Solving Schrödinger Bridges via Maximum Likelihood
Abstract
1. Introduction
- We recast the iterations of the dynamic IPFP algorithm as a regression-based maximum likelihood objective. This is formalised in Theorem 1 and Observation 1. This differs to prior approaches such as [10] where their maximum likelihood formulation solves a density estimation problem. This allows the application of many regression methods from machine learning that scale well to high dimensional problems. Note that this formulation can be parametrised with any method of choice. We chose GPs; however, neural networks would also be well suited,
- Finally we re-implement the approach by [10] and compare approaches across a series of numerical experiments. Furthermore we empirically show how our approach works well in dimensions higher than 2.
2. Technical Background
2.1. Dynamic Formulation
2.1.1. Time Reversal of Diffusions
2.1.2. Stochastic Control Formulation
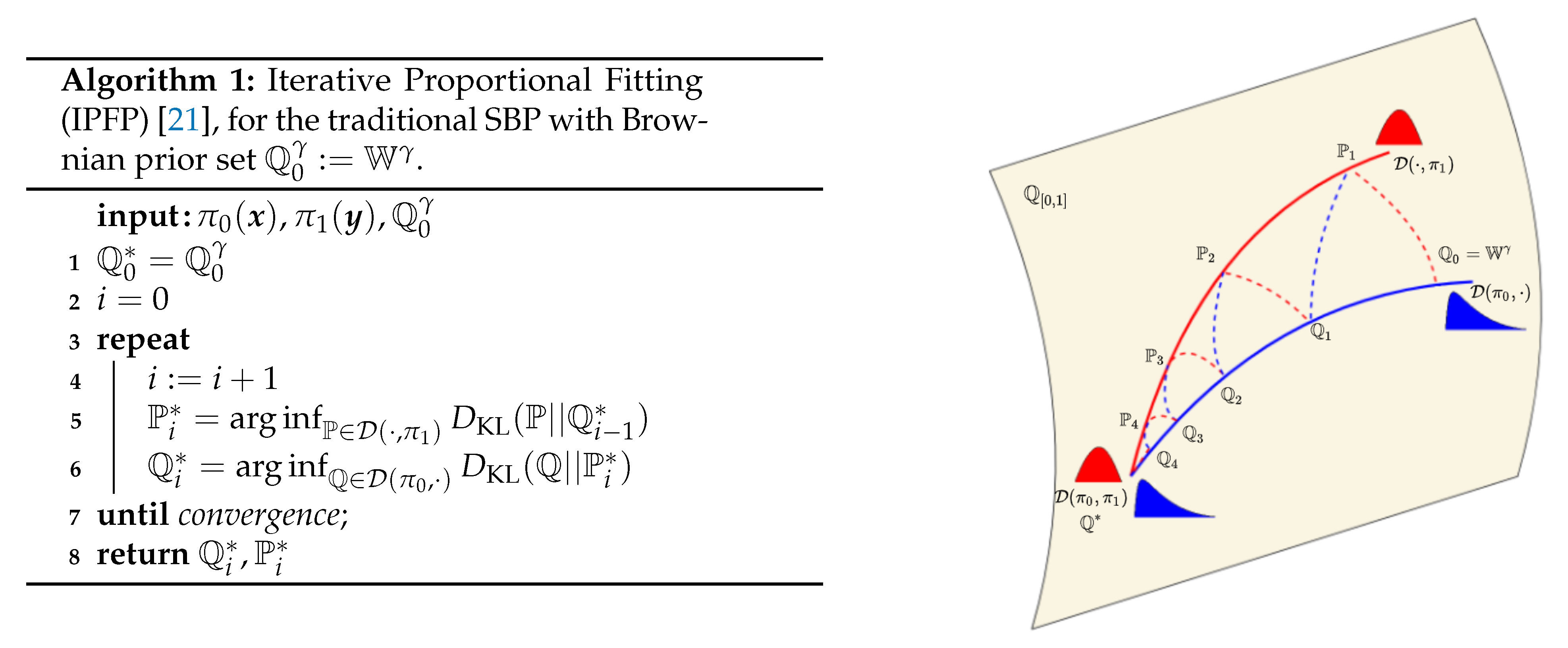
2.2. Iterative Proportional Fitting Procedure
3. Methodology
3.1. Approximate Half Bridge Solving as Optimal Drift Estimation
3.2. On the Need for Time Reversal
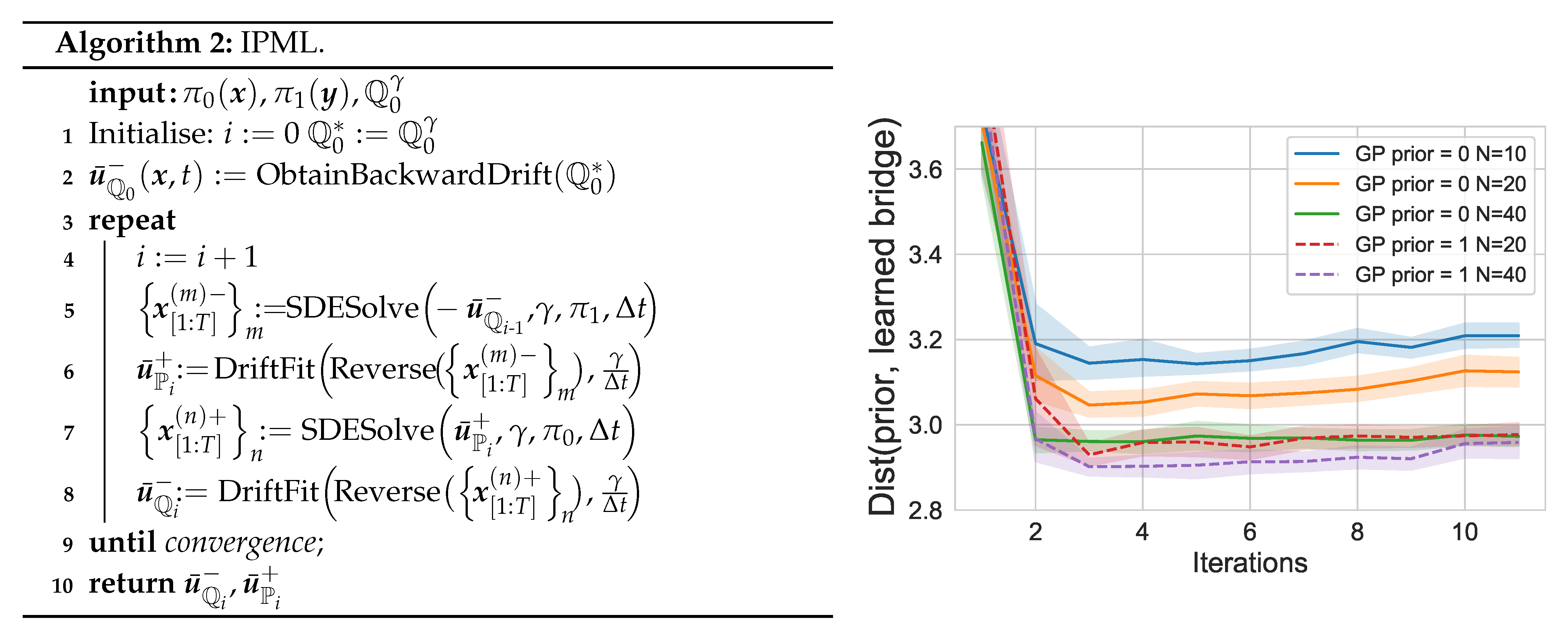
3.3. Iterative Proportional Maximum Likelihood (IPML)
4. Related Methodology
4.1. Sinkhorn–Knop Algorithms
4.2. Data-Driven Schrödinger Bridge (DDSB)
5. Numerical Experiments
5.1. Simple 1D and 2D Distribution Alignment
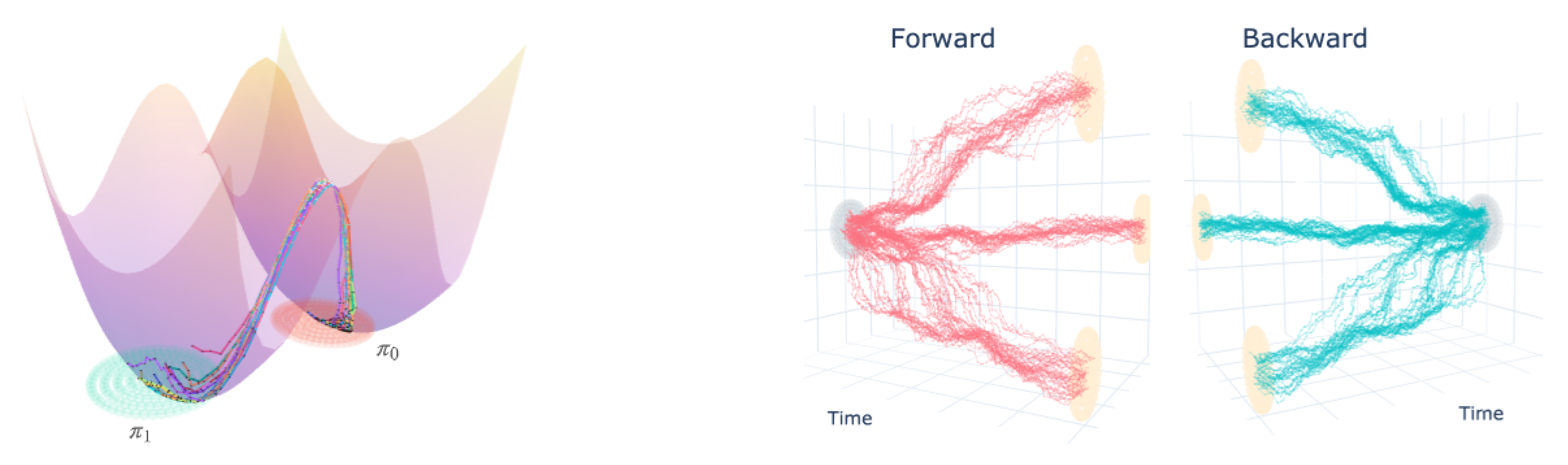
5.2. 2D Double Well Experiments
5.3. Finite Sample/Iteration Convergence
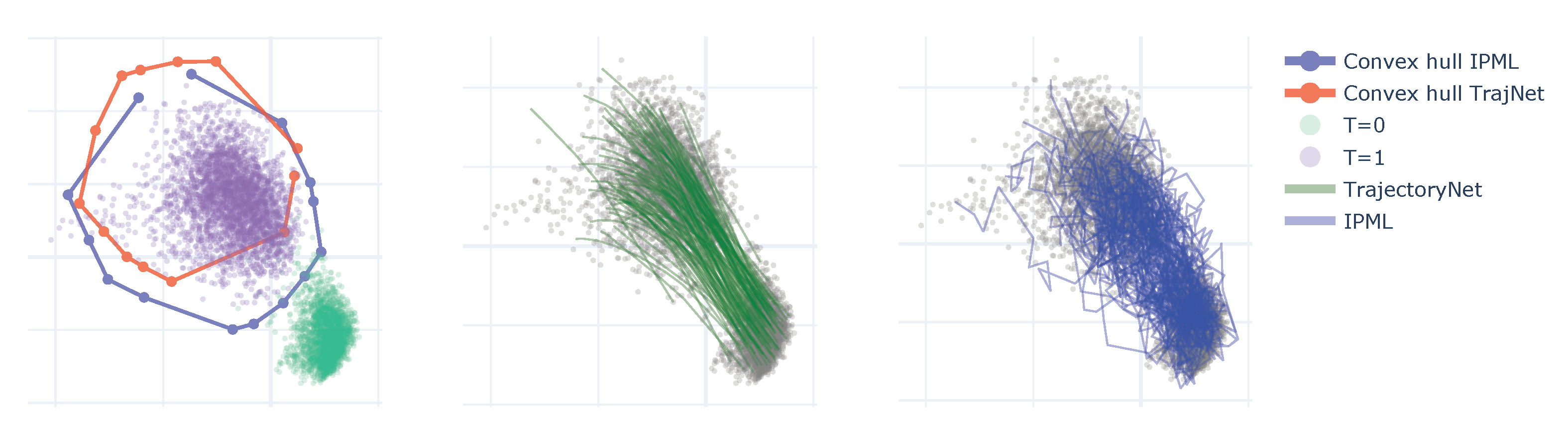
5.4. Single Cell—Embryo Body (EB) Data Set
5.5. Motion Capture
6. Limitations and Opportunities
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Assumptions Across Proofs
- All SDEs considered have –Lipchitz diffusion coefficients as well as satisfying linear growth
- The optimal drifts are elements of a compact space and thus satisfy the HJB equations. Note for the proposes of Theorem 1 this can be relaxed using notions of –convergence,
- All SDEs satisfy a Fokker–Plank equation and thus is differentiable with respect to ,
- The boundary distributions are bounded in that is .
Appendix A. Brief Introduction to the Schrödinger System and Potentials
Appendix B. Disintegration Theorem—Product Rule for Measures
- ,
- is a measurable function known as the canonical projection operator (i.e., and ),
RN Derivative Disintegration
Appendix C. Proof Sketches for Half Bridges
Appendix D. Proof Sketch for Reverse-MLE Consistency
- The density is differentiable with respect to ,
- The optimal drift lies in a compact space (this can be relaxed using notions of –convergence),
- The prior drift coefficient is –Lipchitz and satisfies linear growth.
Extending Theorem 1 to EM Samples
Appendix E. Towards a Finite Sample Analysis of Approximate IPFP Schemes
- The exact IPFP at the ith iteration can be bounded from above as:
- The approximate IPFP projection operators are –Lipchitz
- and the approximate finite sample projection error can be bounded by a constant:
Appendix E.1. GPDriftFit Implementation Details
Appendix E.2. Coupled vs. Decoupled Drift Estimators
Appendix F. Estimates Required by the Sinkhorn–Knop Algorithm
- The Sinkhorn–Knop algorithm requires computing the cost . For more general SDE priors whose transition densities are not available in closed form can be challenging:
- –
- First we have to estimate the empirical distribution for by generating multiple samples from the priors SDE for each in the dataset:
- –
- Once we have samples we must carry out density estimation for each j in order to evaluate .
- The Sinkhorn–Knop algorithm produces discrete potentials, which can be interpolated using the logsumexp formula; however, how do we go from these static potentials to time dependant trajectories?
- –
- From [10] we can obtain expressions for the optimal drift as a function of the time extended potentials:The first integral can be approximated using the Montecarlo approximation via sampling from the prior SDE to draw samples from ; however, computing the potential integral is less clear and requires careful thought.
- –
- Note that in order to estimate the drift we would have to simulate the SDE prior every time we want to evaluate the drift, which itself will be run in another SDE simulation to generate optimal trajectories.
Appendix G. Approximations Required by DDSB
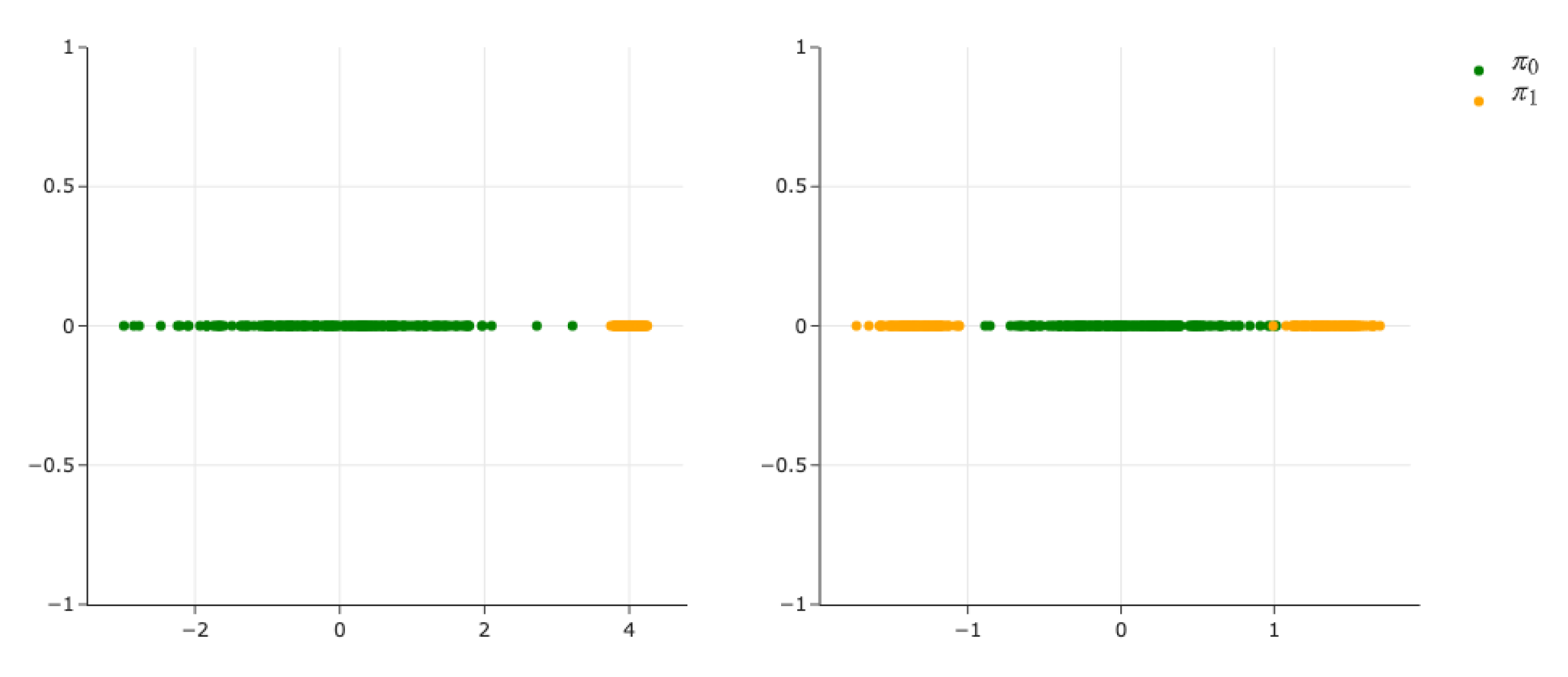
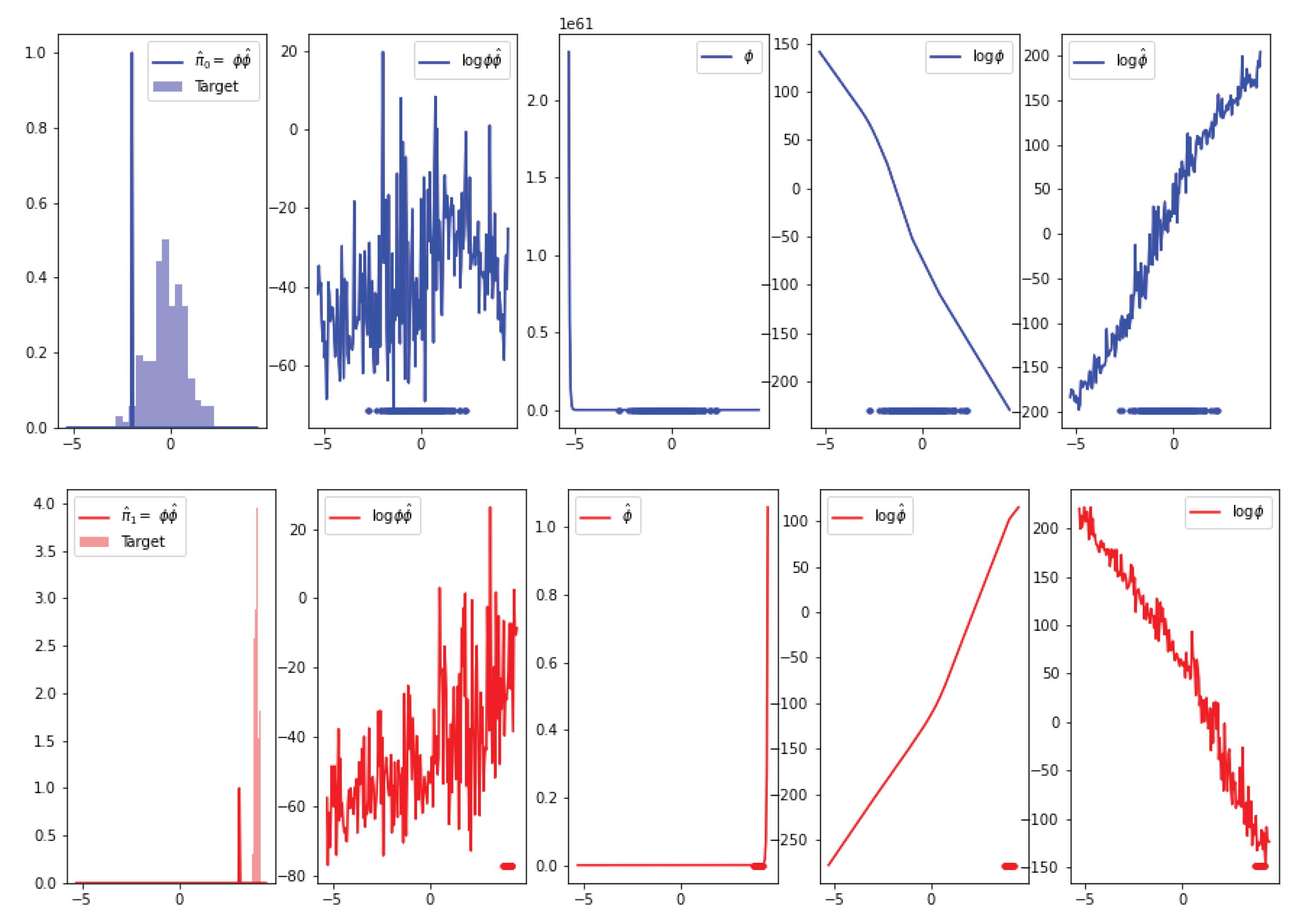
Appendix H. Experiments
Appendix H.1. 1D Experiment
Appendix H.1.1. Delta Collapse in DDSB
Appendix H.2. Well Experiment
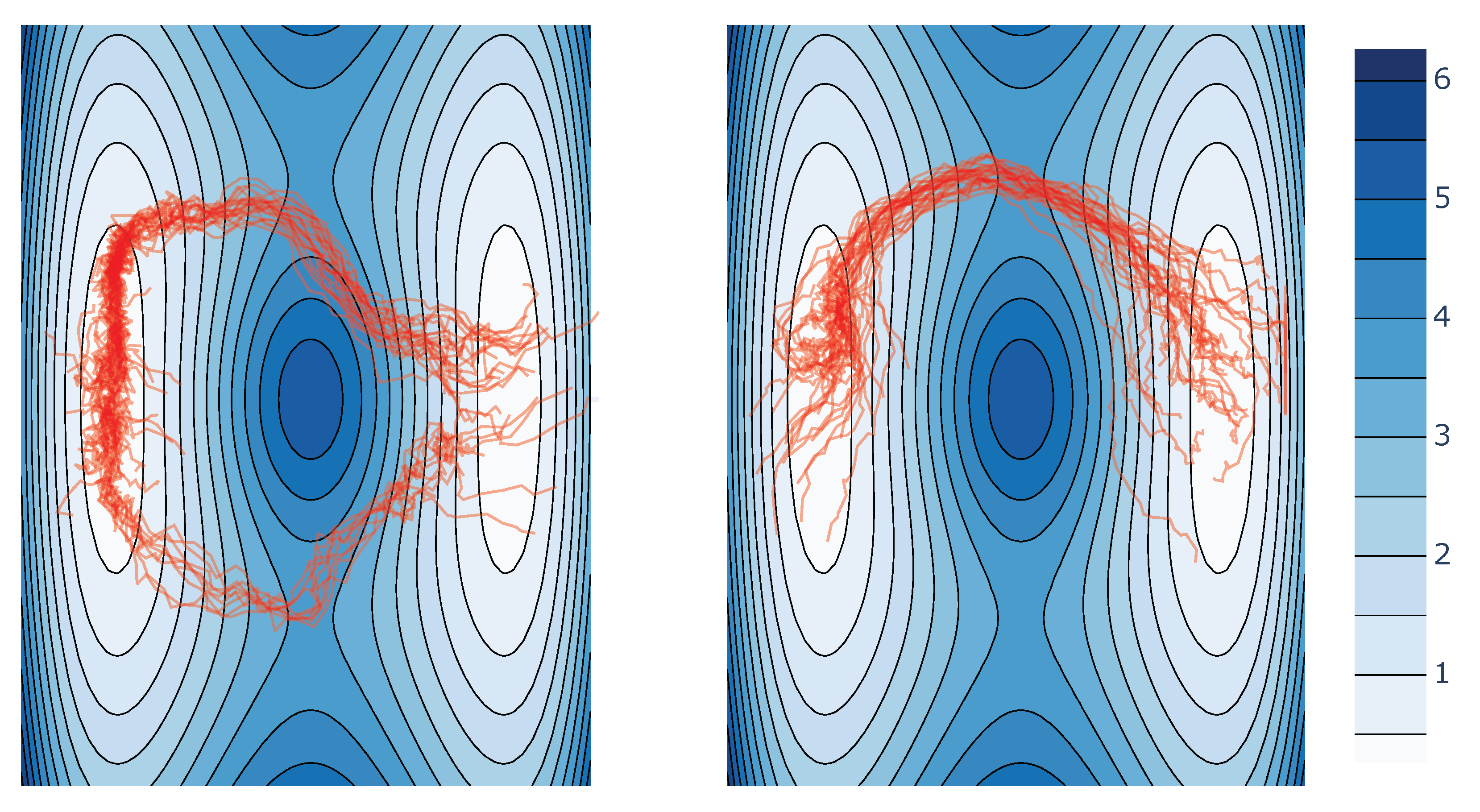
Discussion on Kernel Choice
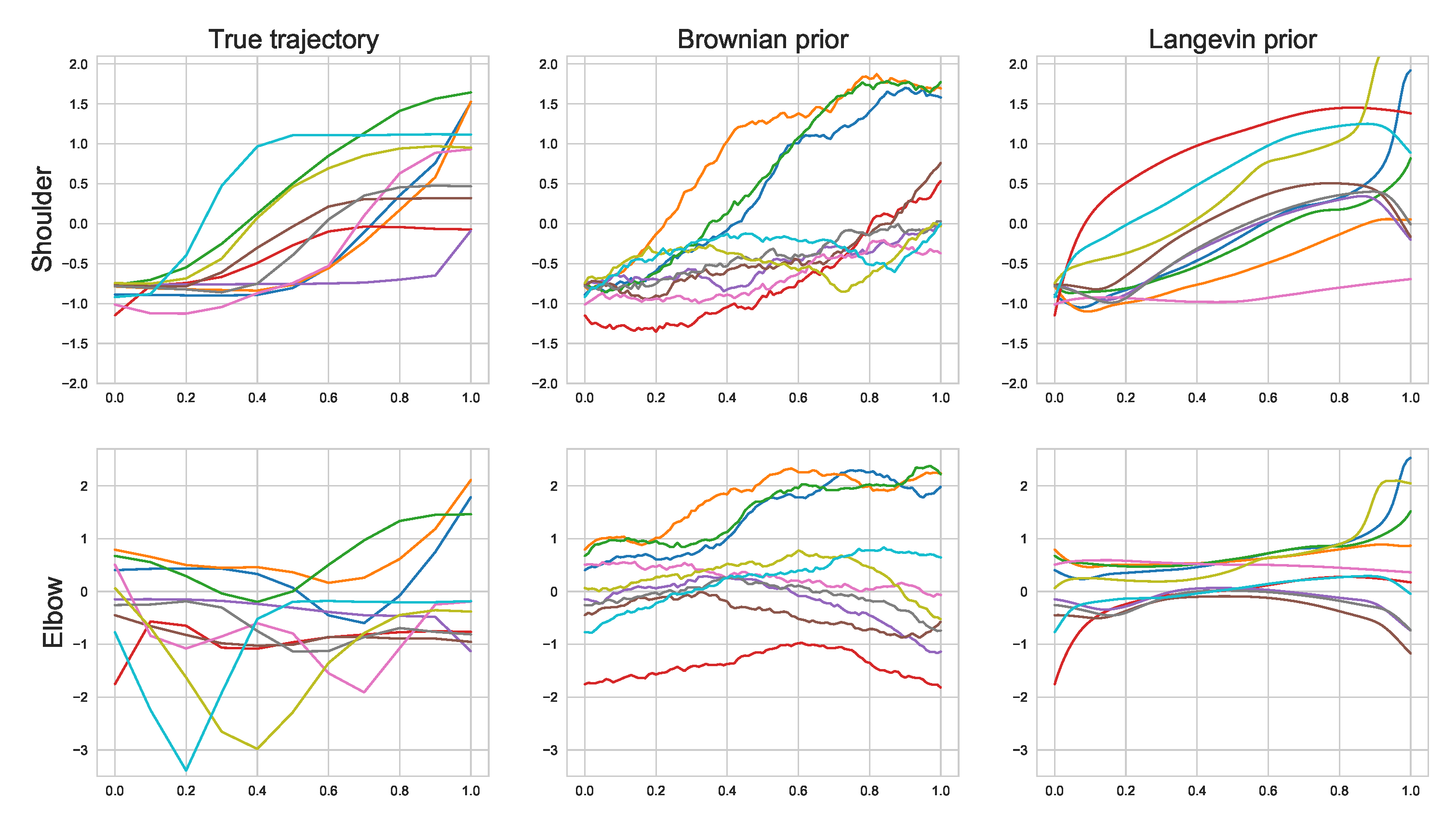
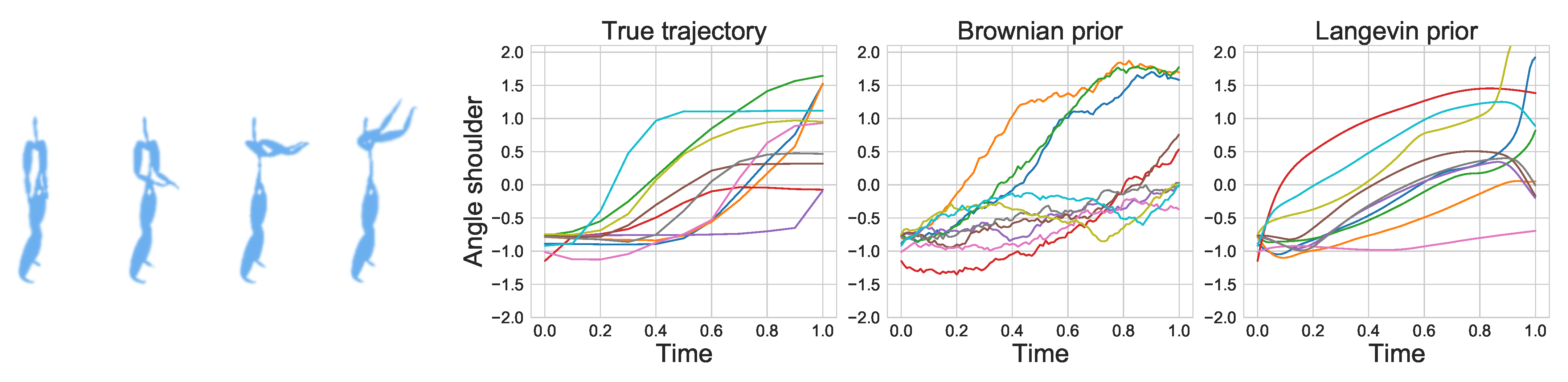
Appendix H.3. Motion Experiment

Appendix H.4. Cell Experiment
Appendix H.5. Computational Resources
Appendix H.5.1. Computational Costs
Appendix H.5.2. Infrastructure Used
References
- Schrödinger, E. Uber die Umkehrung der Naturgesetze; Akademie der Wissenschaften: Berlin, Germany, 1931; pp. 144–153. [Google Scholar]
- Schrödinger, E. Sur la théorie relativiste de l’électron et l’interprétation de la mécanique quantique. Annales de l’Institut Henri Poincaré 1932, 2, 269–310. [Google Scholar]
- Sinkhorn, R.; Knopp, P. Concerning nonnegative matrices and doubly stochastic matrices. Pac. J. Math. 1967, 21, 343–348. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013. [Google Scholar]
- Feydy, J.; Séjourné, T.; Vialard, F.X.; Amari, S.I.; Trouvé, A.; Peyré, G. Interpolating between optimal transport and MMD using Sinkhorn divergences. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Okinawa, Japan, 16 April 2019; pp. 2681–2690. [Google Scholar]
- Chizat, L.; Roussillon, P.; Léger, F.; Vialard, F.X.; Peyré, G. Faster Wasserstein Distance Estimation with the Sinkhorn Divergence. In Proceedings of the 2020 Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Volume 33. [Google Scholar]
- Hennig, P.; Osborne, M.A.; Girolami, M. Probabilistic numerics and uncertainty in computations. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150142. [Google Scholar] [CrossRef]
- Kullback, S. Probability densities with given marginals. Ann. Math. Stat. 1968, 39, 1236–1243. [Google Scholar] [CrossRef]
- Ruschendorf, L. Convergence of the iterative proportional fitting procedure. Ann. Stat. 1995, 23, 1160–1174. [Google Scholar] [CrossRef]
- Pavon, M.; Tabak, E.G.; Trigila, G. The Data Driven Schrödinger Bridge. arXiv 2018, arXiv:1610.02588v4. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Ruttor, A.; Batz, P.; Opper, M. Approximate Gaussian process inference for the drift function in stochastic differential equations. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 2040–2048. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003; pp. 65–84. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-Based Generative Modeling through Stochastic Differential Equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Nelson, E. Dynamical Theories of Brownian Motion; Princeton University Press: Princeton, NJ, USA, 1967; Volume 3. [Google Scholar]
- Anderson, B.D. Reverse-time diffusion equation models. Stoch. Process. Appl. 1982, 12, 313–326. [Google Scholar] [CrossRef]
- Elliott, R.J.; Anderson, B.D. Reverse time diffusions. Stoch. Process. Appl. 1985, 19, 327–339. [Google Scholar] [CrossRef][Green Version]
- Follmer, H. An entropy approach to the time reversal of diffusion processes. Lect. Notes Control Inf. Sci. 1984, 69, 156–163. [Google Scholar]
- Haussmann, U.; Pardoux, E. Time reversal of diffusion processes. In Stochastic Differential Systems Filtering and Control; Springer: Berlin/Heidelberg, Germany, 1985; pp. 176–182. [Google Scholar]
- Pavon, M.; Wakolbinger, A. On free energy, stochastic control, and Schrödinger processes. In Modeling, Estimation and Control of Systems with Uncertainty; Springer: New York, NY, USA, 1991; pp. 334–348. [Google Scholar]
- Cramer, E. Probability measures with given marginals and conditionals: I-projections and conditional iterative proportional fitting. Stat. Decis.—Int. J. Stoch. Methods Models 2000, 18, 311–330. [Google Scholar]
- Bernton, E.; Heng, J.; Doucet, A.; Jacob, P.E. Schrödinger Bridge Samplers. arXiv 2019, arXiv:1912.13170. [Google Scholar]
- Papaspiliopoulos, O.; Pokern, Y.; Roberts, G.O.; Stuart, A.M. Nonparametric estimation of diffusions: A differential equations approach. Biometrika 2012, 99, 511–531. [Google Scholar] [CrossRef]
- Batz, P.; Ruttor, A.; Opper, M. Approximate Bayes learning of stochastic differential equations. Phys. Rev. E 2018, 98, 022109. [Google Scholar] [CrossRef]
- Pokern, Y.; Stuart, A.M.; van Zanten, J.H. Posterior consistency via precision operators for Bayesian nonparametric drift estimation in SDEs. Stoch. Process. Appl. 2013, 123, 603–628. [Google Scholar] [CrossRef]
- De Bortoli, V.; Thornton, J.; Heng, J.; Doucet, A. Diffusion Schrödinger Bridge with Applications to Score-Based Generative Modeling. arXiv 2021, arXiv:2106.01357. [Google Scholar]
- Feydy, J. Geometric Data Analysis, beyond Convolutions. Ph.D. Thesis, Université Paris-Saclay, Gif-sur-Yvette, France, 2020. Available online: https://www.math.ens.fr/$\sim$feydy (accessed on 22 August 2021).
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Papamakarios, G.; Pavlakou, T.; Murray, I. Masked autoregressive flow for density estimation. arXiv 2017, arXiv:1705.07057. [Google Scholar]
- Papamakarios, G. Neural density estimation and likelihood-free inference. arXiv 2019, arXiv:1910.13233. [Google Scholar]
- Wang, G.; Jiao, Y.; Xu, Q.; Wang, Y.; Yang, C. Deep Generative Learning via Schrödinger Bridge. arXiv 2021, arXiv:2106.10410. [Google Scholar]
- Huang, J.; Jiao, Y.; Kang, L.; Liao, X.; Liu, J.; Liu, Y. Schrödinger-Föllmer Sampler: Sampling without Ergodicity. arXiv 2021, arXiv:2106.10880. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Poole, B.; Ho, J. Variational Diffusion Models. arXiv 2021, arXiv:2107.00630. [Google Scholar]
- Tong, A.; Huang, J.; Wolf, G.; Van Dijk, D.; Krishnaswamy, S. Trajectorynet: A dynamic optimal transport network for modeling cellular dynamics. In Proceedings of the International Conference on Machine Learning, Online. 12–18 July 2020; pp. 9526–9536. [Google Scholar]
- McCann, R.J.; Guillen, N. Five lectures on optimal transportation: Geometry, regularity and applications. In Analysis and Geometry of Metric Measure Spaces: Lecture Notes of the Séminaire de Mathématiques Supérieure (SMS) Montréal; American Mathematical Society: Providence, RI, USA, 2011; pp. 145–180. [Google Scholar]
- Schiebinger, G.; Shu, J.; Tabaka, M.; Cleary, B.; Subramanian, V.; Solomon, A.; Gould, J.; Liu, S.; Lin, S.; Berube, P.; et al. Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming. Cell 2019, 176, 928–943. [Google Scholar] [CrossRef]
- Sanguinetti, G.; Lawrence, N.D.; Rattray, M. Probabilistic inference of transcription factor concentrations and gene-specific regulatory activities. Bioinformatics 2006, 22, 2775–2781. [Google Scholar] [CrossRef][Green Version]
- Léonard, C. A survey of the Schrödinger problem and some of its connections with optimal transport. arXiv 2013, arXiv:1308.0215. [Google Scholar] [CrossRef]
- Léonard, C. Some properties of path measures. In Séminaire de Probabilités XLVI; Springer: Cham, Switzerland, 2014; pp. 207–230. [Google Scholar]
- Kunitha, H. On backward stochastic differential equations. Stochastics 1982, 6, 293–313. [Google Scholar] [CrossRef]
- Revuz, D.; Yor, M. Continuous Martingales and Brownian Motion; Springer: Berlin/Heidelberg, Germany, 2013; Volume 293. [Google Scholar]
- Kailath, T. The structure of Radon-Nikodym derivatives with respect to Wiener and related measures. Ann. Math. Stat. 1971, 42, 1054–1067. [Google Scholar] [CrossRef]
- Sottinen, T.; Särkkä, S. Application of Girsanov theorem to particle filtering of discretely observed continuous-time non-linear systems. Bayesian Anal. 2008, 3, 555–584. [Google Scholar] [CrossRef]
- Levy, B.C. Principles of Signal Detection and Parameter Estimation; Springer: Boston, MA, USA, 2008. [Google Scholar]
- Gyöngy, I.; Krylov, N. Existence of strong solutions for Itô’s stochastic equations via approximations. Probab. Theory Relat. Fields 1996, 105, 143–158. [Google Scholar] [CrossRef]
- Sra, S. Scalable nonconvex inexact proximal splitting. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; Volume 25, pp. 530–538. [Google Scholar]
- Álvarez, M.A.; Rosasco, L.; Lawrence, N.D. Kernels for Vector-Valued Functions: A Review. Found. Trends Mach. Learn. 2012, 4, 195–266. [Google Scholar] [CrossRef]
- Evgeniou, T.; Micchelli, C.A.; Pontil, M.; Shawe-Taylor, J. Learning multiple tasks with kernel methods. J. Mach. Learn. Res. 2005, 6, 615–637. [Google Scholar]
- Martino, L.; Elvira, V.; Louzada, F. Effective sample size for importance sampling based on discrepancy measures. Signal Process. 2017, 131, 386–401. [Google Scholar] [CrossRef]
| Unimodal | Bimodal | |||||||
|---|---|---|---|---|---|---|---|---|
| KS | EMD | KS | EMD | KS | EMD | KS | EMD | |
| DDSB | 0.17 | 0.34 | 0.19 | 0.13 | 0.18 | 0.12 | 0.07 | 0.04 |
| IPML | 0.06 | 0.10 | 0.13 | 0.04 | 0.05 | 0.04 | 0.07 | 0.15 |
| T = 1 | T = 2 | T = 3 | T = 4 | T = 5 | Mean | ||
|---|---|---|---|---|---|---|---|
| Path | Full | ||||||
| TrajectoryNet | 0.62 | 1.15 | 1.49 | 1.26 | 0.99 | 1.30 | 1.18 |
| IPML EQ | 0.38 | 1.19 | 1.44 | 1.04 | 0.48 | 1.22 | 1.02 |
| IPML EXP | 0.34 | 1.13 | 1.35 | 1.01 | 0.49 | 1.16 | 0.97 |
| OT | Na | 1.13 | 1.10 | 1.11 | Na | 1.11 | Na |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas, F.; Thodoroff, P.; Lamacraft, A.; Lawrence, N. Solving Schrödinger Bridges via Maximum Likelihood. Entropy 2021, 23, 1134. https://doi.org/10.3390/e23091134
Vargas F, Thodoroff P, Lamacraft A, Lawrence N. Solving Schrödinger Bridges via Maximum Likelihood. Entropy. 2021; 23(9):1134. https://doi.org/10.3390/e23091134
Chicago/Turabian StyleVargas, Francisco, Pierre Thodoroff, Austen Lamacraft, and Neil Lawrence. 2021. "Solving Schrödinger Bridges via Maximum Likelihood" Entropy 23, no. 9: 1134. https://doi.org/10.3390/e23091134
APA StyleVargas, F., Thodoroff, P., Lamacraft, A., & Lawrence, N. (2021). Solving Schrödinger Bridges via Maximum Likelihood. Entropy, 23(9), 1134. https://doi.org/10.3390/e23091134






