Understanding the Nature of the Long-Range Memory Phenomenon in Socioeconomic Systems
Abstract
1. Introduction
2. The Multiplicative Point Process, the Class of Stochastic Differential Equations, and Their Applications
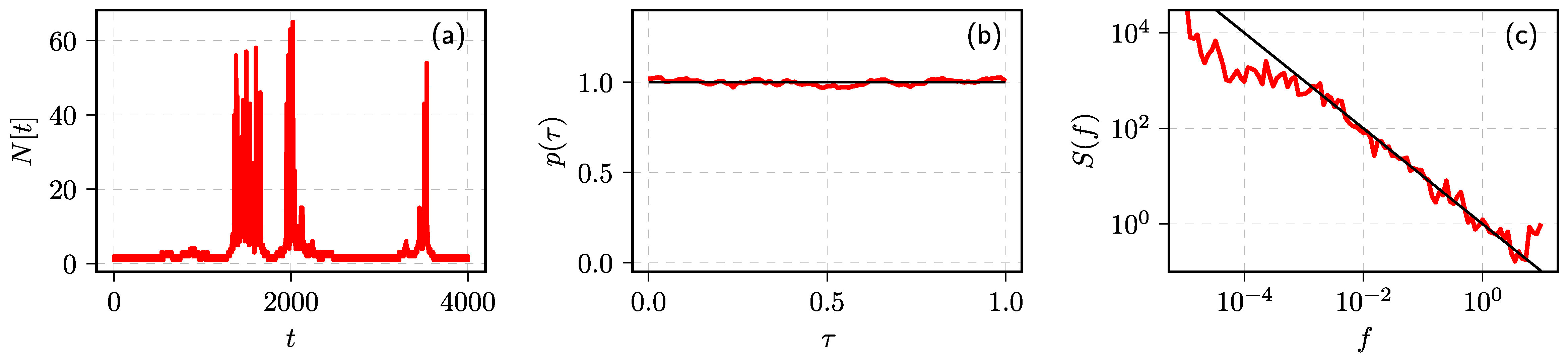
2.1. The Multiplicative Point Process Model
2.2. The Class of Non-Linear Stochastic Differential Equations
2.3. Reproducing the Long-Range Memory Using GARCH(1,1) Process
2.4. Anomalous Diffusion in the Long-Range Memory Process
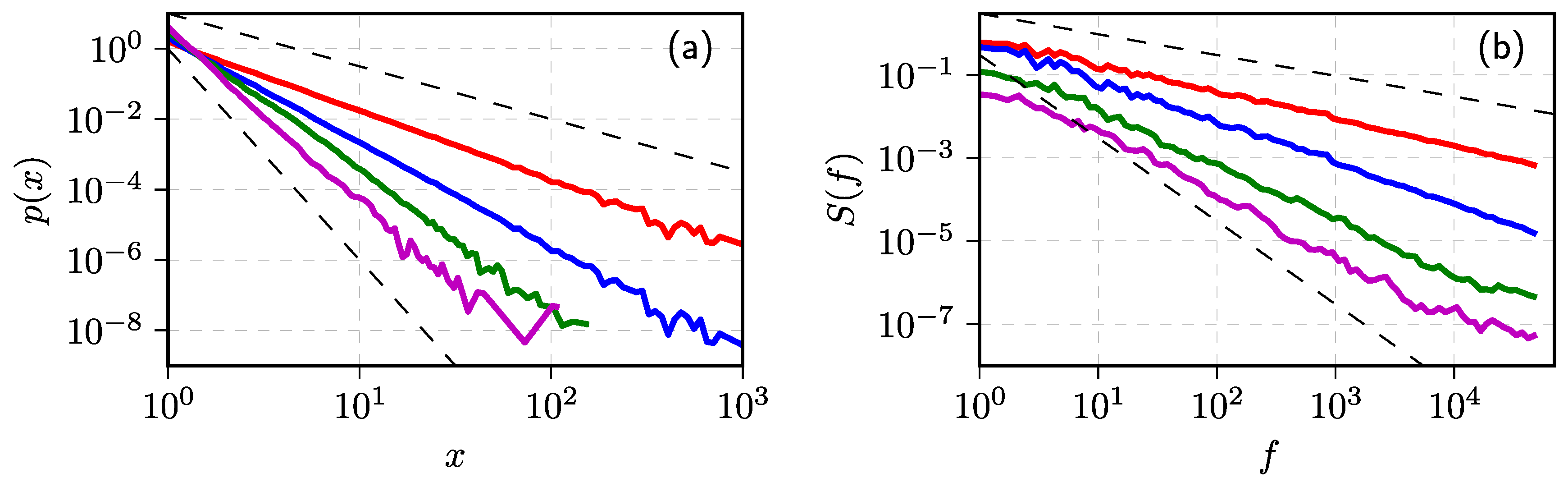
2.5. Inverse Cubic Law for Long-Range Correlated Processes
2.6. Noise with Distributions Other Than Power–Law
2.7. Reproducing Statistical Properties of the Financial Markets
2.8. Variable Step Method for Solving Non-Linear Stochastic Differential Equations
3. Agent-Based Model of the Long-Range Memory in the Financial Markets
3.1. Kirman’s Herding Model
3.2. Kirman’s Herding Model for the Financial Markets
3.3. Kirman’s Herding Model, Voter Model, and the Opinion Dynamics Context
4. Searching for the True Long-Range Memory Test
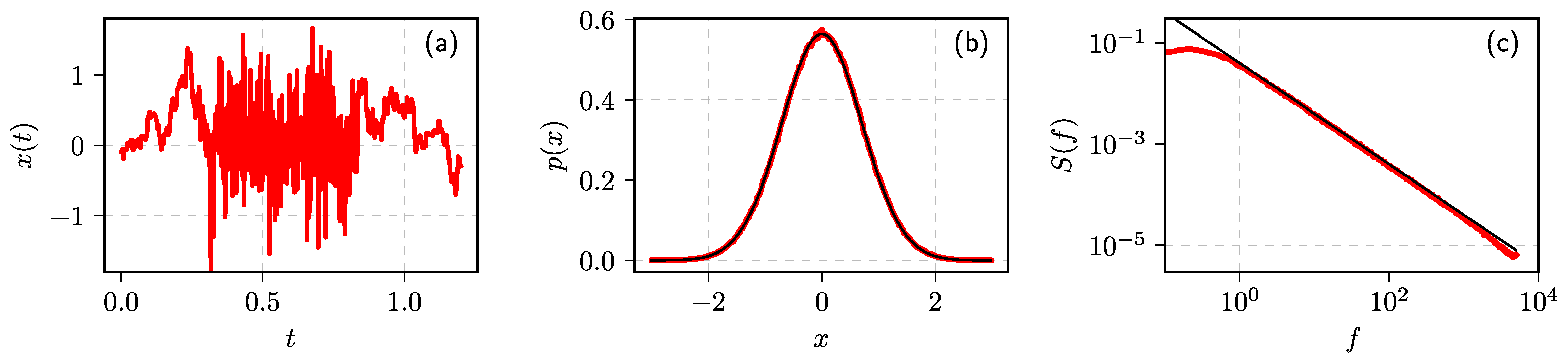
4.1. Fractional Processes with Non-Gaussian Noise
4.2. Numerical Exploration of the Accumulated ARFIMA(0,d,0) Time Series
5. Future Considerations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ABM | agent-based model |
| APFA | Applications of Physics in Financial Analysis |
| ARCH | autoregressive conditional heteroscedasticity |
| ARFIMA | autoregressive fractionally integrated moving average |
| AVE | absolute value estimator |
| BDA | burst and interburst duration analysis |
| COST | European Cooperation in Science and Technology |
| FBM | fractional Brownian motion |
| FGN | fractional Gaussian noise |
| FIGARCH | fractionally integrated GARCH |
| FLSM | fractional Lèvy stable motion |
| FLSN | fractional Lèvy stable noise |
| GARCH | generalized ARCH |
| MSD | mean squared displacement |
| NYSE | New York stock exchange |
| probability density function | |
| PSD | power spectral density |
| SDE | stochastic differential equation |
| VSE | Vilnius stock exchange |
| WSE | Warsaw stock exchange |
References
- Mandelbrot, B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Press, W.H. Flicker noises in astronomy and elsewhere. Comments Astrophys. 1978, 7, 103–119. [Google Scholar]
- Dutta, P.; Horn, P.M. Low-frequency fluctuations in solids: 1/f noise. Rev. Mod. Phys. 1981, 53, 497–516. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/fnoise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- West, B.J.; Shlesinger, M.F. On the ubiquity of 1/f nose. Int. J. Mod. Phys. B 1989, 3, 795–819. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Multifractals and 1/f Noise: Wild Self-Affinity in Physics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Milotti, E. 1/f noise: A pedagogical review. arXiv 2002, arXiv:physics/0204033. [Google Scholar]
- Ward, L.; Greenwood, P. 1/f noise. Scholarpedia 2007, 2, 1537. [Google Scholar] [CrossRef]
- Rodriguez, M.A. Complete spectral scaling of time series: Towards a classification of 1/f noise. Phys. Rev. E 2014, 90, 042122. [Google Scholar] [CrossRef]
- Yadav, A.C.; Kumar, N. Scaling theory for the 1/f noise. arXiv 2021, arXiv:2103.11608. [Google Scholar]
- Taqqu, M.S.; Teverovsky, V.; Willinger, W. Estimators for long-range dependence: An empirical study. Fractals 1995, 3, 785–788. [Google Scholar] [CrossRef]
- Gopikrishnan, P.; Meyer, M.; Amaral, L.; Stanley, H. Inverse cubic law for the distribution of stock price variations. Eur. Phys. J. B 1998, 3, 139–140. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Nunes Amaral, L.A.; Gabaix, X.; Stanley, H.E. Economic fluctuations and anomalous diffusion. Phys. Rev. E 2000, 62, R3023–R3026. [Google Scholar] [CrossRef]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Financ. 2001, 1, 1–14. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Gabaix, X.; Gopikrishnan, P.; Plerou, V.; Stanley, H.E. A theory of power law distributions in financial market fluctuations. Nature 2003, 423, 267–270. [Google Scholar] [CrossRef]
- Farmer, J.D.; Gillemot, L.; Lillo, F.; Mike, S.; Sen, A. What really causes large price changes. Quant. Financ. 2004, 4, 383–397. [Google Scholar] [CrossRef]
- Gabaix, X.; Gopikrishnan, P.; Plerou, V.; Stanley, H.E. Institutional investors and stock market volatility. Q. J. Econ. 2006, 461–504. [Google Scholar] [CrossRef]
- Alfi, V.; Cristelli, M.; Pietronero, L.; Zaccaria, A. Minimal agent based model for financial markets I: Origin and self-organization of stylized facts. Eur. Phys. J. B 2009, 67, 385–397. [Google Scholar] [CrossRef]
- Kaulakys, B.; Vektaris, G. Transition to nonchaotic behaviour in randomly driven systems: Intermittency and 1/f-noise. In Noise in Physical Systems and 1/f Fluctuations, Proceedings of the 13th International Conference, Palanga, Lithuania, 29 May–3 June 1995; World Scientific: Singapore, 1995; pp. 677–680. [Google Scholar]
- Kaulakys, B.; Meskauskas, T. Modeling 1/f noise. Phys. Rev. E 1998, 58, 7013–7019. [Google Scholar] [CrossRef]
- Kaulakys, B. Autoregressive model of 1/f noise. Phys. Lett. A 1999, 257, 37–42. [Google Scholar] [CrossRef][Green Version]
- Kaulakys, B.; Gontis, V.; Alaburda, M. Point process model of 1/f noise vs a sum of Lorentzians. Phys. Rev. E 2005, 71, 1–11. [Google Scholar] [CrossRef]
- Ghosh, A. Econophysics research in India in the last two decades. IIM Kozhikode Soc. Manag. Rev. 2013, 2, 135–146. [Google Scholar] [CrossRef]
- de Area Leao Pereira, E.J.; da Silva, M.F.; Pereira, H. Econophysics: Past and present. Phys. A 2017, 473, 251–261. [Google Scholar] [CrossRef]
- Jovanovic, F.; Schinckus, C. Econophysics and Financial Economics: An Emerging Dialogue; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Gontis, V. Modelling share volume traded in financial markets. Lith. J. Phys. 2001, 41, 551–555. [Google Scholar]
- Gontis, V. Multiplicative stochastic model of the time interval between trades in financial markets. Nonlinear Anal. Model. Control 2002, 7, 43–54. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B. Multiplicative point process as a model of trading activity. Phys. A 2004, 343, 505–514. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B. Modeling financial markets by the multiplicative sequence of trades. Phys. A 2004, 344, 128–133. [Google Scholar] [CrossRef][Green Version]
- Gontis, V.; Kaulakys, B.; Alaburda, M.; Ruseckas, J. Evolution of complex systems and 1/f noise: From physics to financial markets. Solid State Phenom. 2004, 97–98, 65–70. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B.; Ruseckas, J. Point process models of 1/f noise and internet traffic. AIP Conf. Proc. 2005, 776, 144–149. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B. Modeling long-range memory trading activity by stochastic differential equations. Phys. A 2007, 382, 114–120. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B. Long-range memory model of trading activity and volatility. J. Stat. Mech. 2006, 2006, P10016. [Google Scholar] [CrossRef]
- Gontis, V.; Ruseckas, J.; Kononovicius, A. A Non-linear stochastic model of return in financial markets. In Stochastic Control; Myers, C., Ed.; InTech: London, UK, 2010; pp. 559–580. [Google Scholar] [CrossRef]
- Gontis, V.; Ruseckas, J.; Kononovicius, A. A long-range memory stochastic model of the return in financial markets. Phys. A 2010, 389, 100–106. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Nonlinear stochastic model of return matching to the data of New York and Vilnius stock exchanges. Dyn.-Socio-Econ. Syst. 2011, 2, 101–109. [Google Scholar]
- Ruseckas, J.; Gontis, V.; Kaulakys, B. Nonextensive statistical mechanics distributions and dynamics of financial observables from the nonlinear stochastic differential equations. Adv. Complex Syst. 2012, 15, 1250073. [Google Scholar] [CrossRef]
- Ruseckas, J.; Kaulakys, B.; Gontis, V. Herding model and 1/f noise. EPL 2011, 96, 60007. [Google Scholar] [CrossRef]
- Kononovicius, A.; Gontis, V. Agent based reasoning for the non-linear stochastic models of long-range memory. Phys. A 2012, 391, 1309–1314. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Consentaneous agent-based and stochastic model of the financial markets. PLoS ONE 2014, 9, e102201. [Google Scholar] [CrossRef]
- Kononovicius, A.; Ruseckas, J. Order book model with herding behavior exhibiting long-range memory. Phys. A 2019, 525, 171–191. [Google Scholar] [CrossRef]
- Kononovicius, A. Empirical analysis and agent-based modeling of Lithuanian parliamentary elections. Complexity 2017, 2017, 7354642. [Google Scholar] [CrossRef]
- Kononovicius, A. Compartmental voter model. J. Stat. Mech. 2019, 2019, 103402. [Google Scholar] [CrossRef]
- Kononovicius, A. Noisy voter model for the anomalous diffusion of parliamentary presence. J. Stat. Mech. 2020, 2020, 063405. [Google Scholar] [CrossRef]
- Kononovicius, A. Supportive interactions in the noisy voter model. Chaos Solitons Fractals 2021, 143, 110627. [Google Scholar] [CrossRef]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Dong, Y.; Zhan, M.; Kou, G.; Ding, Z.; Liang, H. A survey on the fusion process in opinion dynamics. Inf. Fusion 2018, 43, 57–65. [Google Scholar] [CrossRef]
- Noorazar, H. Recent advances in opinion propagation dynamics. Eur. Phys. J. Plus 2020, 135, 521. [Google Scholar] [CrossRef]
- Gontis, V.; Havlin, S.; Kononovicius, A.; Podobnik, B.; Stanley, H.E. Stochastic model of financial markets reproducing scaling and memory in volatility return intervals. Phys. A 2016, 462, 1091–1102. [Google Scholar] [CrossRef]
- Yamasaki, K.; Muchnik, L.; Havlin, S.; Bunde, A.; Stanley, H. Scaling and memory in volatility return intervals in financial markets. Proc. Natl. Acad. Sci. USA 2005, 102, 9424–9428. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Yamasaki, K.; Havlin, S.; Stanley, H. Scaling and memory of intraday volatility return intervals in stock market. Phys. Rev. E 2006, 73, 026117. [Google Scholar] [CrossRef]
- Wang, F.; Yamasaki, K.; Havlin, S.; Stanley, H. Indication of multiscaling in the volatility return intervals of stock markets. Phys. Rev. E 2008, 77, 016109. [Google Scholar] [CrossRef]
- Denys, M.; Gubiec, T.; Kutner, R.; Jagielski, M.; Stanley, H.E. Universality of market superstatistics. Phys. Rev. E 2016, 94, 042305. [Google Scholar] [CrossRef]
- Redner, S. A Guide to First-Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Ding, M.; Yang, W. Distribution of the first return time in fractional Brownian motion and its application to the study of on-off intermittency. Phys. Rev. E 1995, 52, 207. [Google Scholar] [CrossRef]
- Johnson, J.B. The Schottky effect in low frequency circuits. Phys. Rev. 1925, 26, 71–85. [Google Scholar] [CrossRef]
- Levitin, D.J.; Chordia, P.; Menon, V. Musical rhythm spectra from Bach to Joplin obey a 1/f power law. Proc. Natl. Acad. Sci. USA 2012, 109, 3716–3720. [Google Scholar] [CrossRef]
- Kobayashi, M.; Musha, T. 1/f fluctuation of heartbeat period. IEEE Trans. Biomed. Eng. 1982, 29, 456–457. [Google Scholar] [CrossRef] [PubMed]
- Wagenmakers, E.J.; Farrell, S.; Ratcliff, R. Estimation and interpretation of 1/fα noise in human cognition. Psychon. Bull. Rev. 2004, 11, 579–615. [Google Scholar] [CrossRef] [PubMed]
- Mathiesen, J.; Angheluta, L.; Ahlgren, P.T.H.; Jensen, M.H. Excitable human dynamics driven by extrinsic events in massive communities. Proc. Natl. Acad. Sci. USA 2013, 110, 17259–17262. [Google Scholar] [CrossRef] [PubMed]
- Leonardis, E.; Chapman, S.C.; Foullon, C. Turbulent characteristics in the intensity fluctuations of a solar quiescent prominence observed by the Hinode Solar Optical Telescop. Astrophys. J. 2012, 745, 185. [Google Scholar] [CrossRef]
- Meskauskas, T.; Kaulakys, B. 1/f noise in fractal quaternionic structures. AIP Conf. Proc. 2005, 780, 91–94. [Google Scholar] [CrossRef]
- Ribeiro, L.C.; de Deus, L.G.; Loureiro, P.M.; Albuquerque, E.D.M. Profits and fractal properties: Notes on Marx, countertendencies and simulation models. Rev. Political Econ. 2017, 29, 282–306. [Google Scholar] [CrossRef]
- Ribeiro, L.C.; Rapini, M.S.; Silva, L.A.; Albuquerque, E.M. Growth patterns of the network of international collaboration in science. Scientometrics 2018, 114, 159–179. [Google Scholar] [CrossRef]
- Nakamura, T.; Small, M.; Tanizawa, T. Long-range correlation properties of stationary linear models with mixed periodicities. Phys. Rev. E 2019, 99, 022128. [Google Scholar] [CrossRef] [PubMed]
- Erland, S.; Greenwood, P.E. Constructing 1/ωα noise from reversible Markov chains. Phys. Rev. E 2007, 76, 031114. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin, Germany, 1999. [Google Scholar]
- Kaulakys, B.; Ruseckas, J. Stochastic nonlinear differential equation generating 1/f noise. Phys. Rev. E 2004, 70, 020101. [Google Scholar] [CrossRef] [PubMed]
- Kaulakys, B.; Ruseckas, J.; Gontis, V.; Alaburda, M. Nonlinear stochastic models of 1/f noise and power-law distributions. Phys. A 2006, 365, 217–221. [Google Scholar] [CrossRef]
- Kaulakys, B.; Alaburda, M. Modeling scaled processes and 1/fβ noise using non-linear stochastic differential equations. J. Stat. Mech. 2009, 2009, P02051. [Google Scholar] [CrossRef]
- Ruseckas, J.; Kaulakys, B. 1/f noise from nonlinear stochastic differential equations. Phys. Rev. E 2010, 81, 031105. [Google Scholar] [CrossRef]
- Lera, S.C.; Sornette, D. Currency target-zone modeling: An interplay between physics and economics. Phys. Rev. E 2015, 92, 062828. [Google Scholar] [CrossRef]
- Engle, R. Autoregresive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1008. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Engle, R.; Bollerslev, T. Modeling the persistence of conditional variances. Econom. Rev. 1986, 5, 1–50. [Google Scholar] [CrossRef]
- Potters, M.; Cont, R.; Bouchaud, J.P. Financial markets as adaptive systems. EPL 1998, 41, 239–244. [Google Scholar] [CrossRef][Green Version]
- Giraitis, L.; Robinson, P.M.; Surgailis, D. A model for long memory conditional heteroscedasticity. Ann. Appl. Probab. 2000, 10, 1002–1024. [Google Scholar] [CrossRef]
- Bollerslev, T. Glossary to ARCH (GARCH). CREATES Res. Pap. 2008, 49, 1–46. [Google Scholar] [CrossRef]
- Giraitis, L.; Leipus, R.; Surgailis, D. Recent advances in ARCH modelling. In Long Memory in Economics; Teyssiere, G., Kirman, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 3–38. [Google Scholar]
- Giraitis, L.; Leipus, R.; Surgailis, D. ARCH(∞) models and long memory. In Handbook of Financial Time Series; Anderson, T.G., Davis, R.A., Kreis, J., Mikosh, T., Eds.; Springer Verlag: Berlin, Germany, 2009; pp. 71–84. [Google Scholar] [CrossRef]
- Giraitis, L.; Surgailis, D.; Škarnulis, A. Stationary integrated ARCH(∞) and AR(∞) processes with finite variance. Econom. Theory 2018, 34, 1159–1179. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Joyeux, R. An introduction to long-memory time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Baillie, R.T.; Bollerslev, T.; Mikkelsen, H.O. Fractionally integrated generalized autoregressive conditional heteroskedasticity. J. Econom. 1996, 74, 3–30. [Google Scholar] [CrossRef]
- Tayefi, M.; Ramanathan, T.V. An overview of FIGARCH and related time series models. Austrian J. Stat. 2012, 41, 175–196. [Google Scholar] [CrossRef]
- Kononovicius, A.; Ruseckas, J. Nonlinear GARCH model and 1/f noise. Phys. A 2015, 427, 74–81. [Google Scholar] [CrossRef]
- Nelson, D.B. ARCH models as diffusion approximations. J. Econom. 1990, 45, 7–38. [Google Scholar] [CrossRef]
- Kluppelberg, C.; Lindner, A.; Maller, R. A continuous-time GARCH process driven by a Levy process: Stationarity and second-order behaviour. J. Appl. Probab. 2004, 41, 601–622. [Google Scholar] [CrossRef]
- Kluppelberg, C.; Maller, R.; Szimayer, A. The COGARCH: A Review, with News on Option Pricing and Statistical Inference. In Surveys in Stochastic Processes; EMS press: Berlin, Germany, 2010. [Google Scholar] [CrossRef][Green Version]
- Kazakevicius, R.; Ruseckas, J. Influence of external potentials on heterogeneous diffusion processes. Phys. Rev. E 2016, 94, 032109. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 2002, 51, 187–292. [Google Scholar] [CrossRef]
- ben Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Kazakevičius, R.; Ruseckas, J. Lévy flights in inhomogeneous environments and 1/f noise. Phys. A 2014, 411, 95. [Google Scholar] [CrossRef]
- Kazakevicius, R.; Ruseckas, J. Power-law statistics from nonlinear stochastic differential equations driven by Lévy stable noise. Chaos Solitons Fractals 2015, 81, 432–442. [Google Scholar] [CrossRef]
- Kazakevicius, R.; Ruseckas, J. Anomalous diffusion in nonhomogeneous media: Power spectral density of signals generated by time-subordinated nonlinear Langevin equations. Phys. A 2015, 438, 210–222. [Google Scholar] [CrossRef]
- Kazakevicius, R.; Ruseckas, J. Power law statistics in the velocity fluctuations of Brownian particle in inhomogeneous media and driven by colored noise. J. Stat. Mech. 2015, 2015, P02021. [Google Scholar] [CrossRef][Green Version]
- Ruseckas, J.; Kazakevicius, R.; Kaulakys, B. 1/f noise from point process and time-subordinated Langevin equations. J. Stat. Mech. 2016, 2016, 054022. [Google Scholar] [CrossRef][Green Version]
- Ruseckas, J.; Kazakevicius, R.; Kaulakys, B. Coupled nonlinear stochastic differential equations generating arbitrary distributed observable with 1/f noise. J. Stat. Mech. 2016, 2016, 043209. [Google Scholar] [CrossRef]
- Kaulakys, B.; Alaburda, M.; Ruseckas, J. 1/f noise from the nonlinear transformations of the variables. Mod. Phys. Lett. B 2015, 29, 1550223. [Google Scholar] [CrossRef]
- Kazakevicius, R.; Kononovicius, A. Anomalous diffusion in nonlinear transformations of the noisy voter model. Phys. Rev. E 2021, 103, 032154. [Google Scholar] [CrossRef] [PubMed]
- Kaulakys, B.; Alaburda, M.; Ruseckas, J. Modeling of long-range memory processes with inverse cubic distributions by the nonlinear stochastic differential equations. J. Stat. Mech. 2016, 2016, 054035. [Google Scholar] [CrossRef]
- Pesce, G.; McDaniel, A.; Hottovy, S.; Wehr, J.; Volpe, G. Stratonovich-to-Itô transition in noisy systems with multiplicative feedback. Nat. Commun. 2013, 4, 2733. [Google Scholar] [CrossRef]
- Kaulakys, B.; Alaburda, M.; Gontis, V.; Ruseckas, J. Modeling long-memory processes by stochastic difference equations and superstatistical approach. Braz. J. Phys. 2009, 39, 453–456. [Google Scholar] [CrossRef]
- Tsallis, C. Economics and finance: q-Statistical stylized features galore. Entropy 2017, 19, 457. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B.; Ruseckas, J. Trading activity as driven Poisson process: Comparison with empirical data. Phys. A 2008, 387, 3891–3896. [Google Scholar] [CrossRef][Green Version]
- Ruseckas, J.; Kaulakys, B. Tsallis distributions and 1/f noise from nonlinear stochastic differential equations. Phys. Rev. E 2011, 84, 051125. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, R. Approximations for stochastic differential equations with reflecting convex boundaries. Stoch. Process. Appl. 1995, 59, 295–308. [Google Scholar] [CrossRef]
- Lux, T.; Marchesi, M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature 1999, 397, 498–500. [Google Scholar] [CrossRef]
- Challet, D.; Marsili, M.; Zecchina, R. Statistical mechanics of systems with heterogeneous agents: Minority games. Phys. Rev. Lett. 2000, 84, 1824–1827. [Google Scholar] [CrossRef]
- Cristelli, M.; Pietronero, L.; Zaccaria, A. Critical overview of agent-based models for economics. arxiv 2012, arXiv:1101.1847. [Google Scholar]
- Kirman, A.P. Ants, rationality and recruitment. Q. J. Econ. 1993, 108, 137–156. [Google Scholar] [CrossRef]
- Alfarano, S.; Lux, T.; Wagner, F. Estimation of agent-based models: The case of an asymmetric herding model. Comput. Econ. 2005, 26, 19–49. [Google Scholar] [CrossRef]
- Alfarano, S.; Lux, T.; Wagner, F. Time variation of higher moments in a financial market with heterogeneous agents: An analytical approach. J. Econ. Dyn. Control 2008, 32, 101–136. [Google Scholar] [CrossRef]
- van Kampen, N.G. Stochastic Process in Physics and Chemistry; North Holland: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Walras, L. Elements of Pure Economics; Routledge: London, UK, 2013. [Google Scholar]
- Rak, R.; Drozdz, S.; Kwapien, J.; Oswiecimka, P. Stock returns versus trading volume: Is the correspondence more general? Acta Phys. Pol. B 2013, 44, 2035–2050. [Google Scholar] [CrossRef]
- Kononovicius, A.; Gontis, V. Three state herding model of the financial markets. EPL 2013, 101, 28001. [Google Scholar] [CrossRef]
- Kononovicius, A.; Gontis, V. Control of the socio-economic systems using herding interactions. Phys. A 2014, 405, 80–84. [Google Scholar] [CrossRef]
- Kononovicius, A.; Gontis, V. Herding interactions as an opportunity to prevent extreme events in financial markets. Eur. Phys. J. B 2015, 88, 189. [Google Scholar] [CrossRef]
- Biondo, A.E.; Pluchino, A.; Rapisarda, A.; Helbing, D. Stopping financial avalanches by random trading. Phys. Rev. E 2013, 88, 062814. [Google Scholar] [CrossRef]
- Fernandez-Gracia, J.; Suchecki, K.; Ramasco, J.J.; San Miguel, M.; Eguiluz, V.M. Is the voter model a model for voters? Phys. Rev. Lett. 2014, 112, 158701. [Google Scholar] [CrossRef]
- Sano, F.; Hisakado, M.; Mori, S. Mean field voter model of election to the house of representatives in Japan. In Proceedings of the JPS Conference Proceedings, The Physical Society of Japan, Kanazawa, Japan, 13–18 November 2017; Volume 16, p. 011016. [Google Scholar] [CrossRef][Green Version]
- Braha, D.; de Aguiar, M.A.M. Voting contagion: Modeling and analysis of a century of U.S. presidential elections. PLoS ONE 2017, 12, e0177970. [Google Scholar] [CrossRef]
- Fenner, T.; Kaufmann, E.; Levene, M.; Loizou, G. A multiplicative process for generating a beta-like survival function with application to the UK 2016 EU referendum results. Int. J. Mod. Phys. C 2017, 28, 1750132. [Google Scholar] [CrossRef]
- Fenner, T.; Levene, M.; Loizou, G. A multiplicative process for generating the rank-order distribution of UK election results. Qual. Quant. 2017, 52, 1069–1079. [Google Scholar] [CrossRef]
- Fenner, T.; Levene, M.; Loizou, G. A stochastic differential equation approach to the analysis of the UK 2016 EU referendum polls. J. Phys. Commun. 2018, 2, 055022. [Google Scholar] [CrossRef]
- Levene, M.; Fenner, T. A stochastic differential equation approach to the analysis of the 2017 and 2019 UK general election polls. Int. J. Forecast. 2021, 37, 1227–1234. [Google Scholar] [CrossRef]
- Michaud, J.; Szilva, A. Social influence with recurrent mobility and multiple options. Phys. Rev. E 2018, 97, 062313. [Google Scholar] [CrossRef]
- Marmani, S.; Ficcadenti, V.; Kaur, P.; Dhesi, G. Entropic analysis of votes expressed in Italian elections between 1948 and 2018. Entropy 2020, 22, 523. [Google Scholar] [CrossRef]
- Kononovicius, A.; Ruseckas, J. Continuous transition from the extensive to the non-extensive statistics in an agent-based herding model. Eur. Phys. J. B 2014, 87, 169. [Google Scholar] [CrossRef][Green Version]
- Alfarano, S.; Milakovic, M. Network structure and N-dependence in agent-based herding models. J. Econ. Dyn. Control 2009, 33, 78–92. [Google Scholar] [CrossRef]
- Carro, A.; Toral, R.; San Miguel, M. The noisy voter model on complex networks. Sci. Rep. 2016, 6, 24775. [Google Scholar] [CrossRef]
- Vieira, D.S.; Riveros, J.M.E.; Jauregui, M.; Mendes, R.S. Anomalous diffusion behavior in parliamentary presence. Phys. Rev. E 2019, 99, 042141. [Google Scholar] [CrossRef] [PubMed]
- Willis, H.R. Conformity, independence and anticonformity. Hum. Relat. 1965, 18, 373–388. [Google Scholar] [CrossRef]
- Latane, B. The psychology of social impact. Am. Psychol. 1981, 36, 343–356. [Google Scholar] [CrossRef]
- Bancerowski, P.; Malarz, K. Multi-choice opinion dynamics model based on Latane theory. Eur. Phys. J. 2019, 92, 219. [Google Scholar] [CrossRef]
- Kowalska-Styczeń, A.; Malarz, K. Noise induced unanimity and disorder in opinion formation. PLoS ONE 2020, 15, e0235313. [Google Scholar] [CrossRef]
- de Oliveira, M.J. Isotropic majority-vote model on a square lattice. J. Stat. Phys. 1992, 66, 273–281. [Google Scholar] [CrossRef]
- Vilela, A.L.M.; Stanley, H.E. Effect of strong opinions on the dynamics of the majority-vote model. Sci. Rep. 2018, 8, 8709. [Google Scholar] [CrossRef]
- Galesic, M.; Stein, D.L. Statistical physics models of belief dynamics: Theory and empirical tests. Phys. A 2019, 519, 275–294. [Google Scholar] [CrossRef]
- Castellano, C.; Munoz, M.A.; Pastor-Satorras, R. The non-linear q-voter model. Phys. Rev. E 2009, 80, 041129. [Google Scholar] [CrossRef]
- Jedrzejewski, A.; Sznajd-Weron, K. Statistical physics of opinion formation: Is it a SPOOF? Comptes Rendus Phys. 2019, 20, 244–261. [Google Scholar] [CrossRef]
- Stark, H.U.; Tessone, C.J.; Schweitzer, F. Decelerating microdynamics can accelerate macrodynamics in the voter model. Phys. Rev. Lett. 2008, 101, 018701. [Google Scholar] [CrossRef]
- Stark, H.U.; Tessone, C.J.; Schweitzer, F. Slower is faster: Fostering consensus formation by heterogeneous inertia. Adv. Complex Syst. 2008, 11, 551–563. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Wang, L.; Zhang, Y.; Wang, Z. Freezing period strongly impacts the emergence of a global consensus in the voter model. Sci. Rep. 2014, 4, 3597. [Google Scholar] [CrossRef] [PubMed]
- Artime, O.; Peralta, A.F.; Toral, R.; Ramasco, J.; San Miguel, M. Aging-induced continuous phase transition. Phys. Rev. E 2018, 98, 032104. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A.; Reimann, S. The class of nonlinear stochastic models as a background for the bursty behavior in financial markets. Adv. Complex Syst. 2012, 15, 1250071. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Spurious memory in non-equilibrium stochastic models of imitative behavior. Entropy 2017, 19, 387. [Google Scholar] [CrossRef]
- Kononovicius, A.; Gontis, V. Approximation of the first passage time distribution for the birth-death processes. J. Stat. Mech. 2019, 2019, 073402. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Bessel-like birth-death process. Phys. A 2020, 540, 123119. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Burst and inter-burst duration statistics as empirical test of long-range memory in the financial markets. Phys. A 2017, 483, 266–272. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. The consentaneous model of the financial markets exhibiting spurious nature of long-range memory. Phys. A 2018, 505, 1075–1083. [Google Scholar] [CrossRef]
- Gontis, V. Interplay between endogenous and exogenous fluctuations in financial markets. Acta Phys. Pol. A 2016, 129, 1023–1031. [Google Scholar] [CrossRef]
- Metzler, R.; Oshanin, G.; Redner, S. First-Passage Phenomena and Their Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Burnecki, K.; Weron, A. Fractional Levy stable motion can model subdiffusive dynamics. Phys. Rev. E 2010, 82, 021130. [Google Scholar] [CrossRef]
- Burnecki, K.; Weron, A. Algorithms for testing of fractional dynamics: A practical guide to ARFIMA modelling. J. Stat. Mech. 2014, 2014, P10036. [Google Scholar] [CrossRef]
- Burnecki, K.; Sikora, G. Identification and validation of stable ARFIMA processes with application to UMTS data. Chaos Solitons Fractals 2017, 102, 456–466. [Google Scholar] [CrossRef]
- Klafter, J.; Lim, S.C.; Metzler, R. (Eds.) Fractional Dynamics: Recent Advances; World Scientific: New York, NY, USA, 2012. [Google Scholar]
- Lillo, F.; Farmer, J.D. The long memory of the efficient market. Stud. Nonlinear Dyn. Econom. 2001, 8, 1–35. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Gefen, Y.; Potters, M.; Wyart, M. Fluctuations and response in financial markets: The subtle nature of ’random’ price changes. Quant. Financ. 2004, 4, 176–190. [Google Scholar] [CrossRef]
- Toth, B.; Palit, I.; Lillo, F.; Farmer, J.D. Why is equity order flow so persistent? J. Econ. Dyn. Control 2015, 51, 218–239. [Google Scholar] [CrossRef]
- Gontis, V. Long-range memory test by the burst and inter-burst duration distribution. J. Stat. Mech. 2020, 2020, 093406. [Google Scholar] [CrossRef]
- Huang, R.; Polak, T. LOBSTER: The Limit Order Book Reconstructor; Technical Report; Discussion Paper School of Business and Economics; Humboldt Universitat zu Berlin: Berlin, Germany, 2011. [Google Scholar]
- Gontis, V. Order Flow in the Financial Markets from the Perspective of the Fractional Lévy Stable Motion. arXiv 2021, arXiv:2105.02057. [Google Scholar]
- Smarodinsky, G.; Taqqu, M. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman and Hall: London, UK, 1994. [Google Scholar] [CrossRef]
- Magdziarz, M.; Slezak, J.K.; Wojcik, J. Estimation and testing of the Hurst parameter using p-variation. J. Phys. Math. Theor. 2013, 46, 325003. [Google Scholar] [CrossRef]
- Weron, A.; Burnecki, K. Complete description of all self-similar models driven by Levy stable noise. Phys. Rev. E 2005, 71, 016113. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes; CRC press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Montanari, A.; Taqqu, M.S.; Teverovsky, V. Estimating long-range dependence in the presence of periodicity: An empirical study. Math. Comput. Model. 1999, 29, 217–228. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Mercik, S.; Weron, K.; Burnecki, K.; Weron, A. Enigma of self-similarity of fractional Levy stable motions. Acta Phys. Pol. B 2003, 34, 3773–3791. [Google Scholar]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S. Simulation methods for linear fractional stable motion and FARIMA using the Fast Fourier Transform. Fractals 2004, 12, 95. [Google Scholar] [CrossRef]
- Bassler, K.E.; Gunaratne, G.H.; McCauley, J.L. Markov processes, Hurst exponents, and nonlinear diffusion equations: With application to finance. Phys. A 2006, 369, 343–353. [Google Scholar] [CrossRef]
- McCauley, J.L.; Gunaratne, G.H.; Bassler, K.E. Hurst exponents, Markov processes, and fractional Brownian motion. Phys. A 2007, 379, 1–9. [Google Scholar] [CrossRef]
- Ruseckas, J.; Kaulakys, B.; Alaburda, M. Modelling of 1/f noise by sequences of stochastic pulses of different duration. Lith. J. Phys. 2003, 43, 223–228. [Google Scholar]
- Kutner, R.; Masoliver, J. The continuous time random walk, still trendy: Fifty-year history, state of art and outlook. Eur. Phys. J. B 2017, 90, 50. [Google Scholar] [CrossRef]
- Baronchelli, A. The emergence of consensus: A primer. R. Soc. Open Sci. 2018, 5, 172189. [Google Scholar] [CrossRef] [PubMed]
- Landry, N.; Restrepo, J.G. The effect of heterogeneity on hypergraph contagion models. Chaos 2020, 30, 103117. [Google Scholar] [CrossRef] [PubMed]
- Leibovich, N.; Dechant, A.; Lutz, E.; Barkai, E. Aging Wiener-Khinchin theorem and critical exponents of 1/fβ noise. Phys. Rev. E 2016, 94, 052130. [Google Scholar] [CrossRef]
- Dmitriev, A.; Tsukanova, O.; Maltseva, S. Modeling of microblogging social networks: Dynamical system vs. Random dynamical system. Procedia Comput. Sci. 2017, 122, 812–819. [Google Scholar] [CrossRef]
- Vita, A.D. On the response of power law distributions to fluctuations. Eur. Phys. J. B 2019, 92, 255. [Google Scholar] [CrossRef]
- Ponta, L.; Trinh, M.; Raberto, M.; Scalas, E.; Cincotti, S. Modeling non-stationarities in high-frequency financial time series. Phys. A 2019, 521, 173–196. [Google Scholar] [CrossRef]
- Emenogu, N.G.; Adenomon, M.O. Robustness of GARCH family models to high positive autocorrelation. J. Niger. Stat. Assoc. 2020, 32, 13–28. [Google Scholar]
- Vveinhardt, J.; Streimikiene, D.; Rizwan, A.R.; Nawaz, A.; Rehman, A. Mean reversion: An investigation from Karachi stock exchange sectors. Technol. Econ. Dev. Econ. 2016, 22, 493–511. [Google Scholar] [CrossRef]
- Lima, L.S.; Melgaço, J.H.C. Dynamics of stocks prices based in the Black & Scholes equation and nonlinear stochastic differentials equations. Phys. A 2021, 581, 126220. [Google Scholar] [CrossRef]
- Benhamou, E.; Gobet, E.; Miri, M. Time dependent Heston model. SIAM J. Financ. Math. 2010, 1, 289–325. [Google Scholar] [CrossRef]
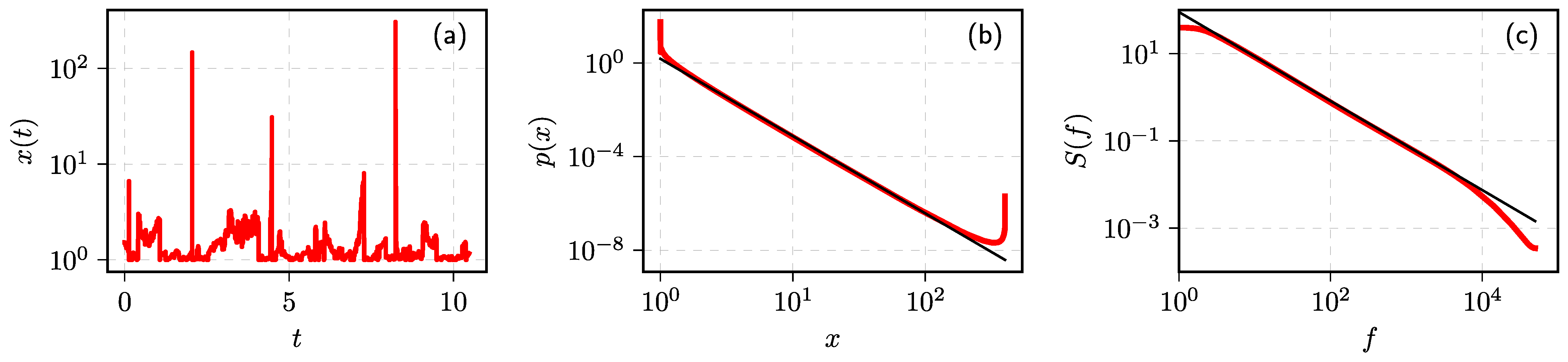
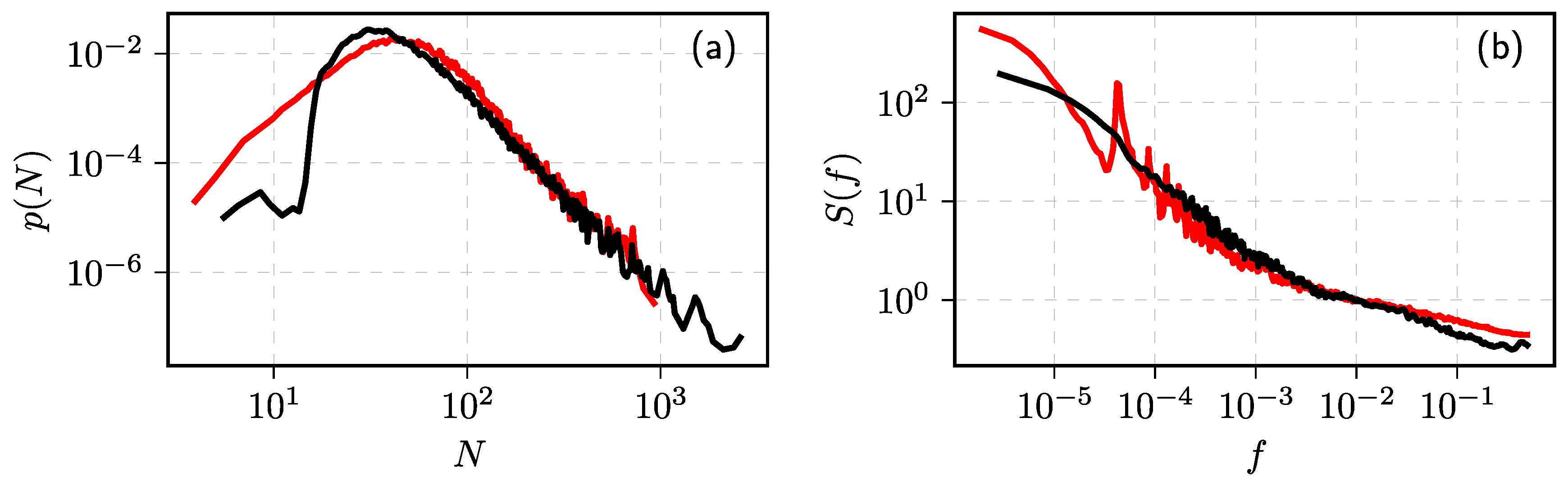
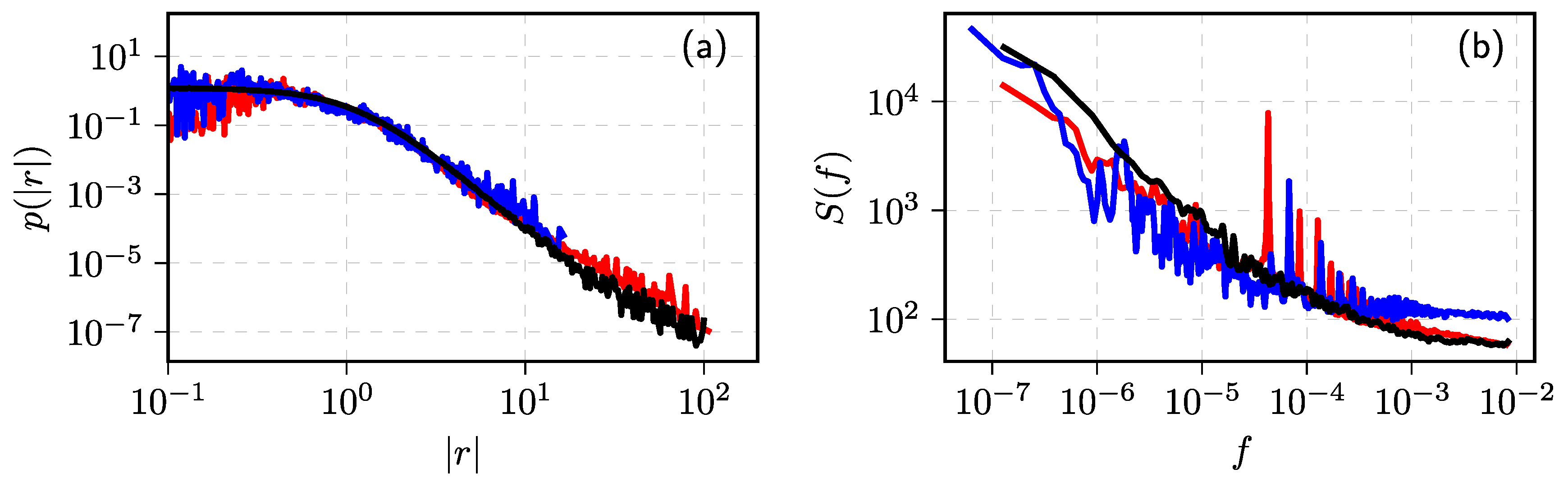
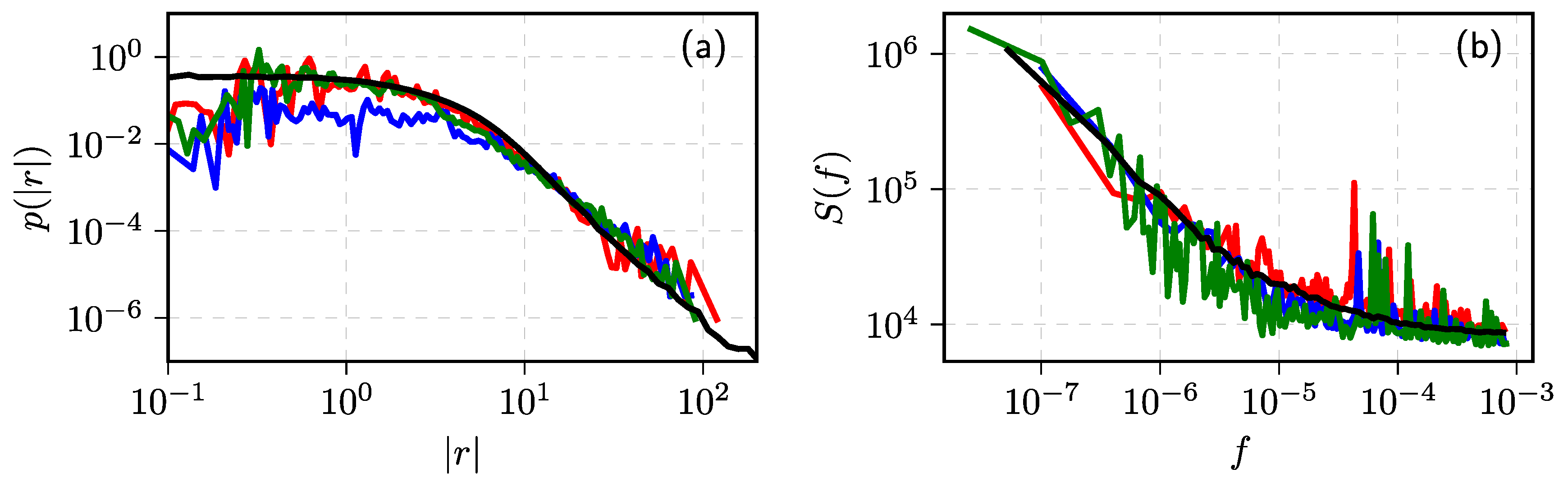
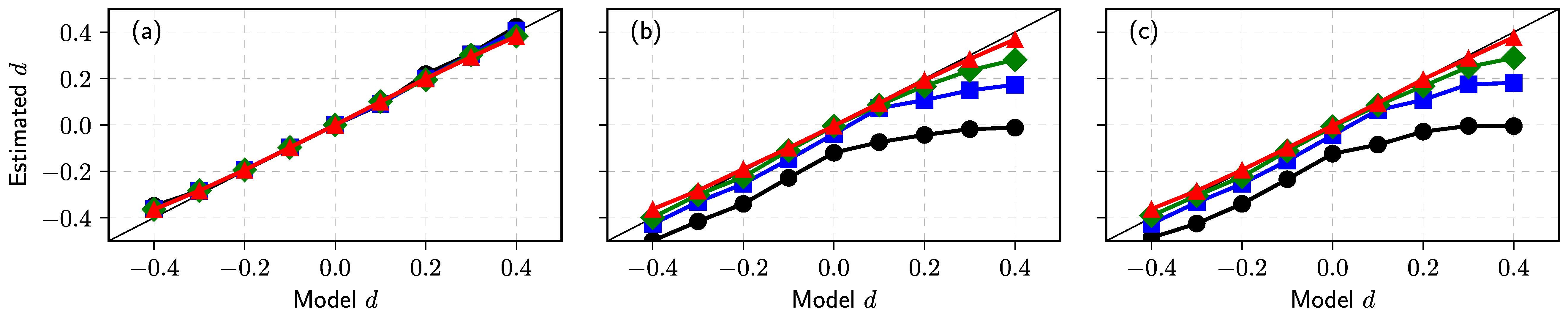

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazakevičius, R.; Kononovicius, A.; Kaulakys, B.; Gontis, V. Understanding the Nature of the Long-Range Memory Phenomenon in Socioeconomic Systems. Entropy 2021, 23, 1125. https://doi.org/10.3390/e23091125
Kazakevičius R, Kononovicius A, Kaulakys B, Gontis V. Understanding the Nature of the Long-Range Memory Phenomenon in Socioeconomic Systems. Entropy. 2021; 23(9):1125. https://doi.org/10.3390/e23091125
Chicago/Turabian StyleKazakevičius, Rytis, Aleksejus Kononovicius, Bronislovas Kaulakys, and Vygintas Gontis. 2021. "Understanding the Nature of the Long-Range Memory Phenomenon in Socioeconomic Systems" Entropy 23, no. 9: 1125. https://doi.org/10.3390/e23091125
APA StyleKazakevičius, R., Kononovicius, A., Kaulakys, B., & Gontis, V. (2021). Understanding the Nature of the Long-Range Memory Phenomenon in Socioeconomic Systems. Entropy, 23(9), 1125. https://doi.org/10.3390/e23091125






