Relationship between Age and Value of Information for a Noisy Ornstein–Uhlenbeck Process
Abstract
:1. Introduction
2. VoI with Application to OU Processes
2.1. VoI Definition
2.2. Noisy OU Process Model
2.3. VoI for the Noisy OU Process
3. Relationship between VoI and AoI
4. Statistical Properties of the VoI in the M/M/1 Queue Model
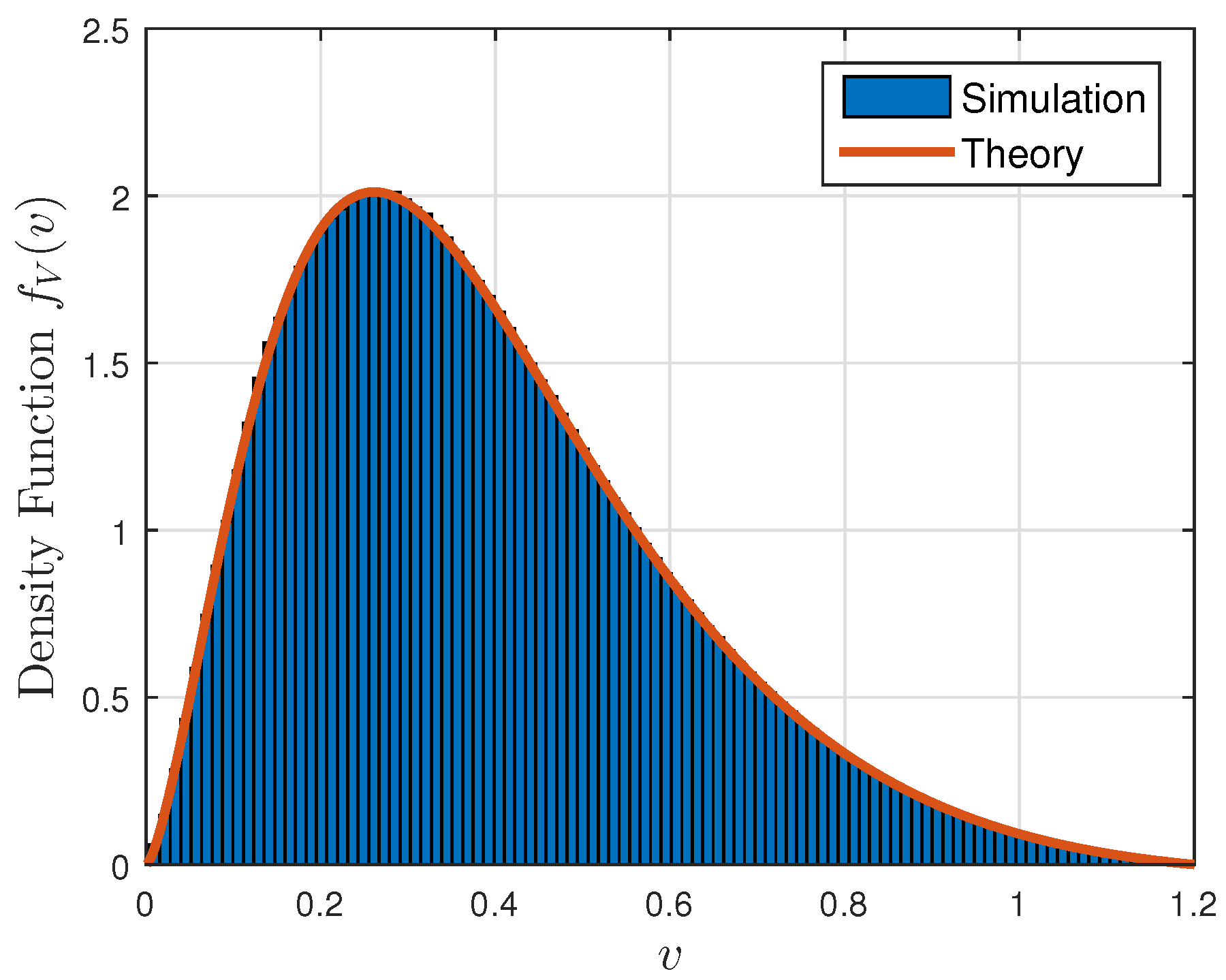
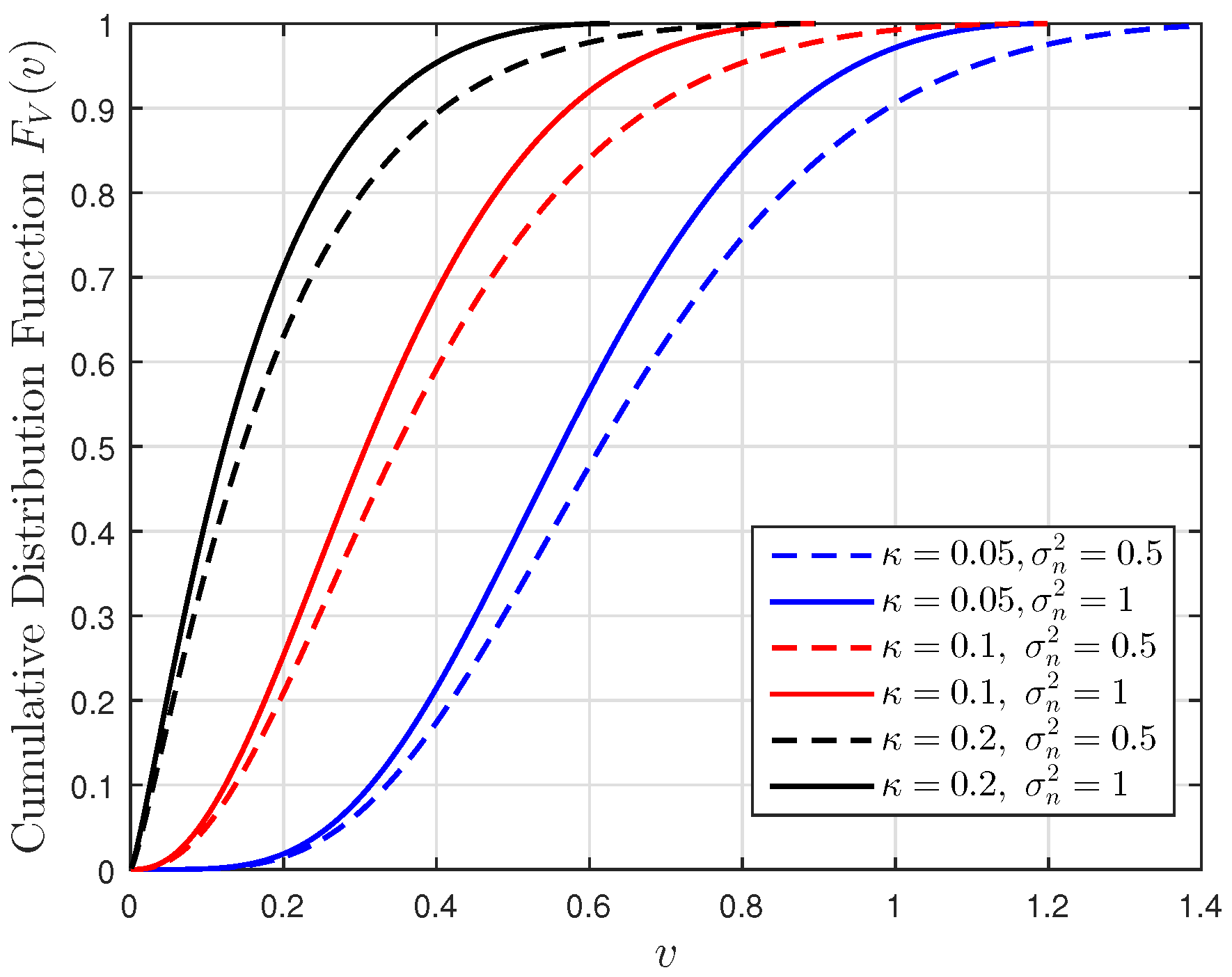
4.1. Distribution of the VoI
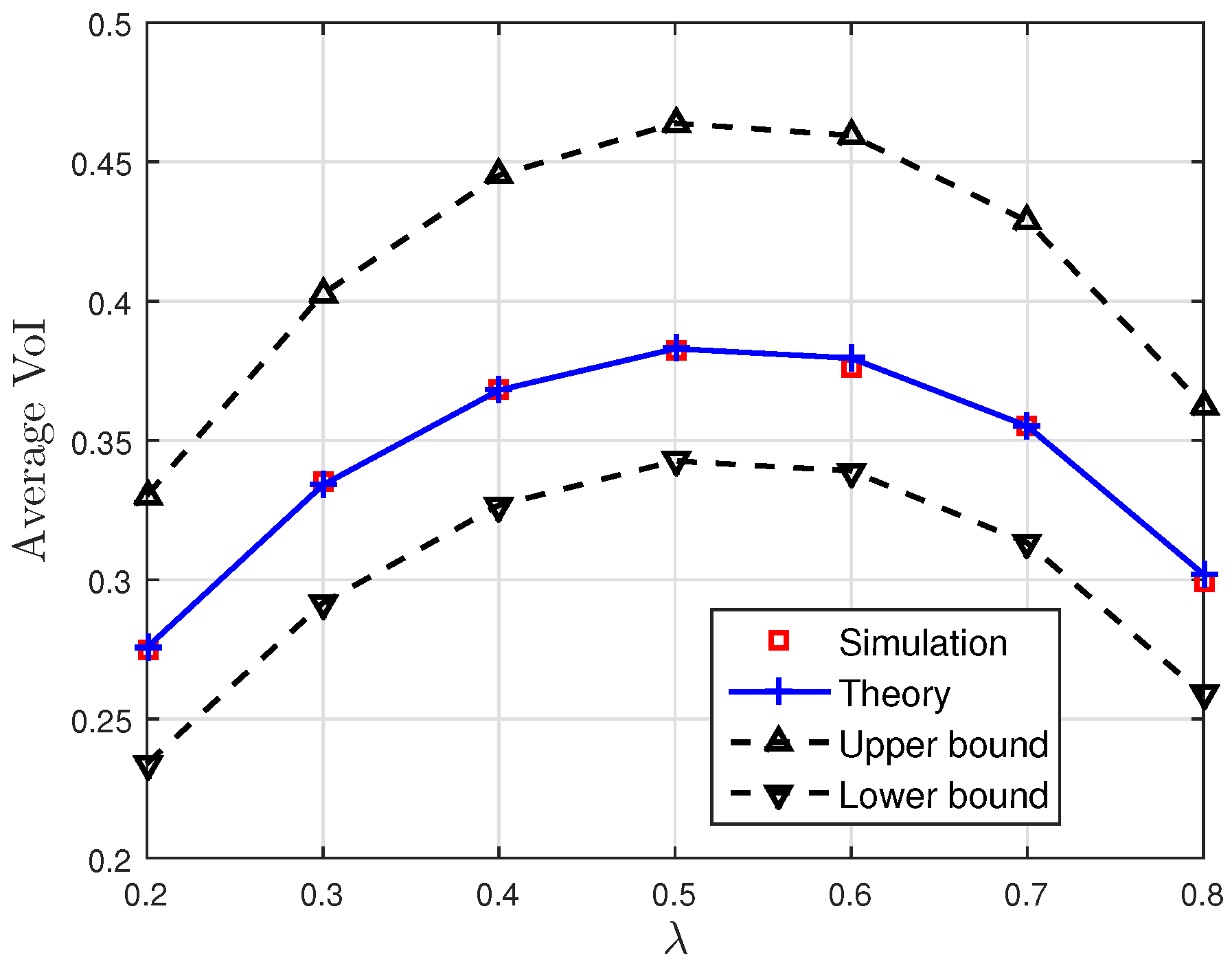
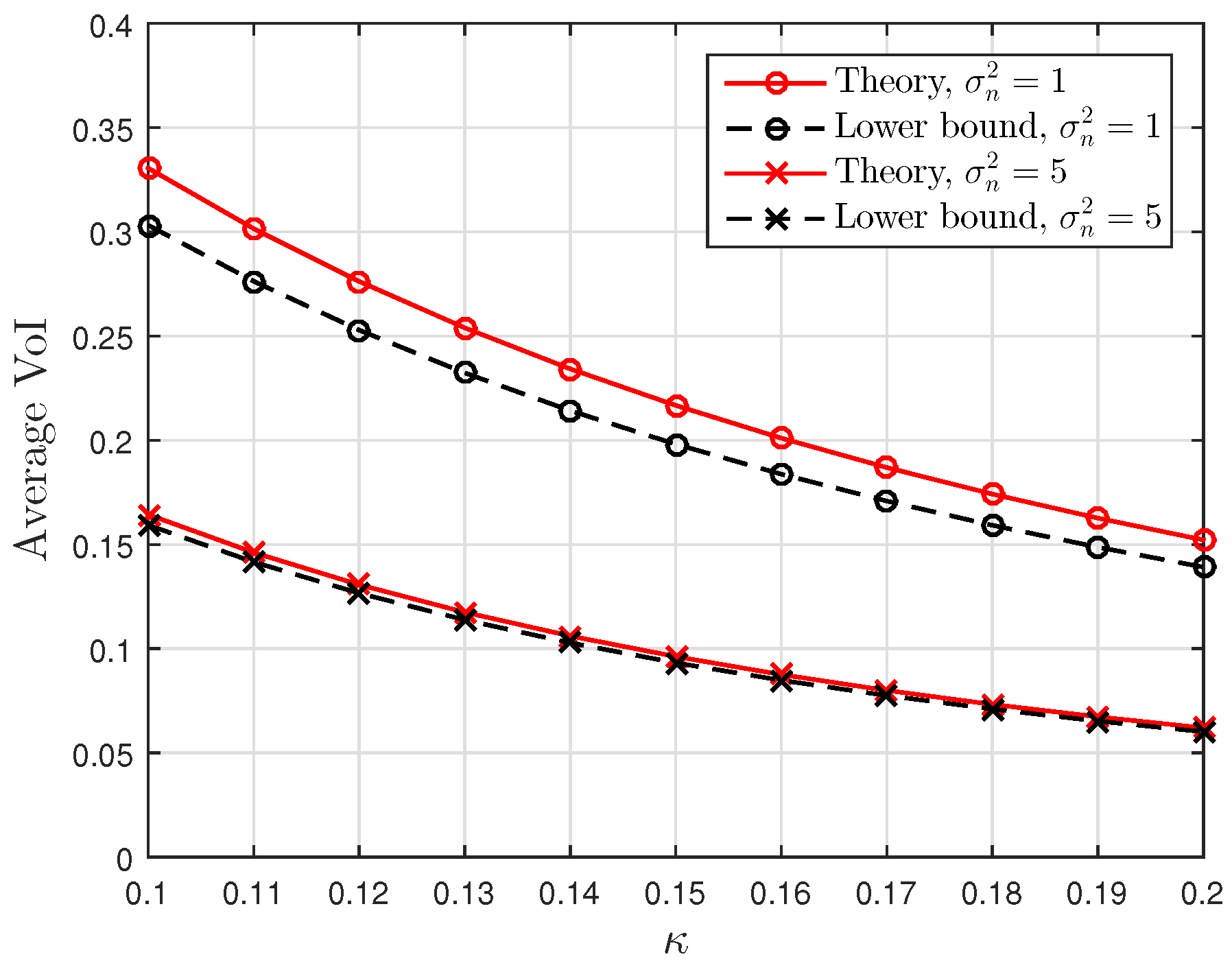
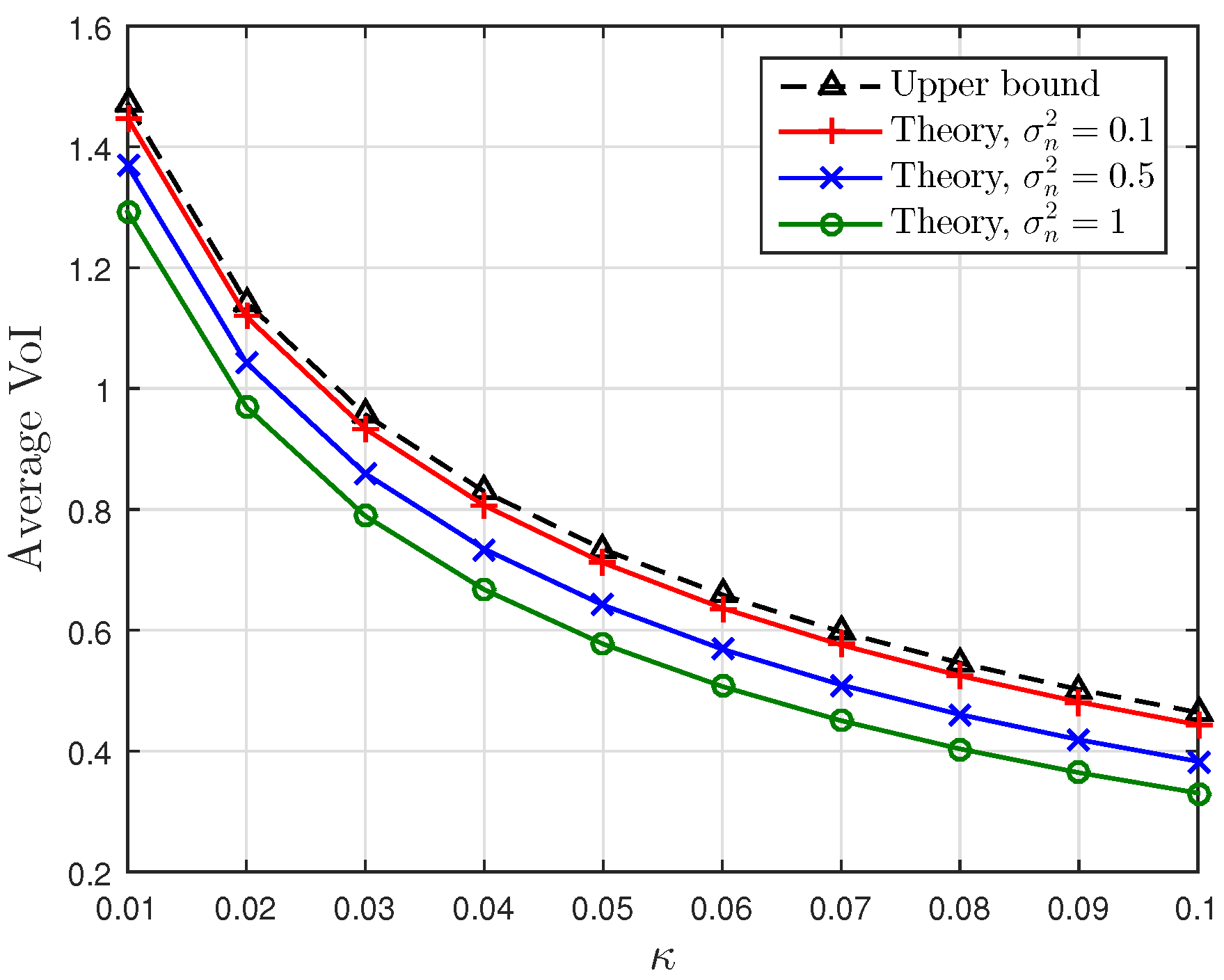
4.2. Moments and Bounds
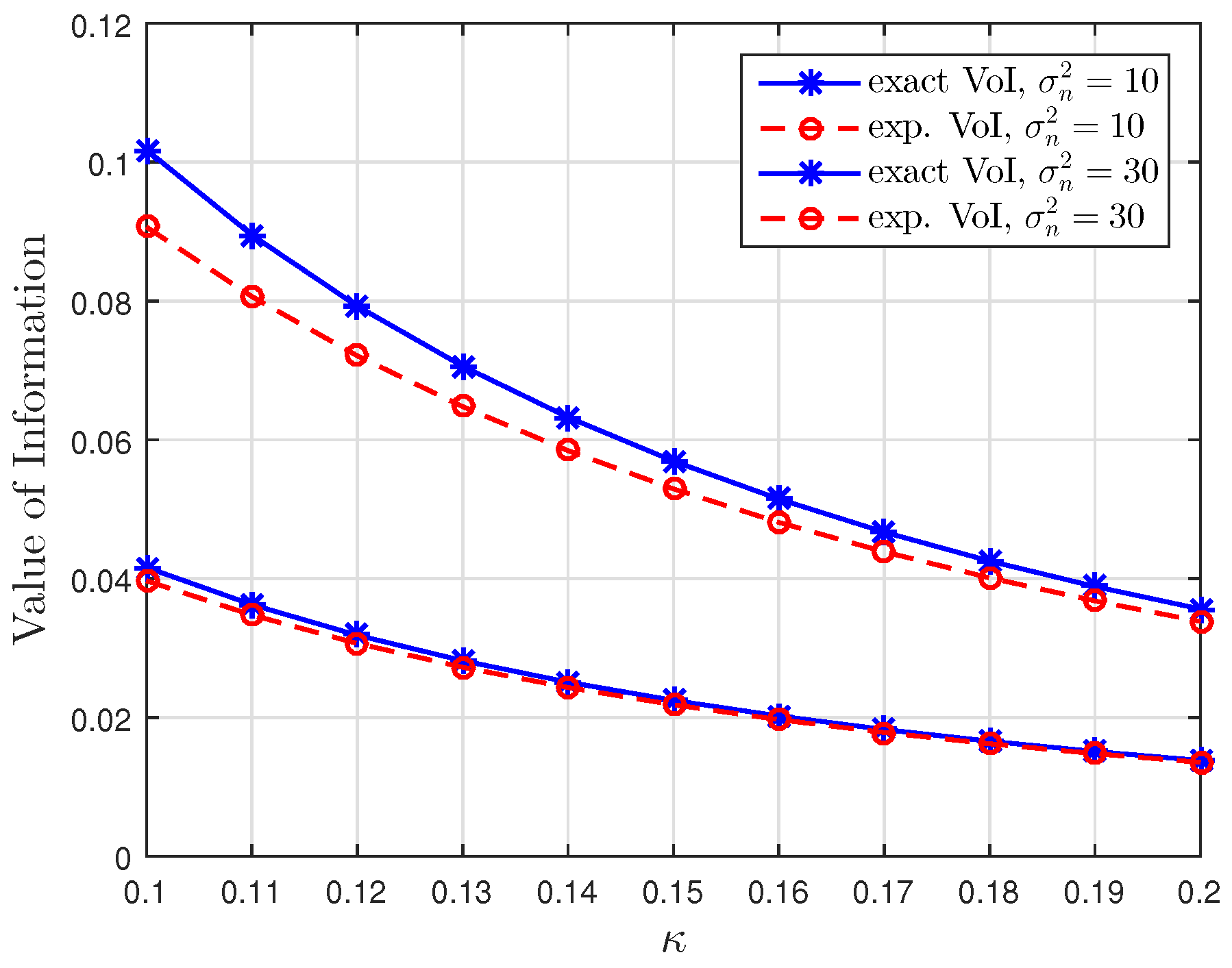
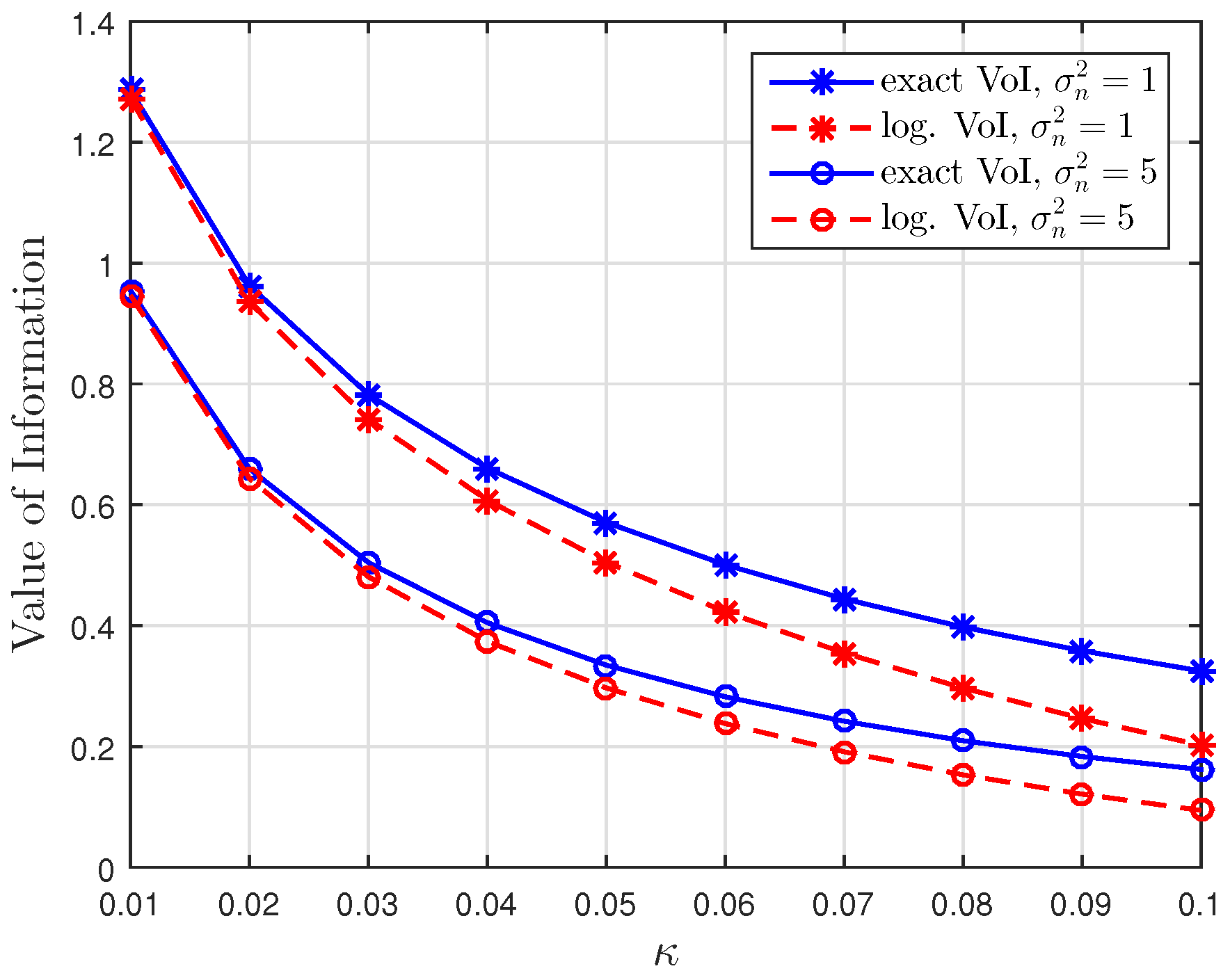
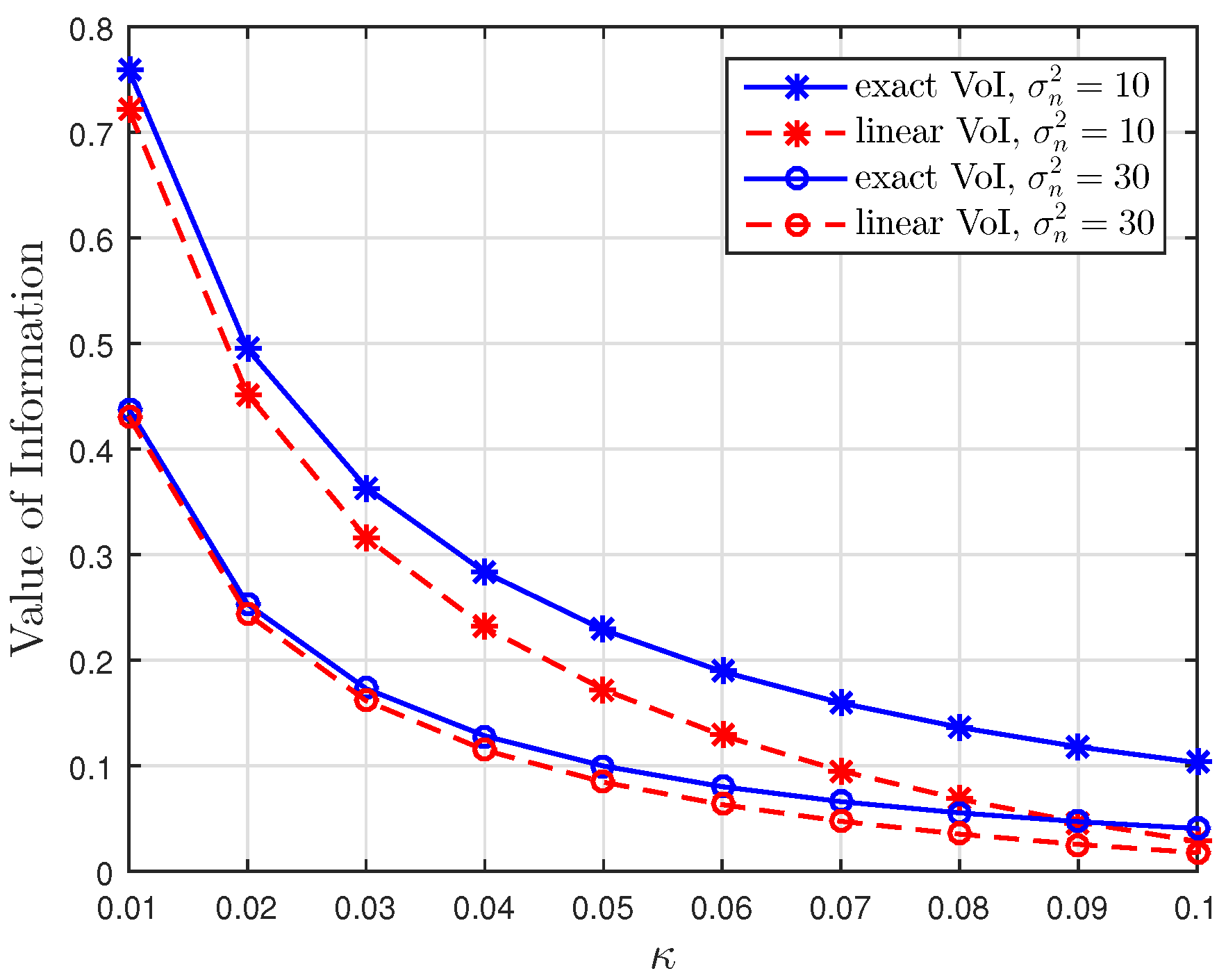
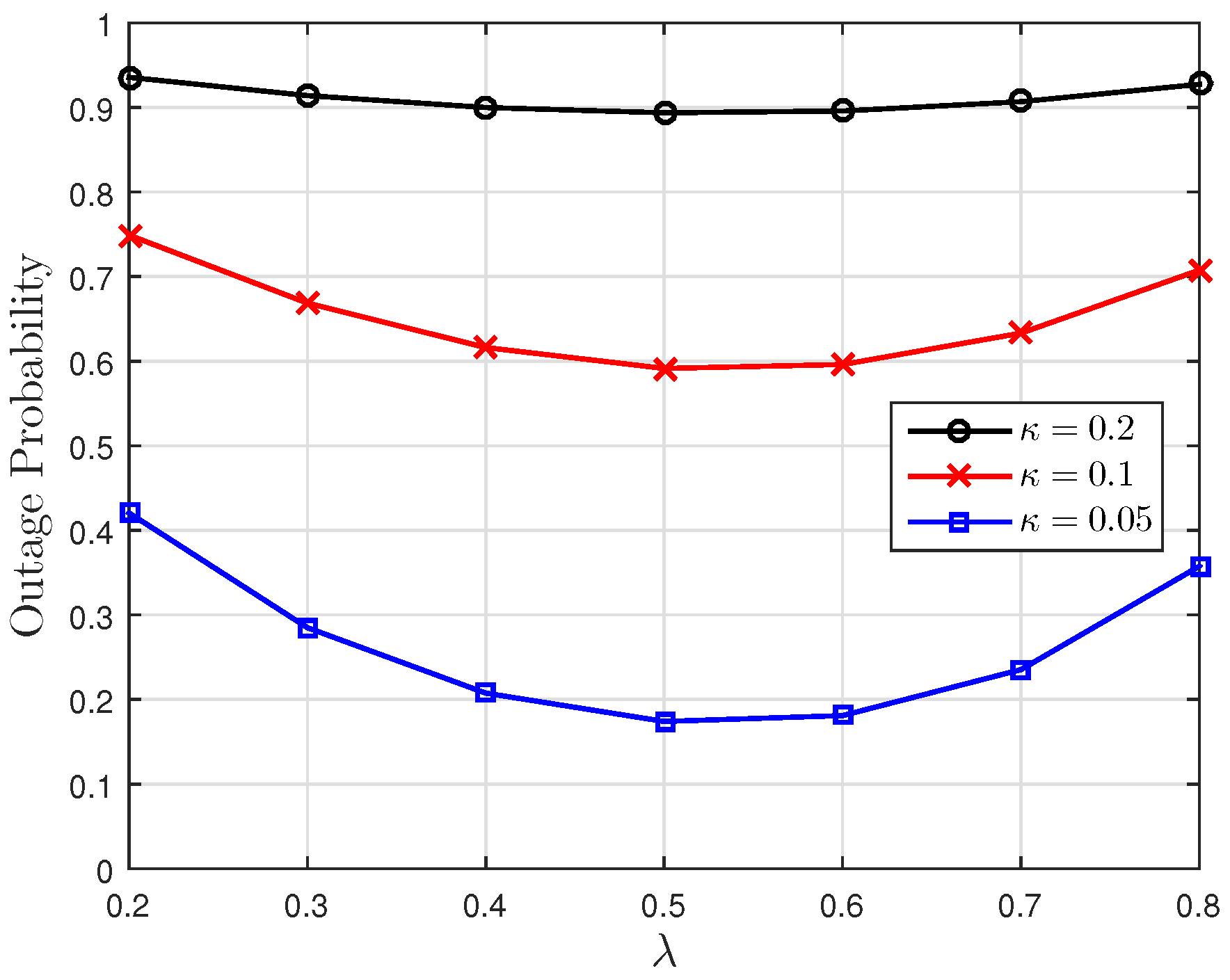
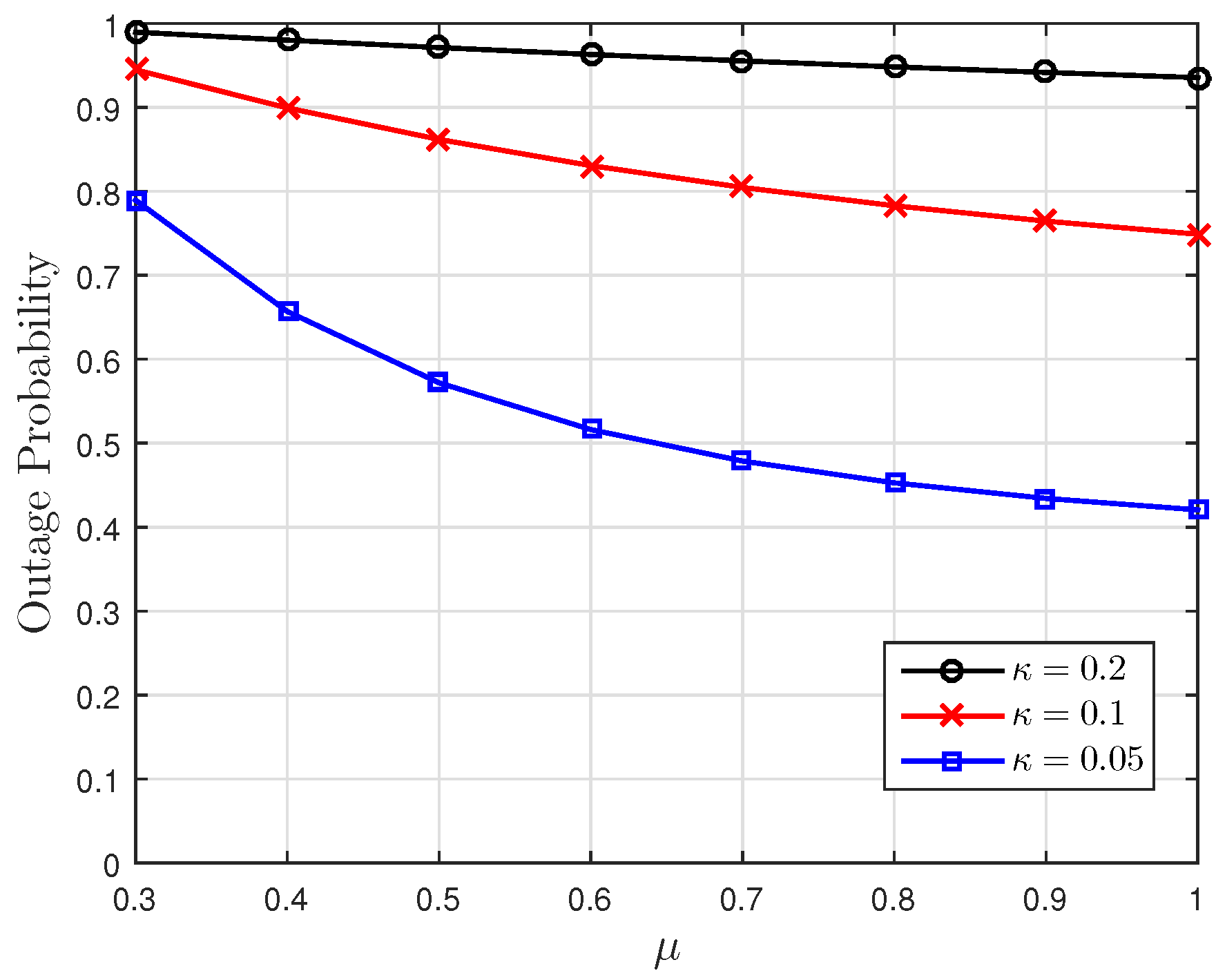
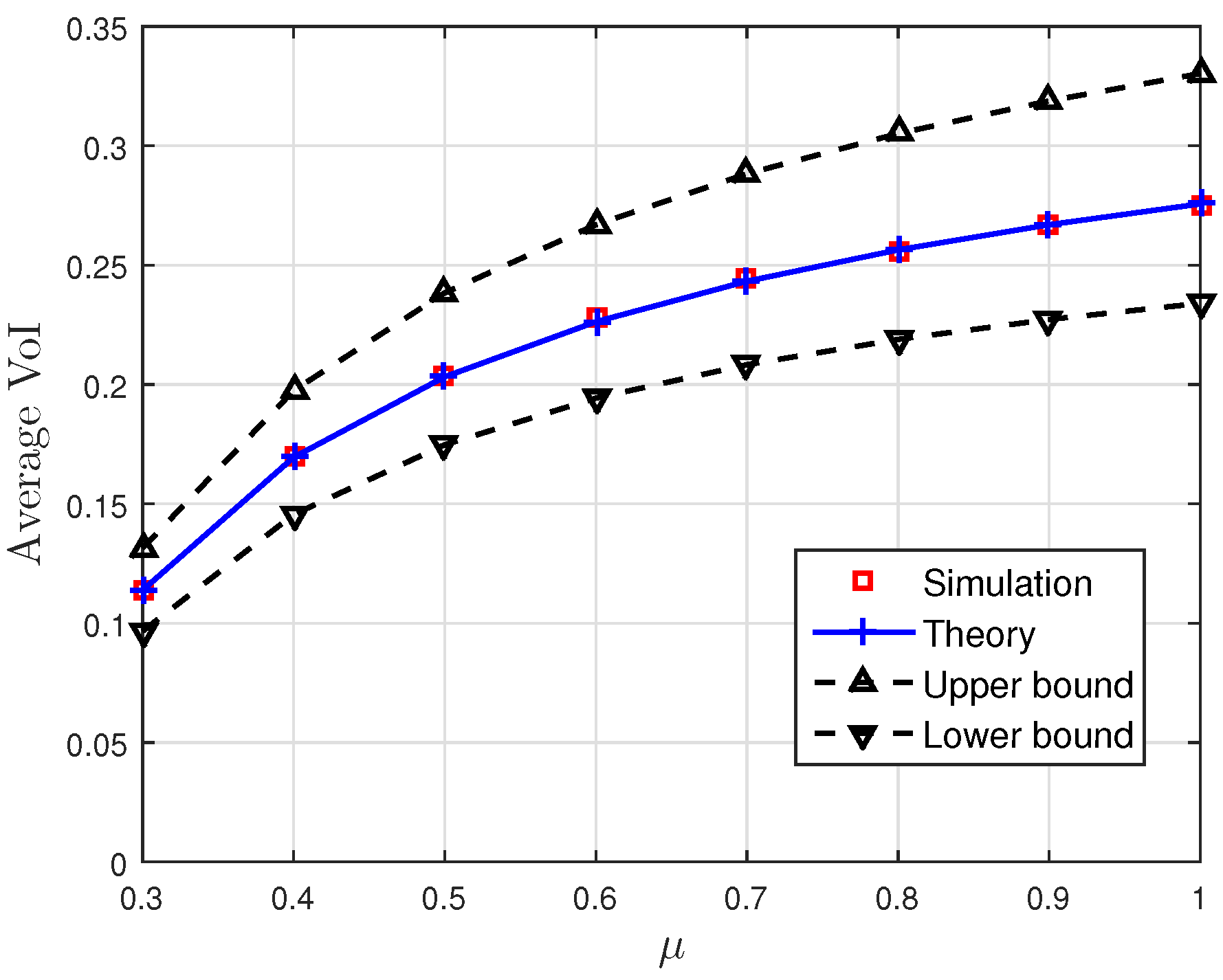
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Monotonicity in μ
Appendix A.2. Proof of Optimal λ Exists
Appendix B. Proof of Proposition 3
Appendix C. Proof of Proposition 4
References
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update? In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 2731–2735. [Google Scholar]
- Yates, R.D.; Kaul, S. Real-time status updating: Multiple sources. In Proceedings of the 2012 IEEE International Symposium on Information Theory Proceedings, Cambridge, MA, USA, 1–6 July 2012; pp. 2666–2670. [Google Scholar]
- Kosta, A.; Pappas, N.; Angelakis, V. Age of Information: A New Concept, Metric, and Tool. Found. Trends Netw. 2017, 12, 162–259. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Yang, J.; Wu, J. Optimal Status Update for Age of Information Minimization with an Energy Harvesting Source. IEEE Trans. Green Commun. Netw. 2018, 2, 193–204. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, X.; Liu, B.; Zhang, P. Joint Data Sampling and Link Scheduling for Age Minimization in Multihop Cyber-Physical Systems. IEEE Commun. Lett. 2019, 8, 765–768. [Google Scholar] [CrossRef]
- He, Q.; Dán, G.; Fodor, V. Joint Assignment and Scheduling for Minimizing Age of Correlated Information. IEEE/ACM Trans. Netw. 2019, 27, 1887–1900. [Google Scholar] [CrossRef]
- Abd-Elmagid, M.A.; Dhillon, H.S. Average Peak Age-of-Information Minimization in UAV-Assisted IoT Networks. IEEE Trans. Veh. Technol. 2019, 68, 2003–2008. [Google Scholar] [CrossRef] [Green Version]
- Abd-Elmagid, M.A.; Pappas, N.; Dhillon, H.S. On the Role of Age of Information in the Internet of Things. IEEE Commun. Mag. 2019, 57, 72–77. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Masuyama, H.; Takine, T.; Tanaka, T. The stationary distribution of the age of information in FCFS single-server queues. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 571–575. [Google Scholar]
- Hu, L.; Chen, Z.; Dong, Y.; Jia, Y.; Liang, L.; Wang, M. Status Update in IoT Networks: Age of Information Violation Probability and Optimal Update Rate. IEEE Internet Things J. 2021, 11329–11344. [Google Scholar] [CrossRef]
- Inoue, Y.; Masuyama, H.; Takine, T.; Tanaka, T. A General Formula for the Stationary Distribution of the Age of Information and Its Application to Single-Server Queues. IEEE Trans. Inf. Theory 2019, 65, 8305–8324. [Google Scholar] [CrossRef] [Green Version]
- Bedewy, A.M.; Sun, Y.; Shroff, N.B. Minimizing the Age of Information Through Queues. IEEE Trans. Inf. Theory 2019, 65, 5215–5232. [Google Scholar] [CrossRef] [Green Version]
- Kaul, S.K.; Yates, R.D. Age of Information: Updates with Priority. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 2644–2648. [Google Scholar]
- Kam, C.; Kompella, S.; Nguyen, G.D.; Wieselthier, J.E.; Ephremides, A. On the Age of Information with Packet Deadlines. IEEE Trans. Inf. Theory 2018, 64, 6419–6428. [Google Scholar] [CrossRef]
- Champati, J.P.; Al-Zubaidy, H.; Gross, J. On the Distribution of AoI for the GI/GI/1/1 and GI/GI/1/2* Systems: Exact Expressions and Bounds. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 37–45. [Google Scholar]
- Sun, Y.; Cyr, B. Sampling for data freshness optimization: Non-linear age functions. J. Commun. Netw. 2019, 21, 204–219. [Google Scholar] [CrossRef]
- Sun, Y.; Uysal-Biyikoglu, E.; Yates, R.D.; Koksal, C.E.; Shroff, N.B. Update or Wait: How to Keep Your Data Fresh. IEEE Trans. Inf. Theory 2017, 63, 7492–7508. [Google Scholar] [CrossRef]
- Zheng, X.; Zhou, S.; Jiang, Z.; Niu, Z. Closed-Form Analysis of Non-Linear Age of Information in Status Updates with an Energy Harvesting Transmitter. IEEE Trans. Wirel. Commun. 2019, 18, 4129–4142. [Google Scholar] [CrossRef] [Green Version]
- Kosta, A.; Pappas, N.; Ephremides, A.; Angelakis, V. Age and value of information: Non-linear age case. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 326–330. [Google Scholar]
- Kosta, A.; Pappas, N.; Ephremides, A.; Angelakis, V. The Cost of Delay in Status Updates and Their Value: Non-Linear Ageing. IEEE Trans. Commun. 2020, 68, 4905–4918. [Google Scholar] [CrossRef] [Green Version]
- Kosta, A.; Pappas, N.; Ephremides, A.; Angelakis, V. The Age of Information in a Discrete Time Queue: Stationary Distribution and Non-Linear Age Mean Analysis. IEEE J. Sel. Areas Commun. 2021, 39, 1352–1364. [Google Scholar] [CrossRef]
- Sun, Y.; Polyanskiy, Y.; Uysal, E. Sampling of the Wiener Process for Remote Estimation over a Channel with Random Delay. IEEE Trans. Inf. Theory 2020, 66, 1118–1135. [Google Scholar] [CrossRef]
- Ornee, T.Z.; Sun, Y. Sampling and Remote Estimation for the Ornstein-Uhlenbeck Process through Queues: Age of Information and Beyond. IEEE/ACM Trans. Netw. 2021, 1–14. [Google Scholar] [CrossRef]
- Zheng, X.; Zhou, S.; Niu, Z. Urgency of Information for Context-Aware Timely Status Updates in Remote Control Systems. IEEE Trans. Wirel. Commun. 2020, 19, 7237–7250. [Google Scholar] [CrossRef]
- Kam, C.; Kompella, S.; Nguyen, G.D.; Wieselthier, J.E.; Ephremides, A. Towards an effective age of information: Remote estimation of a Markov source. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Honolulu, HI, USA, 15–19 April 2018; pp. 367–372. [Google Scholar]
- Sun, Y.; Cyr, B. Information Aging Through Queues: A Mutual Information Perspective. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Wang, Z.; Badiu, M.A.; Coon, J.P. A Value of Information Framework for Latent Variable Models. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Doob, J.L. The Brownian Movement and Stochastic Equations. Ann. Math. 1942, 43, 351–369. [Google Scholar] [CrossRef]
- Conway, J.; Guy, R. The Book of Numbers; Springer New York: New York, NY, USA, 1998. [Google Scholar]
- Andrews, L. Special Functions of Mathematics for Engineers, 2nd ed.; Oxford University Press: Oxford, UK; SPIE Optical Engineering Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Badiu, M.-A.; Coon, J.P. Relationship between Age and Value of Information for a Noisy Ornstein–Uhlenbeck Process. Entropy 2021, 23, 940. https://doi.org/10.3390/e23080940
Wang Z, Badiu M-A, Coon JP. Relationship between Age and Value of Information for a Noisy Ornstein–Uhlenbeck Process. Entropy. 2021; 23(8):940. https://doi.org/10.3390/e23080940
Chicago/Turabian StyleWang, Zijing, Mihai-Alin Badiu, and Justin P. Coon. 2021. "Relationship between Age and Value of Information for a Noisy Ornstein–Uhlenbeck Process" Entropy 23, no. 8: 940. https://doi.org/10.3390/e23080940
APA StyleWang, Z., Badiu, M.-A., & Coon, J. P. (2021). Relationship between Age and Value of Information for a Noisy Ornstein–Uhlenbeck Process. Entropy, 23(8), 940. https://doi.org/10.3390/e23080940





