A Modified Multivariable Complexity Measure Algorithm and Its Application for Identifying Mental Arithmetic Task
Abstract
:1. Introduction
2. Complexity Measure Methods
2.1. PCA and Normalization of the Multivariable Time Series
2.1.1. PCA
2.1.2. Normalization
2.2. Multivariable Ordinal Pattern Representations
2.3. Multivariable Permutation Entropy Algorithms
2.4. Discussion of the Complexity Measurement Methods
- (1)
- The new approach can have more patterns compared with the existing methods like PE and MPE algorithms, and there are patterns in the new approach for multivariate time series, where d is the embedding dimension and m is the dimension of the time series.
- (2)
- Generally, if d takes larger values, there are more patterns. In the real applications, the embedded dimension d can be {2, 3, 4, 5}.
- (3)
- When m becomes to be larger, the number of patterns increase significantly. In the real applications, m could be a large value. Thus, we need a method to shrink the dimension. In this paper, the PCA algorithm is employed to decrease the dimension of the multivariable time series. In the real application, we suggest that the value of m could be smaller than 5.
- (4)
- In general, more patterns mean better recognition of nonlinearity in the time series. Two reasons are presented. Firstly, less patterns mean less computation, but it losses more information. Secondly, if there are more items, the obtained patterns contain more information regarding the nonlinearity in the time series.
- (5)
- In simulations, it is found that there are some “missing” Bandt–Pompe ordinal patterns for some chaotic systems. In fact, the chaotic time series are not random time series. So there is always some “missing” ordinal patterns for the chaotic time series and other nonlinear time series if they are not totally random.
- (6)
- MMPE is an improved version of PE algorithm and MPE algorithm. Its time complexity is .
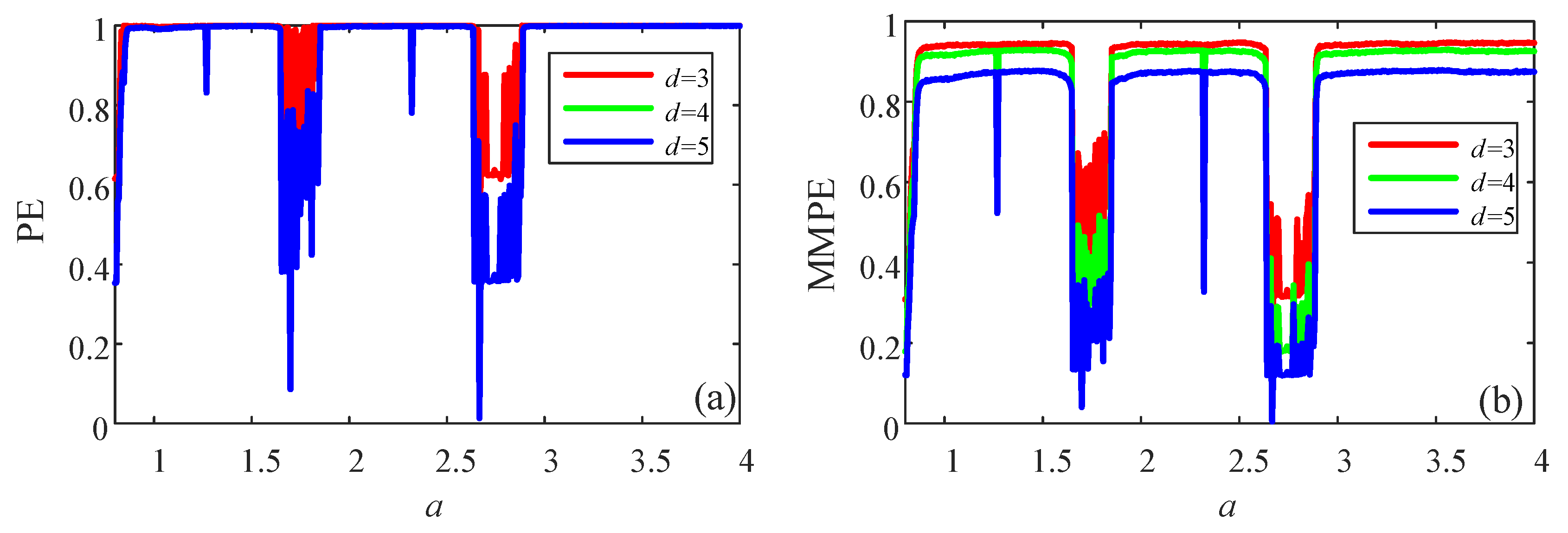
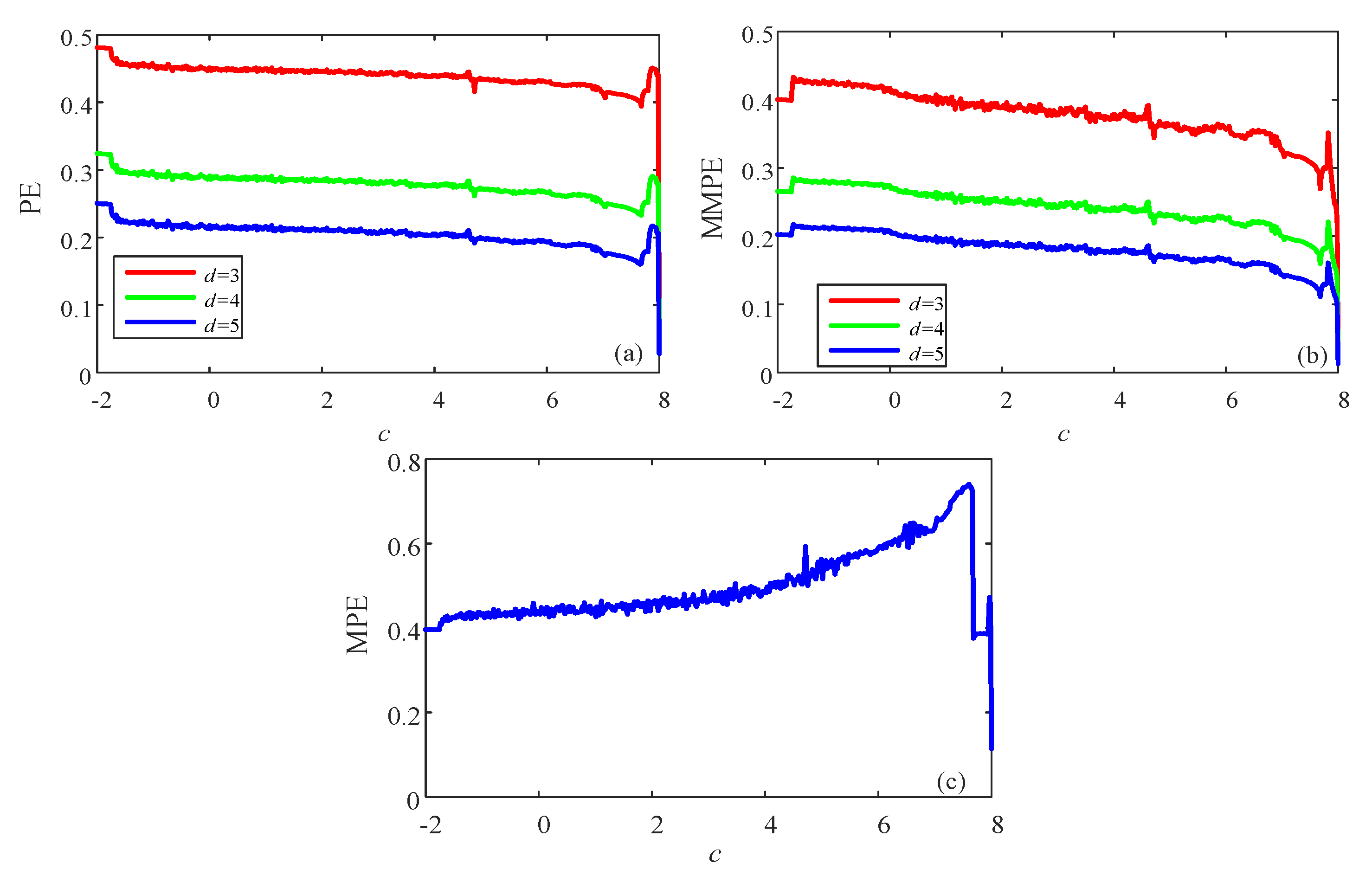
3. Complexity Analysis of Chaotic Systems
4. Determine State of EEG Signals
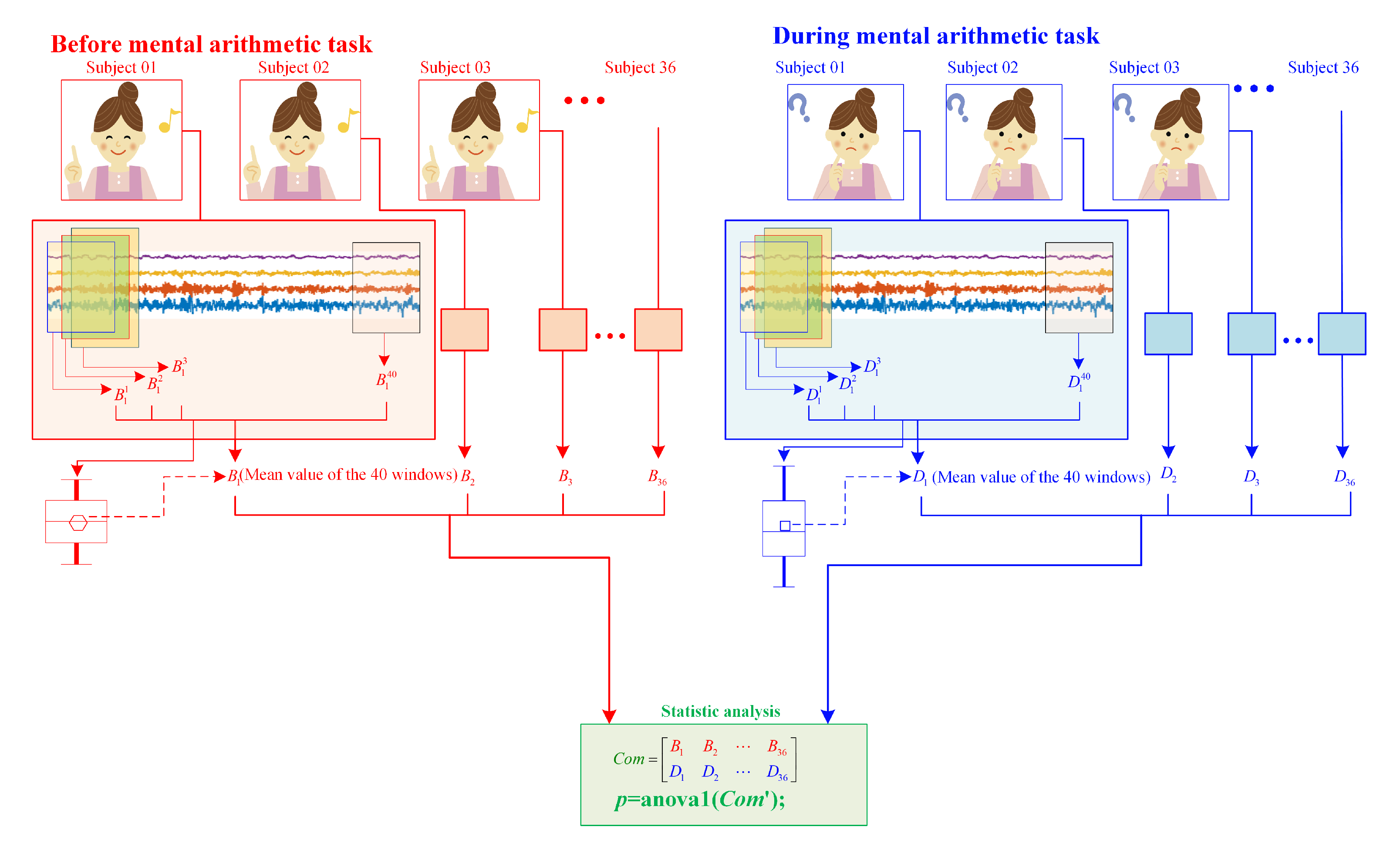
4.1. Data Description
4.2. Complexity Analysis
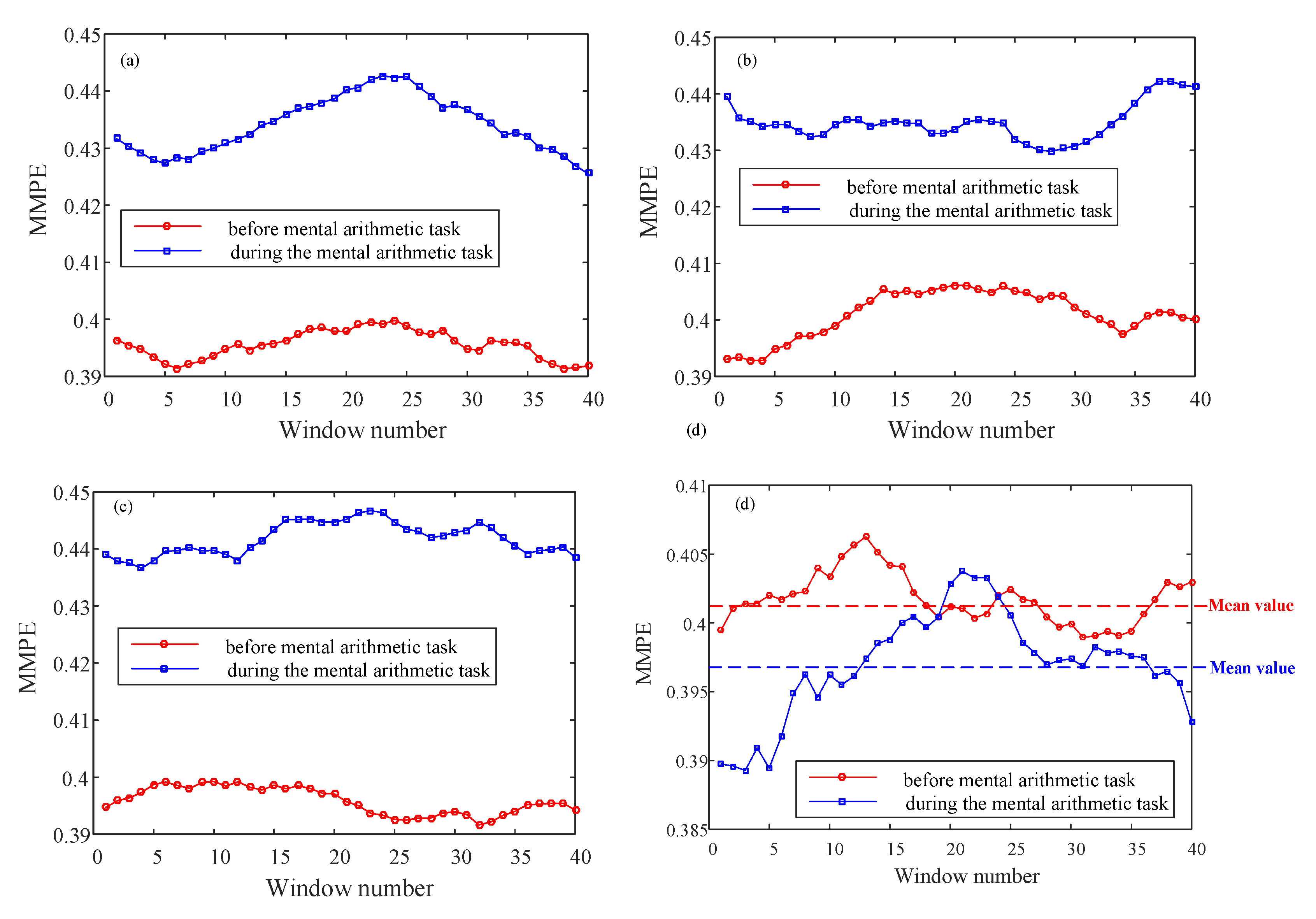
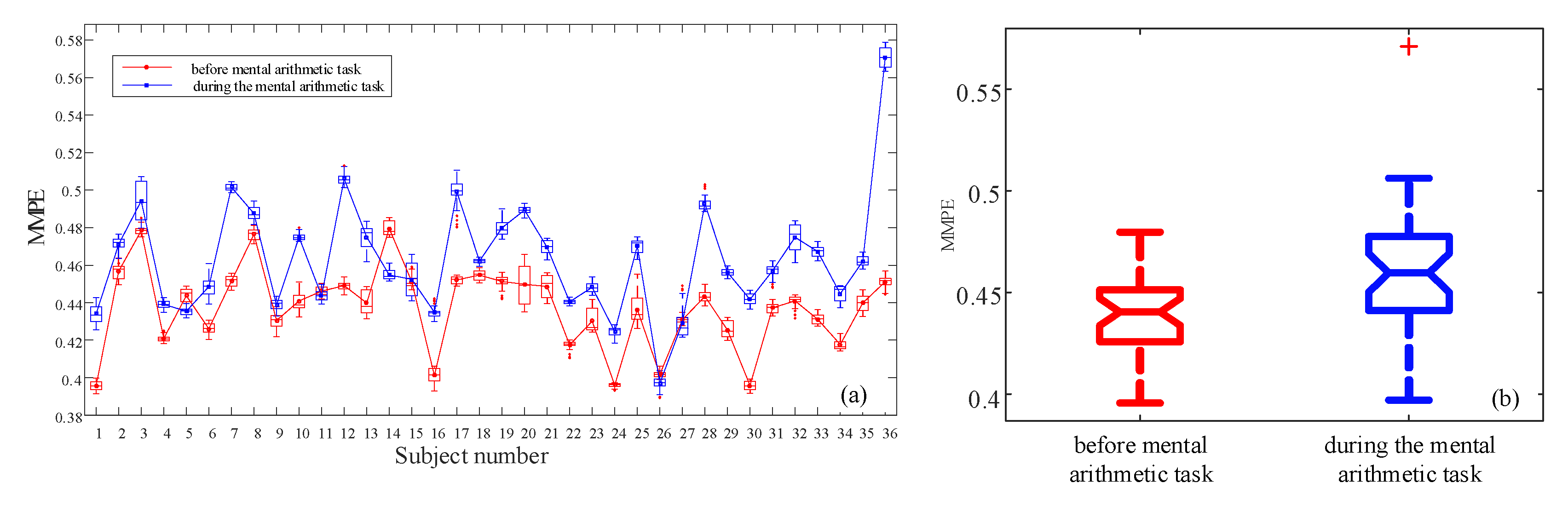
4.2.1. MMPE Analysis
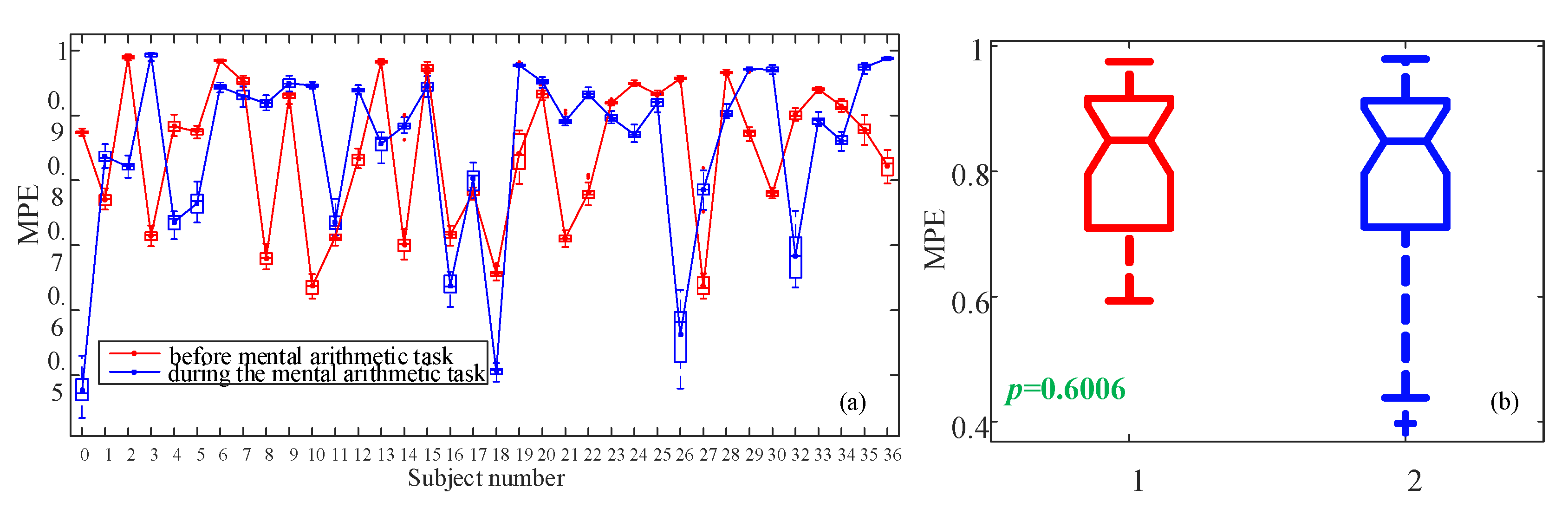
4.2.2. MPE Analysis
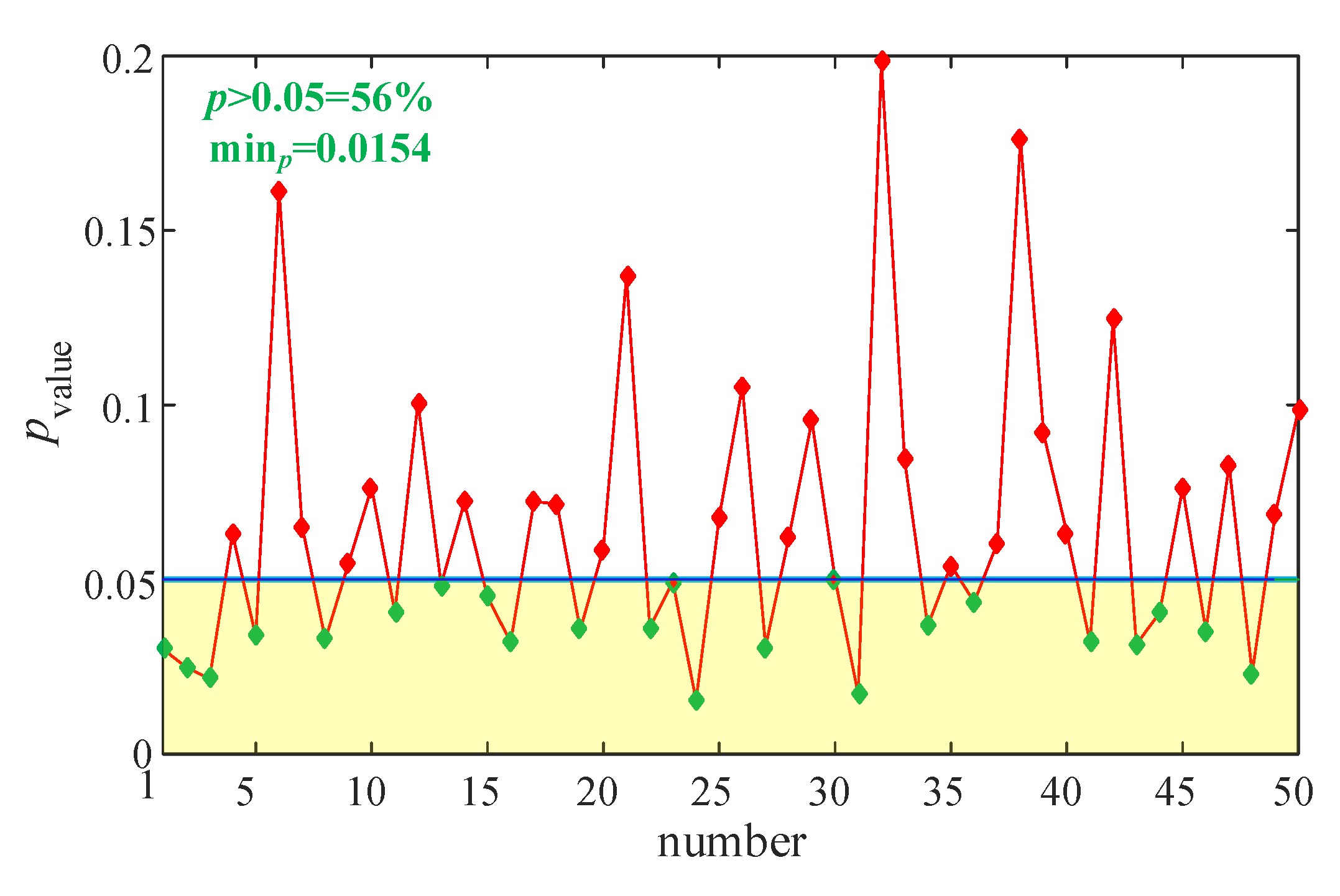
4.2.3. The Necessity of PCA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Redelico, F.O.; Traversaro, F.; García, M.D.C.; Silva, W.; Rosso, O.A.; Risk, M. Classification of Normal and Pre-Ictal EEG Signals Using Permutation Entropies and a Generalized Linear Model as a Classifier. Entropy 2017, 19, 72. [Google Scholar] [CrossRef]
- Tzimourta, K.D.; Afrantou, T.; Ioannidis, P.; Karatzikou, M.; Tzallas, A.T.; Giannakeas, N.; Astrakas, L.G.; Angelidis, P.; Glavas, E.; Grigoriadis, N.; et al. Analysis of electroencephalographic signals complexity regarding Alzheimer’s Disease. Comput. Electr. Eng. 2019, 76, 198–212. [Google Scholar] [CrossRef]
- Namazi, H.; Aghasian, E.; Ala, T.S. Complexity-based classification of EEG signal in normal subjects and patients with epilepsy. Technol. Health Care 2020, 28, 57–66. [Google Scholar] [CrossRef]
- Shi, M.; Zhan, C.; He, H.; Jin, Y.; Wu, R.; Sun, Y.; Shen, B. Renyi distribution entropy analysis of short-term heart rate variability signals and its application in coronary artery disease detection. Front. Physiol. 2019, 10, 809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. Automated diagnosis of atrial fibrillation ECG signals using entropy features extracted from flexible analytic wavelet transform. Biocybern. Biomed. Eng. 2018, 38, 564–573. [Google Scholar] [CrossRef]
- Azami, H.; Arnold, S.E.; Sanei, S.; Chang, Z.; Sapiro, G.; Escudero, J.; Gupta, A.S. Multiscale Fluctuation-Based Dispersion Entropy and Its Applications to Neurological Diseases. IEEE Access 2019, 7, 68718–68733. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, K.; Zhou, G. Asymmetry in Stock Comovements: An Entropy Approach. J. Financ. Quant. Anal. 2017. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J. Transductive Feature Selection Using Clustering-Based Sample Entropy for Temperature Prediction in Weather Forecasting. Entropy 2018, 20, 264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, X.; Shang, P.; Huang, J. Permutation complexity and dependence measures of time series. EPL 2013, 102, 40005. [Google Scholar] [CrossRef]
- Murthy, C.; Srednick, M. Structure of chaotic eigenstates and their entanglement entropy. Phys. Rev. E 2019, 100, 022131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Natiq, H.; Said, M.R.M.; Al-Saidi, N.M.; Kilicman, A. Dynamics and Complexity of a New 4D Chaotic Laser System. Entropy 2019, 21, 34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, Y.; Sun, K.; He, S. Multiscale permutation Rényi entropy and its application for EEG signals. PLoS ONE 2018, 13, e0202558. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.; Peng, C. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Phys. A Stat. Mech. Its Appl. 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y.; Luo, S. A rolling bearing fault diagnosis method based on multi-scale fuzzy entropy and variable predictive model-based class discrimination. Mech. Mach. Theory 2014, 78, 187–200. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar]
- Ye, Y.; Zhang, Y.; Wang, Q.; Wang, Z.; Teng, Z.; Zhang, H. Fault diagnosis of high-speed train suspension systems using multiscale permutation entropy and linear local tangent space alignment. Mech. Sys. Signal Process. 2020, 138, 106565. [Google Scholar] [CrossRef]
- Rezaeezadeh, M.; Shamekhi, S.; Shamsi, M. Attention Deficit Hyperactivity Disorder Diagnosis using non-linear univariate and multivariate EEG measurements: A preliminary study. Phys. Eng. Sci. Med. 2020, 43, 577–592. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wei, S.; Tang, H.; Liu, C. Multivariable fuzzy measure entropy analysis for heart rate variability and heart sound amplitude variability. Entropy 2016, 18, 430. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.U.; Mandic, D. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 84, 061918. [Google Scholar] [CrossRef] [Green Version]
- Mohr, M.; Wilhelm, F.; Hartwig, M.; Möller, R.; Keller, K. New Approaches in Ordinal Pattern Representations for Multivariate Time Series. In Proceedings of the FLAIRS Conference, North Miami Beach, FL, USA, 17–20 May 2020; pp. 124–129. [Google Scholar]
- Duan, R.N.; Zhu, J.Y.; Lu, B. Differential entropy feature for EEG-based emotion classification. In Proceedings of the 2013 6th International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, CA, USA, 6–8 November 2013; Volume 8588, pp. 81–84. [Google Scholar]
- Wang, Q.; Sourina, O. Real-Time Mental Arithmetic Task Recognition From EEG Signals. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 225–232. [Google Scholar] [CrossRef] [PubMed]
- Lim, W.L.; Sourina, O.; Liu, Y.; Wang, L. EEG-based mental workload recognition related to multitasking. In Proceedings of the 2015 10th International Conference on Information, Communications and Signal Processing (ICICS), Singapore, 2–4 December 2015; pp. 1–4. [Google Scholar]
- Chen, T.; Ju, S.; Ren, F.; Fan, M.; Gu, Y. EEG emotion recognition model based on the LIBSVM classifier. Measurement 2020, 164, 108047. [Google Scholar] [CrossRef]
- Chai, R.; Ling, S.H.; San, P.P.; Naik, G.R.; Nguyen, T.N.; Tran, Y.; Craig, A.; Nguyen, H.T. Improving EEG-Based Driver Fatigue Classification Using Sparse-Deep Belief Networks. Front. Neurosci. 2017, 11, 103. [Google Scholar] [CrossRef] [Green Version]
- Billeci, L.; Marino, D.; Insana, L.; Vatti, G.; Varanini, M. Patient-specific seizure prediction based on heart rate variability and recurrence quantification analysis. PLoS ONE 2018, 13, e0204339. [Google Scholar] [CrossRef] [PubMed]
- Deivasigamani, S.; Senthilpari, C.; Yong, W.H. Machine learning method based detection and diagnosis for epilepsy in EEG signal. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 4215–4221. [Google Scholar] [CrossRef]
- Mammone, N.; Duun-Henriksen, J.; Kjaer, T.W.; Morabito, F.C. Differentiating Interictal and Ictal States in Childhood Absence Epilepsy through Permutation Rényi Entropy. Entropy 2015, 17, 4627–4643. [Google Scholar] [CrossRef] [Green Version]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Horgan, J. From Complexity to Perplexity. Sci. Am. 1995, 272, 104–109. [Google Scholar] [CrossRef]
- Larrondo, H.A.; González, C.M.; Martin, M.T.; Plastino, A.; Rosso, O.A. Intensive statistical complexity measure of pseudorandom number generators. Phys. A Stat. Mech. Its Appl. 2005, 356, 133–138. [Google Scholar] [CrossRef]
- Chen, F.; Xu, J.; Gu, F.; Yu, X.; Meng, X.; Qiu, Z. Dynamic process of information transmission complexity in human brains. Biol. Cybern. 2000, 83, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Staniczenko, P.P.A.; Lee, C.; Jones, N. Rapidly detecting disorder in rhythmic biological signals: A spectral entropy measure to identify cardiac arrhythmias. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 011915. [Google Scholar] [CrossRef]
- Pano-Azucena, A.D.; Tlelo-Cuautle, E.; Ovilla-Martinez, B.; Fraga, L.G.D.L.; Li, R. Pipeline FPGA-based Implementations of ANNs for the Prediction of up to 600-steps-ahead of Chaotic Time Series. J. Circuits Syst. Comput. 2020, 2150164. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, A.; Zhang, J.; Zhang, W. A new chaotic feature for EEG classification based seizure diagnosis. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 4651–4655. [Google Scholar]
- Liu, W.; Sun, K.; He, S. SF-SIMM high-dimensional hyperchaotic map and its performance analysis. Nonlinear Dyn. 2017, 89, 2521–2532. [Google Scholar] [CrossRef]
- Sun, K.; Sprott, J. Dynamics of a Simplified Lorenz System. Int. J. Bifurc. Chaos 2009, 19, 1357–1366. [Google Scholar] [CrossRef]
- Guillén-Fernández, O.; Moreno-López, M.F.; Tlelo-Cuautle, E. Issues on Applying One-and Multi-Step Numerical Methods to Chaotic Oscillators for FPGA Implementation. Mathematics 2021, 9, 151. [Google Scholar] [CrossRef]
- Zyma, I.; Tukaev, S.; Seleznov, I.; Kiyono, K.; Popov, A.; Chernykh, M.; Shpenkov, O. Electroencephalograms during Mental Arithmetic Task Performance. Data 2019, 4, 14. [Google Scholar] [CrossRef] [Green Version]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
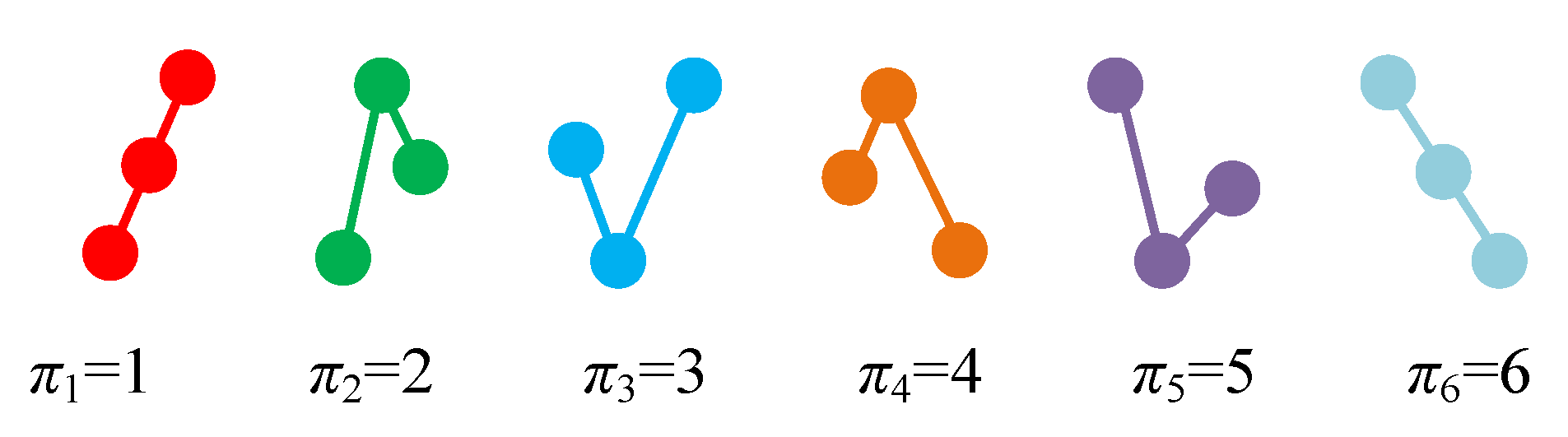







| Method | Characteristic | Advantages | Disadvantages |
|---|---|---|---|
| ApEn [13] SampEn [14] FuzzyEn [15] | Time domain, Phase-space reconstruction Distance between the vectors. | Short time series. | , slow, Not for time series with long length |
| PE [17] | Time domain, Patters from vectors, Shannon entropy. | , Fast. | It cannot detect the periodic state some times, Limited by the patters. |
| Dispersion entropy [16] | Distribution, Patters, Shannon entropy | , fast, Improved version of PE | − |
| Intensive statistical complexity measure [38] | It combines PE algorithm and the probability distribution | , fast, Improved version of PE | Similar as PE algorithm |
| C0 [39] | Frequency domain | FFT, Fast | − |
| Spectral entropy [40] | Frequency domain | Fast; FFT Shannon entropy | − |
| Source | SS | df | MS | F | Prob > F |
|---|---|---|---|---|---|
| Columns | 0.01202 | 1 | 0.01202 | 16.91 | 0.001 |
| Error | 0.04978 | 70 | 0.00071 | ||
| Total | 0.0618 | 71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; He, S.; Sun, K. A Modified Multivariable Complexity Measure Algorithm and Its Application for Identifying Mental Arithmetic Task. Entropy 2021, 23, 931. https://doi.org/10.3390/e23080931
Ma D, He S, Sun K. A Modified Multivariable Complexity Measure Algorithm and Its Application for Identifying Mental Arithmetic Task. Entropy. 2021; 23(8):931. https://doi.org/10.3390/e23080931
Chicago/Turabian StyleMa, Dizhen, Shaobo He, and Kehui Sun. 2021. "A Modified Multivariable Complexity Measure Algorithm and Its Application for Identifying Mental Arithmetic Task" Entropy 23, no. 8: 931. https://doi.org/10.3390/e23080931
APA StyleMa, D., He, S., & Sun, K. (2021). A Modified Multivariable Complexity Measure Algorithm and Its Application for Identifying Mental Arithmetic Task. Entropy, 23(8), 931. https://doi.org/10.3390/e23080931







