Cities on the Coast and Patterns of Movement between Population Growth and Diffusion
Abstract
:1. Introduction
2. Methods
2.1. Strengths and Weaknesses of Urban Modeling Approaches
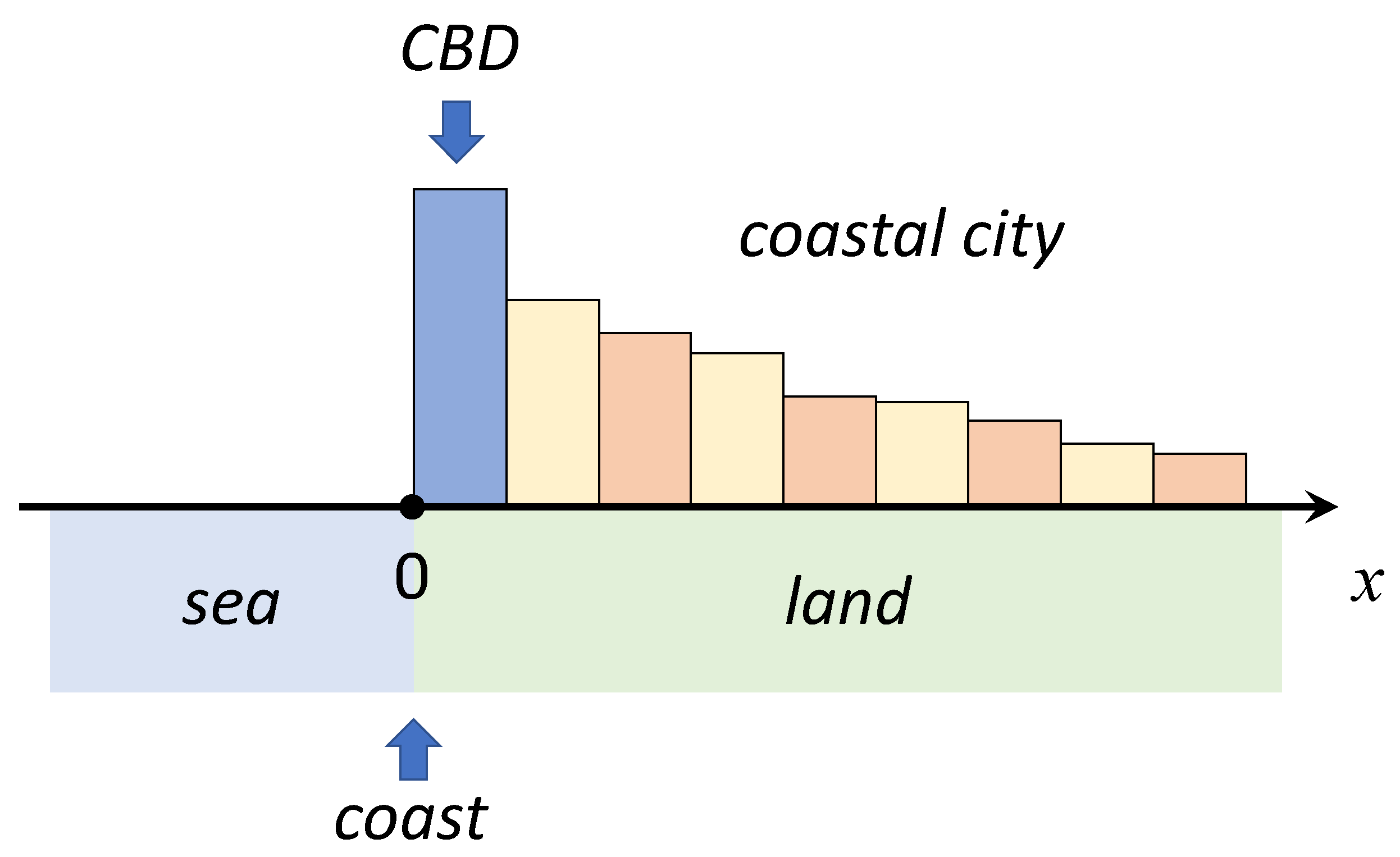
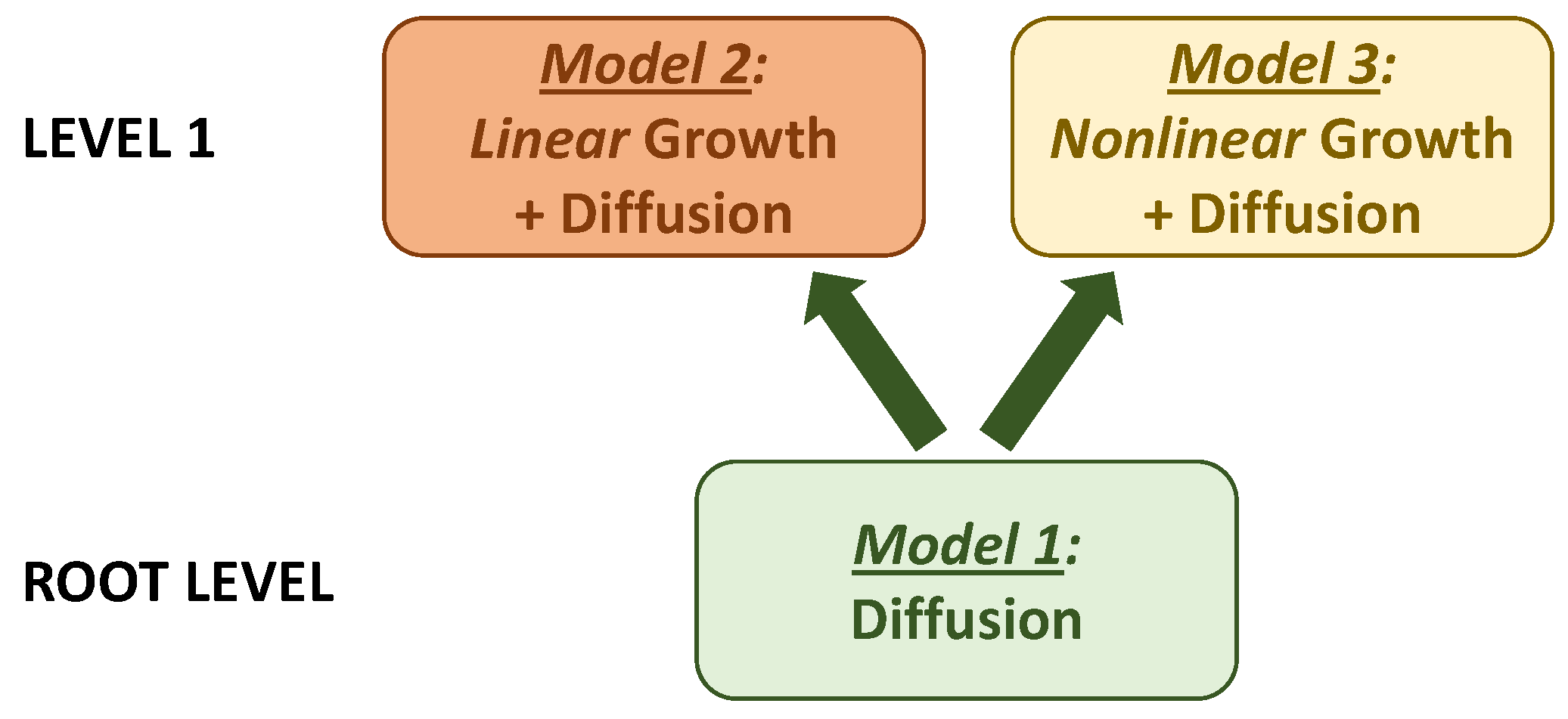
2.2. Modeling the Coastal Urban Dynamics within the Growth-Diffusion Framework
- Model 1: The simple diffusion model, viz.,
- Model 2: The exponential growth-diffusion model, viz.,where r is the population growth rate; and, finally,
- Model 3: the logistic growth-diffusion model, viz.,
3. Results
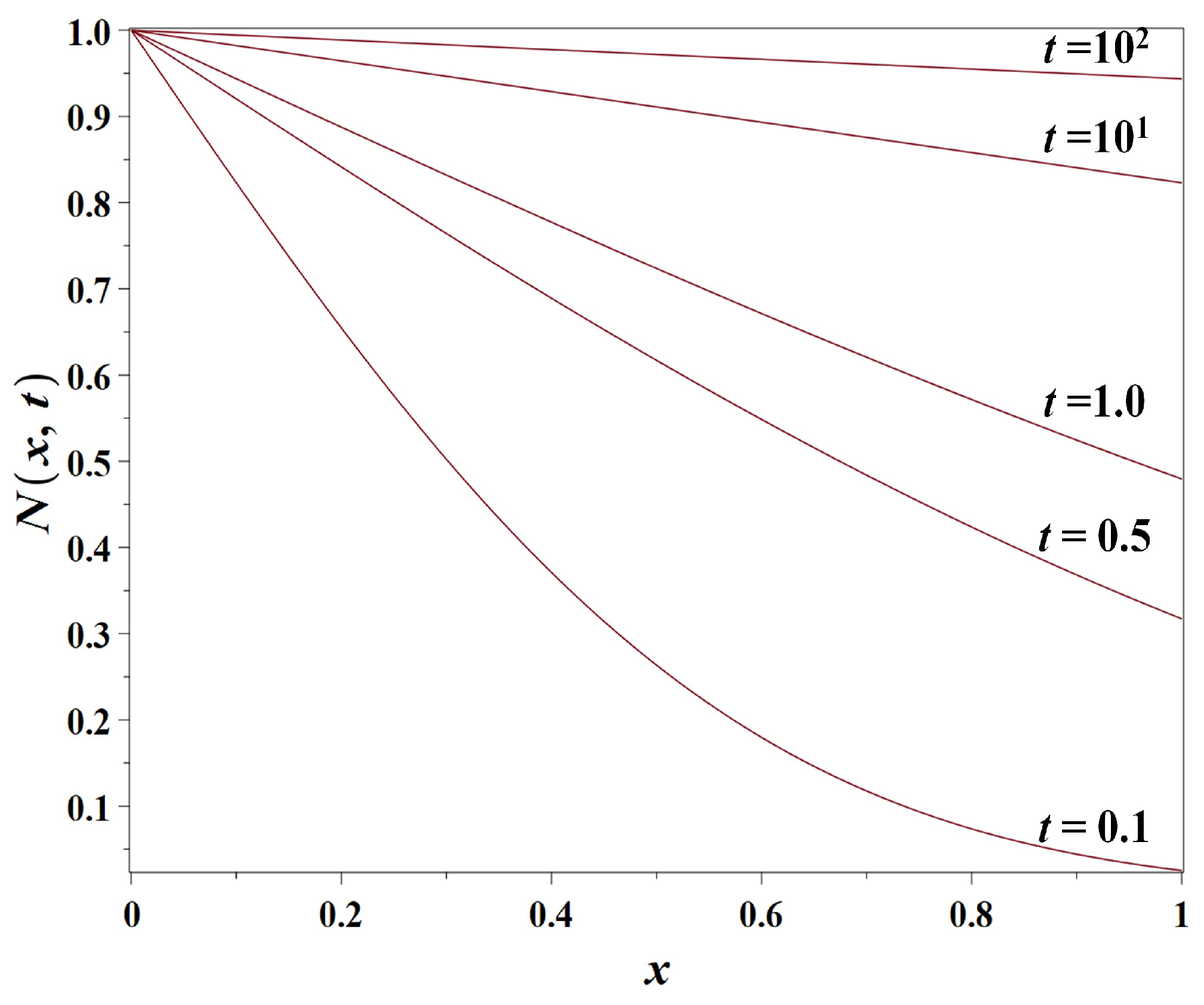
3.1. Model 1: The Simple Diffusion Model
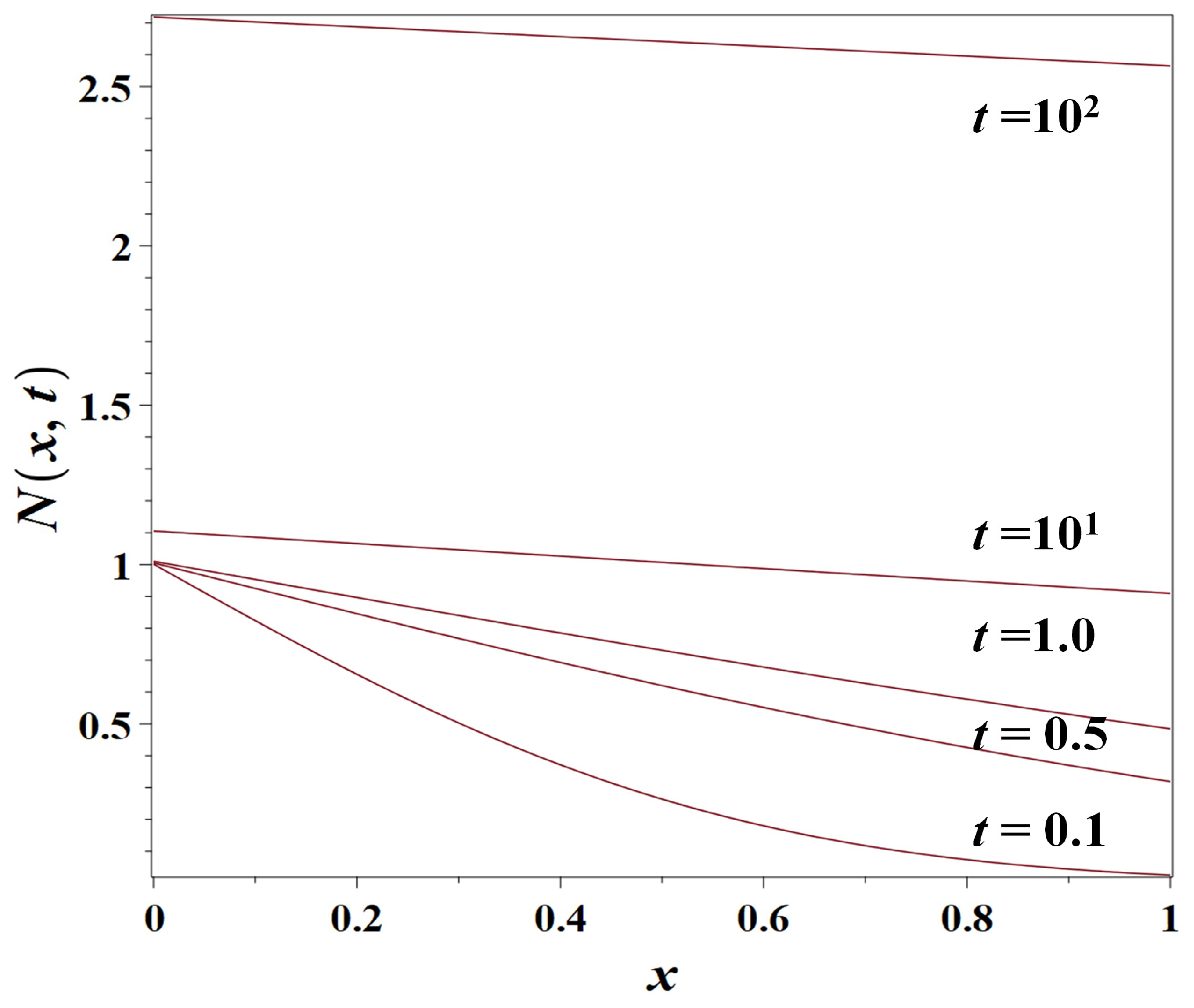
3.2. Model 2: The Exponential Growth-Diffusion Model
3.2.1. Reduction to the Simple Diffusion Model
3.2.2. ‘Synchronized’ Boundary Condition
3.2.3. Constraining the Growth in the Central Business District
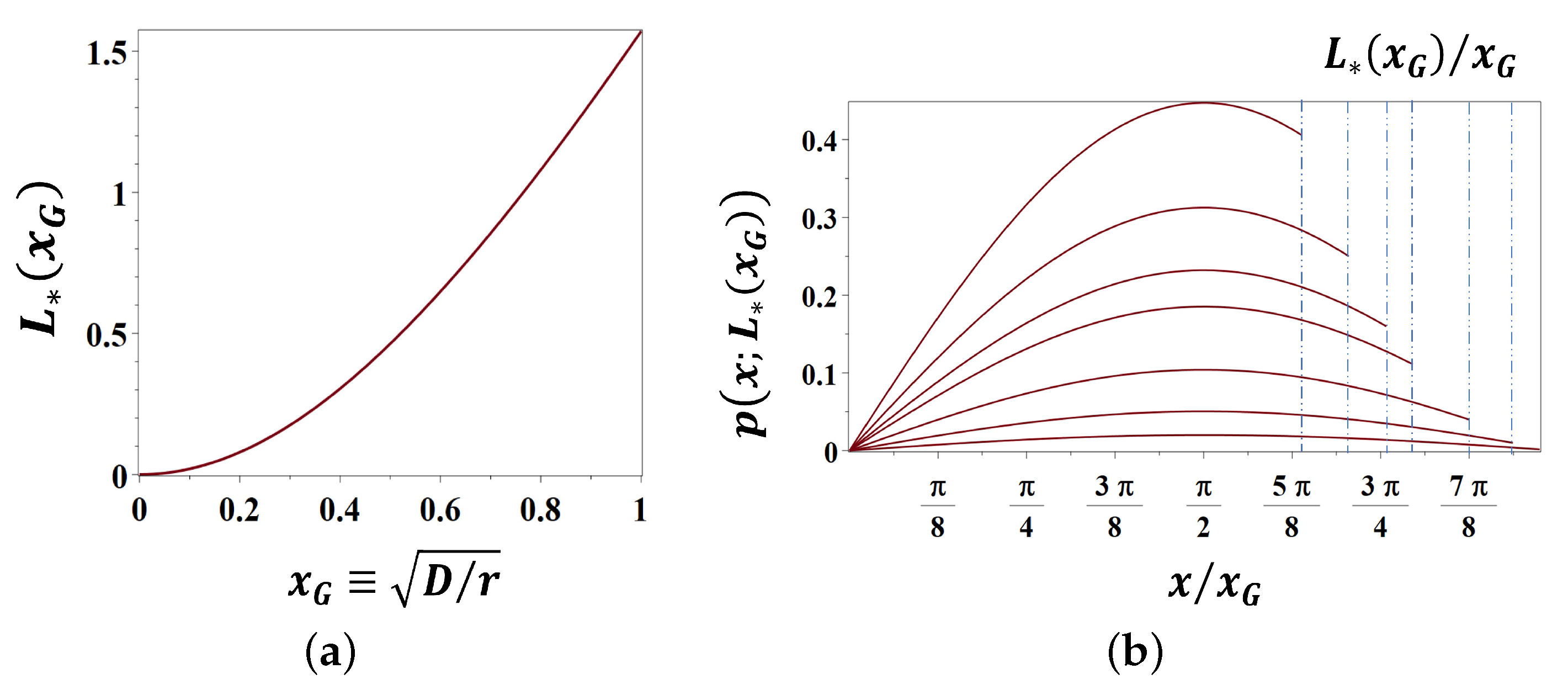
3.2.4. Steady-State Wave Solutions in a Coastal Band
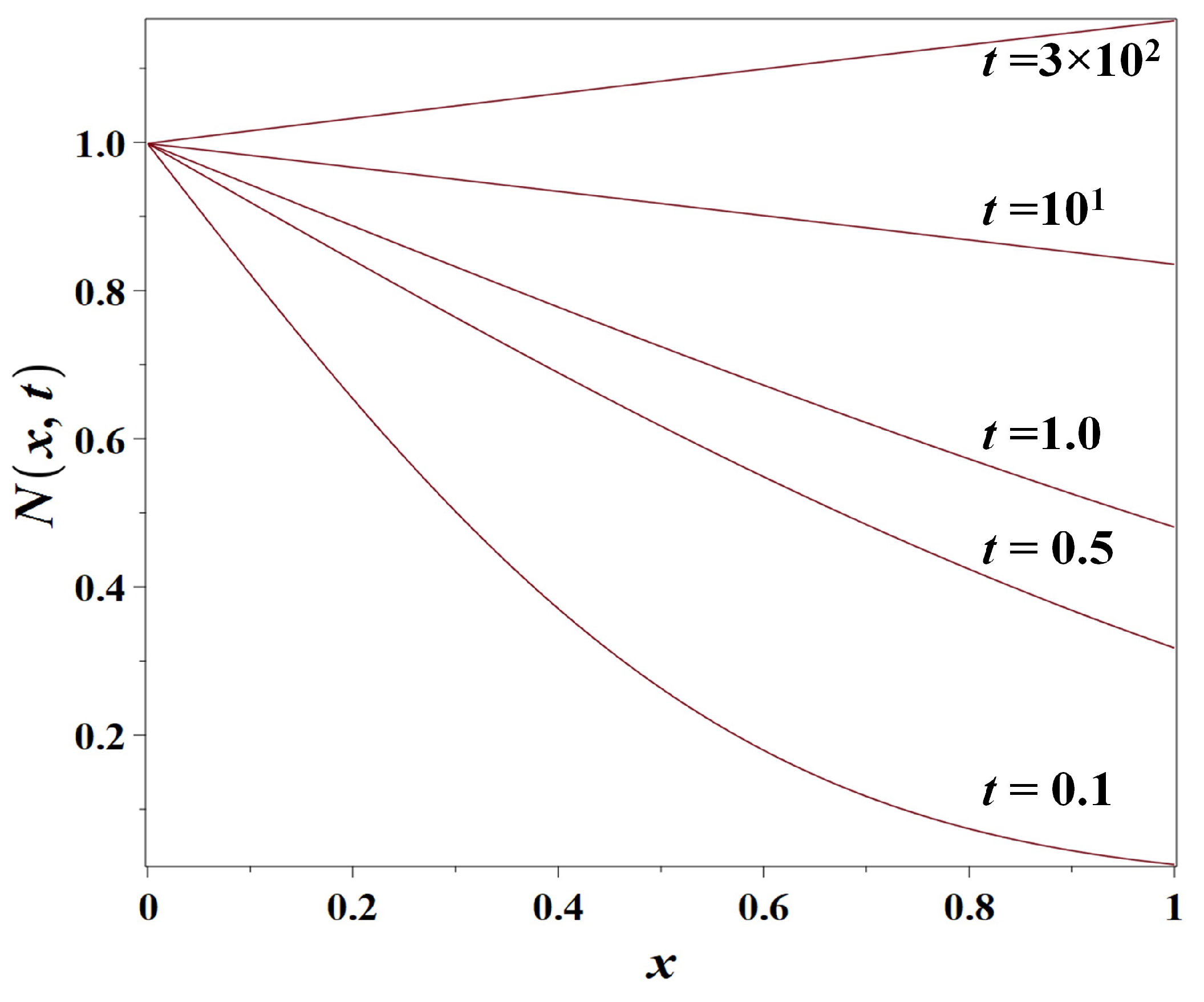
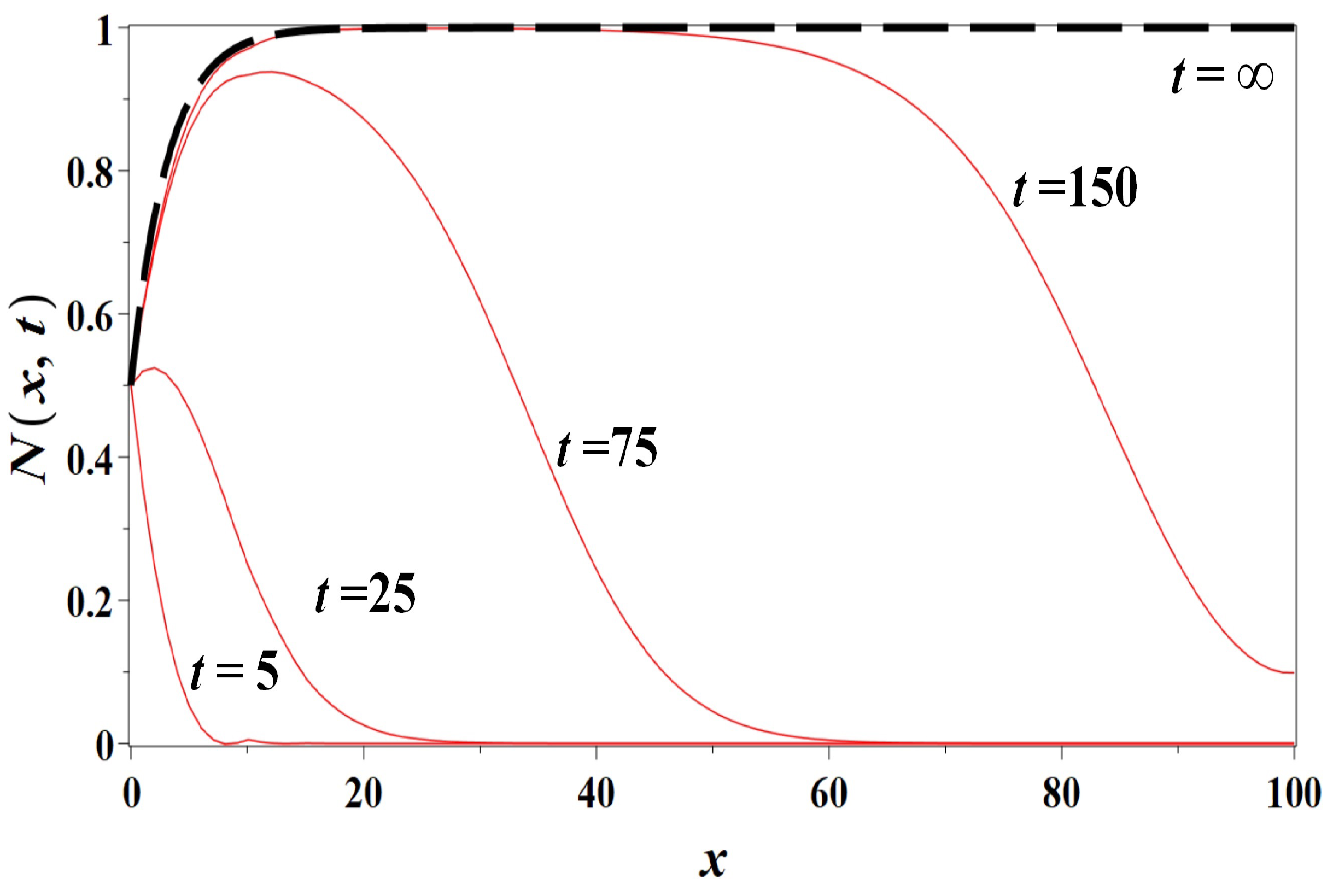
3.3. Model 3: The Logistic Growth-Diffusion Model
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D | one-dimensional |
| 2D | two-dimensional |
| ABM | agent-based modeling |
| AI | artificial intelligence |
| ANN | artificial neural network |
| CA | cellular automata |
| CBD | central business district |
| GIS | geographic information system |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
| probability density function | |
| SD | system dynamics |
Appendix A. Derivation of Total Urban Population for the Simple Diffusion Model (Model 1)
Appendix B. Derivation of the Expected Living Location and the Second Moment for the Simple Diffusion Model (Model 1)
Appendix C. Derivation of Solution for the Exponential Growth-Diffusion Model (Model 2, Case of Regulated Central Business District)
Appendix D. Total Urban Population for the Exponential Growth-Diffusion Model (Model 2, Case of Regulated Central Business District)
Appendix E. Derivation of the Stationary Solution in the Logistic Growth-Diffusion Model (Model 3)
Appendix F. Approximate Stationary Solution in the Logistic Growth-Diffusion Model (Model 3)
References
- Smith, K. We are seven billion. Nat. Clim. Chang. 2011, 1, 331–335. [Google Scholar] [CrossRef]
- Brown, S.; Nicholls, R.J.; Goodwin, P.; Haigh, I.D.; Lincke, D.; Vafeidis, A.T.; Hinkel, J. Quantifying land and people exposed to sea-level rise with no mitigation and 1.5 °C and 2.0 °C rise in global temperatures to year 2300. Earths Future 2018, 6, 583–600. [Google Scholar] [CrossRef]
- McMichael, C.; Dasgupta, S.; Ayeb-Karlsson, S.; Kelman, I. A review of estimating population exposure to sea-level rise and the relevance for migration. Environ. Res. Lett. 2020, 15, 123005. [Google Scholar] [CrossRef] [PubMed]
- World Bank. U.S. GDP 2005–2013. Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.CD?end=2013&start=2005&year_high_desc=true (accessed on 31 May 2021).
- Total Economy of Coastal Areas (NOAA). NOAA Office for Coastal Management, Bureau of Labor Statistics, Bureau of Economic Analysis. Available online: https://coast.noaa.gov/digitalcoast/data/coastaleconomy.html (accessed on 31 May 2021).
- Guaralda, M.; Hearn, G.; Foth, M.; Yigitcanlar, T.; Mayere, S.; Law, L. Towards Australian regional turnaround: Insights into sustainably accommodating post-pandemic urban growth in regional towns and cities. Sustainability 2020, 12, 10492. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef] [Green Version]
- Intergovernmental Panel on Climate Change. Climate Change 2014—Impacts, Adaptation and Vulnerability: Part A: Global and Sectoral Aspects: Working Group II Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef] [Green Version]
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Guillén Bolaños, T.; Bindi, M.; Brown, S.; Camilloni, I.A.; Diedhiou, A.; Djalante, R.; Ebi, K.; et al. The human imperative of stabilizing global climate change at 1.5 °C. Science 2019, 365, eaaw6974. [Google Scholar] [CrossRef] [Green Version]
- Jacob, D.; Kotova, L.; Teichmann, C.; Sobolowski, S.P.; Vautard, R.; Donnelly, C.; Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Damm, A.; et al. Climate impacts in Europe under +1.5 °C global warming. Earths Future 2018, 6, 264–285. [Google Scholar] [CrossRef] [Green Version]
- Pfeifer, S.; Rechid, D.; Reuter, M.; Viktor, E.; Jacob, D. 1.5°, 2°, and 3° global warming: Visualizing European regions affected by multiple changes. Reg. Environ. Chang. 2019, 19, 1777–1786. [Google Scholar] [CrossRef] [Green Version]
- Teichmann, C.; Bülow, K.; Otto, J.; Pfeifer, S.; Rechid, D.; Sieck, K.; Jacob, D. Avoiding extremes: Benefits of staying below +1.5 °C compared to +2.0 °C and +3.0 °C global warming. Atmosphere 2018, 9, 115. [Google Scholar] [CrossRef] [Green Version]
- Weber, T.; Haensler, A.; Rechid, D.; Pfeifer, S.; Eggert, B.; Jacob, D. Analyzing regional climate change in Africa in a 1.5, 2, and 3 °C global warming world. Earths Future 2018, 6, 643–655. [Google Scholar] [CrossRef]
- Smirnov, V.; Ma, Z.; Volchenkov, D. Extreme events and emergency scales. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105350. [Google Scholar] [CrossRef]
- Maribus gGmbH. World Ocean Review 1, Living with the Oceans. A Report on the State of the World’s Oceans, Chapter 3: The Uncertain Future of the Coasts; Maribus gGmbH: Hamburg, Germany, 2010; Available online: https://www.unep.org/resources/report/world-ocean-review-1-living-oceans-report-state-worlds-oceans (accessed on 12 August 2021)ISBN 978-3-86648-012-4.
- Rosenzweig, C.; Solecki, W.; Romero-Lankao, P.; Mehrotra, S.; Dhakal, S.; Ali Ibrahim, S. (Eds.) Climate Change and Cities: Second Assessment Report of the Urban Climate Change Research Network; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Cortekar, J.; Bender, S.; Brune, M.; Groth, M. Why climate change adaptation in cities needs customised and flexible climate services. Clim. Serv. 2016, 4, 42–51. [Google Scholar] [CrossRef] [Green Version]
- Koldunov, N.V.; Kumar, P.; Rasmussen, R.; Ramanathan, A.L.; Nesje, A.; Engelhardt, M.; Tewari, M.; Haensler, A.; Jacob, D. Identifying climate change information needs for the Himalayan Region: Results from the GLACINDIA Stakeholder Workshop and Training Program. Bull. Am. Meteorol. Soc. 2016, 97, ES37–ES40. [Google Scholar] [CrossRef] [Green Version]
- Preuschmann, S.; Hänsler, A.; Kotova, L.; Dürk, N.; Eibner, W.; Waidhofer, C.; Haselberger, C.; Jacob, D. The IMPACT2C web-atlas—Conception, organization and aim of a web-based climate service product. Clim. Serv. 2017, 7, 115–125. [Google Scholar] [CrossRef]
- van den Hurk, B.J.J.M.; Bouwer, L.M.; Buontempo, C.; Döscher, R.; Ercin, E.; Hananel, C.; Hunink, J.E.; Kjellström, E.; Klein, B.; Manez, M.; et al. Improving predictions and management of hydrological extremes through climate services: www.imprex.eu. Clim. Serv. 2016, 1, 6–11. [Google Scholar] [CrossRef]
- Rölfer, L.; Winter, G.; Máñez Costa, M.; Celliers, L. Earth observation and coastal climate services for small islands. Clim. Serv. 2020, 18, 100168. [Google Scholar] [CrossRef]
- Williams, D.S.; Máñez Costa, M.; Celliers, L.; Sutherland, C. Informal settlements and flooding: Identifying strengths and weaknesses in local governance for water management. Water 2018, 10, 871. [Google Scholar] [CrossRef] [Green Version]
- Meadows, D.; Randers, J.; Meadows, D. Limits to Growth: The 30-Year Update; Chelsea Green Publishing Co.: White River Junction, VT, USA, 2004. [Google Scholar]
- Fiddaman, T. Dynamics of climate policy. Syst. Dyn. Rev. 2007, 23, 21–34. [Google Scholar] [CrossRef]
- Hallegatte, S.; Ghil, M. Natural disasters impacting a macroeconomic model with endogenous dynamics. Ecol. Econ. 2008, 68, 582–592. [Google Scholar] [CrossRef] [Green Version]
- Kellie-Smith, O.; Cox, P.M. Emergent dynamics of the climate-economy system in the Anthropocene. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2011, 369, 868–886. [Google Scholar] [CrossRef] [Green Version]
- Herold, M.; Goldstein, N.; Clarke, K. The spatio-temporal form of urban growth: Measurement, analysis and modeling. Remote Sens. Environ. 2003, 85, 95–105. [Google Scholar] [CrossRef]
- Hasselmann, K. Detecting and responding to climate change. Tellus Chem. Phys. Meteorol. 2013, 65, 20088. [Google Scholar] [CrossRef] [Green Version]
- Hasselmann, K.; Kovalevsky, D.V. Simulating animal spirits in actor-based environmental models. Environ. Model. Softw. 2013, 44, 10–24. [Google Scholar] [CrossRef]
- Hasselmann, K.; Cremades, R.; Filatova, T.; Hewitt, R.; Jaeger, C.; Kovalevsky, D.; Voinov, A.; Winder, N. Free-riders to forerunners. Nat. Geosci. 2015, 8, 895–898. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Cellular-automata and fractal urban form—A cellular modeling approach to the evolution of urban land-use patterns. Environ. Plan A 1993, 25, 1175–1199. [Google Scholar] [CrossRef] [Green Version]
- White, R.; Engelen, G. Cellular automata as the basis of integrated dynamic regional modeling. Environ. Plan B 1997, 24, 235–246. [Google Scholar] [CrossRef]
- Cechini, A. Urban modeling by means of cellular automata: Generalised urban automata with the help on-line (AUGH) model. Environ. Plan B 1996, 23, 721–732. [Google Scholar] [CrossRef]
- Sanders, L.; Pumain, D.; Mathian, H.; Guérin-Pace, F.; Bura, S. A multiagent system for the study of urbanism. Environ. Plan B 1997, 24, 287–305. [Google Scholar] [CrossRef] [Green Version]
- Benati, S. A cellular automaton for the simulation of competitive location. Environ. Plan B 1997, 24, 205–218. [Google Scholar] [CrossRef]
- Batty, M.; Shie, Y.; Sun, Z. Modeling urban dynamics through GIS-based cellular automata. Comput. Environ. Urban 1999, 23, 205–233. [Google Scholar] [CrossRef] [Green Version]
- Clarke, K.; Gaydos, L. Loose-coupling a cellular automaton model and GIS: Longterm urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci. 1998, 12, 699–714. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Yeh, A. modeling sustainable urban development by the integration of constrained cellular automata and GIS. Int. J. Geogr. Inform. Sci. 2000, 14, 131–152. [Google Scholar] [CrossRef]
- Solecki, W.D.; Oliveri, C. Downscaling climate change scenarios in an urban land use change model. J. Environ. Manag. 2004, 72, 105–115. [Google Scholar] [CrossRef]
- Hewitt, R.; van Delden, H.; Escobar, F. Participatory land use modeling, pathways to an integrated approach. Environ. Model. Softw. 2014, 52, 149–165. [Google Scholar] [CrossRef]
- Batty, M.; Desyllas, J.; Duxbury, E. The discrete dynamics of small-scale spatial events: Agent-based models of mobility in carnivals and street parades. Int. J. Geogr. Inf. Sci. 2003, 17, 673–697. [Google Scholar] [CrossRef]
- Parker, D.; Berger, T.; Manson, S. Agent-Based Models of Land-Use and Land-Cover Change; LUCC International Project Office: Louvain-la-Neuve, Belgium, 2001; Volume 6. [Google Scholar]
- Filatova, T.; Verburg, P.H.; Parker, D.C.; Stannard, C.A. Spatial agent-based models for socio-ecological systems: Challenges and prospects. Environ. Model. Softw. 2013, 45, 1–7. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, J.M.; Schickhoff, M.; Sengupta, S.; Scheffran, J. Technological and social networks of a pastoralist artificial society: Agent-based modeling of mobility patterns. J. Comput. Soc. Sc. 2021, 1–27. [Google Scholar] [CrossRef]
- Scheffran, J. Conflict and cooperation in energy and climate change: The framework of a dynamic game of power-value interaction. In Jahrbuch für Neue Politische Ökonomie. Band 20: Power and Fairness; Holler, M.J., Kliemt, H., Schmidtchen, D., Streit, M.E., Eds.; Mohr Siebeck: Tübingen, Germany, 2002; pp. 229–254. [Google Scholar]
- Scheffran, J. Adaptive management of energy transitions in long-term climate change. Comput. Manag. Sci. 2008, 5, 259–286. [Google Scholar] [CrossRef]
- BenDor, T.K.; Scheffran, J. Agent-Based Modeling of Environmental Conflict and Cooperation; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2019; 363p. [Google Scholar]
- Nordhaus, W.D. A Question of Balance; Yale University Press: London, UK, 2008. [Google Scholar]
- Tang, Z.; Engel, A.; Pijanowski, B.; Lim, J. Forecasting land use change and its environmental impact at a watershed scale. J. Environ. Manag. 2005, 76, 35–45. [Google Scholar] [CrossRef]
- Medeiros, R.; Cabral, P. Dynamic modeling of urban areas for supporting integrated coastal zone management in the South Coast of São Miguel Island, Azores (Portugal). J. Coast. Conserv. 2013, 17, 805–811. [Google Scholar] [CrossRef]
- USGS Is a Primary Source of Geographic Information Systems (GIS). Available online: https://www.usgs.gov/products/data-and-tools/gis-data (accessed on 12 August 2021).
- Pijanowski, B.; Shellito, B.; Bauer, M.; Sawaya, K. Using GIS, Artificial Neural Networks and Remote Sensing to model urban change in the Minneapolis-St. Paul and Detroit metropolitan areas. In Proceedings of the ASPRS Proceedings, St. Louis, MO, USA, 21–26 April 2001. [Google Scholar]
- Pijanowski, B.; Pithadia, S.; Shellito, B.; Alexandridis, K. Calibrating a neural network-based urban change model for two metropolitan areas of the Upper Midwest of the United States. Int. J. Geogr. Inf. Sci. 2005, 19, 197–215. [Google Scholar] [CrossRef]
- Ray, D.; Pijanowski, B. A backcast land use change model to generate past land use maps: Application and validation at the Muskegon River watershed of Michigan, USA. J. Land Use Sci. 2010, 5, 1–29. [Google Scholar] [CrossRef]
- Baker, W. A review of models of landscape change. Landsc. Ecol. 1989, 2, 111–133. [Google Scholar] [CrossRef]
- Agarwal, C.; Green, G.; Grove, J.; Evans, T.; Schweik, C. A Review and Assessment of Land-Use Change Models: Dynamics of Space, Time, and Human Choice; NE-297; United States Department of Agriculture: Washington, DC, USA, 2000. [Google Scholar]
- EPA. Projecting Land-Use Change: A Summary of Models for Assessing the Effects of Community Growth and Change on Land-Use Patterns; EPA/600/R-00/098; Environmental Protection Agency: Washington, DC, USA, 2000.
- Pontius, R.; Malanson, J. Comparison of the structure and accuracy of two land change models. Int. J. Geogr. Inf. Sci. 2005, 19, 243–265. [Google Scholar] [CrossRef]
- Pijanowski, B.; Shellito, B.; Pithadia, S.; Konstantinos, A. Forecasting and assessing the impact of urban sprawl in coastal watersheds along eastern Lake Michigan. Lakes Reserv. Res. Manag. 2002, 7, 271–285. [Google Scholar] [CrossRef] [Green Version]
- Wu, F. An emprirical model of intra-metropolitan land-use changes in a Chinese city. Environ. Plan B 1998, 25, 245–263. [Google Scholar] [CrossRef]
- Wu, F.; Webster, C. Simulating artificial cities in a GIS environment: Urban growth under alternative regulation regimes. Int. J. Geogr. Inf. Sci. 2000, 14, 625–648. [Google Scholar] [CrossRef]
- Veldkamp, A.; Fresco, L. CLUE: A conceptual model to study the conversion of land use and its effects. Ecol. Model 1996, 85, 253–270. [Google Scholar] [CrossRef]
- Forrester, J.W. Urban Dynamics; MIT Press: Cambridge, MA, USA, 1969; 290p. [Google Scholar]
- Benenson, I.; Torrens, P.M. Geosimulation: Automata-Based Modeling of Urban Phenomena; Wiley: Hoboken, NJ, USA, 2004; Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/0470020997 (accessed on 12 August 2021).
- Kovalevsky, D.; Scheffran, J. Coastal cities affected by sea level rise and Forrester’s ‘Urban Dynamics’. In Proceedings of the 12. Deutsche Klimatagung, Online, 15–18 March 2021. DKT-12-14. [Google Scholar] [CrossRef]
- Sekovski, I.; Armaroli, C.; Calabrese, L.; Mancini, F.; Stecchi, F.; Perini, L. Coupling scenarios of urban growth and flood hazards along the Emilia-Romagna coast (Italy). Nat. Hazards Earth Syst. Sci. 2015, 15, 2331–2346. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Fu, X.; Gu, Y.; Deng, Y.; Peng, Z.-R. An examination of land use impacts of flooding induced by sea level rise. Nat. Hazards Earth Syst. Sci. 2017, 17, 315–334. [Google Scholar] [CrossRef] [Green Version]
- Filatova, T.; Parker, D.; van der Veen, A. Agent-based urban land markets: Agent’s pricing behavior, land prices and urban land use change. J. Artif. Soc. Soc. Simul. 2009, 12, 3. Available online: http://jasss.soc.surrey.ac.uk/12/1/3.html (accessed on 12 August 2021).
- von Szombathely, M.; Albrecht, M.; Antanaskovic, D.; Augustin, J.; Augustin, M.; Bechtel, B.; Bürk, T.; Fischereit, J.; Grawe, D.; Hoffmann, P.; et al. A conceptual modeling approach to health-related urban well-being. Urban Sci. 2017, 1, 17. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.E.; Scheffran, J.; Süsser, D.; Dawson, R.; Chen, Y.D. Assessment of flood losses with household responses: Agent-based simulation in an urban catchment area. Environ. Model. Assess. 2018, 23, 369–388. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.E.; Chan, F.K.S.; Scheffran, J. Climate change, water management and stakeholder analysis in the Dongjiang River basin in South China. Int. J. Water Resour. Dev. 2018, 34, 166–191. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, S.; Scheffran, J.; Kovalevsky, D. A Single-Agent Urban Coastal Adaptation Model: Adaptive decision-making within the VIABLE modeling framework. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. EGU21-12752. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Landry, C.E.; Smith, M.D.; Whitehead, J.C. Economics of coastal erosion and adaptation to sea level rise. Annu. Rev. Resour. Econ. 2016, 8, 119–139. [Google Scholar] [CrossRef]
- Kovalevsky, D.; Scheffran, J. A coastal urban adaptation model with time-discounting, optimizing and satisficing decision making. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. EGU21-12228. [Google Scholar] [CrossRef]
- Blanchard, P.; Volchenkov, D. Markov Chain Methods For Analyzing Urban Networks. J. Stat. Phys. 2008, 132, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, P.; Volchenkov, D. Intelligibility and first passage times in complex urban networks. Proc. R. Soc. A 2008, 464, 2153–2167. [Google Scholar] [CrossRef]
- Blanchard, P.; Volchenkov, D. Mathematical Analysis of Urban Spatial Networks; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Volchenkov, D.; Smirnov, V. The City of Lubbock is Running Away. Integration and Isolation Patterns in the Wandering City. J. Vib. Test. Syst. Dyn. 2019, 3, 121–132. [Google Scholar] [CrossRef]
- Volchenkov, D. Assessing Complexity of Urban Spatial Networks. In The Mathematics of Urban Morphology. Modeling and Simulation in Science, Engineering and Technology; D’Acci, L., Ed.; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-12380-2. [Google Scholar] [CrossRef]
- Müller, I. A History of Thermodynamics: The Doctrine of Energy and Entropy; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Roos, N. Entropic forces in Brownian motion. Am. J. Phys. 2014, 82, 1161–1166. [Google Scholar] [CrossRef] [Green Version]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171. [Google Scholar] [CrossRef]
- Hernando, A.; Hernando, R.; Plastino, A.; Plastino, A.R. The workings of the maximum entropy principle in collective human behavior. J. R. Soc. Interface 2012, 10, 20120758. [Google Scholar] [CrossRef] [Green Version]
- Volchenkov, D. Survival under Uncertainty: An Introduction to Probability Models of Social Structure and Evolution; Springer: Berlin/Heidelberg, Germany, 2016; 240p, ISBN 978-3-319-39419-0. [Google Scholar]
- Wilson, A.G. Entropy in Urban and Regional Modeling; Pion: London, UK, 1970. [Google Scholar]
- Gould, P. Pedagogic Review. Ann. Assoc. Am. Geogr. 1972, 62, 689–700. [Google Scholar] [CrossRef]
- Haggett, P.; Cliff, A.D.; Frey, A. Locational Analysis in Human Geography, Volume 1: Locational Models; Edward Arnold: London, UK, 1977; 605p. [Google Scholar]
- Tobler, W. Cellular geography. In Philosophy in Geography; Gale, S., Olsson, G., Eds.; Reidel: Dortrecht, The Netherlands, 1979; pp. 379–386. [Google Scholar]
- Casti, J.L. ‘Biologizing’ control theory: How to make a control system come alive. Complexity 2002, 4, 10–12. [Google Scholar] [CrossRef]
- Kortschak, D.; Perrels, A. Opportunities for Tool-Assisted Decision Support: The Cases for Energy, Transport and Tourism. Available online: http://www.topdad.eu/upl/files/98433 (accessed on 12 August 2021).
- Emmerling, J.; Drouet, L.; van der Wijst, K.-I.; van Vuuren, D.; Bosetti, V.; Tavoni, M. The role of the discount rate for emission pathways and negative emissions. Environ. Res. Lett. 2019, 14, 104008. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Kramer, L.; Riecke, H. Effects of boundaries on one-dimensional reaction-diffusion equations near threshold. Phys. D Nonlinear Phenom. 1985, 15, 402–420. [Google Scholar] [CrossRef]
- Skellam, J.G. Random dispersal in theoretical populations. Biometrika 1951, 38, 196–218. [Google Scholar] [CrossRef]
- Andow, D.A.; Kareiva, P.M.; Levin, S.A.; Okubo, A. Spread of invading organisms. Landsc. Ecol. 1990, 4, 177–188. [Google Scholar] [CrossRef]
- O’Neill, W. Estimation of a logistic growth and diffusion model describing neighborhood change. J. Geogr. Anal. 1981, 13, 206–224. [Google Scholar] [CrossRef]
- Chapman, E.J.; Byron, C.J. The flexible application of carrying capacity in ecology. Glob. Ecol. Conserv. 2018, 13, e00365. [Google Scholar] [CrossRef]
- Smirnov, V.I. A Course of Higher Mathematics, Volume 2: Advanced Calculus; Pergamon Press: Oxford, NY, USA, 1964; 632p. [Google Scholar]
- Hasselmann, K. Simulating Human Behavior in Macroeconomic Models Applied to Climate Change. In Proceedings of the Dahlem Conference ‘Is There a Mathematics of Social Entities’, Berlin, Germany, 14–19 December 2008; ECF Working Paper 3/2009. Available online: https://globalclimateforum.org/fileadmin/ecf-documents/publications/ecf-working-papers/hasselmann__simultating-human-behavior-in-macroeconomic-models-applied-to-climate-change.pdf (accessed on 12 August 2021).
- United Nations System-Wide Earthwatch, Oceans and Coastal Areas. Available online: http://earthwatch.unep.net/oceans/coastalthreats.php (accessed on 20 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalevsky, D.V.; Volchenkov, D.; Scheffran, J. Cities on the Coast and Patterns of Movement between Population Growth and Diffusion. Entropy 2021, 23, 1041. https://doi.org/10.3390/e23081041
Kovalevsky DV, Volchenkov D, Scheffran J. Cities on the Coast and Patterns of Movement between Population Growth and Diffusion. Entropy. 2021; 23(8):1041. https://doi.org/10.3390/e23081041
Chicago/Turabian StyleKovalevsky, Dmitry V., Dimitri Volchenkov, and Jürgen Scheffran. 2021. "Cities on the Coast and Patterns of Movement between Population Growth and Diffusion" Entropy 23, no. 8: 1041. https://doi.org/10.3390/e23081041
APA StyleKovalevsky, D. V., Volchenkov, D., & Scheffran, J. (2021). Cities on the Coast and Patterns of Movement between Population Growth and Diffusion. Entropy, 23(8), 1041. https://doi.org/10.3390/e23081041







