Secret Communication Systems Using Chaotic Wave Equations with Neural Network Boundary Conditions
Abstract
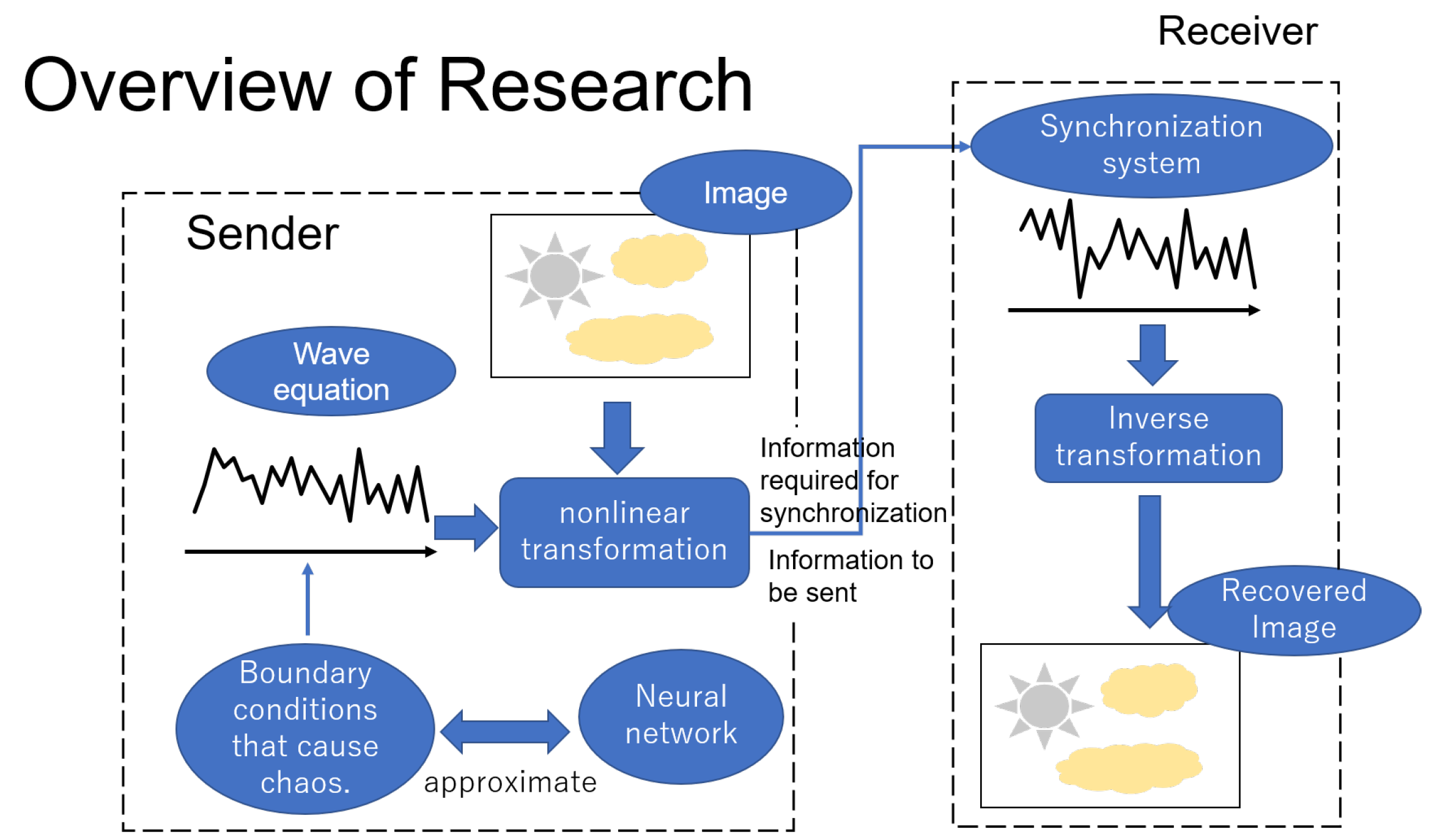
1. Introduction
2. Grayscale Images as Transmission Objects
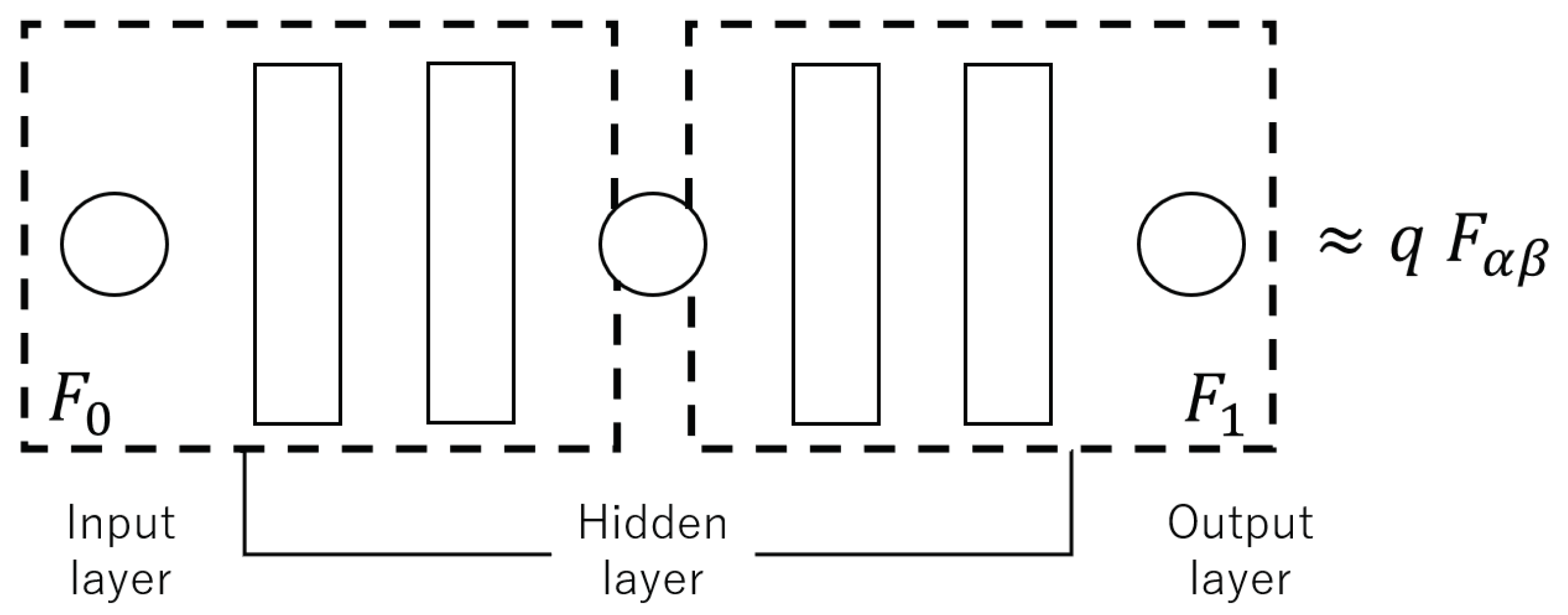
2.1. Wave Equation with the van der Pol Boundary Conditions
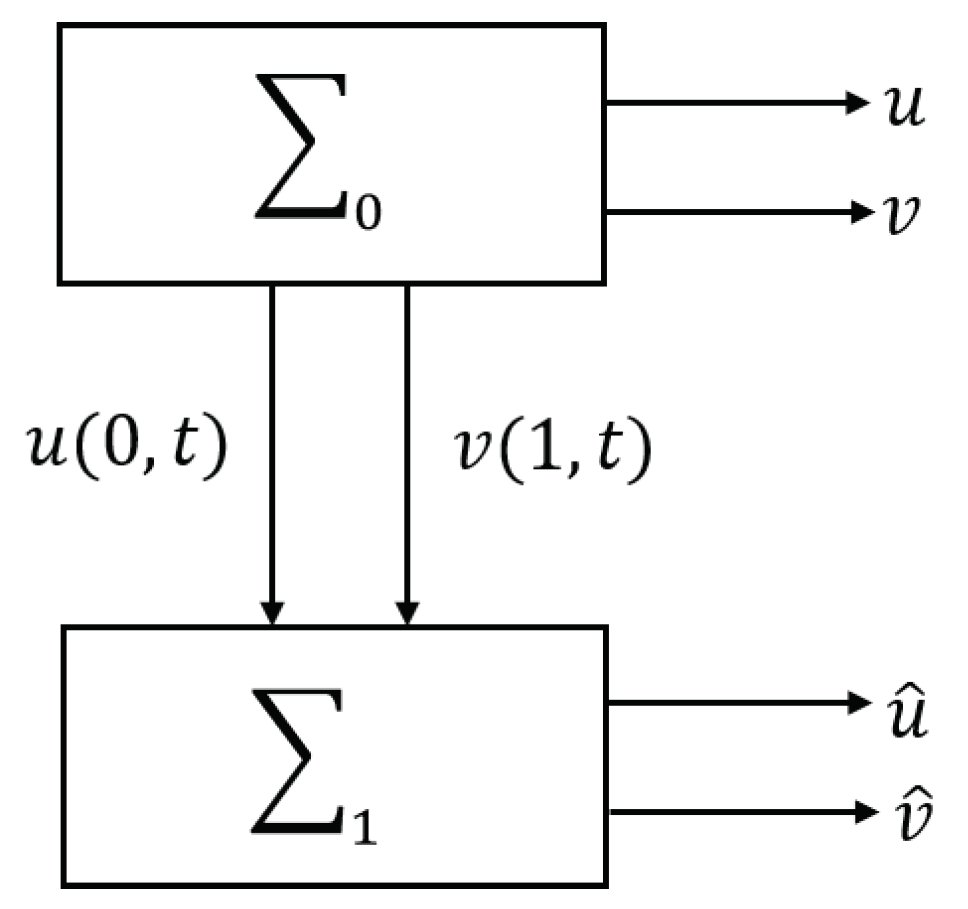
2.2. Synchronization System
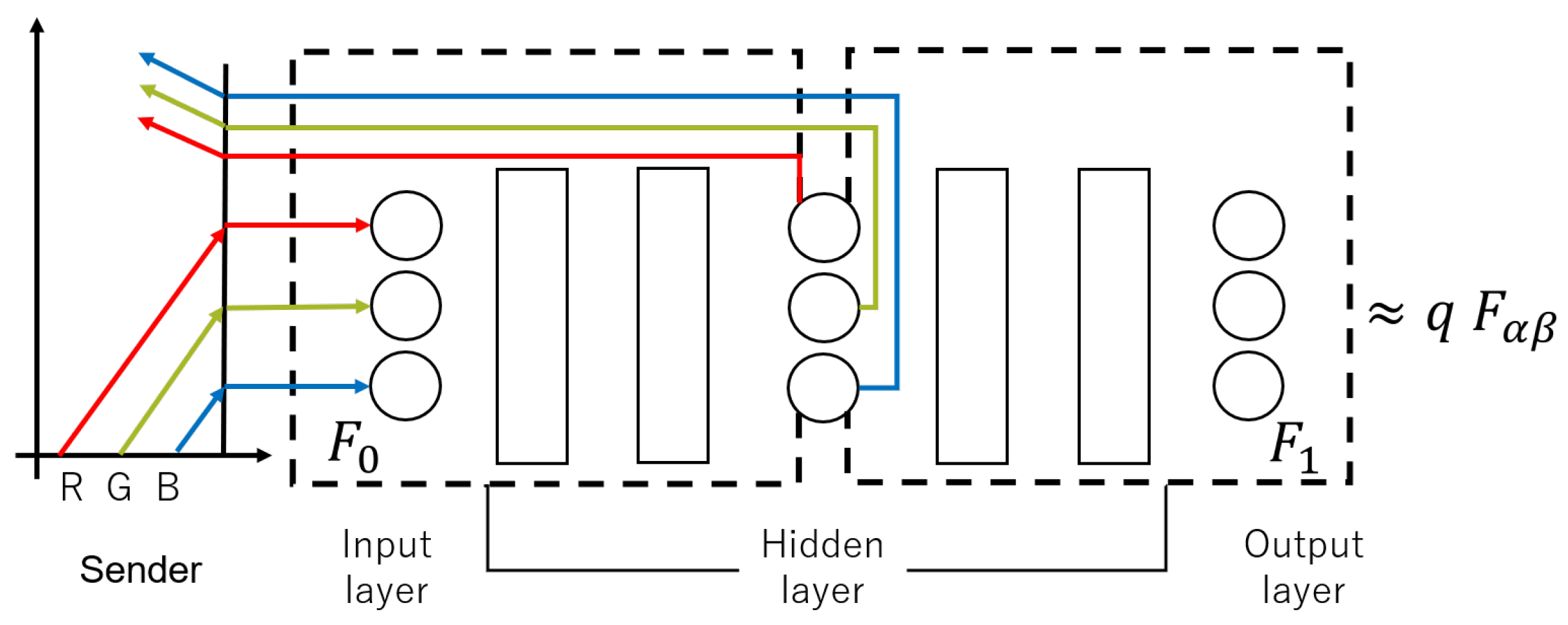
2.3. Proposed Secret Communication System
- (1)
- F has a sensitive dependence on initial conditions within the defined region.
- (2)
2.4. Numerical Experiments
3. Numerical Experiments with Color Images
4. Security Evaluation of the Encrypted Images by the Proposed Method
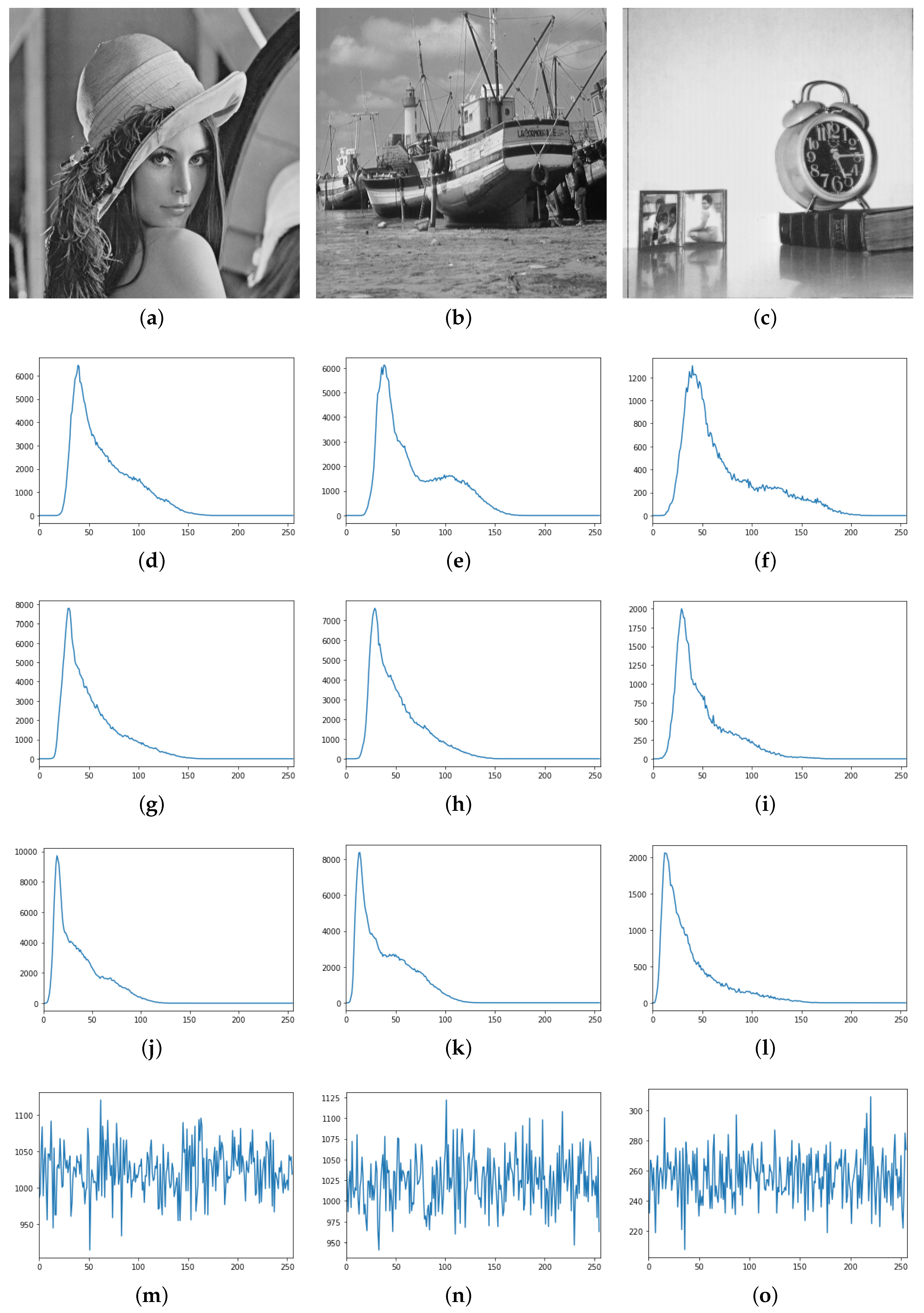
4.1. Randomness Testing of Encrypted Images
4.2. Distinguishability of Encrypted Images
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cuomo, K.M.; Oppenheim, A.V. Circuit Implementation of Synchronized Chaos with Applications to Communications. Phys. Rev. Lett. 1993, 1, 65–68. [Google Scholar] [CrossRef]
- Kocarev, L.; Parlitz, U. General Approach for Chaotic Synchronization with Applications to Communication. Phys. Rev. Lett. 1995, 25, 5028–5031. [Google Scholar] [CrossRef]
- Lin, C.H.; Hu, G.H.; Chan, C.Y.; Yan, J.J. Chaos-Based Synchronized Dynamic Keys and Their Application to Image Encryption with an Improved AES Algorithm. Appl. Sci. 2021, 11, 1329. [Google Scholar] [CrossRef]
- Ushio, T. Chaotically Synchronizing Control and Its Application to Secure Communication. Trans. Inf. Process. Soc. Jpn. 1995, 3, 525–530. [Google Scholar]
- Yoshimura, K. Multichannel Digital Communications by the Synchronization of Globally Coupled Chaotic Systems. Phys. Rev. E 1999, 2, 1648–1657. [Google Scholar] [CrossRef]
- Li, C.; Zhao, F.; Liu, C.; Lei, L.; Zhang, J. A Hyperchaotic Color Image Encryption Algorithm and Security Analysis. Secur. Commun. Netw. 2019, 2019, 8132547. [Google Scholar] [CrossRef]
- Sbiaa, F.; Kotel, S.; Zeghid, M.; Tourki, R.; Machhout, M.; Baganne, A. High-Level Implementation of a Chaotic and AES Based Crypto-System. J. Circuits, Syst. Comput. 2017, 26, 1750122. [Google Scholar] [CrossRef]
- Arab, A.; Rostami, M.J.; Ghavami, B. An image encryption method based on chaos system and AES algorithm. J. Supercomput. 2019, 75, 6663–6682. [Google Scholar] [CrossRef]
- Suri, S.; Vijay, R. An AES–CHAOS-Based Hybrid Approach to Encrypt Multiple Images. In Recent Developments in Intelligent Computing, Communication and Devices; Springer: Singapore, 2017; pp. 3–43. [Google Scholar]
- Liu, Y.; Tong, X.; Hu, S. A family of new complex number chaotic maps based image encryption algorithm. Signal Process. Image Commun. 2013, 28, 1548–1559. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An image encryption algorithm based on hyper-chaos system and DNA plane. Multimed. Tools Appl. 2014, 72, 57–70. [Google Scholar] [CrossRef]
- Kuo, C.L. Design of a fuzzy sliding-mode synchronization controller for two different chaos systems. Comput. Math. Appl. 2011, 61, 2090–2095. [Google Scholar] [CrossRef]
- Moon, S.; Baik, J.-J.; Seo, J.M. Chaos synchronization in generalized Lorenz systems and an application to image encryption. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105708. [Google Scholar] [CrossRef]
- Njah, A.N. Tracking control and synchronization of the new hyperchaotic Liu system via backstepping techniques. Nonlinear Dyn. 2010, 61, 1–9. [Google Scholar] [CrossRef]
- Pai, M.C. Global synchronization of uncertain chaotic systems via discrete-time sliding mode control. Appl. Math. Comput. 2014, 228, 663–671. [Google Scholar] [CrossRef]
- Yau, H.T.; Kuo, C.L.; Yan, J.J. Fuzzy sliding mode control for a class of chaos synchronization with uncertainties. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 333–338. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.X. Adaptive hybrid projective synchronization of uncertain chaotic systems based on backstepping design. Nonlinear Anal. Real World Appl. 2011, 12, 388–393. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization of chaotic systems. Chaos 2015, 25, 097611. [Google Scholar] [CrossRef] [PubMed]
- Sano, H.; Wakaiki, M.; Yaguchi, T. Secure Communication Systems Using Distributed Parameter Chaotic Synchronization. Trans. Soc. Instrum. Control. Eng. 2021, 2, 78–85. [Google Scholar] [CrossRef]
- Chen, G.; Hsu, S.B.; Zhou, J. Chaotic Vibrations of the One-Dimensional Wave Equation due to a Self-Excitation Boundary Condition. Part I: Controlled Hysteresis, Appendix C by G.R. Chen and G. Crosta. Trans. Am. Math. Soc. 1998, 11, 4265–4311. [Google Scholar] [CrossRef]
- Chen, G.; Hsu, S.B.; Zhou, J. Chaotic Vibration of the Wave Equation with Nonlinear Feedback Boundary Control: Progress and Open Questions. In Chaos Control: Theory and Applications; Chen, G.R., Yu, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 25–50. [Google Scholar]
- Li, L.; Huang, Y.; Xiao, M. Observer Design for Wave Equations with Van Der Pol Type Boundary Conditions. SIAM J. Control. Optim. 2012, 3, 1200–1219. [Google Scholar] [CrossRef]
- Naoe, H.K. Tanaka and Y. Takefuji, Information Security Techniques Based on Artificial Neural Network. J. Jpn. Soc. Artif. Intell. 1995, 5, 577–585. [Google Scholar]
- Tariq, M.I.; Memon, N.A.; Ahmed, S. A Review of Deep Learning Security and Privacy Defensive Techniques. Mob. Inf. Syst. 2020, 2020, 6535834. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations; Amer Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Guan, K. Important Notes on Lyapunov Exponents. arXiv 2014, arXiv:1401.3315. [Google Scholar]
- Inoue, Y. Chaos:Definition and Characterization. Jpn. J. Multiph. Flow 1997, 2, 157–162. [Google Scholar] [CrossRef][Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Preishuber, M.; Hütter, T.; Katzenbeisser, S.; Uhl, A. Depreciating Motivation and Empirical Security Analysis of Chaos-Based Image and Video Encryption. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2137–2150. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI Randomness Tests for Image Encryption. Cyber J. Multidiscip. J. Sci. Technol. 2011, 1, 31–38. [Google Scholar]
- Ali, F.; Mohammed, A.H. Content Based Image Retrieval (CBIR) by Statistical Methods. Baghdad Sci. J. 2020, 17, 694–700. [Google Scholar] [CrossRef]
- Seetharaman, K.; Jeyakarthic, M. Statistical distributional approach for scale and rotation invariant color image retrieval using multivariate parametric tests and orthogonality condition. J. Vis. Commun. Image Represent. 2014, 25, 727–739. [Google Scholar] [CrossRef]





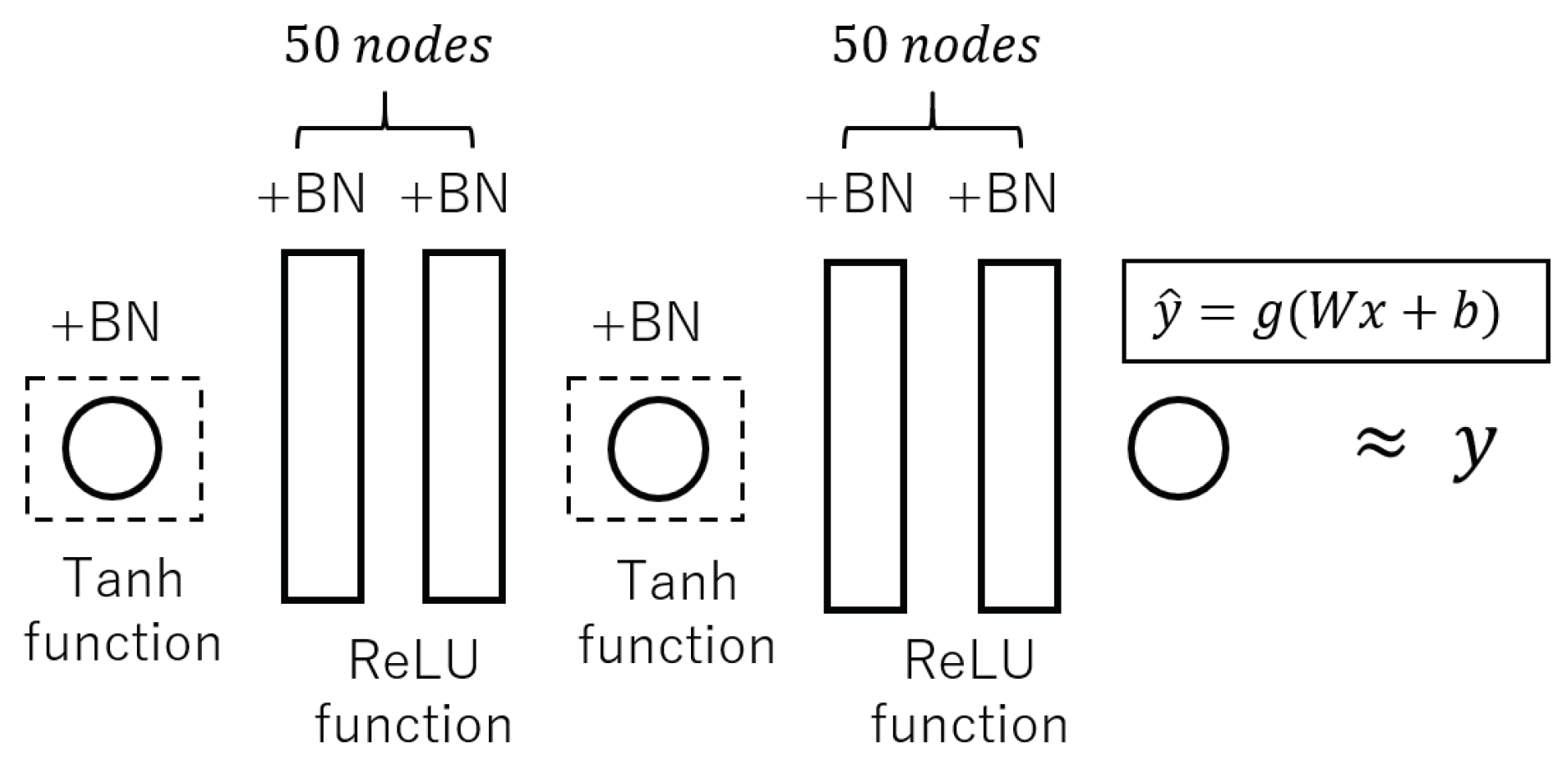
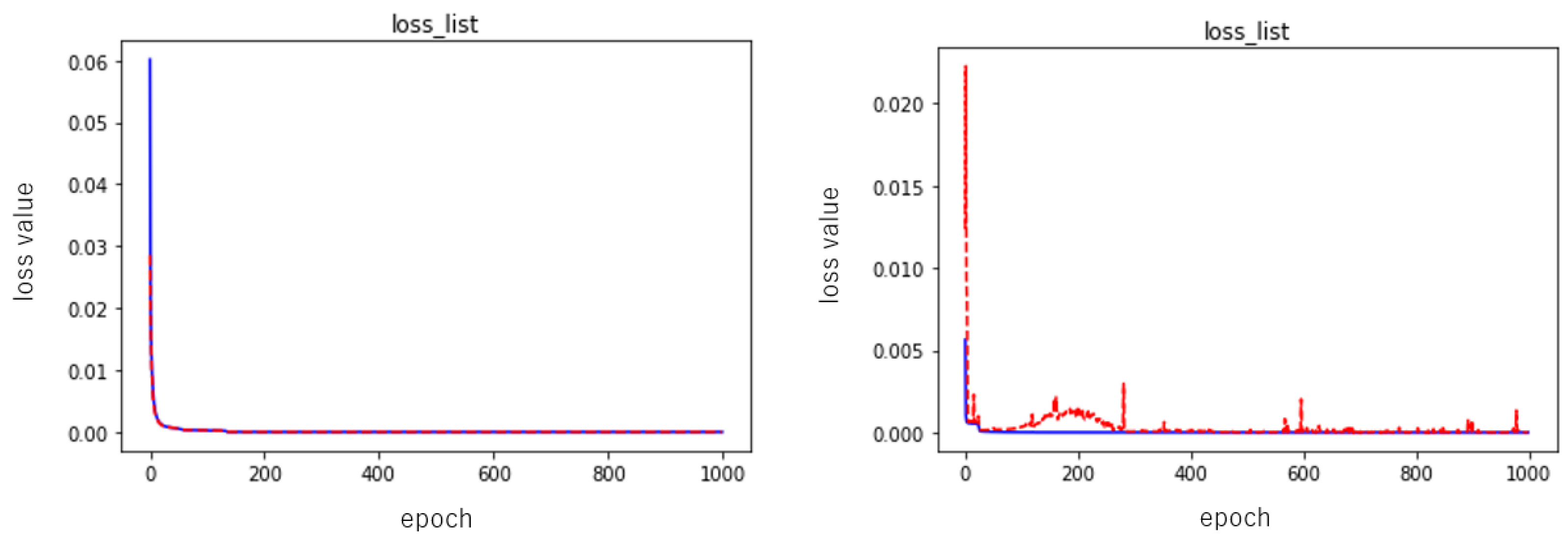










| Epoch | Data Set | Mean ± Standard |
|---|---|---|
| 1000 times | train set | 0.000005 ± 0.000001 |
| test set | 0.000005 ± 0.000001 | |
| Lyapunov exponent | −0.067282 ± 0.102745 | |
| Epoch | Data Set | Mean ± Standard |
|---|---|---|
| 1000 times | train set | 0.000002 ± 0.000001 |
| test set | 0.000275 ± 0.000394 | |
| Lyapunov exponent | 0.024377 ± 0.148675 | |
| Epoch | Data Set | Mean ± Standard |
|---|---|---|
| 1000 times | train set | 0.000694 ± 0.000035 |
| test set | 0.000919 ± 0.000033 | |
| Lyapunov exponent | 0.1144 ± 0.1469 | |
| 0.0038 ± 0.0917 | ||
| −0.1717 ± 0.2333 | ||
| Object | Correlation | UACI | ||||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | ||||
| lena | m = 6 | T = 1 | 0.972642 | 0.972993 | 0.922492 | 36.141486 |
| T = 2 | 0.962627 | 0.962568 | 0.890740 | 39.410799 | ||
| T = 3 | 0.968880 | 0.969089 | 0.915038 | 35.114740 | ||
| m = 7.5 | T = 1 | 0.968823 | 0.969244 | 0.908995 | 39.877836 | |
| T = 2 | 0.954396 | 0.954471 | 0.874803 | 39.730604 | ||
| T = 3 | 0.976311 | 0.976517 | 0.940879 | 35.622222 | ||
| AES | 0.002630 | 0.008785 | 0.000658 | 49.996347 | ||
| boat | m = 6 | T = 1 | 0.980538 | 0.980823 | 0.943327 | 36.728787 |
| T = 2 | 0.961264 | 0.961193 | 0.885866 | 41.783973 | ||
| T = 3 | 0.973791 | 0.973994 | 0.930897 | 39.928194 | ||
| m = 7.5 | T = 1 | 0.972897 | 0.973300 | 0.923706 | 36.761638 | |
| T = 2 | 0.957479 | 0.957473 | 0.874213 | 41.551513 | ||
| T = 3 | 0.973904 | 0.974118 | 0.936444 | 40.359627 | ||
| AES | 0.000163 | 0.000445 | 0.000502 | 50.000055 | ||
| clock | m = 6 | T = 1 | 0.921742 | 0.922687 | 0.806450 | 48.089881 |
| T = 2 | 0.858309 | 0.858372 | 0.664064 | 58.067992 | ||
| T = 3 | 0.888560 | 0.889011 | 0.722784 | 58.823428 | ||
| m = 7.5 | T = 1 | 0.899274 | 0.900966 | 0.770316 | 47.179087 | |
| T = 2 | 0.853312 | 0.957473 | 0.874213 | 56.637741 | ||
| T = 3 | 0.880133 | 0.881703 | 0.754349 | 57.388910 | ||
| AES | 0.005367 | 0.004363 | 0.003360 | 49.929277 | ||
| Object | Correlation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | |||||||||
| R | G | B | R | G | B | R | G | B | |||
| lena | m = 7.5 | T = 1 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.95 | 0.99 | 0.96 |
| T = 2 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | ||
| T = 3 | 0.93 | 0.94 | 0.81 | 0.93 | 0.94 | 0.81 | 0.82 | 0.89 | 0.59 | ||
| m = 8.8 | T = 1 | 0.96 | 0.99 | 0.97 | 0.96 | 0.99 | 0.97 | 0.88 | 0.88 | 0.88 | |
| T = 2 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.97 | 0.96 | 0.98 | 0.96 | ||
| T = 3 | 0.89 | 0.95 | 0.82 | 0.90 | 0.95 | 0.83 | 0.75 | 0.88 | 0.57 | ||
| AES | 5 × | 1 × | −1 × | 1 × | 6 × | 8 × | 1 × | −8 × | 3 × | ||
| boat | m = 7.5 | T = 1 | 0.96 | 1.00 | 0.98 | 0.97 | 1.00 | 0.98 | 0.94 | 0.99 | 0.96 |
| T = 2 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | ||
| T = 3 | 0.92 | 0.97 | 0.92 | 0.93 | 0.97 | 0.92 | 0.82 | 0.94 | 0.86 | ||
| m = 8.8 | T = 1 | 0.96 | 0.99 | 0.97 | 0.96 | 0.99 | 0.97 | 0.93 | 0.99 | 0.95 | |
| T = 2 | 0.98 | 0.99 | 0.97 | 0.98 | 0.99 | 0.97 | 0.96 | 0.98 | 0.96 | ||
| T = 3 | 0.92 | 0.96 | 0.92 | 0.93 | 0.97 | 0.93 | 0.82 | 0.93 | 0.87 | ||
| AES | 6 × | −1 × | −1 × | −3 × | −1 × | −3 × | 1 × | −2 × | −3 × | ||
| veg | m = 7.5 | T = 1 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.94 | 0.99 | 0.96 |
| T = 2 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.88 | 0.98 | 0.98 | 0.97 | ||
| T = 3 | 0.92 | 0.97 | 0.92 | 0.93 | 0.97 | 0.92 | 0.82 | 0.94 | 0.86 | ||
| m = 8.8 | T = 1 | 0.96 | 0.99 | 0.97 | 0.97 | 0.99 | 0.98 | 0.94 | 0.99 | 0.96 | |
| T = 2 | 0.98 | 0.99 | 0.97 | 0.98 | 0.99 | 0.97 | 0.96 | 0.98 | 0.96 | ||
| T = 3 | 0.92 | 0.96 | 0.92 | 0.93 | 0.96 | 0.92 | 0.82 | 0.96 | 0.86 | ||
| AES | 2 × | 2 × | 5 × | −8 × | 2 × | 6 × | 4 × | 4 × | 7 × | ||
| Object | UACI | ||||
|---|---|---|---|---|---|
| R | G | B | |||
| lena | m = 7.5 | T = 1 | 46.293217 | 40.515568 | 24.708355 |
| T = 2 | 43.678409 | 43.262431 | 37.007906 | ||
| T = 3 | 41.407206 | 42.583560 | 29.628579 | ||
| m = 8.8 | T = 1 | 46.454520 | 41.186064 | 24.949227 | |
| T = 2 | 44.341227 | 43.377668 | 33.920451 | ||
| T = 3 | 43.072341 | 40.273322 | 40.672362 | ||
| AES | 50.133255 | 50.047464 | 49.936812 | ||
| boat | m = 7.5 | T = 1 | 35.143726 | 48.660561 | 52.421603 |
| T = 2 | 39.571601 | 55.066602 | 56.038358 | ||
| T = 3 | 47.716444 | 53.135069 | 53.060568 | ||
| m = 8.8 | T = 1 | 35.245613 | 50.609906 | 55.037498 | |
| T = 2 | 38.337034 | 56.456049 | 58.441035 | ||
| T = 3 | 42.331758 | 55.305545 | 56.647502 | ||
| AES | 49.953939 | 50.052023 | 50.175874 | ||
| veg | m = 7.5 | T = 1 | 37.751291 | 54.587069 | 54.226224 |
| T = 2 | 45.768913 | 47.626056 | 62.656476 | ||
| T = 3 | 37.213291 | 48.628576 | 69.999379 | ||
| m = 8.8 | T = 1 | 37.915899 | 54.778044 | 55.353727 | |
| T = 2 | 62.202183 | 48.556424 | 40.446628 | ||
| T = 3 | 33.298991 | 51.570749 | 69.901463 | ||
| AES | 49.956022 | 50.026667 | 49.943955 | ||
| I2 | Lena (m = 6, T = 1) | Boat (m = 7.5, T = 2) | Clock (m = 6, T = 2) | |
|---|---|---|---|---|
| I1 | ||||
| lena (m = 7.5, T = 1) | 0.068396 | 0.0898650 | ||
| 0.112057 | 0.119775 | |||
| 0.999999 | 0.999999 | |||
| boat (m = 7.5, T = 1) | 0.042764 | 0.099446 | ||
| 0.077088 | 0.143051 | |||
| 0.999999 * | 0.999999 | |||
| clock (m = 6, T = 3) | 0.106253 | 0.071040 | ||
| 0.107990 | 0.081516 | |||
| 0.999999 | 0.999999 | |||
| I2 | Lena (m = 8.8, T = 2) | Boat (m = 7.5, T = 2) | Veg (m = 8.8, T = 1) | |
|---|---|---|---|---|
| I1 | ||||
| lena (m = 8.8, T = 3) | 0.047194 | 0.070985 | ||
| 0.103503 | 0.184824 | |||
| 0.999999 | 0.999999 | |||
| boat (m = 7.5, T = 1) | 0.084080 | 0.008566 | ||
| 0.185896 | 0.037862 | |||
| 0.999999 * | 0.999999 | |||
| veg (m = 7.5, T = 1) | 0.092913 | 0.106315 | ||
| 0.191360 | 0.210313 | |||
| 0.999999 | 0.999999 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Sano, H.; Wakaiki, M.; Yaguchi, T. Secret Communication Systems Using Chaotic Wave Equations with Neural Network Boundary Conditions. Entropy 2021, 23, 904. https://doi.org/10.3390/e23070904
Chen Y, Sano H, Wakaiki M, Yaguchi T. Secret Communication Systems Using Chaotic Wave Equations with Neural Network Boundary Conditions. Entropy. 2021; 23(7):904. https://doi.org/10.3390/e23070904
Chicago/Turabian StyleChen, Yuhan, Hideki Sano, Masashi Wakaiki, and Takaharu Yaguchi. 2021. "Secret Communication Systems Using Chaotic Wave Equations with Neural Network Boundary Conditions" Entropy 23, no. 7: 904. https://doi.org/10.3390/e23070904
APA StyleChen, Y., Sano, H., Wakaiki, M., & Yaguchi, T. (2021). Secret Communication Systems Using Chaotic Wave Equations with Neural Network Boundary Conditions. Entropy, 23(7), 904. https://doi.org/10.3390/e23070904






