A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization
Abstract
:1. Introduction
1.1. Summary of the Current Survey Work
1.2. Motivations
1.3. Research Methodology
1.4. Scope of Discussion
1.5. Our Contributions
1.6. Structure of the Paper
2. Common NIOAs
2.1. The Common Process for the 11 NIOAs
2.2. The Principles of the 11 NIOAs
2.2.1. Genetic Algorithm (GA)
| Algorithm 1 GA |
|
2.2.2. Particle Swarm Optimization (PSO) Algorithm
| Algorithm 2 PSO |
|
2.2.3. Artificial Bee Colony (ABC) Algorithm
| Algorithm 3 ABC |
|
2.2.4. Bat Algorithm (BA)
| Algorithm 4 BA |
|
2.2.5. Immune Algorithm (IA)
| Algorithm 5 IA |
|
2.2.6. Firefly Algorithm (FA)
| Algorithm 6 FA |
|
2.2.7. Cuckoo Search (CS) Algorithm
| Algorithm 7 CS |
|
2.2.8. Differential Evolution (DE) Algorithm
| Algorithm 8 DE |
|
2.2.9. Gravitational Search Algorithm (GSA)
| Algorithm 9 GSA |
|
2.2.10. Grey Wolf Optimizer (GWO)
| Algorithm 10 GWO |
|
2.2.11. Harmony Search (HS) Optimization
| Algorithm 11 HS |
|
3. Theoretical Comparison and Analysis of the 11 NIOAs
3.1. Common Characteristics
3.2. Variant Methods of Common NIOAs
3.3. Differences
4. Performance Comparison and Analysis for the 11 NIOAs
4.1. The Description of BBOB Test Functions
4.2. Performance Comparison and Analysis on Benchmark Functions
4.2.1. The Comparison and Analysis on the Accuracy, Stability and Parameter Sensitivity
4.2.2. The Efficiency Comparison and Analysis
4.2.3. The Comparison of Running Time
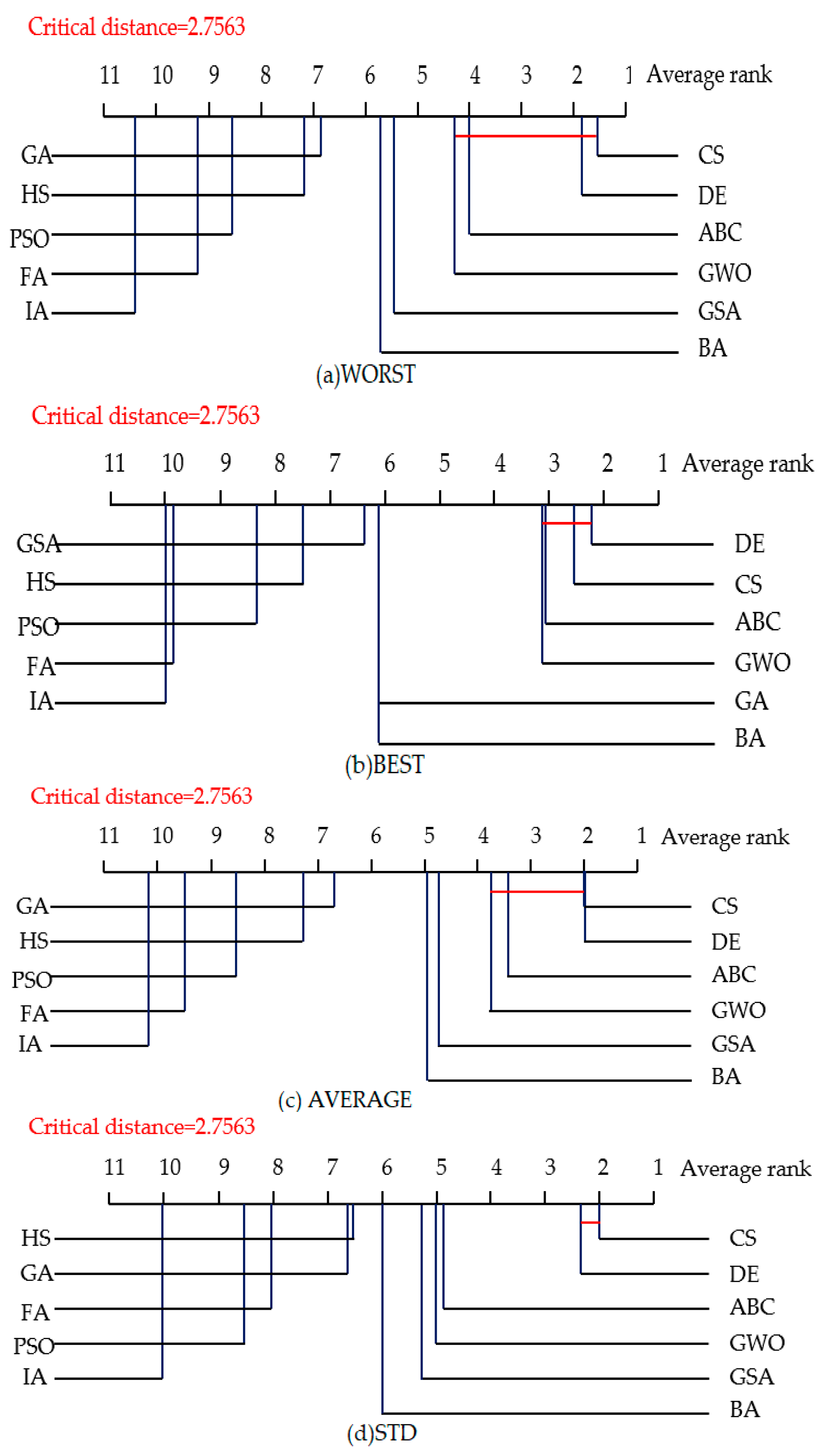
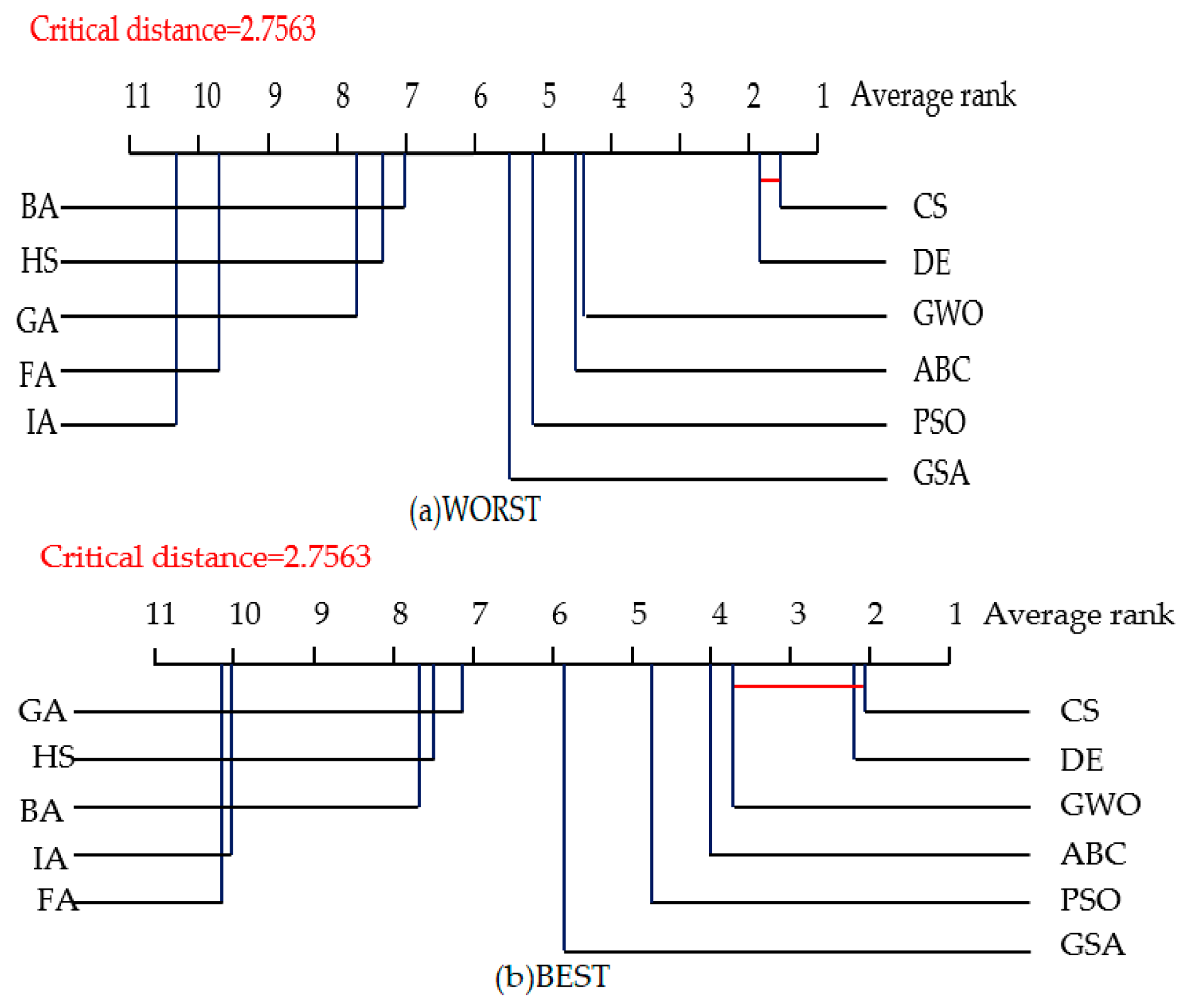
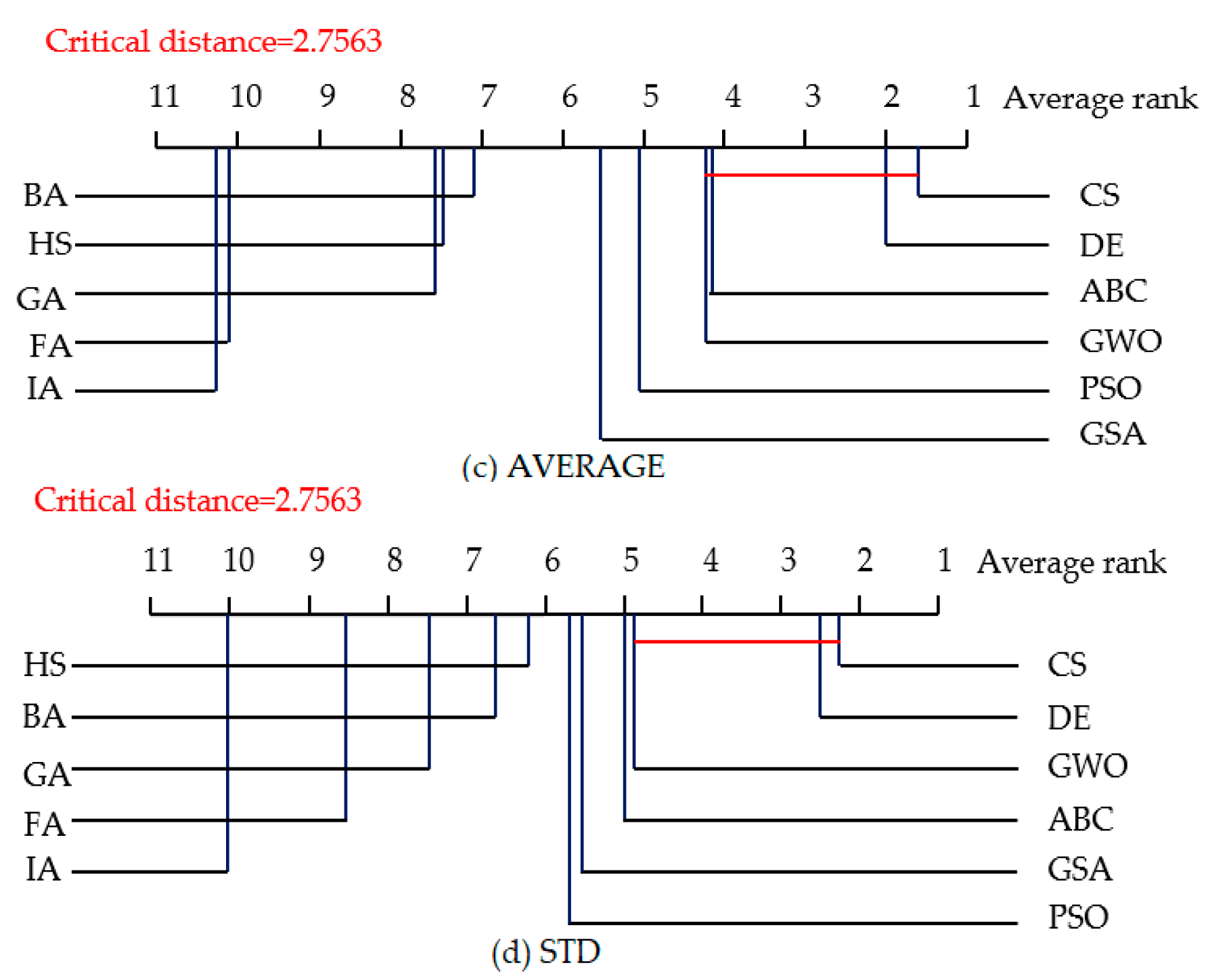
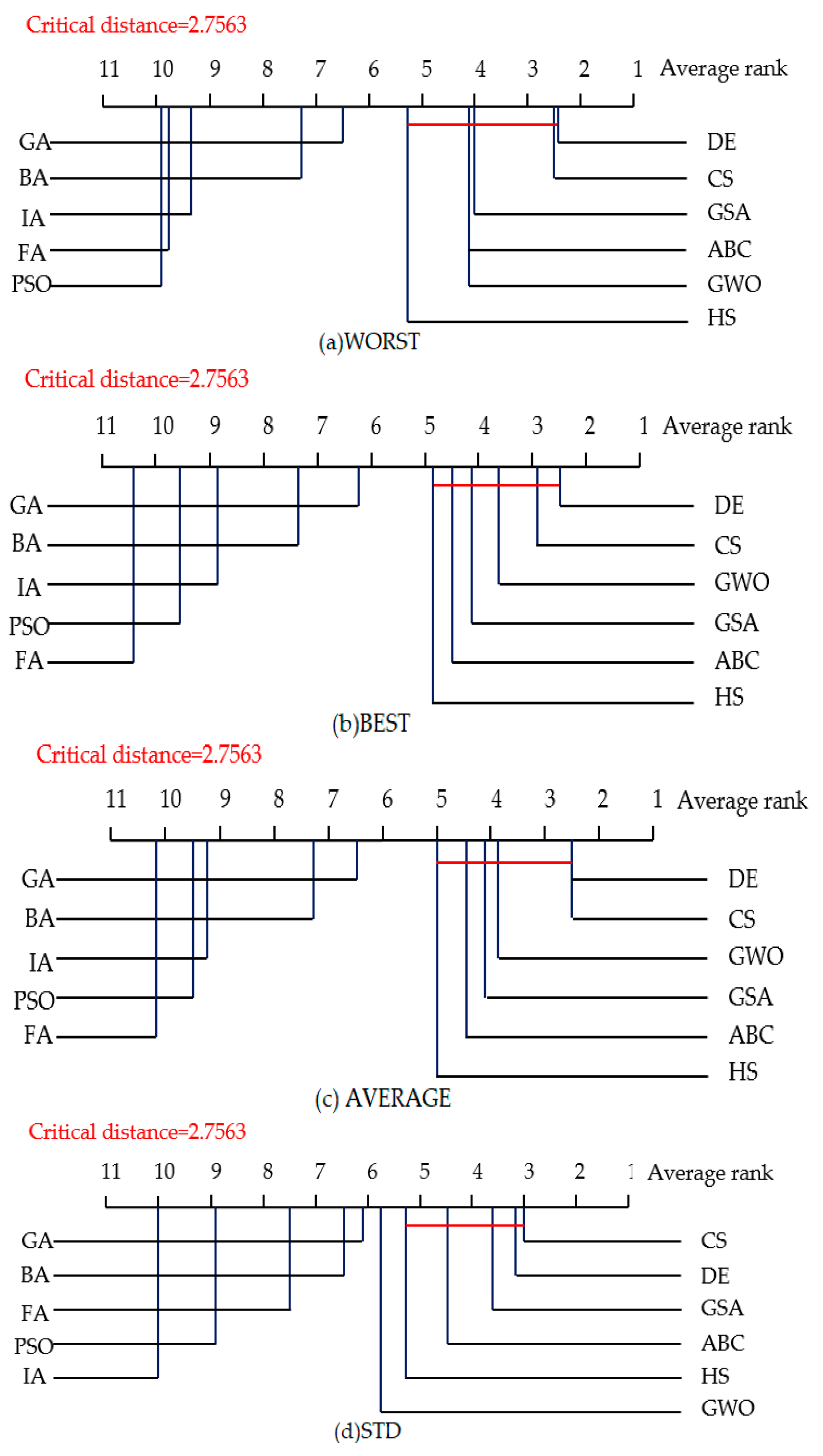
4.3. Statistical Tests for Algorithm Comparison
4.4. Performance Comparison on Engineering Optimization Problem
5. Challenges and Future Directions
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fister, I., Jr.; Yang, X.S.; Brest, J.; Fister, D. A Brief Review of Nature-Inspired Algorithms for Optimization. Elektrotehniški Vestn. 2013, 80, 116–122. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Space. J. Glob. Opt. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Dervis, K.; Bahriye, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the 1st European Conference on Artificial Life, York, UK, 11–13 November 1991; pp. 134–142. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the 2009 World Congress on Nature and Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S. Nature-Inspired Metaheutistic Algorithms; Luniver Press: Beckington, UK, 2008. [Google Scholar]
- Bersini, H.; Varela, F.J. The Immune Recruitment Mechanism: A Selective Evolutionary Strategy. In Proceedings of the International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991; pp. 520–526. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Esmat, R.; Hossein, N.P.; Saeid, S. GSA: A Gravitational Search Algorithm. Inform. Sci. 2009, 179, 2232–2248. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Lim, T.Y. Structured population genetic algorithms: A literature survey. Artif. Intell. Rev. 2014, 41, 385–399. [Google Scholar] [CrossRef]
- Rezaee Jordehi, A. Particle swarm optimisation for dynamic optimisation problems: A review. Neural Comput. Appl. 2014, 25, 1507–1516. [Google Scholar] [CrossRef]
- Dervis, K.; Beyza, G.; Celal, O.; Nurhan, K. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar]
- Chawla, M.; Duhan, M. Bat Algorithm: A Survey of the State-Of-The-Art. Appl. Artif. Intell. 2015, 29, 617–634. [Google Scholar] [CrossRef]
- Dasgupta, D.; Yu, S.H.; Nino, F. Recent Advances in Artificial Immune Systems: Models and Applications. Appl. Soft Comput. 2011, 11, 1574–1587. [Google Scholar] [CrossRef]
- Fister, I., Jr.; Yang, X.S.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef] [Green Version]
- Mohamad, A.B.; Zain, A.M.; Bazin, N.E.N. Cuckoo search algorithm for optimization problems—A literature review and its applications. Appl. Artif. Intell. 2014, 28, 419–448. [Google Scholar] [CrossRef]
- Swagatam, D.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar]
- Esmat, R.; Elaheh, R.; Hossein, N.P. A comprehensive survey on gravitational search algorithm. Swarm Evol. Comput. 2018, 41, 141–158. [Google Scholar]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Hatta, N.M.; Zain, A.M.; Sallehuddin, R.; Shayfull, Z.; Yusoff, Y. Recent studies on optimisation method of Grey Wolf Optimiser (GWO): A review (2014–2017). Artif. Intell. Rev. 2019, 52, 2651–2683. [Google Scholar] [CrossRef]
- Alia, O.M.; Mandava, R. The variants of the harmony search algorithm: An overview. Artif. Intell. Rev. 2011, 36, 49–68. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kar, A.K. Swarm Intelligence: A Review of Algorithms. In Nature-Inspired Computing and Optimization; Springer: Berlin/Heidelberg, Germany, 2017; pp. 475–494. [Google Scholar]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef] [Green Version]
- Kar, A.K. Bio inspired computing–A review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Chu, S.C.; Huang, H.C.; Roddick, J.F. Overview of Algorithms for Swarm Intelligence. In Proceedings of the 3rd International Conference on Computational Collective Intelligence, GdyNIOA, Poland, 21–23 September 2011; pp. 28–41. [Google Scholar]
- Parpinelli, R.S. New inspirations in swarm intelligence: A survey. Int. J. Bio-Inspir. Comput. 2011, 3, 1–16. [Google Scholar] [CrossRef]
- Monismith, D.R.; Mayfield, B.E. Slime Mold as a Model for Numerical Optimization. In Proceedings of the 2008 IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008. [Google Scholar]
- Havens, T.C.; Spain, C.J.; Salmon, N.G.; Keller, J.M. Roach Infestation Optimization. In Proceedings of the 2008 IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008. [Google Scholar]
- Abbass, H.A. MBO: Marriage in Honey Bees Optimization A Haplometrosis Polygynous Swarming Approach. In Proceedings of the 2001 IEEE Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; pp. 207–214. [Google Scholar]
- Burnet, F.M. The Clonal Selection Theory of Acquired Immunity; Cambridge Univ. Press: Cambridge, UK, 1959. [Google Scholar]
- Xiao, R.B.; Wang, L. Artificial Immune System Principle, Models, Analysis and Perspectives. Chin. J. Comput. 2002, 25, 1281–1292. [Google Scholar]
- Reynolds, C. Flocks, herds, and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Safe. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Beyer, H.G. Self-adaptive genetic algorithms with simulated binary crossover. Evol. Comput. 2001, 9, 197–221. [Google Scholar] [CrossRef] [PubMed]
- Payne, A.W.R.; Glen, R.C. Molecular Recognition Using A Binary Genetic Search Algorithm. J. Mol. Graph. Model. 1993, 11, 74–91. [Google Scholar] [CrossRef]
- Stanimirović, Z.; Kratica, J.; Dugošija, D. Genetic algorithms for solving the discrete ordered median problem. Eur. J. Oper. Res. 2007, 182, 983–1001. [Google Scholar] [CrossRef]
- Leung, Y.W.; Wang, Y.P. An Orthogonal Genetic Algorithm with Quantization for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2001, 5, 41–53. [Google Scholar] [CrossRef] [Green Version]
- Tsai, J.T.; Liu, T.K.; Chou, J.H. Hybrid Taguchi-genetic algorithm for global numerical optimization. IEEE Trnas. Evol. Comput. 2004, 8, 365–377. [Google Scholar] [CrossRef]
- Sarma, K.C.; Adeli, H. Fuzzy genetic algorithm for optimization of steel structures. J. Struct. Eng. 2000, 126, 596–604. [Google Scholar] [CrossRef]
- Yuan, X.H.; Yuan, Y.B.; Zhang, Y.C. A hybrid chaotic genetic algorithm for short-term hydro system scheduling. Math. Comput. Simul. 2002, 59, 319–327. [Google Scholar] [CrossRef]
- Jiao, L.C.; Wang, L. A Novel Genetic Algorithm Based on Immunity. IEEE Trans. Syst. Man Cybern. 2000, 30, 552–561. [Google Scholar] [CrossRef] [Green Version]
- Juang, C.F. A Hybrid of genetic algorithm and particle swarm optimization for recurrent network design. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Li, B.B.; Wang, L. A hybrid quantum-inspired genetic algorithm for multiobjective flow shop scheduling. IEEE Trans. Syst. Man Cybern. Part B 2007, 37, 576–591. [Google Scholar] [CrossRef]
- Tripathi, P.K.; Bandyopadhyay, S.; Pal, S.K. Multi-Objective Particle Swarm Optimization with time variant inertia and acceleration coefficients. Inform. Sci. 2007, 177, 5033–5049. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; Shawki, A.; Robert, D. Strength Pareto Particle Swarm Optimization and Hybrid EA-PSO for Multi-Objective Optimization. Evol. Comput. 2010, 18, 127–156. [Google Scholar]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S.H. Adaptive Particle Swarm Optimization. IEEE Trans. Syst. Man Cybern. Part B 2009, 39, 1362–1381. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.H.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation 2001, Soul, Korea, 27–30 May 2001; pp. 101–106. [Google Scholar]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary Particle Swarm Optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Liao, C.J.; Tseng, C.T.; Luarn, P. A discrete version of particle swarm optimization for flowshop scheduling problems. Comput. Oper. Res. 2007, 34, 3099–3111. [Google Scholar] [CrossRef]
- Zhao, X.C. A perturbed particle swarm algorithm for numerical optimization. Appl. Soft Comput. 2010, 10, 119–124. [Google Scholar]
- Wang, Y.; Liu, J.H. Chaotic particle swarm optimization for assembly sequence planning. Robot. Comput. Integr. Manuf. 2010, 26, 212–222. [Google Scholar] [CrossRef]
- Liu, H.; Cai, Z.X.; Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Santucci, V.; Milani, A. Particle Swarm Optimization in the EDAs Framework. In Proceedings of the 15th Online World Conference on Soft Computing in Industrial Applications, Electr Network, Online, 15–17 November 2010; pp. 87–96. [Google Scholar]
- Plevris, V.; Papadrakakis, M. A Hybrid Particle Swarm-Gradient Algorithm for Global Structural Optimization. Comput. Civ. Infrastruct. Eng. 2011, 26, 48–68. [Google Scholar] [CrossRef]
- Bachlaus, M.; Pandey, M.K.; Mahajan, C. Designing an integrated multi-echelon agile supply chain network: A hybrid taguchi-particle swarm optimization approach. J. Intell. Manuf. 2008, 19, 747–761. [Google Scholar] [CrossRef]
- Akbari, R.; Hedayatzadeh, R.; Ziarati, K.; Hassanizadeh, B. A multi-objective artificial bee colony algorithm. Swarm Evol. Comput. 2012, 2, 39–52. [Google Scholar] [CrossRef]
- Song, X.Y.; Yan, Q.F.; Zhao, M. An adaptive artificial bee colony algorithm based on objective function value information. Appl. Soft Comput. 2017, 55, 384–401. [Google Scholar] [CrossRef]
- Kashan, M.H.; Nahavandi, N.; Kashan, A.H. DisABC: A new artificial bee colony algorithm for binary optimization. Appl. Soft Comput. 2012, 12, 342–352. [Google Scholar] [CrossRef]
- Pan, Q.K.; Tasgetiren, M.F.; Suganthan, P.N.; Chua, T.J. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem. Inform. Sci. 2011, 181, 2455–2468. [Google Scholar] [CrossRef]
- Teimouri, R.; Baseri, H. Forward and backward predictions of the friction stir welding parameters using fuzzy-artificial bee colony-imperialist competitive algorithm systems. J. Intell. Manuf. 2015, 26, 307–319. [Google Scholar] [CrossRef]
- Xu, C.F.; Duan, H.B.; Liu, F. Chaotic artificial bee colony approach to Uninhabited Combat Air Vehicle (UCAV) path planning. Aerosp. Sci. Technol. 2010, 14, 535–541. [Google Scholar] [CrossRef]
- Jadon, S.S.; Tiwari, R.; Sharma, H.; Bansal, J.C. Hybrid Artificial Bee Colony algorithm with Differential Evolution. Appl. Soft Comput. 2017, 58, 11–24. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.J.; Xu, Q. Structural inverse analysis by hybrid simplex artificial bee colony algorithms. Comput. Struct. 2009, 87, 861–870. [Google Scholar] [CrossRef]
- Yang, X.S. Bat algorithm for multi-objective optimisation. Int. J. Bio-Inspir. Comput. 2011, 3, 267–274. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load frequency control: Self Adaptive Modified Bat Algorithm. Int. J. Electr. Power Energy Syst. 2015, 71, 254–261. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Osaba, E.; Yang, X.S.; Diaz, F.; Lopez-Garcia, P.; Carballedo, R. An improved discrete bat algorithm for symmetric and asymmetric Traveling Salesman Problems. Eng. Appl. Artif. Intell. 2016, 48, 59–71. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.H. A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization. J. Appl. Math. 2013, 2013, 696491. [Google Scholar] [CrossRef]
- Perez, J.; Valdez, F.; Castillo, O. Modification of the Bat Algorithm using Fuzzy Logic for Dynamical Parameter Adaptation. In Proceedings of the IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015; pp. 464–471. [Google Scholar]
- Gandomi, A.H.; Yang, X.S. Chaotic bat algorithm. J. Comput. Sci.-NETH 2014, 5, 224–232. [Google Scholar] [CrossRef]
- Fister, I.; Fong, S.; Brest, J.; Fister, I. A Novel Hybrid Self-Adaptive Bat Algorithm. Sci. World J. 2014, 2014, 709738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Wang, W.J.; Cui, L.Z.; Sun, H.; Zhao, J.; Wang, Y.; Xue, Y. A hybrid multi-objective firefly algorithm for big data optimization. Appl. Soft Comput. 2018, 69, 806–815. [Google Scholar] [CrossRef]
- Baykasoglu, A.; Ozsoydan, F.B. Adaptive firefly algorithm with chaos for mechanical design optimization problems. Appl. Soft Comput. 2015, 36, 152–164. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, B.; Chai, H.T.; Alma, Z.Q.; Yang, G.F. Identification of DNA-binding proteins using multi-features fusion and binary firefly optimization algorithm. BMC Bioinform. 2016, 17, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Sayadi, M.K.; Hafezalkotob, A.; Naini, S.G.J. Firefly-inspired algorithm for discrete optimization problems: An application to manufacturing cell formation. J. Manuf. Syst. 2013, 32, 78–84. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.H.; Duan, H.; Wang, H.Q. A New Improved Firefly Algorithm for Global Numerical Optimization. J. Comput. Theor. Nanos 2014, 11, 477–485. [Google Scholar] [CrossRef]
- Chandrasekaran, K.; Simon Sishaj, P. Optimal deviation based firefly algorithm tuned fuzzy design for multi-objective UCP. IEEE Trans. Power Syst. 2013, 28, 460–471. [Google Scholar] [CrossRef]
- Coelho dos Santos, L.; de Andrade Bernert, D.L.; Mariani, V.C. A Chaotic Firefly Algorithm Applied to Reliability-Redundancy Optimization. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation, New Orleans, LA, USA; 2011; pp. 517–521. [Google Scholar]
- Abdullah, A.; Deris, S.; Mohamad, M.S.; Hashim, S.Z.M. A new hybrid firefly algorithm for complex and nonlinear problem. In Distributed Computing and Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2012; pp. 673–680. [Google Scholar]
- Satapathy, P.; Dhar, S.; Dash, P.K. Stability improvement of PV-BESS diesel generator-based microgrid with a new modified harmony search-based hybrid firefly algorithm. IET Renew. Power Gen. 2017, 11, 566–577. [Google Scholar] [CrossRef]
- Luh, G.C.; Chueh, C.H.; Liu, W.W. Moia: Multi-objective immune algorithm. Eng. Optim. 2003, 35, 143–164. [Google Scholar] [CrossRef]
- Shao, X.G.; Cheng, L.J.; Cai, W.S. An adaptive immune optimization algorithm for energy minimization problems. J. Chem. Phys. 2004, 120, 11401–11406. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.C.; Song, B.Q.; Huang, P.Y.; Wen, Z.C.; Weng, J.L.; Fan, Y. An improved discrete immune optimization algorithm based on PSO for QoS-driven web service composition. Appl. Soft Comput. 2012, 12, 2208–2216. [Google Scholar] [CrossRef]
- Tsai, J.T.; Ho, W.H.; Liu, T.K.; Chou, J.H. Improved immune algorithm for global numerical optimization and job-shop scheduling problems. Appl. Math. Comput. 2007, 194, 406–424. [Google Scholar] [CrossRef]
- Sahan, S.; Polat, K.; Kodaz, H.; Günes¸, S. A new hybrid method based on fuzzy-artificial immune system and k-nn algorithm for breast cancer diagnosis. Comput. Biol. Med. 2007, 37, 415–423. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Qian, F.; Du, W.L. A chaotic immune algorithm with fuzzy adaptive parameters. Asia-Pac. J. Chem. Eng. 2008, 3, 695–705. [Google Scholar] [CrossRef]
- Lin, Q.Z.; Zhu, Q.L.; Huang, P.Z.; Chen, J.Y.; Ming, Z.; Yu, J.P. A novel hybrid multi-objective immune algorithm with adaptive differential evolution. Comput. Oper. Res. 2015, 62, 95–111. [Google Scholar] [CrossRef]
- Ali Riza, Y. An effective hybrid immune-hill climbing optimization approach for solving design and manufacturing optimization problems in industry. J. Mater. Process. Tech. 2009, 209, 2773–2780. [Google Scholar]
- Chandrasekaran, K.; Simon Sishaj, P. Multi-objective scheduling problem: Hybrid approach using fuzzy assisted cuckoo search algorithm. Swarm Evol. Comput. 2012, 5, 1–16. [Google Scholar] [CrossRef]
- Mlakar, U.; Fister, I.; Fister, I. Hybrid self-adaptive cuckoo search for global optimization. Swarm Evol. Comput. 2016, 29, 47–72. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pereira, L.A.M.; Almeida, T.N.S.; Papa, J.P.; Souza, A.N.; Romos, C.C.O.; Yang, X.S. BCS: A Binary Cuckoo Search algorithm for feature selection. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems, Beijing, China, 19–23 May 2013; pp. 465–468. [Google Scholar]
- Ouaarab, A.; Ahiod, B.; Yang, X.S. Discrete cuckoo search algorithm for the travelling salesman problem. Neural Comput. Appl. 2014, 24, 1659–1669. [Google Scholar] [CrossRef]
- Guerrero, M.; Castillo, O.; Garcia, M. Fuzzy dynamic parameters adaptation in the Cuckoo Search Algorithm using Fuzzy logic. In Proceedings of the IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015; pp. 441–448. [Google Scholar]
- Wang, G.G.; Deb, S.; Gandomi, A.H.; Zhang, Z.J.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Kanagaraj, G.; Ponnambalam, S.G.; Jawahar, N.; Nilakantan, J.M. An effective hybrid cuckoo search and genetic algorithm for constrained engineering design optimization. Eng. Optim. 2014, 46, 1331–1351. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Zhao, X.J.; Chu, H.C.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Ali, M.; Siarry, P.; Pant, M. An efficient Differential Evolution based algorithm for solving multi-objective optimization problems. Eur. J. Oper. Res. 2012, 217, 404–416. [Google Scholar] [CrossRef]
- Cui, L.Z.; Li, G.H.; Lin, Q.Z.; Chen, J.Y.; Lu, N. Adaptive differential evolution algorithm with novel mutation strategies in multiple sub-populations. Comput. Oper. Res. 2016, 65, 155–173. [Google Scholar] [CrossRef]
- Wang, L.; Pan, Q.K.; Suganthan, P.N.; Wang, W.H.; Wang, Y.M. A novel hybrid discrete differential evolution algorithm for blocking flow shop scheduling problems. Comput. Oper. Res. 2010, 27, 509–520. [Google Scholar] [CrossRef]
- Pan, Q.K.; Tasgetiren, M.F.; Liang, Y.C. A discrete differential evolution algorithm for the permutation flowshop scheduling problem. Comput. Ind. Eng. 2008, 55, 795–816. [Google Scholar] [CrossRef] [Green Version]
- Maulik, U.; Saha, I. Modified differential evolution based fuzzy clustering for pixel classification in remote sensing imagery. Pattern Recognit. 2009, 42, 2135–2149. [Google Scholar] [CrossRef]
- Dos Santos, C.L.; Ayala, H.V.H.; Mariani, V.C. A self-adaptive chaotic differential evolution algorithm using gamma distribution for unconstrained global optimization. Appl. Math. Comput. 2014, 234, 452–459. [Google Scholar]
- Li, X.; Yin, M. Parameter estimation for chaotic systems by hybrid differential evolution algorithm and artificial bee colony algorithm. Nonlinear Dynam 2014, 77, 61–71. [Google Scholar] [CrossRef]
- Sayah, S.; Hamouda, A. A hybrid differential evolution algorithm based on particle swarm optimization for nonconvex economic dispatch problems. Appl. Soft Comput. 2013, 13, 1608–1619. [Google Scholar] [CrossRef]
- Wang, L.; Zou, F.; Hei, X.H.; Yang, D.D.; Chen, D.B.; Jiang, Q.Y.; Cao, Z.J. A hybridization of teaching–learning-based optimization and differential evolution for chaotic time series prediction. Neural Comput. Appl. 2014, 25, 1407–1422. [Google Scholar] [CrossRef]
- Reza, H.H.; Modjtaba, R. A multi-objective gravitational search algorithm. In Proceedings of the 2nd International Conference on Computational Intelligence, Communication Systems and Networks, Liverpool, UK, 28–30 July 2010; pp. 7–12. [Google Scholar]
- Mirjalili, S.; Lewis, A. Adaptive gbest-guided gravitational search algorithm. Neural Comput. Appl. 2014, 25, 1569–1584. [Google Scholar] [CrossRef]
- Yuan, X.H.; Ji, B.; Zhang, S.Q.; Tian, H.; Hou, Y.H. A new approach for unit commitment problem via binary gravitational search algorithm. Appl. Soft Comput. 2014, 22, 249–260. [Google Scholar] [CrossRef]
- Mohammad Bagher, D.; Hossein, N.P.; Mashaallah, M. A discrete gravitational search algorithm for solving combinatorial optimization problems. Inform. Sci. 2014, 258, 94–107. [Google Scholar]
- Sombra, A.; Valdez, F.; Melin, P.; Castillo, O. A new gravitational search algorithm using fuzzy logic to parameter adaptation. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 1068–1074. [Google Scholar]
- Gao, S.C.; Vairappan, C.; Wang, Y.; Cao, Q.P.; Tang, Z. Gravitational search algorithm combined with chaos for unconstrained numerical optimization. Appl. Math. Comput. 2014, 231, 48–62. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ji, Z.C.; Shen, Y.X. A novel hybrid particle swarm optimization and gravitational search algorithm for solving economic emission load dispatch problems with various practical constraints. Int. J. Electr. Power 2014, 55, 628–644. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. A novel hybrid gravitational search and pattern search algorithm for load frequency control of nonlinear power system. Appl. Soft Comput. 2015, 29, 310–327. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho Leandro Dos, S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Rodriguez, L.; Castillo, O.; Soria, J. Grey wolf optimizer with dynamic adaptation of parameters using fuzzy logic. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 3116–3123. [Google Scholar]
- Li, L.G.; Sun, L.J.; Guo, J.; Qi, J.; Xu, B.; Li, S.J. Modified Discrete Grey Wolf Optimizer Algorithm for Multilevel Image Thresholding. Comput. Intel Neurosci. 2017, 2017, 3116–3123. [Google Scholar] [CrossRef] [PubMed]
- Radu-Emil, P.; Radu-Codrut, D.; Emil, M.P. Grey Wolf optimizer algorithm-based tuning of fuzzy control systems with reduced parametric sensitivity. IEEE Trans. Ind. Electron. 2017, 64, 527–534. [Google Scholar]
- Mehak, K.; Sankalap, A. Chaotic grey wolf optimization algorithm for constrained optimization problems. J. Comput. Des. Eng. 2018, 5, 458–472. [Google Scholar]
- Zhang, S.; Luo, Q.F.; Zhou, Y.Q. Hybrid Grey Wolf Optimizer Using Elite Opposition-Based Learning Strategy and Simplex Method. Int. J. Comput. Int. Appl. 2017, 6, 1–38. [Google Scholar] [CrossRef]
- Zhang, X.M.; Kang, Q.; Cheng, J.F.; Wang, X. A novel hybrid algorithm based on Biogeography-Based Optimization and Grey Wolf Optimizer. Appl. Soft Comput. 2018, 67, 197–214. [Google Scholar] [CrossRef]
- Gao, K.Z.; Suganthan, P.N.; Pan, Q.K.; Chua, T.J.; Cai, T.X.; Chong, C.S. Pareto-based grouping discrete harmony search algorithm for multi-objective flexible job shop scheduling. Inform. Sci. 2014, 289, 76–90. [Google Scholar] [CrossRef]
- Wang, L.; Yang, R.X.; Xu, Y.; Niu, Q.; Pardalos, P.M.; Fei, M. An improved adaptive binary Harmony Search algorithm. Inform. Sci. 2013, 232, 58–87. [Google Scholar] [CrossRef]
- Geem, Z.W. Novel derivative of harmony search algorithm for discrete design variables. Appl. Math. Comput. 2008, 199, 223–230. [Google Scholar] [CrossRef]
- Peraza, C.; Valdez, F.; Garcia, M.; Melin, P.; Castillo, O. A New Fuzzy Harmony Search Algorithm using Fuzzy Logic for Dynamic Parameter Adaptation. Algorithms 2016, 9, 69. [Google Scholar] [CrossRef]
- Alatas, B. Chaotic harmony search algorithms. Appl. Math. Comput. 2010, 216, 2687–2699. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Yang, J.D. A hybrid harmony search algorithm for the flexible job shop scheduling problem. Appl. Soft Comput. 2013, 13, 3259–3272. [Google Scholar] [CrossRef]
- Layeb, A. A hybrid quantum inspired harmony search algorithm for 0–1 optimization problems. J. Comput. Appl. Math. 2013, 253, 14–25. [Google Scholar] [CrossRef]
- Wang, Z.W.; Qin, C.; Wan, B.T.; Song, W.W. An Adaptive Fuzzy Chicken Swarm Optimization Algorithm. Math. Probl. Eng. 2021, 2021, 8896794. [Google Scholar]
- Li, Z.Y.; Wang, W.Y.; Yan, Y.Y.; Li, Z. PS-ABC: A hybrid algorithm based on particle swarm and artificial bee colony for high-dimensional optimization problems. Expert Syst. Appl. 2015, 42, 8881–8895. [Google Scholar] [CrossRef]
- Pan, T.S.; Dao, T.K.; Nguyen, T.T.; Chu, S.C. Hybrid Particle Swarm Optimization with Bat Algorithm. In Proceedings of the 8th International Conference on Genetic and Evolutionary Computing, Nanchang, China, 18–20 October 2015; pp. 37–47. [Google Scholar]
- Soerensen, K. Metaheuristics—the metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [Google Scholar] [CrossRef]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Joines, J.; Houck, C. On the use of non-stationary penalty functions to solve nonlinear constrained optimization problems with GA’s. In Proceedings of the 1st IEEE Conference on Evolutionary Computation, Orlando, FL, USA, 27–29 June 1994; pp. 579–584. [Google Scholar]
- He, J.; Yao, X. Drift analysis and average time complexity of evolutionary algorithms. Artif. Intell. 2001, 127, 57–85. [Google Scholar] [CrossRef] [Green Version]
- Mohammad Reza, B.; Zbigniew, M. Analysis of Stability, Local Convergence, and Transformation Sensitivity of a Variant of the Particle Swarm Optimization Algorithm. IEEE Trans. Evol. Comput. 2016, 20, 370–385. [Google Scholar]
- Mohammad Reza, B.; Zbigniew, M. Stability Analysis of the Particle Swarm Optimization Without Stagnation Assumption. IEEE Trans. Evol. Comput. 2016, 20, 814–819. [Google Scholar]
- Chen, W.N.; Zhang, J.; Lin, Y.; Chen, N.; Zhan, Z.H.; Chung, H.S.H.; Li, Y.; Shi, Y.H. Particle Swarm Optimization with an Aging Leader and Challengers. IEEE Trans. Evol. Comput. 2013, 17, 241–258. [Google Scholar] [CrossRef]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–15 May 2002; pp. 1671–1676. [Google Scholar]
- Huang, C.W.; Li, Y.X.; Yao, X. A Survey of Automatic Parameter Tuning Methods for Metaheuristics. IEEE Trans. Evol. Comput. 2020, 24, 201–216. [Google Scholar] [CrossRef]
- Hart, E.; Ross, P. GAVEL—A New Tool for Genetic Algorithm Visualization. IEEE Trans. Evol. Comput. 2001, 5, 335–348. [Google Scholar] [CrossRef]
- Ryoji, T.; Hisao, I. A Review of Evolutionary Multimodal Multiobjective Optimization. IEEE Trans. Evol. Comput. 2020, 24, 193–200. [Google Scholar]
- Ma, X.L.; Li, X.D.; Zhang, Q.F.; Tang, K.; Liang, Z.P.; Xie, W.X.; Zhu, Z.X. A Survey on Cooperative Co-Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2019, 23, 421–440. [Google Scholar] [CrossRef]
- Jin, Y.C.; Wang, H.D.; Chugh, T.; Guo, D.; Miettinen, K. Data-Driven Evolutionary Optimization: An Overview and Case Studies. IEEE Trans. Evol. Comput. 2019, 23, 442–458. [Google Scholar] [CrossRef]
- Djenouri, Y.; Fournier-Viger, P.; Lin, J.C.W.; Djenouri, D.; Belhadi, A. GPU-based swarm intelligence for Association Rule Mining in big databases. Intell. Data Anal. 2019, 23, 57–76. [Google Scholar] [CrossRef]
- Wang, J.L.; Gong, B.; Liu, H.; Li, S.H. Multidisciplinary approaches to artificial swarm intelligence for heterogeneous computing and cloud scheduling. Appl. Intell. 2015, 43, 662–675. [Google Scholar] [CrossRef]
- De, D.; Ray, S.; Konar, A.; Chatterjee, A. An evolutionary SPDE breeding-based hybrid particle swarm optimizer: Application in coordination of robot ants for camera coverage area optimization. In Proceedings of the 1st International Conference on Pattern Recognition and Machine Intelligence, Kolkata, India, 20–22 December 2005; pp. 413–416. [Google Scholar]
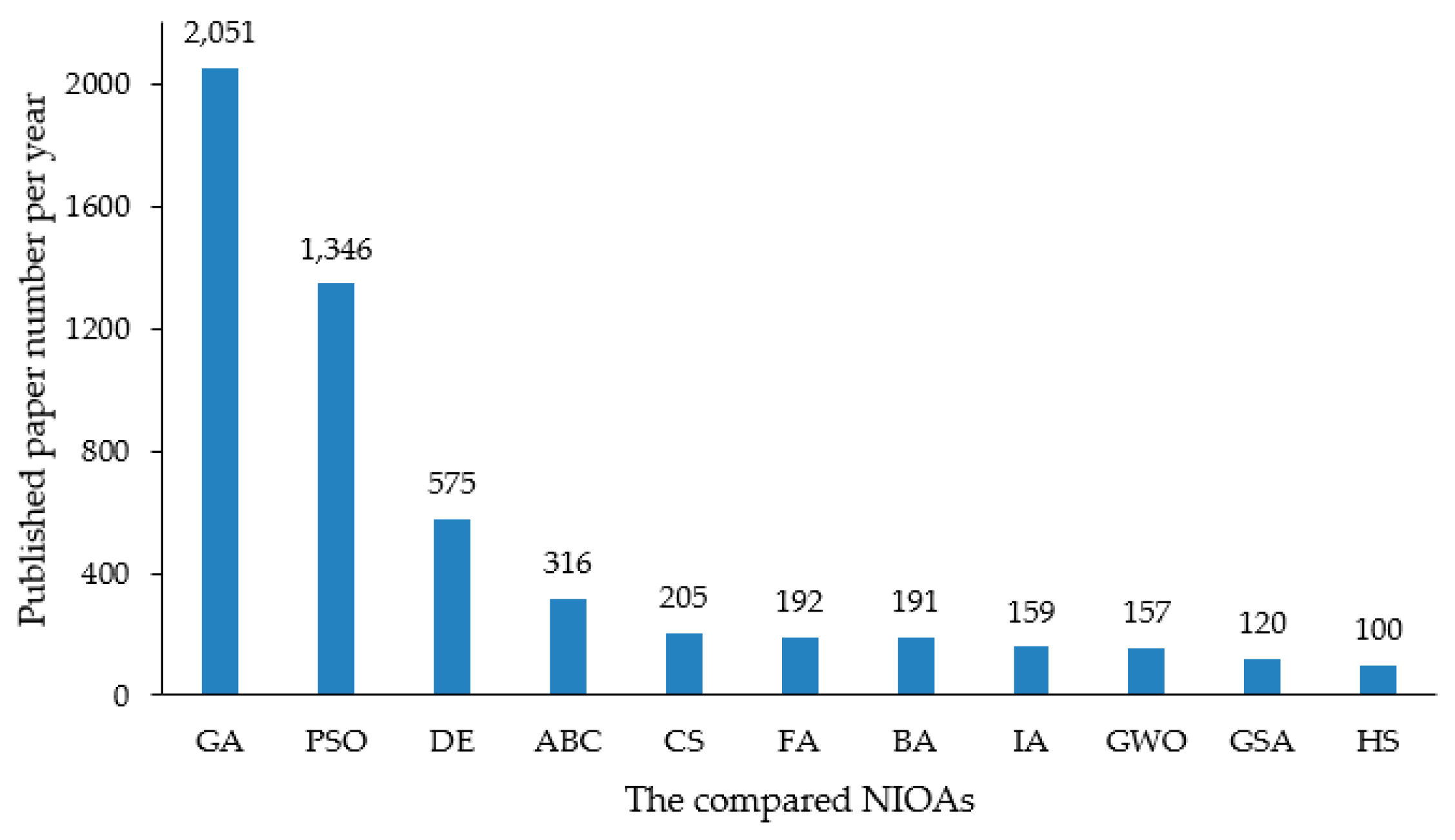


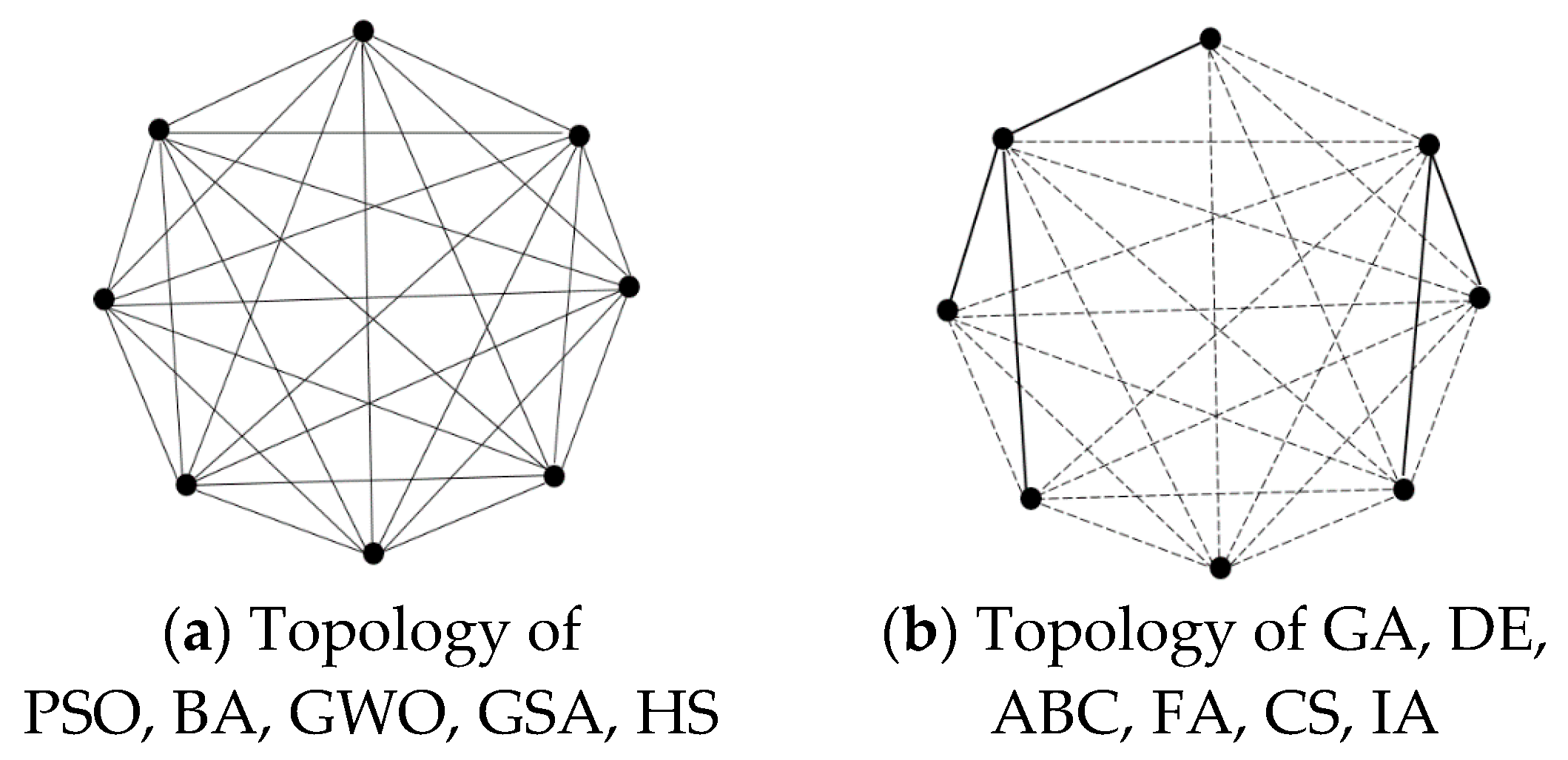

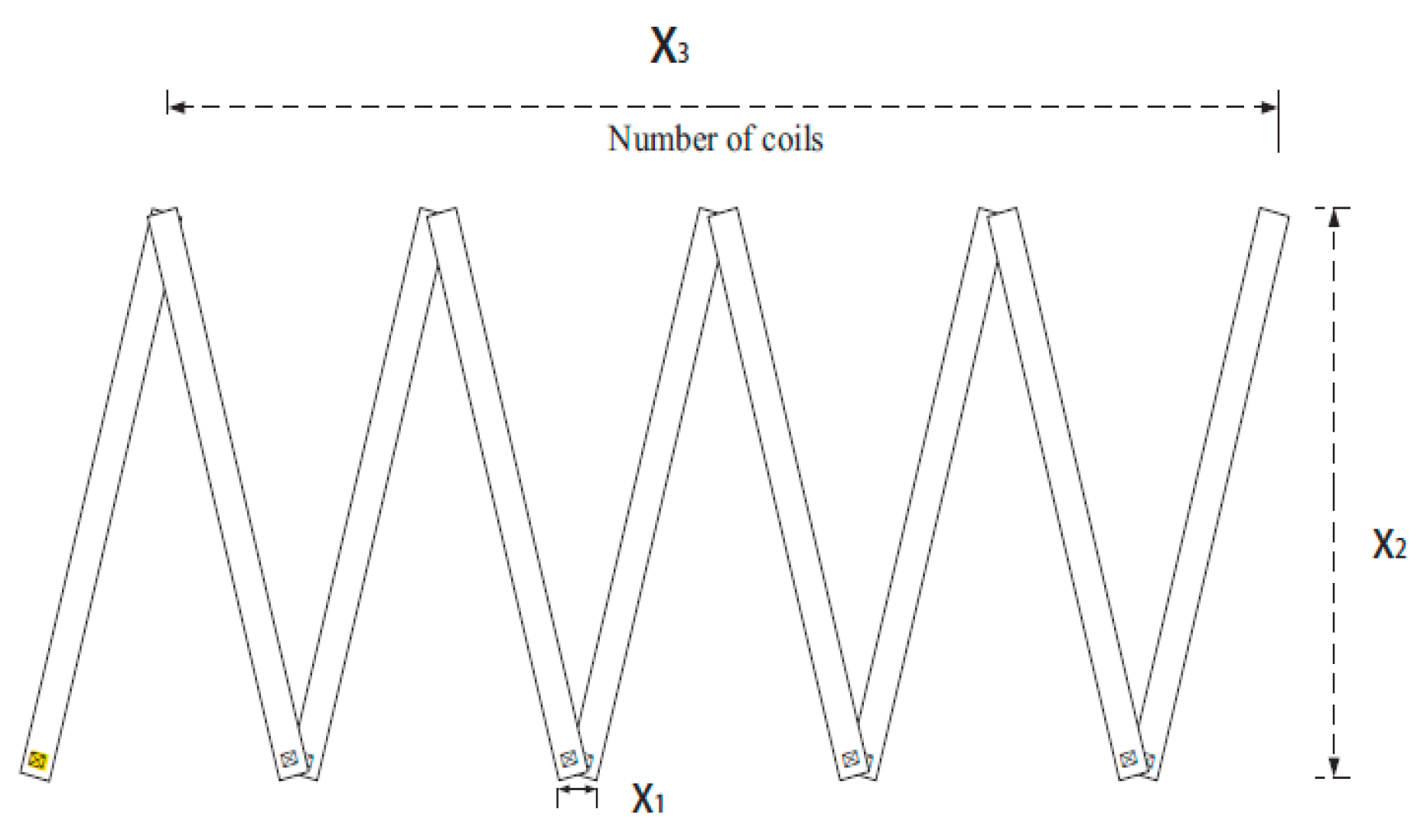
| Conceptions | Symbols | Description |
|---|---|---|
| Space dimension | The problem space description | |
| Population size | Individual quantity | |
| Iteration times | Algorithm termination condition | |
| Individual position | The expression of the ith solution on the tth iteration, also used to represent the ith individual | |
| Local best solution | Local best solution of the ith individual on the tth iteration | |
| Global best solution | Global best solution of the whole populationon the tth iteration | |
| Fitness function | Unique standard to evaluate solutions | |
| Precision threshold | Algorithm termination condition |
| NIOAs | Multiple Objectives | Adaptive | Spatial Property | Hybridization | ||||
|---|---|---|---|---|---|---|---|---|
| Discrete | Continuous | Fuzzy Theory | Chaos Theory | Combination among NIOAs | Others | |||
| GA | [37]3594 [38]44334 | [39]204 | [40]142 [41]73 | [42]1405 [43]831 | [44]305 | [45]195 | [46]420 [47]1373 | [43]831 [48]355 |
| PSO | [49]800 [50]67 | [51]2363 [52]914 | [53]732 [54]640 | [55]296 | [52]914 | [56]252 | [57]381 [58]11 | [59]214 [60]154 [50]67 |
| ABC | [61]334 | [62]47 | [63]235 [64]851 | [5]3932 | [65]42 | [66]197 | [67]122 | [68]428 |
| BA | [69]433 | [70]204 | [71]560 [72]285 | [73]136 | [74]27 | [75]158 | [76]64 | [73]136 |
| FA | [77]81 | [78]66 | [79]43 [80]165 | [81]142 | [82]45 | [83]140 | [84]99 | [85]56 |
| IA | [86]166 | [87]97 | [88]157 | [89]141 | [90]205 [91]17 | [91]17 | [92]166 | [93]230 |
| CS | [94]192 | [95]114 | [96]142 [97]438 | [7]2801 | [98]41 | [99]104 | [100]77 | [101]308 |
| DE | [102]350 | [103]198 | [104]375 [105]219 | [4]1925 | [106]251 | [107]86 | [108]70 [109]257 | [110]81 |
| GSA | [111]135 | [112]216 | [113]133 [114]114 | [12]5909 | [115]154 | [116]145 | [117]253 | [118]152 |
| GWO | [119]627 | [120]60 | [121]28 | [16]6135 | [122]225 | [123]188 | [124]29 | [125]105 |
| HS | [126]221 | [127]186 | [128]429 | [18]6808 | [129]38 | [130]345 | [131]194 | [132]133 |
| NIOAs | Time Complexity | Comments |
|---|---|---|
| PSO | Tupd = Tvec + Tpos = D∙M + D∙M = 2∙D∙M; O(TPSO) = O(D∙M + (3∙D∙M + M)∙N) ≈ O(D∙M∙N) | Tupd denotes the cost of updating velocity (Tvec) and position (Tpos) |
| GA | Tupd = Tcross + Tmut = D∙M + D∙M = 2∙D∙M; O(TGA) = O(D∙M + (2∙M∙D + M)∙N) ≈ O(D∙M∙N) | Tupd denotes the cost of crossover (Tcross) and mutation (Tmut) operations |
| ABC | Tupd = Temp + Tsct + Tonk = D∙M/2 + D∙M/2 + M = D∙M + M; O(TABC) =O(D∙M + (2∙M∙D + 2M)∙N) ≈ O(D∙M∙N) | Tupd denotes the cost of updating the positions of employed foragers (Temp), scouts (Tsct) and onlookers (Tonk) |
| BA | Tupd = Tfreq + Tvec + Tpos = D∙M+ D∙M+ D∙M = 3∙D∙M; O(TBA) = O(D∙M + (4∙M∙D + M)∙N) ≈ O(D∙M∙N) | Tupd denotes the cost of updating the frequency (Tfreq), velocity (Tvec) and positions (Tpos) |
| IA | Tupd = Tden + Tact + Tcross+ Tmut =M∙M + M+ D∙M + D∙M = M(M + 1) + 2 D∙M; O(TIA) = O(D∙M +(M∙(M +4) + 3∙M∙D)∙N) ≈ O(D∙M∙N + M∙M∙N) =O((D + M)∙M∙N) | Tupd is the cost of updating the density (Tden), activity (Tact), crossover (Tcross) and mutation (Tmut) operations |
| FA | Tupd = M∙M∙D; O(TFA) = O(D∙M +(M∙M∙D + M∙D + M)∙N) ≈ O(D∙M2∙N) | Tupd is the cost of updating the positions of fireflies |
| CS | Tupd = 2∙M∙D; O(TCS) = O(D∙M + (3∙M∙D + M)∙N) ≈ O(D∙M∙N) | Tupd is the cost of updating the host nests of cuckoos |
| DE | Tupd = M∙D+ M∙D+ M; O(TDE) = O(D∙M +(4M∙D + 2∙M)∙N) ≈ O(D∙M∙N) | Tupd is the cost of crossover mutation and selection operations |
| GSA | Tupd = Tgrav + Tvec + Tpos = M∙M+ M∙D+ M∙D; O(TGSA) = O(D∙M + (M∙M + 3∙M∙D + M)∙N) ≈ O(D∙M∙N + M∙M∙N) = O((D + M)∙M∙N) | Tupd is the cost of updating gravitational acceleration (Tgrav), velocity (Tvec) and position (Tpos) |
| GWO | Tupd = M∙D; O(TGWO) = O(D∙M + (2M∙D + M)∙N) ≈ O(D∙M∙N) | Tupd denotes the cost of updating the positions of wolves |
| HS | Tupd = M∙D; O(THS) = O(D∙M + (2M∙D + M)∙N) ≈ O(D∙M∙N) | Tupd is the cost of updating harmony vectors |
| Algorithms | Parameters I | Parameters II |
|---|---|---|
| GA | = 1, = 0.8, = 0.2 | = 1, = 0.75, = 0.25 |
| PSO | = 2, = 2 | = 1.5, = 1.5 |
| ABC | , Limit = 20 | , Limit = 30 |
| BA | = 0.9, = 0.9 = 100, = 1, = 100, = 1 | = 0.8, = 0.8 = 150, = 1, = 150, = 1 |
| IA | = 0.8, = 0.2 | = 0.75, = 0.25 |
| FA | = 0.6, step = 0.4, = 1 | = 0.5, step = 0.5, = 1.1 |
| CS | = 1, = 0.25 | = 1.1, = 0.15 |
| DE | F = 0.5, CR = 0.1 | F = 0.6, CR = 0.2 |
| GSA | = 100, = 20 | = 90, = 15 |
| GWO | None | None |
| HS | HMCR = 0.995, PAR = 0.4, BW = 1 | HMCR = 0.85, PAR = 0.5, BW = 0.9 |
| Criteria | WORST | AVERGAE | BEST | STD | |
|---|---|---|---|---|---|
| NIOAs | |||||
| DE | D = 10 | 10 (F5, F6, F8, F9, F10, F17, F20, F27, F29, F30) | 10 (F5, F6, F8, F9, F10, F17, F19, F20, F27, F30) | 13 (F6, F9, F11, F14, F15, F16, F17, F18, F19, F20, F21, F27, F30) | 7 (F5, F6, F8, F9, F23, F28, F30) |
| D = 50 | 9 (F4, F6, F8, F16, F20, F25, F27, F28, F30) | 8 (F6, F9, F11, F20, F25, F27, F29, F30) | 8 (F6, F9, F11, F20, F22, F25, F27, F30) | 7 (F4, F6, F21, F25, F27, F28, F30) | |
| CS | D = 10 | 17 (F2, F3, F4, F11, F12, F13, F14, F15, F16,F18, F19, F21, F23, F24, F25, F26, F28) | 16 (F2, F3, F4, F11, F12, F13, F14, F15, F16, F18, F21, F22, F24, F25, F26, F28) | 7 (F2, F3, F4, F12, F13, F25, F26) | 17 (F2, F3, F4, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F27, F29) |
| D = 50 | 8 (F3, F12, F14, F15, F18, F19, F24, F29) | 10 (F1, F3, F4, F12, F13, F14, F15, F18, F19, F28) | 8 (F3, F4, F12, F13, F14, F18, F19, F28) | 9 (F3, F10, F14, F15, F16, F18, F19, F22, F29) | |
| HS | D = 10 | - | - | - | - |
| D = 50 | 2 (F9, F23) | 2 (F8, F23) | 5 (F5, F8, F21, F23, F29) | 3 (F9, F23, F24) | |
| GSA | D = 10 | 4 (F1, F7, F9, F22) | 3 (F1, F7, F9) | 3 (F1, F7, F9) | 5 (F1, F7, F9, F22, F25) |
| D = 50 | 6 (F1, F2, F7, F11, F13, F26) | 3 (F2, F7, F26) | 4 (F1, F2, F7, F26) | 9 (F1, F2, F5, F7, F8, F11, F12, F13, F26) | |
| GWO | D = 10 | - | 1 (F29) | 3 (F5, F8, F22) | 2 (F25, F26) |
| D = 50 | 3 (F5, F17, F21) | 7 (F5, F10, F16, F17, F21, F22, F24) | 3 (F16, F17, F24) | - | |
| ABC | D = 10 | - | 1 (F23) | 5 (F10, F23, F24, F28, F29) | - |
| D = 50 | 2 (F10, F22) | - | - | 1 (F17) | |
| PSO | D = 10 | - | - | 1 (F6) | - |
| D = 50 | - | - | 2 (F10, F15) | - | |
| FA | D = 10 | - | - | - | - |
| D = 50 | - | - | - | 1 (F20) | |
| BA | - | - | - | - | |
| GA | - | - | - | - | |
| IA | - | - | - | - | |
| Criteria | WORST | AVERGAE | BEST | STD | |
|---|---|---|---|---|---|
| NIOAs | |||||
| DE | D = 10 | 11 (F5, F6, F8, F10, F14, F15, F17, F18, F19, F20, F30) | 12 (F5, F6, F8, F15, F17, F18, F19, F20, F23, F27, F29, F30) | 14 (F5, F6, F8, F9, F14, F15, F16, F17, F18, F19, F20, F23, F27, F30) | 9 (F5, F6, F8, F15, F18, F19, F25, F28, F30) |
| D = 50 | 7 (F4, F6, F20, F25, F26, F27, F28) | 4 (F6, F9,F25, F27) | 5 (F6, F9, F25, F27, F30) | 5 (F4, F6, F25, F27, F28) | |
| CS | D = 10 | 16 (F1, F2, F3, F4, F11, F12, F13, F16, F21, F23, F24, F25, F26, F28, F29) | 14 (F2, F3, F4, F11, F12, F13, F14,F16, F21, F22, F24, F25, F26, F28) | 11 (F2, F3, F4, F11, F12, F13, F21, F22, F25, F26, F28) | 15 (F1, F2, F3, F4, F11, F12, F13, F14, F16, F17, F20, F21, F23, F27, F29) |
| D = 50 | 12 (F1, F2, F11, F12, F13, F14, F15, F18, F19, F24, F29, F30) | 13 (F1, F2, F4, F11, F12, F13, F14, F15, F18, F19, F28, F29, F30) | 11 (F2, F4, F11, F12, F13, F14,F15, F18, F19, F28, F29) | 12 (F1, F2, F11, F12, F13, F14, F15, F17, F18, F19, F29, F30) | |
| HS | D = 10 | - | - | - | 1 (F24) |
| D = 50 | - | - | - | 7 (F5, F8, F16, F21, F23, F24, F26) | |
| GSA | D = 10 | 3 (F7, F9, F22) | 3 (F1, F7, F9) | 3 (F1, F7, F9) | 3 (F7, F9, F22) |
| D = 50 | 2 (F7, F10) | 3 (F7, F10, F26) | 4 (F1, F7, F10, F26) | - | |
| GWO | D = 10 | - | 1 (F10) | 2 (F10, F29) | - |
| D = 50 | 7 (F5, F8, F16, F17, F21, F22, F23) | 9 (F5, F8, F16, F17, F20, F21, F22, F23, F24) | 8 (F5, F8, F16, F17, F20, F21, F23, F24) | - | |
| ABC | D = 10 | - | - | - | 1 (F26) |
| D = 50 | - | - | 1 (F22) | - | |
| PSO | D = 10 | - | - | 1 (F24) | - |
| D = 50 | 1 (F3) | 1 (F3) | 1 (F3) | 3 (F3, F7) | |
| FA | D = 10 | - | - | - | 1 (F10) |
| D = 50 | - | - | - | 2 (F20, F22) | |
| GA | D = 10 | - | - | - | - |
| D = 50 | 1 (F9) | - | - | 2 (F9, F10) | |
| BA | - | - | - | - | |
| IA | - | - | - | - | |
| Criteria | WORST | AVERGAE | BEST | STD | |
|---|---|---|---|---|---|
| NIOAs | |||||
| DE | D = 10 | - | - | - | - |
| D = 50 | 7 (F1 **, F2, F9, F12, F13 ***, F15 **, F30 **) | 8 (F1 **, F2, F7, F10, F12, F13 **, F15, F30) | 7 (F2, F3, F7, F8, F10, F18, F22) | 11 (F1 **, F2, F3, F4, F9, F12, F13 **, F15, F18, F22, F30 **) | |
| CS | D = 10 | - | - | - | - |
| D = 50 | 2 (F1, F18) | 1 (F18) | 2 (F8, F12) | 2 (F14, F29) | |
| HS | D = 10 | - | - | - | - |
| D = 50 | 8 (F1 ***, F2, F4, F5, F9, F12 **, F13, F30) | 8 (F1 ***, F2 **, F4, F8, F12 **, F13, F19, F30) | 8 (F1 **, F2, F4, F8, F12 **, F13, F19, F30) | 10 (F1 ***, F2, F4, F9, F12 **, F13, F15, F18, F25, F30) | |
| GSA | D = 10 | - | - | - | - |
| D = 50 | 6 (F1, F2, F9, F12 **, F13, F14 **) | 3 (F12 ***, F14, F22) | 4 (F8, F14, F19, F22) | 7 (F2 **, F9, F12 ***, F13, F14 **, F18, F19) | |
| GWO | D = 10 | - | - | - | - |
| D = 50 | 4 (F1, F9, F18, F19) | 3 (F4, F7, F13) | 3 (F1, F2, F19) | 3 (F13, F19, F24) | |
| ABC | D = 10 | 2 (F18, F30) | 2 (F18, F30) | 2 (F18, F30) | 2 (F18, F30) |
| D = 50 | 6 (F1, F11, F12, F13, F18, F19) | 2 (F1, F15) | 1 (F19) | 4 (F12, F13, F14, F19) | |
| PSO | D = 10 | 12 (F1 **, F2, F3, F7, F9, F12 **, F13, F14, F15, F18, F19, F30) | 11 (F1 **, F2, F3, F9, F12, F13, F14, F15, F18, F19, F30) | 8 (F1 **, F3, F9, F12, F13, F14, F18, F30) | 12 (F1 ***, F2 **, F3 **, F7, F9, F12, F13, F14, F15 **, F18, F19, F30) |
| D = 50 | 12 (F1 **, F2, F3 **, F4 **, F11, F12, F13 **, F14 **, F15 **, F18 **, F19 **, F30) | 14 (F1 **, F2 **, F3 **, F4 **, F11, F12 **, F13 **, F14 ***, F15 **, F18, F19 **, F26, F28, F30 **) | 15 (F1 ***, F2 **, F3 **, F4 **, F9, F11, F12 **, F13 **, F14 **, F15 **, F18 **, F19 **, F26, F28, F30) | 12 (F1 **, F2 **, F3 **, F4 **, F11 ***, F12, F13 **, F14 ***, F15 ***, F18 **, F19 ***, F30 **) | |
| FA | D = 10 | - | - | - | - |
| D = 50 | 4 (F2, F14, F17, F29) | 4 (F12, F14, F18, F29) | 4 (F12, F14, F15, F17) | 4 (F1, F13, F14, F17) | |
| BA | D = 10 | - | - | - | - |
| D = 50 | 3 (F2, F11, F19) | 6 (F2, F3, F12, F14, F15, F26) | 2 (F3, F9) | 6 (F2, F4, F11, F13, F19, F28) | |
| GA | D = 10 | 3 (F1, F18, F19) | 1 (F1) | 1 (F1) | 2 (F1, F18) |
| D = 50 | 4 (F15, F19, F26, F30) | 6 (F1, F14, F15, F18, F19, F26) | 5 (F1 **, F13, F15, F18, F26) | 4 (F1, F11, F15, F30) | |
| IA | D = 10 | - | - | - | - |
| D = 50 | - | 1 (F14) | - | 2 (F1, F13) |
| Dimensions | NIOAs Parameters | Criteria | ||
|---|---|---|---|---|
| 10-dimensional space | Parameters I | WORST | 89.9707 | 1.8634 |
| BEST | 79.0949 | |||
| AVERAGE | 94.9530 | |||
| STD | 34.6416 | |||
| Parameters II | WORST | 80.1552 | ||
| BEST | 78.3713 | |||
| AVERAGE | 95.4905 | |||
| STD | 27.9553 | |||
| 50-dimensional space | Parameters I | WORST | 68.9997 | |
| BEST | 69.7277 | |||
| AVERAGE | 71.4619 | |||
| STD | 32.7366 | |||
| Parameters II | WORST | 61.3683 | ||
| BEST | 92.1188 | |||
| AVERAGE | 75.6435 | |||
| STD | 14.9259 |
| Algorithm | WORST | AVERAGE | BEST | STD |
|---|---|---|---|---|
| GA | 0.029080 | 0.016709 | 0.012691 | 0.004163 |
| PSO | 0.030457 | 0.015028 | 0.012746 | 0.005420 |
| ABC | 0.016446 | 0.014202 | 0.012827 | 0.001062 |
| BA | 0.044217 | 0.023193 | 0.013194 | 0.011202 |
| IA | 0.031477 | 0.021735 | 0.013134 | 0.006702 |
| FA | 0.012880 | 0.012733 | 0.012718 | 3.48 × 10−5 |
| CS | 0.012670 | 0.012666 | 0.012665 | 1.27 × 10−6 |
| DE | 0.013397 | 0.013007 | 0.012755 | 0.000201 |
| GSA | 0.013073 | 0.012953 | 0.012740 | 9.06 × 10−5 |
| GWO | 0.012821 | 0.012715 | 0.012672 | 3.00 × 10−5 |
| HS | 0.032620 | 0.020375 | 0.012877 | 0.006328 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Qin, C.; Wan, B.; Song, W.W. A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization. Entropy 2021, 23, 874. https://doi.org/10.3390/e23070874
Wang Z, Qin C, Wan B, Song WW. A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization. Entropy. 2021; 23(7):874. https://doi.org/10.3390/e23070874
Chicago/Turabian StyleWang, Zhenwu, Chao Qin, Benting Wan, and William Wei Song. 2021. "A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization" Entropy 23, no. 7: 874. https://doi.org/10.3390/e23070874
APA StyleWang, Z., Qin, C., Wan, B., & Song, W. W. (2021). A Comparative Study of Common Nature-Inspired Algorithms for Continuous Function Optimization. Entropy, 23(7), 874. https://doi.org/10.3390/e23070874








