1. Preliminaries
In a previous paper [
1], we introduced the Sisyphus random walk as an infinite Markov chain that moves on the space state
and that, at every step, can either jump one unit rightward or return to the initial state from where it is restarted. The system was named after the king of Ephyra, Sisyphus, who was condemned to lift a heavy stone in an endless cycle.
Here, we generalize the above idea and consider a random walk on the integers whose dynamics alternates deterministic linear motion with resets which drive the system to the starting point at the random times . At every clock tick, the position of the random walker is such that either increases one unit, or returns to the ground state, whereupon the evolution continues. Such resetting occurs through an independent mechanism superimposed onto the original semi-deterministic evolution. Once is reset to the origin at , it begins the evolution anew from scratch which is deterministic between resets.
Using translational invariance, we can suppose that with no loss of generality. Concretely, starting from , three possibilities exist for the future position : the system may remain at provided a reset occurs at ; otherwise, it goes one unit to the right with probability or to the left with probability . In addition, if the system has wandered into the positives so that at a certain time is (respectively ) then, at time , it may either be reset to the origin with arbitrary probability or else increase (respectively, decrease) one unit to (respectively ).
Such apparent simplicity is misleading, as this simple evolution law can exhibit a surprisingly complex and rich behavior. Indeed, at each site, we allow arbitrary probabilities for the random walk to reset to the origin and, additionally, the possibility to move both in the positive and negative integers. The only restriction in this general dynamics is the requirement that
be a Markov chain. The resulting system is a natural, non-trivial generalization of that of [
1], which is recovered when the reset probability is independent of the location and when
.
In a different setting, such a system may be used as an idealized model of the random dynamics of a “mobile” in a trap, say, who is trying to climb stepwise a ladder or wall given that, at every step, there is a probability of slipping to the bottom, resulting in the need to restart again. Here, the natural question would be the determination of the location probability and expected time to escape the trap.
A related mechanism—Sisyphus cooling— was proposed by Claude Cohen-Tannoudji in certain optical contexts to the effect that an atom may climb up a potential hill, till suddenly it is returned to some ground state where it can restart anew. The hallmark of such systems is the possibility to display “back-to-square-one” behavior, a feature common in real life systems. Indeed, the study of stochastic processes subject to random resets is a problem that has attracted great interest in recent years after the seminal work of Manrubia and Zanette [
2] and Evans and Majumadar [
3]. Presently, the dynamics of systems with resets is being subjected to intense study, see the recent review [
4]. Other mechanisms for random walks that are suddenly refreshed to the starting position are considered in [
5,
6,
7]. Brownian motion with resets is considered in [
3,
8] while in [
9] the propagator of Brownian motion under time-dependent resetting is obtained (see also [
10] for further elaboration). In [
11], these ideas are applied to the case of a compound Poisson process with positive jumps and constant drift. Further elaboration appears in [
12]. Reset mechanisms have also been thoroughly applied to search strategies in mathematical and physical contexts as well as to behavioral ecology, see [
10,
13,
14,
15,
16,
17,
18]. Surprisingly, strategies that incorporate reset to pure search are advantageous in certain contexts in ecology and biophysics and molecular dynamics, [
19,
20,
21,
22]. A generalization of the Kardar–Parisi–Zhang (KPZ) equation that describes fluctuating interfaces and polymers under resetting is covered in [
23]. Dynamical systems with resets have also been used as proxies of the classical integrate-and-fire models of neuron dynamics, see [
24,
25]. In the context of Lévy flights with resetting, see the interesting papers [
26,
27]. For other applications, see also the recent papers [
28,
29,
30,
31,
32,
33,
34,
35].
As commented, the main aim of this paper is to study the main features of the semi-deterministic random walk with resets
. The evolution rules for such a random walk are described in
Section 2. We then study the propensity towards resetting of the system. According to this important property, we denote systems as reset averse, neutral or reset-inclined, and characterize them in terms of the transition probabilities and behavior of
. In
Section 3, we study the stationary distribution that the system approaches for large time.
Section 4 considers first-passage problems and, in particular, two-sided exit probabilities; concretely, given levels
we study the probability that
x reaches
before having reached
and distributions of the escape time. First passage times (FPT) also play a key role in statistical decision models, or to devise optimal strategies for seeking information; the rate at which a Brownian particle, under the influence of a metastable potential, escapes from a potential well is also a critical subject in the study of polymers, the so-called Kramers problem [
36].
Under the simplest election and constant, we have that the distribution of the FPT to level is that of the number of trials required in an unfair coin-toss to obtain k consecutive successes, a classical problem in probability. Even with , the distribution of such a problem is not trivial.
2. The Model
The evolution rules for the random walk
are as follows. Let
be the initial position. We suppose that, if for any
is
, then the random walk satisfies
We denote
the probability that, starting form zero, the system moves away from the origin at the next instant and
the probability that, if the system abandons the originat time
t, it goes to position
. To ease notation, for any value
p, we set
,
. Besides
is the Kronecker delta.
Further, we suppose that the random walk
is a Markov chain where, if
, the only allowed transitions are either to site
if no reset occurs, which happens with probability
; or else to
, when a reset occurs, with probability
. Here, the sequence
satisfies that
for all
n. It follows that the chain has the transition rules
and 0 otherwise. We also suppose that the infinite product with general term
satisfies
This mild requirement does not imply that
(see Equation (
12) below).
The model considered in [
1] is recovered assuming
and that the jump-probability is constant:
.
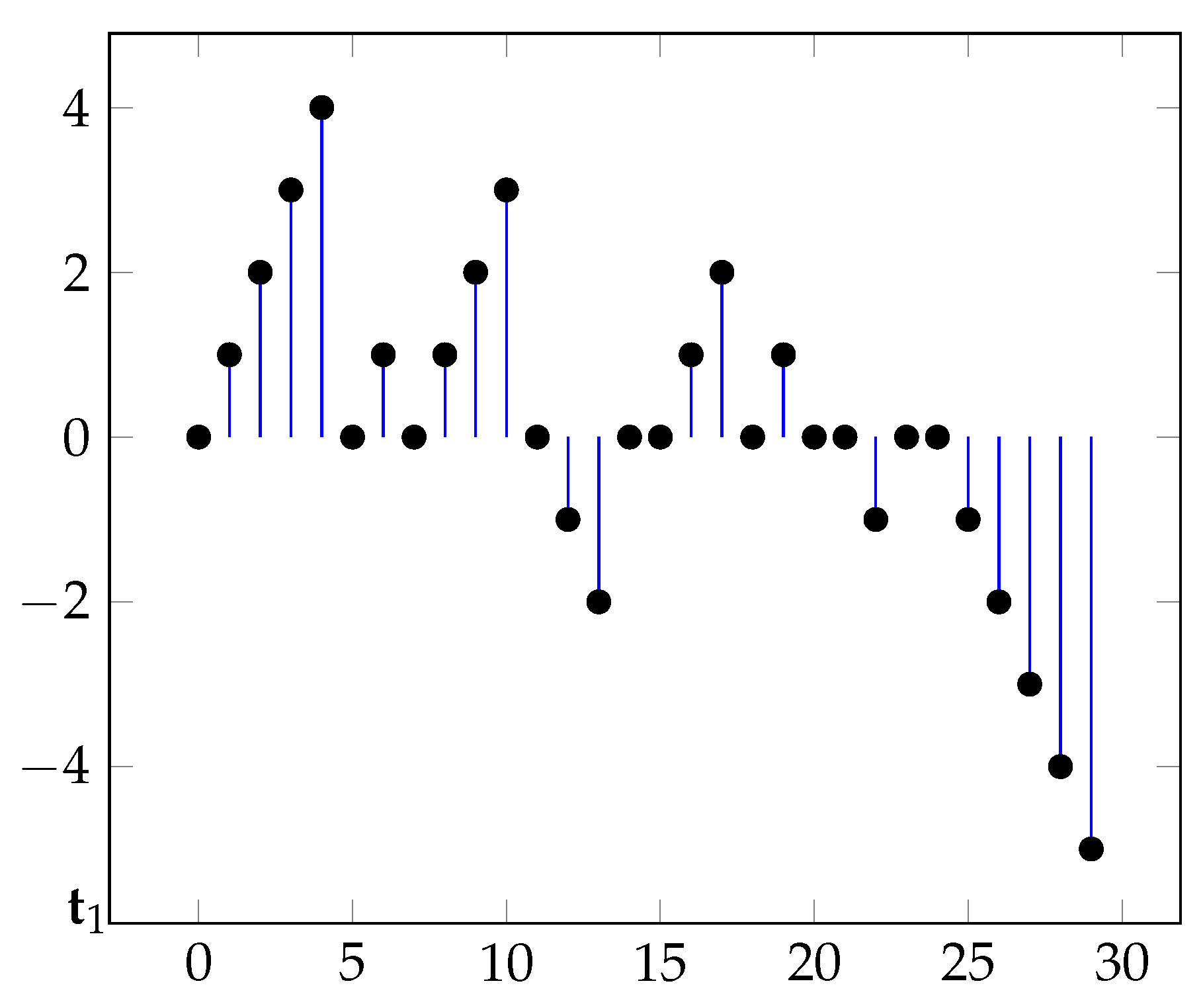
Figure 1 displays a typical sample path.
2.1. Reset Times
We denote as
the random time at which the first reset happens. Here, we consider its distribution probability
. Similarly, we denote as
the random time at which the
reset happens. To this end, note that for
the reset takes place at time
n if in all previous times no reset has occurred—and so
and
. Thus, we have transitions
and the corresponding probability
where
is a proper random variable, in view of Equation (
5).
The following representation clarifies the meaning and different roles of
and
and
We relate both probabilities. We introduce recursively a sequence
via
and
. Note then that
This can be inverted as
where
is the cumulative distribution function (cdf) of
and
. Recalling that
we finally have that Equation (
6) can be inverted as
2.2. Reset Averse and Reset-Inclined Systems
One of the most defining traits in the random walk (
2)–(
4) is what we call propensity towards resetting, a measure of how likely is that the resetting mechanism is triggered as the time from the last reset increases. We say that a system is inclined towards resetting if such a probability grows as the distance to the origin increases:
for all
n. Intuitively, for a reset-inclined system, the greater the time since the last visit (alternatively, the farthest off) the more anxious to return to the origin becomes the random walk. If this probability decreases (respectively, remains unchanged), we say that the system is reset-averse or reset-neutral. Reset-neutral chains correspond to having
for all
n. This is the choice considered in [
1]. In this case
Actually, we are interested in this property for large
n. We say that a system is ultimately averse, neutral or, respectively, inclined towards resetting if, as the time from the last reset tends to infinity, the reset probability
satisfies
The selection
corresponds to an ultimately reset-inclined system. Here, we have
and
A simple calculation yields
, which is bounded with respect to the parameter
.
Finally, the choice
corresponds to a reset-averse system. Here, the chain has power law decay tails:
The selections (
13) and (
14) reflect that the probability to commit an error that sends the walker to square one diminishes (increases) with every step. This may be put down to a capability to learn or, in contrast, to forget or grow tired with the distance to the origin. Equation (
14) corresponds to
—and hence to learning—while, if
, then Zipf law (
13)
follows.
Equation (
14) may also arise due to uncertainty in the relevant parameters. Suppose we accept the basic model (
11) to hold but are ignorant of the value of parameter
. Besides, we accept that all values for
are equally likely; in this situation, the parameter
should be assumed to have Uniform
distribution. Bayes theorem implies that the distribution at posteriori of
must be given by Equation (
14):
We next show that the above behavior is ubiquitous, so the reset propensity is directly related with the tail’s behavior. Indeed, since the sequence
is strictly monotone and
as
, the Stolz–Cesáro theorem gives
Requiring
, we obtain that asymptotically
must grow as
which is the paradigmatic example of ultimately neutral systems. Note that such
has medium tails. By contrast, tails of the form
give
if
and
if
. The exponential case
, i.e., the geometric distribution, marks the crossover between these cases.
Note that slowly, power-law decaying, sequences such as
also correspond to reset-averse systems ultimately. Thus, heavy tails of the sequence
correspond to reset-averse systems while the opposite holds with medium and light (super-exponential) tails such as those in Equations (
11) and (
18).
Table 1 summarizes all the possibilities.
More complicated tails can be handled noting the behavior of ultimately averse, neutral or inclined reset systems under sums and products. We use
to denote that
(thus,
or 1). Hence, with obvious notation, the sums and product rules for
read
where the symbol
is used to mean that if
As an example, for
, consider the hybrid system
where
. Here,
and tails display mixed exponential and power-law decay. Hence,
correspond to an ultimately neutral system. This is corroborated by an exact evaluation of
. Equation (
10) yields that
2.3. Comments on Markovianness
The fact that the system has a capability for learning (or to forget, see Equations (
11), (
13) and (
14)) suggests the existence of some “memory” in the dynamics, a fact that cast doubt upon the Markovian nature of the model. Actually, there is some hidden memory, although not in
.
This apparent paradox has interesting implications and can be developed further as we now explain. At any time
t, let
be the process that counts the number of resets
“observed” in the time window
. Thus,
if
. Given that
any additional information may result in information relevant to predict its future: if additionally, say
, we infer that a reset has occurred exactly at
t, a valuable information. Hence,
is generically non-Markovian. The only exception is the system (
11); here,
follows a binomial distribution with success parameter
:
By contrast, suppose we know
. This information amounts to saying that the previous reset occurred at
and hence pins down the history of the process after
, viz
. By contrast, the history of the process previous to
remains unknown. Should additional information be provided, it would not help predict the future of
x, since at
the process started anew; hence, only the history after
is relevant, but this is already known. Thus, we arrive at the counter-intuitive fact that
needs not be Markovian but
is. Likewise, the vector chain
is Markovian.
3. Equilibrium Distribution
Here, we consider the large time distribution of the random walk. Call
the limit of the process and
its distribution. When it exists it is also a stationary state, in the sense that if it has initially this distribution then it will not abandon it.
satisfies the system
where
is the transition probability matrix defined in Equation (
3):
To handle this, we divide the matrix in upper and lower parts, connected only by the column and rows with index 0, i.e.,
where
is essentially obtained from
by reflection and
reads (including the
column)
By insertion, we find
along with the recursive system
Solving recursively, we find
Normalization gives
which requires
, i.e.,
must decay at least as
. In this case, defining
, the stationary distribution is
The probability that the random walk has drifted to site n for large times decreases as
does, see
Table 1. Hence, for reset-averse systems,
displays heavy tails (which may even decay in a weak, algebraic way), and so there exists a non-negligible probability to find the system away from the origin at large times. This agrees with the “unwillingness” of the system to return to the origin. The opposite holds for reset-inclined systems where this probability will decrease quicker than exponentially. Concretely, for the cases (
11) and (
13), the stationary distribution is
Finally, for system (
14), there is neither an equilibrium nor a stationary distribution, indicating that the chain spreads out far from the origin and does not settle to an equilibrium.
Writing Equation (
21) as
, it states that the total probability flux from all states
n into
m,
, must equal the flux from state
m into the rest of states. Hence,
satisfies a global balance equations, viz Equation (
21). This does not imply that
is an equilibrium state, only a limit state; for an equilibrium distribution it must satisfy the far stronger “detailed balance” condition:
—which does not hold. This was to be expected since detailed balance guarantees time-reversibility of the dynamics, a trait that the system at hand clearly does not exhibit, as a simple inspection of the trajectories shows.
In the absence of any information, the maximum entropy principle yields that the distribution with maximum entropy should be chosen on the basis that it is the least-informative one. Within the class with fixed finite mean, it is well known that this corresponds to a geometric distribution. It follows from Equation (
28) that this implies that the model satisfies Equation (
11). We conclude that the reset neutral chain (
11) satisfying
, for all
n, and arbitrary
has the remarkable properties of being the only selection that corresponds to a truly Markovian situation (i.e., for both
and the arrival process
) and the one that gives the maximum entropy for fixed mean.
4. Escape Probabilities
In a classical study, W. Feller [
37] showed that most recurrent properties of general diffusion processes can be codified in terms of two of the functions that define escape probabilities from an interval
. Given that the process has started from a general
, Feller considers the “scale and speed functions”, defined as
and shows that they solve certain differential equations (see [
37] for an overview). Here, for any
, we introduce the “hitting time”
which represents the lapse of time necessary to travel from the starting value to
a.
We perform a similar study here and determine, for given levels , the probability that the random walk reaches a before having reached . Note that by translational invariance the case when starts from general is immediately reduced to that with .
We start noting that when resets are switched off the only source of randomness lies in the first displacement of the random walk away from ; hence, for all n if . In this case, —the minimum time to hit either or —is a binary random variable that takes values a and b with probabilities and . Besides, .
Obviously, will increase when a reset mechanism is introduced; it is, however, tempting to think that resets do not affect the escape probabilities, namely still holds. However this is not correct! To dispel such a misinterpretation, note that resets introduce a bias which favors the closest barrier against the farthest one. This is similar to the classical waiting time paradox where cycles with very large inter-reset times have a greater probability than smaller ones. Intuitively, if restarts occur very often, the possibility to reach the farthest barrier diminishes. We now determine this probability.
A very simple argument goes as follows. Consider the probability
that the random walk
reaches
before having reached
when we know that
hits
a or
in the given cycle. The event that escape occurs at a given cycle, say, the first, is
with probability
Hence, the probability that escape occurs via the upper barrier can be evaluated as the probability of
conditional on the event
E having happened:
The reasoning when escape occurs at a general given cycle is a bit more involved but does not change the result.
Denote
the corresponding probability when no resets are introduced. Then,
which means that resets increase the probability to hit first the closest barrier, as expected. Further, when
Equation (
32) yields
.
We thus have for the neutral chain (
11), the reset-averse chain (
13) and the reset-inclined chain (
14), respectively
In the second equality, we introduce , which measures the departure from symmetry of the problem and suppose for ease of notation.