Analyzing Transverse Momentum Spectra of Pions, Kaons and Protons in p–p, p–A and A–A Collisions via the Blast-Wave Model with Fluctuations

Abstract

The transverse momentum spectra of different types of particles, ${\pi }^{\pm }$, $K^{\pm }$, p and $\overline{p}$, produced at mid-(pseudo)rapidity in different centrality lead–lead (Pb–Pb) collisions at 2.76 TeV; proton–lead (p–Pb) collisions at 5.02 TeV; xenon–xenon (Xe–Xe) collisions at 5.44 TeV; and proton–proton (p–p) collisions at 0.9, 2.76, 5.02, 7 and 13 TeV, were analyzed by the blast-wave model with fluctuations. With the experimental data measured by the ALICE and CMS Collaborations at the Large Hadron Collider (LHC), the kinetic freeze-out temperature, transverse flow velocity and proper time were extracted from fitting the transverse momentum spectra. In nucleus–nucleus (A–A) and proton–nucleus (p–A) collisions, the three parameters decrease with the decrease of event centrality from central to peripheral, indicating higher degrees of excitation, quicker expansion velocities and longer evolution times for central collisions. In p–p collisions, the kinetic freeze-out temperature is nearly invariant with the increase of energy, though the transverse flow velocity and proper time increase slightly, in the considered energy range.

1. Introduction

In high-energy collisions, one of the most important questions is the identification of various phases of dense matter. Quark-gluon plasma (QGP) [1,2,3], which is considered a new state of matter, was produced in the early universe shortly after the Big Bang, prior to the condensation in hadrons. High energy nucleus–nucleus (heavy ion) collisions at the large hadron collider (LHC) [4,5,6,7,8] provide another excellent environment with high temperatures and high density under which QGP are expected to form and to live for a longer lifetime than that at the relativistic heavy ion collider (RHIC) [9]. Presently, the LHC has performed four different types of collisions, proton–proton (p–p), proton–lead (p–Pb), lead–lead (Pb–Pb) and xenon–xenon (Xe–Xe) collisions, at different collision energies. The former two with low multiplicity are not expected to form QGP due to small systems and less energy deposition, though the deconfinement of quarks and gluons may appear. The latter two are expected to form QGP due to large systems and high energy. It is possible that the former two with high multiplicity will also form QGP due to violent collisions.

Kinetic freeze-out temperature, transverse flow velocity and proper time are three important parameters with which to characterize the thermal properties of different stages during high-energy p–p, proton–nucleus (p–A) and nucleus–nucleus (A–A) collisions. The proper time reflects the time elapsed from the initial collisions to the stage of kinetic freeze-out. A large proper time represents that the interacting system has a long life. Temperature is an important concept in the physics of high-energy collisions. Usually, papers [6,10,11,12,13] use four types of temperature: initial temperature, chemical freeze-out temperature, kinetic freeze-out temperature and effective temperature. Firstly, the initial temperature describes the excitation degree of the interacting system at the initial stage of collisions. Secondly, the chemical freeze-out temperature describes the excitation degree of the interacting system at the stage of chemical equilibrium, where the chemical components (relative fractions) of particles are no longer changed. Thirdly, the kinetic freeze-out temperature describes the excitation degree of the interacting system at the stage of kinetic and thermal equilibrium in which the (transverse) momentum spectra of particles are no longer changed. Fourthly, the effective temperature is not a real temperature; it is related to particle mass and describes the sum of the excitation degree of the interacting system and the effect of transverse flow at the stage of kinetic freeze-out, where the transverse flow resulted from the impact and squeeze reflects the hydrodynamic expansion of the interacting system.

Generally, since the initial stage of collisions happens earlier than (or alongside) the stage of chemical freeze-out, the initial temperature is larger than (or equal to) the chemical freeze-out temperature. The chemical freeze-out temperature is equal to or larger than the kinetic freeze-out temperature, as the chemical equilibrium comes about at the same time as or before the kinetic equilibrium. It is usually obtained from the particle ratios [14,15,16]. The effective temperature is larger than the kinetic freeze-out temperature due to mass and flow effects [17,18]. It can be extracted from the transverse momentum spectra by using some distribution laws, such as the standard (Boltzmann, Fermi–Dirac and Bose–Einstein) distributions, the Tsallis distribution and so forth. The kinetic freeze-out temperature can be extracted from the transverse momentum spectra using models such as the blast-wave model with Boltzmann–Gibbs statistics, the blast-wave model with Tsallis statistics and the blast-wave model with fluctuations. Usually, the initial, chemical freeze-out and kinetic freeze-out temperatures are real temperatures.

We were very interested in studying the transverse excitation, the dynamic expansion characteristic and the lifetime of the interacting system, as their relation is important for mapping the phase diagram, and with them we could obtain some information about the proper time. In order to extract some quantities and study their dependences on event centrality and collision energy, we may use some models to analyze the particle spectra. These models include, but are not limited to, the blast-wave model with Boltzmann–Gibbs statistics [19,20], the blast-wave model with Tsallis statistics [21,22,23] and the alternative method [24,25,26,27,28] based on the standard distribution (including Boltzmann, Fermi-Dirac and Bose–Einstein distributions) or Tsallis distribution. The blast-wave model is a traditional and current method; it has very widespread applicability. The model makes the simple assumption that particles are locally thermalized in a hard-sphere, uniform-density source at a kinetic freeze-out temperature and are moving with a common collective manner in a transverse radial flow velocity field. In the alternative method, the kinetic freeze-out temperature is regarded as the intercept in the linear relation between effective temperature and rest mass, and the transverse flow velocity is regarded as the slope in the linear relation between mean transverse momenta and mean energy. Like the alternative method, too, the traditional blast-wave model can only extract the kinetic freeze-out temperature and transverse flow velocity. By inheritance and through development, the blast-wave model with fluctuations can extract the kinetic freeze-out temperature, transverse flow velocity and proper time simultaneously.

To understand the thermal properties of different stages of high energy collisions, we applied the blast-wave model with fluctuations to study the transverse momentum ($p_T$) spectra of different particles produced in A–A, p–A and p–p collisions at the LHC. The kinetic freeze-out temperature ($T_0$), transverse flow velocity (${\beta }_T$) and uncorrected proper time ($\tau$) were extracted from Pb–Pb collisions at 2.76 TeV; p–Pb collisions at 5.02 TeV; Xe–Xe collisions at 5.44 TeV; and p–p collisions at 0.9, 2.76, 5.02, 7 and 13 TeV. The cited experimental data were measured by the ALICE [29,30,31,32] and CMS Collaborations [33,34]. The changing trends of related parameters with event centrality and collision energy were then obtained and analyzed.

The paper is organized as follows. The formalism and method are briefly described in Section 2. Results and discussion are given in Section 3. Finally, we summarize our main observations and conclusions in Section 4.

2. Formalism and Method

High-energy collisions are complex processes in which many emission sources are formed. Sources with the same excitation degree may form a local equilibrium state which can be described by the standard distribution. For different equilibrium states which have different excitation degrees, different temperature parameters may be used. At the same time, we neglect the quantum effect and chemical potential due to their small influences on the $p_T$ spectra in high-energy collisions.

According to the invariant phase-space source emission distribution of Schnedermann, Sollfrank and Heinz (SSH) [19], Tomášik, Wiedemann and Heinz [35] further developed the blast-wave model with fluctuations. In this model the invariant momentum distribution is calculated by integrating over the space-time coordinates of the source function. According to [35,36], the blast-wave model with fluctuations results in the invariant momentum distribution as follows:

$$\begin{array}{cc}\hfill E\frac{d^{3}N}{d{p}^3}=& \frac{\tau m_T}{4{\pi }^2{\hslash }^3}coshy{\int }_0^{R}rdrG\left(r\right)e^{{\mu }_0/T_0}\hfill \\ \hfill & \times I_0\left[\frac{p_T}{T_0}sinh{\eta }_T\left(r\right)\right]{\int }_{{\eta }_{smin}}^{{\eta }_{smax}}d{\eta }_{s}cosh{\eta }_{s}H\left({\eta }_s\right)\hfill \\ \hfill & \times exp\left[-\frac{m_T}{T_0}coshycosh{\eta }_T\left(r\right)cosh{\eta }_s\right],\hfill \end{array}$$

(1)

where $\tau$ is the proper time considered by us as an uncorrected quantity, $m_T=\sqrt{p_T^2+m_0^2}$ is the transverse mass, $m_0$ is the rest mass, ${\mu }_0$ is chemical potential—which is chosen to be 0 at high energy, $T_0$ is the kinetic freeze-out temperature of emission source, $I_0$ is the modified Bessel functions of the first kind,

$$\begin{array}{c}\hfill {\eta }_T\left(r\right)=\frac{1}{2}ln\frac{1+\beta \left(r\right)}{1-\beta \left(r\right)}\end{array}$$

(2)

is the transverse flow rapidity, $\beta \left(r\right)={\beta }_S{(r/R)}^{n_0}$ is a self-similar flow profile, ${\beta }_S$ is the flow velocity on the surface of the thermal source, r and R are, respectively, the radial position and its maximum in the thermal system, ${\eta }_s$ is the source rapidity, $n_0$ is a free parameter which is customarily chosen to be 2 [19] due to the quadratic profile resembling the solutions of hydrodynamics closest [37] and $G\left(r\right)$ and $H\left({\eta }_s\right)$ are, respectively, the transverse and longitudinal source distributions. Generally, transverse flow velocity is ${\beta }_T=(2/R^2){\int }_0^{R}r\beta \left(r\right)dr=2{\beta }_S/(n_0+2)$. In the case of $n_0=2$ as used in [19], we have ${\beta }_T=0.5{\beta }_S$ [38]. $n_0$ is not a sensitive quantity. It does not matter if $n_0=1$ or $n_0=2$. When we choose $n_0=1$, the results are similar. To be compatible with [35,36], we used $n_0=2$.

For a single source emission, one has ${\eta }_s=0$, $G\left(r\right)=1$ and $H\left({\eta }_s\right)=1$. In the natural system of units, where $\hslash =1$, Equation (1) is simplified as follows:

$$\begin{array}{cc}\hfill E\frac{d^{3}N}{d{p}^3}=& \frac{\tau }{4{\pi }^2}{m}_{T}coshy{\int }_0^{R}rdr{e}^{{\mu }_0/T_0}\hfill \\ \hfill & \times I_0\left[\frac{p_T}{T_0}sinh{\eta }_T\left(r\right)\right]\hfill \\ \hfill & \times exp\left[-\frac{m_T}{T_0}coshycosh{\eta }_T\left(r\right)\right].\hfill \end{array}$$

(3)

The blast-wave model with fluctuations results in the united density function of y and $p_T$ as follows:

$$\begin{array}{cc}\hfill \frac{d^{2}N}{dyd{p}_T}=& \frac{\tau }{2\pi }{p}_T{m}_{T}coshy{\int }_0^{R}rdr{e}^{({\mu }_0/T_0)}\hfill \\ \hfill & \times I_0\left[\frac{p_T}{T_0}sinh{\eta }_T\left(r\right)\right]\hfill \\ \hfill & \times exp\left[-\frac{m_T}{T_0}coshycosh{\eta }_T\left(r\right)\right].\hfill \end{array}$$

(4)

According to the general expression of invariant momentum, the normalized factor in Equation (1) is $\tau /4{\pi }^2=gV/{\left(2\pi \right)}^3$. For pseudoscalar particles ${\pi }^{+}$, ${\pi }^{-}$, $K^{+}$ and $K^{-}$, the degeneracy factor is $g=1$. For p and $\overline{p}$, we have $g=2$ due to their spin being $1/2$. For sphere volume, $V=(4/3)\pi R^3$, where R is the maximum range of light particles at the kinetic freeze-out. Then, we obtain the real or corrected proper time ${\tau }_0={\left(1.5\tau \right)}^{1/3}$ for emissions of ${\pi }^{+}$, ${\pi }^{-}$, $K^{+}$ and $K^{-}$; and ${\tau }_0={\left(0.75\tau \right)}^{1/3}$ for emissions of p and $\overline{p}$.

3. Results and Discussion

Figure 1 presents the transverse momentum spectra, ($1/N_{EV}){\left(2\pi p_T\right)}^{-1}{d}^{2}N/\left(dyd{p}_T\right)$, of (a) ${\pi }^{+}$, (b) ${\pi }^{-}$, (c) $K^{+}$, (d) $K^{-}$, (e) p and (f) $\overline{p}$ produced in Pb–Pb collisions in different centralities at $\sqrt{s_{NN}}=2.76$ TeV in the rapidity range $\left|y\right|<0.5$. $N_{EV}$ which is usually omitted on the vertical axis denotes the number of events. The symbols represent the experimental data measured by the ALICE Collaboration in different centralities [29] and the curves are our fitting results by using the blast-wave model with fluctuations, i.e., Equation (4). In the fitting, the method of least squares was used to get the minimized ${\chi }^2$. The substantially near event centralities, the values of free parameters’ kinetic freeze-out temperature $T_0$, the transverse flow velocity ${\beta }_T$ and proper time $\tau$; and the ${\chi }^2$ degrees of freedom (dof) and corrected proper time ${\tau }_0$ corresponding to the fit are listed in Table 1. In some cases, the ${\chi }^2$ is large, which indicates that the fitting was qualitative and approximately acceptable, and the large dispersion between the curve and data exists. In most cases, one can see the good approximate descriptions of the model results for the experimental data of the ALICE Collaboration in the $p_T$ spectra of the identified particles produced in different centralities for Pb–Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV.

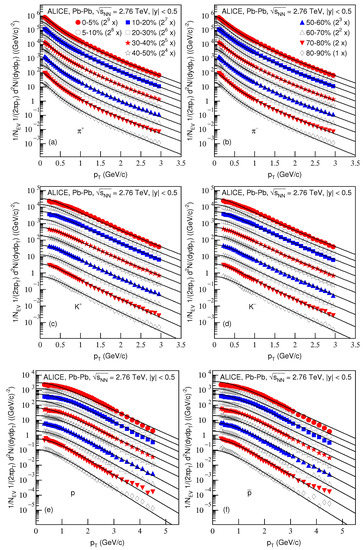
Figure 1. Transverse momentum spectra of (a) ${\pi }^{+}$, (b) ${\pi }^{-}$, (c) $K^{+}$, (d) $K^{-}$, (e) p and (f) $\overline{p}$ produced in Pb–Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV in the rapidity range $\left|y\right|<0.5$. The closed (open) symbols represent the experimental data measured by the ALICE Collaboration in centralities 0–5%, 5–10%, 10–20%, 20–30%, 30–40%, 40–50%, 50–60%, 60–70%, 70–80% and 80–90% [29]; the spectra for the same particle in different centralities were multiplied by the factor of $2^n$ for the clarity—n changed from 9 to 0 with the event centrality changing from 0–5% to 80–90%. The curves are our fitting results obtained by using the blast-wave model with fluctuations, Equation (4).

Table 1. Values of parameters ($T_0$, ${\beta }_T$ and $\tau$), ${\chi }^2$, dof and ${\tau }_0$ corresponding to the fits of the blast-wave model with fluctuations. The collision types, centrality and particle types are listed for clarity.

Figure	Centrality	Particle	${\mathit{T}}_0$ (GeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	$\mathit{\tau }$ (fm/c)	${\mathit{\chi }}^2$/dof	${\mathit{\tau }}_0$ (fm/c)
1a	0–5%	${\pi }^{+}$	$0.075\pm 0.006$	$0.477\pm 0.006$	203,000.0 ± 20,900.0	50.7/38	$67.276\pm 2.309$
Pb–Pb	5–10%		$0.075\pm 0.004$	$0.477\pm 0.004$	170,000.0 ± 18,000.0	48.8/38	$63.413\pm 2.238$
	10–20%		$0.075\pm 0.004$	$0.477\pm 0.004$	130,000.0 ± 14,000.0	44.3/38	$57.989\pm 2.082$
	20–30%		$0.075\pm 0.004$	$0.477\pm 0.004$	90,000.0 ± 9900.0	50.5/38	$51.299\pm 1.881$
	30–40%		$0.075\pm 0.004$	$0.477\pm 0.004$	56,000.0 ± 6100.0	28.4/38	$43.795\pm 1.590$
	40–50%		$0.075\pm 0.004$	$0.477\pm 0.004$	34,000.0 ± 3700.0	19.5/38	$37.084\pm 1.345$
	50–60%		$0.074\pm 0.004$	$0.477\pm 0.004$	19,000.0 ± 2200.0	44.1/38	$30.546\pm 1.179$
	60–70%		$0.074\pm 0.004$	$0.477\pm 0.004$	10,000.0 ± 1200.0	43.5/38	$24.662\pm 0.986$
	70–80%		$0.069\pm 0.004$	$0.480\pm 0.004$	$6900.0\pm 780.0$	335.9/38	$21.792\pm 0.821$
	80–90%		$0.066\pm 0.004$	$0.479\pm 0.004$	$2900.0\pm 310.0$	97.6/38	$16.324\pm 0.582$
1b	0–5%	${\pi }^{-}$	$0.075\pm 0.006$	$0.478\pm 0.006$	198,000.0 ± 20,600.0	68.6/38	$66.719\pm 2.314$
Pb–Pb	5–10%		$0.075\pm 0.004$	$0.478\pm 0.004$	165,000.0 ± 17,000.0	58.2/38	$62.785\pm 2.156$
	10–20%		$0.075\pm 0.004$	$0.478\pm 0.004$	128,000.0 ± 13,000.0	43.7/38	$57.690\pm 1.953$
	20–30%		$0.075\pm 0.004$	$0.478\pm 0.004$	85,000.0 ± 9500.0	32.6/38	$50.331\pm 1.875$
	30–40%		$0.075\pm 0.004$	$0.478\pm 0.004$	54,000.0 ± 5900.0	22.2/38	$43.267\pm 1.576$
	40–50%		$0.075\pm 0.004$	$0.478\pm 0.004$	33,000.0 ± 3700.0	15.2/38	$36.717\pm 1.372$
	50–60%		$0.074\pm 0.004$	$0.478\pm 0.004$	19,000.0 ± 2200.0	25.0/38	$30.546\pm 1.179$
	60–70%		$0.074\pm 0.004$	$0.478\pm 0.004$	10,000.0 ± 1200.0	45.0/38	$24.662\pm 0.986$
	70–80%		$0.069\pm 0.004$	$0.480\pm 0.004$	$6600.0\pm 700.0$	184.1/38	$21.472\pm 0.759$
	80–90%		$0.066\pm 0.004$	$0.478\pm 0.004$	$2900.0\pm 310.0$	98.3/38	$16.324\pm 0.582$
1c	0–5%	$K^{+}$	$0.148\pm 0.006$	$0.424\pm 0.010$	$9900.0\pm 1000.0$	87.9/33	$24.580\pm 0.828$
Pb–Pb	5–10%		$0.148\pm 0.006$	$0.424\pm 0.010$	$8500.0\pm 1800.0$	68.7/33	$23.362\pm 1.649$
	10–20%		$0.148\pm 0.006$	$0.424\pm 0.010$	$6400.0\pm 800.0$	58.2/33	$21.253\pm 0.886$
	20–30%		$0.148\pm 0.006$	$0.424\pm 0.010$	$4400.0\pm 550.0$	40.2/33	$18.758\pm 0.782$
	30–40%		$0.148\pm 0.006$	$0.424\pm 0.010$	$2800.0\pm 400.0$	18.5/33	$16.134\pm 0.768$
	40–50%		$0.148\pm 0.006$	$0.424\pm 0.010$	$1700.0\pm 300.0$	14.9/33	$13.662\pm 0.804$
	50–60%		$0.148\pm 0.006$	$0.414\pm 0.010$	$900.0\pm 110.0$	24.9/33	$11.052\pm 0.450$
	60–70%		$0.146\pm 0.006$	$0.414\pm 0.010$	$500.0\pm 80.0$	20.8/33	$9.086\pm 0.485$
	70–80%		$0.137\pm 0.005$	$0.414\pm 0.008$	$350.0\pm 60.0$	92.5/33	$8.067\pm 0.461$
	80–90%		$0.133\pm 0.005$	$0.414\pm 0.008$	$140.0\pm 40.0$	50.3/33	$5.944\pm 0.566$
1d	0–5%	$K^{-}$	$0.148\pm 0.006$	$0.424\pm 0.010$	10,100.0 ± 1100.0	58.3/33	$24.744\pm 0.898$
Pb–Pb	5–10%		$0.148\pm 0.006$	$0.424\pm 0.010$	$8400.0\pm 1600.0$	55.3/33	$23.270\pm 1.477$
	10–20%		$0.148\pm 0.006$	$0.424\pm 0.010$	$6300.0\pm 780.0$	46.7/33	$21.142\pm 0.873$
	20–30%		$0.148\pm 0.006$	$0.424\pm 0.010$	$4300.0\pm 550.0$	25.3/33	$18.614\pm 0.794$
	30–40%		$0.148\pm 0.006$	$0.424\pm 0.010$	$2800.0\pm 400.0$	13.3/33	$16.134\pm 0.768$
	40–50%		$0.148\pm 0.006$	$0.424\pm 0.010$	$1700.0\pm 300.0$	14.8/33	$13.662\pm 0.804$
	50–60%		$0.148\pm 0.006$	$0.414\pm 0.010$	$960.0\pm 110.0$	13.4/33	$11.292\pm 0.431$
	60–70%		$0.146\pm 0.006$	$0.414\pm 0.010$	$500.0\pm 80.0$	25.8/33	$9.086\pm 0.485$
	70–80%		$0.137\pm 0.005$	$0.414\pm 0.008$	$350.0\pm 60.0$	95.0/33	$8.067\pm 0.461$
	80–90%		$0.133\pm 0.005$	$0.414\pm 0.008$	$140.0\pm 40.0$	66.7/33	$5.944\pm 0.566$
1e	0–5%	p	$0.350\pm 0.006$	$0.260\pm 0.010$	$185.0\pm 22.0$	243.0/39	$5.177\pm 0.205$
Pb–Pb	5–10%		$0.350\pm 0.006$	$0.260\pm 0.010$	$150.0\pm 28.0$	238.1/39	$4.827\pm 0.300$
	10–20%		$0.345\pm 0.006$	$0.260\pm 0.010$	$133.0\pm 20.0$	160.8/39	$4.638\pm 0.232$
	20–30%		$0.336\pm 0.006$	$0.260\pm 0.010$	$102.0\pm 22.0$	120.9/39	$4.245\pm 0.305$
	30–40%		$0.331\pm 0.006$	$0.260\pm 0.010$	$70.0\pm 17.0$	87.9/39	$3.744\pm 0.303$
	40–50%		$0.331\pm 0.006$	$0.250\pm 0.010$	$44.0\pm 9.0$	68.1/39	$3.208\pm 0.219$
	50–60%		$0.331\pm 0.006$	$0.210\pm 0.010$	$26.0\pm 6.0$	53.4/39	$2.692\pm 0.207$
	60–70%		$0.319\pm 0.006$	$0.210\pm 0.010$	$17.0\pm 3.0$	101.5/39	$2.336\pm 0.137$
	70–80%		$0.287\pm 0.006$	$0.220\pm 0.010$	$15.0\pm 3.0$	222.7/39	$2.241\pm 0.149$
	80–90%		$0.251\pm 0.006$	$0.249\pm 0.010$	$10.0\pm 2.0$	95.6/39	$1.957\pm 0.131$
1f	0–5%	$\overline{p}$	$0.350\pm 0.006$	$0.260\pm 0.010$	$185.0\pm 22.0$	174.0/39	$5.177\pm 0.205$
Pb–Pb	5–10%		$0.350\pm 0.006$	$0.260\pm 0.010$	$150.0\pm 28.0$	197.0/39	$4.827\pm 0.300$
	10–20%		$0.345\pm 0.006$	$0.260\pm 0.010$	$133.0\pm 20.0$	143.6/39	$4.638\pm 0.232$
	20–30%		$0.336\pm 0.006$	$0.260\pm 0.010$	$102.0\pm 22.0$	106.2/39	$4.245\pm 0.305$
	30–40%		$0.331\pm 0.006$	$0.260\pm 0.010$	$75.0\pm 18.0$	81.8/39	$3.832\pm 0.307$
	40–50%		$0.331\pm 0.006$	$0.250\pm 0.010$	$44.0\pm 9.0$	101/39	$3.208\pm 0.219$
	50–60%		$0.331\pm 0.006$	$0.210\pm 0.010$	$29.0\pm 6.0$	47.0/39	$2.791\pm 0.193$
	60–70%		$0.319\pm 0.006$	$0.210\pm 0.010$	$17.0\pm 3.0$	92.1/39	$2.336\pm 0.137$
	70–80%		$0.287\pm 0.006$	$0.220\pm 0.010$	$15.0\pm 3.0$	144.1/39	$2.241\pm 0.149$
	80–90%		$0.251\pm 0.006$	$0.249\pm 0.010$	$10.0\pm 2.0$	115.1/39	$1.957\pm 0.131$
3a	0–5%	(${\pi }^{+}+{\pi }^{-})/2$	$0.077\pm 0.004$	$0.481\pm 0.004$	163,500.0 ± 22,250.0	78.1/38	$62.595\pm 2.839$
p–Pb	5–10%		$0.075\pm 0.004$	$0.481\pm 0.004$	143,500.0 ± 19,680.0	62.3/38	$59.930\pm 2.740$
	10–20%		$0.075\pm 0.004$	$0.481\pm 0.004$	123,500.0 ± 16,550.0	82.3/38	$57.006\pm 2.546$
	20–40%		$0.074\pm 0.004$	$0.481\pm 0.004$	103,500.0 ± 15,500.0	170.6/38	$53.746\pm 2.683$
	40–60%		$0.074\pm 0.003$	$0.479\pm 0.004$	72,000.0 ± 10,650.0	183.1/38	$47.622\pm 2.348$
	60–80%		$0.073\pm 0.003$	$0.477\pm 0.004$	47,000.0 ± 6200.0	277.2/38	$41.311\pm 1.817$
	80–100%		$0.069\pm 0.003$	$0.475\pm 0.004$	22,000.0 ± 2305.0	516.5/38	$32.075\pm 1.120$
3b	0–5%	($K^{+}+K^{-})/2$	$0.139\pm 0.005$	$0.448\pm 0.010$	12,000.0 ± 1805.0	15.8/28	$26.207\pm 1.314$
p–Pb	5–10%		$0.139\pm 0.005$	$0.448\pm 0.010$	$9500.0\pm 1410.0$	5.7/28	$24.244\pm 1.199$
	10–20%		$0.139\pm 0.005$	$0.446\pm 0.010$	$8000.0\pm 2005.0$	2.7/28	$22.894\pm 1.913$
	20–40%		$0.139\pm 0.005$	$0.438\pm 0.010$	$6300.0\pm 965.0$	7.4/28	$21.142\pm 1.079$
	40–60%		$0.136\pm 0.005$	$0.432\pm 0.010$	$5000.0\pm 670.0$	35.0/28	$19.574\pm 0.874$
	60–80%		$0.130\pm 0.005$	$0.428\pm 0.010$	$3700.0\pm 448.0$	50.0/28	$17.705\pm 0.715$
	80–100%		$0.112\pm 0.005$	$0.425\pm 0.010$	$3450.0\pm 410.0$	125.9/28	$17.297\pm 0.685$
3c	0–5%	($p+\overline{p})/2$	$0.221\pm 0.007$	$0.393\pm 0.014$	$2150.0\pm 291.0$	41.8/36	$11.726\pm 0.529$
p–Pb	5–10%		$0.221\pm 0.007$	$0.393\pm 0.014$	$1650.0\pm 232.0$	26.7/36	$10.736\pm 0.503$
	10–20%		$0.221\pm 0.007$	$0.385\pm 0.014$	$1445.0\pm 223.0$	21.3/36	$10.272\pm 0.528$
	20–40%		$0.218\pm 0.006$	$0.374\pm 0.014$	$1245.0\pm 185.0$	37.6/36	$9.774\pm 0.484$
	40–60%		$0.206\pm 0.006$	$0.364\pm 0.014$	$1245.0\pm 185.0$	57.7/36	$9.774\pm 0.484$
	60–80%		$0.191\pm 0.006$	$0.355\pm 0.014$	$1195.0\pm 166.0$	116.1/36	$9.641\pm 0.446$
	80–100%		$0.169\pm 0.005$	$0.324\pm 0.014$	$1195.0\pm 166.0$	192.5/36	$9.641\pm 0.446$
5a	0–5%	(${\pi }^{+}+{\pi }^{-})/2$	$0.101\pm 0.006$	$0.468\pm 0.007$	67,892.5 ± 8920.0	19.5/38	$46.697\pm 2.045$
Xe–Xe	5–10%		$0.101\pm 0.006$	$0.468\pm 0.007$	49,892.5 ± 6044.0	19.2/38	$42.141\pm 1.702$
	10–20%		$0.101\pm 0.006$	$0.468\pm 0.007$	41,392.5 ± 4678.0	23.9/38	$39.598\pm 1.492$
	20–30%		$0.101\pm 0.006$	$0.468\pm 0.007$	27,892.5 ± 3462.0	40.6/38	$34.716\pm 1.436$
	30–40%		$0.099\pm 0.006$	$0.468\pm 0.007$	20,392.5 ± 2569.0	42.4/38	$31.274\pm 1.313$
	40–50%		$0.097\pm 0.006$	$0.468\pm 0.007$	13,142.5 ± 1581.0	53.0/38	$27.014\pm 1.083$
	50–60%		$0.094\pm 0.000$	$0.468\pm 0.000$	$8642.5\pm 1056.0$	109.1/38	$23.491\pm 0.957$
	60–70%		$0.094\pm 0.006$	$0.468\pm 0.007$	$4642.5\pm 559.0$	79.8/38	$19.096\pm 0.766$
	70–90%		$0.091\pm 0.006$	$0.468\pm 0.007$	$2042.5\pm 349.0$	69.3/38	$14.524\pm 0.827$
5b	0–5%	($K^{+}+K^{-})/2$	$0.155\pm 0.006$	$0.423\pm 0.010$	$8392.5\pm 1418.0$	18.1/30	$23.263\pm 1.310$
Xe–Xe	5–10%		$0.155\pm 0.006$	$0.423\pm 0.010$	$6892.5\pm 833.0$	13.5/30	$21.785\pm 0.878$
	10–20%		$0.155\pm 0.006$	$0.423\pm 0.010$	$5192.5\pm 569.0$	10.5/30	$19.822\pm 0.724$
	20–30%		$0.155\pm 0.006$	$0.423\pm 0.010$	$3692.5\pm 478.0$	5.4/30	$17.693\pm 0.763$
	30–40%		$0.152\pm 0.006$	$0.423\pm 0.010$	$2342.5\pm 355.0$	3.4/30	$15.203\pm 0.768$
	40–50%		$0.152\pm 0.006$	$0.423\pm 0.010$	$1606.0\pm 205.0$	5.1/30	$13.405\pm 0.570$
	50–60%		$0.152\pm 0.006$	$0.420\pm 0.010$	$906.0\pm 121.0$	5.4/30	$11.077\pm 0.493$
	60–70%		$0.148\pm 0.006$	$0.418\pm 0.010$	$552.5\pm 66.0$	13.8/30	$9.393\pm 0.374$
	70–90%		$0.139\pm 0.005$	$0.405\pm 0.008$	$277.5\pm 30.0$	20.2/30	$7.467\pm 0.269$
5c	0–5%	($p+\overline{p})/2$	$0.374\pm 0.009$	$0.221\pm 0.016$	$147.5\pm 23.0$	37.9/32	$4.800\pm 0.250$
Xe–Xe	5–10%		$0.374\pm 0.009$	$0.221\pm 0.016$	$119.5\pm 22.0$	37.6/32	$4.475\pm 0.275$
	10–20%		$0.374\pm 0.009$	$0.221\pm 0.016$	$92.5\pm 16.0$	30.6/32	$4.109\pm 0.237$
	20–30%		$0.374\pm 0.009$	$0.221\pm 0.016$	$65.0\pm 13.0$	19.4/32	$3.653\pm 0.244$
	30–40%		$0.374\pm 0.009$	$0.221\pm 0.016$	$42.5\pm 10.0$	14.1/32	$3.171\pm 0.249$
	40–50%		$0.364\pm 0.009$	$0.208\pm 0.016$	$32.5\pm 6.5$	11.0/32	$2.899\pm 0.193$
	50–60%		$0.348\pm 0.009$	$0.196\pm 0.016$	$22.5\pm 5.5$	13.8/32	$2.565\pm 0.209$
	60–70%		$0.327\pm 0.007$	$0.180\pm 0.013$	$18.5\pm 3.5$	17.5/32	$2.403\pm 0.152$
	70–90%		$0.290\pm 0.006$	$0.176\pm 0.013$	$12.5\pm 2.5$	41.7/29	$2.109\pm 0.141$

To see the dispersions of the curve from the data, Figure 1 continued (Figure 2) presents the ratios of data/fit. The panels a*–f* correspond to Figure 1a–f, respectively. The different closed (open) symbols represent the data/fit values corresponding to different centralities marked in Figure 2. Indeed, in some $p_T$ regions, the ratios are large. This means that the dispersions between the curve and data are large, and the fits are only qualitative and approximate in some cases.

Figure 2. The ratios of data/fit. Panels (a*–f*) correspond to Figure 1a–f, respectively. The different closed (open) symbols represent the data/fit values corresponding to different centralities marked in the Figure 1.

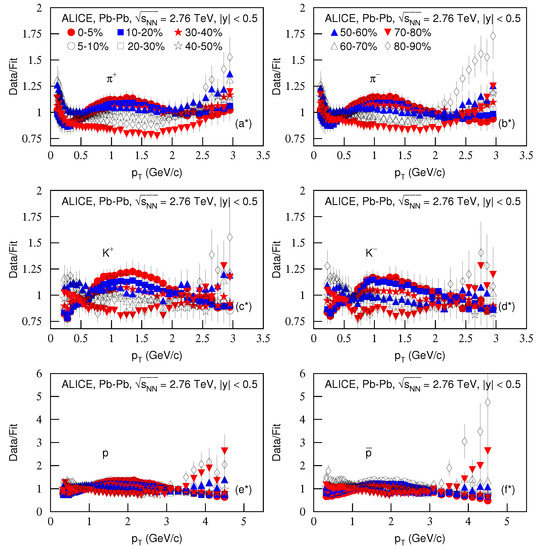
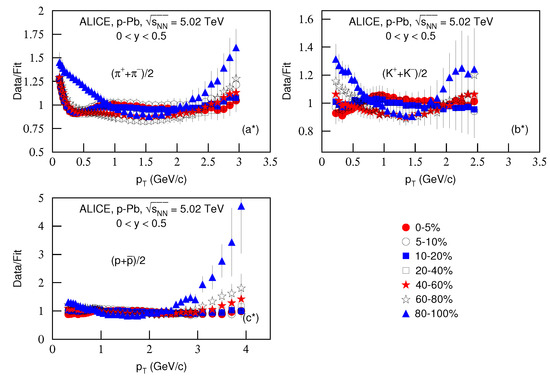
Figure 3 is the same as Figure 1, but it shows the spectra of (a) $({\pi }^{+}+{\pi }^{-}$)/2, (b) $(K^{+}+K^{-})/2$ and (c) $(p+\overline{p})/2$ produced in p–Pb collisions at $\sqrt{s_{NN}}=5.02$ TeV in $0<y<0.5$. The symbols represent the experimental data measured by the ALICE Collaboration [30]. The related parameters and the centralities are listed together in Table 1. One can see the good approximation the model produced of the experimental data of the ALICE Collaboration in the $p_T$ spectra of identified particles produced in different centrality p–Pb collisions at $\sqrt{s_{NN}}=5.02$ TeV.

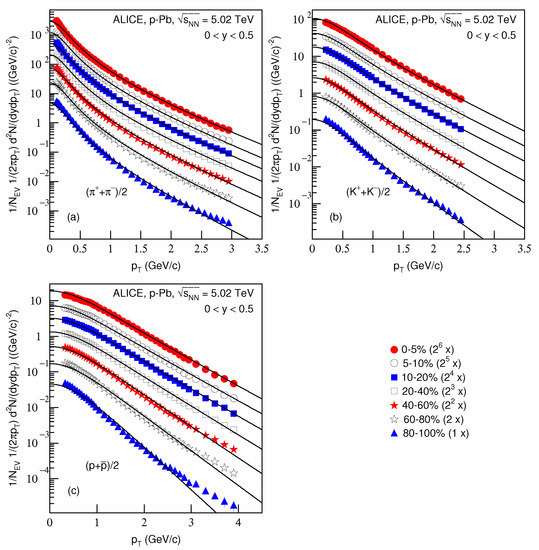
Figure 3. Same as Figure 1, but showing the spectra of (a) $({\pi }^{+}+{\pi }^{-})/2$, (b) $(K^{+}+K^{-})/2$ and (c) $(p+\overline{p})/2$ produced in p–Pb collisions at $\sqrt{s_{NN}}=5.02$ TeV in $0<y<0.5$. The closed (open) symbols represent the experimental data measured by the ALICE Collaboration in centralities 0–5%, 5–10%, 10–20%, 20–40%, 40–60%, 60–80% and 80–100% [30]. The spectra are scaled by the factor of $2^n$, where n changes from 6 to 0 with the event centrality changing from 0–5% to 80–100%.

Figure 4 is the same as Figure 2, but it presents the ratios of data/fit, in which panels a*–c* correspond to Figure 3a–c, respectively. The different closed (open) symbols represent the data/fit values corresponding to different centralities marked in the figure. One can see again that, in some $p_T$ regions, the ratios are large, which means large dispersions between the curve and data. In some cases, the fits are only qualitative and approximate.

Figure 4. Same as Figure 2, but panels (a*–c*) correspond to Figure 3a–c, respectively.

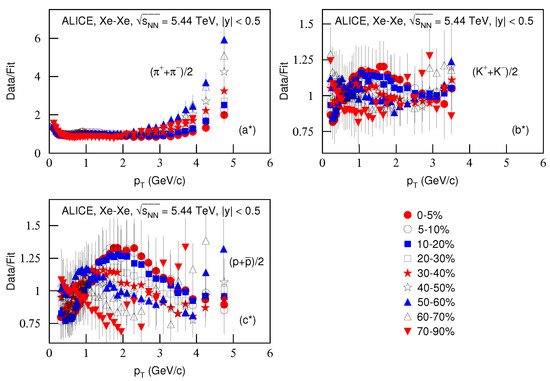
Figure 5 is the same as Figure 1 and Figure 3, but it shows the spectra, ($1/N_{EV})d^{2}N/\left(dyd{p}_T\right)$, of (a) $({\pi }^{+}+{\pi }^{-})/2$, (b) $(K^{+}+K^{-})/2$ and (c) $(p+\overline{p})/2$ produced in Xe–Xe collisions at $\sqrt{s_{NN}}=5.44$ TeV in $\left|y\right|<0.5$. The symbols represent the experimental data measured by the ALICE Collaboration [31]. The related parameters and the centralities are listed together in Table 1. One can see the good approximation the model produced of the experimental data of the ALICE Collaboration in the $p_T$ spectra of particles produced in different centrality Xe–Xe collisions at $\sqrt{s_{NN}}=5.44$ TeV.

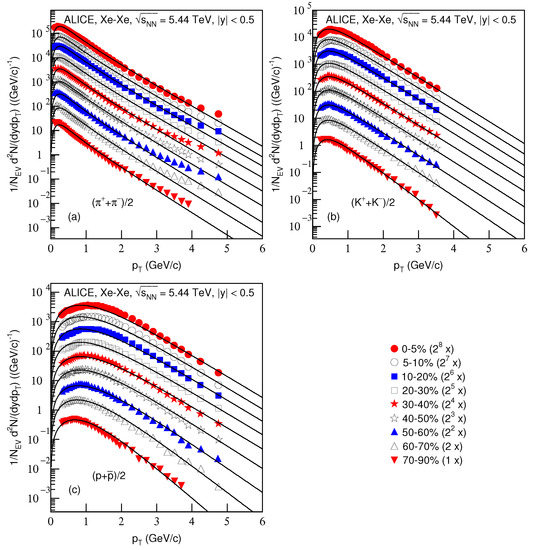
Figure 5. Same as Figure 1, but showing the spectra of (a) $({\pi }^{+}+{\pi }^{-})/2$, (b) $(K^{+}+K^{-})/2$ and (c) $(p+\overline{p})/2$ produced in Xe–Xe collisions at $\sqrt{s_{NN}}=5.44$ TeV in $\left|y\right|<0.5$. The closed (open) symbols represent the experimental data measured by the ALICE Collaboration in centralities 0–5%, 5–10%, 10–20%, 20–30%, 30–40%, 40–50%, 50–60%, 60–70% and 70–90% [31]. The spectra were scaled by the factor of $2^n$; n changed from 8 to 0 with the event centrality changing from 0–5% to 70–90%.

Figure 6 is the same as Figure 2 and Figure 4, but it presents the ratios of data/fit in which panels a*–c* correspond to Figure 5a–c, respectively. The different closed (open) symbols represent the data/fit values corresponding to different centralities marked in the figure. The same conclusions obtained from Figure 2 and Figure 4 can be obtained from Figure 6.

Figure 6. Same as Figure 2, but panels (a*–c*) correspond to Figure 5a–c, respectively.

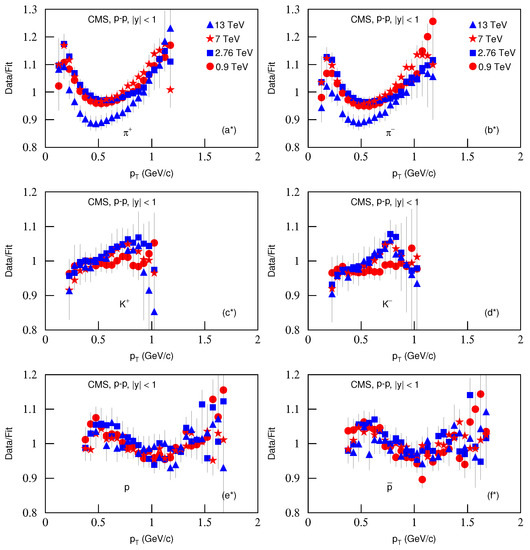
Figure 7 is the same as Figure 5, but it shows the spectra of (a) ${\pi }^{+}$, (b) ${\pi }^{-}$, (c) $K^{+}$, (d) $K^{-}$, (e) p and (f) $\overline{p}$ produced in p–p collisions in $\left|y\right|<1$. The symbols represent the experimental data measured by the CMS Collaboration at $\sqrt{s}=0.9$, 2.76, 7 and 13 TeV [33,34]. The energy and related parameters are listed in Table 2. One can see the good approximation the model produced of the experimental data of the CMS Collaboration in the $p_T$ spectra of identified particles produced in p–p collisions at different energies.

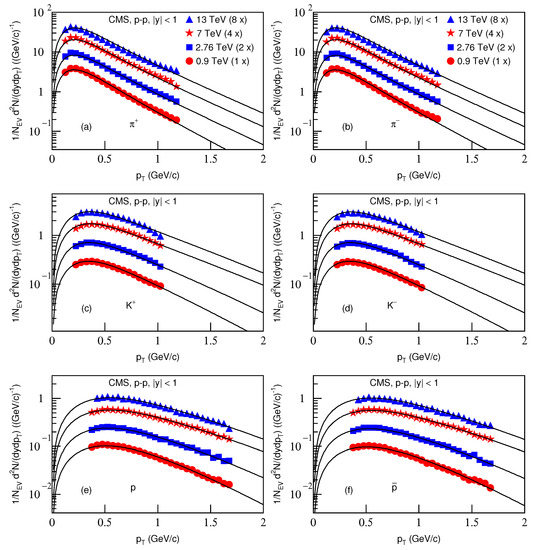
Figure 7. Same as Figure 5, but showing the spectra of (a) ${\pi }^{+}$, (b) ${\pi }^{-}$, (c) $K^{+}$, (d) $K^{-}$, (e) p and (f) $\overline{p}$, produced in p–p collisions in $\left|y\right|<1$. The symbols represent the experimental data measured by the CMS Collaboration at $\sqrt{s}=0.9$, 2.76, 7 and 13 TeV [33,34]; the spectra for the same particle in different centralities were multiplied by different amounts shown in the panels for clarity. The spectra were scaled by a factor of $2^n$; n changed from 0 to 3 with the energy changing from 0.9 to 2.76 TeV.

Table 2. Values of parameters ($T_0$, ${\beta }_T$ and $\tau$), ${\chi }^2$, dof and ${\tau }_0$ corresponding to the fits of blast-wave model with fluctuations. The collision type, energy type and particle type are listed for clarity.

Figure	Energy (TeV)	Particle	${\mathit{T}}_0$ (GeV)	${\mathit{\beta }}_{\mathit{T}}$ (c)	$\mathit{\tau }$ (fm/c)	${\mathit{\chi }}^2$/dof	${\mathit{\tau }}_0$ (fm/c)
7a	0.9	${\pi }^{+}$	$0.100\pm 0.005$	$0.423\pm 0.010$	10,785.0 ± 1110.0	84.9/19	$25.291\pm 0.868$
p–p	2.76		$0.100\pm 0.005$	$0.444\pm 0.013$	12,785.0 ± 1300.0	105.3/19	$26.767\pm 0.907$
	7		$0.100\pm 0.005$	$0.449\pm 0.015$	15,785.0 ± 1590.0	120.3/19	$28.715\pm 0.964$
	13		$0.100\pm 0.005$	$0.452\pm 0.015$	15,785.0 ±1585.0	132.7/19	$28.715\pm 0.961$
7b	0.9	${\pi }^{-}$	$0.100\pm 0.005$	$0.423\pm 0.010$	10,725.0 ± 1110.0	117.9/19	$25.244\pm 0.871$
p–p	2.76		$0.100\pm 0.005$	$0.444\pm 0.013$	12,705.0 ± 1300.0	85.7/19	$26.711\pm 0.911$
	7		$0.100\pm 0.005$	$0.449\pm 0.015$	15,815.0 ± 1590.0	116.0/19	$28.733\pm 0.963$
	13		$0.100\pm 0.005$	$0.452\pm 0.015$	15,785.0 ± 1585.0	113.4/19	$28.715\pm 0.961$
7c	0.9	$K^{+}$	$0.110\pm 0.004$	$0.423\pm 0.012$	$6885.0\pm 722.0$	3.3/14	$21.777\pm 0.761$
p–p	2.76		$0.110\pm 0.004$	$0.440\pm 0.015$	$8585.0\pm 883.0$	21.2/14	$23.439\pm 0.804$
	7		$0.114\pm 0.004$	$0.455\pm 0.016$	$8685.0\pm 890.0$	20.2/14	$23.530\pm 0.804$
	13		$0.114\pm 0.004$	$0.455\pm 0.016$	$7605.0\pm 766.0$	5.2/14	$22.511\pm 0.756$
7d	0.9	$K^{-}$	$0.110\pm 0.004$	$0.423\pm 0.012$	$6885.0\pm 722.0$	16.7/14	$21.777\pm 0.761$
p–p	2.76		$0.110\pm 0.004$	$0.440\pm 0.015$	$8585.0\pm 883.0$	23.3/14	$23.439\pm 0.804$
	7		$0.114\pm 0.004$	$0.455\pm 0.016$	$8685.0\pm 890.0$	22.9/14	$23.530\pm 0.804$
	13		$0.114\pm 0.004$	$0.455\pm 0.016$	$7685.0\pm 776.0$	6.5/14	$22.590\pm 0.760$
7e	0.9	p	$0.148\pm 0.003$	$0.333\pm 0.013$	$5688.0\pm 665.0$	37.9/24	$16.218\pm 0.632$
p–p	2.76		$0.148\pm 0.003$	$0.367\pm 0.015$	$7044.0\pm 810.0$	48.9/24	$17.416\pm 0.668$
	7		$0.151\pm 0.003$	$0.396\pm 0.016$	$7544.0\pm 839.0$	21.2/24	$17.819\pm 0.661$
	13		$0.151\pm 0.003$	$0.396\pm 0.017$	$6844.0\pm 688.0$	15.3/23	$17.250\pm 0.578$
7f	0.9	$\overline{p}$	$0.148\pm 0.003$	$0.333\pm 0.013$	$5408.0\pm 644.0$	66.8/24	$15.948\pm 0.633$
p–p	2.76		$0.148\pm 0.003$	$0.367\pm 0.015$	$6824.0\pm 786.0$	37.9/24	$17.233\pm 0.662$
	7		$0.151\pm 0.003$	$0.396\pm 0.016$	$7444.0\pm 820.0$	23.4/24	$17.740\pm 0.651$
	13		$0.151\pm 0.003$	$0.396\pm 0.017$	$6744.0\pm 480.0$	11.9/23	$17.166\pm 0.407$
9	5.02	(${\pi }^{+}+{\pi }^{-})/2$	$0.100\pm 0.003$	$0.459\pm 0.010$	11,242.5 ± 1055.0	187.6/28	$25.644\pm 0.802$
		($K^{+}+K^{-})/2$	$0.110\pm 0.003$	$0.457\pm 0.010$	$7457.5\pm 833.0$	13.7/23	$22.365\pm 0.833$
		($p+\overline{p})/2$	$0.149\pm 0.002$	$0.374\pm 0.010$	$4542.5\pm 499.0$	23.5/21	$15.047\pm 0.551$

Figure 8 is the same as Figure 6, but it presents the ratios of data/fit, in which panels a*–f* correspond to Figure 7a–f, respectively. The different closed symbols represent the data/fit values corresponding to different energies marked in the figure. The same conclusions obtained from Figure 2, Figure 4 and Figure 6 can be obtained from Figure 8.

Figure 8. Same as Figure 6, but panels (a*–f*) correspond to Figure 7a–f, respectively.

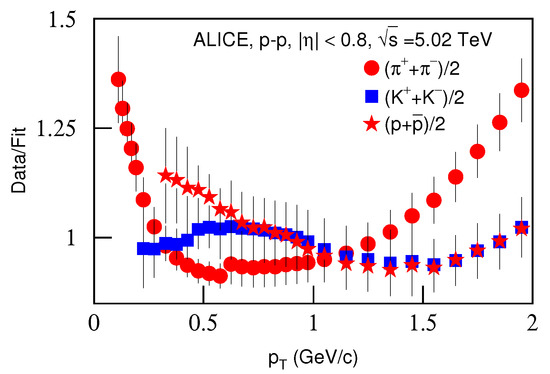
Figure 9 is the same as Figure 1, but it shows the spectra of (a) $({\pi }^{+}+{\pi }^{-})/2$, (b) $(K^{+}+K^{-})/2$ and (c) $(p+\overline{p})/2$ produced in p–p collisions in the pseudorapidity range $\left|\eta \right|<0.8$. The symbols represent the experimental data measured by the ALICE Collaboration at $\sqrt{s}=5.02$ TeV [34]. The energy and related parameters are listed in Table 2. One can see the good approximation the model produced of the experimental data of the ALICE Collaboration in the $p_T$ spectra of identified particles produced in p–p collisions at $\sqrt{s}=5.02$ TeV.

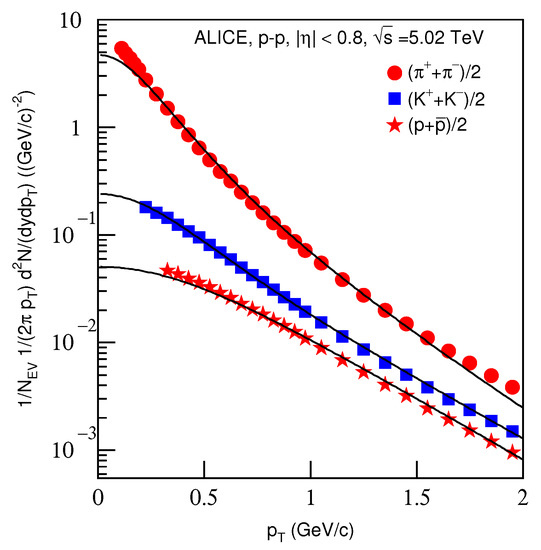
Figure 9. Same as Figure 1, but showing the spectra of $({\pi }^{+}+{\pi }^{-})/2$, $(K^{+}+K^{-})/2$ and $(p+\overline{p})/2$ produced in p–p collisions in the pseudorapidity range $\left|\eta \right|<0.8$. The symbols represent the experimental data measured by the ALICE Collaboration at $\sqrt{s}=5.02$ TeV [32].

Figure 10 is the same as Figure 2, but it presents the ratios of data/fit corresponding to Figure 9. The different closed symbols represent the data/fit values corresponding to different particles marked in the figure. The same conclusions obtained in the above discussions can be obtained from Figure 10.

Figure 10. Same as Figure 2, but showing the ratios of data/fit corresponding to Figure 9.

From Figure 1, Figure 3, Figure 5, Figure 7 and Figure 9, one can see that we have used the species-dependent parameters to fit the spectra of pions, kaons and protons. This is not the usual way to use the blast-wave model, which fits various spectra simultaneously. We have examined the simultaneous fit of the model for various spectra and know that narrow and different $p_T$ ranges have to be used for different particles. We do not think that the simultaneous fitting of various spectra can be better in wide $p_T$ ranges. Instead, we may use the individual fit for different spectra and obtain better fits. If needed, we may use the parameters averaged by weighting the yields of different particles to give the simultaneous fit. In fact, the simultaneous fit was not needed in this case, though what we show by the end of this section is a weighted average of proper times for different particles. As will be seen, the individual fit reveals and confirms the mass-dependent differential kinetic freeze-out scenario.

From the above discussions we know that, according to the blast-wave model with fluctuations, we can obtain not only the kinetic freeze-out temperature and transverse flow velocity but also the proper time. The advantage of this model is that the information about proper time can be obtained. This is very important for us to understand the specific evolution of high-energy collisions. The proper time reflects the lifetime of the interacting system. We may discuss the change rule of the proper time by this model. This is an important innovation of the present work. However, the disadvantage of the model is also obvious. In some cases, one component model cannot fit the data well. In fact, it is only applicable to the low-$p_T$ region, but not to the high-$p_T$ region. This problem is not only a disadvantage in the blast-wave model with fluctuations, but also a disadvantage in all thermal models.

To study the change trend of parameters with centrality and energy, Figure 11 shows the dependencies of kinetic freeze-out temperature $T_0$ on (a)–(c) centrality C and (d) energy $\sqrt{s}$ for the production of different particles in (a) Pb–Pb, (b) p–Pb, (c) Xe–Xe and (d) p–p collisions. Different symbols represent different meanings shown in the panels. One can see that, from peripheral to central collisions, $T_0$ slightly increases. The reasons are the more violent interactions in central collisions, where there are higher degrees of excitation, and more participant nucleons being involved in the collisions. $T_0$ also increases with the increase of particle mass. This is an evidence of a mass-dependent differential kinetic freeze-out scenario or a multiple kinetic freeze-out scenario [12,39]. In addition, with the increase of energy, $T_0$ is nearly invariant at the LHC energies, which implies the nearly saturated density in QGP phase. In p–p collisions, the dependence of $T_0$ on energy is similar to that in peripheral nuclear (A–A and p–A) collisions.

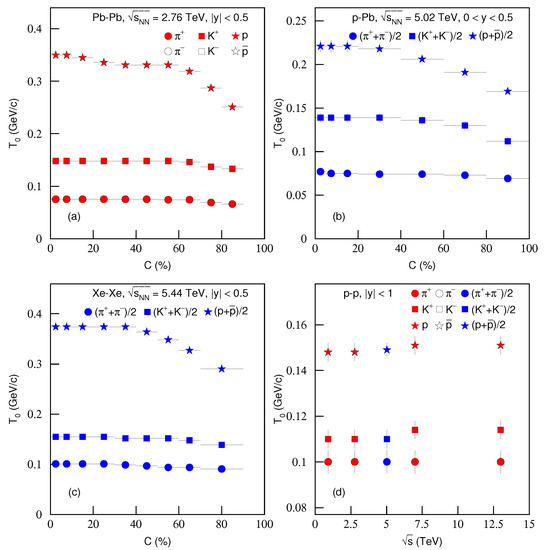
Figure 11. Dependencies of kinetic freeze-out temperature $T_0$ on (a–c) centrality C and (d) energy $\sqrt{s}$ for the productions of (a) ${\pi }^{+}$, ${\pi }^{-}$, $K^{+}$, $K^{-}$, p and $\overline{p}$ in different centrality Pb–Pb collisions at 2.76 TeV; (b) $({\pi }^{+}+{\pi }^{-})/2$, $(K^{+}+K^{-})/2$ and $(p+\overline{p})/2$ in different centrality p–Pb collisions at 5.02 TeV; (c) $({\pi }^{+}+{\pi }^{-})/2$, $(K^{+}+K^{-})/2$ and $(p+\overline{p})/2$ in different centrality Xe–Xe collisions at 5.44 TeV; and (d) ${\pi }^{+}$, ${\pi }^{-}$, $K^{+}$, $K^{-}$, p and $\overline{p}$ at 0.9, 2.76, 7 and 13 TeV, along with $({\pi }^{+}+{\pi }^{-})/2$, $(K^{+}+K^{-})/2$ and $(p+\overline{p})/2$ at 5.02 TeV. The red closed and black open symbols in panel (a) represent positively and negatively charged particles respectively, which are quoted from Table 1. The blue closed symbols in panels (b,c) represent positively plus negatively charged particles divided by 2, which are quoted from Table 1. The red closed (black open) and blue closed symbols in panel (d) represent positively (negatively) and positively plus negatively charged particles divided by 2, which are quoted from Table 2.

Figure 12 is the same as Figure 11, but it shows the dependence of transverse flow velocity ${\beta }_T$ on (a)–(c) centrality C and (d) energy $\sqrt{s}$. Different symbols represent different ${\beta }_T$ of different particles. One can see in general the slight increase of ${\beta }_T$ from peripheral to central collisions. With the increase of energy, ${\beta }_T$ increases slightly. The present work confirms our previous work [27,40,41] which used the intercept-slope method and obtained a slight larger ${\beta }_T$ in central collisions than in peripheral collisions. In our opinion, the flow is produced in the inner core of the interacting system. Even for peripheral or proton–proton collisions, there is non-zero flow velocity. From Figure 12, one can also see the mass-dependent ${\beta }_T$ in most cases. A heavy particle corresponds to a small ${\beta }_T$ due to its large inertia. The differences in ${\beta }_T$ for different particles decrease with the increase of $\sqrt{s}$, where ${\beta }_T$ is large at high $\sqrt{s}$. This reflects that we can neglect the mass effect in a strong flow field.

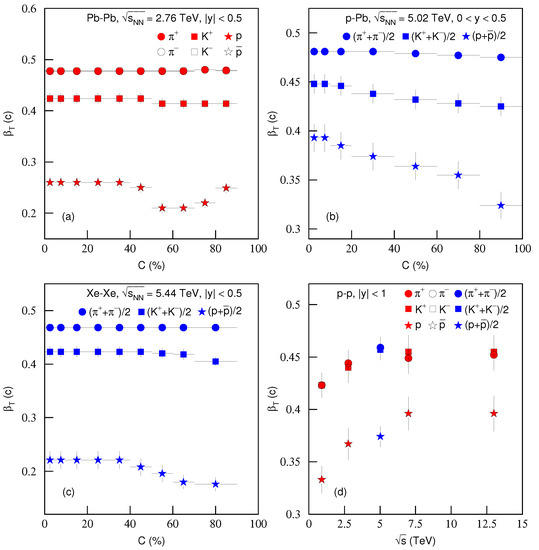
Figure 12. Same as Figure 11, but showing the dependencies of transverse flow velocity ${\beta }_T$ on (a–c) centrality C and (d) energy $\sqrt{s}$.

In the fit process, the free parameters $T_0$ and ${\beta }_T$ were not fixed. We looked for the most appropriate parameters according to the values of ${\chi }^2$ in various cases. That is, we obtained the results without bias. As the two parameters were sensitive to the results, they had far less freedom to vary. However, it was inevitable that there would be a correlation between the parameters. The values of $T_0$ and ${\beta }_T$ are not independent of centrality classes of up to 60% centrality in nuclear collisions. The same $T_0$ and ${\beta }_T$ indicate that the given interaction system has the same excitation degree, expansion characteristic and matter form from 0 to 60% centrality. The same matter can be QGP from the considered central to semi-central collisions.

Figure 13 is the same as Figure 11, but it shows the dependencies of proper time ${\tau }_0$ on (a)–(c) centrality C and (d) energy $\sqrt{s}$. Different symbols represent different ${\tau }_0$ for different particles. One can see the increase of ${\tau }_0$ from peripheral to central collisions in panels (a–c), as the number of participant nucleons increases from peripheral to central collisions. Due to the large number of binary collisions by the re-scattering of partons, the system with more participants reached equilibrium slowly. However, the small number of participant nucleons led to the system to go quickly to equilibrium.

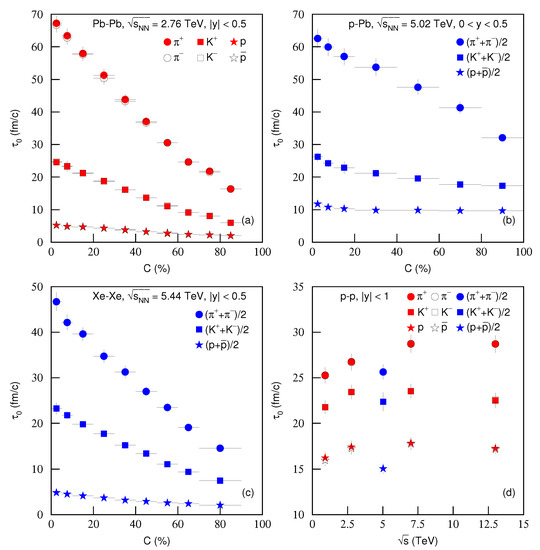
Figure 13. Same as Figure 11, but showing the dependencies of proper time ${\tau }_0$ on (a–c) centrality C and (d) energy $\sqrt{s}$.

Figure 13 also proves the mass-dependent differential scenario from ${\tau }_0$. The heavier the particle is, the smaller ${\tau }_0$ is, which shows the early freeze-out of heavier particles as compared to the lighter particles. This also suggests that different particles have different freeze-out surfaces [39,42]. The result that pions correspond to a much larger ${\tau }_0$ than protons means that the protons stop interacting while pions are still interacting. Due to protons having larger $m_0$ than pions, protons are left behind during the system evolution from the origin of collisions in the radial direction, which is the behavior of hydrodynamics [43]. In Figure 13d, one can see, with the increase of energy, that ${\tau }_0$ increases slightly or is nearly invariant. This is consistent with Figure 11d and Figure 12d.

To study further the dependence of proper time on centrality C and energy $\sqrt{s}$, Figure 14a shows the dependencies of the average proper time $⟨{\tau }_0⟩$ and the average root-mean-square proper time $\sqrt{⟨{\tau }_0^2⟩}$ on C. The red closed and black open symbols represent $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$, respectively, which are from Pb–Pb, p–Pb and Xe–Xe collisions and are also listed in Table 3 with the impact parameter b. These averages were obtained by different particle weights due to different contribution fractions of ${\pi }^{\pm }$, $K^{\pm }$, p and $\overline{p}$. One can see the clear increase of $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ from peripheral to central collisions. The reasons are the more violent interactions in central collisions in which there is a higher degree of excitation, and the higher number of participant nucleons involved.

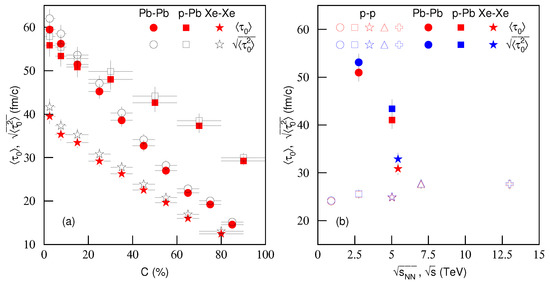
Figure 14. Dependencies of (a) average proper time $⟨{\tau }_0⟩$ and root-mean-square proper time $\sqrt{⟨{\tau }_0^2⟩}$ on centrality C and (b) $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ on energy $\sqrt{s_{NN}}$ ($\sqrt{s}$). In panel (a), the red closed and black open symbols represent $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$, respectively, from Pb–Pb, p–Pb and Xe–Xe collisions, which are listed in Table 3. In panel (b), the red and blue open symbols represent $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$, respectively, from p–p collisions, which are listed in Table 4. The red and blue closed symbols represent $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ respectively from Pb–Pb, p–Pb and Xe–Xe collisions, which are also listed in Table 4.

Table 3. Values of collision type, centrality, impact parameter b, average proper time $⟨{\tau }_0⟩$ and root-mean-square proper time $\sqrt{⟨{\tau }_0^2⟩}$, where $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ are calculated due to different particle weights.

Figure	Centrality	b (fm)	$⟨{\mathit{\tau }}_0⟩$ (fm/c)	$\sqrt{⟨{\mathit{\tau }}_0^2⟩}$ (fm/c)
14a	0–5%	2.117	$59.491\pm 2.055$	$62.021\pm 2.140$
Pb–Pb	5–10%	3.867	$56.202\pm 2.055$	$58.501\pm 2.075$
	10–20%	5.468	$51.435\pm 1.814$	$53.588\pm 1.877$
	20–30%	7.083	$45.199\pm 1.687$	$47.088\pm 1.745$
	30–40%	8.391	$38.598\pm 1.433$	$40.247\pm 1.473$
	40–50%	9.514	$32.736\pm 1.246$	$34.128\pm 1.271$
	50–60%	10.521	$26.972\pm 1.046$	$28.179\pm 1.088$
	60–70%	11.443	$21.870\pm 0.891$	$22.814\pm 0.918$
	70–80%	12.293	$19.225\pm 0.725$	$20.038\pm 0.740$
	80–90%	13.087	$14.595\pm 0.562$	$15.176\pm 0.557$
14a	0–5%	1.237	$55.816\pm 2.546$	$57.894\pm 2.633$
p–Pb	5–10%	2.258	$53.393\pm 2.452$	$55.429\pm 2.539$
	10–20%	3.196	$50.846\pm 2.377$	$52.776\pm 2.403$
	20–40%	4.520	$48.017\pm 2.399$	$49.828\pm 2.489$
	40–60%	5.853	$42.627\pm 2.091$	$44.155\pm 2.172$
	60–80%	6.935	$37.301\pm 1.635$	$38.492\pm 1.690$
	80–100%	7.866	$29.258\pm 1.036$	$29.974\pm 1.054$
14a	0–5%	1.817	$39.521\pm 1.784$	$41.663\pm 1.853$
Xe–Xe	5–10%	3.320	$35.303\pm 1.433$	$37.289\pm 1.507$
	10–20%	4.698	$33.435\pm 1.262$	$35.271\pm 1.327$
	20–30%	6.086	$29.178\pm 1.220$	$30.805\pm 1.278$
	30–40%	7.209	$26.290\pm 1.135$	$27.793\pm 1.180$
	40–50%	8.179	$22.541\pm 0.916$	$23.879\pm 0.961$
	50–60%	9.042	$19.634\pm 0.816$	$20.801\pm 0.852$
	60–70%	9.829	$16.016\pm 0.647$	$16.938\pm 0.680$
	70–90%	10.900	$12.463\pm 0.688$	$13.075\pm 0.731$

Figure 14b shows the dependencies of $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ on energy $\sqrt{s_{NN}}$ ($\sqrt{s}$). The red and blue open symbols represent $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$, respectively, from p–p collisions. The red and blue closed symbols represent $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$, respectively, from Pb–Pb, p–Pb and Xe–Xe collisions, which were calculated from Table 3 in the range of $b=0$–8 fm by different weights ($\propto b$) due to different contribution fractions. The cases of large b were not included to reduce the influence of the cold nuclear effect. The results for p–p collisions corresponding to red and blue open symbols were calculated by different particle weights. The values of proper times used in Figure 14b are also listed in Table 4. In p–p collisions, one can see that with an increase of energy, $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ are slightly increscent or nearly invariant. In nuclear collisions, at similar energies, the considered proper times for Pb–Pb collisions are larger than those for p–Pb collisions, and the latter are larger than Xe–Xe collisions. Generally, nuclear collisions correspond to larger proper times than p–p collisions.

Table 4. Values of collision type, energy, average proper time $⟨{\tau }_0⟩$ and root-mean-square proper time $\sqrt{⟨{\tau }_0^2⟩}$, where $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ were calculated due to different impact parameter weights.

Figure	Energy (TeV)	$⟨{\mathit{\tau }}_0⟩$ (fm/c)	$\sqrt{⟨{\mathit{\tau }}_0^2⟩}$ (fm/c)
14b	0.9	$24.030\pm 0.861$	$24.173\pm 0.855$
p–p	2.76	$25.488\pm 0.894$	$25.628\pm 0.890$
	5.02	$24.801\pm 0.794$	$24.914\pm 0.795$
	7	$27.621\pm 0.931$	$27.779\pm 0.935$
	13	$27.520\pm 0.942$	$27.690\pm 0.940$
Pb–Pb	2.76	$50.967\pm 1.843$	$53.092\pm 1.898$
p–Pb	5.02	$41.031\pm 1.847$	$43.379\pm 1.977$
Xe–Xe	5.44	$30.834\pm 1.277$	$32.848\pm 1.346$

Figure 14a shows that the order of $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ is Pb–Pb > p–Pb > Xe–Xe in central collisions. However, $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ in peripheral p–Pb collisions are larger than those in peripheral Pb–Pb and Xe–Xe collisions. This is caused by the cold nuclear effect in A–A collisions. In order to avoid the cold nuclear effect, we considered only the weighted average of the events from central to semi-central Pb–Pb and Xe–Xe collisions. This was the case for A–A collisions in Figure 14b, for which one can see the order of $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ was Pb–Pb > p–Pb > Xe–Xe > p–p. This order is concordant with that of the maximum size between the projectile and target, and that of the other size if the maximum size is the same. This is direct evidence for the statement that the maximum size of the nucleus determines the lifetime of the interacting system, and the other size also affects it. The larger the maximum size, the longer the system lifetime. If the maximum sizes are the same, the larger other size will determine the longer system lifetime.

To see the common property of the symmetric and asymmetric collisions, Figure 15 shows the dependencies of $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ on impact parameter b. The symbols have the same meaning as Figure 14a. One can see that the large differences in Figure 14a disappear in Figure 15. No matter the symmetric and asymmetric collisions, $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ decrease with increases of impact parameter b. In the plot of $⟨{\tau }_0⟩$ and $\sqrt{⟨{\tau }_0^2⟩}$ versus impact parameter, there is no obvious difference between symmetric and asymmetric collisions. We may say that, compared with the centrality-dependent proper times, the results of impact parameter-dependent proper times are more concordant among different collisions.

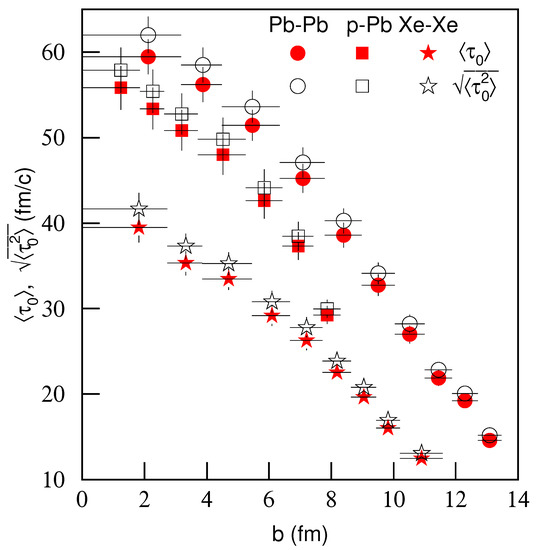
Figure 15. Same as Figure 14a, but showing the dependencies of average proper time $⟨{\tau }_0⟩$ and root-mean-square proper time $\sqrt{⟨{\tau }_0^2⟩}$ on impact parameter b.

4. Summary and Conclusions

We summarize here our main observations and conclusions.

(a) We analyzed the transverse momentum spectra of ${\pi }^{\pm }$, $K^{\pm }$, p and $\overline{p}$ produced in different centrality Pb–Pb collisions at $\sqrt{s_{NN}}=2.76$ TeV, p–Pb collisions at $\sqrt{s_{NN}}=5.02$ TeV and Xe–Xe collisions at $\sqrt{s_{NN}}=5.44$ TeV. The experimental data measured by the ALICE Collaborations were approximately fitted by the blast-wave model with fluctuations. Meanwhile, the transverse momentum spectra of ${\pi }^{\pm }$, $K^{\pm }$, p and $\overline{p}$ produced in p–p collisions at $\sqrt{s_{NN}}=0.9$, 2.76, 5.02, 7 and 13 TeV were analyzed. The experimental data measured by the ALICE and CMS Collaborations were approximately fitted by the model. The kinetic freeze-out temperature, transverse flow velocity and proper time were extracted.

(b) The kinetic freeze-out temperature and transverse flow velocity increase or do not vary with increases of event centrality from peripheral to central collisions, indicating higher excitation degree and greater expansion velocity of the system in central collisions. The average proper time increases with increasing event centrality from peripheral to central collisions, indicating longer lifetime of the system in central collisions. This means that in central collisions, the system needs longer average proper time to reach equilibrium. The heavier particles correspond to shorter proper time, showing the early freeze-out of heavier particles as compared to the lighter particles. From kinetic freeze-out temperature, transverse flow velocity and proper time, the mass-dependent differential kinetic freeze-out scenario or multiple kinetic freeze-out scenario is confirmed.