Accuracy-Risk Trade-Off Due to Social Learning in Crowd-Sourced Financial Predictions
Abstract
1. Introduction
Contributions
- We present an experimental procedure where we exposed 2037 participants to social and non-social information during 7 independent rounds of predicting financial asset prices (S&P 500, gold and WTI Oil). We collected 4634 prediction sets which include participants’ predictions before and after information exposure, as well as the information they were exposed to. We are releasing this data here.
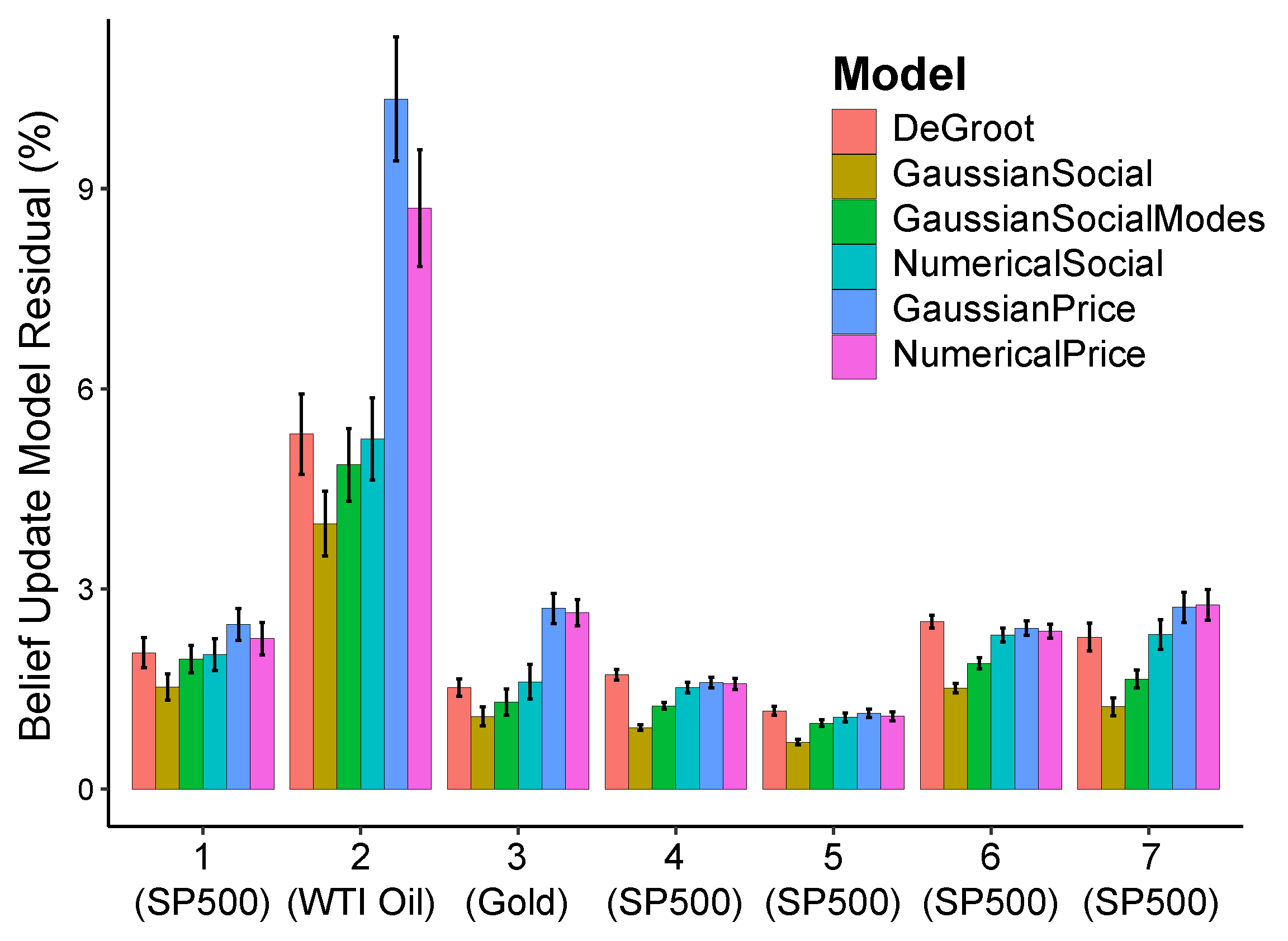
- Using computational models inspired by Bayesian models of cognition [28,29] to investigate the belief update strategy of participants, we observe that a simple model that approximates the likelihood (evidence) to be a unimodal Gaussian beats a more complex Monte Carlo approach. This suggests that our participants exhibit the attribute substitution heuristic of human decision-making [30], whereby a complicated problem is solved by approximating it with a simpler, less accurate model.
- We observe that participants prefer to learn from social information rather than from non-social information, another interesting information processing heuristic.
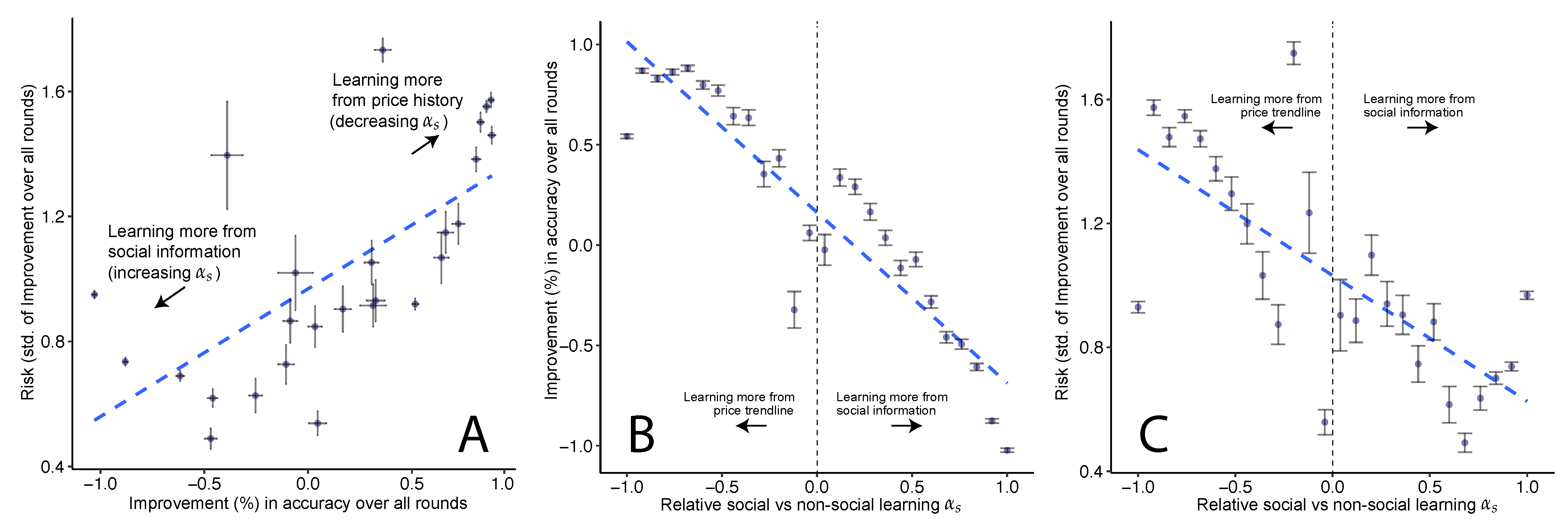
- Our main contribution: we observe a Pareto frontier between accuracy and risk. As the average accuracy of the crowd over the different prediction rounds increases, so does the risk in the crowd’s predictive accuracy. We further observe that this trade-off is mediated by the amount of social learning i.e., the extent to which participants pay attention to each other’s judgments.
- We deployed one of our prediction tasks just before the Brexit vote during which there was a great deal of market uncertainty [31], and we observe that during such uncertain times social learning leads to higher accuracy.
2. Related Work
2.1. Collective Intelligence and Social Learning
2.2. Accuracy-Risk Trade-Off
3. Materials and Methods
3.1. Experimental Design
- Predictions are made of complex and difficult-to-predict phenomena so that our results are applicable to the real-world platform applications.
- Predictions are made over many independent prediction rounds so that the risk of the crowd over these different tasks can be estimated.
- A ground-truth is needed against which we can compare our dataset to judge the external validity of individual and collective performance metric.
- The social and non-social information each participant was exposed to after their initial pre-exposure prediction is recorded so that we can later model how different types of information influenced them in updating their belief into their post-exposure prediction.
3.2. Data Collection
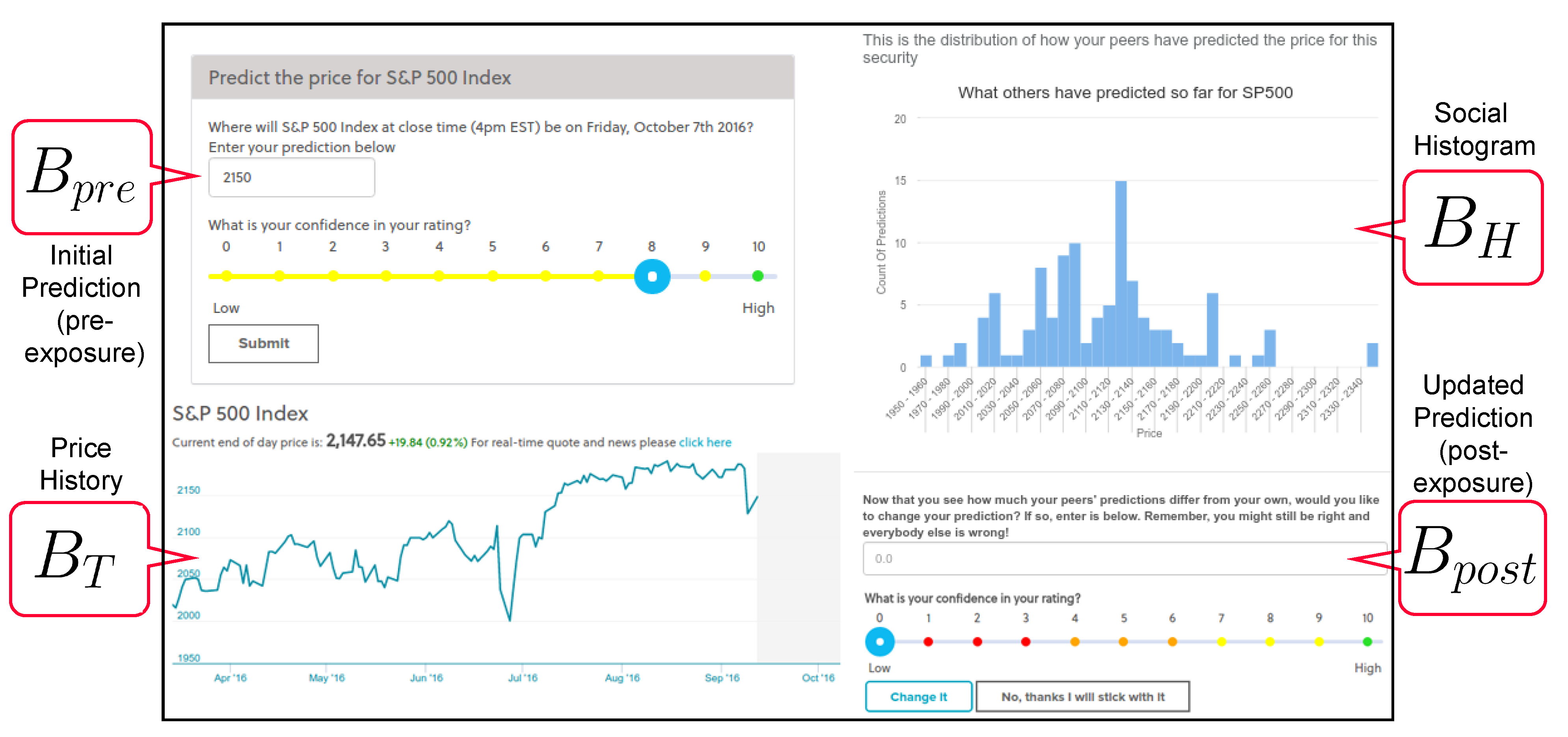
- A “pre-exposure” belief prediction , which is independent of both social information and price history. For example, a participant might show-up on the platform and predict that the closing price of the S&P 500 to be 2001 on 24 June 2016.
- The predictions within the social information histogram shown to each participant after each initial prediction. Additionally, we display a 6-month time series of the asset’s price up to this point.
- The revised “post-exposure” prediction . For example, after seeing the social histogram and asset price history, a participant might update their belief to 2201. Since the real price (the ground-truth V) ended up being 2037.41, this participant became more accurate after information exposure (they went from 2001 to 2201).
3.3. Modeling and Estimation
- In Section 3.3.1, we describe how we model individual belief update: how a participant updates their prediction from a pre-exposure belief to a post-exposure prediction using a variety of models that are either Monte Carlo methods or simpler approximate methods inspired by Bayesian models of cognition [28,29]. This allows us to understand how participants update their belief after information exposure.
- In Section 3.3.2, using the models described earlier, we detail how to estimate the relative amount of social vs. non-social learning for each prediction to understand how much social vs. non-social data were factored into a prediction’s belief update. We then introduce our methodology for selecting predictions based on the estimated amount of social vs. non-social learning. This allows us to make aggregate predictions—at the platform level—based on a pre-specified amount of social learning.
- In Section 3.3.3, we detail how the accuracy and risk—at the platform level—of selected subsets are measured, and how they are used to investigate whether a Pareto trade-off exists between accuracy and risk and whether it is mediated by the relative amount of social vs. non-social learning.
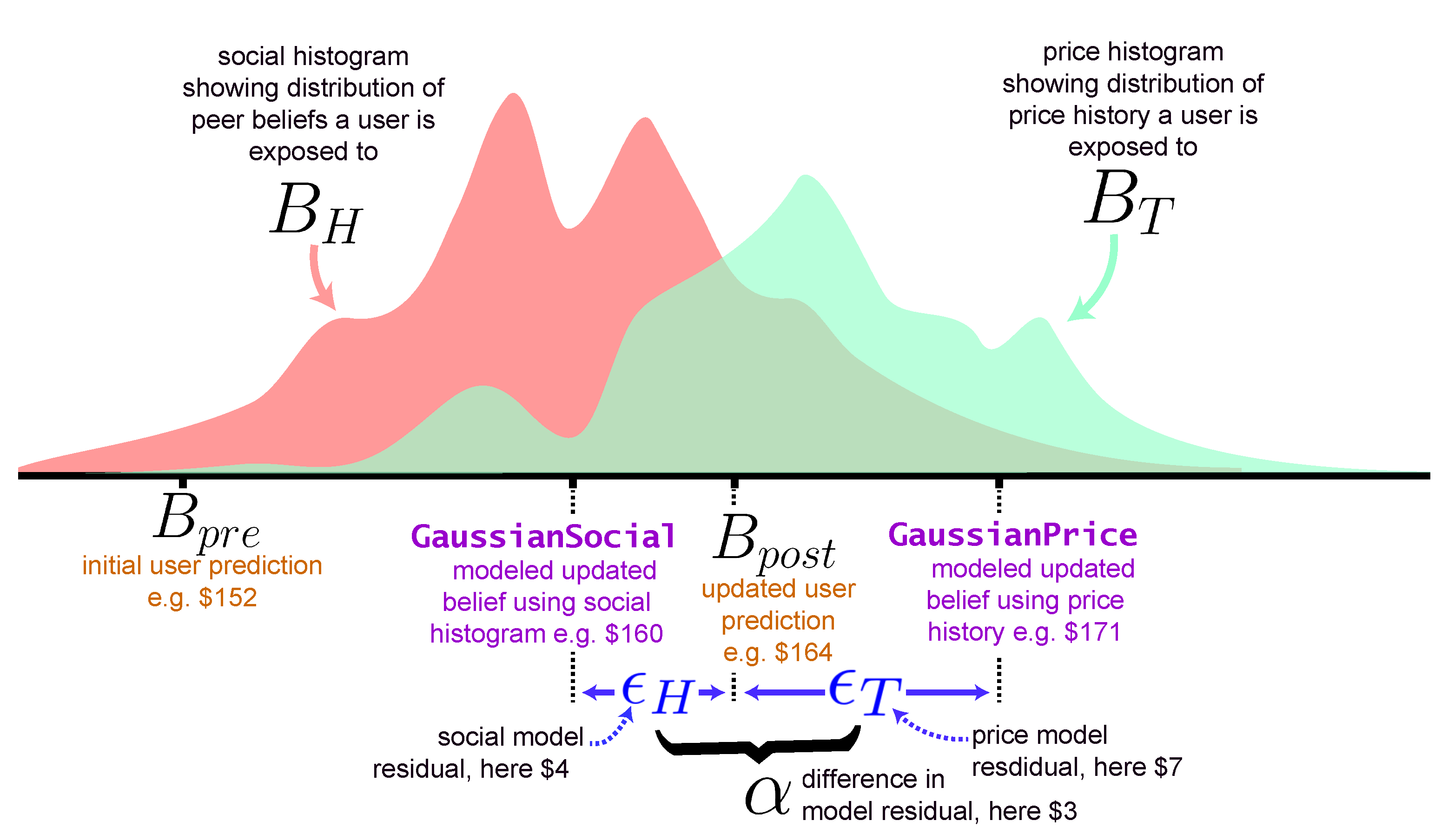
3.3.1. Modeling Belief Updates
3.3.2. Subsetting Predictions Based on Social Learning
3.3.3. Evaluating Improvement of Subsets
4. Results
4.1. Belief Update Models
4.2. Accuracy-Risk Trade-Off
4.3. Performance under High Uncertainty
5. Discussion
5.1. Collective Intelligence System Design Implications
5.2. Information Processing and Decision-Making Heuristics
5.3. Limitations and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diallo, N.; Shi, W.; Xu, L.; Gao, Z.; Chen, L.; Lu, Y.; Shah, N.; Carranco, L.; Le, T.C.; Surez, A.B.; et al. eGov-DAO: A better government using blockchain based decentralized autonomous organization. In Proceedings of the 2018 International Conference on eDemocracy & eGovernment (ICEDEG), Ambato, Ecuador, 4–6 April 2018; pp. 166–171. [Google Scholar]
- Lang, M.; Bharadwaj, N.; Di Benedetto, C.A. How crowdsourcing improves prediction of market-oriented outcomes. J. Bus. Res. 2016, 69, 4168–4176. [Google Scholar] [CrossRef]
- Lawrence, K. Memes, Reddit, and Robinhood: Analyzing the GameStop Saga. 2021. Available online: http://sk.sagepub.com/cases/memes-reddit-and-robinhood-analyzing-the-gamestop-saga (accessed on 10 May 2021).
- Hu, D.; Jones, C.M.; Zhang, V.; Zhang, X. The Rise of Reddit: How Social Media Affects Retail Investors and Short-Sellers’ Roles in Price Discovery. 2021. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3807655 (accessed on 10 May 2021).
- Lazer, D.; Friedman, A. The network structure of exploration and exploitation. Adm. Sci. Q. 2007, 52, 667–694. [Google Scholar] [CrossRef]
- Olorunda, O.; Engelbrecht, A.P. Measuring exploration/exploitation in particle swarms using swarm diversity. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1128–1134. [Google Scholar]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1671–1676. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Domingos, P. A unified bias-variance decomposition. Proceedings of 17th International Conference on Machine Learning, Stanford, CA, USA, 29 June–2 July 2000; pp. 231–238. [Google Scholar]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Gagliardi, F. Instance-based classifiers applied to medical databases: Diagnosis and knowledge extraction. Artif. Intell. Med. 2011, 52, 123–139. [Google Scholar] [CrossRef] [PubMed]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Gammerman, A.; Vovk, V. Hedging predictions in machine learning. Comput. J. 2007, 50, 151–163. [Google Scholar] [CrossRef]
- Joyce, J.M.; Vogel, R.C. The uncertainty in risk: Is variance unambiguous? J. Financ. 1970, 25, 127–134. [Google Scholar] [CrossRef]
- Modigliani, F.; Leah, M. Risk-adjusted performance. J. Portf. Manag. 1997, 23, 45. [Google Scholar] [CrossRef]
- Ghysels, E.; Santa-Clara, P.; Valkanov, R. There is a risk-return trade-off after all. J. Financ. Econ. 2005, 76, 509–548. [Google Scholar] [CrossRef]
- Chavez-Demoulin, V.; Embrechts, P.; Nešlehová, J. Quantitative models for operational risk: Extremes, dependence and aggregation. J. Bank. Financ. 2006, 30, 2635–2658. [Google Scholar] [CrossRef]
- Asmussen, S.; Kroese, D.P. Improved algorithms for rare event simulation with heavy tails. Adv. Appl. Probab. 2006, 38, 545–558. [Google Scholar] [CrossRef]
- Shevchenko, P.V.; Wuthrich, M.V. The structural modelling of operational risk via Bayesian inference: Combining loss data with expert opinions. J. Oper. Risk 2006, 1, 3–26. [Google Scholar] [CrossRef]
- Chapelle, A.; Crama, Y.; Hübner, G.; Peters, J.P. Practical methods for measuring and managing operational risk in the financial sector: A clinical study. J. Bank. Financ. 2008, 32, 1049–1061. [Google Scholar] [CrossRef]
- Cruz, M.G. Modeling, Measuring and Hedging Operational Risk; Wiley: New York, NY, USA, 2002; Volume 346. [Google Scholar]
- Galton, F. Vox populi (The wisdom of crowds). Nature 1907, 75, 450–451. [Google Scholar] [CrossRef]
- Golub, B.; Jackson, M.O. Naive learning in social networks and the wisdom of crowds. Am. Econ. J. Microecon. 2010, 2, 112–149. [Google Scholar] [CrossRef]
- Nofer, M.; Hinz, O. Are crowds on the internet wiser than experts? The case of a stock prediction community. J. Bus. Econ. 2014, 84, 303–338. [Google Scholar] [CrossRef]
- Becker, J.; Brackbill, D.; Centola, D. Network dynamics of social influence in the wisdom of crowds. Proc. Natl. Acad. Sci. USA 2017, 114, 201615978. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.M.; Steyvers, M.; Merkle, E.C.; Budescu, D.V.; Wallsten, T.S. Forecast aggregation via recalibration. Mach. Learn. 2014, 95, 261–289. [Google Scholar] [CrossRef]
- Madirolas, G.; de Polavieja, G.G. Improving collective estimations using resistance to social influence. PLoS Comput. Biol. 2015, 11, e1004594. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Tenenbaum, J.B. Optimal predictions in everyday cognition. Psychol. Sci. 2006, 17, 767–773. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, T.L.; Kemp, C.; Tenenbaum, J.B. Bayesian models of cognition. In The Cambridge Handbook of Computational Psychology; Sun, R., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 1–49. [Google Scholar]
- Kahneman, D.; Frederick, S. Representativeness Revisited: Attribute Substitution in Intuitive Judgment. Available online: https://www.cambridge.org/core/books/heuristics-and-biases/representativeness-revisited-attribute-substitution-in-intuitive-judgment/AAB5D933A3F944CFB5CB02265D376C8F (accessed on 10 May 2021).
- Oehler, A.; Horn, M.; Wendt, S. Brexit: Short-term stock price effects and the impact of firm-level internationalization. Financ. Res. Lett. 2017, 22, 175–181. [Google Scholar] [CrossRef]
- Kennedy, J. Swarm intelligence. In Handbook of Nature-Inspired and Innovative Computing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 187–219. [Google Scholar]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Bonabeau, E.; Marco, D.D.R.D.F.; Dorigo, M.; Théraulaz, G.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Number 1; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Woolley, A.W.; Chabris, C.F.; Pentland, A.; Hashmi, N.; Malone, T.W. Evidence for a collective intelligence factor in the performance of human groups. Science 2010, 330, 686–688. [Google Scholar] [CrossRef]
- Malone, T.W.; Laubacher, R.; Dellarocas, C. The collective intelligence genome. MIT Sloan Manag. Rev. 2010, 51, 21. [Google Scholar] [CrossRef]
- Lorenz, J.; Rauhut, H.; Schweitzer, F.; Helbing, D. How social influence can undermine the wisdom of crowd effect. Proc. Natl. Acad. Sci. USA 2011, 108, 9020–9025. [Google Scholar] [CrossRef]
- Muchnik, L.; Aral, S.; Taylor, S.J. Social influence bias: A randomized experiment. Science 2013, 341, 647–651. [Google Scholar] [CrossRef]
- Salganik, M.J.; Dodds, P.S.; Watts, D.J. Experimental study of inequality and unpredictability in an artificial cultural market. Science 2006, 311, 854–856. [Google Scholar] [CrossRef] [PubMed]
- Moussaïd, M.; Kämmer, J.E.; Analytis, P.P.; Neth, H. Social influence and the collective dynamics of opinion formation. PLoS ONE 2013, 8, e78433. [Google Scholar] [CrossRef] [PubMed]
- Almaatouq, A.; Noriega-Campero, A.; Alotaibi, A.; Krafft, P.; Moussaid, M.; Pentland, A. Adaptive social networks promote the wisdom of crowds. Proc. Natl. Acad. Sci. USA 2020, 117, 11379–11386. [Google Scholar] [CrossRef]
- Adjodah, D.; Calacci, D.; Dubey, A.; Goyal, A.; Krafft, P.; Moro, E.; Pentland, A. Leveraging Communication Topologies Between Learning Agents in Deep Reinforcement Learning. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems, Auckland, New Zealand, 9–13 May 2020. [Google Scholar]
- Lim, S.L.; Quercia, D.; Finkelstein, A. StakeSource: Harnessing the power of crowdsourcing and social networks in stakeholder analysis. In Proceedings of the 2010 ACM/IEEE 32nd International Conference on Software Engineering, Cape Town, South Africa, 2–8 May 2010; Volume 2, pp. 239–242. [Google Scholar]
- Chen, P.Y.; Cheng, S.M.; Ting, P.S.; Lien, C.W.; Chu, F.J. When crowdsourcing meets mobile sensing: A social network perspective. IEEE Commun. Mag. 2015, 53, 157–163. [Google Scholar] [CrossRef]
- Lerman, K.; Ghosh, R. Information contagion: An empirical study of the spread of news on Digg and Twitter social networks. In Proceedings of the Fourth International AAAI Conference on Weblogs and Social Media (ICWSM), Washington, DC, USA, 23–26 May 2010. [Google Scholar]
- Lerman, K.; Hogg, T. Using a model of social dynamics to predict popularity of news. In Proceedings of the 19th International Conference on World Wide Web (WWW), Raleigh, NC, USA, 26–30 April 2010; pp. 621–630. [Google Scholar]
- Stoddard, G. Popularity dynamics and intrinsic quality in reddit and hacker news. In Proceedings of the Ninth International AAAI Conference on Web and Social Media (ICWSM), Oxford, UK, 26–29 May 2015. [Google Scholar]
- Celis, L.E.; Krafft, P.M.; Kobe, N. Sequential voting promotes collective discovery in social recommendation systems. In Proceedings of the Tenth International AAAI Conference on Web and Social Media, Cologne, Germany, 17–20 May 2016. [Google Scholar]
- Karger, D.R.; Oh, S.; Shah, D. Budget-optimal task allocation for reliable crowdsourcing systems. Oper. Res. 2014, 62, 1–24. [Google Scholar] [CrossRef]
- Holt, C.A.; Laury, S.K. Risk aversion and incentive effects. Am. Econ. Rev. 2002, 92, 1644–1655. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. In Handbook of the Fundamentals of Financial Decision Making: Part I; World Scientific: Singapore, 2013; pp. 99–127. [Google Scholar]
- Hintze, A.; Olson, R.S.; Adami, C.; Hertwig, R. Risk sensitivity as an evolutionary adaptation. Sci. Rep. 2015, 5, 8242. [Google Scholar] [CrossRef]
- Zhang, R.; Brennan, T.J.; Lo, A.W. The origin of risk aversion. Proc. Natl. Acad. Sci. USA 2014, 111, 17777–17782. [Google Scholar] [CrossRef] [PubMed]
- Binswanger, H.P.; Sillers, D.A. Risk aversion and credit constraints in farmers’ decision-making: A reinterpretation. J. Dev. Stud. 1983, 20, 5–21. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Green, K.C.; Graefe, A. Golden rule of forecasting: Be conservative. J. Bus. Res. 2015, 68, 1717–1731. [Google Scholar] [CrossRef]
- Passino, K.M.; Seeley, T.D. Modeling and analysis of nest-site selection by honeybee swarms: The speed and accuracy trade-off. Behav. Ecol. Sociobiol. 2006, 59, 427–442. [Google Scholar] [CrossRef]
- Valentini, G.; Hamann, H.; Dorigo, M. Efficient decision-making in a self-organizing robot swarm: On the speed versus accuracy trade-off. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, Istanbul, Turkey, 4–8 May 2015; pp. 1305–1314. [Google Scholar]
- Krause, J.; Ruxton, G.D.; Krause, S. Swarm intelligence in animals and humans. Trends Ecol. Evol. 2010, 25, 28–34. [Google Scholar] [CrossRef]
- Wolf, M.; Kurvers, R.H.; Ward, A.J.; Krause, S.; Krause, J. Accurate decisions in an uncertain world: Collective cognition increases true positives while decreasing false positives. Proc. R. Soc. B Biol. Sci. 2013, 280, 20122777. [Google Scholar] [CrossRef]
- Ward, A.J.; Herbert-Read, J.E.; Sumpter, D.J.; Krause, J. Fast and accurate decisions through collective vigilance in fish shoals. Proc. Natl. Acad. Sci. USA 2011, 108, 2312–2315. [Google Scholar] [CrossRef]
- Dumas, B.; Fleming, J.; Whaley, R.E. Implied volatility functions: Empirical tests. J. Financ. 1998, 53, 2059–2106. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Shiller, R.J. Stock prices, earnings, and expected dividends. J. Financ. 1988, 43, 661–676. [Google Scholar] [CrossRef]
- Fama, E.F. Random walks in stock market prices. Financ. Anal. J. 1995, 51, 75–80. [Google Scholar] [CrossRef]
- Dixon, E.; Enos, E.; Brodmerkle, S. A/b Testing of a Webpage. U.S. Patent 7,975,000, 2013. Available online: https://patents.google.com/patent/US20060162071A1/en (accessed on 10 May 2021).
- Maniadakis, M.; Trahanias, P. Time models and cognitive processes: A review. Front. Neurorobotics 2014, 8, 7. [Google Scholar] [CrossRef] [PubMed]
- Park, C.H.; Irwin, S.H. What do we know about the profitability of technical analysis? J. Econ. Surv. 2007, 21, 786–826. [Google Scholar] [CrossRef]
- Neftci, S.N. Naive trading rules in financial markets and wiener-kolmogorov prediction theory: A study of “technical analysis”. J. Bus. 1991, 64, 549–571. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Kerckhove, C.V.; Martin, S.; Gend, P.; Rentfrow, P.J.; Hendrickx, J.M.; Blondel, V.D. Modelling influence and opinion evolution in online collective behaviour. PLoS ONE 2016, 11, e0157685. [Google Scholar] [CrossRef]
- Soll, J.B.; Larrick, R.P. Strategies for revising judgment: How (and how well) people use others’ opinions. J. Exp. Psychol. Learn. Mem. Cogn. 2009, 35, 780. [Google Scholar] [CrossRef]
- Foster, F.D.; Viswanathan, S. Strategic trading when agents forecast the forecasts of others. J. Financ. 1996, 51, 1437–1478. [Google Scholar] [CrossRef]
- Posada, M.; Hernandez, C.; Lopez-Paredes, A. Learning in continuous double auction market. In Artificial Economics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 41–51. [Google Scholar]
- Hartigan, J.A.; Hartigan, P.M. The dip test of unimodality. Ann. Stat. 1985, 13, 70–84. [Google Scholar] [CrossRef]
- Donnelly, N.; Cave, K.; Welland, M.; Menneer, T. Breast screening, chicken sexing and the search for oil: Challenges for visual cognition. Geol. Soc. Lond. Spec. Publ. 2006, 254, 43–55. [Google Scholar] [CrossRef]
- Nisbett, R.E.; Ross, L. Human Inference: Strategies and Shortcomings of Social Judgment. 1980. Available online: https://philpapers.org/rec/nishis (accessed on 10 May 2021).
- Dave, C.; Wolfe, K.W. On confirmation bias and deviations from Bayesian updating. Retrieved 2003, 24, 2011. [Google Scholar]
- Nickerson, R.S. Confirmation bias: A ubiquitous phenomenon in many guises. Rev. Gen. Psychol. 1998, 2, 175–220. [Google Scholar] [CrossRef]
- Mataric, M.J. Designing emergent behaviors: From local interactions to collective intelligence. In Proceedings of the Second International Conference on Simulation of Adaptive Behavior, Honolulu, HI, USA, 13 April 1993; pp. 432–441. [Google Scholar]
- Tenenbaum, J.B.; Kemp, C.; Griffiths, T.L.; Goodman, N.D. How to grow a mind: Statistics, structure, and abstraction. Science 2011, 331, 1279–1285. [Google Scholar] [CrossRef] [PubMed]
- Vul, E.; Pashler, H. Measuring the crowd within probabilistic representations within individuals. Psychol. Sci. 2008, 19, 645–647. [Google Scholar] [CrossRef]
- Lewandowsky, S.; Griffiths, T.L.; Kalish, M.L. The wisdom of individuals: Exploring people’s knowledge about everyday events using iterated learning. Cogn. Sci. 2009, 33, 969–998. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Griffiths, T.L.; Kemp, C. Theory-based Bayesian models of inductive learning and reasoning. Trends Cogn. Sci. 2006, 10, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.L.; Saxe, R.; Tenenbaum, J.B. Action understanding as inverse planning. Cognition 2009, 113, 329–349. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Judgment under uncertainty: Heuristics and biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef]
- Nisbett, R.E.; Kunda, Z. Perception of social distributions. J. Personal. Soc. Psychol. 1985, 48, 297. [Google Scholar] [CrossRef]
- Lindskog, M. Is the Intuitive Statistician Eager or Lazy?: Exploring the Cognitive Processes of Intuitive Statistical Judgments. Ph.D. Thesis, Acta Universitatis Upsaliensis, 2013. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A677471&dswid=8406 (accessed on 10 May 2021).
- Hoffman, A.B.; Rehder, B. The costs of supervised classification: The effect of learning task on conceptual flexibility. J. Exp. Psychol. Gen. 2010, 139, 319. [Google Scholar] [CrossRef]
- Malkiel, B.G.; Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Fama, E.F. The behavior of stock-market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Shanteau, J. Psychological characteristics and strategies of expert decision makers. Acta Psychol. 1988, 68, 203–215. [Google Scholar] [CrossRef]
- Koehler, D.J.; Brenner, L.; Griffin, D. The calibration of expert judgment: Heuristics and biases beyond the laboratory. Heuristics Biases Psychol. Intuitive Judgm. 2002, 686–715. Available online: https://psycnet.apa.org/record/2003-02858-039 (accessed on 10 May 2021).
- Lakshminarayanan, V.R.; Chen, M.K.; Santos, L.R. The evolution of decision-making under risk: Framing effects in monkey risk preferences. J. Exp. Soc. Psychol. 2011, 47, 689–693. [Google Scholar] [CrossRef]
- Mallpress, D.E.; Fawcett, T.W.; Houston, A.I.; McNamara, J.M. Risk attitudes in a changing environment: An evolutionary model of the fourfold pattern of risk preferences. Psychol. Rev. 2015, 122, 364. [Google Scholar] [CrossRef] [PubMed]
- Kenrick, D.T.; Griskevicius, V. The Rational Animal: How Evolution Made Us Smarter than We Think; Basic Books (AZ), 2013; Available online: https://psycnet.apa.org/record/2013-31943-000 (accessed on 10 May 2021).
- Josef, A.K.; Richter, D.; Samanez-Larkin, G.R.; Wagner, G.G.; Hertwig, R.; Mata, R. Stability and change in risk-taking propensity across the adult life span. J. Personal. Soc. Psychol. 2016, 111, 430. [Google Scholar] [CrossRef] [PubMed]
- Cronqvist, H.; Siegel, S. The genetics of investment biases. J. Financ. Econ. 2014, 113, 215–234. [Google Scholar] [CrossRef]
- Santos, L.R.; Rosati, A.G. The evolutionary roots of human decision making. Annu. Rev. Psychol. 2015, 66, 321–347. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S. Decision-making under risk: Integrating perspectives from biology, economics, and psychology. Personal. Soc. Psychol. Rev. 2014, 18, 280–307. [Google Scholar] [CrossRef]
- Azuma, R.; Daily, M.; Furmanski, C. A review of time critical decision making models and human cognitive processes. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006; p. 9. [Google Scholar]
- Cohen, I. Improving time-critical decision making in life-threatening situations: Observations and insights. Decis. Anal. 2008, 5, 100–110. [Google Scholar] [CrossRef]
- Van Knippenberg, D.; Dahlander, L.; Haas, M.R.; George, G. Information, Attention, and Decision Making. 2015. Available online: https://psycnet.apa.org/record/2015-33332-001 (accessed on 10 May 2021).
- Lubell, M.; Scholz, J.T. Cooperation, reciprocity, and the collective-action heuristic. Am. J. Political Sci. 2001, 45, 160–178. [Google Scholar] [CrossRef]
- Rand, D.G.; Brescoll, V.L.; Everett, J.A.; Capraro, V.; Barcelo, H. Social heuristics and social roles: Intuition favors altruism for women but not for men. J. Exp. Psychol. Gen. 2016, 145, 389. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal distributions across the sciences: Keys and clues: On the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy way to characterize log-normal distributions, which can provide deeper insight into variability and probability—Normal or log-normal: That is the question. BioScience 2001, 51, 341–352. [Google Scholar]
- Dehaene, S.; Izard, V.; Spelke, E.; Pica, P. Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science 2008, 320, 1217–1220. [Google Scholar] [CrossRef] [PubMed]
- Kao, A.B.; Berdahl, A.M.; Hartnett, A.T.; Lutz, M.J.; Bak-Coleman, J.B.; Ioannou, C.C.; Giam, X.; Couzin, I.D. Counteracting estimation bias and social influence to improve the wisdom of crowds. J. R. Soc. Interface 2018, 15, 20180130. [Google Scholar] [CrossRef]
- Payne, J.W.; Payne, J.W.; Bettman, J.R.; Johnson, E.J. The Adaptive Decision Maker; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Schneider, W.; Shiffrin, R.M. Controlled and automatic human information processing: I. Detection, search, and attention. Psychol. Rev. 1977, 84, 1. [Google Scholar] [CrossRef]
- Barkoczi, D.; Galesic, M. Social learning strategies modify the effect of network structure on group performance. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Krafft, P.M.; Della Penna, N.; Pentland, A.S. An experimental study of cryptocurrency market dynamics. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, Montreal, QC, Canada, 21–26 April 2018; pp. 1–13. [Google Scholar]
- Plackett, R.L.; Burman, J.P. The design of optimum multifactorial experiments. Biometrika 1946, 33, 305–325. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Pearl, J. Causal diagrams for empirical research. Biometrika 1995, 82, 669–688. [Google Scholar] [CrossRef]
- Rubin, D.B. Causal inference using potential outcomes: Design, modeling, decisions. J. Am. Stat. Assoc. 2005, 100, 322–331. [Google Scholar] [CrossRef]
- Alquist, R.; Kilian, L. What do we learn from the price of crude oil futures? J. Appl. Econom. 2010, 25, 539–573. [Google Scholar] [CrossRef]
- French, K.R. Detecting spot price forecasts in futures prices. J. Bus. 1986, 59, S39–S54. [Google Scholar] [CrossRef]
- Kim, Y.S.; Walls, L.A.; Krafft, P.; Hullman, J. A Bayesian Cognition Approach to Improve Data Visualization. In Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems, Scotland, UK, 4–9 May 2019; p. 682. [Google Scholar]
- Vul, E.; Goodman, N.; Griffiths, T.L.; Tenenbaum, J.B. One and done? Optimal decisions from very few samples. Cogn. Sci. 2014, 38, 599–637. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, S. Brexit Myth on FTSE and DAX Companies: A Review. Available at SSRN 3517139. 2020. Available online: https://www.researchgate.net/profile/Shubhada-Deshpande-2/publication/338502066_Brexit_Myth_on_FTSE_and_DAX_Companies_A_Review/links/5e183584a6fdcc2837662070/Brexit-Myth-on-FTSE-and-DAX-Companies-A-Review.pdf (accessed on 10 May 2021).
- Cox, J.; Griffith, T. Political Uncertainty and Market Liquidity: Evidence from the Brexit Referendum and the 2016 US Presidential Election. Available at SSRN 3092335. 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3092335 (accessed on 10 May 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adjodah, D.; Leng, Y.; Chong, S.K.; Krafft, P.M.; Moro, E.; Pentland, A. Accuracy-Risk Trade-Off Due to Social Learning in Crowd-Sourced Financial Predictions. Entropy 2021, 23, 801. https://doi.org/10.3390/e23070801
Adjodah D, Leng Y, Chong SK, Krafft PM, Moro E, Pentland A. Accuracy-Risk Trade-Off Due to Social Learning in Crowd-Sourced Financial Predictions. Entropy. 2021; 23(7):801. https://doi.org/10.3390/e23070801
Chicago/Turabian StyleAdjodah, Dhaval, Yan Leng, Shi Kai Chong, P. M. Krafft, Esteban Moro, and Alex Pentland. 2021. "Accuracy-Risk Trade-Off Due to Social Learning in Crowd-Sourced Financial Predictions" Entropy 23, no. 7: 801. https://doi.org/10.3390/e23070801
APA StyleAdjodah, D., Leng, Y., Chong, S. K., Krafft, P. M., Moro, E., & Pentland, A. (2021). Accuracy-Risk Trade-Off Due to Social Learning in Crowd-Sourced Financial Predictions. Entropy, 23(7), 801. https://doi.org/10.3390/e23070801





