Improved Q-Learning Algorithm Based on Approximate State Matching in Agricultural Plant Protection Environment
Abstract
1. Introduction
- Designing a reinforcement learning model for UAV pesticide spraying in the agricultural plant protection environment;
- Proposing an Approximate State Matching Q-learning algorithm to solve the policy learning problem in the agricultural plant protection environment;
- Analyzing the performance of the algorithm and explain the reason that it performs better than the classic Q-learning algorithm in the form of theorems;
- Testing and evaluating the performance of the proposed method on datasets generated based on real agricultural plant protection environment.
2. Background
2.1. Related Work
- The DRL algorithm may take longer than the traditional Q learning algorithm, and DRL may require better computer equipment;
- DRL includes many and complex neural network structures. The optimization of neural networks is a difficult problem. It is possible that a small structural change may cause the experimental results to vary greatly, and it is difficult for us to know the reason for it.
2.2. Reinforcement Learning
| Algorithm 1 Q–Learning Algorithm |
| Input: State set S, Action set A, Reward function R Output: Q table 1: Initialize Q table 2: while the number of iterations do 3: Return s to the initial state 4: while s is not terminal do 5: Choose a from A using policy derived from (e.g., greedy) 6: Take action a, observe r, 7: 8: 9: end while 10: end while 11: Return Q |
3. Problem Description
3.1. State
- (1)
- The history of actions includes not only the information of position, but also other information such as energy cost. For instance, and have the same position but different energy cost.
- (2)
- Since in the initial state, the UAV does not know the exact position of the mission, it is necessary to add a dimension to record where the UAV has been sprayed with pesticides, but this will cause the convergence rate to be greatly slowed down. Using the history of actions can solve this problem, because in the learning process, only the state of spraying pesticides at the correct position will be rewarded.
- (3)
- Only considering the position state may lead to the wrong cycle in the learning process, for instance, if the UAV can get a reward for returning to the base station, it will continue to execute the action of returning to the base station. In addition, using the history of actions as an aid can avoid this situation.
- (4)
- Using the history of actions as a state space can be seen as the limited expansion of using coordinates as state space. This is because the action spray pesticide (s) and supplementary energy (e) are a special action. For instance, and are , but the advantages and disadvantages of the two in action selection are obviously different. Similarly, and are , but their actual effects may be the same (both sprayed in the wrong position) or different (one sprayed in the correct position). For these actions, it is not enough to add a dimension to record whether they are executed. We also need to know where and when these actions are executed. Thus, using the history of actions as a state space can help us find the optimal policy.
- (5)
- Such state space expansion seems infinite, to solve this problem we will propose the Approximate State Matching Q-learning Algorithm in Section 4.1.
- (6)
- Of course, we can also find the optimal strategy by increasing the number of iterations and randomness. However, this situation can only be verified through experiments, but it is difficult to analyze theoretically. In this work, we are committed to improving the traditional Q learning algorithm and explore theoretically why the improved algorithm is better than the traditional algorithm, as we did in Section 4.2.
3.2. Actions
3.3. Transition
- In general, the transition fuction of state is to add the executed action to the current state.
- In order to indicate the number of tasks that UAVs have completed in the current state, we set for each state s. represents the number of tasks that have been completed in state s. Thus, in the initial state, , when a task is completed and is added to state s.
- If all tasks are completed, the state will transition to the end state.
- If the UAV runs out of energy, the state will clear all actions but keep to record the number of tasks that have been completed.
3.4. Reward
- UAV starts from the base station, arrives at the position of plant protection tasks, and sprays pesticides.
- The position and pesticides required of different tasks are different.
- When the energy is insufficient, the UAV needs to return to supplement.
- The base station is the end point of Back (b), and the position no longer changes if b continues to be executed.
- When executing action e, UAVs will return to the position of the base station and replenishes energy.
- After it completes a task, the UAV will execute the next task that is assigned.
- When UAVs have multiple tasks, they need to be executed sequentially (i.e., UAVs can not skip the current task and execute the next one).
4. Problem Solution
4.1. Approximate State Matching Q-Learning Algorithm
| Algorithm 2 Selecting a Similar Set Based on Energy Cost |
| Input: States s Output: Similar set of s 1: Create a empty stack 2: while do 3: a is the action that pops from the head of state s 4: if then 5: Clear the stack 6: else 7: Push a to the stack 8: end if 9: end while 10: Measure the length of the and mark it as l 11: 12: 13: while do 14: Select from 15: executing Line 1 to Line 10 with 16: if then 17: 18: 19: else 20: 21: end if 22: end while 23: Return |
| Algorithm 3 Selecting a Similar Set Based on Vertical Position |
| Input: States s Output: Similar set of s 1: Create 2 empty stack: , 2: while do 3: a is the action that pops from the head of state s 4: if then 5: Push a to 6: else if then 7: if then 8: Pop an element from 9: end if 10: else if then 11: Clear 12: else if then 13: Push a to and clear 14: end if 15: end while 16: Measure the length of the and and mark them as and respectively 17: 18: 19: while do 20: Select from 21: Calculate and by executing Line 1 to Line 16 with 22: if and then 23: 24: 25: else 26: 27: end if 28: end while 29: Return |
| Algorithm 4 Approximate State Matching Q-learning Algorithm |
| Input: Environment Output: Learned Q table 1: Initialize Q table 2: while the number of iterations do 3: Return s to the initial state 4: while s is not terminal state do 5: if s is not in Q table then 6: Add s to the Q table and initialize s 7: end if 8: if s is a Guided State then 9: Choose a from A using policy derived from 10: else 11: Select the similar set of s using Algorithm 2 12: for all 13: Choose a from A using policy derived from 14: if then 15: Select the similar set of s using Algorithm 3 16: for all 17: Choose a from A using policy derived from 18: end if 19: end if 20: Take action a, observe and 21: 22: 23: end while 24: end while 25: Return Q table |
4.2. Analysis of Algorithms
5. Experiment
5.1. Data Generation
5.1.1. UAV Specifications
5.1.2. Farm Information
5.1.3. Data Simulation
5.2. Evaluation Indicator
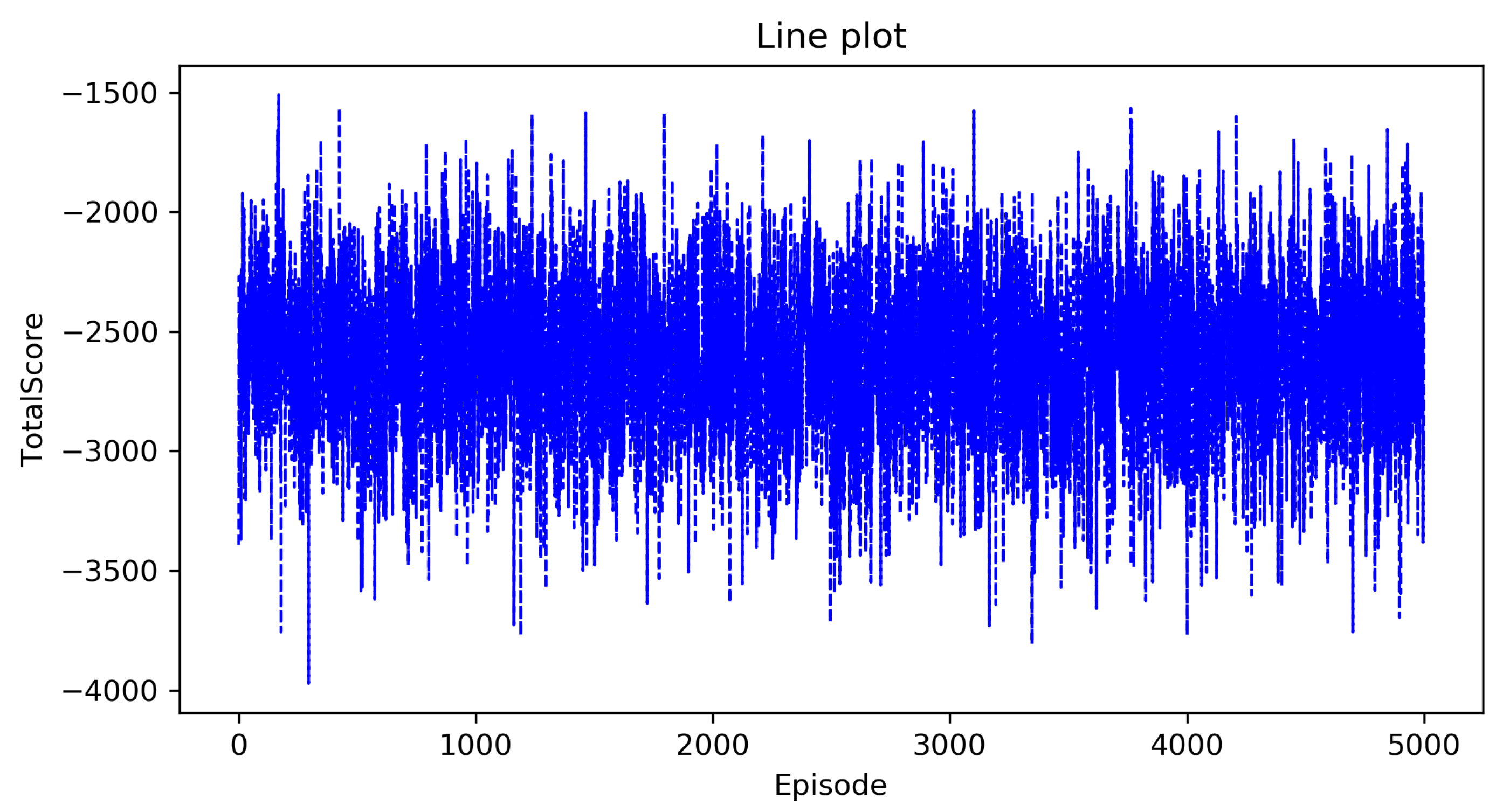
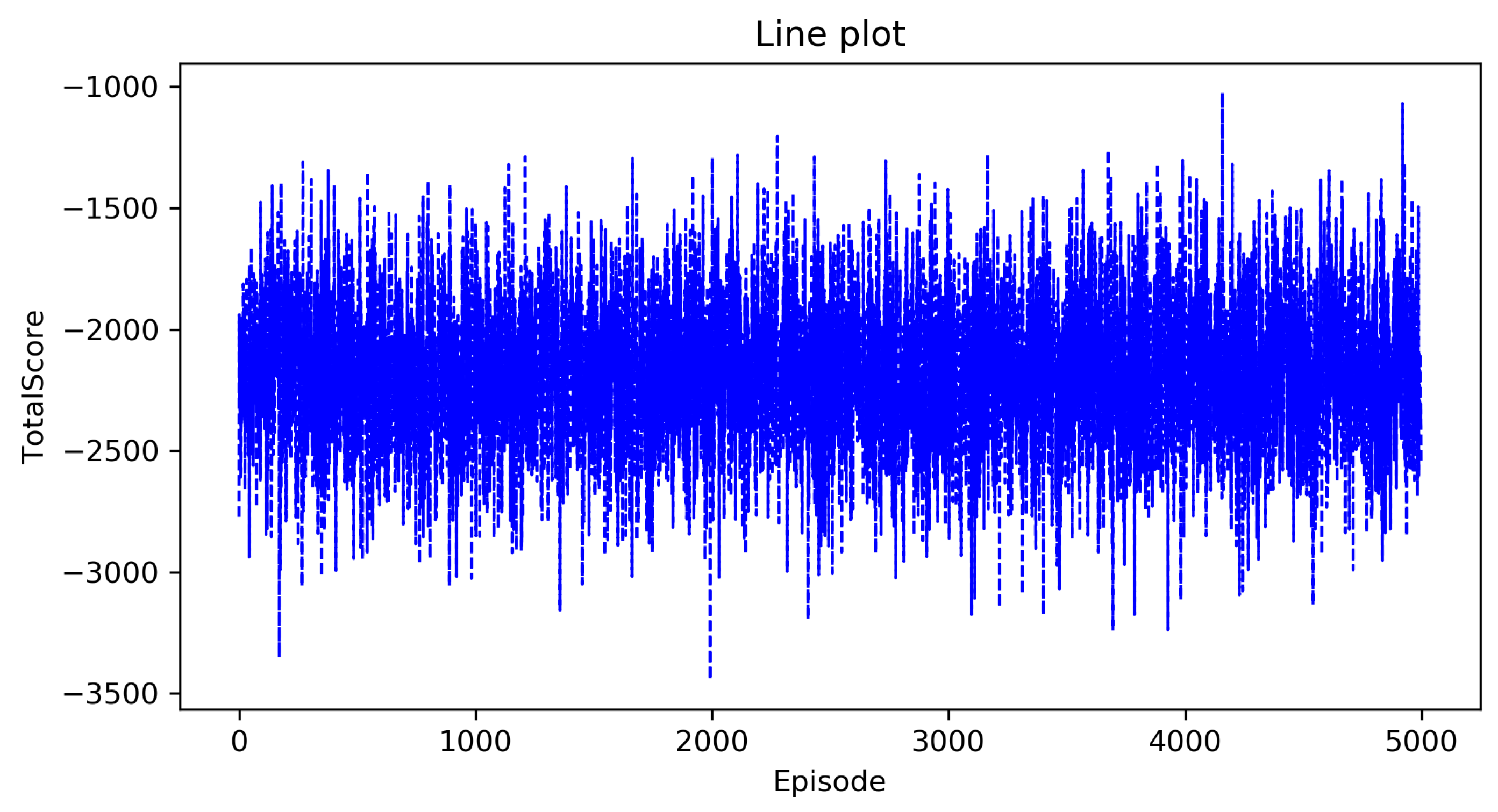
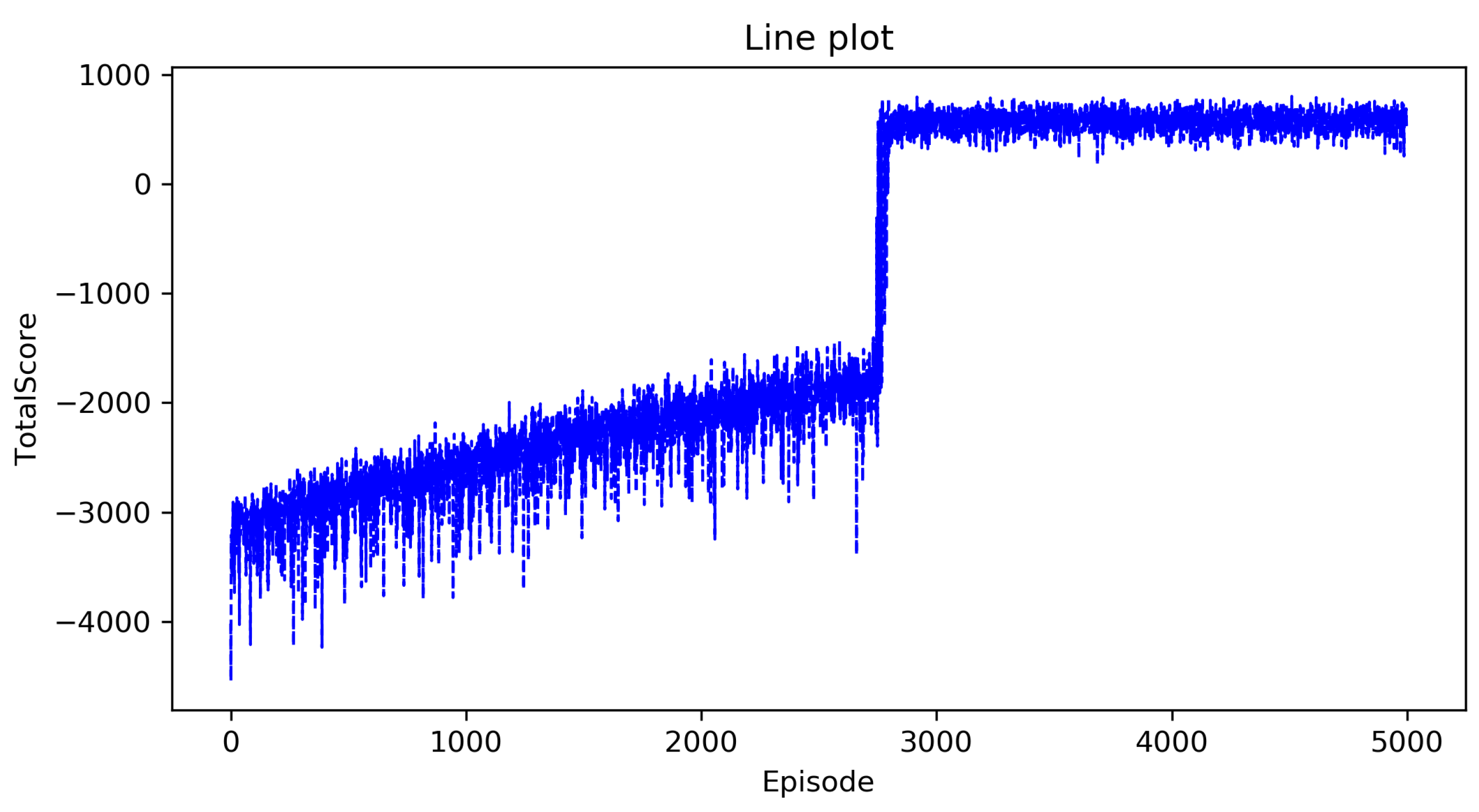
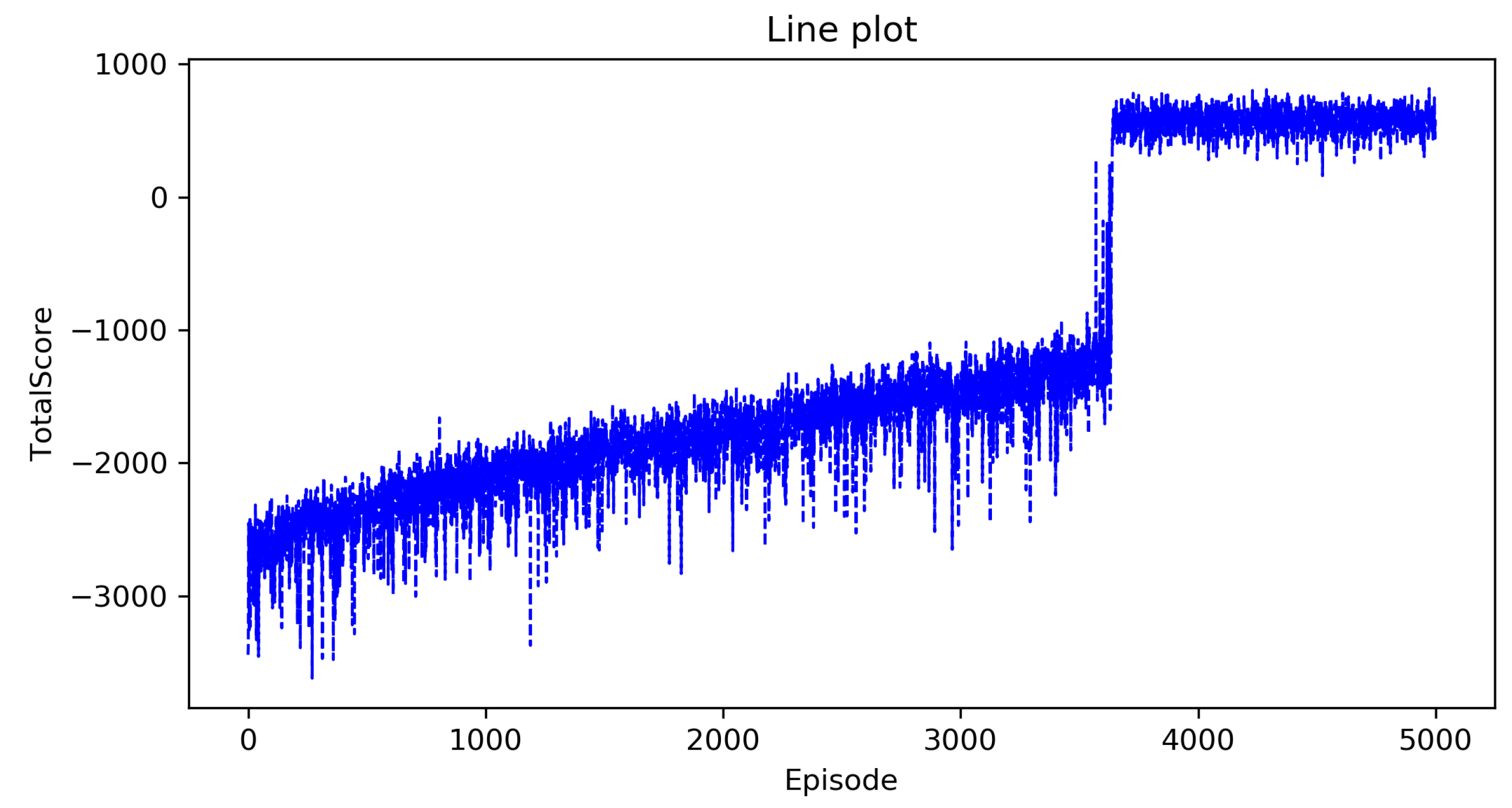
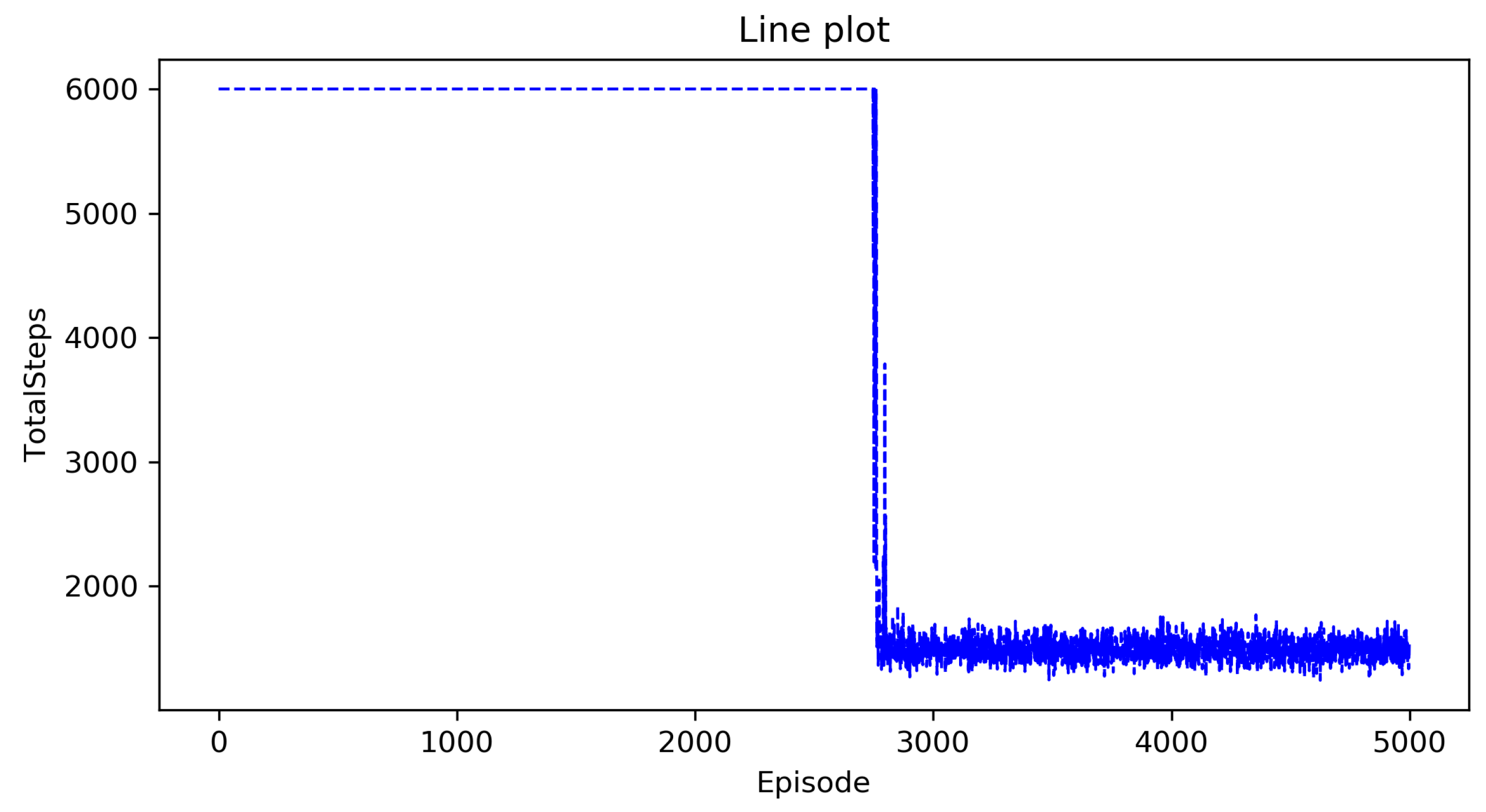
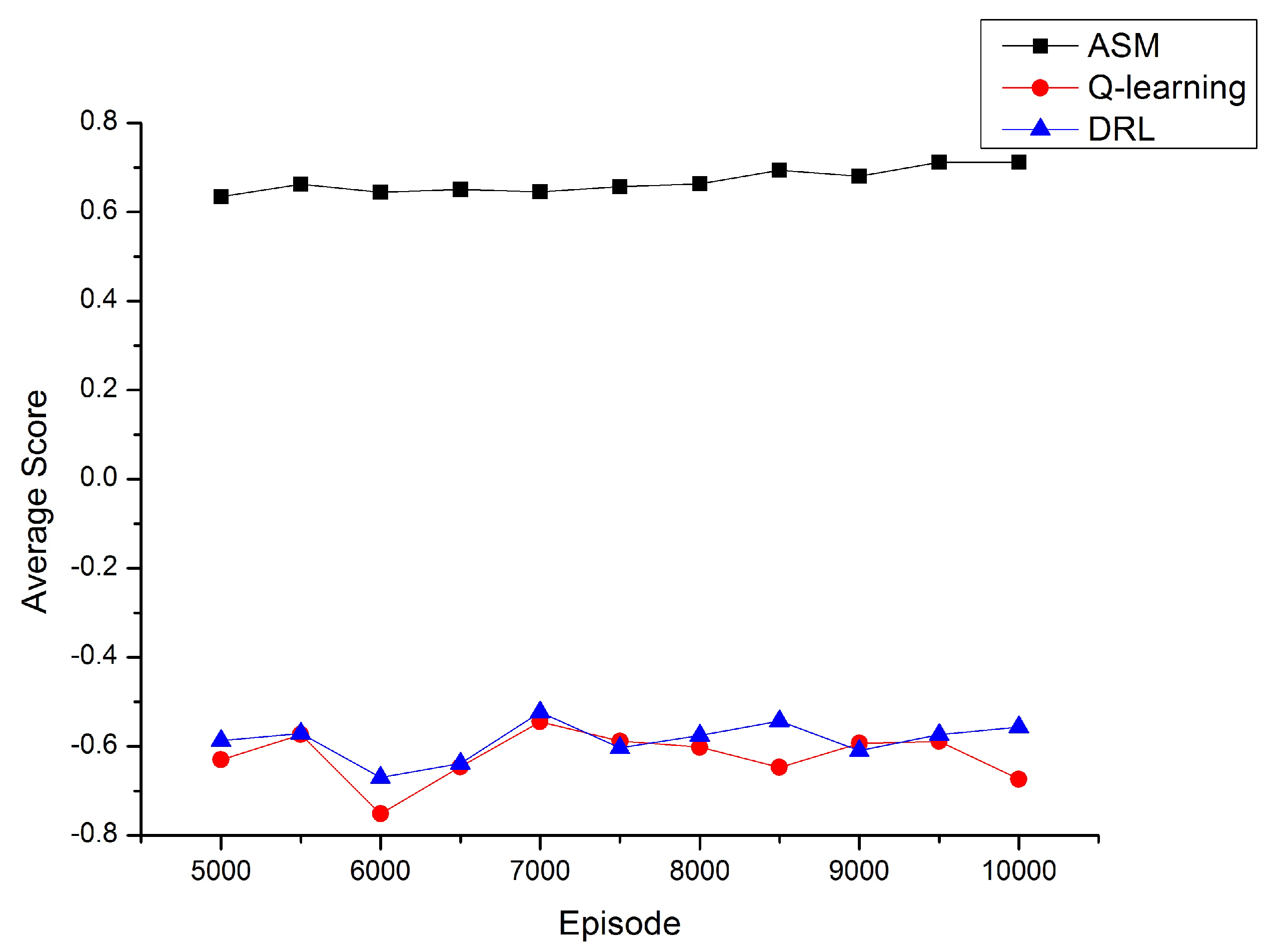
5.3. Result
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Peters, J. Policy gradient methods. Scholarpedia 2010, 5, 3698. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Y.; Xu, X.; Dai, H. Efficient Training Techniques for Multi-Agent Reinforcement Learning in Combat Tasks. IEEE Access 2019, 7, 109301–109310. [Google Scholar] [CrossRef]
- Khriji, L.; Touati, F.; Benhmed, K.; Al-Yahmedi, A. Mobile robot Navigation Based on Q-Learning Technique. Int. J. Adv. Robot. Syst. 2011, 8, 4. [Google Scholar] [CrossRef]
- Sun, L.; Zhai, J.; Qin, W. Crowd Navigation in an Unknown and Dynamic Environment Based on Deep Reinforcement Learning. IEEE Access 2019, 7, 109544–109554. [Google Scholar] [CrossRef]
- Nguyen, H.; La, H. Review of Deep Reinforcement Learning for Robot Manipulation. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019. [Google Scholar]
- Jeyaratnam, J. Acute pesticide poisoning: A major global health problem. World Health Stat. Q. 1990, 43, 139–144. [Google Scholar] [PubMed]
- Sun, F.; Wang, X.; Zhang, R. Fair Task Allocation When Cost of Task Is Multidimensional. Appl. Sci. 2020, 10, 2798. [Google Scholar] [CrossRef]
- Wang, G.; Han, Y.; Li, X.; Andaloro, J.; Lan, Y. Field evaluation of spray drift and environmental impact using an agricultural unmanned aerial vehicle (UAV) sprayer. Sci. Total Environ. 2020, 737, 139793. [Google Scholar] [CrossRef]
- Wang, G.; Yubin, L.; Qi, H.; Chen, P.; Hewitt, A.J.; Han, Y. Field evaluation of an unmanned aerial vehicle (UAV) sprayer: Effect of spray volume on deposition and the control of pests and disease in wheat. Pest Manag. Sci. 2019, 75, 1546–1555. [Google Scholar] [CrossRef]
- Ajmeri, N.; Guo, H.; Murukannaiah, P.K.; Singh, M.P. Robust Norm Emergence by Revealing and Reasoning about Context: Socially Intelligent Agents for Enhancing Privacy. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 28–34. [Google Scholar]
- Hao, J.; Leung, H.F. The dynamics of reinforcement social learning in cooperative multiagent systems. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (IJCAI ’13), Beijing, China, 3–9 August 2013; pp. 184–190. [Google Scholar]
- Bo, X.; Liping, C.; Yu, T. Path planning Based on Minimum Enerny Consumption for plant Protection UAVs in Sorties. Trans. Chin. Soc. Agric. Mach. 2015, 46, 36–42. [Google Scholar]
- Wang, Y.; Chen, H.; Li, Y.; Li, H. Path Planning Method Based on Grid-GSA for Plant Protection UAV. Trans. Chin. Soc. Agric. Mach. 2017, 48, 29–37. [Google Scholar]
- Wang, Y.; Chen, H.; Li, H. 3D Path Planning Approach Based on Gravitational Search Algorithm for Sprayer UAV. Trans. Chin. Soc. Agric. Mach. 2018, 49, 28–33. [Google Scholar]
- Sun, F.; Wang, X.; Zhang, R. Task scheduling system for UAV operations in agricultural plant protection environment. J. Ambient. Intell. Humaniz. Comput. 2020, 1–15. [Google Scholar] [CrossRef]
- Tang, J. Conflict Detection and Resolution for Civil Aviation: A Literature Survey. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 20–35. [Google Scholar] [CrossRef]
- Tang, J.; Zhu, F.; Piera, M.A. A causal encounter model of traffic collision avoidance system operations for safety assessment and advisory optimization in high-density airspace. Transp. Res. Part C Emerg. Technol. 2018, 96, 347–365. [Google Scholar] [CrossRef]
- Conte, R.; Dignum, F. From Social Monitoring to Normative Influence. J. Artif. Soc. Soc. Simul. 2001, 4, 7. [Google Scholar]
- Alechina, N.; Dastani, M.; Logan, B. Programming norm-aware agents. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems—Volume 2, Valencia, Spain, 4–8 June 2012; pp. 1057–1064. [Google Scholar]
- Gasparini, L.; Norman, T.J.; Kollingbaum, M.J. Severity-sensitive norm-governed multi-agent planning. Auton. Agents Multi-Agent Syst. 2018, 32, 26–58. [Google Scholar] [CrossRef]
- Meneguzzi, F.; Luck, M. Norm-based behaviour modification in BDI agents. In Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems (AAMAS ’09)—Volume 1, Budapest, Hungary, 10–15 May 2009; pp. 177–184. [Google Scholar]
- Dignum, F.; Morley, D.; Sonenberg, E.; Cavedon, L. Towards socially sophisticated BDI agents. In Proceedings of the Fourth International Conference on MultiAgent Systems; IEEE Computer Society: Washington, DC, USA, 2000; pp. 111–118. [Google Scholar]
- Fagundes, M.S.; Billhardt, H.; Ossowski, S. Normative reasoning with an adaptive self-interested agent model based on Markov decision processes. In Proceedings of the 12th Ibero-American Conference on Advances in Artificial Intelligence (IBERAMIA’10), Bahía Blanca, Argentina, 1–5 November 2010; pp. 274–283. [Google Scholar]
- Ajmeri, N.; Jiang, J.; Chirkova, R.; Doyle, J.; Singh, M.P. Coco: Runtime reasoning about conflicting commitments. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI’16), New York, NY, USA, 9–15 July 2016; pp. 17–23. [Google Scholar]
- van Riemsdijk, M.B.; Dennis, L.; Fisher, M.; Hindriks, K.V. A Semantic Framework for Socially Adaptive Agents: Towards strong norm compliance. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems (AAMAS ’15), Istanbul, Turkey, 4–8 May 2015; pp. 423–432. [Google Scholar]
- Watkins, C.J.C.H. Learning from Delayed Rewards. Ph.D. Thesis, King’s College, University of Cambridge, Cambridge, UK, 1989. [Google Scholar]
- Smart, W.; Kaelbling, L.P. Effective reinforcement learning for mobile robots. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 4, pp. 3404–3410. [Google Scholar]
- Martinez-Gil, F.; Lozano, M.; Fernández, F. Multi-agent reinforcement learning for simulating pedestrian navigation. In Proceedings of the 11th International Conference on Adaptive and Learning Agents, Taipei, Taiwan, 2 May 2011; pp. 54–69. [Google Scholar]
- Casadiego, L.; Pelechano, N. From One to Many: Simulating Groups of Agents with Reinforcement Learning Controllers. In Proceedings of the Intelligent Virtual Agents: 15th International Conference (IVA 2015), Delft, The Netherlands, 26–28 August 2015; pp. 119–123. [Google Scholar]
- Li, S.; Xu, X.; Zuo, L. Dynamic path planning of a mobile robot with improved Q-learning algorithm. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 409–414. [Google Scholar]
- Bianchi, R.A.C.; Ribeiro, C.H.C.; Costa, A.H.R. Heuristically Accelerated Q–Learning: A New Approach to Speed Up Reinforcement Learning. In Proceedings of the Brazilian Symposium on Artificial Intelligence; Springer: Berlin, Germany, 2004; pp. 245–254. [Google Scholar]
- Matignon, L.; Laurent, G.; Piat, N.L.F. A study of FMQ heuristic in cooperative multi-agent games. In Proceedings of the 7th International Conference on Autonomous Agents and Multiagent Systems. Workshop 10: Multi-Agent Sequential Decision Making in Uncertain Multi-Agent Domains, Aamas’08; International Foundation for Autonomous Agents and Multiagent Systems: Richland County, SC, USA, 2008; Volume 1, pp. 77–91. [Google Scholar]
- Ng, A.Y.; Russell, S.J. Algorithms for Inverse Reinforcement Learning. In Proceedings of the Seventeenth International Conference on Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2000; Volume 67, pp. 663–670. [Google Scholar]
- Henry, P.; Vollmer, C.; Ferris, B.; Fox, D. Learning to navigate through crowded environments. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 981–986. [Google Scholar]
- Anschel, O.; Baram, N.; Shimkin, N. Averaged-DQN: Variance reduction and stabilization for deep reinforcement learning. In Proceedings of the 34th International Conference on Machine Learning—Volume 70, Sydney, Australia, 6–11 August 2017; pp. 176–185. [Google Scholar]
- Wang, P.; Li, H.; Chan, C.Y. Continuous Control for Automated Lane Change Behavior Based on Deep Deterministic Policy Gradient Algorithm. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1454–1460. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, P.; Pan, C.; Zhang, S. Multi-Agent Deep Reinforcement Learning-Based Cooperative Spectrum Sensing With Upper Confidence Bound Exploration. IEEE Access 2019, 7, 118898–118906. [Google Scholar] [CrossRef]
- Matta, M.; Cardarilli, G.C.; Nunzio, L.D.; Fazzolari, R.; Giardino, D.; Nannarelli, A.; Re, M.; Spanò, S. A Reinforcement Learning-Based QAM/PSK Symbol Synchronizer. IEEE Access 2019, 7, 124147–124157. [Google Scholar] [CrossRef]
- Littman, M.L.; Szepesvári, C. A Generalized Reinforcement-Learning Model: Convergence and Applications. In Proceedings of the Machine Learning, Thirteenth International Conference (ICML ’96), Bari, Italy, 3–6 July 1996. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Science, D. MG-1200P Flight Battery User Guide. Available online: https://dl.djicdn.com/downloads/mg_1p/20180705/MG-12000P+Flight+Battery+User+Guide_Multi.pdf (accessed on 5 July 2018).
- Cai, P.; Lin, M.; Huang, A. Research on the Informatization Construction of Agricultural Cooperatives—A Case Study of Rural Areas in Southern Fujian. J. Jiangxi Agric. 2012, 24, 175–178. [Google Scholar]
- News, N. Japanese Companies Develop New UAVs to Cope with Aging Farmers. Available online: https://news.163.com/air/18/0904/15/DQSCN107000181O6.html (accessed on 5 July 2018).

| Symbols | Implication |
|---|---|
| State collection of UAVs in an agricultural plant protection environment. | |
| Action collection of UAVs in a agricultural plant protection environment. | |
| State transition function in a plant protection environment. | |
| Reward function in a plant protection environment. | |
| Number of states in the stack. | |
| The Q value of action a in state s. | |
| The temporary Q value is used to assist the selection of action. | |
| Collection of states with similar positions. | |
| Collection of states with similar energy. |
| Action | Implication |
|---|---|
| Forward | UAV goes forward one step, the distance of the step is fixed. Each Forward action performed costs 1 unit of energy. |
| Back | UAV goes back one step, the step of go back is the same as the step of go forward. Each Back action performed costs 1 unit of energy, which is the same as the energy cost of going Forward. |
| Left | UAV goes left one step, the step of go back is the same as the step of go forward. Each Back action performed costs 1 unit of energy, which is the same as the energy cost going Forward. |
| Right | UAV goes right one step, the step of go back is the same as the step of go forward. Each Back action performed costs 1 unit of energy, which is the same as the energy cost of going Forward. |
| Spray Pesticides | The UAV sprays pesticides once and costs 1 unit of energy, which is the same as the energy cost going Forward and Back. |
| Supplement Energy | The UAV returns to the base station and replenishes energy. |
| State | f | b | p | e |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | ||||
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| Model | MG-12000P MAH- V |
| Capacity | 12,000 mAh |
| Compatible Aircraft Models | DJI MG-1P |
| Voltage | V |
| Battery Type | LiPo 12S |
| Energy | 532 Wh |
| Net Weight | kg |
| Max Charging Power | 1200 W |
| Control range | 3000 m |
| Work Coverage Width | 4–7 m |
| Working Speed | 7 m/s |
| Flight Speed | 12 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, F.; Wang, X.; Zhang, R. Improved Q-Learning Algorithm Based on Approximate State Matching in Agricultural Plant Protection Environment. Entropy 2021, 23, 737. https://doi.org/10.3390/e23060737
Sun F, Wang X, Zhang R. Improved Q-Learning Algorithm Based on Approximate State Matching in Agricultural Plant Protection Environment. Entropy. 2021; 23(6):737. https://doi.org/10.3390/e23060737
Chicago/Turabian StyleSun, Fengjie, Xianchang Wang, and Rui Zhang. 2021. "Improved Q-Learning Algorithm Based on Approximate State Matching in Agricultural Plant Protection Environment" Entropy 23, no. 6: 737. https://doi.org/10.3390/e23060737
APA StyleSun, F., Wang, X., & Zhang, R. (2021). Improved Q-Learning Algorithm Based on Approximate State Matching in Agricultural Plant Protection Environment. Entropy, 23(6), 737. https://doi.org/10.3390/e23060737






