Principled Decision-Making Workflow with Hierarchical Bayesian Models of High-Throughput Dose-Response Measurements
Abstract
1. Introduction
- An overview of the model and data to orient the reader (Section 2).
- Steps taken to validate correctness of the hierarchical Bayesian model (Section 3).
- An outline of how Bayesian posteriors can be used for principled decisions (Section 4).
- Further discussion of the advantages of hierarchical models, as well as limitations of this specific implementation (Section 5).
- Concluding thoughts on the promise of hierarchical Bayesian estimation in high-throughput assays (Section 6).
2. Model and Data Overview
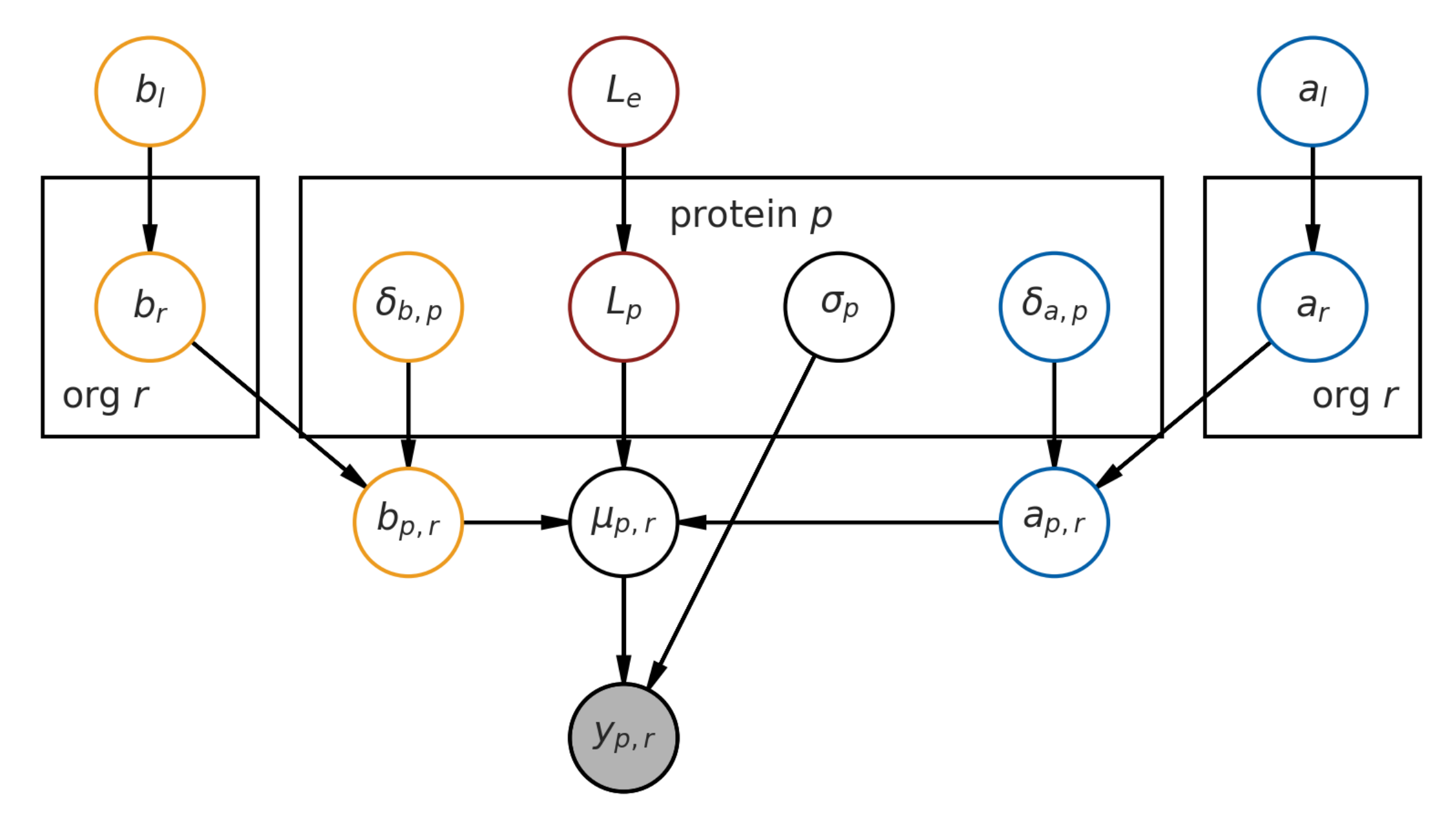
2.1. Base Model Definition
2.2. Data Characteristics and Summary Statistics
- The species and extraction method that a protein was isolated from;
- The protein ID (a unique identifier encompassing its gene name);
- The gene from which the protein was expressed;
- The temperature at which an observation was taken;
- The fold change of the detected stable protein at that temperature, relative to the level at the lowest measured temperature.
3. Validation of Model Implementation
3.1. Melting Curves
3.2. Posterior Variance
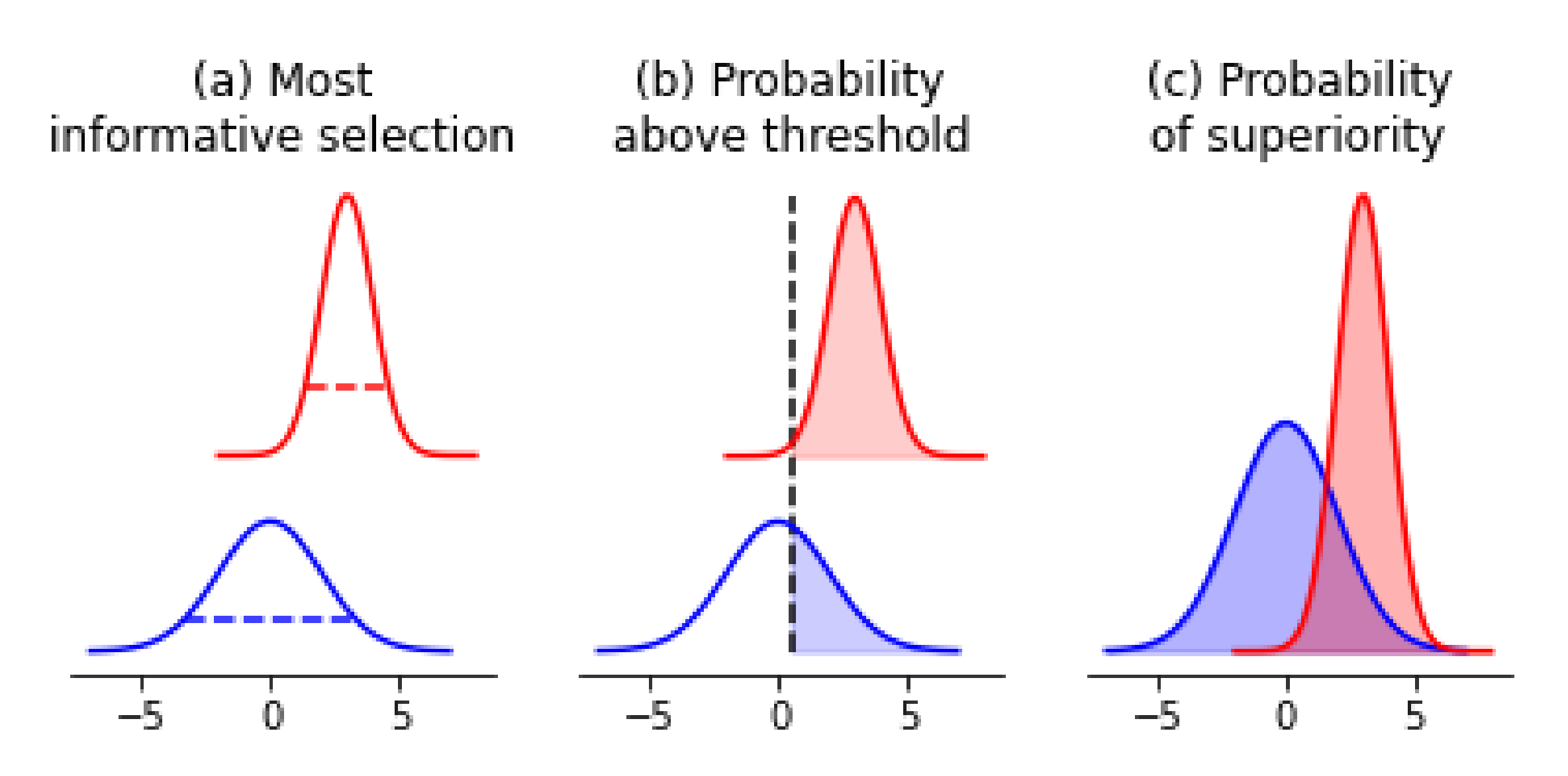
4. Principled Bayesian Decision-Making in High-Throughput Settings
- Which samples need higher-quality confirmatory measurements?
- Which samples should we take forward for further investigation in other measurement modes?
4.1. Acquiring Informative Measurements
4.2. Confirming Optimal Measurements
4.3. Prioritizing Samples for Further Modification
5. Discussion
5.1. Hierarchical Bayesian Methods Enable Reasonable Estimates Where Separate Curve-Fitting Fails to Provide One
5.2. Limitations of Our Model and Inferential Procedure
6. Conclusions: The Promise of Hierarchical Bayesian Models in High-Throughput Biological Measurements
7. Materials and Methods
7.1. Hierarchical Bayesian Estimation Model
7.2. High-Throughput Measurement Data
7.3. Separate Curve-Fitting
7.4. Posterior Curves
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADVI | Automatic Differentiation Variational Inference |
References
- Zhang, J.; Chung, T.; Oldenburg, K. A Simple Statistical Parameter for Use in Evaluation and Validation of high-throughput Screening Assays. J. Biomol. Screen. 1999, 4, 67–73. [Google Scholar] [CrossRef] [PubMed]
- Sui, Y.; Wu, Z. Alternative statistical parameter for high-throughput screening assay quality assessment. J. Biomol. Screen. 2007, 12, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Malo, N.; Hanley, J.; Cerquozzi, S.; Pelletier, J.; Nadon, R. Statistical practice in high-throughput screening data analysis. Nat. Biotechnol. 2006, 24, 167–175. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.; Reif, D.M.; Reich, B.J. Hierarchical dose–response modeling for high-throughput toxicity screening of environmental chemicals. Biometrics 2014, 70, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Shterev, I.D.; Dunson, D.B.; Chan, C.; Sempowski, G.D. Bayesian multi-plate high-throughput screening of compounds. Sci. Rep. 2018, 8, 9551. [Google Scholar] [CrossRef]
- Jensen, S.T.; Shirley, K.E.; Wyner, A.J. Bayesball: A Bayesian hierarchical model for evaluating fielding in major league baseball. Ann. Appl. Stat. 2009, 3, 491–520. [Google Scholar] [CrossRef]
- Ahn, W.Y.; Krawitz, A.; Kim, W.; Busemeyer, J.R.; Brown, J.W. A model-based fMRI analysis with hierarchical Bayesian parameter estimation. Decision 2013, 1, 8–23. [Google Scholar] [CrossRef]
- Gustafson, P. Large hierarchical Bayesian analysis of multivariate survival data. Biometrics 1997, 53, 230–242. [Google Scholar] [CrossRef] [PubMed]
- Tonkin-Hill, G.; Lees, J.A.; Bentley, S.D.; Frost, S.D.; Corander, J. Fast hierarchical Bayesian analysis of population structure. Nucleic Acids Res. 2019, 47, 5539–5549. [Google Scholar] [CrossRef] [PubMed]
- Messner, M.J.; Chappell, C.L.; Okhuysen, P.C. Risk assessment for Cryptosporidium: A hierarchical Bayesian analysis of human dose response data. Water Res. 2001, 35, 3934–3940. [Google Scholar] [CrossRef]
- Kruschke, J. Bayesian estimation supersedes the t test. J. Exp. Psychol. Gen. 2013, 142, 573–603. [Google Scholar] [CrossRef] [PubMed]
- Jarzab, A.; Kurzawa, N.; Hopf, T.; Moerch, M.; Zecha, J.; Leijten, N.; Bian, Y.; Musiol, E.; Maschberger, M.; Stoehr, G.; et al. Meltome atlas-thermal proteome stability across the tree of life. Nat. Methods 2020, 17, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Savitski, M.M.; Reinhard, F.B.; Franken, H.; Werner, T.; Savitski, M.F.; Eberhard, D.; Molina, D.M.; Jafari, R.; Dovega, R.B.; Klaeger, S.; et al. Tracking cancer drugs in living cells by thermal profiling of the proteome. Science 2014, 346, 1255784. [Google Scholar] [CrossRef]
- Schafer, J.L. Multiple imputation: A primer. Stat. Methods Med. Res. 1999, 8, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic Differentiation Variational Inference. J. Mach. Learn. Res. 2017, 18, 1–45. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Brookes, D.; Park, H.; Listgarten, J. Conditioning by adaptive sampling for robust design. In Proceedings of Machine Learning Research; PMLR: Long Beach, CA, USA, 2019; Volume 97, pp. 773–782. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]



| Run Name | Mean | StDev | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|
| A. thaliana seedling lysate | 43.8 | 1.5 | 34.6 | 43.1 | 43.9 | 44.5 | 49.6 |
| B. subtilis lysate | 43.7 | 3.0 | 36.8 | 41.9 | 43.8 | 44.8 | 58.4 |
| C. elegans lysate | 44.0 | 3.5 | 34.2 | 42.2 | 44.5 | 45.4 | 57.6 |
| D. melanogaster lysate | 43.3 | 2.6 | 39.2 | 41.9 | 42.5 | 43.7 | 54.6 |
| E. coli cells | 54.1 | 3.5 | 45.4 | 51.8 | 53.8 | 55.7 | 67.1 |
| E. coli lysate | 55.2 | 4.6 | 45.9 | 51.8 | 54.1 | 57.9 | 67.3 |
| G. stearothermophilus lysate | 81.9 | 5.7 | 59.7 | 77.7 | 81.3 | 85.8 | 97.3 |
| M. musculus BMDC lysate | 49.4 | 2.0 | 44.0 | 48.2 | 49.4 | 50.7 | 60.0 |
| M. musculus liver lysate | 51.0 | 2.2 | 44.4 | 49.7 | 51.0 | 51.8 | 64.1 |
| O. antarctica lysate | 48.8 | 4.5 | 36.5 | 46.0 | 47.5 | 51.3 | 63.7 |
| P. torridus lysate | 72.9 | 3.6 | 65.2 | 70.5 | 72.2 | 74.5 | 83.6 |
| S. cerevisiae lysate | 47.1 | 2.3 | 40.9 | 45.7 | 46.8 | 48.4 | 55.4 |
| T. thermophilus cells | 108.5 | 8.5 | 80.7 | 104.8 | 110.3 | 114.5 | 125.0 |
| T. thermophilus lysate | 107.3 | 8.4 | 79.2 | 101.8 | 109.0 | 113.4 | 125.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, E.J.; Kummer, A. Principled Decision-Making Workflow with Hierarchical Bayesian Models of High-Throughput Dose-Response Measurements. Entropy 2021, 23, 727. https://doi.org/10.3390/e23060727
Ma EJ, Kummer A. Principled Decision-Making Workflow with Hierarchical Bayesian Models of High-Throughput Dose-Response Measurements. Entropy. 2021; 23(6):727. https://doi.org/10.3390/e23060727
Chicago/Turabian StyleMa, Eric J., and Arkadij Kummer. 2021. "Principled Decision-Making Workflow with Hierarchical Bayesian Models of High-Throughput Dose-Response Measurements" Entropy 23, no. 6: 727. https://doi.org/10.3390/e23060727
APA StyleMa, E. J., & Kummer, A. (2021). Principled Decision-Making Workflow with Hierarchical Bayesian Models of High-Throughput Dose-Response Measurements. Entropy, 23(6), 727. https://doi.org/10.3390/e23060727






