Shall I Work with Them? A Knowledge Graph-Based Approach for Predicting Future Research Collaborations
Abstract
1. Introduction
- We investigate whether the integration of unstructured textual data into a single knowledge graph affects the performance of a link prediction model.
- We study the effect of previously proposed graph kernels-based approaches on the performance of an ML model, as far as the link prediction problem is concerned.
- We propose a three-phase pipeline that enables the exploitation of structural and textual information, as well as of pre-trained word embeddings.
- We empirically test our approach through various feature combinations with respect to the link prediction problem.
2. Background and Related Work
2.1. Graph Related Concepts
2.2. Graph Measures and Indices
2.3. Graph Kernels
2.3.1. Pyramid Match Graph Kernel
2.3.2. Propagation Kernel
2.4. Graph-Based Text Representations
2.5. Word Embeddings
2.6. Predicting Future Research Collaborations
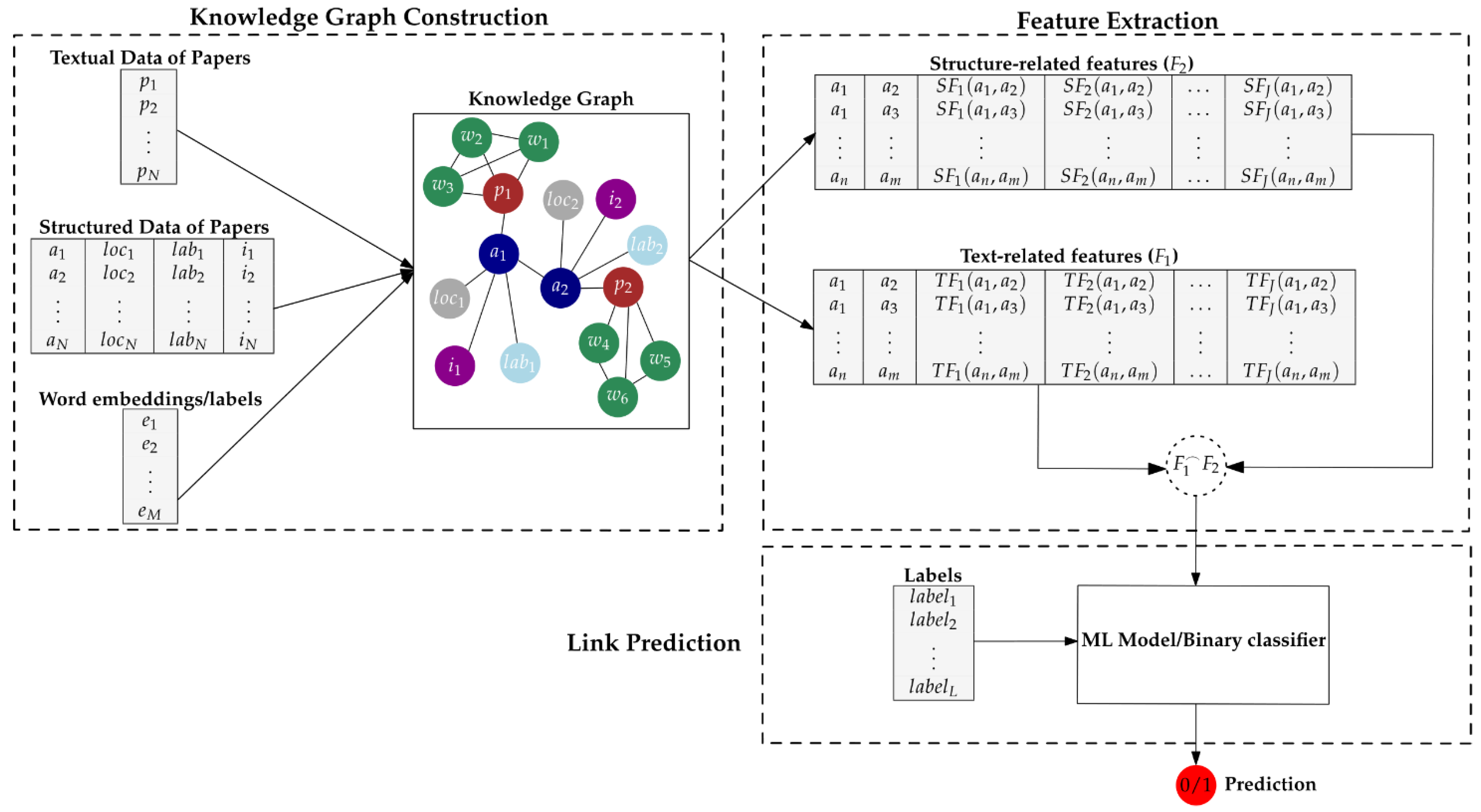
3. The Proposed Approach
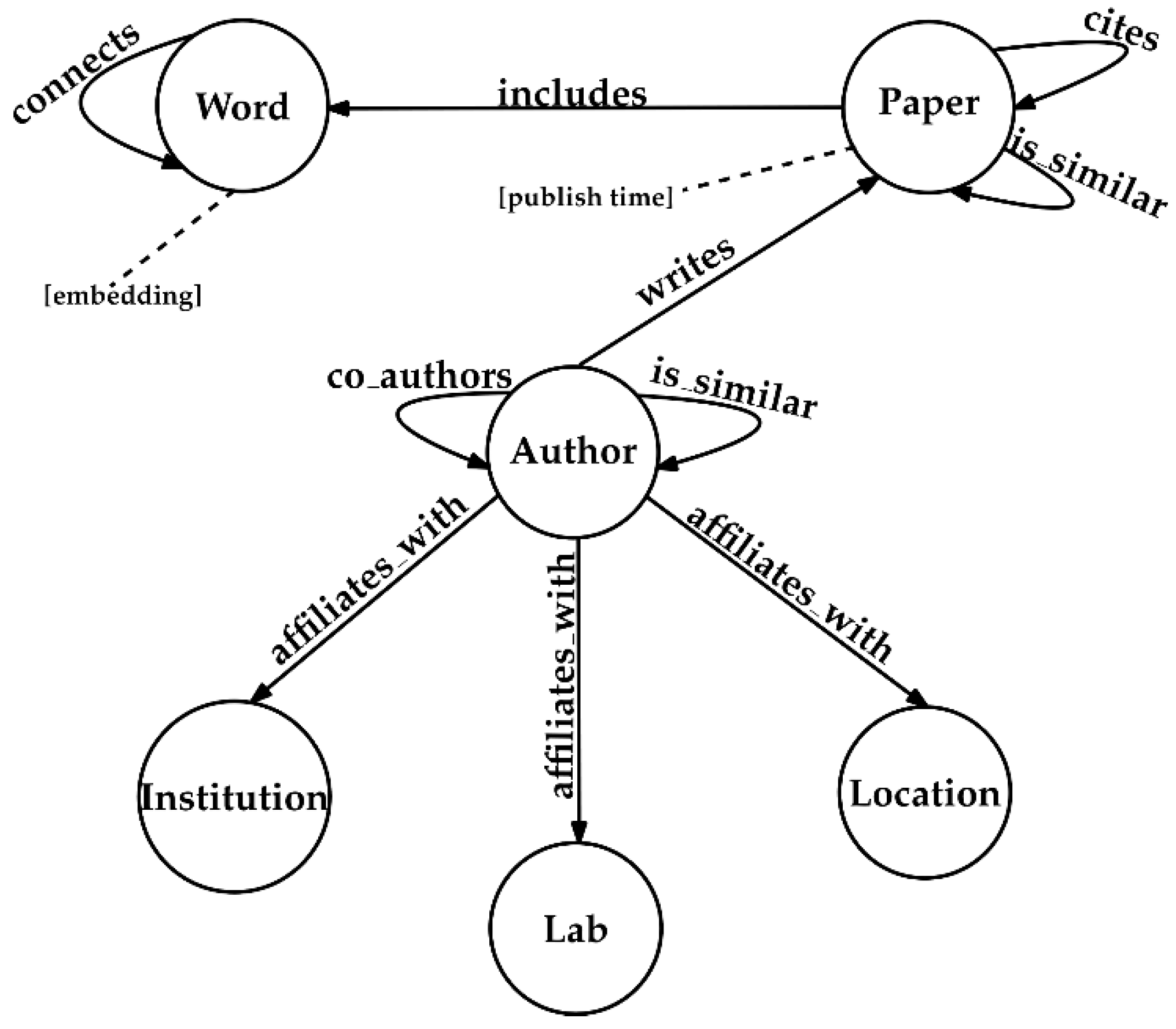
3.1. Knowledge Graph Construction
3.2. Feature Extraction
3.3. Link Prediction
4. Experimental Evaluation
4.1. Evaluation Metrics
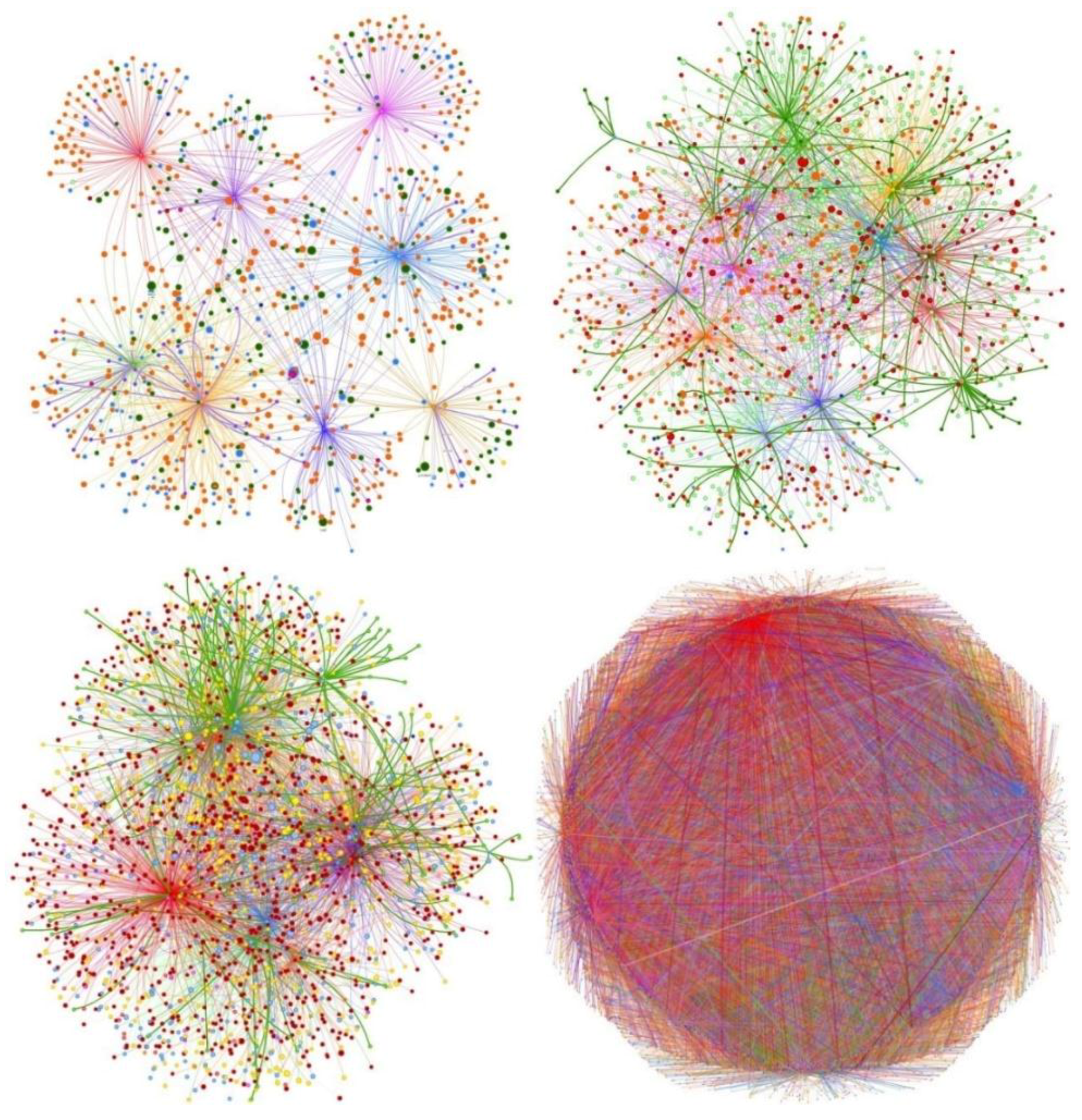
4.2. The CORD-19 Dataset
Generation of Datasets for Predicting Future Research Collaborations
4.3. Baseline Feature Combinations
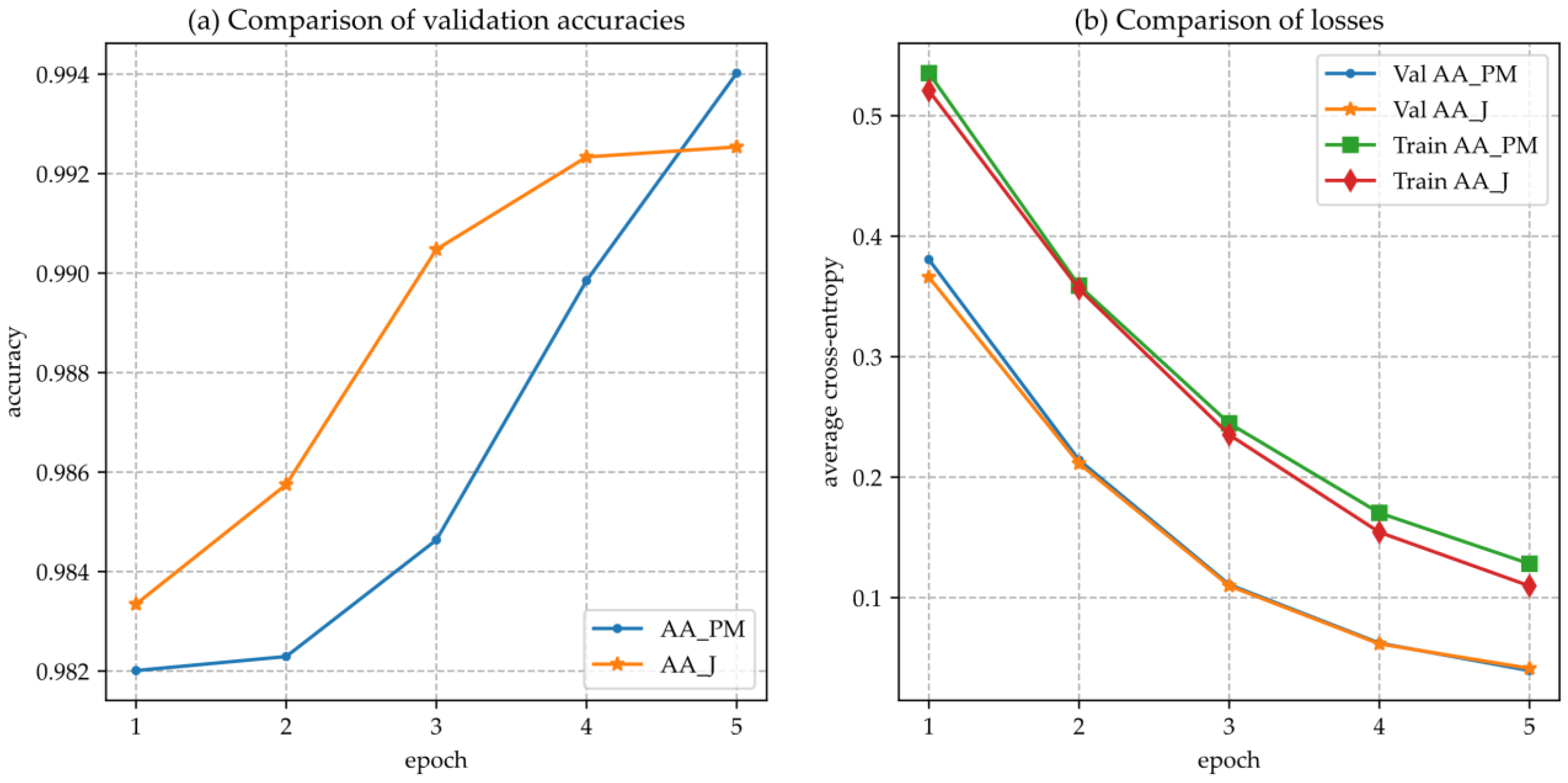
4.4. Evaluation Results
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nathani, D.; Chauhan, J.; Sharma, C.; Kaul, M. Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019. [Google Scholar]
- Vahdati, S.; Palma, G.; Nath, R.J.; Lange, C.; Auer, S.; Vidal, M.E. Unveiling scholarly communities over knowledge graphs. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; pp. 103–115. [Google Scholar]
- Ponomariov, B.; Boardman, C. What is co-authorship? Scientometrics 2016, 109, 1939–1963. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge graph embedding: A survey of approaches and applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Veira, N.; Keng, B.; Padmanabhan, K.; Veneris, A. Unsupervised Embedding Enhancements of Knowledge Graphs using Textual Associations. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI), Macao, China, 10–16 August 2019. [Google Scholar]
- Giarelis, N.; Kanakaris, N.; Karacapilidis, N. An Innovative Graph-Based Approach to Advance Feature Selection from Multiple Textual Documents. In IFIP International Conference on Artificial Intelligence Applications and Innovations; Springer: Cham, Switerland, 2020; pp. 96–106. [Google Scholar]
- Giarelis, N.; Kanakaris, N.; Karacapilidis, N. On a novel representation of multiple tex-tual documents in a single graph. In Proceedings of the 12th KES International Conference on Intelligent Decision Technologies (KES-IDT-20), Split, Croatia, 17–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Giarelis, N.; Kanakaris, N.; Karacapilidis, N. On the Utilization of Structural and Textual Information of a Scientific Knowledge Graph to Discover Future Research Collaborations: A Link Prediction Perspective. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; pp. 437–450. [Google Scholar]
- West, D. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Vathy-Fogarassy, Á.; Abonyi, J. Graph-Based Clustering and Data Visualization Algorithms; Springer: London, UK, 2013. [Google Scholar]
- Li, S.; Huang, J.; Zhang, Z.; Liu, J.; Huang, T. Similarity-based future common neighbors model for link prediction in complex networks. Sci. Rep. 2018, 8, 17014. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical Mechanics of Complex Networks; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Adamic, L.A.; Adar, E. Friends and neighbors on the Web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vandoise Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Nikolentzos, G.; Siglidis, G.; Vazirgiannis, M. Graph Kernels: A Survey. arXiv 2019, arXiv:1904.12218. [Google Scholar]
- Gärtner, T.; Flach, P.; Wrobel, S. On graph kernels: Hardness results and efficient alternatives. In Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2003; pp. 129–143. [Google Scholar]
- Vishwanathan, S.N.; Schraudolph, N.N.; Kondor, R.; Karsten, M. Graph Kernels. J. Mach. Learn. Res. 2010, 11, 1201–1242. [Google Scholar]
- Borgwardt, K.M.; Kriegel, H.P. Shortest-path kernels on graphs. In Proceedings of the IEEE International Conference on Data Mining, ICDM, Houston, TX, USA, 27–30 November 2005; pp. 74–81. [Google Scholar]
- Ramon, J.; Gärtner, T. Expressivity versus Efficiency of Graph Kernels. In First International Workshop on Mining Graphs, Trees and Sequences; 2003; Available online: https://www.ics.uci.edu/~welling/teatimetalks/kernelclub04/graph-kernels.pdf (accessed on 25 April 2021).
- Nikolentzos, G.; Meladianos, P.; Vazirgiannis, M. Matching Node Embeddings for Graph Similarity. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Neumann, M.; Garnett, R.; Bauckhage, C.; Kersting, K. Propagation kernels: Efficient graph kernels from propagated information. Mach. Learn. 2016, 102, 209–245. [Google Scholar] [CrossRef]
- Rousseau, F.; Vazirgiannis, M. Graph-of-word and TW-IDF: New approach to Ad Hoc IR. In Proceedings of the International Conference on Information and Knowledge Management (CIKM), San Francisco, CA, USA, 27 October 27–1 November 2013; pp. 59–68. [Google Scholar]
- Rousseau, F.; Kiagias, E. Text Categorization as a Graph Classification Problem. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015. [Google Scholar]
- Almeida, F.; Xexéo, G. Word Embeddings: A Survey. arXiv 2019, arXiv:1901.09069. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Distributed Representations of Words and Phrases and their Compositionality. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. GloVe: Global Vectors for Word Representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Joulin, A.; Grave, E.; Bojanowski, P.; Douze, M.; Jégou, H.; Mikolov, T. FastText.zip: Compressing text classification models. In Proceedings of the International Conference on Language Resources and Evaluation (LREC), Portorož, Slovenia, 23–28 May 2016. [Google Scholar]
- Kholghi, M.; De Vine, L.; Sitbon, L.; Zuccon, G.; Nguyen, A. The Benefits of Word Embeddings Features for Active Learning in Clinical Information Extraction. In Proceedings of the Australasian Language Technology Association Workshop, Melbourne, Australia, 5–7 December 2016. [Google Scholar]
- Andreas, J.; Klein, D. How much do word embeddings encode about syntax? In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (ACL), Baltimore, MA, USA, 23–25 June 2014.
- Van Der Heijden, N.; Abnar, S.; Shutova, E. A Comparison of Architectures and Pretraining Methods for Contextualized Multilingual Word Embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, New York Hilton Midtown, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Kusner, M.J.; Sun, Y.; Kolkin, N.I.; Weinberger, K.Q. From Word Embeddings to Document Distances. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Ye, X.; Shen, H.; Ma, X.; Bunescu, R.; Liu, C. From Word Embeddings to Document Similarities for Improved Information Retrieval in Software Engineering. In Proceedings of the IEEE/ACM 38th International Conference on Software Engineering, Austin, TX, USA, 14–22 May 2016; pp. 404–415. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed Representations of Sentences and Documents. In Proceedings of the 31st International Conference on Machine Learning (PMLR), Bejing, China, 21–26 June 2014. [Google Scholar]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2003, 58, 1019–1031. [Google Scholar] [CrossRef]
- Sun, Y.; Barber, R. Co-Author Relationship Prediction in Heterogeneous Bibliographic Networks. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Kaohsiung, Taiwan, 25–27 July 2011; pp. 121–128. [Google Scholar]
- Guns, R.; Rousseau, R.; Rousseau, R. Recommending research collaborations using link prediction and random forest classifiers. Scientometrics 2014, 101, 1461–1473. [Google Scholar] [CrossRef]
- Huang, J.; Zhuang, Z.; Li, J.; Giles, C.L. Collaboration over time: Characterizing and modeling network evolution. In Proceedings of the 2008 International Conference on Web Search and Data Mining, Palo Alto, CA, USA, 11–12 February 2008; pp. 107–116. [Google Scholar]
- Yu, Q.; Long, C.; Shao, H.; He, P.; Duan, Z. Predicting Co-Author Relationship in Medical Co-Authorship Networks. PLoS ONE 2014, 9, e101214. [Google Scholar] [CrossRef] [PubMed]
- Fire, M.; Tenenboim, L.; Lesser, O.; Puzis, R.; Rokach, L.; Elovici, Y. Link Prediction in Social Networks using Computationally Efficient Topological Features. In Proceedings of the 2011 IEEE Third International Conference on Privacy, Security, Risk and Trust and 2011 IEEE Third International Conference on Social Computing, Boston, MA, USA, 9–11 October 2011; pp. 73–80. [Google Scholar]
- Julian, K.; Lu, W. Application of Machine Learning to Link Prediction. arXiv 2016. Available online: http://cs229.stanford.edu/proj2016/report/JulianLu-Application-of-Machine-Learning-to-Link-Prediction-report.pdf (accessed on 25 April 2021).
- Panagopoulos, G.; Tsatsaronis, G.; Varlamis, I. Detecting rising stars in dynamic collaborative networks. J. Inform. 2017, 11, 198–222. [Google Scholar] [CrossRef]
- Aggarwal, C. Machine Learning for Text; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; Cournapeau, D.; Pedregosa, F.; Varoquaux, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 11, 198–222. [Google Scholar]
- Siglidis, G.; Nikolentzos, G.; Limnios, S.; Giatsidis, C.; Skianis, K.; Vazirgianis, M. Grakel: A graph kernel library in python. J. Mach. Learn. Res. 2018, 21, 1–5. [Google Scholar]
- Wang, L.L.; Lo, K.; Chandrasekhar, Y.; Reas, R.; Yang, J.; Eide, D.; Funk, K.; Kinney, R.; Liu, Z.; Merrill, W.; et al. CORD-19: The COVID-19 open research dataset. arXiv 2020, arXiv:2004.10706v4. [Google Scholar]
- Wang, Z.; Li, J.; Liu, Z.; Tang, J. Text-enhanced Representation Learning for Knowledge Graph. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 1–6 June 2018; pp. 745–755. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428v3. [Google Scholar]
- CSIRO’s Data61. StellarGraph Machine Learning Library, GitHub Repository. 2018. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Ying, R.; Bourgeois, D.; You, J.; Zitnik, M.; Leskovec, J. GNNExplainer: Generating Explanations for Graph Neural Networks. arXiv 2019, arXiv:1903.03894v4. [Google Scholar]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2021, 23, 18. [Google Scholar] [CrossRef]
- Pho, P.; Mantzaris, A.V. Regularized Simple Graph Convolution (SGC) for improved interpretability of large datasets. J. Big Data 2020, 7, 91. [Google Scholar] [CrossRef]
- Molokwu, B.C.; Kobti, Z. Event Prediction in Complex Social Graphs via Feature Learning of Vertex Embeddings. In Neural Information Processing; Gedeon, T., Wong, K.W., Lee, M., Eds.; Springer International Publishing: Cham, Switerland, 2019; pp. 573–580. [Google Scholar]
- Tran, P.V. Learning to Make Predictions on Graphs with Autoencoders. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Turin, Italy, 1–3 October 2018; pp. 237–245. [Google Scholar] [CrossRef]
| Dataset ID | |Training Subset Samples| | |Testing Subset Samples| |
|---|---|---|
| D1 | 1000 | 330 |
| D2 | 1000 | 330 |
| D3 | 1000 | 330 |
| D4 | 1000 | 330 |
| D5 | 1000 | 330 |
| D6 | 1000 | 330 |
| D7 | 6000 | 1890 |
| D8 | 9900 | |
| D9 | 1000 | 330 |
| D10 | 1000 | 330 |
| Feature | Description | Type |
|---|---|---|
| adamic adar | The sum of the inverse logarithm of the degree of the set of common neighbor ‘Author’ nodes shared by a pair of nodes. | Structural (SF) |
| common neighbors | The number of neighbor ‘Author’ nodes that are common for a pair of ‘Author’ nodes. | Structural (SF) |
| preferential attachment | The product of the in-degree values of a pair of ‘Author’ nodes. | Structural (SF) |
| total neighbors | The product of the in-degree values of a pair of ‘Author’ nodes. | Structural (SF) |
| pyramid match | The similarity of the text of the graph-of-docs graphs of two nodes of ‘Author’ type using the Pyramid match graph kernel. The Propagation graph kernel incorporates the terms, the corresponding label of each term and the structure of the text into its formula, aiming to calculate the similarity between two texts. | Textual (TF) |
| propagation | The similarity of the text of the graph-of-docs graphs of two nodes of ‘Author’ type using the Propagation graph kernel. The Propagation graph kernel incorporates the terms, the corresponding word embedding of each term and the structure of the text into its formula, aiming to calculate the similarity between two texts. | Textual (TF) |
| weisfeiler pyramid match | The similarity of the text of the graph-of-docs graphs of two nodes of ‘Author’ type using the Weisfeiler Lehman framework and the Pyramid match graph kernel. The Weisfeiler Pyramid match graph kernel incorporates the terms, the corresponding label of each term and the structure of the text into its formula, aiming to calculate the similarity between two texts. | Textual (TF) |
| jaccard | The similarity of the text of the graph-of-docs graphs of two nodes of ‘Author’ type using the Jaccard coefficient. The Jaccard index deals only with the absence or the presence of a term into a text. | Structural and Textual (SF and TF) |
| Label | It denotes an edge of the ‘co_authors’ type between two nodes of the ‘Author’ type. A positive value (1) represents the existence, while a negative value (0) represents the absence of the edge. | Class |
| Feature Combination Name | Features Included | Proposed In |
|---|---|---|
| ALL | Adamic Adar, Common Neighbors, Preferential attachment, Total Neighbors, Pyramid match, Weisfeiler Pyramid match, Jaccard, Propagation | [8] |
| PM | Pyramid Match | [20] |
| WPM | Weisfeiler Pyramid match | [20] |
| AA_J (baseline) | Adamic Adar, Jaccard | [8] |
| AA (baseline) | Adamic Adar | [13] |
| p | Propagation | [21] |
| J (baseline) | Jaccard | [14,38] |
| AA_WPM | Adamic Adar, Weisfeiler Pyramid match | |
| AA_P | Adamic Adar, Propagation | |
| AA_PM | Adamic Adar, Pyramid match |
| Feature Combination | Accuracy | Recall | Precision |
|---|---|---|---|
| ALL | 0.6588 | 0.9963 * | 0.6345 |
| J | 0.5093 | 0.0233 | 1.0 |
| AA | 0.9818 | 0.9643 | 0.9995 |
| AA_J | 0.9834 | 0.9671 | 0.9998 |
| p | 0.6669 | 0.5589 | 0.8157 |
| PM | 0.838 | 0.6965 | 0.9752 |
| WPM | 0.9476 | 0.9044 | 0.9905 |
| AA_P | 0.9652 | 0.9923 * | 0.9625 |
| AA_PM | 0.998 * | 0.9966 * | 0.9995 |
| AA_WPM | 0.9986 * | 0.9977 * | 0.9995 |
| Feature Combination | Accuracy | Recall | Precision | Train Loss | Test Loss | Abs Loss Difference |
|---|---|---|---|---|---|---|
| ALL | 0.9908 | 0.9931 * | 0.9886 | 0.102 | 0.0499 | 0.0521 |
| J | 0.5093 | 0.0233 | 1.0 | 0.6647 | 0.6858 | 0.0211 |
| AA | 0.9922 | 0.985 | 0.9995 | 0.1303 | 0.0497 | 0.0806 |
| AA_J | 0.9925 | 0.9856 | 0.9995 | 0.1097 | 0.0413 | 0.0684 |
| p | 0.6954 | 0.5045 | 0.8624 | 0.6289 | 0.6057 | 0.0232 |
| PM | 0.8452 | 0.7085 | 0.9816 | 0.3219 | 0.399 | 0.0771 |
| WPM | 0.9248 | 0.859 | 0.9905 | 0.2612 | 0.239 | 0.0222 |
| AA_P | 0.9923 | 0.9851 | 0.9995 | 0.1311 | 0.0464 | 0.0847 |
| AA_PM | 0.994 * | 0.9886 * | 0.9995 | 0.1281 | 0.0395 | 0.0886 |
| AA_WPM | 0.9932 | 0.987 | 0.9995 | 0.1108 | 0.0372 | 0.0736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanakaris, N.; Giarelis, N.; Siachos, I.; Karacapilidis, N. Shall I Work with Them? A Knowledge Graph-Based Approach for Predicting Future Research Collaborations. Entropy 2021, 23, 664. https://doi.org/10.3390/e23060664
Kanakaris N, Giarelis N, Siachos I, Karacapilidis N. Shall I Work with Them? A Knowledge Graph-Based Approach for Predicting Future Research Collaborations. Entropy. 2021; 23(6):664. https://doi.org/10.3390/e23060664
Chicago/Turabian StyleKanakaris, Nikos, Nikolaos Giarelis, Ilias Siachos, and Nikos Karacapilidis. 2021. "Shall I Work with Them? A Knowledge Graph-Based Approach for Predicting Future Research Collaborations" Entropy 23, no. 6: 664. https://doi.org/10.3390/e23060664
APA StyleKanakaris, N., Giarelis, N., Siachos, I., & Karacapilidis, N. (2021). Shall I Work with Them? A Knowledge Graph-Based Approach for Predicting Future Research Collaborations. Entropy, 23(6), 664. https://doi.org/10.3390/e23060664






