A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies
Abstract
1. Introduction
2. A CF Fractional Model of HIV/AIDS with a Treatment Compartment
3. Equilibrium Point of the Model
4. Sensitivity Analysis
5. Necessary Conditions for Optimality of an FOCP
6. Fractional Optimal Control of the HIV/AIDS Model
7. Numerical Simulations
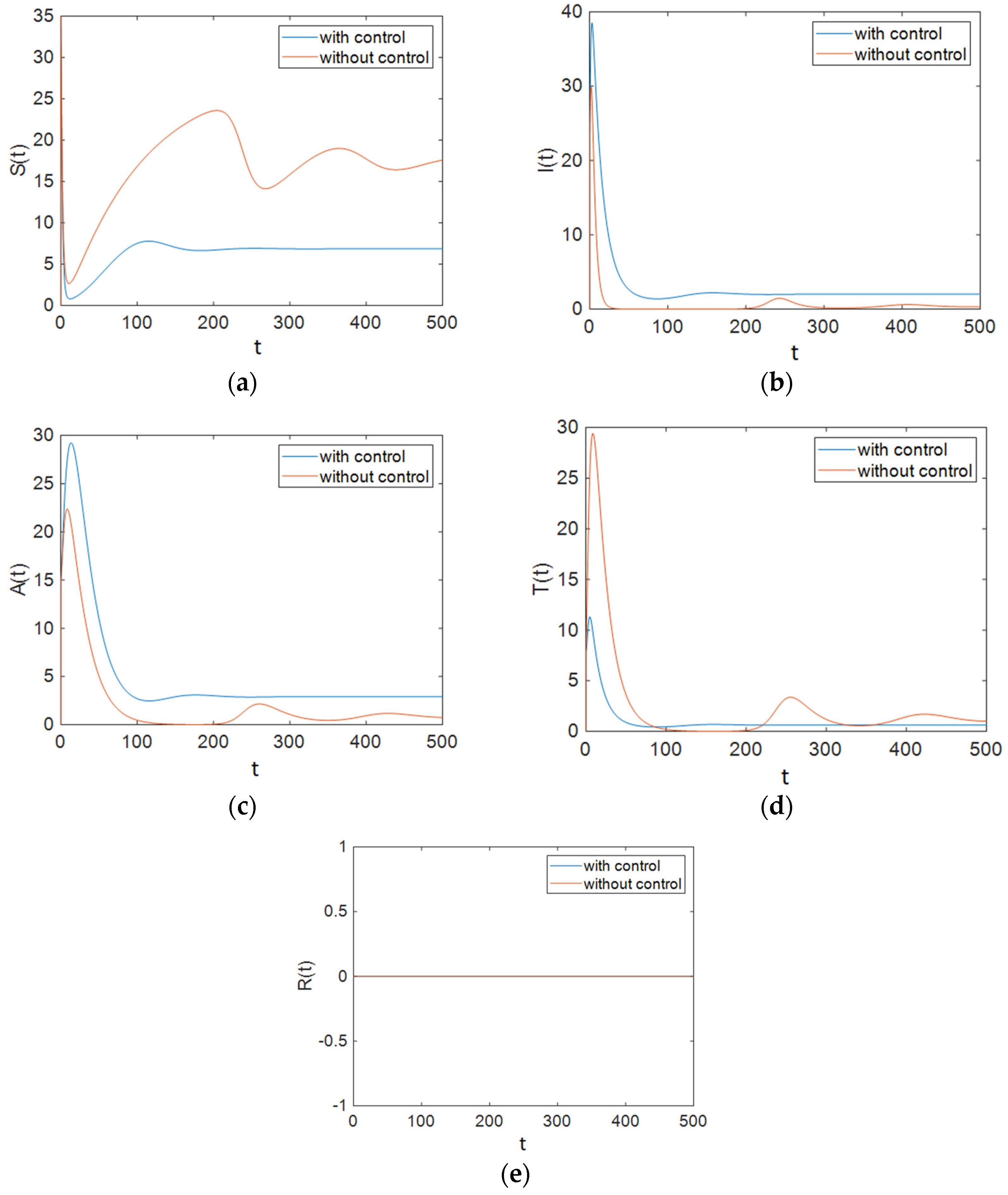
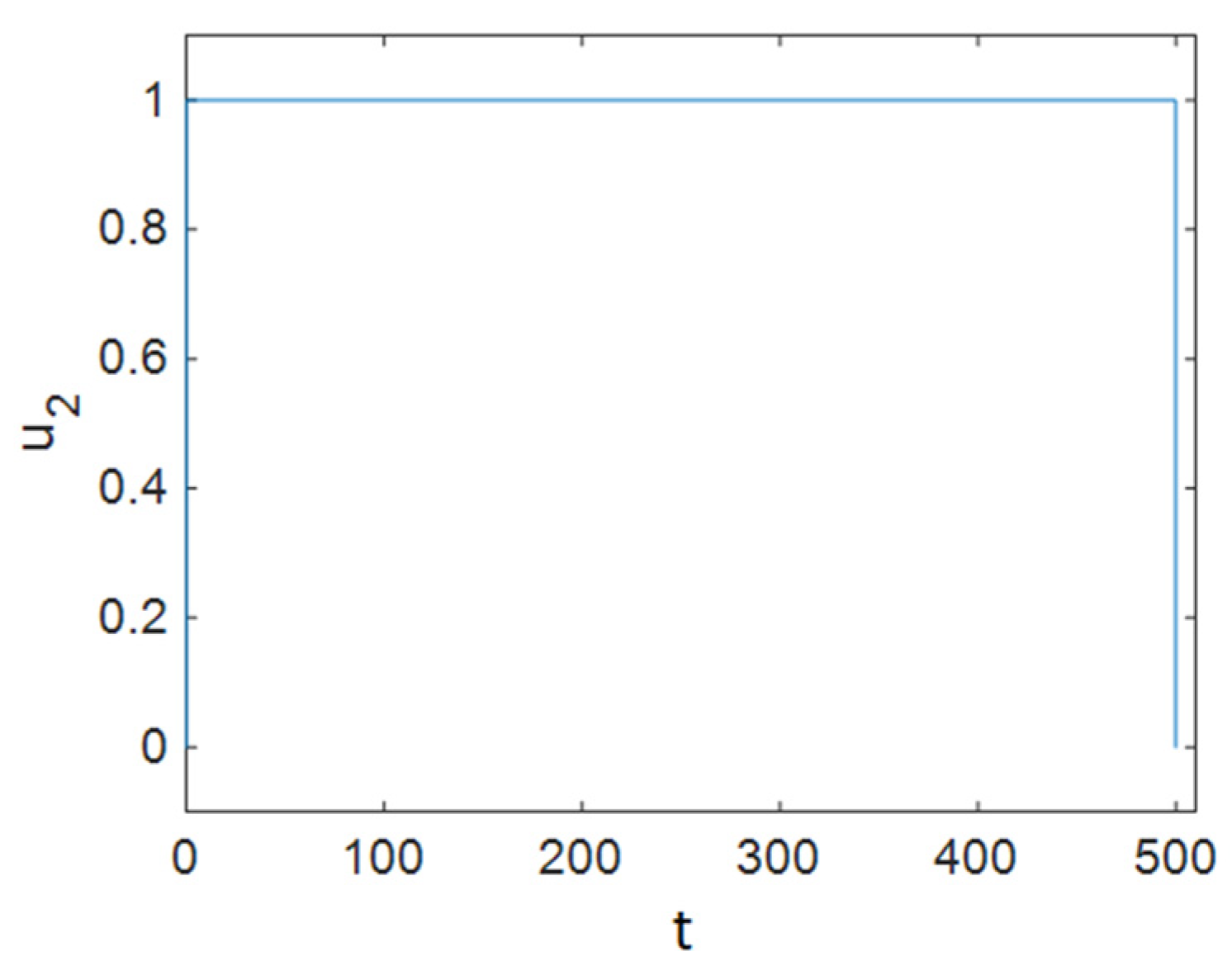
7.1. Strategy A: Control Using Treatment Alone
7.2. Strategy B: Control Using Treatment and Changes in People’s Sexual Habits
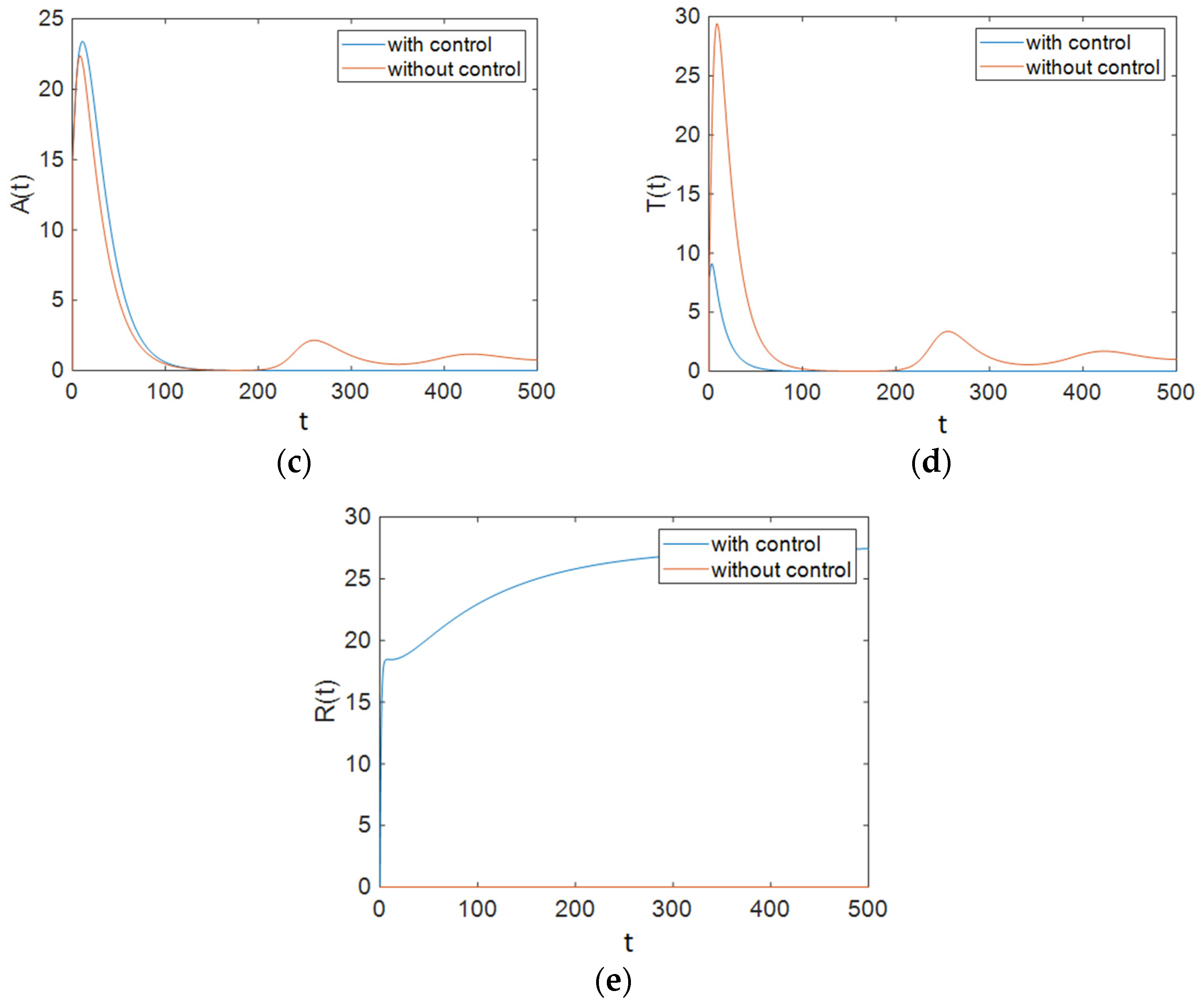
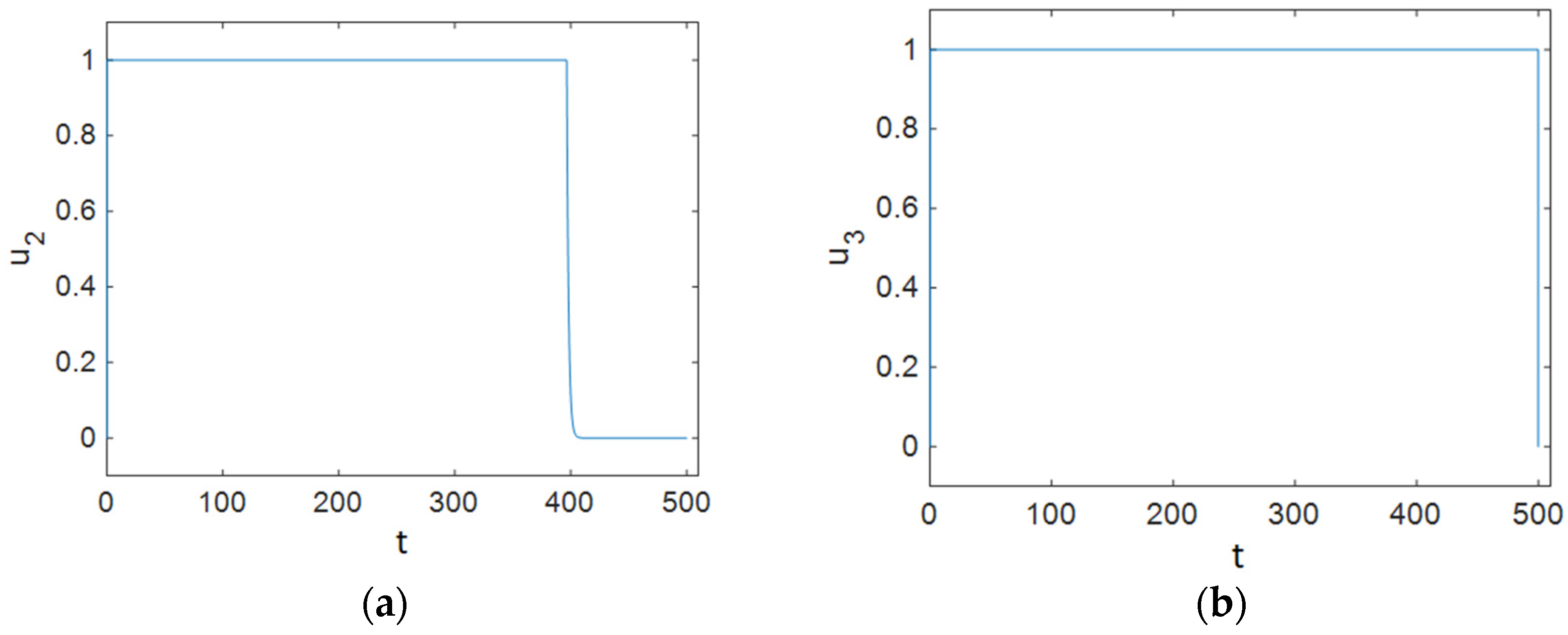
7.3. Strategy C: Control Using Prevention, Treatment, and Changes in Sexual Habits
7.4. Comparing Different Strategies
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elaiw, A.M.; Xia, X. HIV Dynamics: Analysis and Robust Multirate MPC-Based Treatment Schedules; Military Technical College: Cairo, Egypt, 2008; pp. 1–28. [Google Scholar]
- Egonmwan, A.O.; Okuonghae, D. Analysis of a mathematical model for tuberculosis with diagnosis. J. Appl. Math. Comput. 2019, 59, 129–162. [Google Scholar] [CrossRef]
- Pathak, S.; Maiti, A.; Samanta, G.P. Rich dynamics of an SIR epidemic model. Nonlinear Anal. Model. Control 2010, 15, 71–81. [Google Scholar] [CrossRef]
- Brauer, F. Some simple epidemic models. Math. Biosci. Eng. 2006, 3, 1. [Google Scholar] [CrossRef]
- Anderson, R.M.; Medley, G.F.; May, R.M.; Johnson, A.M. A preliminary study of the transmission dynamics of the human immunodeficiency virus (HIV), the causative agent of AIDS. Math. Med. Biol. J. IMA 1986, 3, 229–263. [Google Scholar] [CrossRef] [PubMed]
- Case, K.K.; Johnson, L.F.; Mahy, M.; Marsh, K.; Supervie, V.; Eaton, J.W. Summarizing the results and methods of the 2019 Joint United Nations Programme on HIV/AIDS HIV estimates. AIDS 2019, 33 (Suppl. 3), S197–S201. [Google Scholar] [CrossRef] [PubMed]
- Owolabi, K.M.; Atangana, A. Mathematical analysis and computational experiments for an epidemic system with nonlocal and nonsingular derivative. Chaos Solitons Fractals 2019, 126, 41–49. [Google Scholar] [CrossRef]
- Khajanchi, S.; Nieto, J.J. Mathematical modeling of tumor-immune competitive system, considering the role of time delay. Appl. Math. Comput. 2019, 340, 180–205. [Google Scholar] [CrossRef]
- Li, G.; Jin, Z. Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos Solitons Fractals 2005, 25, 1177–1184. [Google Scholar] [CrossRef]
- Tripathi, A.; Naresh, R.; Sharma, D. Modeling the effect of screening of unaware infectives on the spread of HIV infection. Appl. Math. Comput. 2007, 184, 1053–1068. [Google Scholar] [CrossRef]
- Jabbari, A.; Kheiri, H.; Jodayree Akbarfam, A.; Bekir, A. Dynamical analysis of the avian-human influenza epidemic model using multistage analytical method. Int. J. Biomath. 2016, 9, 1650090. [Google Scholar] [CrossRef]
- Bernoulli, D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l’inoculation pour la prévenir. Hist. Acad. R. Sci. Paris Mem. 1760, 811, 1–45. [Google Scholar]
- Ackermann, J.; Al-Bender, F.; Aliane, N.; Anderson, B.D.O.; Armstrong, B.S.R.; Astolfi, A.; Astrom, K.J.; Barhen, J.; Baumgartner, K.; Berenguel, M. 2008 Index IEEE Control Systems Magazine. IEEE Control Syst. Mag. 2008, 28, 148–156. [Google Scholar]
- Jahanshahi, H. Smooth control of HIV/AIDS infection using a robust adaptive scheme with decoupled sliding mode supervision. Eur. Phys. J. Spec. Top. 2018, 227, 707–718. [Google Scholar] [CrossRef]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelasticallydamped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Ahmed, E.; Hashish, A.; Rihan, F.A. On fractional order cancer model. J. Fract. Calc. Appl. Anal. 2012, 3, 1–6. [Google Scholar]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Soradi-Zeid, S.; Jahanshahi, H.; Yousefpour, A.; Bekiros, S. King algorithm: A novel optimization approach based on variable-order fractional calculus with application in chaotic financial systems. Chaos Solitons Fractals 2020, 132, 109569. [Google Scholar] [CrossRef]
- Wang, S.; Bekiros, S.; Yousefpour, A.; He, S.; Castillo, O.; Jahanshahi, H. Synchronization of fractional time-delayed financial system using a novel type-2 fuzzy active control method. Chaos Solitons Fractals 2020, 136, 109768. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.-T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Chen, S.-B.; Jahanshahi, H.; Abba, O.A.; Solís-Pérez, J.E.; Bekiros, S.; Gómez-Aguilar, J.F.; Yousefpour, A.; Chu, Y.-M. The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization. Chaos Solitons Fractals 2020, 140, 110223. [Google Scholar] [CrossRef]
- Chen, S.-B.; Soradi-Zeid, S.; Jahanshahi, H.; Alcaraz, R.; Gómez-Aguilar, J.F.; Bekiros, S.; Chu, Y.-M. Optimal control of time-delay fractional equations via a joint application of radial basis functions and collocation method. Entropy 2020, 22, 1213. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.-B.; Soradi-Zeid, S.; Alipour, M.; Chu, Y.-M.; Gomez-Aguilar, J.F.; Jahanshahi, H. Optimal control of nonlinear time-delay fractional differential equations with Dickson polynomials. Fractals 2020. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Alotaibi, N.D. A fractional-order SIRD model with time-dependent memory indexes for encompassing the multi-fractional characteristics of the COVID-19. Chaos Solitons Fractals 2021, 143, 110632. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jahanshahi, H.; Jafari, S.; Weldegiorgis, R.; Karthikeyan, A.; Duraisamy, P. Coexisting attractors in a fractional order hydro turbine governing system and fuzzy PID based chaos control. Asian J. Control 2021, 23, 894–907. [Google Scholar] [CrossRef]
- Xiong, P.-Y.; Jahanshahi, H.; Alcaraz, R.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alsaadi, F.E. Spectral entropy analysis and synchronization of a multi-stable fractional-order chaotic system using a novel neural network-based chattering-free sliding mode technique. Chaos Solitons Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sajjadi, S.S.; Bekiros, S.; Aly, A.A. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller. Chaos Solitons Fractals 2021, 144, 110698. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Bekiros, S.; Zambrano-Serrano, E.; Orozco-López, O.; Lahmiri, S.; Jahanshahi, H.; Aly, A.A. Artificial macro-economics: A chaotic discrete-time fractional-order laboratory model. Chaos Solitons Fractals 2021, 145, 110776. [Google Scholar] [CrossRef]
- Li, J.-F.; Jahanshahi, H.; Kacar, S.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alotaibi, N.D.; Alharbi, K.H. On the variable-order fractional memristor oscillator: Data security applications and synchronization using a type-2 fuzzy disturbance observer-based robust control. Chaos Solitons Fractals 2021, 145, 110681. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.-M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, H. A fractional-order differential equation model of HIV infection of CD4+ T-cells. Math. Comput. Model. 2009, 50, 386–392. [Google Scholar] [CrossRef]
- Rihan, F.A. Numerical modeling of fractional-order biological systems. Hindawi Abstr. Appl. Anal. 2013, 2013. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Carvalho, A.R.M. New findings on the dynamics of HIV and TB coinfection models. Appl. Math. Comput. 2014, 242, 36–46. [Google Scholar] [CrossRef]
- Dutta, A.; Adak, A.; Gupta, P.K. Analysis of fractional-order deterministic HIV/AIDS model during drug therapy treatment. In Soft Computing for Problem Solving; Springer: Cham, Switzerland, 2020; pp. 1–8. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Alsaedi, A.; Nieto, J.J.; Venktesh, V. Fractional electrical circuits. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. New aspects of fractional Biswas–Milovic model with Mittag-Leffler law. Math. Model. Nat. Phenom. 2019, 14, 303. [Google Scholar] [CrossRef]
- Kumar, D.; Tchier, F.; Singh, J.; Baleanu, D. An efficient computational technique for fractal vehicular traffic flow. Entropy 2018, 20, 259. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. Analysis and application of new fractional Adams–Bashforth scheme with Caputo–Fabrizio derivative. Chaos Solitons Fractals 2017, 105, 111–119. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Al Qurashi, M.; Baleanu, D. Analysis of logistic equation pertaining to a new fractional derivative with non-singular kernel. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B. Analysis of the Keller–Segel model with a fractional derivative without singular kernel. Entropy 2015, 17, 4439–4453. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Atangana, A. Blind in a commutative world: Simple illustrations with functions and chaotic attractors. Chaos Solitons Fractals 2018, 114, 347–363. [Google Scholar] [CrossRef]
- Moore, E.J.; Sirisubtawee, S.; Koonprasert, S. A Caputo–Fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Differ. Equ. 2019, 2019, 200. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, S.; Xie, Y.; Gui, W.; Tang, Z.; Ma, T.; Niyoyita, J.P. Learning local Gabor pattern-based discriminative dictionary of froth images for flotation process working condition monitoring. IEEE Trans. Ind. Inform. 2020, 17, 4437–4448. [Google Scholar] [CrossRef]
- Liu, J.; He, J.; Xie, Y.; Gui, W.; Tang, Z.; Ma, T.; He, J.; Niyoyita, J.P. Illumination-Invariant flotation froth color measuring via Wasserstein distance-based CycleGAN with structure-preserving constraint. IEEE Trans. Cybern. 2020, 51, 839–852. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. Optimal FPID control approach for a docking maneuver of two spacecraft: Translational motion. J. Aerosp. Eng. 2017, 30, 04017011. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. An optimal fuzzy PID control approach for docking maneuver of two spacecraft: Orientational motion. Eng. Sci. Technol. Int. J. 2017, 20, 293–309. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Chen, D.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Aly, A.A. Enhancement of the performance of nonlinear vibration energy harvesters by exploiting secondary resonances in multi-frequency excitations. Eur. Phys. J. Plus 2021, 136, 1–22. [Google Scholar] [CrossRef]
- Bekiros, S.; Jahanshahi, H.; Bezzina, F.; Aly, A.A. A novel fuzzy mixed H2/H∞ optimal controller for hyperchaotic financial systems. Chaos Solitons Fractals 2021, 146, 110878. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Shahriari-Kahkeshi, M.; Alcaraz, R.; Wang, X.; Singh, V.P.; Pham, V.-T. Entropy analysis and neural network-based adaptive control of a non-equilibrium four-dimensional chaotic system with hidden attractors. Entropy 2019, 21, 156. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Rajagopal, K.; Akgul, A.; Sari, N.N.; Namazi, H.; Jafari, S. Complete analysis and engineering applications of a megastable nonlinear oscillator. Int. J. NonLinear Mech. 2018, 107, 126–136. [Google Scholar] [CrossRef]
- Ying, H.; Lin, F.; MacArthur, R.D.; Cohn, J.A.; Barth-Jones, D.C.; Ye, H.; Crane, L.R. A self-learning fuzzy discrete event system for HIV/AIDS treatment regimen selection. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2007, 37, 966–979. [Google Scholar] [CrossRef]
- Ying, H.; Lin, F.; MacArthur, R.D.; Cohn, J.A.; Barth-Jones, D.C.; Ye, H.; Crane, L.R. A fuzzy discrete event system approach to determining optimal HIV/AIDS treatment regimens. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 663–676. [Google Scholar] [CrossRef]
- Brandt, M.E.; Chen, G. Feedback control of a biodynamical model of HIV-1. IEEE Trans. Biomed. Eng. 2001, 48, 754–759. [Google Scholar] [CrossRef]
- Jeffrey, A.M.; Xia, X.; Craig, I.K. When to initiate HIV therapy: A control theoretic approach. IEEE Trans. Biomed. Eng. 2003, 50, 1213–1220. [Google Scholar] [CrossRef]
- Kwon, H.-D. Optimal treatment strategies derived from a HIV model with drug-resistant mutants. Appl. Math. Comput. 2007, 188, 1193–1204. [Google Scholar] [CrossRef]
- Kirschner, D.; Lenhart, S.; Serbin, S. Optimal control of the chemotherapy of HIV. J. Math. Biol. 1997, 35, 775–792. [Google Scholar] [CrossRef] [PubMed]
- Barão, M.; Lemos, J.M. Nonlinear control of HIV-1 infection with a singular perturbation model. Biomed. Signal Process. Control 2007, 2, 248–257. [Google Scholar] [CrossRef]
- Ge, S.S.; Tian, Z.; Lee, T.H. Nonlinear control of a dynamic model of HIV-1. IEEE Trans. Biomed. Eng. 2005, 52, 353–361. [Google Scholar] [CrossRef]
- Ko, J.H.; Kim, W.H.; Chung, C.C. Optimized structured treatment interruption for HIV therapy and its performance analysis on controllability. IEEE Trans. Biomed. Eng. 2006, 53, 380–386. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Bani-Yaghoub, M.; Gautam, R.; Shuai, Z.; Van Den Driessche, P.; Ivanek, R. Reproduction numbers for infections with free-living pathogens growing in the environment. J. Biol. Dyn. 2012, 6, 923–940. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Li, L. Optimality conditions for fractional variational problems with Caputo-Fabrizio fractional derivatives. Adv. Differ. Equ. 2017, 2017, 357. [Google Scholar] [CrossRef]
- Kheiri, B.; Abdalla, A.; Osman, M.; Ahmed, S.; Hassan, M.; Bachuwa, G. Vitamin D deficiency and risk of cardiovascular diseases: A narrative review. Clin. Hypertens. 2018, 24, 9. [Google Scholar] [CrossRef]


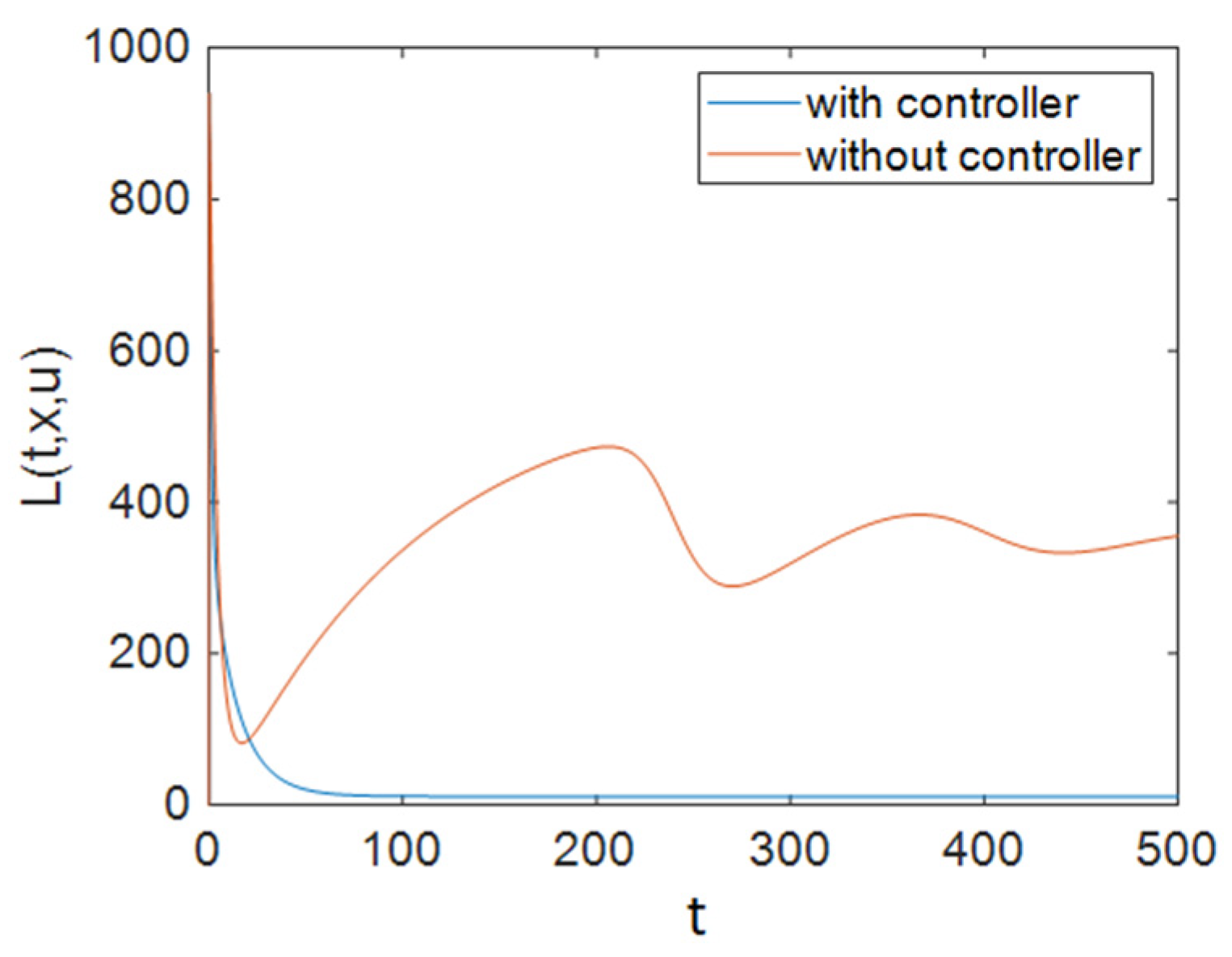
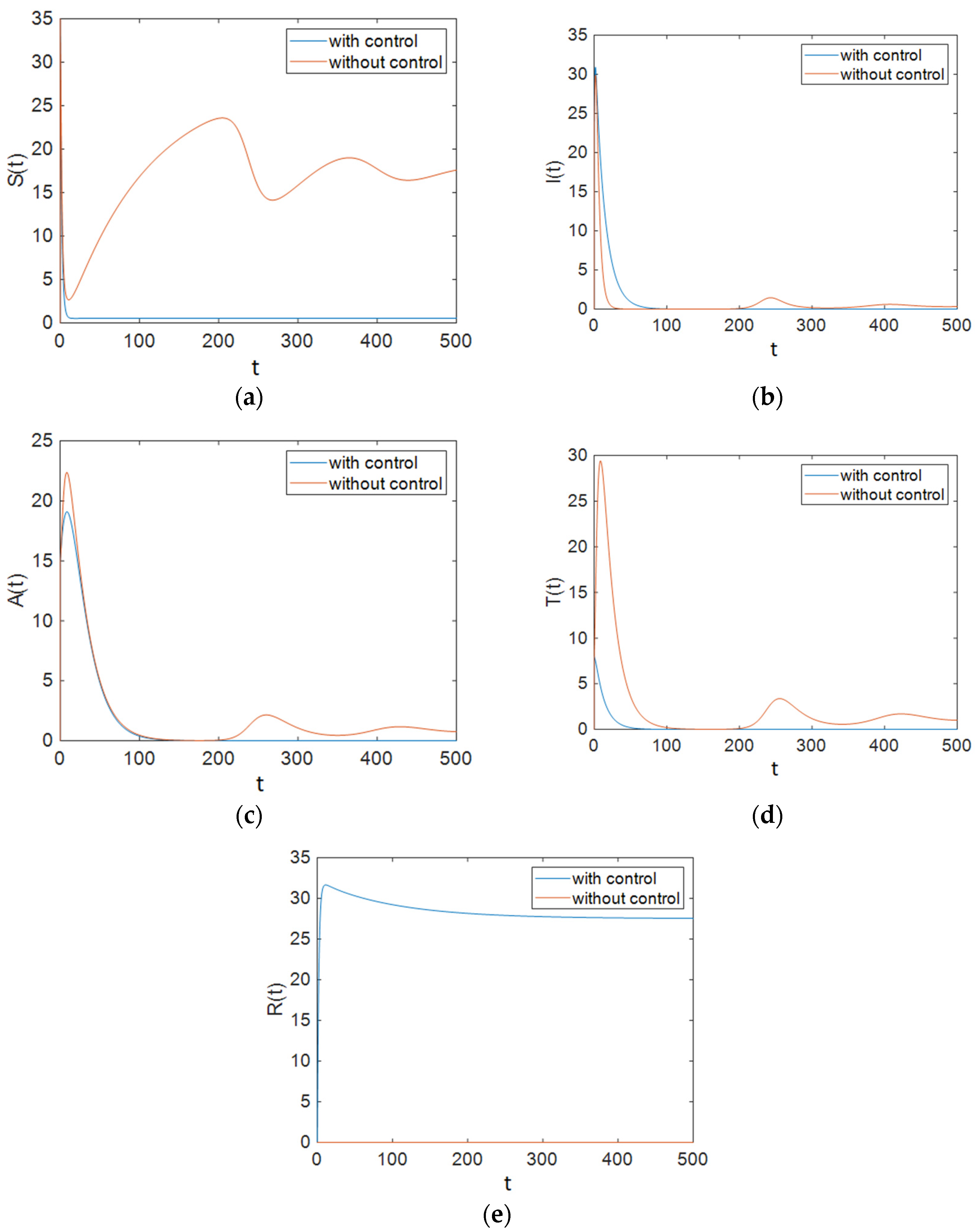

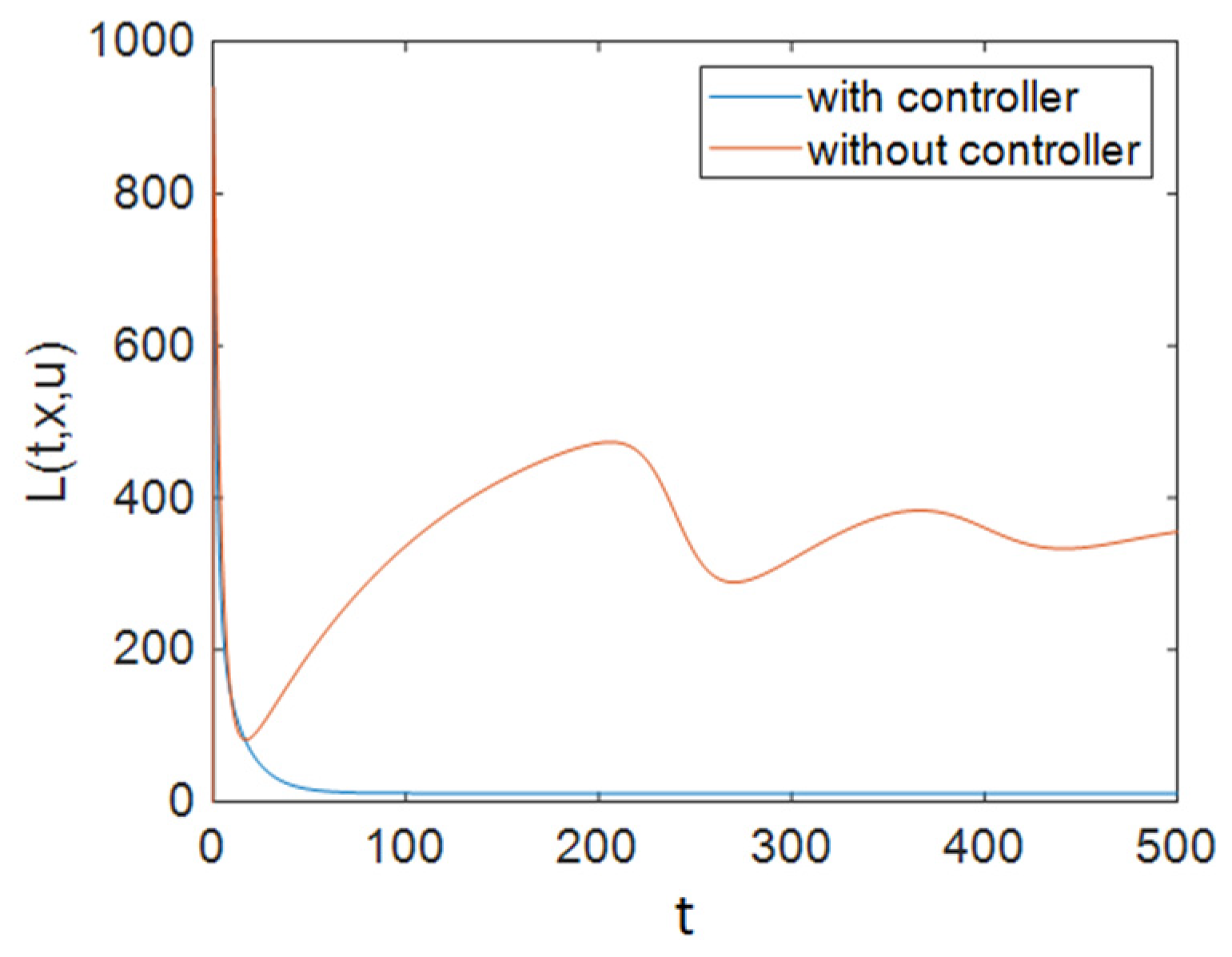
| Parameter | Description | Value |
|---|---|---|
| The recruitment of susceptible people into the population | 0.55 | |
| The contact rate between susceptible and infectious people | 0.03 | |
| The natural death rate | 0.0196 | |
| The rate at which leave the infectious class and become individuals with full-blown AIDS | 0.15 | |
| The rate at which people with HIV receive treatment | 0.35 | |
| The rate at which treated individuals leave this compartment and return to the infectious compartment | 0.08 | |
| The rate at which individuals in the treated compartment leave this class and enter the AIDS compartment | 0.03 | |
| The disease-induced death rate for individuals of the AIDS compartment | 0.0909 | |
| The disease-induced death rate for individuals of the treated compartment | 0.0667 | |
| The rate at which susceptible people change their sexual habits | 0.03 |
| Parameter | Description | Sensitivity Index |
|---|---|---|
| The recruitment of susceptible individuals into the population | 1 | |
| The contact rate between susceptible and infectious individuals | 1 | |
| The rate at which treated individuals leave this compartment and return to the infectious compartment | −0.7231 | |
| The rate at which individuals in the treated compartment leave this class and enter the AIDS compartment | 0.1865 | |
| The disease-induced death rate for individuals of the AIDS compartment | 0.0 | |
| The disease-induced death rate for individuals of the treated compartment | 0.4147 | |
| The rate at which susceptible people change their sexual habits | 0.1333 |
| Parameter | |||
|---|---|---|---|
| 0.0000 | 0.1237 | 0.1237 | |
| −1.0000 | −0.8762 | −0.8762 | |
| 0.7231 | −0.0894 | −0.4970 | |
| −0.1865 | 0.0230 | −0.1297 | |
| 0.0000 | 0.0000 | 0.0000 | |
| −0.4147 | 0.0513 | −0.2885 | |
| −0.7382 | 0.6213 | 0.6213 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Jahanshahi, H.; Wang, M.-K.; Bekiros, S.; Liu, J.; Aly, A.A. A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies. Entropy 2021, 23, 610. https://doi.org/10.3390/e23050610
Wang H, Jahanshahi H, Wang M-K, Bekiros S, Liu J, Aly AA. A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies. Entropy. 2021; 23(5):610. https://doi.org/10.3390/e23050610
Chicago/Turabian StyleWang, Hua, Hadi Jahanshahi, Miao-Kun Wang, Stelios Bekiros, Jinping Liu, and Ayman A. Aly. 2021. "A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies" Entropy 23, no. 5: 610. https://doi.org/10.3390/e23050610
APA StyleWang, H., Jahanshahi, H., Wang, M.-K., Bekiros, S., Liu, J., & Aly, A. A. (2021). A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies. Entropy, 23(5), 610. https://doi.org/10.3390/e23050610








