Dynamics Analysis of a Wireless Rechargeable Sensor Network for Virus Mutation Spreading
Abstract
:1. Introduction
1.1. Research Background
1.2. Related Work
1.3. Contributions
- An epidemic model suitable for WRSNs is established to describe the propagation process of malwares (the virus and mutated virus).
- To analyze and calculate the basic reproductive numbers and . Then, considering the existence of equilibrium of the system, the local and global asymptotic stability is proved by adopting the characteristic equation and the Lyapunov principle. Numerical simulation is carried out to confirm the results.
- By constructing the objective function and applying Pontryagin’s maximum principle, we can obtain the optimal control variable which satisfies the optimal control objective of the security problem.
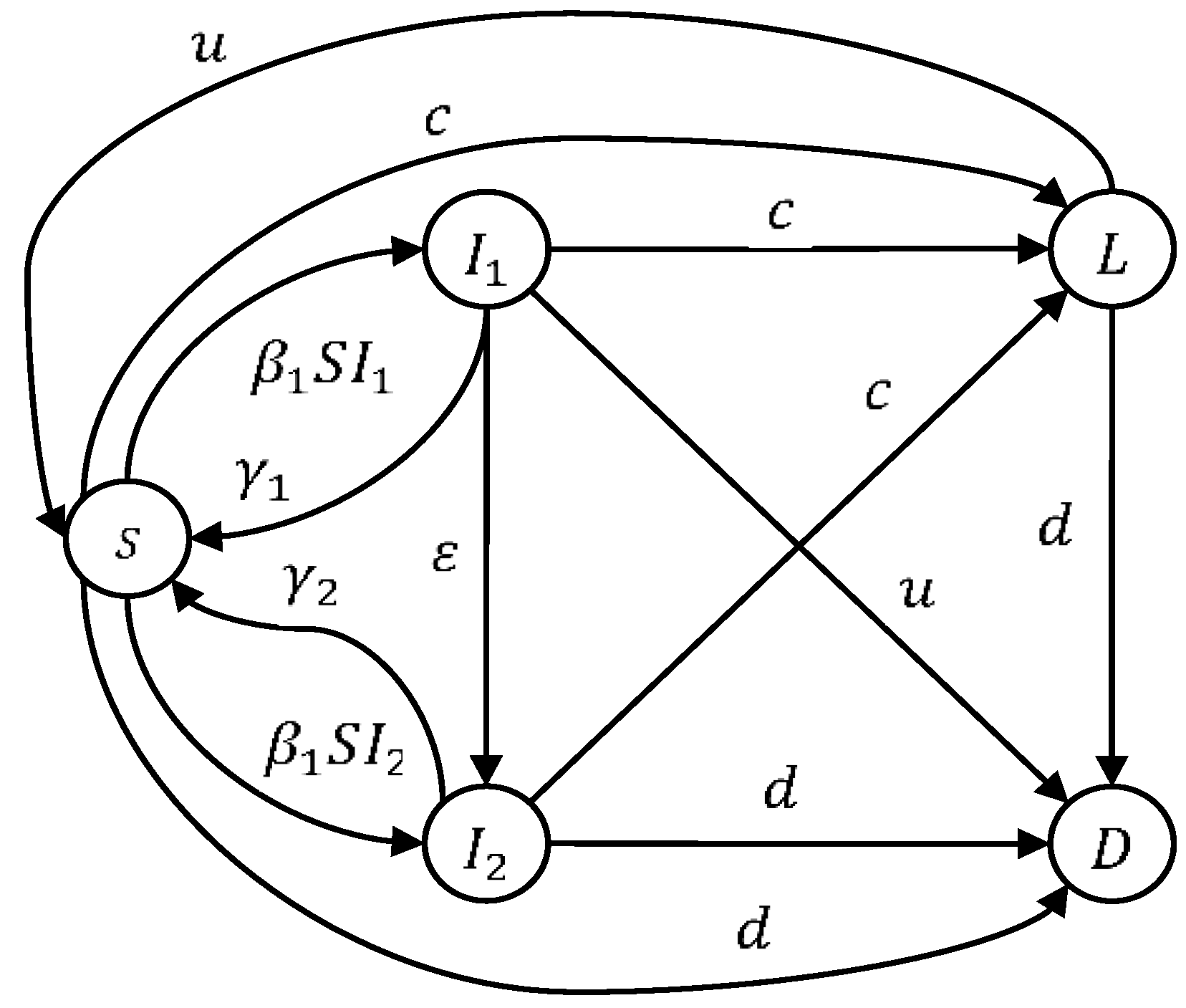
2. Epidemic Modeling
2.1. Model Analysis
2.2. Computing the Equilibrium Points and Basic Reproductive Number
3. Dynamic Stability Analysis
3.1. Local Stability
3.2. Global Stability
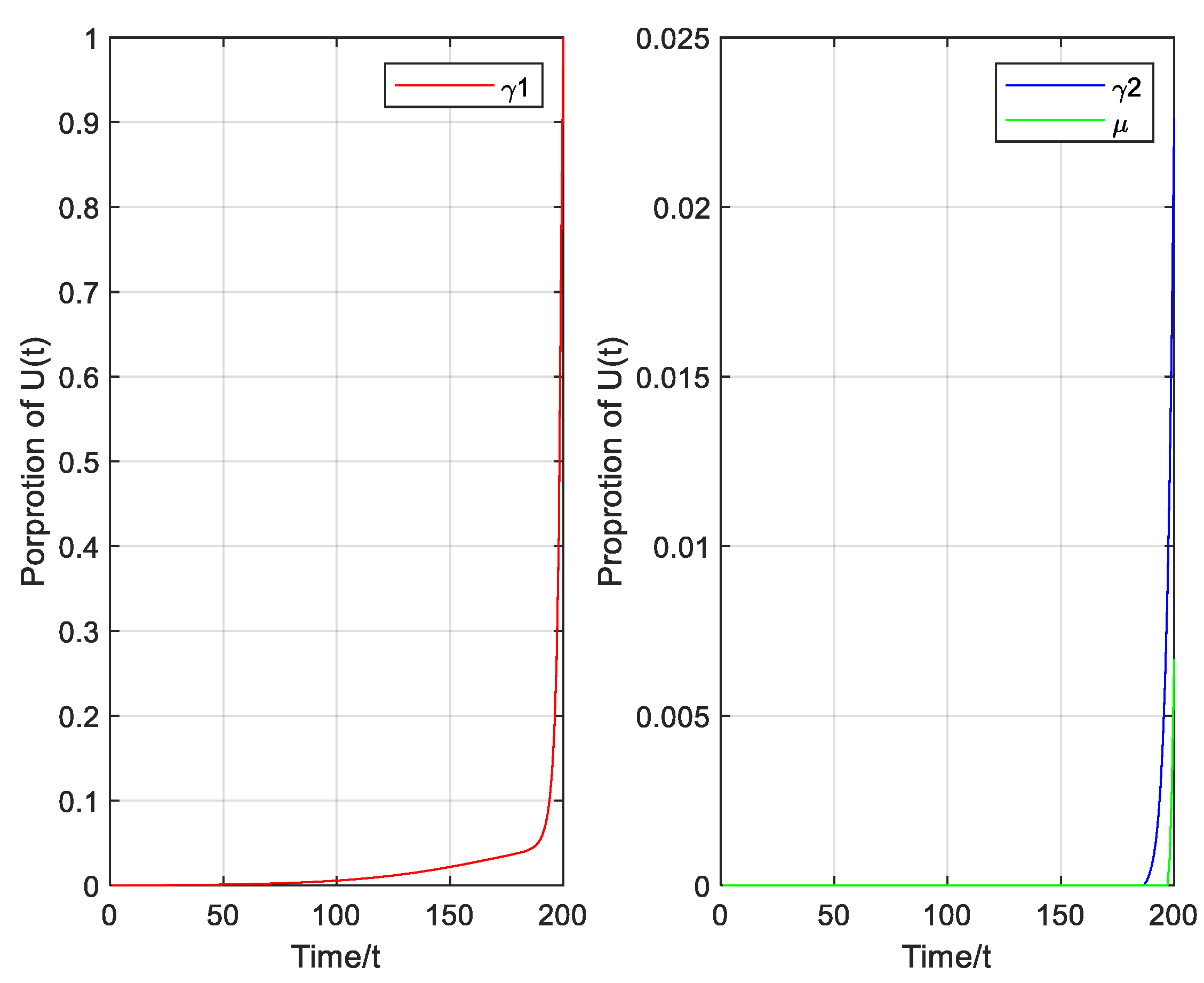
4. Optimal Strategy
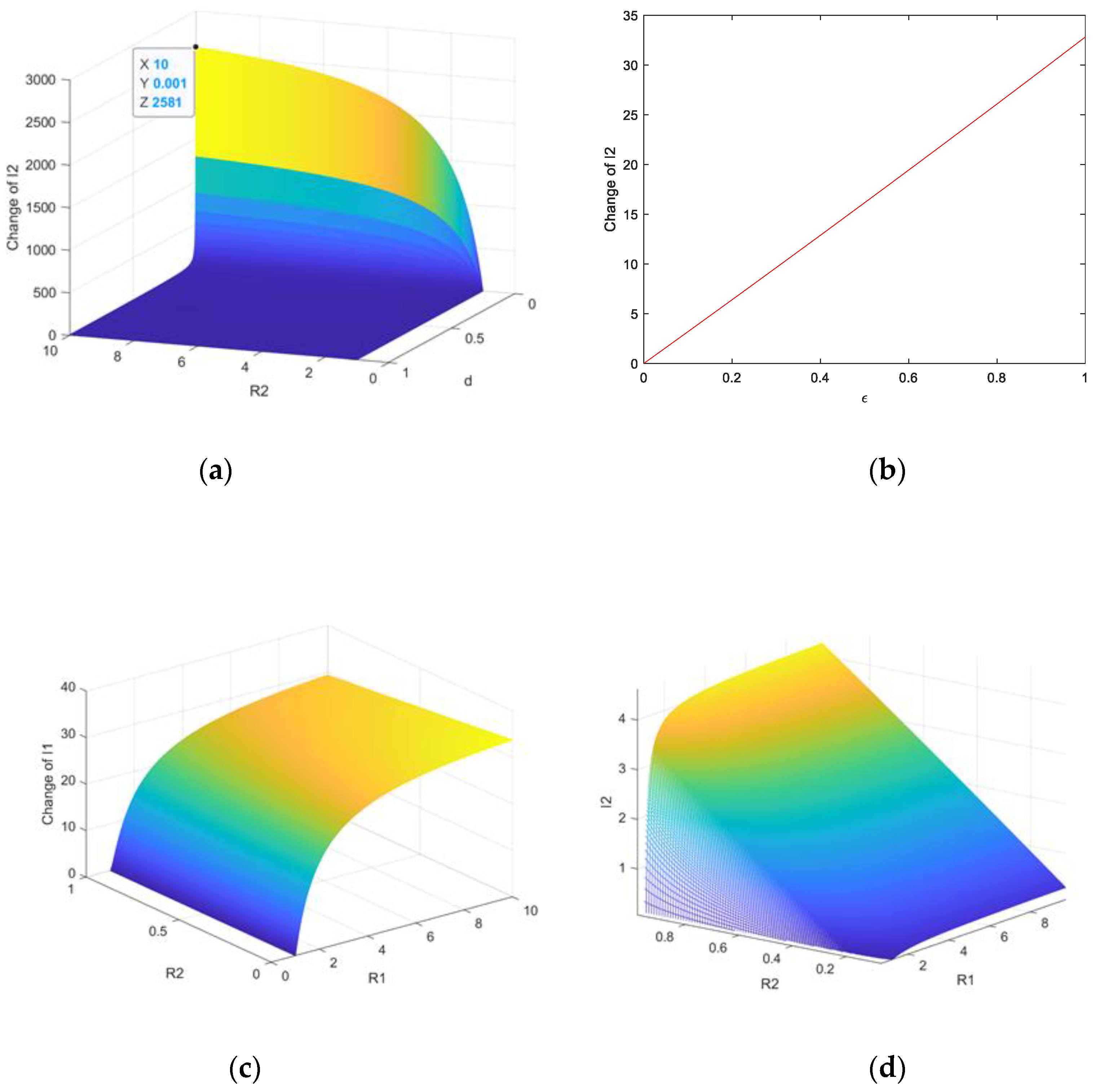
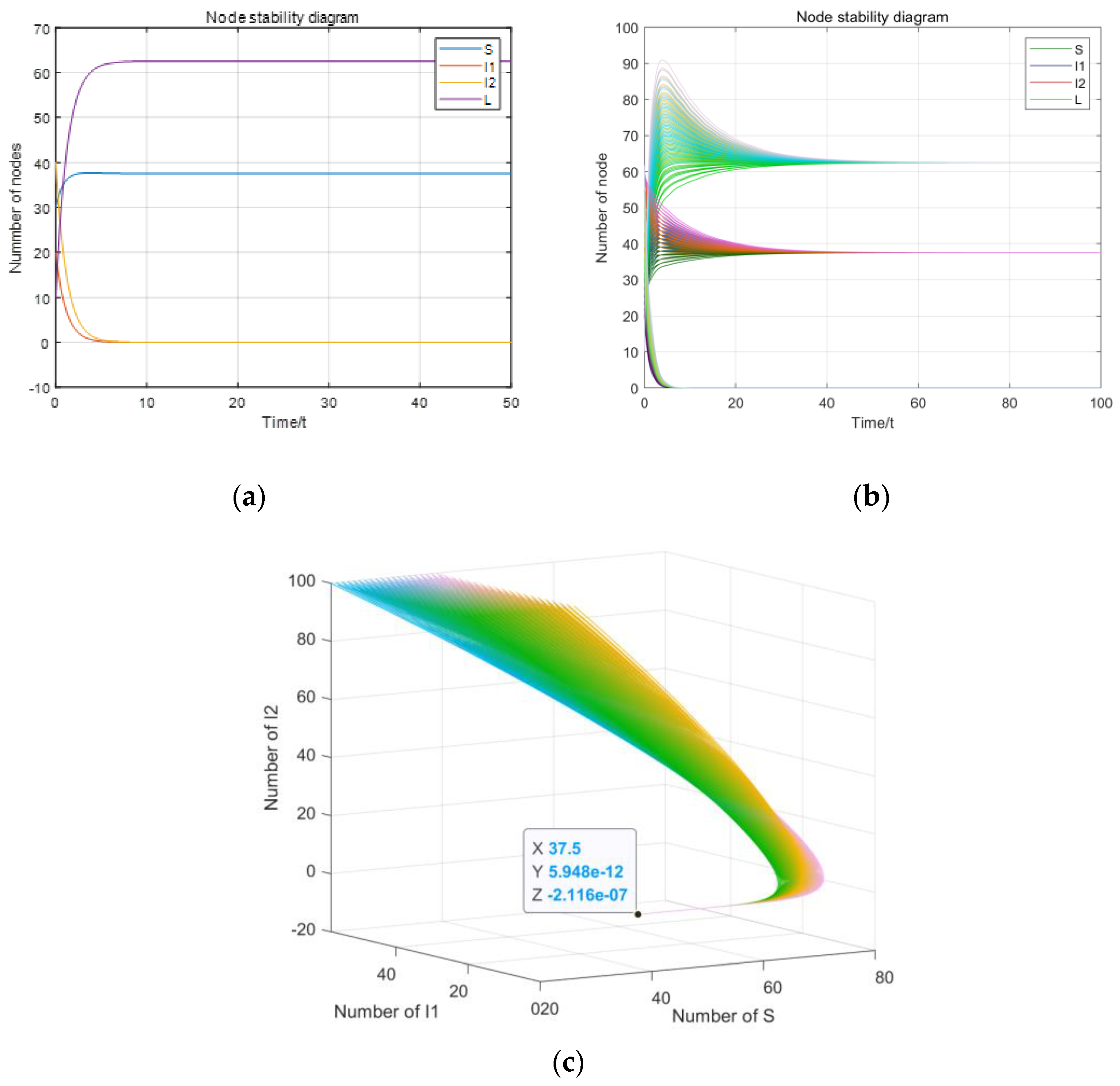
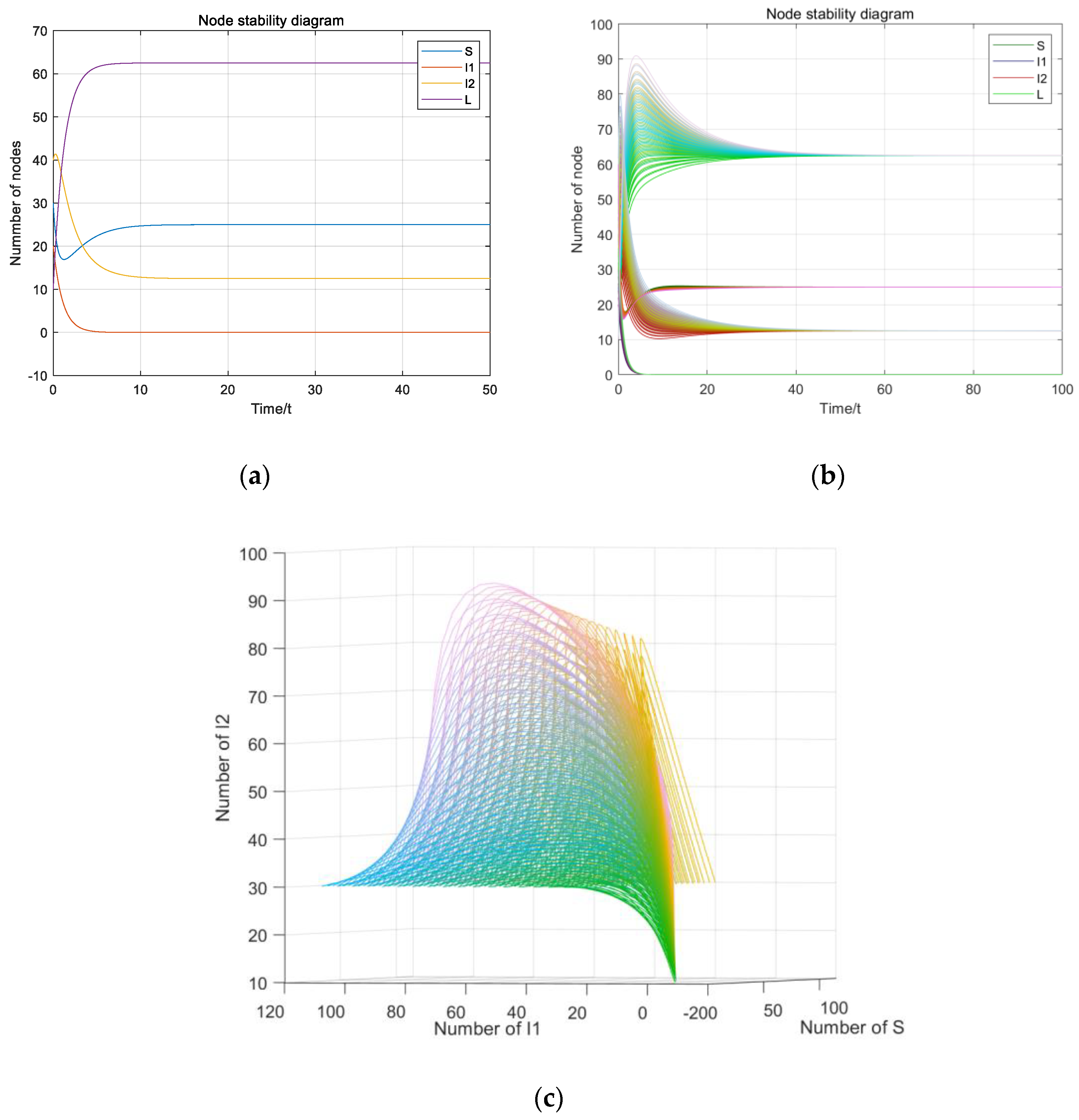
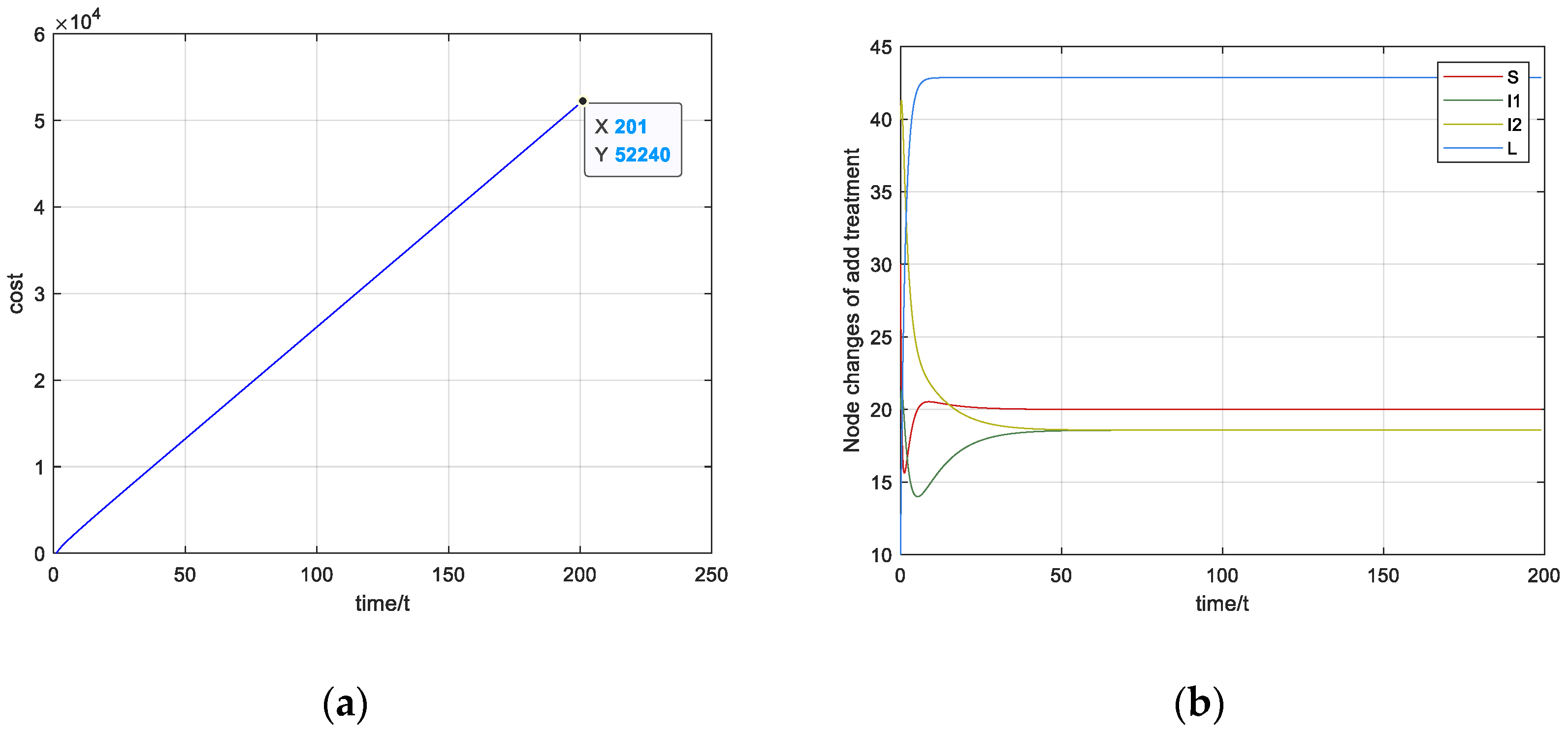
5. Numerical Simulation
5.1. Stability Simulation
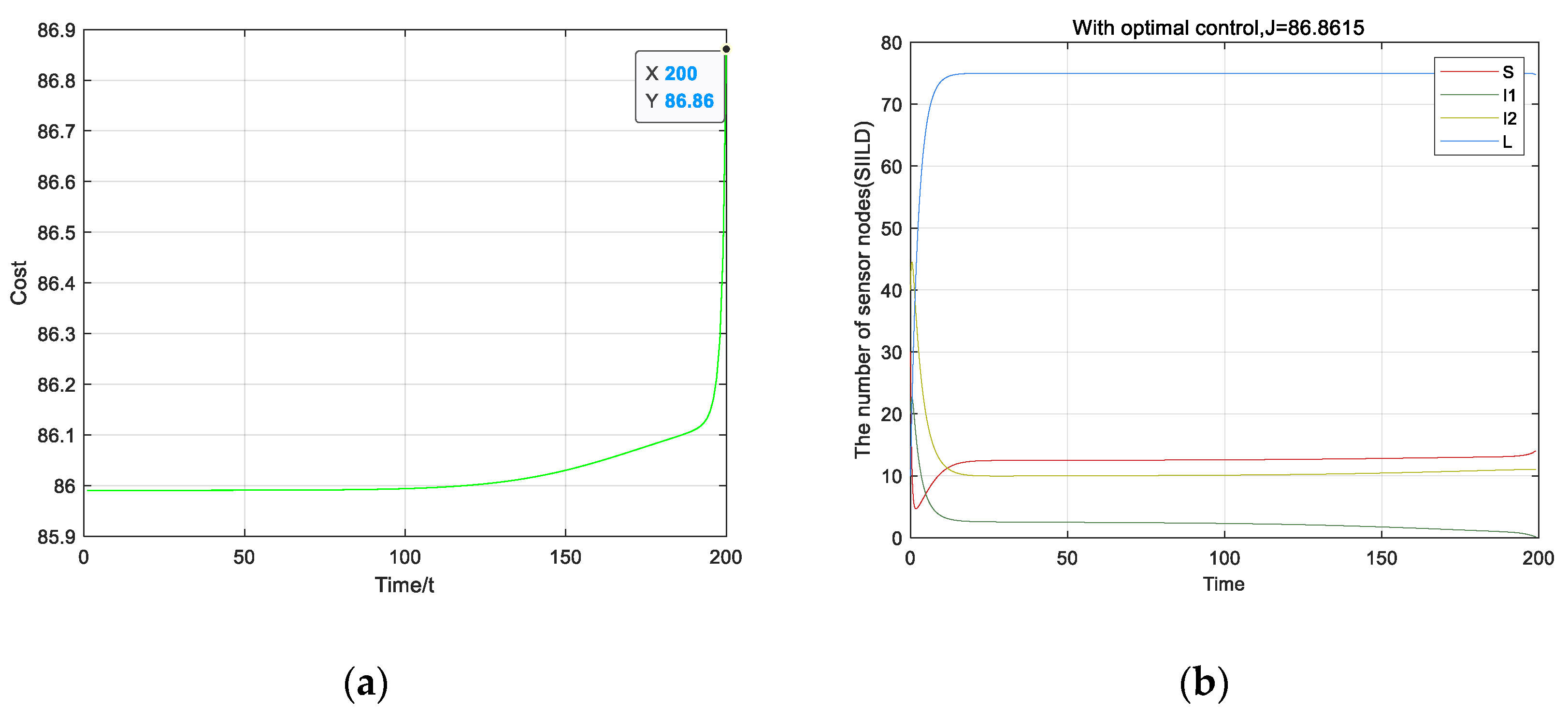
5.2. Optimal Strategy Simulation
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lenin, R.B.; Ramaswamy, S. Performance analysis of wireless sensor networks using queuing networks. Ann. Oper. Res. 2015, 233, 237–261. [Google Scholar] [CrossRef]
- Rashid, B.; Rehmani, M.H. Applications of wireless sensor networks for urban areas: A survey. J. Netw. Comput. Appl. 2016, 60, 192–219. [Google Scholar] [CrossRef]
- Singh, S.; Saini, H.S. Learning-Based Security Technique for Selective Forwarding Attack in Clustered WSN. Wirel. Pers. Commun. 2021, 118, 7789–7814. [Google Scholar] [CrossRef]
- Yu, D.; Kang, J.; Dong, J. Service Attack Improvement in Wireless Sensor Network Based on Machine Learning. Microprocess. Microsyst. 2020, 80, 103637. [Google Scholar] [CrossRef]
- Shi, L.; Liu, Q.; Shao, J.; Cheng, Y. Distributed Localization in Wireless Sensor Networks under Denial-of-Service Attacks. J. Artic. 2020, 5, 493–498. [Google Scholar]
- Bonaci, T.; Bushnell, L.; Poovendran, R. Node capture attacks in wireless sensor networks: A system theoretic approach. In Proceedings of the 49th IEEE Conference on Decision & Control, Atlanta, GA, USA, 15–17 December 2010. [Google Scholar]
- Rasheed, A.; Mahapatra, R.N. The three-tier security scheme in wireless sensor networks with mobile sinks. Trans. Parallel Distrib. Syst. IEEE 2012, 23, 958–965. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Wang, C. Wireless Rechargeable Sensor Networks; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Lin, C.; Shang, Z.; Du, W.; Ren, J.K.; Wang, L.; Wu, G.W. CoDoC: A Novel Attack for Wireless Rechargeable Sensor Networks through Denial of Charge. In Proceedings of the IEEE INFOCOM 2019, Paris, France, 29 April–2 May 2019. [Google Scholar]
- He, T.; Chin, K.W.; Soh, S. On using wireless power transfer to increase the max flow of rechargeable wireless sensor networks. In Proceedings of the IEEE ISSNIP, Singapore, 7–9 April 2015; pp. 1–6. [Google Scholar]
- Sun, J.; Dong, M.I.; Wang, T.; Li, D.Q. Research on the Mutation of Computer Virus. Sci. Technol. Eng. 2006, 2006, 1926–1928. [Google Scholar]
- Shafie, A.E.; Niyato, D.; Al-Dhahir, N. Security of Rechargeable Energy-Harvesting Transmitters in Wireless Networks. IEEE Wireless Commun. Lett. 2016, 5, 384–387. [Google Scholar] [CrossRef] [Green Version]
- Bhushan, B.; Sahoo, G. E2SR2: An acknowledgement-based mobile sink routing protocol with rechargeable sensors for wireless sensor networks. Wirel. Netw. 2019, 25, 2697–2721. [Google Scholar] [CrossRef]
- Kephart, J.O.; White, S.R. Directed-Graph Epidemiological Models of Computer Viruses. In Proceedings of the IEEE Computer Society Symposium on Research in Security & Privacy, Oakland, CA, USA, 4–6 May 1992; pp. 71–102. [Google Scholar]
- Kephart, J.O.; White, S.R. Measuring and Modeling Computer Virus Prevalence. In Proceedings of the 1993 IEEE Computer Society Symposium on Research in Security and Privacy, Oakland, CA, USA, 23–26 May 1993; pp. 2–15. [Google Scholar]
- Cao, Y.L.; Wang, X.M.; He, Z.B. Optimal Security Strategy for Malware Propagation in Mobile Wireless Sensor Networks. Acta Electron. Sin. 2016, 44, 1851. [Google Scholar]
- Zheng, Y.; Zhu, J.; Lai, C. A SEIQR Model considering the Effects of Different Quarantined Rates on Worm Propagation in Mobile Internet. Math. Probl. Eng. 2020, 2020, 16. [Google Scholar] [CrossRef]
- Han, X.F.; Li, F.; Meng, X. Dynamics Analysis of a Nonlinear Stochastic SEIR Epidemic system with Varying Population Size. Entropy 2018, 20, 376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.; Peng, B.; Zhong, X. Epidemic Analysis of Wireless Rechargeable Sensor Networks Based on an Attack–Defense Game Model. Sensors 2021, 21, 594. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Peng, B.; Zhong, X. Attack-Defense Game between Malicious Programs and Energy-Harvesting Wireless Sensor Networks Based on Epidemic Modeling. Complexity 2020, 2020, 13. [Google Scholar]
- Liu, G.; Peng, B.; Zhong, X. A novel epidemic model for wireless rechargeable sensor network security. Sensors 2020, 21, 123. [Google Scholar] [CrossRef]
- Liu, G.; Peng, B.; Zhong, X. Differential Games of Rechargeable Wireless Sensor Networks against Malicious Programs Based on SILRD Propagation Model. Complexity 2020, 2020, 5686413. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J. Global Analysis of an Epidemic Model with Virus Auto Variation. J. Biomath. 2008, 23, 101–106. [Google Scholar]
- Li, D.M.; Li, C.C.; Xu, Y.J. The Stability of a Class of SEIR Epidemic Model with Virus Mutate. J. Harbin Univ. Sci. Technol. 2014, 19, 106–109. [Google Scholar]
- Gao, J.; Zhang, T. Analysis on an SEIR Epidemic Model with Logistic Death Rate of Virus Mutation. J. Math. Res. Appl. 2019, 39, 43–52. [Google Scholar]
- Tong, Y.H.; Li, L.P. The Time Delay Epidemic Model with Spontaneous Virus Variation. J. Shanxi Datong Univ. 2013, 29, 1674-0874. [Google Scholar]
- Li, D.M.; Fu, Y.L.; Gao, T.Q.; Li, C.C. Stability Analysis of a Class of SIR Epidemic Model with Delayed Spontaneous Variation of Virus. J. Harbin Univ. Sci. Technol. 2020, 25, 170–176. [Google Scholar]
- Xu, D.G.; Xu, X.Y.; Yang, C.H.; Gui, W.H. Global Stability of a Variation Epidemic Spreading Model on Complex Networks. Math. Probl. Eng. Theory Methods Appl. 2015, 2015, 365049. [Google Scholar] [CrossRef] [Green Version]
- Cai, L.; Xiang, J.; Li, X.; Lashari, A.A. A two-strain epidemic model with mutant strain and vaccination. J. Appl. Math. Comput. 2012, 40, 125–142. [Google Scholar] [CrossRef]
- Xu, D.; Xu, X.; Xie, Y.; Yang, C. Optimal control of an SIVRS epidemic spreading model with virus variation based on complex networks. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 200–210. [Google Scholar] [CrossRef]
- Lyapunov, A.M.; Walker, J.A. The General Problem of the Stability of Motion. J. Appl. Mech. 1994, 55, 531–534. [Google Scholar] [CrossRef] [Green Version]
- Wu, X. On zeros of polynomial and vector solutions of associated polynomial system from Vieta theorem. Appl. Numer. Math. 2003, 44, 415–423. [Google Scholar] [CrossRef]
- Fu, M.H.; Liang, H.L. An improved precise Runge-Kutta integration. Acta Scientiarum Naturalium Universitatis Sunyatseni 2009, 5, 1–5. [Google Scholar]


| Authors | Research Field | Model | Content |
|---|---|---|---|
| Yang et al. [23] | Dynamic analysis of the virus mutation model | SIS | Proof of the local and global stability of the system |
| Dong-Mei et al. [24] | Model analysis of disease viruses mutated in the process of transmission | SEIR | Proof of the local and global stability of the system that considers the exposed |
| Gao et al. [25] | An SEIR epidemic model analysis with logistic death rate of virus mutation | SEIR | Proof of the local and global stability of the system that considers the logistic death rate of virus mutation |
| Tong et al. [26] | Dynamic model analysis with delay of the virus mutation | SIS | Proof of the local and global stability of the system that considers the time delay |
| Dong-Mei et al. [27] | SIR model analysis with delay of the virus mutation | SIR | Proof of the local and global stability of the system that considers recovered factor and the time delay |
| De-gang et al. [28] | A variation epidemic model’s propagation and analysis in complex networks | SIVR | Proof of the local and global stability of the system |
| Cai et al. [29] | Model analysis of spread of the pathogen with mutant strain and vaccination | SIVR | Proof of the local and global stability and analysis of the Hopf bifurcation of the system |
| Xu et al. [30] | Optimal control of the SIVRS epidemic spreading model with virus mutation in complex networks | SIVRS | Considers the optimal strategy and calculates the optimal control results of the system |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Peng, Z.; Liang, Z.; Li, J.; Cheng, L. Dynamics Analysis of a Wireless Rechargeable Sensor Network for Virus Mutation Spreading. Entropy 2021, 23, 572. https://doi.org/10.3390/e23050572
Liu G, Peng Z, Liang Z, Li J, Cheng L. Dynamics Analysis of a Wireless Rechargeable Sensor Network for Virus Mutation Spreading. Entropy. 2021; 23(5):572. https://doi.org/10.3390/e23050572
Chicago/Turabian StyleLiu, Guiyun, Zhimin Peng, Zhongwei Liang, Junqiang Li, and Lefeng Cheng. 2021. "Dynamics Analysis of a Wireless Rechargeable Sensor Network for Virus Mutation Spreading" Entropy 23, no. 5: 572. https://doi.org/10.3390/e23050572
APA StyleLiu, G., Peng, Z., Liang, Z., Li, J., & Cheng, L. (2021). Dynamics Analysis of a Wireless Rechargeable Sensor Network for Virus Mutation Spreading. Entropy, 23(5), 572. https://doi.org/10.3390/e23050572









