Unifying Large- and Small-Scale Theories of Coordination
Abstract
1. Introduction: Biological Coordination

2. The Birth of Coordination Dynamics: The HKB Model
3. The Extended HKB Model
4. The Kuramoto Model
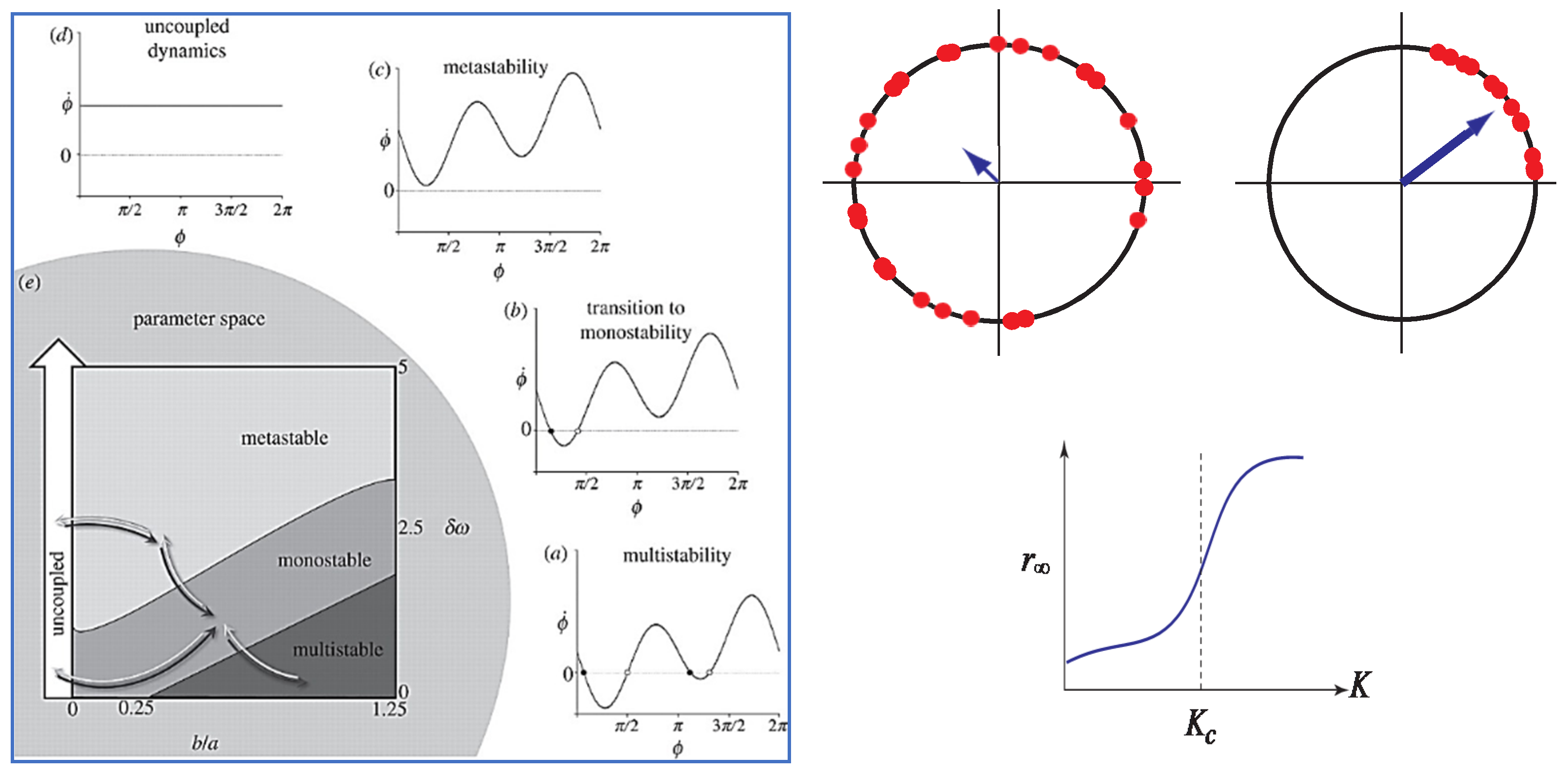
5. Coordinating the Few and the Many
6. Toward Unification: The Marriage of HKB and Kuramoto
“We dance round in a ring and suppose but the secret sits in the middle and knows.”(Robert Frost)
7. The Generalized HKB Model of Coordination Dynamics
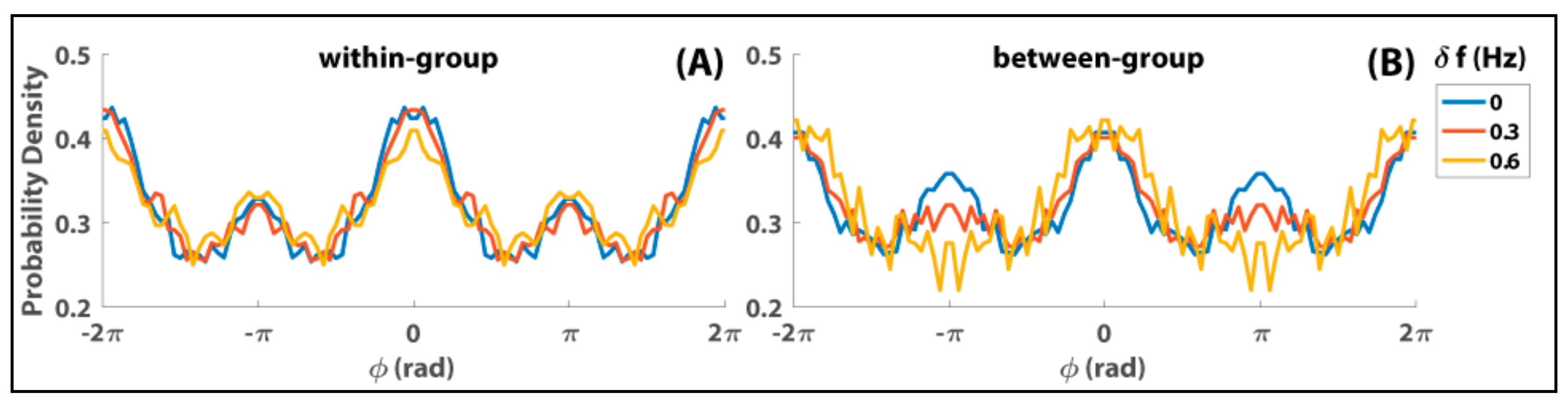
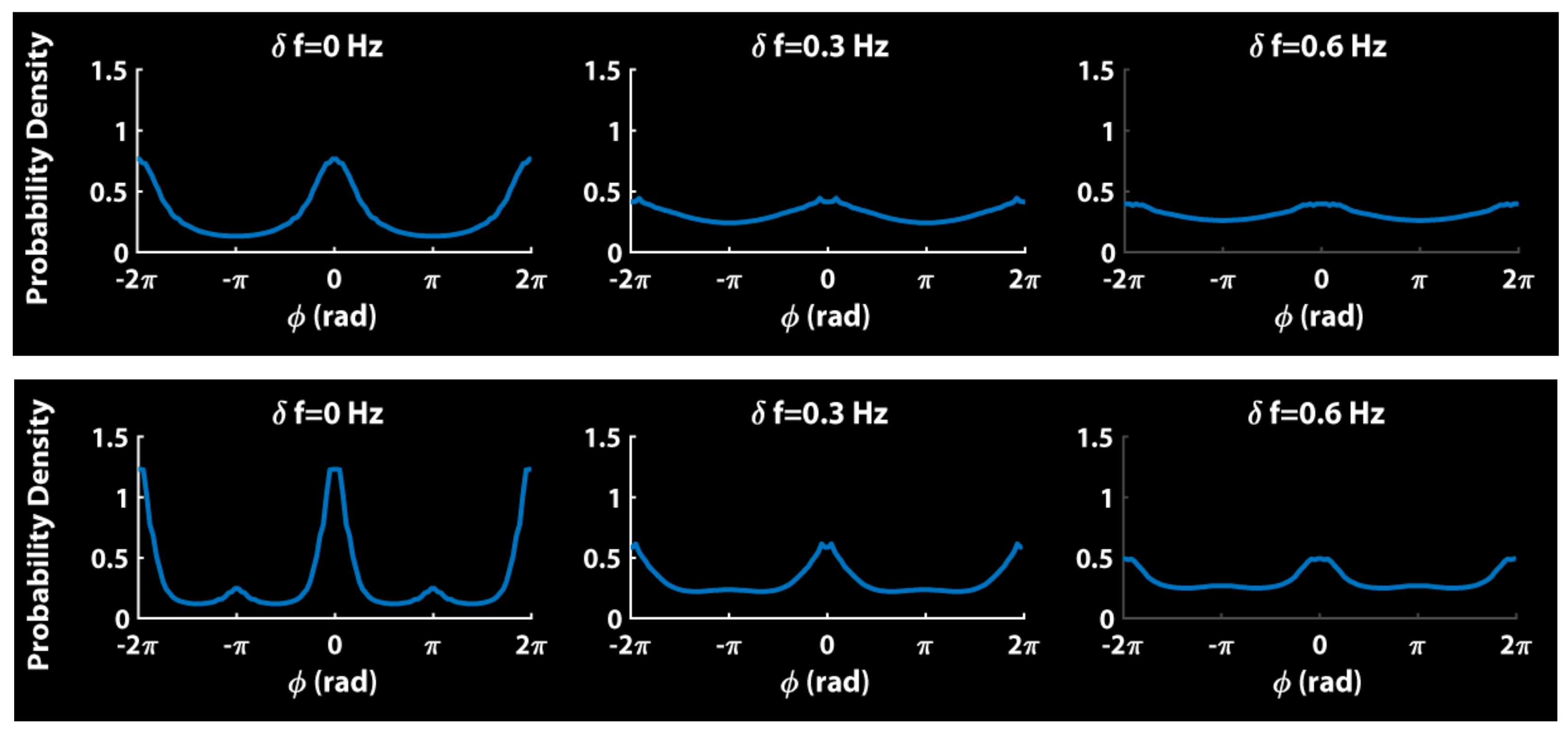
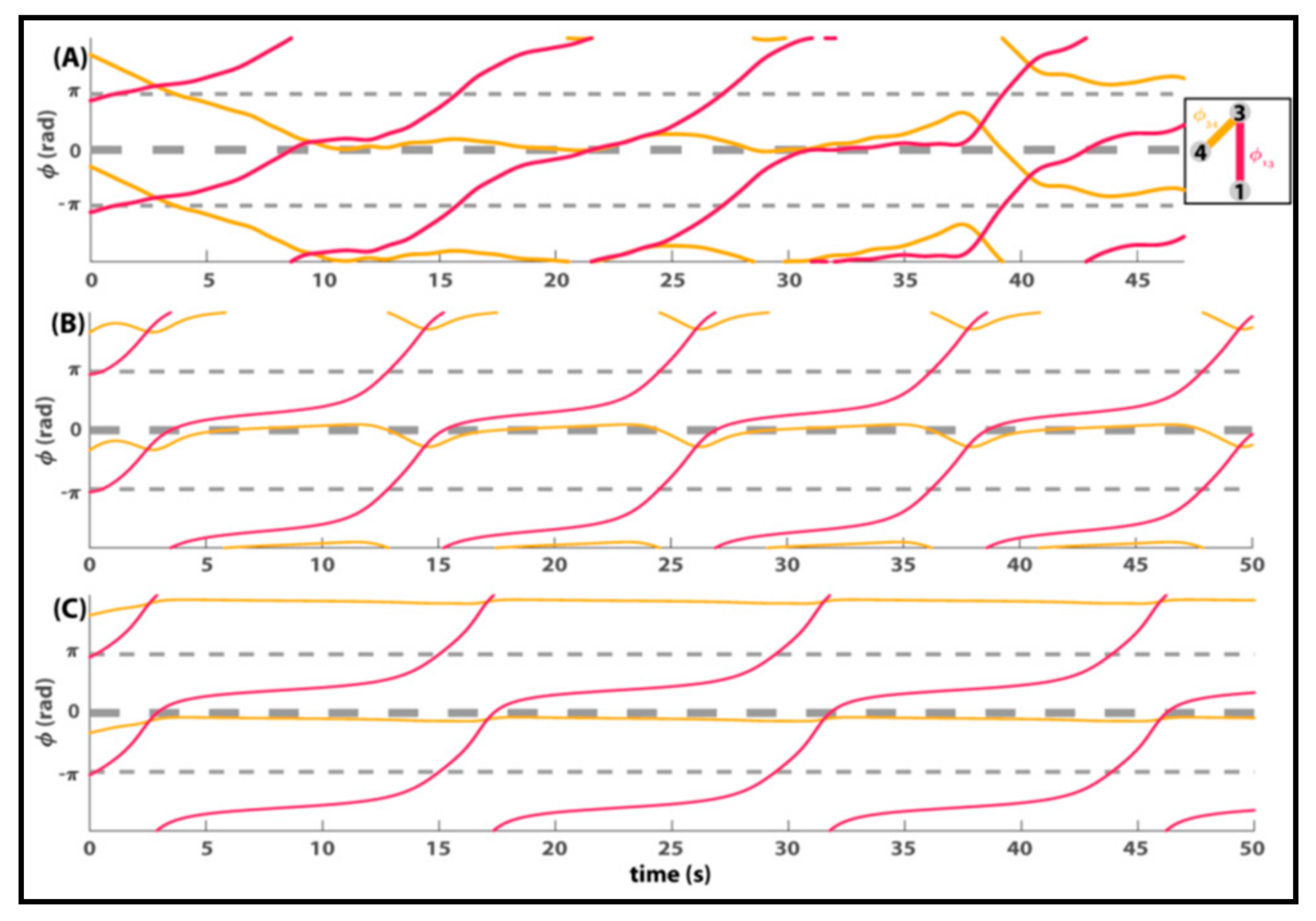
8. Relevance of Generalized HKB to Small and Mid-Size Group Coordination
9. Some Implications and Future Directions…
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haugeland, J. Artificial Intelligence: The Very Idea; The MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Kelso, J.A.S. Coordination Dynamics. In Encyclopedia of Complexity and System Science; Meyers, R.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1537–1564. [Google Scholar]
- Kelso, J.A.S.; Haken, H. New laws to be expected in the organism: Synergetics of brain and behavior. In What is Life? The Next 50 Years; Murphy, M., O’Neill, L., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 137–160. [Google Scholar]
- Sheets-Johnstone, M. The Primacy of Movement; John Benjamins Publishing Company: Amsterdam, The Netherlands, 1999. [Google Scholar]
- DeLuca, C.; Jantzen, K.J.; Comani, S.; Bertollo, M.; Kelso, J.A.S. Striatal activity during intentional switching depends on pattern stability. J. Neurosci. 2010, 30, 3167–3174. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Dynamic Patterns: The Self-Organization of Brain and Behavior; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Kostrubiec, V.; Zanone, P.-G.; Fuchs, A.; Kelso, J.A.S. Beyond the blank slate: Routes to learning new coordination patterns depend on the intrinsic dynamics of the learner —experimental evidence and theoretical model. Front. Hum. Neurosci. 2012, 6, 212. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.D.; Snapp-Childs, W.; Coats, R.; Bingham, G.P. Learning a coordinated rhythmic movement with task-appropriate coordination feedback. Exp. Brain Res. 2010, 205, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Zanone, P.G.; Kelso, J.A.S. The evolution of behavioral attractors with learning: Nonequilibrium phase transitions. J. Exp. Psychol. Hum. Percept. Perform. 1992, 18, 403–421. [Google Scholar] [CrossRef]
- Schöner, G.; Kelso, J.A.S. Dynamic pattern generation in behavioral and neural systems. Science 1988, 239, 1513–1520. [Google Scholar] [CrossRef]
- Haken, H. The Science of Structure: Synergetics; Van Nostrand Reinhold: New York, NY, USA, 1984. [Google Scholar]
- Haken, H. Synergetics, an Introduction: Non-Equilibrium Phase Transitions and Self-Organization in Physics, Chemistry and Biology; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Haken, H. Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems. Rev. Mod. Phys. 1975, 47, 67–121. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Tuller, B. A dynamical basis for action systems. In Handbook of Cognitive Neuroscience; Gazzaniga, M.S., Ed.; Plenum: New York, NY, USA, 1984; pp. 321–356. [Google Scholar]
- Turvey, M.T.; Fitch, H.; Tuller, B. The Bernstein perspective: I. The problem of degrees of freedom and context-conditioned variability. In Human Motor Behavior: An Introduction; Kelso, J.A.S., Ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1982; pp. 239–252. [Google Scholar]
- Beer, R.D. Dynamical approaches to cognitive science. Trends Cogn. Sci. 2000, 4, 91–99. [Google Scholar] [CrossRef]
- Chemero, A. Dynamical explanation and mental representations. Trends Cogn. Sci. 2001, 5, 141–142. [Google Scholar] [CrossRef]
- Port, R.F.; van Gelder, T. (Eds.) Mind as Motion: Explorations in the Dynamics of Cognition; The MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Thelen, E.; Smith, L. A Dynamic Systems Approach to the Development of Cognition and Action; The MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Kelso, J.A.S. On the oscillatory basis of movement. Bull. Psychon. Soc. 1981, 18, 63. [Google Scholar]
- Kelso, J.A.S. Phase transitions and critical behavior in human bimanual coordination. Am. J. Physiol. Integr. Comp. Physiol. 1984, 246, R1000–R1004. [Google Scholar] [CrossRef] [PubMed]
- Kelso, J.A.S.; Southard, D.L.; Goodman, D. On the nature of human interlimb coordination. Science 1979, 203, 1029–1031. [Google Scholar] [CrossRef] [PubMed]
- Kelso, J.A.S.; Holt, K.G.; Rubin, P.; Kugler, P.N. Patterns of human interlimb coordination emerge from the properties of non-linear, limit cycle oscillatory processes: Theory and data. J. Mot. Behav. 1981, 13, 226–261. [Google Scholar] [CrossRef] [PubMed]
- Mechsner, F.; Kerzel, D.; Knoblich, G.; Prinz, W. Perceptual basis of bimanual coordination. Nat. Cell Biol. 2001, 414, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Kugler, P.N.; Kelso, J.A.S.; Turvey, M.T. Coordinative structures as dissipative structures I. Theoretical lines of convergence. In Tutorials in Motor Behavior; Stelmach, G.E., Requin, J., Eds.; North Holland: Amsterdam, The Netherlands, 1980; pp. 1–40. [Google Scholar]
- Kelso, J.A.S.; Scholz, J.P. Cooperative Phenomena in Biological Motion. In Complex Systems: Operational Approaches in Neurobiology, Physics and Computers; Haken, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Haken, H.; Kelso, J.A.S.; Bunz, H. A theoretical model of phase transitions in human hand movements. Biol. Cybern. 1985, 51, 347–356. [Google Scholar] [CrossRef] [PubMed]
- Schöner, G.; Haken, H.; Kelso, J.A.S. A stochastic theory of phase transitions in human hand movement. Biol. Cybern. 1986, 53, 247–257. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Instabilities and phase transitions in human brain and behavior. Front. Hum. Neurosci. 2010, 4, 23. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.A.; Dakos, V.; Van De Koppel, J.; Van De Leemput, I.A.; Levin, S.A.; Van Nes, E.H.; et al. Anticipating Critical Transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Scholz, J.P.; Schöner, G. Nonequilibrium phase transitions in coordinated biological motion: Critical fluctuations. Phys. Lett. A 1986, 118, 279–284. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Schöner, G.; Scholz, J.P.; Haken, H. Phase locked modes, phase transitions and component oscillators in coordinated biological motion. Phys. Scr. 1987, 35, 79–87. [Google Scholar] [CrossRef]
- Scholz, J.; Kelso, J.; Schöner, G. Nonequilibrium phase transitions in coordinated biological motion: Critical slowing down and switching time. Phys. Lett. A 1987, 123, 390–394. [Google Scholar] [CrossRef]
- Winfree, A.T. (Purdue University, West Lafayette, IN, USA). Personal Communication, 1982.
- Pennycuick, C.J. Newton Rules Biology: A Physical Approach to Biological Problems; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Aramaki, Y.; Honda, M.; Okada, T.; Sadato, N. Neural correlates of the spontaneous phase transition during bimanual coordination. Cereb. Cortex 2006, 16, 1338–1348. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Bressler, S.L.; Buchanan, S.; DeGuzman, G.C.; Ding, M.; Fuchs, A.; Holroyd, T. A phase transition in human brain and behavior. Phys. Lett. A 1992, 169, 134–144. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Fuchs, A.; Holroyd, T.; Lancaster, R.; Cheyne, D.; Weinberg, H. Dynamic cortical activity in the human brain reveals motor equivalence. Nature 1998, 392, 814–818. [Google Scholar] [CrossRef]
- Meyer-Lindenberg, A.; Ziemann, U.; Hajak, G.; Cohen, L.; Berman, K.F. Transitions between dynamical states of differing stability in the human brain. Proc. Natl. Acad. Sci. USA 2002, 99, 10948–10953. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Jirsa, V.K. How do neural connectivity and time delays influence bimanual coordination? Biol. Cybern. 2006, 96, 265–278. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, S.C. The neuronal basis of bimanual coordination: Recent neurophysiological evidence and functional models. Acta Psychol. 2002, 110, 139–159. [Google Scholar] [CrossRef]
- Fuchs, A.; Jirsa, V.K.; Kelso, J.A.S. Theory of the relation between human brain activity (MEG) and hand movements. Neuroimage 2000, 11, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, A.; Jirsa, V.K.; Kelso, J.A.S. Issues in the coordination of human brain activity and motor behavior. Neuroimage 2000, 11, 375–377. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jirsa, V.K.; Kelso, J.A.S. Spatiotemporal pattern formation in neural systems with heterogeneous connection topologies. Phys. Rev. E 2000, 62, 8462–8465. [Google Scholar] [CrossRef] [PubMed]
- Jirsa, V.K.; Fuchs, A.; Kelso, J.A.S. Connecting cortical and behavioral dynamics: Bimanual coordination. Neural Comput. 1998, 10, 2019–2045. [Google Scholar] [CrossRef]
- Jirsa, V.K.; Friedrich, R.; Haken, H.; Kelso, J.A.S. A theoretical model of phase transitions in the human brain. Biol. Cybern. 1994, 71, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Granatosky, M.C.; Bryce, C.M.; Hanna, J.; Fitzsimons, A.; Laird, M.F.; Stilson, K.; Wall, C.E.; Ross, C.F. Inter-stride variability triggers gait transitions in mammals and birds. Proc. R. Soc. B Biol. Sci. 2018, 285, 20181766. [Google Scholar] [CrossRef] [PubMed]
- Hoyt, D.F.; Taylor, C.R. Gait and the energetics of locomotion in horses. Nature 1981, 292, 239–240. [Google Scholar] [CrossRef]
- Jantzen, K.J.; Steinberg, F.L.; Kelso, J.A.S. Coordination dynamics of large-scale neural circuitry underlying rhythmic sensorimotor Behavior. J. Cogn. Neurosci. 2009, 21, 2420–2433. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Van Syoc, B.; Yang, R.; Kuehn, T.; Smith, D.; Zhu, Q. Using visual and/or kinesthetic information to stabilize intrinsic bimanual coordination patterns is a function of movement frequency. Psychol. Res. 2021, 85, 865–878. [Google Scholar] [CrossRef] [PubMed]
- Lagarde, J.; Kelso, J.A.S. Binding of movement, sound and touch: Multimodal coordination dynamics. Exp. Brain Res. 2006, 173, 673–688. [Google Scholar] [CrossRef] [PubMed]
- Haken, H. Information and Self-Organization; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Abbott, L.F. Where are the switches in this thing? In 23 Problems in Systems Neuroscience; Van Hemmen, J.L., Sejnowski, T.J., Eds.; Oxford University Press: Oxford, UK, 2006; pp. 423–433. [Google Scholar]
- Aguilera, M.; Bedia, M.G.; Santos, B.A.; Barandiaran, X.E. The situated HKB model: How sensorimotor spatial coupling can alter oscillatory brain dynamics. Front. Comput. Neurosci. 2013, 7, 117. [Google Scholar] [CrossRef] [PubMed]
- Kelso, J.A.S.; Dumas, G.; Tognoli, E. Outline of a general theory of behavior and brain coordination. Neural Netw. 2013, 37, 120–131. [Google Scholar] [CrossRef]
- Tognoli, E.; Zhang, M.; Fuchs, A.; Beetle, C.B.; Kelso, J.A.S. Coordination Dynamics: A foundation for understanding social behavior. Special Issue on Sensorimotor Foundations of Social Cognition. Front. Hum. Neurosci. 2020, 14, 317. [Google Scholar] [CrossRef]
- Kelso, J.A.S.; Jeka, J.J. Symmetry breaking dynamics of human multilimb coordination. J. Exp. Psychol. Hum. Percept. Perform. 1992, 18, 645–668. [Google Scholar] [CrossRef] [PubMed]
- Kelso, J.A.S.; DelColle, J.; Schöner, G. Action Perception as a pattern formation process. In Attention and Performance XIII; Jeannerod, M., Ed.; Erlbaum: Hillsdale, NJ, USA, 1990; pp. 139–169. [Google Scholar]
- Fuchs, A.; Jirsa, V.K.; Haken, H.; Kelso, J.A.S. Extending the HKB-Model of coordinated movement to oscillators with different eigenfrequencies. Biol. Cybern. 1996, 74, 21–30. [Google Scholar] [CrossRef]
- Richardson, M.J.; Schmidt, R.C.; Kay, B.A. Distinguishing the noise and attractor strength of coordinated limb movements using recurrence analysis. Biol. Cybern. 2006, 96, 59–78. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Self-organizing dynamical systems. In International Encyclopaedia of Social and Behavioral Sciences; Smelser, N.J., Baltes, P.B., Eds.; Pergamon: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Kelso, J.A.S. Metastable coordination dynamics of brain and behavior. Brain Neural Netw. 2001, 8, 125–130. [Google Scholar] [CrossRef][Green Version]
- Kelso, J.A.S. The complementary nature of coordination dynamics: Toward a science of the in-between. In Uncertainty and Surprise; Daniel, R.M., Driebe, D., Eds.; Springer Series in Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 77–85. [Google Scholar]
- Kelso, J.A.S. Multistability and metastability: Understanding dynamic coordination in the brain. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 906–918. [Google Scholar] [CrossRef] [PubMed]
- Tognoli, E.; Kelso, J.A.S. The Metastable Brain. Neuron 2014, 81, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, A. Nonlinear Dynamics in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fuchs, A.; Jirsa, V.K. (Eds.) Coordination: Neural, Behavioral and Social Dynamics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Frank, T.D.; Silva, P.L.; Turvey, M.T. Symmetry axiom of Haken–Kelso–Bunz coordination dynamics revisited in the context of cognitive activity. J. Math. Psychol. 2012, 56, 149–165. [Google Scholar] [CrossRef]
- Leise, T.; Cohen, A. Nonlinear oscillators at our fingertips. Am. Math. Mon. 2007, 114, 14–28. [Google Scholar] [CrossRef]
- Post, A.A.; Peper, C.E.; Beek, P.J. Relative phase dynamics in perturbed interlimb coordination: The effects of frequency and amplitude. Biol. Cybern. 2000, 83, 529–542. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Post, A.A.; Peper, C.E.; Daffertshofer, A.; Beek, P.J. Relative phase dynamics in perturbed interlimb coordination: Stability and stochasticity. Biol. Cybern. 2000, 83, 443–459. [Google Scholar] [CrossRef] [PubMed]
- Słowiński, P.; Al-Ramadhani, S.; Tsaneva-Atanasova, K. Relaxation oscillations and canards in the Jirsa–Kelso excitator model: Global flow perspective. Eur. Phys. J. Spéc. Top. 2018, 227, 591–601. [Google Scholar] [CrossRef]
- Słowiński, P.; Al-Ramadhani, S.; Tsaneva-Atanasova, K. Neurologically motivated coupling functions in models of motor coordination. Siam J. Appl. Dyn. Syst. 2020, 19, 208–232. [Google Scholar] [CrossRef]
- Haken, H. Principles of Brain Functioning; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Zhang, M.; Dumas, G.; Kelso, J.A.S.; Tognoli, E. Enhanced emotional responses during social coordination with a virtual partner. Int. J. Psychophysiol. 2016, 104, 33–43. [Google Scholar] [CrossRef]
- Kelso, J.A.S. The informational character of self-organized coordination dynamics. Hum. Mov. Sci. 1994, 13, 393–413. [Google Scholar] [CrossRef]
- Haken, H.; Portugali, J. Information Adaptation: The Interplay between Shannon Information and Semantic Information in Cognition; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Collins, J.J.; Stewart, I.N. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlinear Sci. 1993, 3, 349–392. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I.; Buono Collins, J.J. The role of symmetry in locomotor central pattern generators and animal gaits. Nature 1999, 401, 693–695. [Google Scholar] [CrossRef]
- Schöner, G.; Jiang, W.; Kelso, J.A.S. A synergetic theory of quadrupedal gaits and gait transitions. J. Theor. Biol. 1990, 142, 359–391. [Google Scholar] [CrossRef]
- Taga, G.; Yamaguchi, Y.; Shimizu, H. Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment. Biol. Cybern. 2019, 65, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Jeka, J.J.; Kelso, J.A.S. Manipulating symmetry in the coordination dynamics of human movement. J. Exp. Psychol. Hum. Percept. Perform. 1995, 21, 360–374. [Google Scholar] [CrossRef]
- Jeka, J.J.; Kelso, J.A.S.; Kiemel, T. Pattern switching in human multilimb coordination dynamics. Bull. Math. Biol. 1993, 55, 829–845. [Google Scholar] [CrossRef]
- Kovacs, A.J.; Wang, Y.; Kennedy, D.M. Accessing interpersonal and intrapersonal coordination dynamics. Exp. Brain Res. 2019, 238, 17–27. [Google Scholar] [CrossRef] [PubMed]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Strogatz, S.H. Sync: The Emerging Science of Spontaneous Order; Hyperion: New York, NY, USA, 2003. [Google Scholar]
- Winfree, A.T. The Geometry of Biological Time; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Pikovsky, A.; Rosenblum, M.; Kurtz, J. Synchronization: A Universal Concept in Nonlinear Science; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Von Holst, E. The Behavioral Physiology of Animals and Men; University of Miami Press: Coral Gables, FL, USA, 1937. [Google Scholar]
- Jeka, J.J.; Kelso, J.A.S. The dynamic pattern approach to coordinated behavior: A tutorial review. In Perspectives on the Coordination of Movement; Wallace, S.A., Ed.; North Holland Publishers: Amsterdam, The Netherlands, 1989; pp. 3–45. [Google Scholar]
- Edelman, G.M.; Mountcastle, V.B. (Eds.) The Mindful Brain; MIT Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Beek, P.J.; Peper, C.; Daffertshofer, A. Modeling rhythmic interlimb coordination: Beyond the Haken–Kelso–Bunz model. Brain Cogn. 2002, 48, 149–165. [Google Scholar] [CrossRef] [PubMed]
- Beek, P.J.; Rikkert, W.E.I.; Van Wieringen, P.C. Limit cycle properties of rhythmic forearm movements. J. Exp. Psychol. Hum. Percept. Perform. 1996, 22, 1077–1093. [Google Scholar] [CrossRef]
- Kay, B.A.; Kelso, J.A.S.; Saltzman, E.L.; Schöner, G. The space time behavior of single and bimanual rhythmical movements: Data and limit cycle model. J. Exp. Psychol. Hum. Percept. Perform. 1987, 13, 178–192. [Google Scholar] [CrossRef]
- Kay, B.A.; Saltzman, E.L.; Kelso, J.A.S. Steady state and perturbed rhythmical movements: Dynamical modeling using a variety of analytic tools. J. Exp. Psychol. Hum. Percept. Perform. 1991, 17, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Breakspear, M.; Heitmann, S.; Daffertshofer, A. Generative Models of Cortical Oscillations: Neurobiological Implications of the Kuramoto Model. Front. Hum. Neurosci. 2010, 4, 190. [Google Scholar] [CrossRef]
- Iberall, A.S. A field and circuit thermodynamics for integrative physiology. I-Introduction to the general notions. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1977, 2, R171–R180. [Google Scholar] [CrossRef] [PubMed]
- Soodak, H.; Iberall, A. Homeokinetics: A physical science for complex systems. Science 1978, 201, 579–582. [Google Scholar] [CrossRef]
- Morowitz, H.J. Energy Flow in Biology; Oxbow Press: Woodbridge, CT, USA, 1979. [Google Scholar]
- Yates, F.E.; Marsh, D.J.; Iberall, A.S. Integration of the whole organism: A foundation for a theoretical biology. In Challenging Biological Problems: Directions towards Their Solution; Behnke, J.A., Ed.; Oxford UP: New York, NY, USA, 1972; pp. 110–132. [Google Scholar]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Zhang, M.; Beetle, C.; Kelso, J.A.S.; Tognoli, E. Connecting empirical phenomena and theoretical models of biological coordination across scales. J. Royal. Soc. Interface 2019, 16, 20190360. [Google Scholar] [CrossRef]
- Zhang, M.; Kelso, J.A.S.; Tognoli, E. Critical diversity: Divided or united states of social coordination. PLoS ONE 2018, 13, e0193843. [Google Scholar] [CrossRef]
- Jantzen, K.J.; Steinberg, F.L.; Kelso, J.A.S. Brain networks underlying human timing behavior are influenced by prior context. Proc. Natl. Acad. Sci. USA 2004, 101, 6815–6820. [Google Scholar] [CrossRef]
- Nordham, C.A.; Tognoli, E.; Fuchs, A.; Kelso, J.A.S. How interpersonal coordination affects individual behavior (and vice- versa): Experimental analysis and adaptive HKB model of social memory. Ecol. Psychol. 2018, 30, 224–249. [Google Scholar] [CrossRef] [PubMed]
- Oullier, O.; De Guzman, G.C.; Jantzen, K.J.; Lagarde, J.; Kelso, J.A.S. Social coordination dynamics: Measuring human bonding. Soc. Neurosci. 2008, 3, 178–192. [Google Scholar] [CrossRef] [PubMed]
- Richardson, M.J.; Marsh, K.L.; Isenhower, R.W.; Goodman, J.R.L.; Schmidt, R.C. Rocking together: Dynamics of unintentional and intentional interpersonal coordination. Hum. Mov. Sci. 2007, 26, 867–891. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.C.; Carello, C.; Turvey, M.T. Phase transitions and critical fluctuations in the visual coordination of rhythmic movements between people. J. Exp. Psychol. Hum. Percept. Perform. 1990, 16, 227–247. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.C.; Richardson, M.J. Dynamics of Interpersonal Coordination. In Coordination: Neural, Behavioral and Social Dynamics; Fuchs, A., Jirsa, V.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 281–307. [Google Scholar]
- Zhang, M. The Coordination Dynamics of Multiple Agents. Ph.D. Thesis, Florida Atlantic University, Boca Raton, FL, USA, December 2018. [Google Scholar]
- Rabinovich, M.I.; Zaks, M.A.; Varona, P. Sequential dynamics of complex networks in mind: Consciousness and creativity. Phys. Rep. 2020, 883, 1–32. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Principles of Coordination: Synergies of Synergies. In Complex Systems in Sport: Linking Theory and Practice; Torrents, C., Passos, P., Cos, F., Eds.; Frontiers in Science e–Book; Frontiers Media SA: Lausanne, Switzerland, 2017; pp. 13–17. [Google Scholar] [CrossRef]
- Pattee, H.H. Physical Theories of Biological Coordination. In Topics in the Philosophy of Biology; Grene, M., Mendelsohn, E., Eds.; Boston Studies XXVII; Reidel: Kufstein, Austria, 1976; pp. 152–173. [Google Scholar]
- Lumsden, J.; Miles, L.K.; Macrae, C.N. Sync or sink? Interpersonal synchrony impacts self–esteem. Front. Psychol. 2014, 5, 1064. [Google Scholar] [CrossRef] [PubMed]
- Dotov, D.; Bosnyak, D.; Trainor, L.J. Collective music listening: Movement energy is enhanced by groove and visual social cues. Q. J. Exp. Psychol. 2021. [Google Scholar] [CrossRef] [PubMed]
- Mayo, O.; Gordon, I. In and out of synchrony—Behavioral and physiological dynamics of dyadic interpersonal coordination. Psychophysiology 2020, 57, e13574. [Google Scholar] [CrossRef] [PubMed]
- Feldman, R. Bio–behavioral synchrony: A model for integrating biological and microsocial behavioral processes in the study of parenting. Parenting 2012, 12, 154–164. [Google Scholar] [CrossRef]
- Codrons, E.; Bernardi, N.F.; Vandoni, M.; Bernardi, L. Spontaneous group synchronization of movements and respiratory rhythms. PLoS ONE 2014, 9, e107538. [Google Scholar] [CrossRef] [PubMed]
- Tognoli, E.; Lagarde, J.; DeGuzman, G.C.; Kelso, J.A.S. The phi complex as a neuromarker of human social coordination. Proc. Natl. Acad. Sci. USA 2007, 104, 8190–8195. [Google Scholar] [CrossRef] [PubMed]
- Valencia, A.L.; Froese, T. What binds us? Inter–brain neural synchronization and its implications for theories of human consciousness. Neurosci. Conscious. 2020, 2020, niaa010. [Google Scholar] [CrossRef] [PubMed]
- Alderisio, F.; Bardy, B.G.; Di Bernardo, M. Entrainment and synchronization in networks of Rayleigh–van der Pol oscillators with diffusive and Haken–Kelso–Bunz couplings. Biol. Cybern. 2016, 110, 151–169. [Google Scholar] [CrossRef] [PubMed]
- Noy, L.; Dekel, E.; Alon, U. The mirror game as a paradigm for studying the dynamics of two people improvising motion together. Proc. Natl. Acad. Sci. USA 2011, 108, 20947–20952. [Google Scholar] [CrossRef] [PubMed]
- Frank, T.D.; Richardson, M.J. On a test statistic for the Kuramoto order parameter of synchronization: An illustration for group synchronization during rocking chairs. Phys. D Nonlinear Phenom. 2010, 239, 2084–2092. [Google Scholar] [CrossRef]
- Richardson, M.J.; Garcia, R.L.; Frank, T.D.; Gregor, M.; Marsh, K.L. Measuring group synchrony: A cluster–phase method for analyzing multivariate movement time–series. Front. Physiol. 2012, 3, 405. [Google Scholar] [CrossRef]
- Nalepka, P.; Lamb, M.; Kallen, R.W.; Shockley, K.; Chemero, A.; Saltzman, E.; Richardson, M.J. Human social motor solutions for human–machine interaction in dynamical task contexts. Proc. Natl. Acad. Sci. USA 2019, 116, 1437–1446. [Google Scholar] [CrossRef] [PubMed]
- Petkoski, S.; Jirsa, V.K. Transmission time delays organize the brain network synchronization. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20180132. [Google Scholar] [CrossRef] [PubMed]
- Peper, C.E.; Beek, P.J. Are frequency–induced transitions in rhythmic coordination mediated by a drop in amplitude? Biol. Cybern. 1998, 79, 291–300. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Avitabile, D.; Słowiński, P.; Bardy, B.; Tsaneva–Atanasova, K. Beyond in–phase and anti–phase coordination in a model of joint action. Biol. Cybern. 2016, 110, 201–216. [Google Scholar] [CrossRef] [PubMed]
- Dotov, D.G.; De Cock, V.C.; Geny, C.; Ihalainen, P.; Moens, B.; Leman, M.; Bardy, B.; Bella, S.D. The role of interaction and predictability in the spontaneous entrainment of movement. J. Exp. Psychol. Gen. 2019, 148, 1041–1057. [Google Scholar] [CrossRef] [PubMed]
- Bardy, B.G.; Calabrese, C.; De Lellis, P.; Bourgeaud, S.; Colomer, C.; Pla, S.; Di Bernardo, M. Moving in unison after perceptual interruption. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Alderisio, F.; Fiore, G.; Salesse, R.N.; Bardy, B.G.; di Bernardo, M. Interaction patterns and individual dynamics shape the way we move in synchrony. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Rio, K.W.; Dachner, G.C.; Warren, W.H. Local interactions underlying collective motion in human crowds. Proc. R. Soc. B Biol. Sci. 2018, 285, 20180611. [Google Scholar] [CrossRef] [PubMed]
- Warren, W.H. Collective motion in human crowds. Curr. Dir. Psychol. Sci. 2018, 27, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.D. Synchronization: The key to effective communication in animal collectives. Trends Cogn. Sci. 2018, 22, 844–846. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.D.; Krause, J. Self–organization and collective behavior in vertebrates. Adv. Study Behav. 2003, 32, 1–75. [Google Scholar] [CrossRef]
- Camazine, S.; Deneubourg, J.-L.; Franks, N.R.; Sneyd, J.; Theraulaz, G.; Bonabeau, E. Self–Organization in Biological Systems; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Matheny, M.H.; Emenheiser, J.; Fon, W.; Chapman, A.; Salova, A.; Rohden, M.; Li, J.; de Badyn, M.H.; Pósfai, M.; Duenas–Osorio, L.; et al. Exotic states in a simple network of nanomechanical oscillators. Science 2019, 363, eaav7932. [Google Scholar] [CrossRef] [PubMed]
- Dyson, F. Origins of Life; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Alderson, T.H.; Bokde, A.L.; Kelso, J.A.S.; Maguire, L.; Coyle, D. Metastable neural dynamics in Alzheimer’s disease is disrupted by lesions to the structural connectome. NeuroImage 2018, 183, 438–455. [Google Scholar] [CrossRef]
- Alderson, T.H.; Bokde, A.L.W.; Kelso, J.A.S.; Maguire, L.; Coyle, D. Metastable neural dynamics underlies cognitive performance across multiple behavioural paradigms. Hum. Brain Mapp. 2020, 41, 3212–3234. [Google Scholar] [CrossRef] [PubMed]
- Buzsáki, G.; Freeman, W. Editorial overview: Brain rhythms and dynamic coordination. Curr. Opin. Neurobiol. 2015, 31, v–ix. [Google Scholar] [CrossRef] [PubMed]
- Buzsáki, G.; Logothetis, N.; Singer, W. Scaling Brain Size, Keeping Timing: Evolutionary Preservation of Brain Rhythms. Neuron 2013, 80, 751–764. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Kalies, W.D.; Kelso, J.A.S.; Tognoli, E. Topological portraits of multiscale coordination dynamics. J. Neurosci. Methods 2020, 339, 108672. [Google Scholar] [CrossRef] [PubMed]
- Newell, K.M.; Liu, Y.-T. Collective variables and task constraints in movement coordination, control and skill. J. Mot. Behav. 2020, 1–27. [Google Scholar] [CrossRef]
- Anderson, P.W. More is different. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, A.; Kelso, J.A.S. Coordination Dynamics and Synergetics: From Finger Movements to Brain Patterns and Ballet Dancing. In Complexity and Synergetics; Mueller, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 301–316. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelso, J.A.S. Unifying Large- and Small-Scale Theories of Coordination. Entropy 2021, 23, 537. https://doi.org/10.3390/e23050537
Kelso JAS. Unifying Large- and Small-Scale Theories of Coordination. Entropy. 2021; 23(5):537. https://doi.org/10.3390/e23050537
Chicago/Turabian StyleKelso, J. A. Scott. 2021. "Unifying Large- and Small-Scale Theories of Coordination" Entropy 23, no. 5: 537. https://doi.org/10.3390/e23050537
APA StyleKelso, J. A. S. (2021). Unifying Large- and Small-Scale Theories of Coordination. Entropy, 23(5), 537. https://doi.org/10.3390/e23050537





