Comparative Assessment of Various Low-Dissipation Combined Models for Three-Terminal Heat Pump Systems
Abstract
1. Introduction
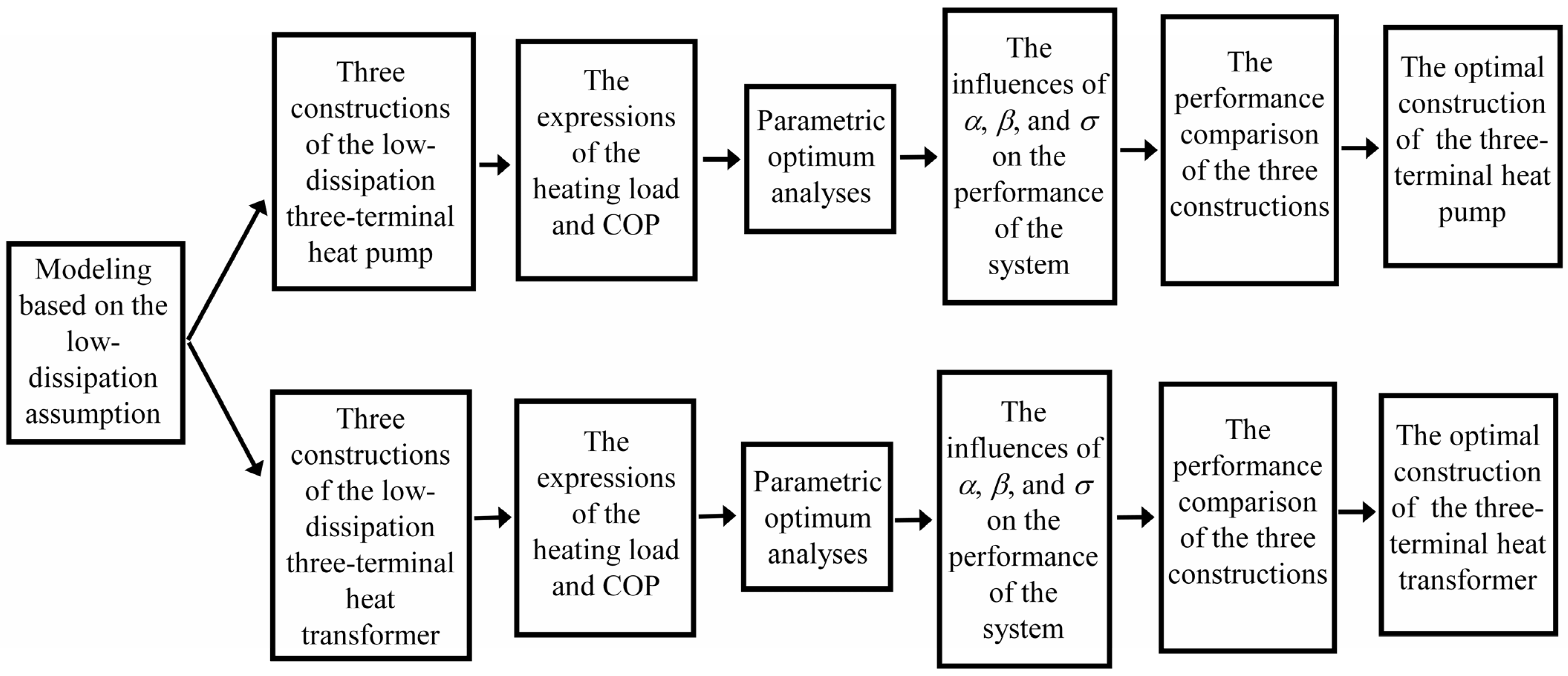
2. Model Descriptions
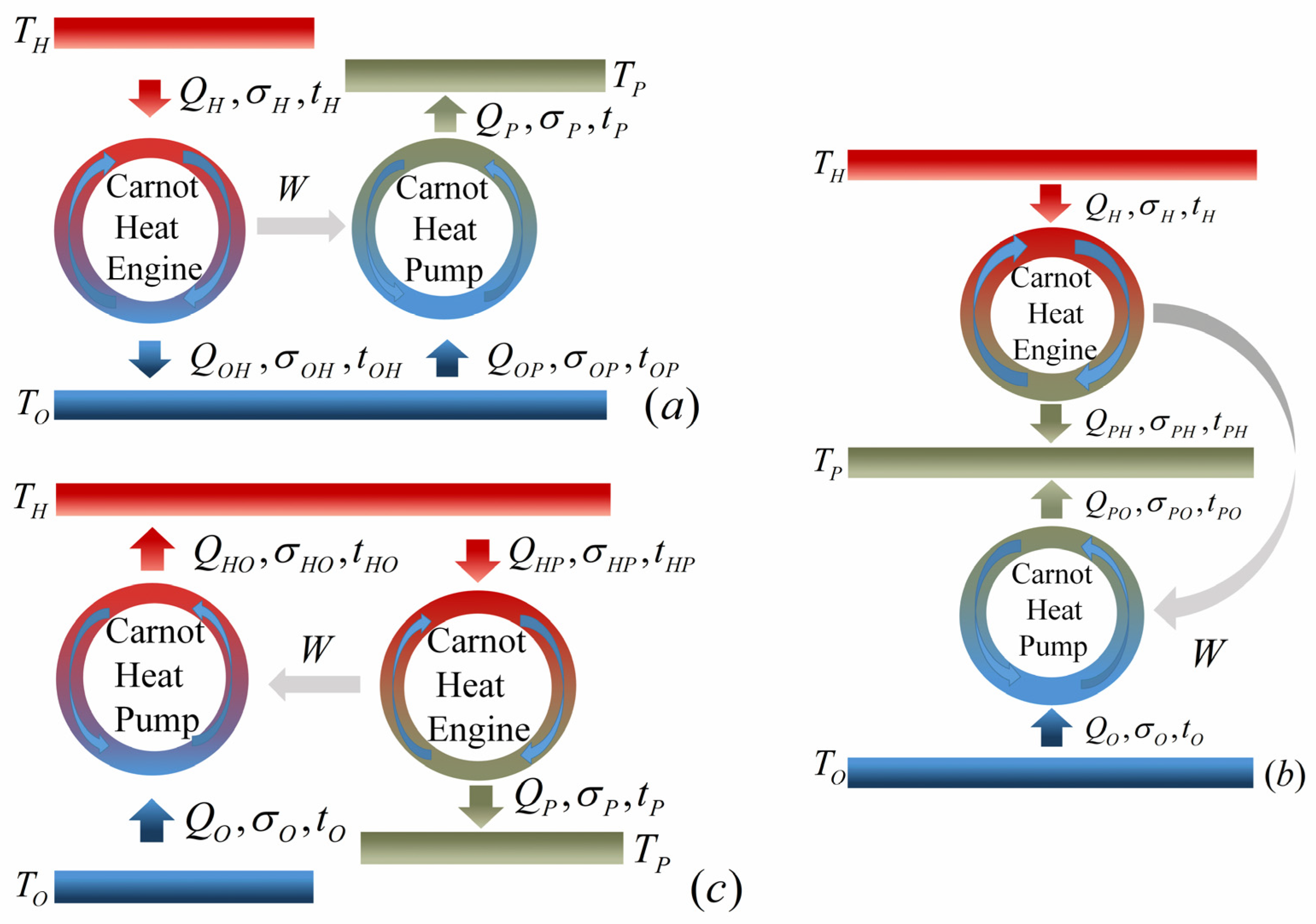
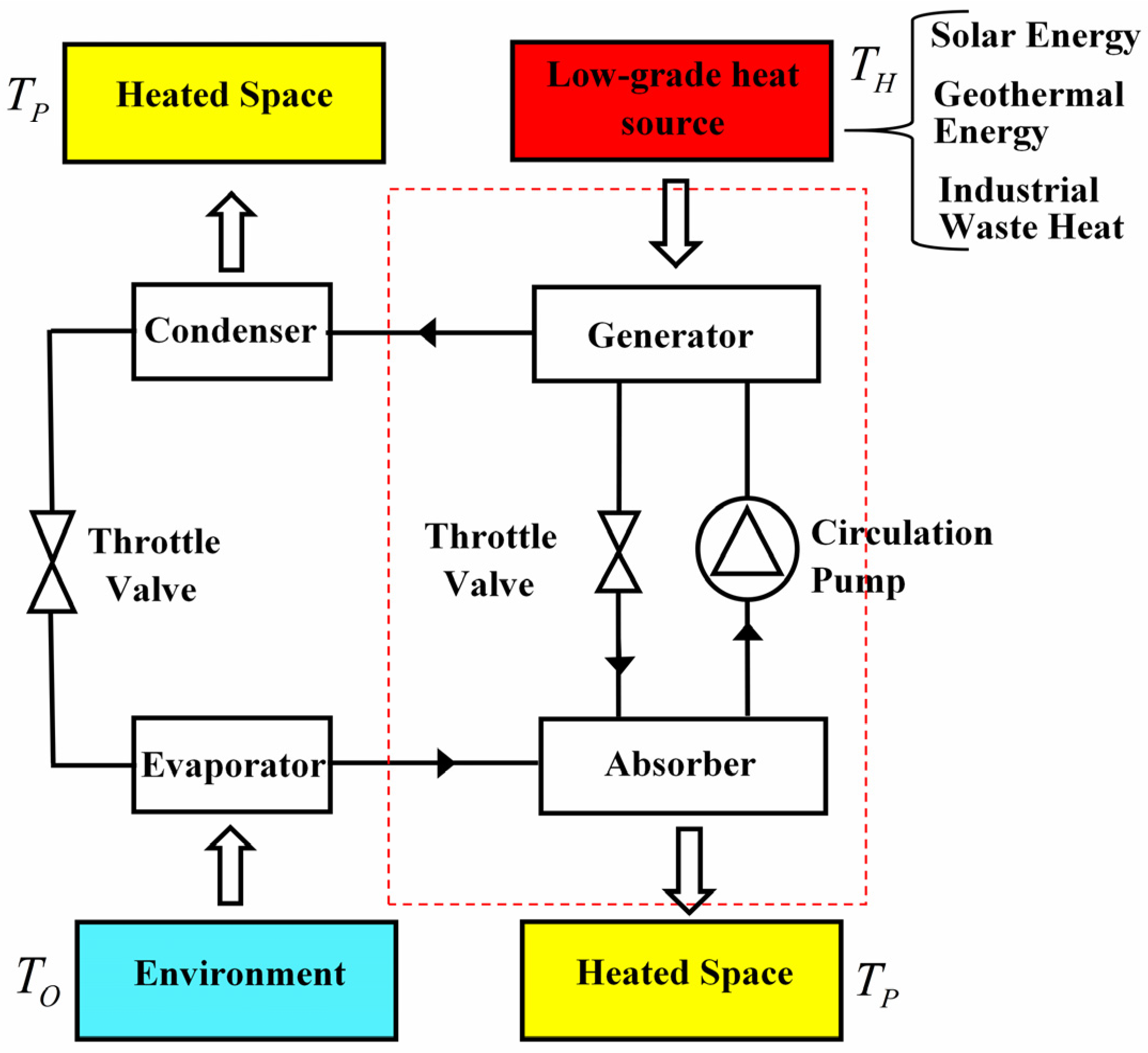
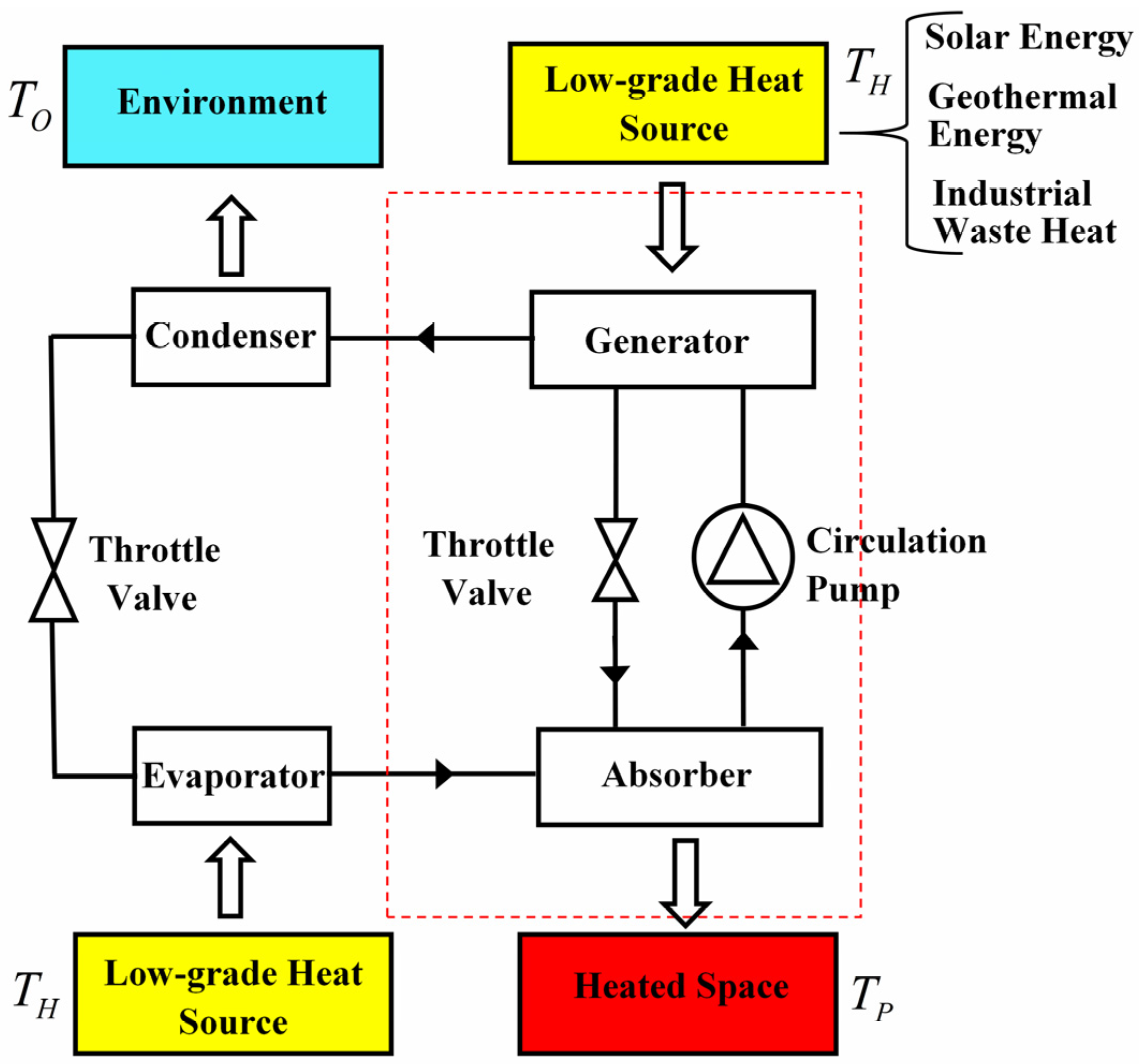
2.1. Low-Dissipation Three-Terminal Heat Pump
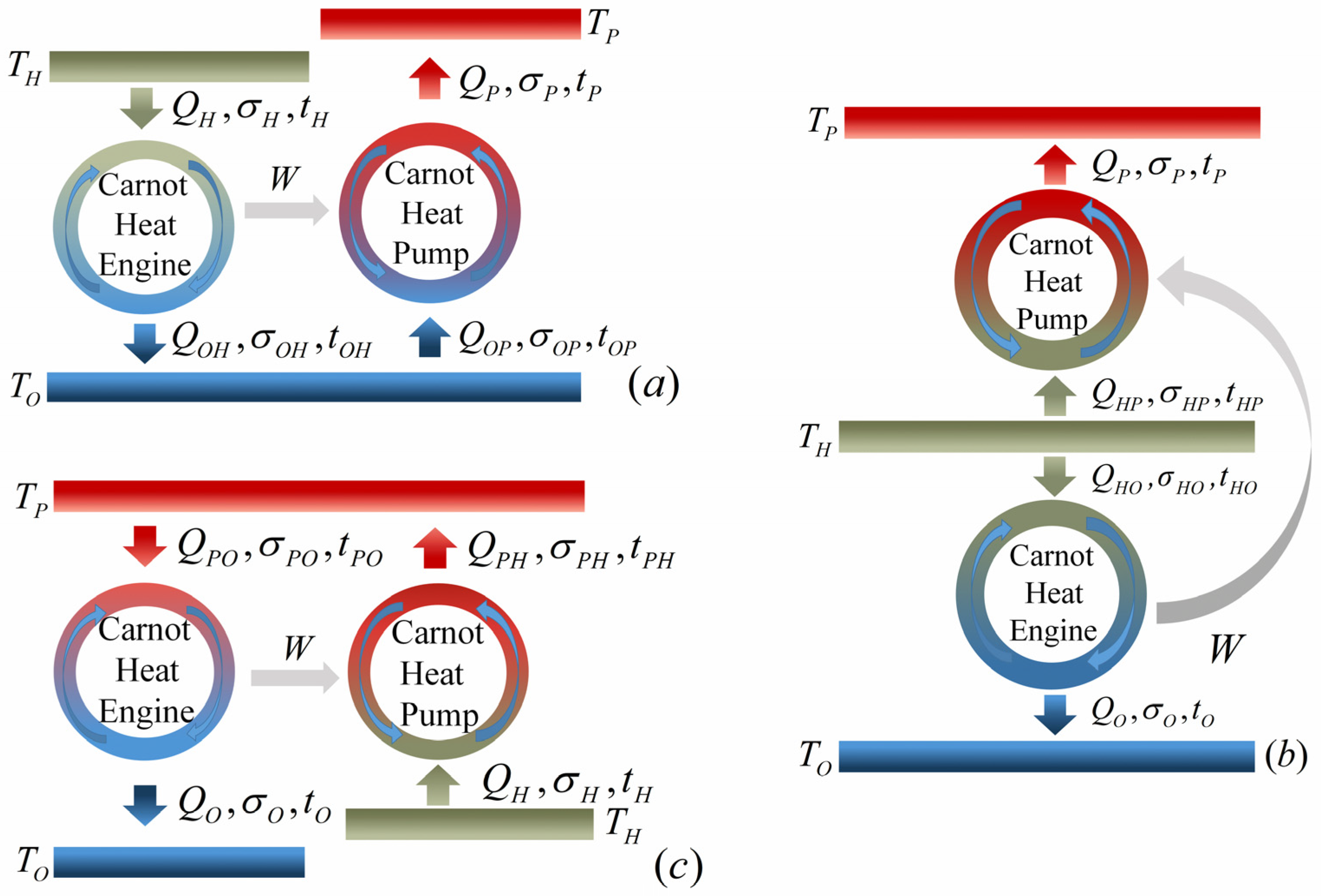
2.2. Low-Dissipation Three-Terminal Heat Transformer
3. Parametric Optimum Analyses
3.1. Optimal Coefficient of Performance and the Corresponding Parametric Optimizations for Three-Terminal Heat Pump
3.2. Optimal Coefficient of Performance and the Corresponding Parametric Optimizations for Three-Terminal Heat Transformer
4. Results and Discussion
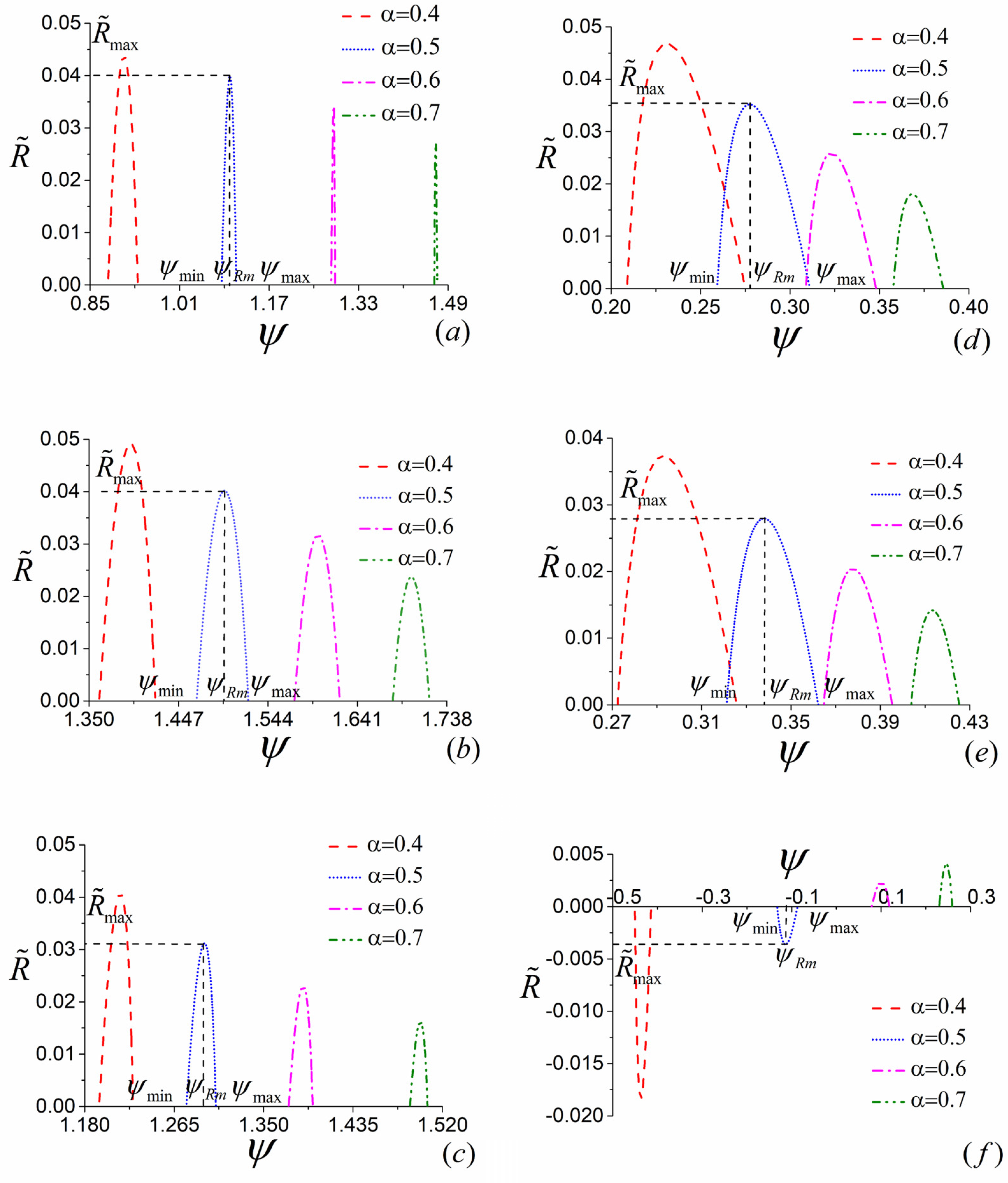
4.1. The Influence of
4.2. The Influence of
4.3. The Influence of
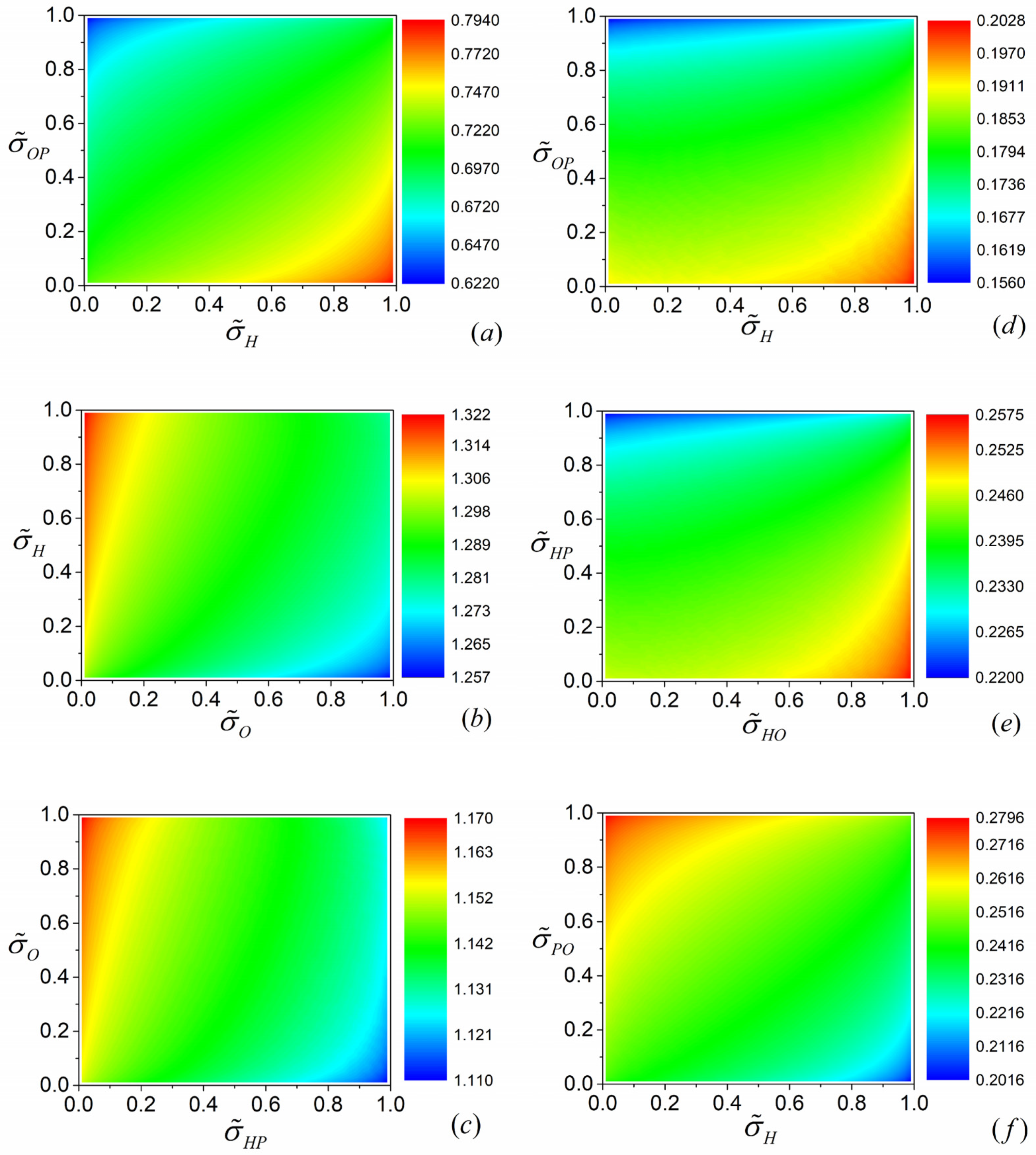
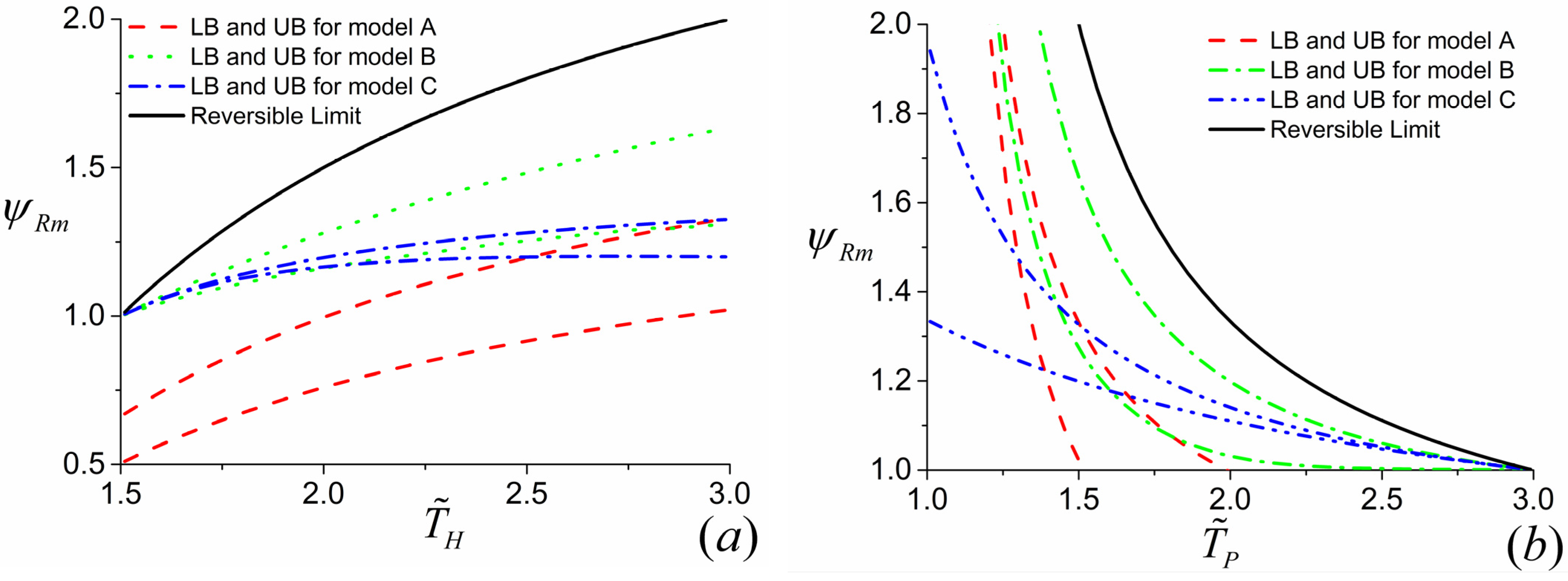
4.4. Upper and Lower Bounds
4.5. Extensions for the Three-Terminal Chemical Pump and Chemical Potential Transformer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin letters | |
| size ratio of two subsystems for the three-terminal heat pump | |
| size ratio of two subsystems for the three-terminal heat transformer | |
| heat () | |
| heating load () | |
| dimensionless heating load | |
| entropy () | |
| temperature () | |
| dimensionless temperature | |
| time () | |
| dimensionless time | |
| work () | |
| Greek letters | |
| parameter of deviation from reversible limit | |
| dissipation symmetry between two subsystems | |
| coefficient of performance of Carnot heat pump subsystem | |
| efficiency of Carnot heat engine subsystem | |
| chemical potential () | |
| dissipation parameter (s) | |
| dimensionless dissipation parameter | |
| cycle time () | |
| dimensionless cycle time | |
| coefficient of performance of the three-terminal heat pump/transformer | |
| Subscript and Superscript | |
| model a | |
| model b | |
| model c | |
| high temperature/chemical potential source | |
| , , , , , , , , | several heat-transfer processes in the three-terminal heat pump systems (please see Figure 2 and Figure 3) |
| Carnot heat engine subsystem | |
| Carnot heat pump subsystem | |
| maximum | |
| minimum | |
| low temperature/chemical potential source | |
| heated/pumped space | |
| maximum heating load state | |
| reversible condition | |
| thp | three-terminal heat pump |
| three-terminal heat transformer | |
| Abbreviations | |
| COP | coefficient of performance |
References
- Proesmans, K.; Cleuren, B.; Van den Broeck, C. Power-efficiency-dissipation relations in linear thermodynamics. Phys. Rev. Lett. 2016, 116, 220601. [Google Scholar] [CrossRef]
- Wang, H.; He, J.; Wang, J. Endoreversible quantum heat engines in the linear response regime. Phys. Rev. E 2017, 96, 012152. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, L.; Sun, F. Progress in finite time thermodynamic studies for internal combustion engine cycles. Entropy 2016, 18, 139. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Hernandez, A.C. Optimization, stability, and entropy in endoreversible heat engines. Entropy 2020, 22, 1323. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yan, Z. The effect of heat-transfer law on performance of a two-heat-source endoreversible cycle. J. Chem. Phys. 1989, 90, 3740–3743. [Google Scholar] [CrossRef]
- Esposito, M.; Kawai, R.; Lindenberg, K.; Van den Broeck, C. Efficiency at maximum power of low-dissipation Carnot engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef] [PubMed]
- Schmiedl, T.; Seifert, U. Efficiency at maximum power: An analytically solvable model for stochastic heat engines. Europhys. Lett. 2008, 81, 20003. [Google Scholar] [CrossRef]
- Rojas-Gamboa, D.A.; Rodriguez, J.I.; Gonzalez-Ayala, J.; Angulo-Brown, F. Ecological efficiency of finite-time thermodynamics: A molecular dynamics study. Phys. Rev. E 2018, 98, 022130. [Google Scholar] [CrossRef] [PubMed]
- Dorfman, K.E.; Xu, D.; Cao, J. Efficiency at maximum power of a laser quantum heat engine enhanced by noise-induced coherence. Phys. Rev. E 2018, 97, 042120. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Tu, Z.C.; Hernandez, A.C.; Roco, J.M.M. Coefficient of performance at maximum figure of merit and its bounds for low-dissipation Carnot-like refrigerators. Phys. Rev. E 2012, 86, 011127. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Wang, Y.; Chen, J. Universal efficiency bounds of weak-dissipative thermodynamic cycles at the maximum power output. Phys. Rev. E 2013, 87, 012133. [Google Scholar] [CrossRef]
- Abiuso, P.; Perarnau-Llobet, M. Optimal cycles for low-dissipation heat engines. Phys. Rev. Lett. 2020, 124, 110606. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; He, J.; Ma, Y. Efficiency at maximum power of a heat engine working with a two-level atomic system. Phys. Rev. E 2013, 87, 042119. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Chen, J. General performance characteristics and parametric optimum bounds of irreversible chemical engines. J. Appl. Phys. 2012, 112, 103504. [Google Scholar] [CrossRef]
- Johal, R.S. Performance optimization of low-dissipation thermal machines revisited. Phys. Rev. E 2019, 100, 052101. [Google Scholar] [CrossRef] [PubMed]
- Hernández, A.C.; Medina, A.; Roco, J.M.M. Time, entropy generation, and optimization in low-dissipation heat devices. New J. Phys. 2015, 17, 075011. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, D.; Dong, H.; Sun, C. Universal constraint for efficiency and power of a low-dissipation heat engine. Phys. Rev. E 2018, 98, 042112. [Google Scholar] [CrossRef]
- Singh, V.; Johal, R.S. Low-dissipation Carnot-like heat engines at maximum efficient power. Phys. Rev. E 2018, 98, 062132. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Santillán, M.; Reyes-Ramírez, I.; Calvo-Hernández, A.C. Link between optimization and local stability of a low-dissipation heat engine: Dynamic and energetic behaviors. Phys. Rev. E 2018, 98, 032142. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Santillan, M.; Santos, M.J.; Hernandez, A.C.; Roco, J.M.M. Optimization and stability of heat engines: The role of entropy evolution. Entropy 2018, 20, 865. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Efficiency at maximum power of minimally nonlinear irreversible heat engines. Europhys. Lett. 2012, 97, 10004. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K.; Roco, J.M.M.; Hernandez, A.C. Heat devices in nonlinear irreversible thermodynamics. Phys. Rev. E 2015, 91, 052140. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Medina, A.; Roco, J.M.M.; Hernandez, A.C. Entropy generation and unified optimization of Carnot-like and low-dissipation refrigerators. Phys. Rev. E 2018, 97, 022139. [Google Scholar] [CrossRef] [PubMed]
- Johal, R.S. Heat engines at optimal power: Low-dissipation versus endoreversible model. Phys. Rev. E 2017, 96, 012151. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Hernandez, A.C. Carnot-like heat engines versus low-dissipation models. Entropy 2017, 19, 182. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, H.; Hu, Z.; Hou, S. Performance evaluation of a new hybrid system consisting of a photovoltaic module and an absorption heat transformer for electricity production and heat upgrading. Energy 2021, 216, 119270. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, T.; Sun, F.; Wu, C. Optimal cooling load and COP relationship of a four-heat reservoir endoreversible absorption refrigeration cycle. Entropy 2004, 6, 316–326. [Google Scholar] [CrossRef]
- Xia, D.; Chen, L.; Sun, F. Optimal performance of an endoreversible three-mass-reservoir chemical pump with diffusive mass transfer law. Appl. Math. Model. 2010, 34, 140–145. [Google Scholar] [CrossRef]
- Little, A.B.; Garimella, S. Comparative assessment of alternative cycles for waste heat recovery and upgrade. Energy 2011, 36, 4492–4504. [Google Scholar] [CrossRef]
- Erdman, P.A.; Bhandari, B.; Fazio, R.; Pekola, J.P.; Taddei, F. Absorption refrigerators based on Coulomb-coupled single-electron systems. Phys. Rev. B 2018, 98, 045433. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Huang, C.; Lin, G.; Chen, J. Thermoelectric performance and optimization of three-terminal quantum dot nano-devices. Energy 2016, 95, 593–601. [Google Scholar] [CrossRef]
- Guo, J.; Yang, H.; Zhang, H.; Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Hernandez, A.C. Thermally driven refrigerators: Equivalent low-dissipation three-heat-source model and comparison with experimental and simulated results. Energy Convers. Manage. 2019, 198, 111917. [Google Scholar] [CrossRef]
- Guo, J.; Yang, H.; Gonzalez-Ayala, J.; Roco, J.M.M.; Medina, A.; Hernandez, A.C. The equivalent low-dissipation combined cycle system and optimal analyses of a class of thermally driven heat pumps. Energy Convers. Manage. 2020, 220, 113100. [Google Scholar] [CrossRef]
- Huang, F.F. Engineering Thermodynamics Fundamental and Applications; Macmillan Publishing Co.: New York, NY, USA, 1976. [Google Scholar]
- Chen, J.; Yan, Z. Equivalent combined systems of three-heat-source heat pumps. J. Chem. Phys. 1989, 90, 4951. [Google Scholar] [CrossRef]
- Lin, G.; Chen, J.; Wu, C.; Hua, B. The equivalent combined cycle of an irreversible chemical pump and its performance analysis. Int. J. Ambient Energy 2002, 23, 97–102. [Google Scholar] [CrossRef]
- Lin, G.; Chen, J.; Wu, C. The equivalent combined cycle of an irreversible chemical potential transformer and its optimal performance. Int. J. Energy 2002, 2, 119–124. [Google Scholar] [CrossRef]
- Bakhtiari, B.; Fradette, L.; Legros, R.; Paris, J. A model for analysis and design of H2O-LiBr absorption heat pumps. Energy Convers. Manage. 2011, 52, 1439–1448. [Google Scholar] [CrossRef]
- Sun, J.; Fu, L.; Zhang, S.; Hou, W. A mathematical model with experiments of single effect absorption heat pump using LiBr-H2O. Appl. Therm. Eng. 2010, 30, 2753–2762. [Google Scholar] [CrossRef]
- Xu, Z.; Mao, H.; Liu, D.; Wang, R. Waste heat recovery of power plant with large scale serial absorption heat pumps. Energy 2018, 165, 1097–1105. [Google Scholar] [CrossRef]
- Sujatha, I.; Venkatarathnam, G. Performance of a vapour absorption heat transformer operating with ionic liquids and ammonia. Energy 2017, 141, 924–936. [Google Scholar] [CrossRef]
- Hong, S.J.; Lee, C.H.; Kim, S.M.; Kim, I.G.; Kwon, O.K.; Park, C.W. Analysis of single stage steam generating absorption heat transformer. Appl. Therm. Eng. 2018, 144, 1109–1116. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Hernandez, A.C.; Roco, J.M.M. Irreversible and endoreversible behaviors of the LD-model for heat devices: The role of the time constraints and symmetries on the performance at maximum χ figure of merit. J. Stat. Mech. 2016, 2016, 073202. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Cao, H.; Yang, H.; Guo, J. Comparative Assessment of Various Low-Dissipation Combined Models for Three-Terminal Heat Pump Systems. Entropy 2021, 23, 513. https://doi.org/10.3390/e23050513
Li Z, Cao H, Yang H, Guo J. Comparative Assessment of Various Low-Dissipation Combined Models for Three-Terminal Heat Pump Systems. Entropy. 2021; 23(5):513. https://doi.org/10.3390/e23050513
Chicago/Turabian StyleLi, Zhexu, Haibo Cao, Hanxin Yang, and Juncheng Guo. 2021. "Comparative Assessment of Various Low-Dissipation Combined Models for Three-Terminal Heat Pump Systems" Entropy 23, no. 5: 513. https://doi.org/10.3390/e23050513
APA StyleLi, Z., Cao, H., Yang, H., & Guo, J. (2021). Comparative Assessment of Various Low-Dissipation Combined Models for Three-Terminal Heat Pump Systems. Entropy, 23(5), 513. https://doi.org/10.3390/e23050513




