LPA-MNI: An Improved Label Propagation Algorithm Based on Modularity and Node Importance for Community Detection
Abstract
:1. Introduction
2. Related Work
| Algorithm 1: LPA. |
| Input: |
| Output: The result of community detection |
|
3. Methods
3.1. Rough Community Detection
3.2. Label Update Strategy
3.3. The Framework of LPA-MNI Algorithm
| Algorithm 2: LPA-MNI. |
| Input: |
| Output: The result of community detection |
|
3.4. Computational Complexity
4. Results and Discussion
4.1. Evaluation Metrics
4.2. Experiments on Real-World Networks
4.2.1. The Networks with Known Community Structure
4.2.2. The Networks with Unknown Community Structure
4.3. Experiments on Artificial Synthetic Networks
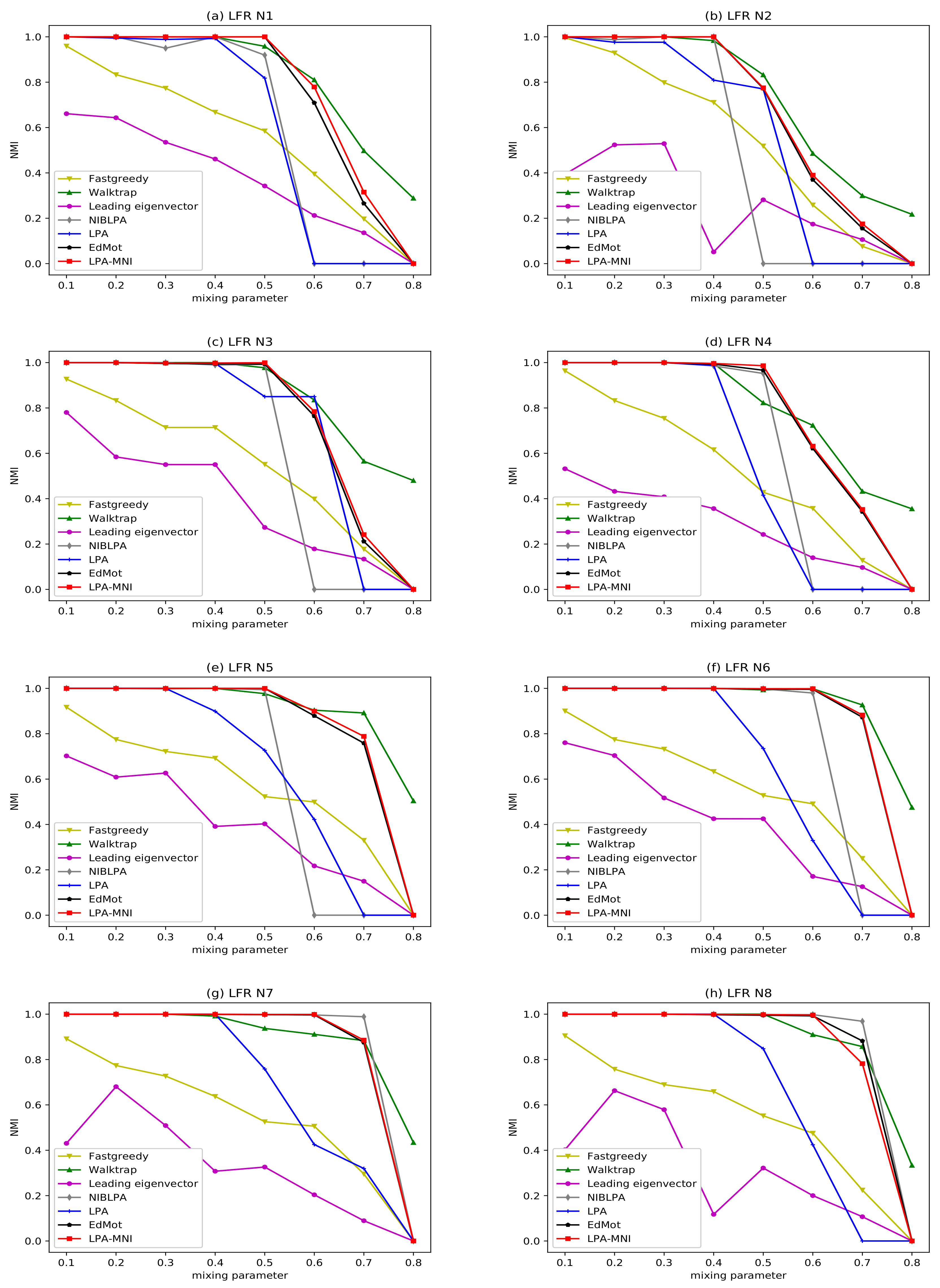
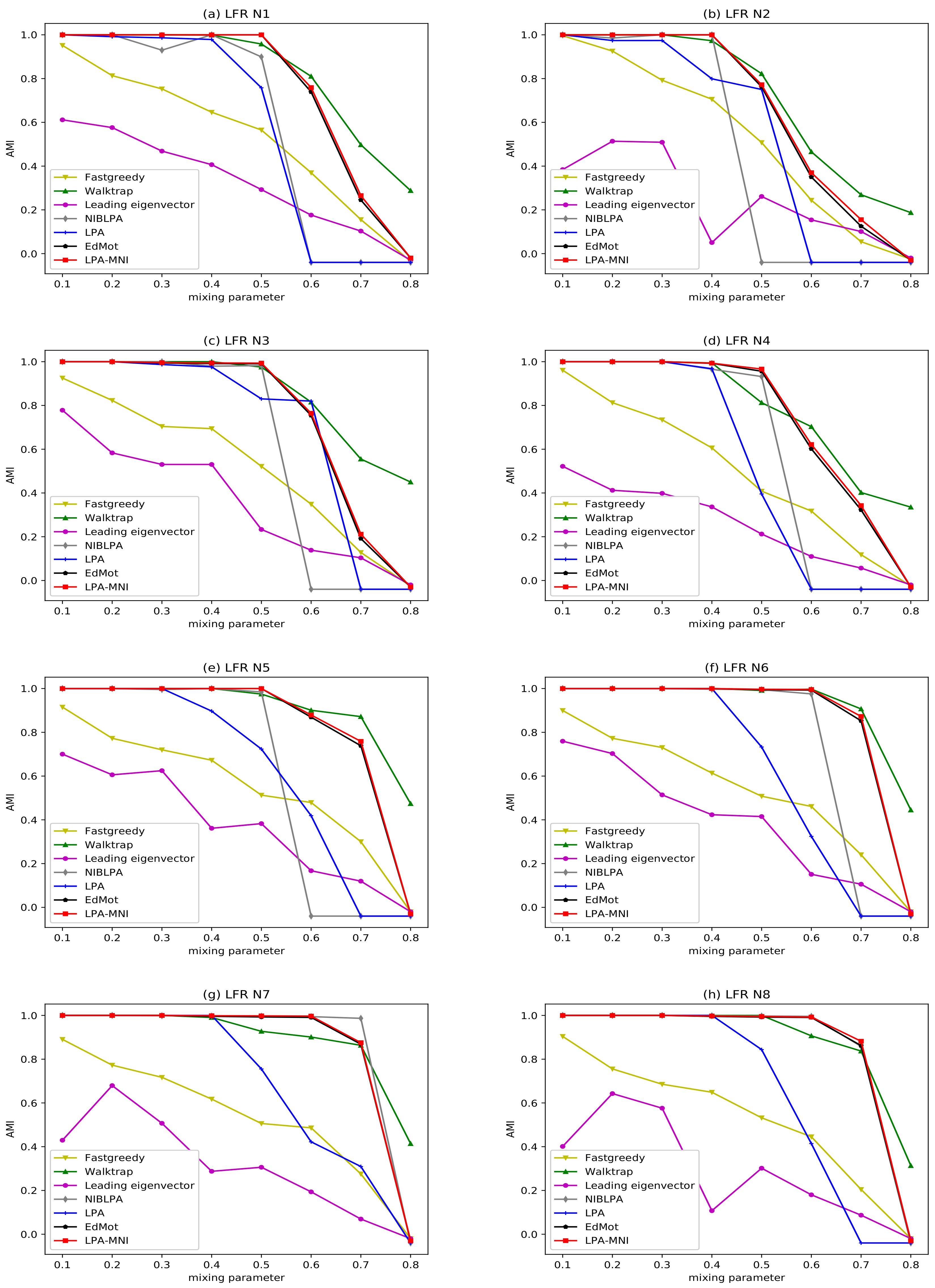
4.3.1. Experiment on LFR Benchmark Networks
4.3.2. Experiment on GN Benchmark Networks
4.4. Comparison of Computational Complexity
4.5. Critical Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ji, Z.; Pi, H.; Wei, W.; Xiong, B.; Woźniak, M.; Damasevicius, R. Recommendation Based on Review Texts and Social Communities: A Hybrid Model. IEEE Access 2019, 7, 40416–40427. [Google Scholar] [CrossRef]
- Shang, J.; Wu, H.; Zhou, S.; Zhong, J.; Feng, Y.; Qiang, B. IMPC: Influence maximization based on multi-neighbor potential in community networks. Phys. A Stat. Mech. Appl. 2018, 512, 1085–1103. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radicchi, F.; Castellano, C.; Cecconi, F.; Loreto, V.; Parisi, D. Defining and identifying communities in networks. Proc. Natl. Acad. Sci. USA 2004, 101, 2658–2663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 036104. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef] [Green Version]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding community structure in very large networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. 2008, 2008, 155–168. [Google Scholar] [CrossRef] [Green Version]
- Guimerà, R.; Sales-Pardo, M.; Amaral, L.A.N. Modularity from fluctuations in random graphs and complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 70, 025101. [Google Scholar] [CrossRef] [Green Version]
- Gui, C.; Zhang, R.; Hu, R.; Huang, G.; Wei, J. Overlapping communities detection based on spectral analysis of line graphs. Phys. A Stat. Mech. Appl. 2018, 498, 50–65. [Google Scholar] [CrossRef]
- Zhang, X.; Newman, M.E. Multiway spectral community detection in networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 92, 052808. [Google Scholar] [CrossRef] [Green Version]
- Barthelemy, M.; Fortunato, S. Resolution limit in community detection. Proc. Natl. Acad. Sci. USA 2007, 104, 36–41. [Google Scholar]
- Chen, M.; Kuzmin, K.; Szymanski, B.K. Community Detection via Maximization of Modularity and Its Variants. IEEE Trans. Comput. Soc. Syst. 2014, 1, 46–65. [Google Scholar] [CrossRef] [Green Version]
- GãMez, S.; Jensen, P.; Arenas, A. Analysis of community structure in networks of correlated data. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 016114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Zhao, H. Normalized modularity optimization method for community identification with degree adjustment. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 88, 052802. [Google Scholar] [CrossRef]
- Yuan, Q.; Liu, B. Community detection via an efficient nonconvex optimization approach based on modularity. Comput. Stat. Data Anal. 2021, 157, 107163. [Google Scholar] [CrossRef]
- Pons, P.; Latapy, M. Computing communities in large networks using random walks. In International Symposium on Computer and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2005; pp. 284–293. [Google Scholar]
- Rosvall, M.; Bergstrom, C.T. Maps of Random Walks on Complex Networks Reveal Community Structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Dongen, S. Graph Clustering by Flow Simulation. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 2000. [Google Scholar]
- Behera, R.K.; Rath, S.K.; Misra, S.; Damaševičius, R.; Maskeliūnas, R. Large Scale Community Detection Using a Small World Model. Appl. Sci. 2017, 7, 1173. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.; Feng, Z.; Ren, Z. Community detection using Ant Colony Optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 3072–3078. [Google Scholar]
- Guerrero, M.; Montoya, F.G.; Baños, R.; Alcayde, A.; Gil, C. Adaptive community detection in complex networks using genetic algorithms. Neurocomputing 2017, 266, 101–113. [Google Scholar] [CrossRef]
- Cai, Q.; Gong, M.; Shen, B.; Ma, L.; Jiao, L. Discrete particle swarm optimization for identifying community structures in signed social networks. Neural Netw. 2014, 58, 4–13. [Google Scholar] [CrossRef]
- Ali, E.; Hafez, A.I.; Hassanien, A.E.; Fahmy, A.A. A Discrete Bat Algorithm for the Community Detection Problem. In Hybrid Artificial Intelligent Systems; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Zhang, Y.; Liu, Y.; Li, J.; Zhu, J.; Yang, C.; Yang, W.; Wen, C. WOCDA: A whale optimization based community detection algorithm. Phys. A Stat. Mech. Appl. 2019, 539, 122937. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation learning on graphs: Methods and applications. arXiv Preprint 2017, arXiv:1709.05584. [Google Scholar]
- Yang, J.; Leskovec, J. Overlapping Community Detection at Scale: A Nonnegative Matrix Factorization Approach. In Proceedings of the Sixth ACM International Conference on Web Search and Data Mining, Rome, Italy, 4–8 February 2013; ACM: New York, NY, USA, 2013; pp. 587–596. [Google Scholar]
- Li, S.; Jiang, L.; Wu, X.; Han, W.; Zhao, D.; Wang, Z. A weighted network community detection algorithm based on deep learning. Appl. Math. Comput. 2021, 401, 126012. [Google Scholar]
- Yan, C.; Chang, Z. Modularized tri-factor nonnegative matrix factorization for community detection enhancement. Phys. A Stat. Mech. Appl. 2019, 533, 122050. [Google Scholar] [CrossRef]
- Yan, C.; Chang, Z. Modularized convex nonnegative matrix factorization for community detection in signed and unsigned networks. Phys. A Stat. Mech. Appl. 2020, 539, 122904. [Google Scholar] [CrossRef]
- Luo, W.; Lu, N.; Ni, L.; Zhu, W.; Ding, W. Local community detection by the nearest nodes with greater centrality. Inf. Sci. 2020, 517, 377–392. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, Z.; Liu, C.; Su, Y.; Zhang, X. Community detection in complex networks with an ambiguous structure using central node based link prediction. Knowl.-Based Syst. 2020, 195, 105626. [Google Scholar] [CrossRef]
- Li, X.; Zhou, S.; Liu, J.; Lian, G.; Chen, G.; Lin, C.W. Communities detection in social network based on local edge centrality. Phys. A Stat. Mech. Appl. 2019, 531, 121552. [Google Scholar] [CrossRef]
- Liu, S.; Xia, Z. A two-stage BFS local community detection algorithm based on node transfer similarity and Local Clustering Coefficient. Phys. A Stat. Mech. Appl. 2020, 537, 122717. [Google Scholar] [CrossRef]
- Sheng, J.; Liu, C.; Chen, L.; Wang, B.; Zhang, J. Research on Community Detection in Complex Networks Based on Internode Attraction. Entropy 2020, 22, 1383. [Google Scholar] [CrossRef] [PubMed]
- Chunaev, P. Community detection in node-attributed social networks: A survey. Comput. Sci. Rev. 2020, 37, 100286. [Google Scholar] [CrossRef]
- Mercorio, F.; Mezzanzanica, M.; Moscato, V.; Picariello, A.; Sperli, G. DICO: A Graph-DB Framework for Community Detection on Big Scholarly Data. IEEE Trans. Emerg. Top. Comput. 2019, 1. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 76, 036106. [Google Scholar] [CrossRef] [Green Version]
- Kothari, R.; Jain, V. Learning from labeled and unlabeled data. Int. Jt. Conf. Neural Netw. 2002, 3175, 2803–2808. [Google Scholar]
- Gui, Q.; Deng, R.; Xue, P.; Cheng, X. A community discovery algorithm based on boundary nodes and label propagation. Pattern Recognit. Lett. 2018, 109, 103–109. [Google Scholar] [CrossRef]
- Ma, T.; Xia, Z. An improved label propagation algorithm based on node importance and random walk for community detection. Mod. Phys. Lett. B 2017, 31, 1750162. [Google Scholar] [CrossRef]
- Xing, Y.; Meng, F.; Zhou, Y.; Zhu, M.; Shi, M.; Sun, G. A Node Influence Based Label Propagation Algorithm for Community Detection in Networks. Sci. World J. 2014, 5, 627581. [Google Scholar] [CrossRef]
- Zhang, X.K.; Ren, J.; Song, C.; Jia, J.; Zhang, Q. Label propagation algorithm for community detection based on node importance and label influence. Phys. Lett. A 2017, 381, 2691–2698. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, J.; Dengaob, L.I. A Stable Label Propagation Algorithm for Community Detection. J. Taiyuan Univ. Technol. 2013, 4, 493–495. [Google Scholar]
- Barber, M.J.; Clark, J.W. Detecting network communities by propagating labels under constraints. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 026129. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Murata, T. Advanced modularity-specialized label propagation algorithm for detecting communities in networks. Phys. A Stat. Mech. Appl. 2012, 389, 1493–1500. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Szymanski, B.K. Community Detection Using a Neighborhood Strength Driven Label Propagation Algorithm. In Proceedings of the 2011 IEEE Network Science Workshop, IEEE Computer Society, West Point, NY, USA, 22–24 June 2011; pp. 188–195. [Google Scholar]
- Cordasco, G.; Gargano, L. Community detection via semi-synchronous label propagation algorithms. In Proceedings of the IEEE International Workshop on Business Applications of Social Network Analysis, Bangalore, India, 15 December 2011; pp. 1–8. [Google Scholar]
- Gui, C.; Zhang, R.; Zhao, Z.; Wei, J.; Hu, R. LPA-CBD An Improved Label Propagation Algorithm Based on Community Belonging Degree for Community Detection. Int. J. Mod. Phys. C 2018, 29, 1850011. [Google Scholar] [CrossRef]
- Gregory, S. Finding overlapping communities in networks by label propagation. New J. Phys. 2010, 12, 2011–2024. [Google Scholar] [CrossRef]
- Xie, J.; Szymanski, B.K.; Liu, X. SLPA: Uncovering Overlapping Communities in Social Networks via a Speaker-Listener Interaction Dynamic Process. In Proceedings of the IEEE International Conference on Data Mining Workshops, Vancouver, BC, Canada, 11 December 2012; pp. 344–349. [Google Scholar]
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef] [Green Version]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2004, 340, 378–382. [Google Scholar]
- Burt, R.S.; Minor, M.J. Applied Network Analysis: A Methodological Introduction; SAGE Publications: Beverly Hills, CA, USA, 1983. [Google Scholar]
- Li, P.Z.; Huang, L.; Wang, C.D.; Lai, J.H. EdMot: An Edge Enhancement Approach for Motif-Aware Community Detection. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 479–487. [Google Scholar] [CrossRef] [Green Version]
- Danon, L.; Díazguilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. 2005, 2005, 09008. [Google Scholar] [CrossRef]
- McCarthy, A.D.; Chen, T.; Rudinger, R.; Matula, D.W. Metrics Matter in Community Detection. Complex Networks and Their Applications VIII; Cherifi, H., Gaito, S., Mendes, J.F., Moro, E., Rocha, L.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 164–175. [Google Scholar]
- Chakraborty, T.; Dalmia, A.; Mukherjee, A.; Ganguly, N. Metrics for Community Analysis: A Survey. ACM Comput. Surv. 2017, 50. [Google Scholar] [CrossRef]
- Lusseau, D. The emergent properties of a dolphin social network. Proc. Biol. Sci. 2003, 270 (Suppl. 2), S186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knuth, D.E. The Stanford GraphBase: A Platform for Combinatorial Computing; ACM: New York, NY, USA, 1993; pp. 41–43. [Google Scholar]
- Gleiser, P.M.; Danon, L. Community Structure in Jazz. Adv. Complex Syst. 2003, 6, 565–573. [Google Scholar] [CrossRef] [Green Version]
- Glance, N.; Glance, N. The political blogosphere and the 2004 U.S. election: Divided they blog. Int. Workshop Link Discov. 2005, 36–43. [Google Scholar] [CrossRef]
- Rossi, R.A.; Ahmed, N.K. The network data repository with interactive graph analytics and visualization. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 4292–4293. [Google Scholar]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph evolution: Densification and shrinking diameters. Acm Trans. Knowl. Discov. Data 2007, 1, 2. [Google Scholar] [CrossRef]
- Newman, M.E. The Structure of Scientific Collaboration Networks. Proc. Natl. Acad. Sci. USA 2001, 98, 404–409. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Fu, Y.; Shang, M. A fast and efficient heuristic algorithm for detecting community structures in complex networks. Phys. A Stat. Mech. Appl. 2012, 388, 2741–2749. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 78, 046110. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Networks | C | ||||
|---|---|---|---|---|---|
| Karate [54] | 34 | 78 | 17 | 4.588 | 0.256 |
| Dolphins [62] | 62 | 159 | 12 | 5.129 | 0.309 |
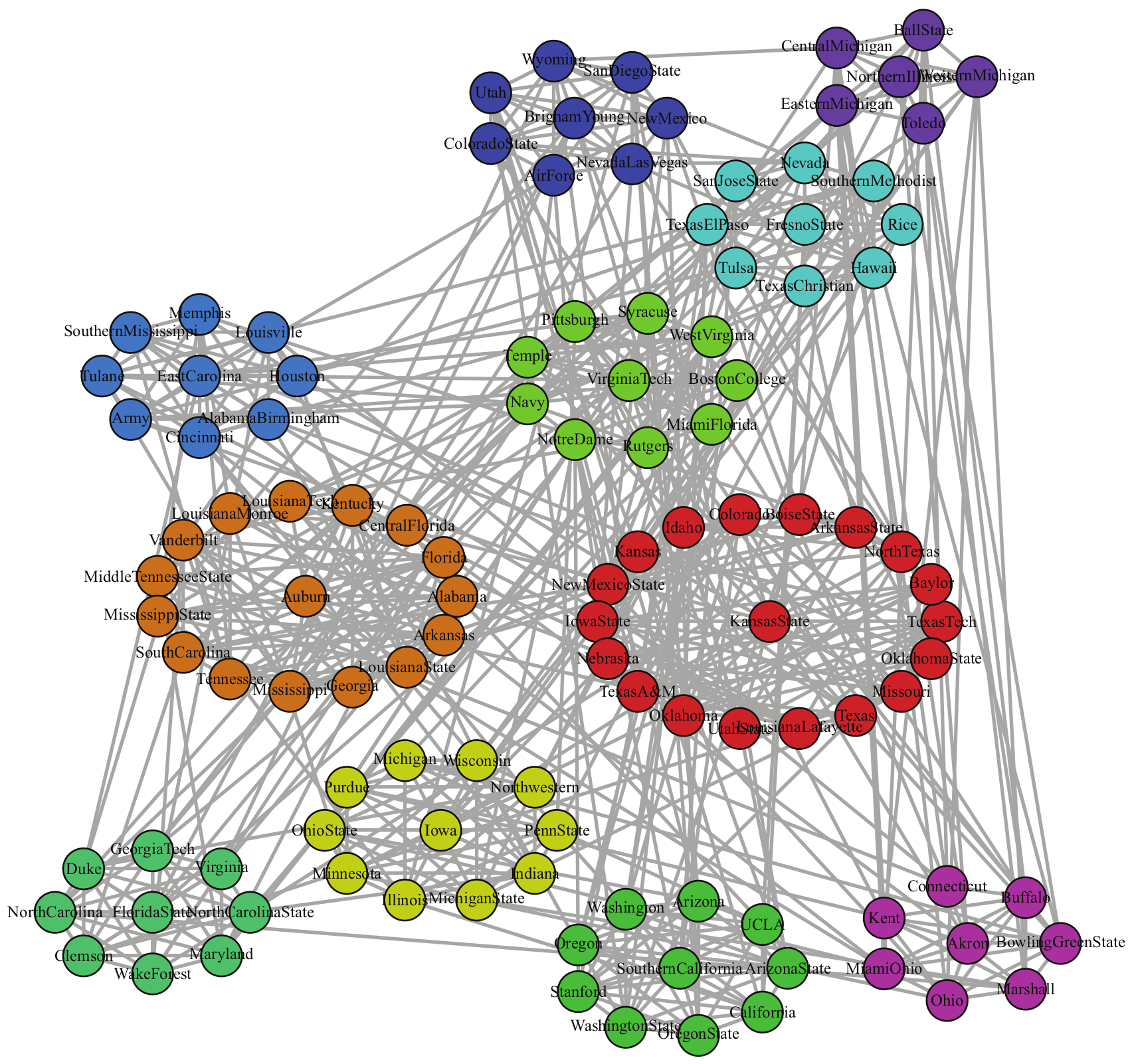
| Football [4] | 115 | 613 | 12 | 10.661 | 0.407 |
| Riskmap | 42 | 83 | 6 | 3.952 | 0.435 |
| Lesmis [63] | 77 | 254 | 36 | 6.597 | 0.499 |
| Jazz [64] | 198 | 2742 | 100 | 28.563 | 0.520 |
| PolBlogs [65] | 1222 | 16,714 | 351 | 27.355 | 0.226 |
| Yeast [66] | 2375 | 11,693 | 118 | 9.847 | 0.469 |
| Ca_Hep [67] | 9877 | 25,973 | 65 | 5.259 | 0.284 |
| Astro-ph [67] | 16,706 | 121,251 | 360 | 14.516 | 0.426 |
| Cond_mat [68] | 16,726 | 47,594 | 107 | 5.691 | 0.360 |
| Cond_mat2005 [68] | 40,421 | 175,692 | 278 | 8.693 | 0.650 |
| Community ID | Members |
|---|---|
| 1 | 1,2,3,4,5,6,7,8,11,12,13,14,17,18,20,22 |
| 2 | 9,10,15,16,19,21,23,24,25,26,27,28,29,30,31,32,33,34 |
| Algorithm | Fastgreedy | LPA | Leading Eigenvector | Walktrap | NIBLPA | EdMot | LPA-MNI |
|---|---|---|---|---|---|---|---|
| CN | 3 | 2 | 4 | 5 | 3 | 3 | 2 |
| Q | 0.380 | 0.292 ± 0.292 | 0.393 | 0.353 | 0.352 | 0.412 | 0.372 |
| NMI | 0.692 | 0.585 ± 0.415 | 0.677 | 0.504 | 0.625 | 0.602 | 1 |
| AMI | 0.681 | 0.571 ± 0.403 | 0.661 | 0.473 | 0.618 | 0.581 | 1 |
| Algorithm | Fastgreedy | LPA | Leading Eigenvector | Walktrap | NIBLPA | EdMot | LPA-MNI |
|---|---|---|---|---|---|---|---|
| CN | 4 | 3 | 5 | 4 | 5 | 4 | 4 |
| Q | 0.495 | 0.492 ± 214 | 0.491 | 0.489 | 0.452 | 0.518 | 0.527 |
| NMI | 0.787 | 0.732 ± 0.210 | 0.679 | 0.692 | 0.721 | 0.830 | 0.843 |
| AMI | 0.773 | 0.722 ± 0.110 | 0.652 | 0.671 | 0.719 | 0.815 | 0.833 |
| Algorithm | Fastgreedy | LPA | Leading Eigenvector | Walktrap | NIBLPA | EdMot | LPA-MNI |
|---|---|---|---|---|---|---|---|
| CN | 6 | 9 | 8 | 10 | 9 | 9 | 11 |
| Q | 0.549 | 0.576 ± 0.072 | 0.492 | 0.602 | 0.542 | 0.604 | 0.582 |
| NMI | 0.697 | 0.880 ± 0.114 | 0.698 | 0.887 | 0.707 | 0.889 | 0.889 |
| AMI | 0.650 | 0.866 ± 0.102 | 0.633 | 0.856 | 0.685 | 0.859 | 0.870 |
| Network | Metrics | Fastgreedy | LPA | Leading Eigenvector | Walktrap | NIBLPA | EdMot | LPA-MNI |
|---|---|---|---|---|---|---|---|---|
| Riskmap | Q | 0.625 | 0.534 ± 0.126 | 0.546 | 0.623 | 0.634 | 0.634 | 0.634 |
| Lesmis | Q | 0.501 | 0.348 ± 0.049 | 0.532 | 0.521 | 0.348 | 0.525 | 0.527 |
| Jazz | Q | 0.439 | 0.282 ± 0.105 | 0.394 | 0.438 | 0.293 | 0.444 | 0.415 |
| PolBlogs | Q | 0.426 | 0.418 ± 0.129 | 0.424 | 0.425 | 0.422 | 0.237 | 0.427 |
| Yeast | Q | 0.700 | 0.657 ± 0.020 | 0.628 | 0.677 | 0.660 | 0.728 | 0.678 |
| Ca_Hep | Q | 0.716 | 0.631 ± 0.045 | 0.583 | 0.663 | 0.628 | 0.669 | 0.675 |
| Astro-ph | Q | 0.633 | 0.551 ± 0.107 | 0.595 | 0.636 | 0.606 | 0.546 | 0.687 |
| Cond_mat | Q | 0.778 | 0.720 ± 0.016 | 0.588 | 0.741 | 0.698 | 0.745 | 0.750 |
| Condmat_mat2005 | Q | 0.631 | 0.445 ± 0.173 | 0.359 | 0.599 | 0.558 | 0.626 | 0.629 |
| Network | N | |||||||
|---|---|---|---|---|---|---|---|---|
| LFR N1 | 1000 | 15 | 50 | 2 | 1 | 10 | 50 | 0.1–0.8 |
| LFR N2 | 1000 | 15 | 50 | 2 | 1 | 20 | 100 | 0.1–0.8 |
| LFR N3 | 2000 | 15 | 50 | 2 | 1 | 10 | 50 | 0.1–0.8 |
| LFR N4 | 2000 | 15 | 50 | 2 | 1 | 20 | 100 | 0.1–0.8 |
| LFR N5 | 5000 | 25 | 50 | 2 | 1 | 20 | 50 | 0.1–0.8 |
| LFR N6 | 5000 | 25 | 50 | 2 | 1 | 20 | 100 | 0.1–0.8 |
| LFR N7 | 10,000 | 25 | 50 | 2 | 1 | 20 | 50 | 0.1–0.8 |
| LFR N8 | 10,000 | 25 | 50 | 2 | 1 | 20 | 100 | 0.1–0.8 |
| Algorithm | Time Complexity |
|---|---|
| Fastgreedy | |
| LPA | |
| Leading eigenvector | |
| Walktrap | |
| NIBLPA | |
| EdMot | |
| LPA-MNI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, R.; Zhao, Z.; Liu, X. LPA-MNI: An Improved Label Propagation Algorithm Based on Modularity and Node Importance for Community Detection. Entropy 2021, 23, 497. https://doi.org/10.3390/e23050497
Li H, Zhang R, Zhao Z, Liu X. LPA-MNI: An Improved Label Propagation Algorithm Based on Modularity and Node Importance for Community Detection. Entropy. 2021; 23(5):497. https://doi.org/10.3390/e23050497
Chicago/Turabian StyleLi, Huan, Ruisheng Zhang, Zhili Zhao, and Xin Liu. 2021. "LPA-MNI: An Improved Label Propagation Algorithm Based on Modularity and Node Importance for Community Detection" Entropy 23, no. 5: 497. https://doi.org/10.3390/e23050497
APA StyleLi, H., Zhang, R., Zhao, Z., & Liu, X. (2021). LPA-MNI: An Improved Label Propagation Algorithm Based on Modularity and Node Importance for Community Detection. Entropy, 23(5), 497. https://doi.org/10.3390/e23050497





