Novel Features for Binary Time Series Based on Branch Length Similarity Entropy
Abstract
1. Introduction
2. Materials and Methods
2.1. BLS Entropy and Its Profile
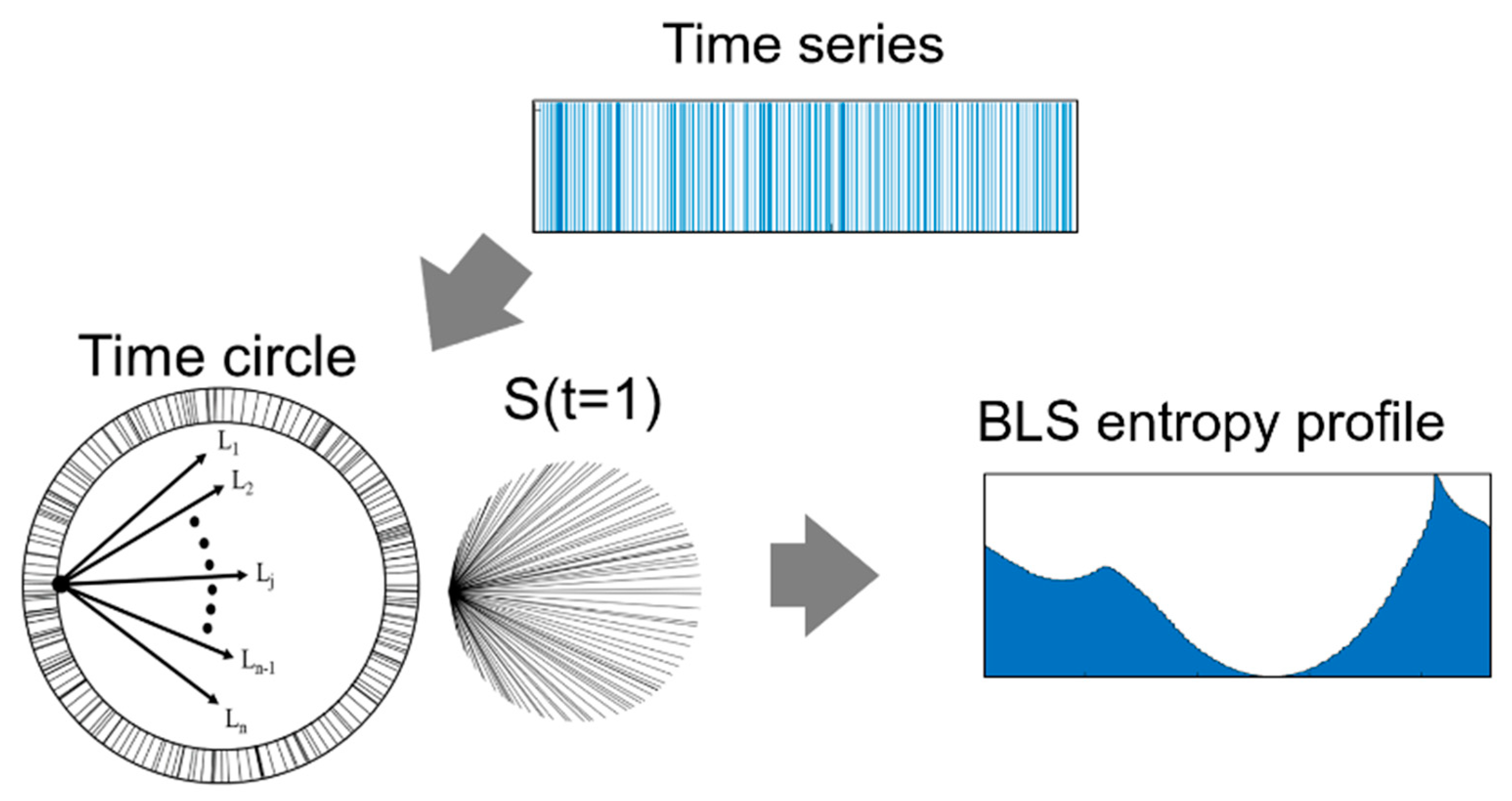
2.2. Time Circle for a Time Series
3. Results
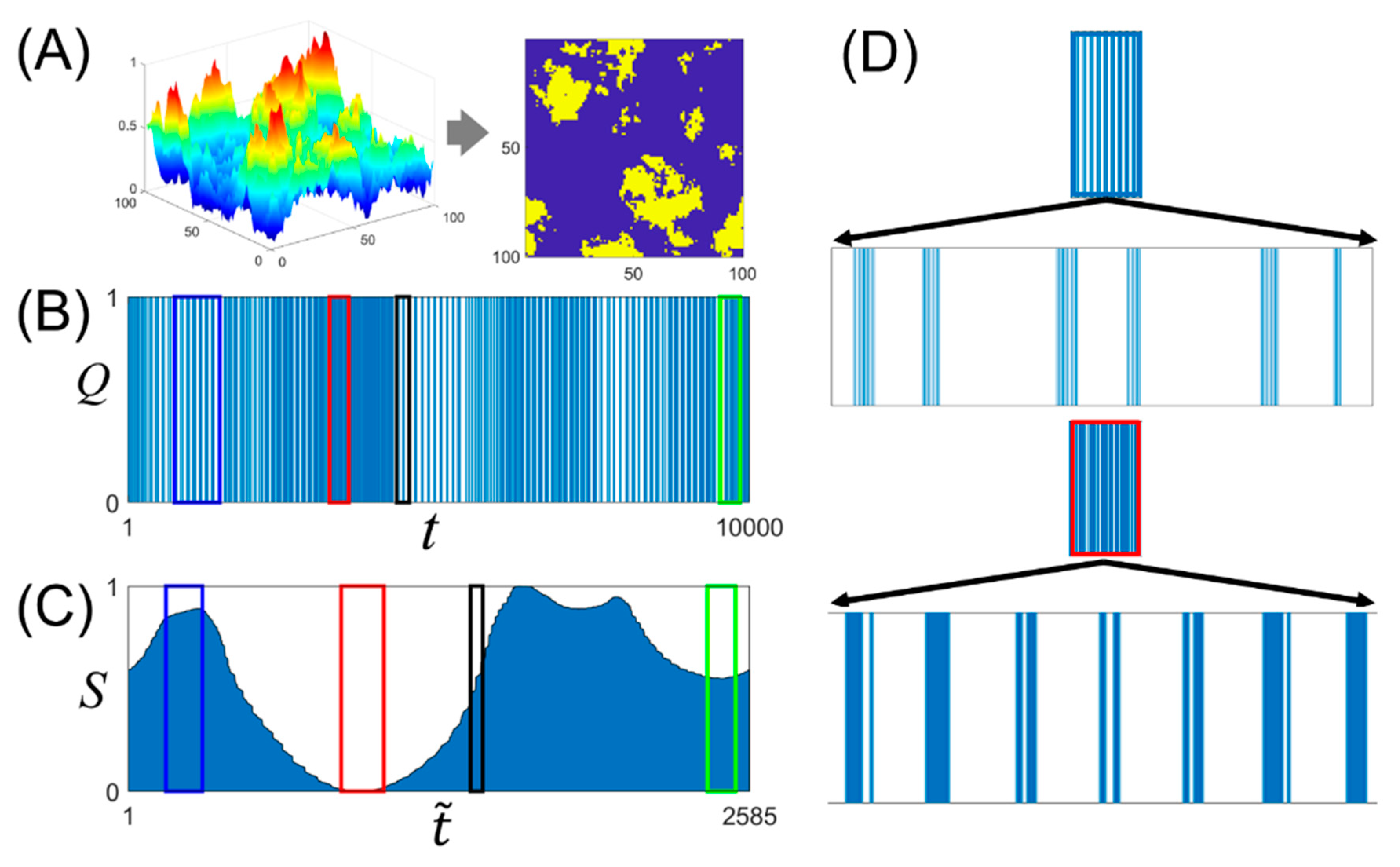
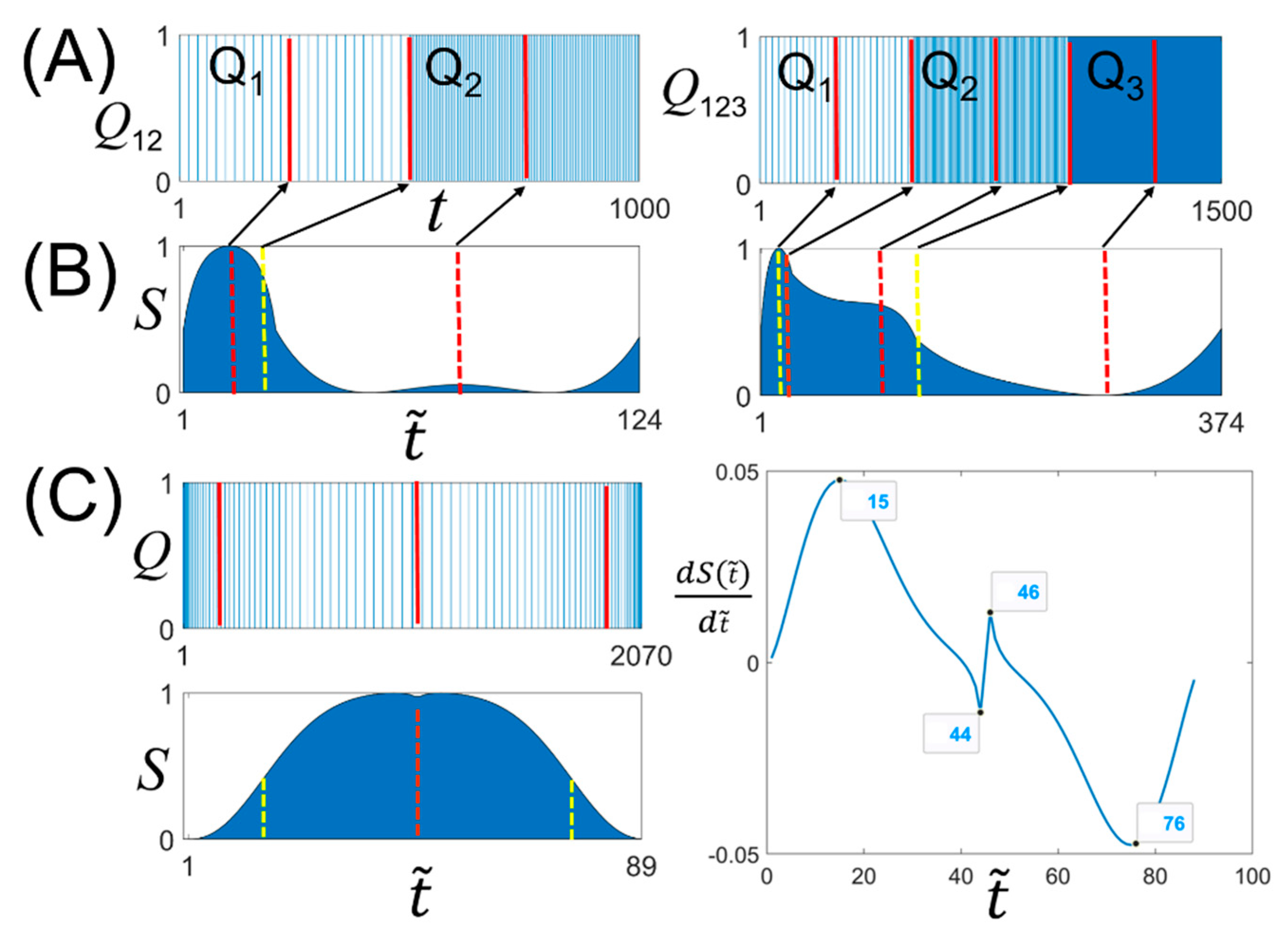
3.1. Characteristic Features of Binary Time-Series Appearing in the BLS Entropy Profile
3.2. Application: Characterization of Crawling Trajectories of Caenorhabditis Elegans
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Izakian, H.; Pedrycz, W.; Jamal, I. Fuzzy clustering of time series data using dynamic time warping distance. Eng. Appl. Artif. Intell. 2015, 39, 235–244. [Google Scholar] [CrossRef]
- Sadahiro, Y.; Kobayashi, T. Exploratory analysis of time series data: Detection of partial similarities, clustering, and visualization. Comput. Environ. Urban Syst. 2014, 45, 24–33. [Google Scholar] [CrossRef]
- Guo, C.; Jia, H.; Zhang, N. Time Series Clustering Based on ICA for Stock Data Analysis. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–17 October 2008; pp. 1–4. [Google Scholar]
- Tuncel, K.S.; Baydogan, M.G. Autoregressive forests for multivariate time series modeling. Pattern Recognit. 2018, 73, 202–215. [Google Scholar] [CrossRef]
- Harvill, J.L.; Ravishanker, N.; Ray, B.K. Bispectral-based methods for clustering time series. Comput. Stat. Data Anal. 2013, 64, 113–131. [Google Scholar] [CrossRef]
- Di Salvo, R.; Montalto, P.; Nunnari, G.; Neri, M.; Puglisi, G. Multivariate time series clustering on geophysical data recorded at Mt. Etna from 1996 to 2003. J. Volcanol. Geotherm. Res. 2013, 251, 65–74. [Google Scholar] [CrossRef]
- Aach, J.; Church, G.M. Aligning gene expression time series with time warping algorithms. Bioinformatics 2001, 17, 495–508. [Google Scholar] [CrossRef]
- Zhang, G.P. A neural network ensemble method with jittered training data for time series forecasting. Inf. Sci. 2007, 177, 5329–5346. [Google Scholar] [CrossRef]
- Keogh, E.J.; Kasetty, S. On the Need for Time Series Data Mining Benchmarks: A Survey and Empirical Demonstration. Data Min. Knowl. Discov. 2003, 7, 349–371. [Google Scholar] [CrossRef]
- Yi, B.K.; Faloutsos, C. Fast Time Sequence Indexing for Arbitrary Lp Norms; VLDB: San Francisco, CA, USA, 2000; pp. 385–394. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. 2009, 41, 1–72. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The great time series classification bake off: A review and experimental evaluation of recent algorithmic advances. Data Min. Knowl. Discov. 2017, 31, 606–660. [Google Scholar] [CrossRef]
- Preea, H.; Herwiga, B.; Grubera, T.; Sicka, B.; David, K.; Lukowiczc, P. On general purpose time series similarity measures and their use as kernel functions in support vector machines. Inf. Sci. 2014, 281, 478–495. [Google Scholar] [CrossRef]
- Megalooikonomou, V.; Wang, Q.; Li, G.; Faloutsos, C. A Multiresolution Symbolic Representation of Time Series. In Proceedings of the 21st International Conference on Data Engineering (ICDE’05), Tokyo, Japan, 5–8 April 2005; pp. 668–679. [Google Scholar]
- Persoon, E.; Fu, K.-S. Shape Discrimination Using Fourier Descriptors. IEEE Trans. Syst. Man Cybern. 1977, 7, 170–179. [Google Scholar] [CrossRef]
- Lines, J.; Bag, A. Time series classification with ensembles of elastic distance measures. Data Min. Knowl. Discov. 2015, 29, 565–592. [Google Scholar] [CrossRef]
- Richards, C.W.; Hemami, H. Identification of three-dimensional objects using fourier descriptors of the boundary curve. IEEE Trans. SMC 1974, 4, 371–378. [Google Scholar] [CrossRef]
- Struzik, Z.; Siebes, A. Measuring time series similarity through large singular features revealed with wavelet transformation. In Proceedings of the Tenth International Workshop on Database and Expert Systems Applications. DEXA 99, Florence, Italy, 1–3 September 1999; pp. 162–166. [Google Scholar]
- Kopenkov, V.N. Efficient algorithms of local discrete wavelet transform with Haar-like bases. Pattern Recognit. Image Anal. 2008, 18, 654–661. [Google Scholar] [CrossRef]
- Rocha, T.; Paredes, S.; Carvalho, P.; Henriques, J. An efficient strategy for evaluating similarity between time series based on Wavelet / Karhunen-Loève transforms. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; Volume 2012, pp. 6216–6219. [Google Scholar]
- Popivanov, I.; Miller, R. Similarity search over time-series data using wavelets. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2003; pp. 212–221. [Google Scholar]
- Bagnall, A.; Janacek, G. A Run Length Transformation for Discriminating Between Auto Regressive Time Series. J. Classif. 2014, 31, 154–178. [Google Scholar] [CrossRef][Green Version]
- Ghassempour, S.; Girosi, F.; Maeder, A. Clustering Multivariate Time Series Using Hidden Markov Models. Int. J. Environ. Res. Public Health 2014, 11, 2741–2763. [Google Scholar] [CrossRef] [PubMed]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2015. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Tran, Q.K.; Song, S.K. Water Level Forecasting based on Deep Learning: A Use Case of rinity River-Texas-The United States. J. KIISE 2017, 44, 607–612. [Google Scholar] [CrossRef]
- Yang., K.; Shahabi, C. A PCA-based Similarity Measure for Multivariate Time Series. In Proceedings of the MMDB04, Washington, DC, USA, 13 November 2004; pp. 65–74. [Google Scholar]
- Wei, L.; Hua, Z.; JianFeng, Q.; Chen, L.; Afang, J. Based on time series similarity matching algorithm for earthquake prediction research. In Proceedings of the 2010 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), Chengdu, China, 20–22 August 2010; Volume 4, p. V4-57. [Google Scholar]
- Lhermittea, S.; Verbesselt, J.; Verstraeten, W.W.; Coppine, P. A comparison of time series similarity measures for classifica3ion and change detection of ecosystem dynamics. Remote Sens. Environ. 2011, 115, 3129–3152. [Google Scholar] [CrossRef]
- Rafiei, D.; Mendelzon, A. Similarity-based queries for time series data. ACM SIGMOD Rec. 1997, 26, 13–25. [Google Scholar] [CrossRef]
- Kostadinova, E.; Boeva, V.; Boneva, L.; Tsiporkova, E. An Integrative DTW-based imputation method for gene expression time series data. In Proceedings of the 2012 6th IEEE International Conference Intelligent Systems, Sofia, Bulgaria, 6–8 September 2012; pp. 258–263. [Google Scholar]
- Kedem, B.; Fokianos, K. Regression Models for Time Series Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2002; Volume 488. [Google Scholar]
- Bellégo, C.; Ferrara, L. Forecasting Euro-Area Recessions Using Time-Varying Binary Response Models for Financial Markets. SSRN Electron. J. 2009. [Google Scholar] [CrossRef]
- Adães, J.; Pires, J.C.M. Analysis and Modelling of PM2.5 Temporal and Spatial Behaviors in European Cities. Sustainability 2019, 11, 6019. [Google Scholar] [CrossRef]
- Lee, S.-H.; Bardunias, P.; Su, N.-Y.; Sang-Hee, L. A Novel Approach to Shape Recognition Using Shape Outline. J. Korean Phys. Soc. 2010, 56, 1016–1019. [Google Scholar] [CrossRef]
- Lee, S.-H. Robustness of Branch Length Similarity Entropy Approach for Noise-added Shape Recognition. J. Korean Phys. Soc. 2010, 57, 501–505. [Google Scholar] [CrossRef]
- Lee, S.-H.; Park, C.-M.; Choi, U. A New Measure to Characterize the Degree of Self-Similarity of a Shape and Its Applicability. Entropy 2020, 22, 1061. [Google Scholar] [CrossRef]
- With, K. The Application of Neutral Landscape Models in Conservation Biology. Aplicacion de Modelos de Paisaje Neutros en la Biologia de la Conservacion. Conserv. Biol. 1997, 11, 1069–1080. [Google Scholar] [CrossRef]
- Fang-Yen, C.; Wyart, M.; Xie, J.; Kawai, R.; Kodger, T.; Chen, S.; Wen, Q.; Samuel, A.D.T. Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 2010, 107, 20323–20328. [Google Scholar] [CrossRef]
- Faumont, S.; Miller, A.C.; Lockery, S.R. Chemosensory behavior of semi-restrainedCaenorhabditis elegans. J. Neurobiol. 2005, 65, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Kaletta, T.; Hengartner, M.O. Finding function in novel targets: C. elegans as a model organism. Nat. Rev. Drug Discov. 2006, 5, 387–399. [Google Scholar] [CrossRef] [PubMed]
- Miśkiewicz, J. Analysis of Time Series Correlation. The Choice of Distance Metrics and Network Structure. Acta Phys. Pol. A 2012, 121, B-89. [Google Scholar] [CrossRef]
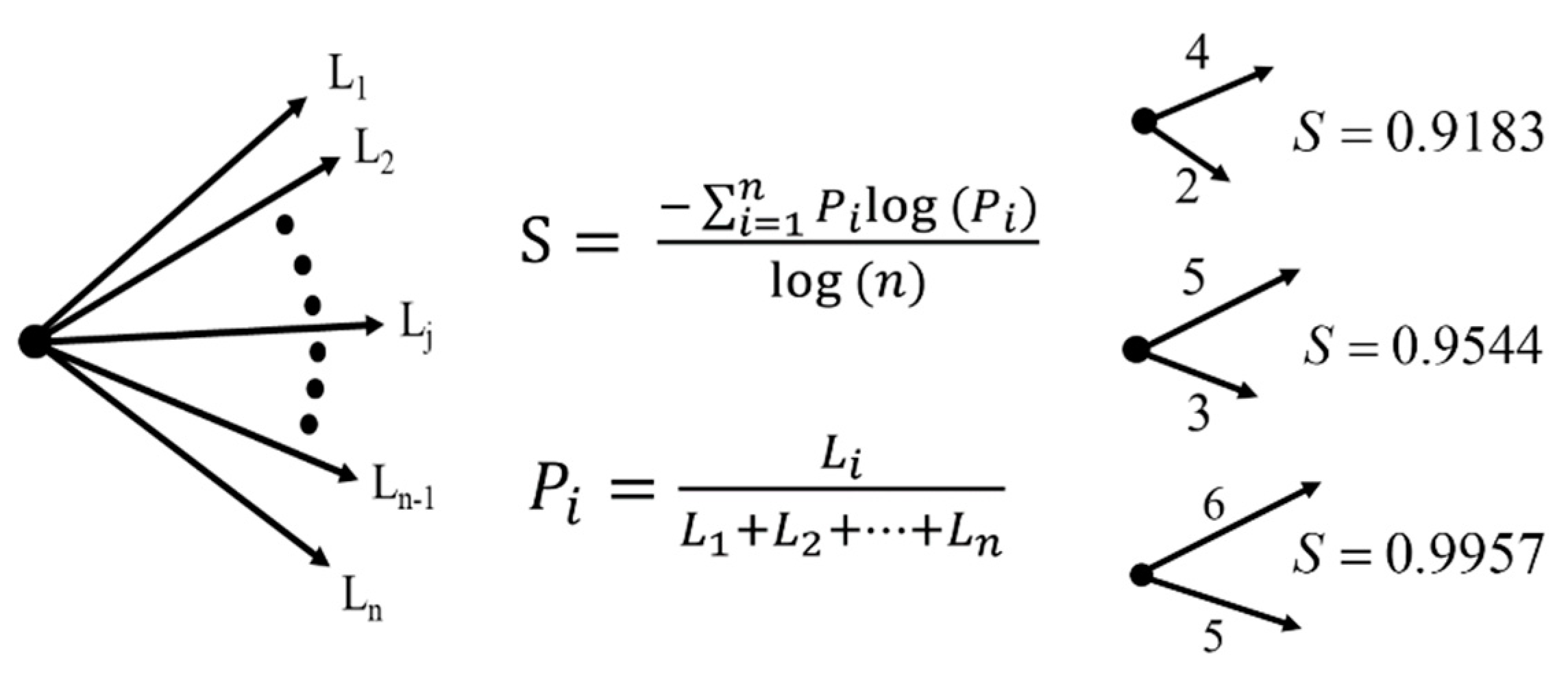

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-H.; Park, C.-M. Novel Features for Binary Time Series Based on Branch Length Similarity Entropy. Entropy 2021, 23, 480. https://doi.org/10.3390/e23040480
Lee S-H, Park C-M. Novel Features for Binary Time Series Based on Branch Length Similarity Entropy. Entropy. 2021; 23(4):480. https://doi.org/10.3390/e23040480
Chicago/Turabian StyleLee, Sang-Hee, and Cheol-Min Park. 2021. "Novel Features for Binary Time Series Based on Branch Length Similarity Entropy" Entropy 23, no. 4: 480. https://doi.org/10.3390/e23040480
APA StyleLee, S.-H., & Park, C.-M. (2021). Novel Features for Binary Time Series Based on Branch Length Similarity Entropy. Entropy, 23(4), 480. https://doi.org/10.3390/e23040480





