Estimation of Feeding Composition of Industrial Process Based on Data Reconciliation
Abstract
1. Introduction
2. Preliminaries
2.1. Data Reconciliation
2.2. M-Estimator
- •
- is is continuous;
- •
- ;
- •
- and is integrable
- •
- , for ;
- •
- .
- •
- IF is limited;
- •
- IF is continuous or piecewise continuous;
- •
- ;
- •
- IF is nearly linear near the origin (, for small ), but this characteristic is not necessary;
- •
- the rejection point of IF (the point where IF is zero) is finite to suppress large deviations.
3. Data Reconciliation Based on a Novel Robust Estimator
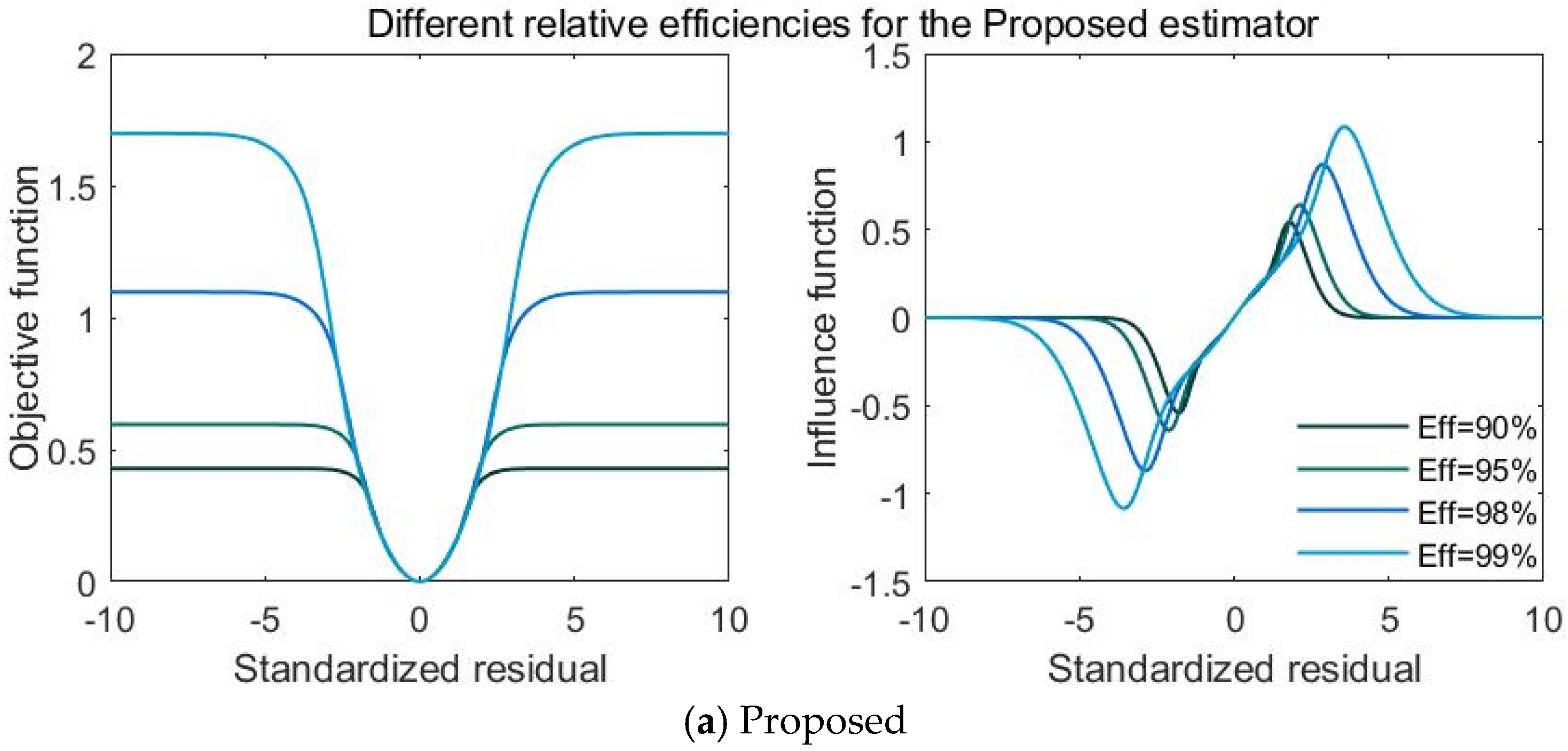
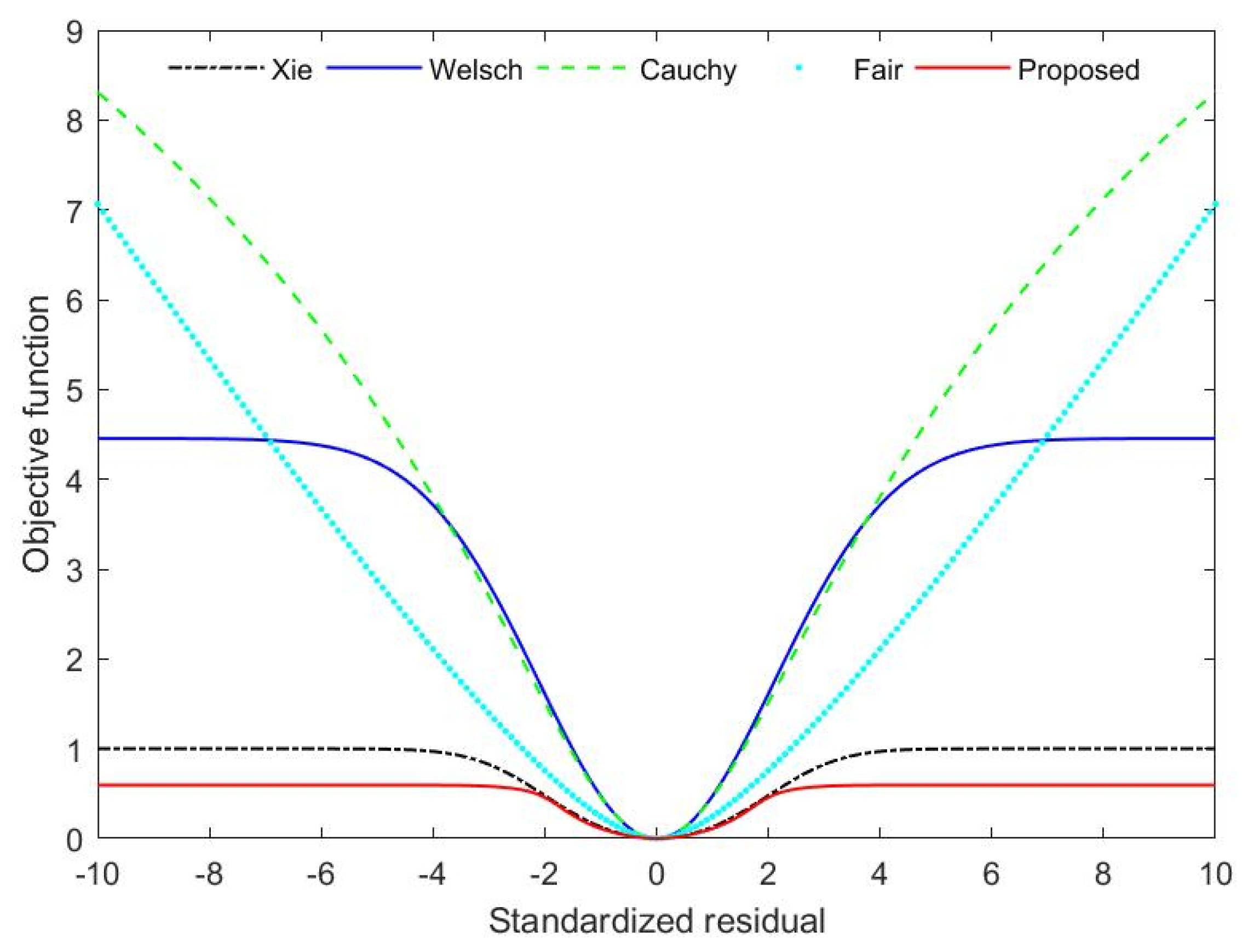
3.1. A Novel Robust Estimator
3.2. The Tuning Parameter of the Novel Robust Estimator
3.3. Linear Case
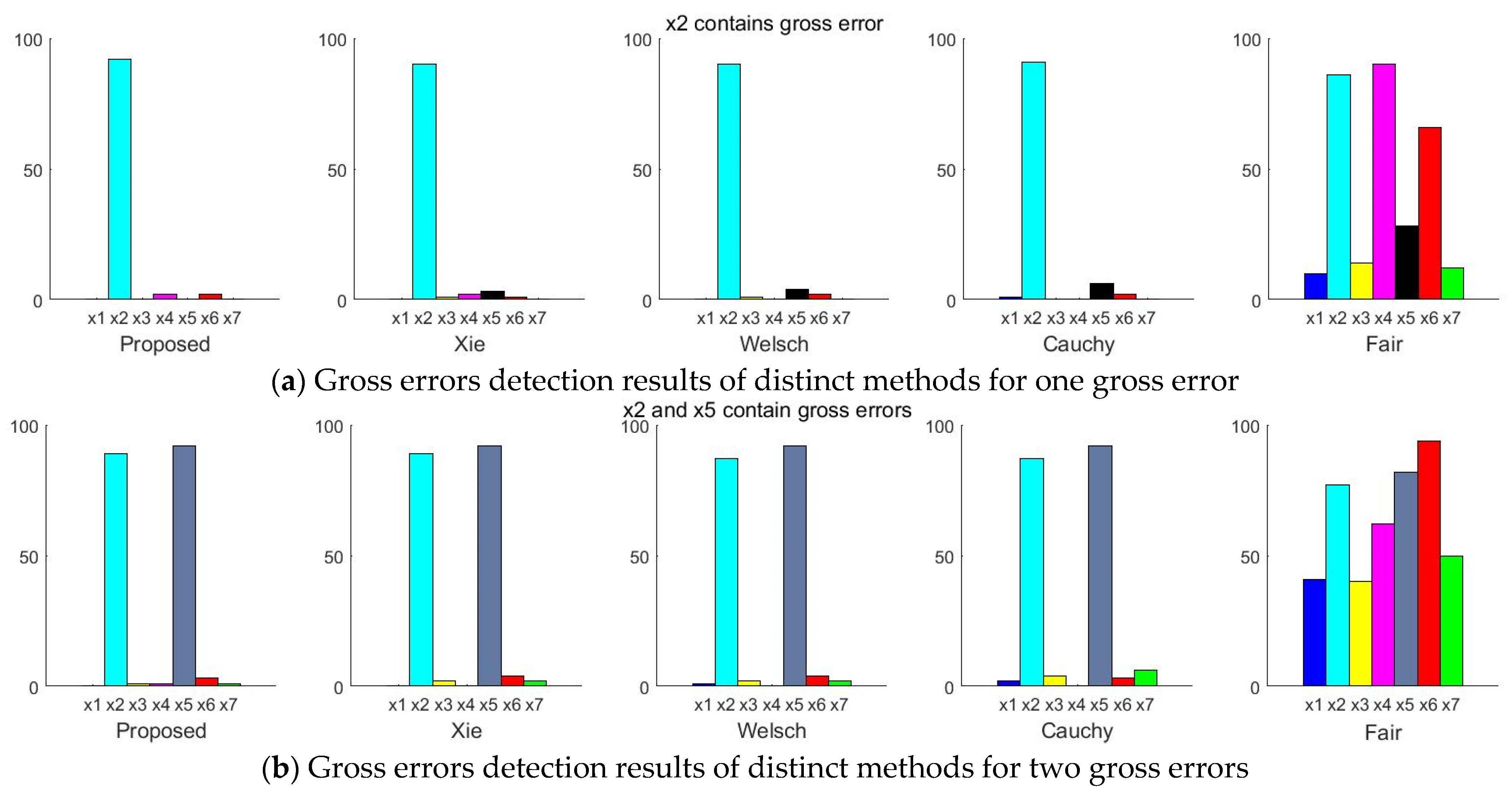
3.3.1. There Are Two Gross Errors in the Measurement Variables
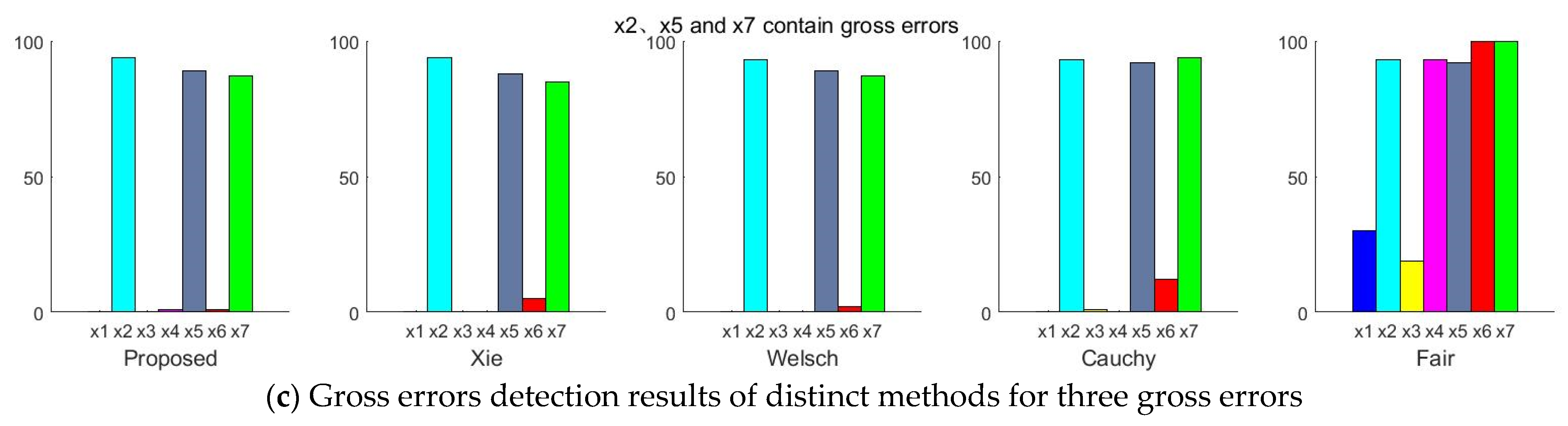
3.3.2. There Are Three Gross Errors in the Measurement Variables
3.4. Nonlinear Case
4. Feeding Composition Estimation Based on Iterative Data Reconciliation
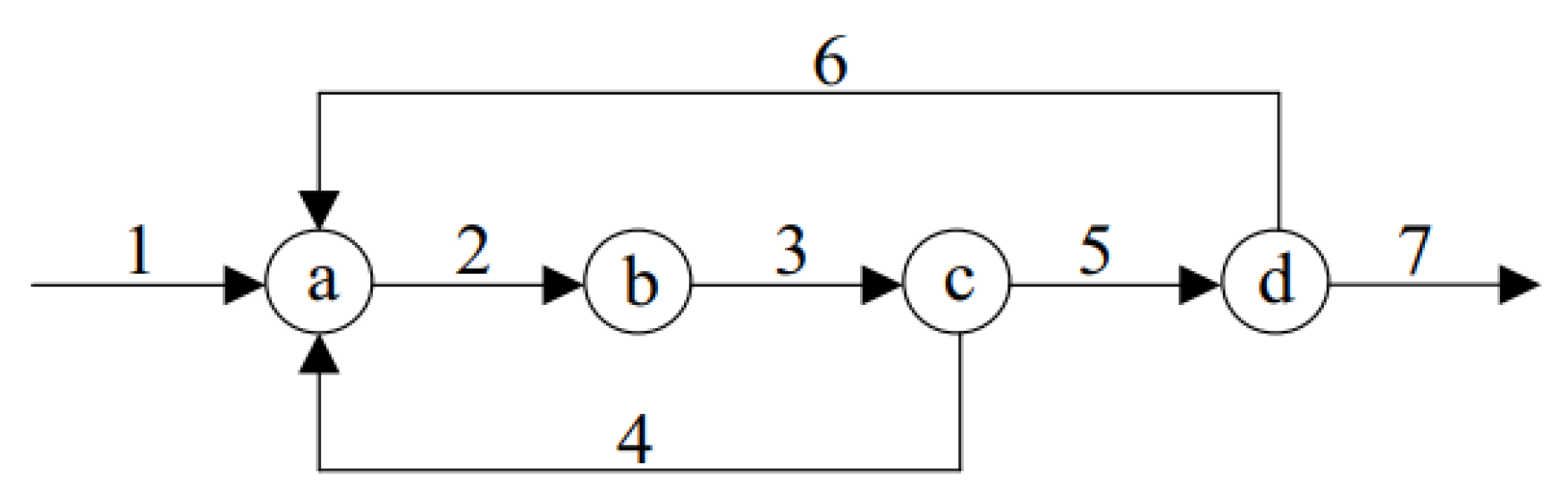
4.1. Industrial Process Description
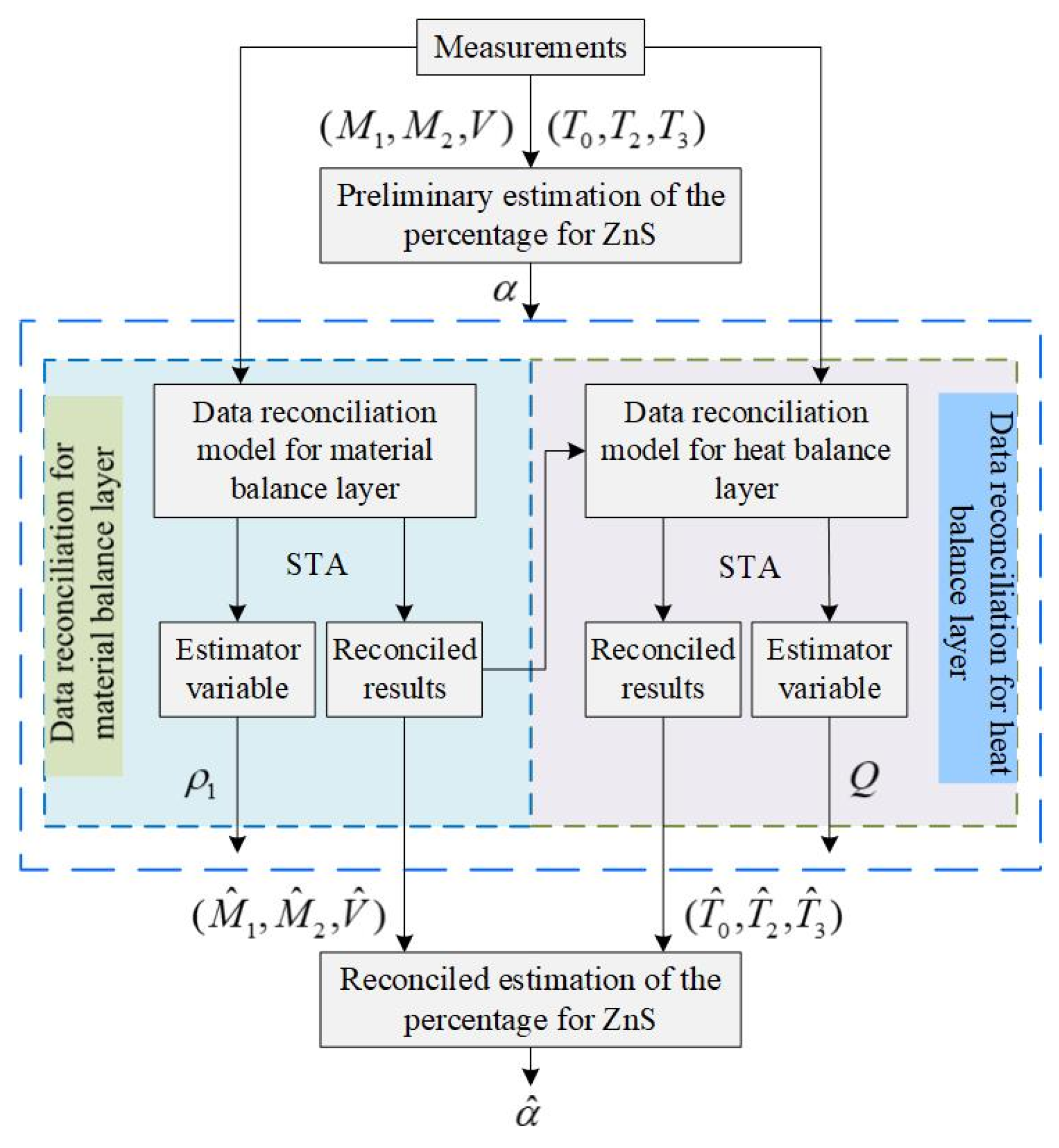
4.2. Iterative Robust Hierarchical Data Reconciliation and Composition Estimation Framework
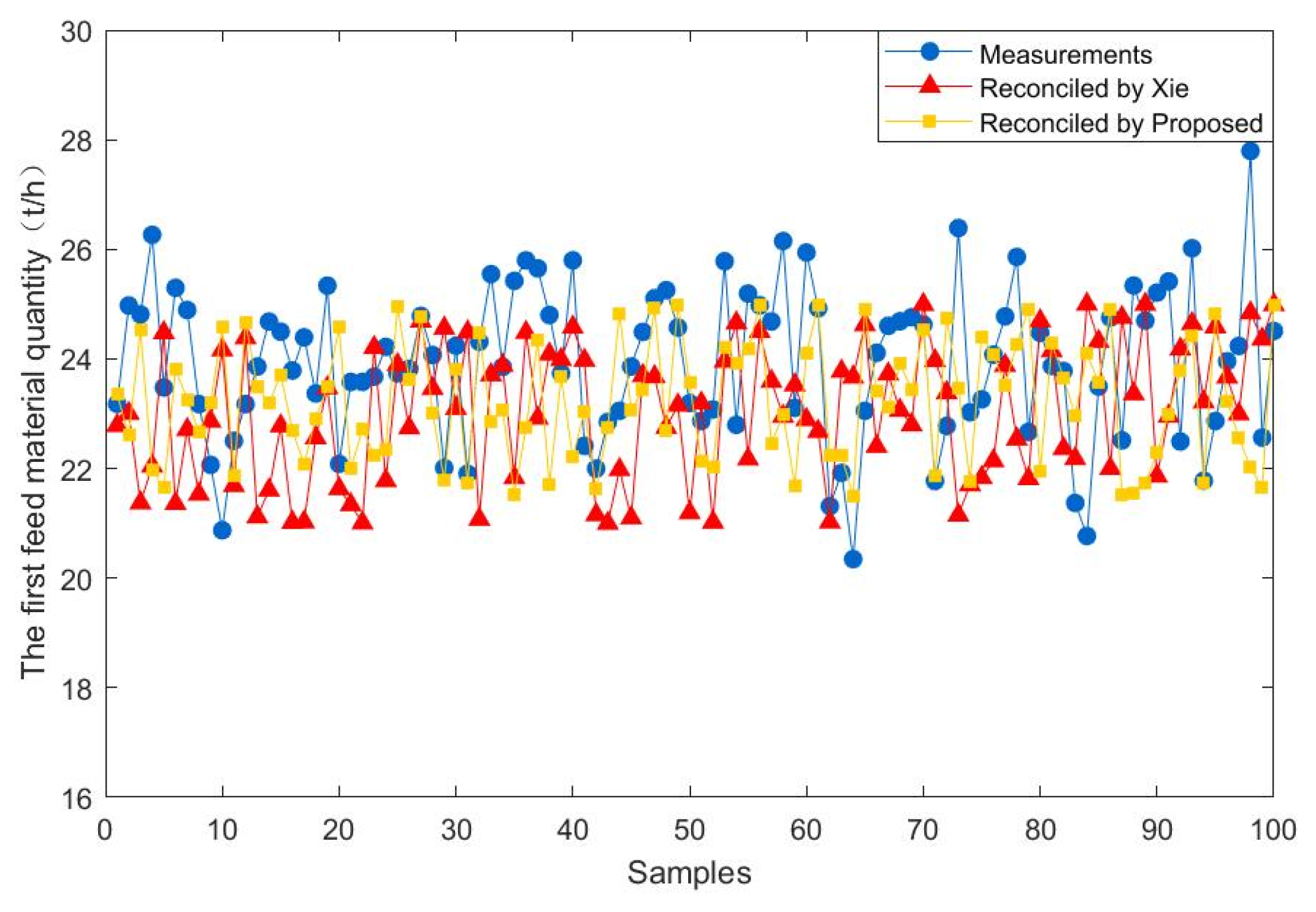
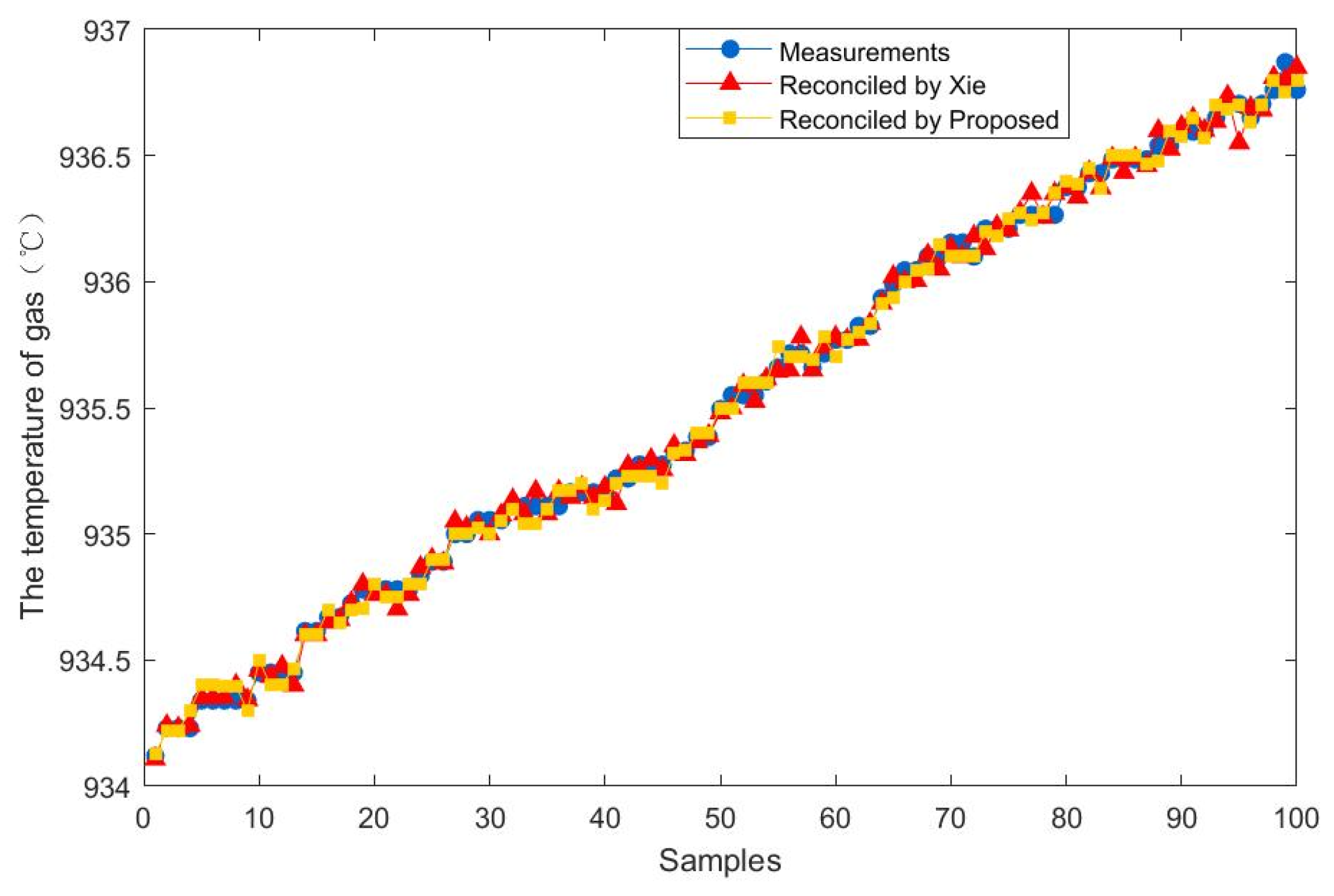
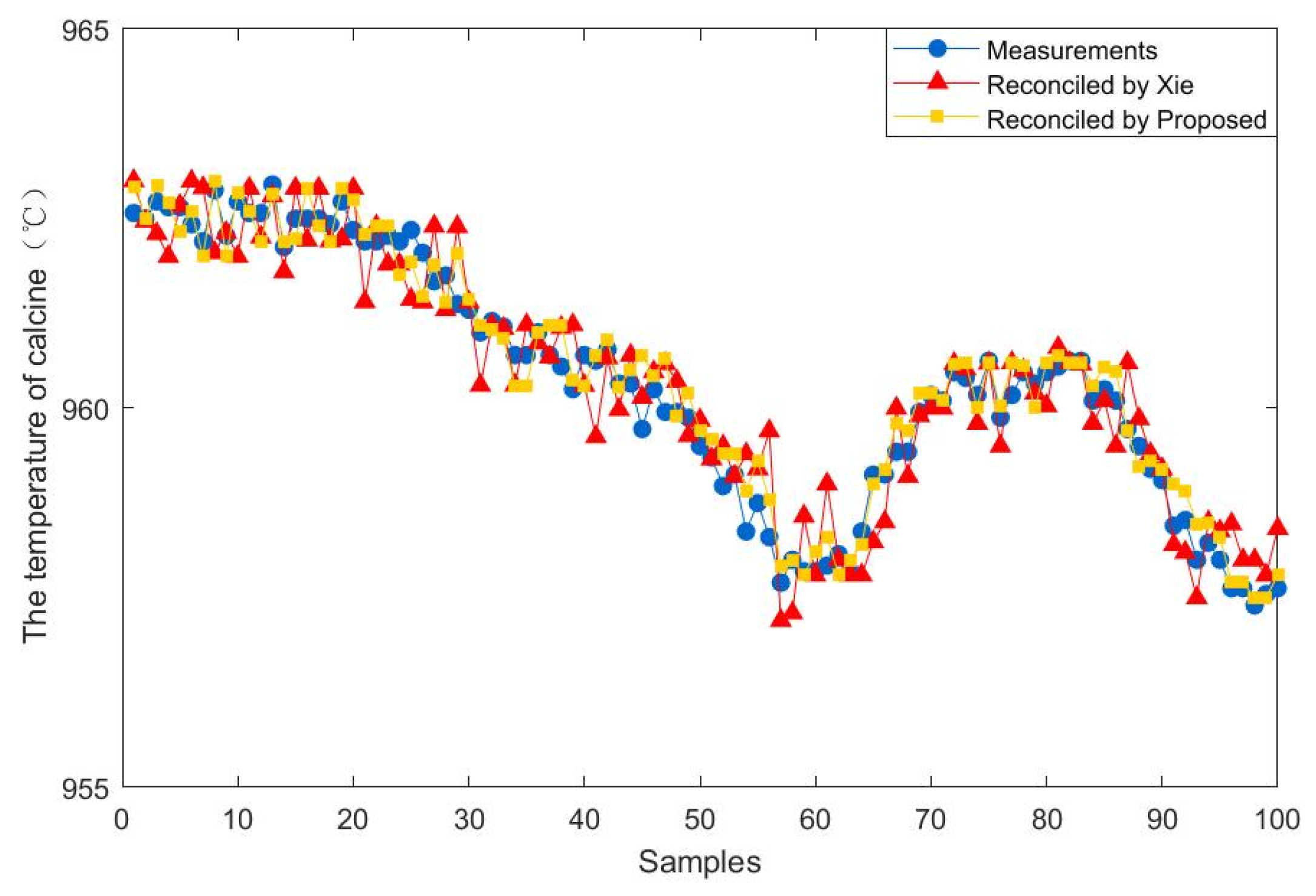
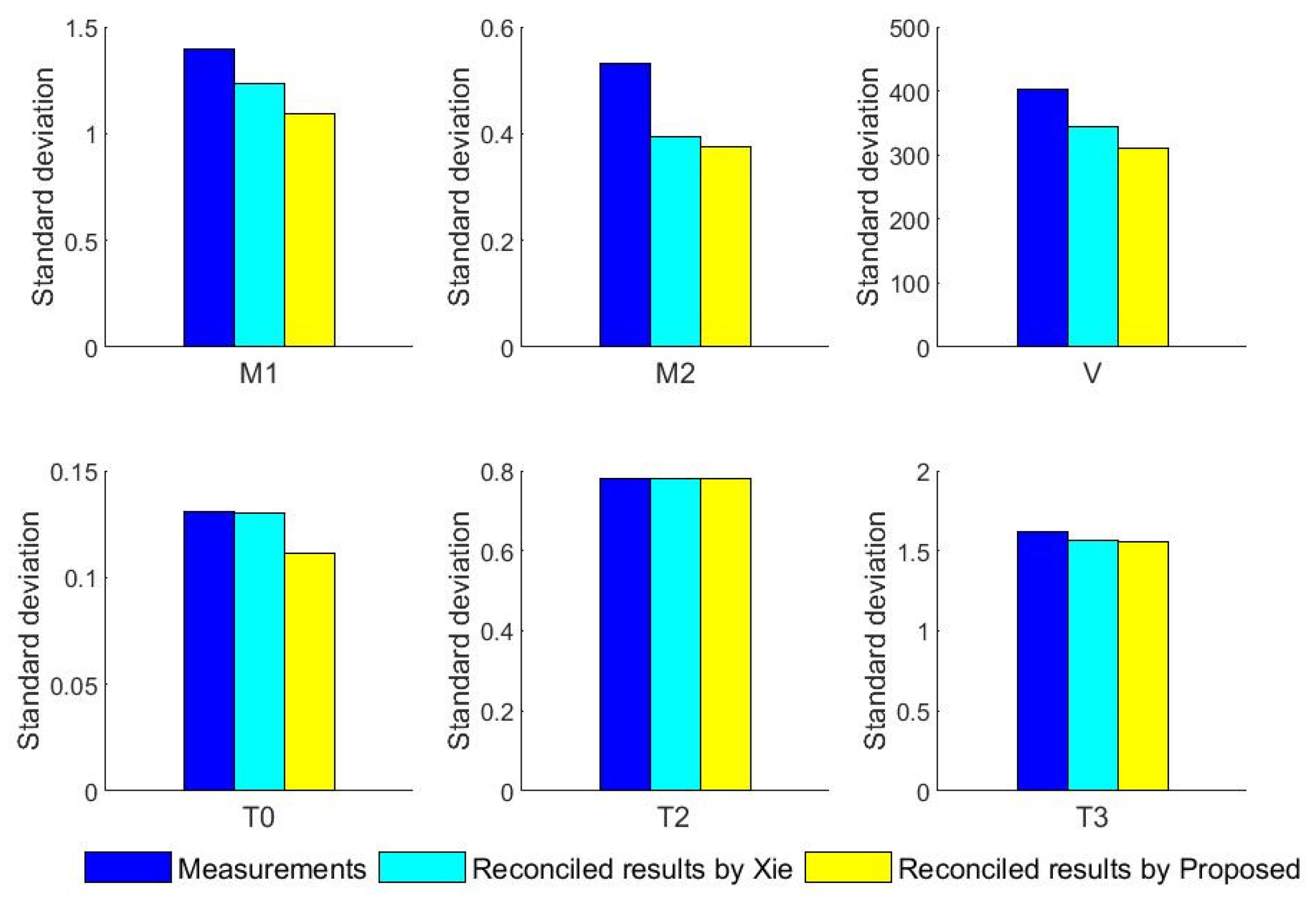
5. Results from Real Industrial Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuehn, D.R.; Davidson, H. Computer control II. Mathematics of control. Chem. Eng. Prog. 1961, 57, 44–47. [Google Scholar]
- Narasimhan, S.; Jordache, C. Data Reconciliation and Gross Error Detection: An Intelligent Use of Process Data; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Prata, D.M.; Lima, E.L.; Pinto, J.C. In-Line Monitoring of Bulk Polypropylene Reactors Based on Data Reconciliation Procedures. Macromol. Symp. 2008, 271, 26–37. [Google Scholar] [CrossRef]
- Prata, D.M.; Lima, E.L.; Pinto, J.C. Nonlinear Dynamic Data Reconciliation in Real Time in Actual Processes. Comput. Aided Chem. Eng. 2009, 27, 47–54. [Google Scholar]
- Abu-El-Zeet, Z.H.; Roberts, P.D.; Becerra, V.M. Enhancing model predictive control using dynamic data reconciliation. Alche J. 2002, 48, 324–333. [Google Scholar] [CrossRef]
- Sun, B.; Yang, C.; Wang, Y.; Gui, W.; Craig, I.; Olivier, L. A comprehensive hybrid first principles/machine learning modeling framework for complex industrial processes. J. Process Control 2020, 86, 30–43. [Google Scholar] [CrossRef]
- Faber, R.; Arellano-Garcia, H.; Li, P.; Wozny, G. An optimization framework for parameter estimation of large-scale systems. Chem. Eng. Process. 2007, 46, 1085–1095. [Google Scholar] [CrossRef]
- Schladt, M.; Hu, B. Soft Sensor Based on Nonlinear Steady-State Data Reconciliation in the Process Industry. Chem. Eng. Process. 2007, 46, 1107–1115. [Google Scholar] [CrossRef]
- Su, Q.; Bommireddy, Y.; Shah, Y.; Ganesh, S.; Moreno, M.; Liu, J.; Gonzalez, M.; Yasdanpanah, N.; O’Connor, T.; Reklaitis, G.V.; et al. Data reconciliation in the Quality-byDesign (QbD) implementation of pharmaceutical continuous tablet manufacturing. Int. J. Pharm. 2019, 563, 259–272. [Google Scholar] [CrossRef]
- Chiari, M.; Bussani, G.; Grotolli, M.G.; Pierucci, S. On-line Data Reconciliation and Optimisation: Refinery Applications. Comput. Chem. Eng. 1997, 21, s1185–s1190. [Google Scholar] [CrossRef]
- Lee, M.H.; Lee, S.J.; Han, C.; Chang, K.S.; Kim, S.H.; Sang, H.Y. Hierarchical on-line data reconciliation and optimization for an industrial utility plant. Comput. Chem. Eng. 1998, 22, s247–s254. [Google Scholar] [CrossRef]
- Almásy, G.A.; Sztanó, T. Checking and correction of measurements on the basis of linear system model. Probl. Control Inf. Theory 1975, 4, 57–69. [Google Scholar]
- Mah, R.S.H.; Tamhane, A.C. Detection of gross errors in process data. Aiche J. 2010, 28, 828–830. [Google Scholar] [CrossRef]
- Mah, R.S.; Stanley, G.M.; Downing, D.M. Reconciliation and rectification of process flow and inventory data. Ind. Eng. Chem. Process Des. Dev. 1976, 15, 175–183. [Google Scholar] [CrossRef]
- Narasimhan, S.; Mah, R.S.H. Generalized likelihood ratio method for gross error identification. Aiche J. 1987, 33, 1514–1521. [Google Scholar] [CrossRef]
- Tong, H.; Crowe, C.M. Detection of gross erros in data reconciliation by principal component analysis. Aiche J. 2010, 41, 1712–1722. [Google Scholar] [CrossRef]
- Yu, M.; Hong-Ye, S.U.; Jian, C.H.U. A support vector regression approach for recursive simultaneous data reconciliation and gross error detection in nonlinear dynamical systems. Acta Autom. Sin. 2009, 35, 707–716. [Google Scholar]
- Zhang, Z.; Chen, J. Simultaneous data reconciliation and gross error detection for dynamic systems using particle filter and measurement test. Comput. Chem. Eng. 2014, 69, 66–74. [Google Scholar] [CrossRef]
- Yuan, Y.; Khatibisepehr, S.; Huang, B.; Li, Z. Bayesian method for simultaneous gross error detection and data reconciliation. Aiche J. 2015, 61, 3232–3248. [Google Scholar] [CrossRef]
- Tjoa, I.B.; Biegler, L.T. Simultaneous strategies for data reconciliation and gross error detection of nonlinear systems. Comput. Chem. Eng. 1991, 15, 679–690. [Google Scholar] [CrossRef]
- Johnson, L.P.M.; Kramer, M.A. Maximum likelihood data rectification: Steady-state systems. Alche J. 1995, 41, 2415–2426. [Google Scholar] [CrossRef]
- Arora, N.; Biegler, L.T. Redescending estimators for data reconciliation and parameter estimation. Comput. Chem. Eng. 2001, 25, 1585–1599. [Google Scholar] [CrossRef]
- Wang, D.; Romagnoli, J.A. A Framework for Robust Data Reconciliation Based on a Generalized Objective Function. Ind. Eng. Chem. Res. 2003, 42, 3075–3084. [Google Scholar] [CrossRef]
- Özyurt, D.B.; Pike, R.W. Theory and practice of simultaneous data reconciliation and gross error detection for chemical processes. Comput. Chem. Eng. 2004, 28, 381–402. [Google Scholar] [CrossRef]
- Ragot, J.; Chadli, M.; Maquin, D. Mass balance equilibration: A robust approach using contaminated distribution. Aiche J. 2005, 51, 1569–1575. [Google Scholar] [CrossRef]
- Prata, D.M.; Schwaab, M.; Lima, E.L.; Pinto, J.C. Simultaneous robust data reconciliation and gross error detection through particle swarm optimization for an industrial polypropylene reactor. Chem. Eng. Sci. 2010, 65, 4943–4954. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; Chen, X.; Wang, K.; Qian, J. Quasi-weighted least squares estimator for data reconciliation. Comput. Chem. Eng. 2010, 34, 154–162. [Google Scholar] [CrossRef]
- Llanos, C.E.; Sanchéz, M.C.; Maronna, R.A. Robust estimators for data reconciliation. Ind. Eng. Chem. Res. 2015, 54, 5096–5105. [Google Scholar] [CrossRef]
- Alighardashi, H.; Magbool Jan, N.; Huang, B. Expectation Maximization Approach for Simultaneous Gross Error Detection and Data Reconciliation Using Gaussian Mixture Distribution. Ind. Eng. Chem. Res. 2017, 56, 14530–14544. [Google Scholar] [CrossRef]
- Xie, S.; Yang, C.; Yuan, X.; Wang, X.; Xie, Y. A novel robust data reconciliation method for industrial processes. Control Eng. Pract. 2019, 83, 203–212. [Google Scholar] [CrossRef]
- de Menezes, D.Q.F.; Prata, D.M.; Secchi, A.R.; Pinto, J.C. A review on robust M-estimators for regression analysis. Comput. Chem. Eng. 2021, 147, 107254. [Google Scholar] [CrossRef]
- Rey, W.J.J. Introduction to Robust and Quasi-Robust Statistical Methods; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Fair, R.C. On the robust estimation of econometric models. Ann. Econ. Soc. Meas. 1974, 3, 667. [Google Scholar]
- Jin, S.Y.; Li, X.W.; Huang, Z.J.; Meng, L. A new target function for robust data reconciliation. Ind. Eng. Chem. Res. 2012, 51, 10220–10224. [Google Scholar] [CrossRef]
- Hoaglin, D.C.; Mosteller, F.; Tukey, J.W. Understanding Robust and Exploratory Data Analysis; Wiley: New York, NY, USA, 1983; Volume 3. [Google Scholar]
- Albuquerque, J.S.; Biegler, L.T. Data reconciliation and gross-error detection for dynamic systems. Aiche J. 1996, 42, 2841–2856. [Google Scholar] [CrossRef]
- Shevlyakov, G.; Morgenthaler, S.; Shurygin, A. Redescending m-estimators. J. Stat. Plann. Inference 2008, 138, 2906–2917. [Google Scholar] [CrossRef][Green Version]
- Zhou, X.J.; Yang, C.H.; Gui, W.H. State transition algorithm. J. Ind. Manag. Optim. 2012, 8, 1039–1056. [Google Scholar] [CrossRef]







| M-Estimator | Tuning Parameter | |
|---|---|---|
| 1 | Welsch | |
| 2 | Xie | |
| 3 | Proposed |
| Stream | True | Original Meas. | Meas. with Gross Error | Proposed | Xie | Welsch | Cauchy | Fair |
|---|---|---|---|---|---|---|---|---|
| 5 | 4.995 | 4.995 | 5.0111 | 5.0152 | 5.0346 | 5.0519 | 5.1777 | |
| 15 | 14.91 | 16.91 | 15.0420 | 15.0540 | 15.1202 | 15.1970 | 15.6413 | |
| 15 | 15.01 | 15.01 | 15.0420 | 15.0540 | 15.1202 | 15.1970 | 15.6413 | |
| 5 | 5.002 | 5.002 | 4.9987 | 4.9985 | 5.0053 | 5.0230 | 5.1795 | |
| 10 | 9.98 | 10.98 | 10.0433 | 10.0555 | 10.1149 | 10.1740 | 10.4618 | |
| 5 | 5.019 | 5.019 | 5.0322 | 5.0403 | 5.0803 | 5.1221 | 5.2841 | |
| 5 | 5.014 | 5.014 | 5.0111 | 5.0152 | 5.0346 | 5.0519 | 5.1777 | |
| SSE | -- | -- | -- | 0.0067 | 0.0110 | 0.0510 | 0.1287 | 1.2117 |
| TER | -- | -- | -- | 0.9424 | 0.9263 | 0.8457 | 0.7606 | 0.2953 |
| RER | -- | -- | -- | 0.9101 | 0.8838 | 0.7501 | 0.6008 | −0.2626 |
| Stream | True | Original Meas. | Meas. with Gross Error | Proposed | Xie | Welsch | Cauchy | Fair |
|---|---|---|---|---|---|---|---|---|
| 5 | 4.995 | 4.995 | 5.0080 | 5.0164 | 5.0574 | 5.0323 | 4.3533 | |
| 15 | 14.91 | 16.91 | 15.0390 | 15.0552 | 15.1425 | 15.1802 | 15.1833 | |
| 15 | 15.01 | 15.01 | 15.0390 | 15.0552 | 15.1425 | 15.1802 | 15.1833 | |
| 5 | 5.002 | 5.002 | 4.9991 | 4.9984 | 5.0037 | 5.0244 | 5.3066 | |
| 10 | 9.98 | 10.98 | 10.0399 | 10.0568 | 10.1388 | 10.1558 | 9.8767 | |
| 5 | 5.019 | 5.019 | 5.0320 | 5.0404 | 5.0814 | 5.1235 | 5.5233 | |
| 5 | 5.014 | 3.514 | 5.0080 | 5.0164 | 5.0574 | 5.0323 | 4.3533 | |
| SSE | -- | -- | -- | 0.0058 | 0.0115 | 0.0731 | 0.1071 | 1.2866 |
| TER | -- | -- | -- | 0.9743 | 0.9642 | 0.9111 | 0.8954 | 0.3474 |
| RER | -- | -- | -- | 0.9641 | 0.9470 | 0.8621 | 0.8446 | 0.1268 |
| Stream | Standard Deviation | True | Meas. | Proposed | Xie | Welsch | Cauchy | Fair |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 4.5124 | 4.5360 | 4.5378 | 4.5280 | 4.5379 | 4.5796 | 4.4727 | |
| 0.6 | 5.5819 | 5.9070 | 5.5754 | 5.5655 | 5.5331 | 5.5360 | 5.6514 | |
| 0.2 | 1.9260 | 1.8074 | 1.9221 | 1.9223 | 1.9200 | 1.9153 | 1.9321 | |
| 0.2 | 1.4560 | 1.4653 | 1.4653 | 1.4842 | 1.4924 | 1.5096 | 1.4655 | |
| 0.5 | 4.8545 | 4.5491 | 4.8156 | 4.8010 | 4.8083 | 4.7882 | 4.7870 | |
| -- | 11.070 | -- | 11.0988 | 11.1178 | 11.1939 | 11.2079 | 10.9076 | |
| -- | 0.6147 | -- | 0.6143 | 0.6160 | 0.6187 | 0.6168 | 0.6104 | |
| -- | 2.0504 | -- | 2.0469 | 2.0349 | 2.0317 | 2.0345 | 2.0372 | |
| SSE | -- | -- | -- | 0.0031 | 0.0067 | 0.0222 | 0.0333 | 0.0377 |
| TER | -- | -- | -- | 0.8950 | 0.8192 | 0.7751 | 0.6631 | 0.7994 |
| RER | -- | -- | -- | 0.8805 | 0.8008 | 0.7324 | 0.5930 | 0.7693 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, Y.; Jiang, M.; Feng, Z.; Sun, B. Estimation of Feeding Composition of Industrial Process Based on Data Reconciliation. Entropy 2021, 23, 473. https://doi.org/10.3390/e23040473
Luan Y, Jiang M, Feng Z, Sun B. Estimation of Feeding Composition of Industrial Process Based on Data Reconciliation. Entropy. 2021; 23(4):473. https://doi.org/10.3390/e23040473
Chicago/Turabian StyleLuan, Yusi, Mengxuan Jiang, Zhenxiang Feng, and Bei Sun. 2021. "Estimation of Feeding Composition of Industrial Process Based on Data Reconciliation" Entropy 23, no. 4: 473. https://doi.org/10.3390/e23040473
APA StyleLuan, Y., Jiang, M., Feng, Z., & Sun, B. (2021). Estimation of Feeding Composition of Industrial Process Based on Data Reconciliation. Entropy, 23(4), 473. https://doi.org/10.3390/e23040473





