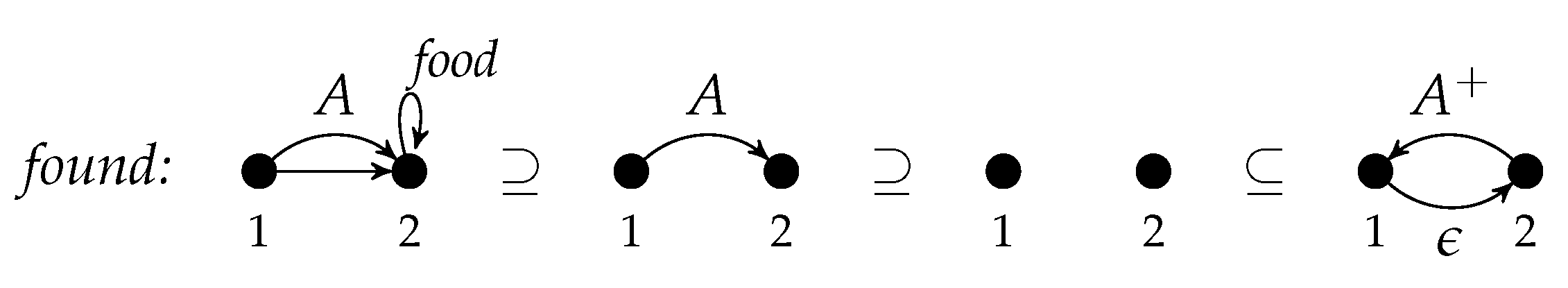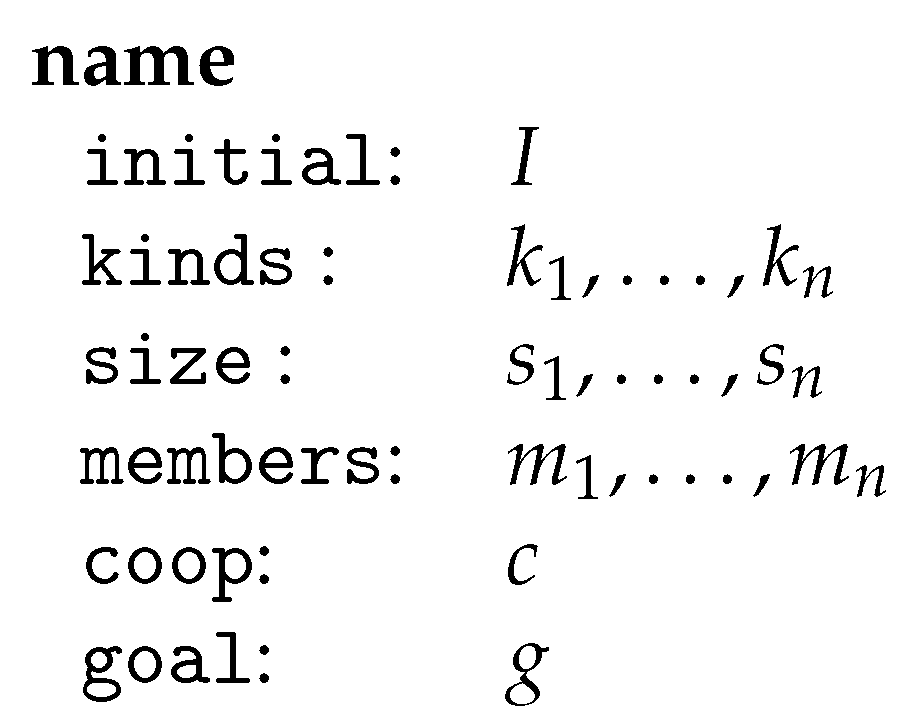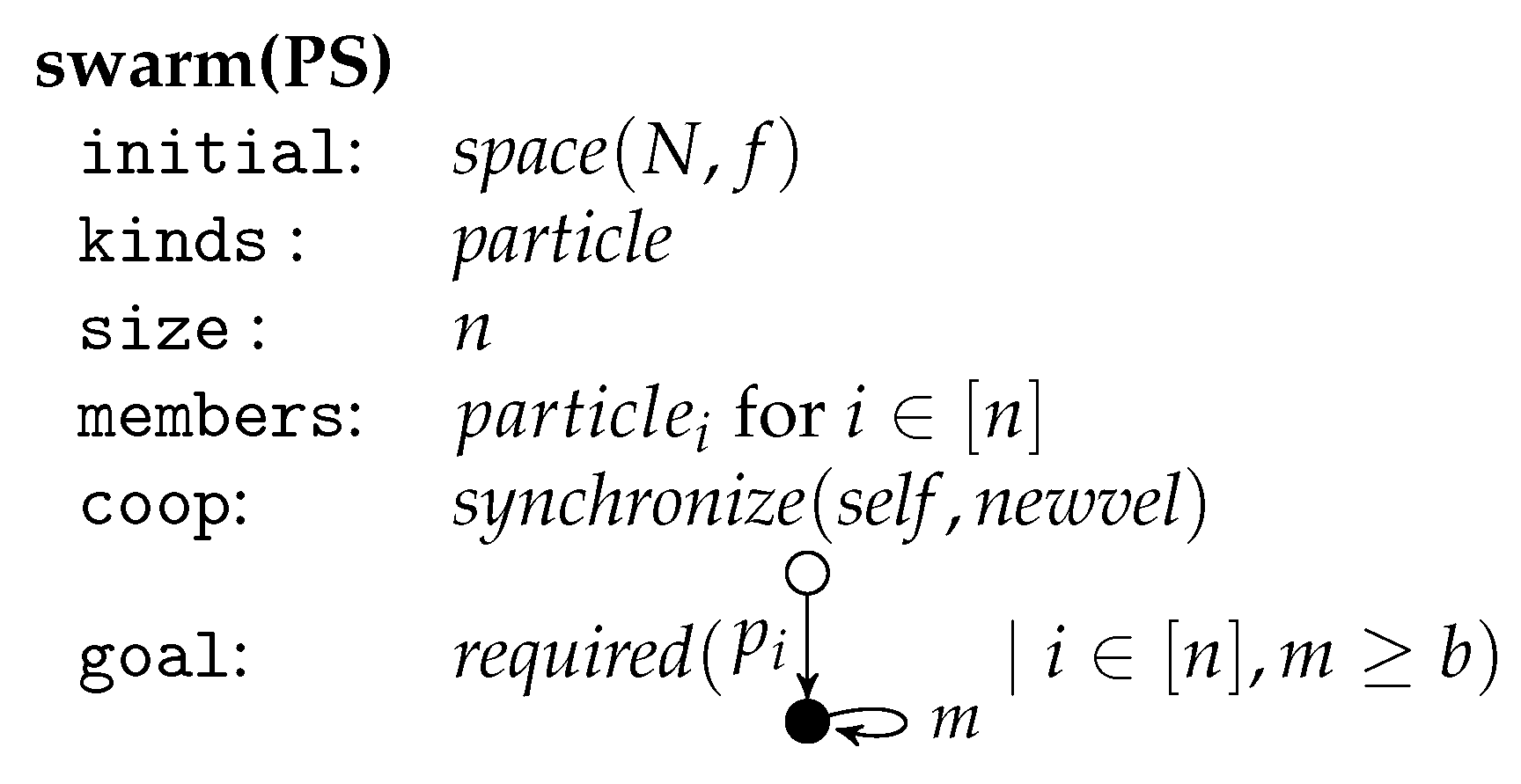1. Introduction
The idea of swarm computation is to design systems that mimic the problem-solving behavior of swarms in nature like ant colonies, bee hives, bird flocks, fish schools, etc. One encounters quite a variety of swarm concepts and swarm algorithms in the literature (see, e.g., [
1,
2,
3,
4,
5,
6,
7,
8,
9]). Moreover, there are several general computational approaches like cellular automata, particle swarms and ant colony optimization that are subsumed under the heading of swarm intelligence. In this paper, we propose graph-transformational swarms as a unifying framework using the methods of graph transformation. The notion of graph-transformational swarms is flexible enough to cover a variety of swarm concepts and provides a mathematical basis for the analysis of swarms with respect to correctness and efficiency. The hope is that different models of swarm computation can be better compared with each other within a common framework and that results for one model can be carried over to other models more easily. Moreover, the graph-transformational approach allows to employ graph-transformation tools for simulation, model checking and SAT solving in a standardized way.
A graph-transformational swarm consists of an arbitrary number of members of a finite number of different kinds. The members act simultaneously in a common environment which is represented as a graph. Moreover, there may be a cooperation condition to regulate the interaction and cooperation of the members as well as a goal to be reached. Kinds and members are modeled as graph transformation units (see, e.g., [
10]) which are computational devices based on rules. The key is that the framework of graph transformation provides the concept of parallel rule application to formalize the simultaneous actions of swarm members. First ideas of graph-transformational swarms are presented by [
11] and [
12] where typical applications of ant colony optimization algorithms are modeled, but a general definition of graph transformational swarms is missing. A short draft version of this paper appeared as [
13]. A good part of the paper is also integrated into the first author’s PhD thesis [
14].
The paper is organized in the following way. In
Section 2, the basic notions of graph transformation are recalled.
Section 3 introduces graph-transformational swarms. In
Section 4, an illustrating example is given: a simple ant colony the ants of which forage for food in a pheromone-driven manner. To demonstrate the power of our approach, we embed cellular automata in
Section 5 and particle swarms in
Section 6.
2. Graph Transformation
In this section, we recall the basic elements of graph transformation as far as needed in this paper (for more details, see, e.g., [
15,
16,
17]). We consider directed edge-labeled graphs and their derivation by applications of rules. The graph transformation approach is chosen in such a way that rules can be applied in parallel and that their parallel applicability follows from the applicability of each of the involved rules and an additional independence condition. Moreover, we use the notion of graph transformation units which comprise a set of rules and a control condition. Such a unit is a computational device that models the derivation of graphs while the control condition is obeyed. Units are used as members of swarms, and the parallelism makes sure that the members can act simultaneously (cf.
Section 3).
2.1. Directed Edge-Labeled Graphs
Let be a set of labels with . A (directed edge-labeled) graph over is a system where V is a set of nodes, E is a set of edges, and are mappings assigning a source , a target and a label to every edge .
An edge e with is a loop. If is labeled with z, e is also called a z-edge or a z-loop resp. An edge with label * represents an unlabeled edge. In drawings of graphs, the label * is omitted. The components V, E, s, t, and l of G are also denoted by , , , , and , respectively. The empty graph is denoted by ∅. The class of all directed edge-labeled graphs over is denoted by .
The disjoint union of two graphs G and H is defined as where ⊎ denotes the disjoint union of sets and for if and otherwise.
For graphs , a graph morphism is a pair of mappings and which are structure-preserving, i.e., , , and for all . If the mappings and are inclusions, then G is called a subgraph of denoted by The match of G with respect to the morphism g is the subgraph .
2.2. Graph Transformation Rules
A
rule consists of three graphs
such that
. A
rule with positive context consists of four graphs
C,
L,
K, and
R such that
is a rule and
. If
C equals
L, it is omitted in
r. The components
C,
L,
K, and
R are called
positive context,
left-hand side,
gluing graph, and
right-hand side, respectively. Sample rules are always presented with the inclusion symbols so that left-hand side, gluing graph, right-hand side, and a possible positive context are clear from their positions. In order to avoid too much technical detail, we assume that the node sets of
L and
K are equal. This means that rule applications do not delete nodes.
Figure 1 shows the rule
found a variant of which is used in
Section 4 for modeling a simple ant colony.
The gluing graph consists of two nodes, say u and v, as well as an unlabeled edge from u to v and a food-loop at v. The left-hand side consists of the gluing graph and an A-edge from u to v. The right-hand side consists of the gluing graph and an -edge from v to u as well as an -edge from u to v.
Intuitively, the application of a rule replaces an occurrence of L in some graph by R such that the occurrence of K is kept. Hence, the application of the rule found reverses an A-edge into an -edge provided that it is attached to a node with a food-loop. Additionally, it inserts an -edge.
A rule with positive context
is applied in the same way as
provided that the occurence of
L is located within an occurrence of
C. If the left-hand-side of the rule
found is regarded as positive context, we can remove the
food-loop as well as the unlabeled edge from the remaining three rule components, because they are not changed. The result is displayed in
Figure 2 where the two nodes of the gluing graph are numbered to fix their inclusion into the other graphs. It is worth noting that the rule in
Figure 1 and the rule in
Figure 2 are semantically equivalent.
Formally, the application of with to a graph consists of the following three steps.
- (1)
Choose a match of L in G subject to the identification condition, which requires that those items that are identified via g belong to the gluing graph K, i.e., for implies or . (Without the identification condition, the Parallelization Theorem below would not hold.)
- (2)
Remove the edges of and call the resulting graph Z.
- (3)
Add the right-hand side R to Z by gluing Z with R in yielding the graph H with and . The edges of Z keep their labels, sources, and targets so that The edges of R keep their labels; they also keep their sources and targets provided that those belong to Otherwise, they are redirected to the image of their original source or target, i.e., for with and for with
A rule with positive context
is applied to
G in the same way provided that the morphism
can be extended to
C.
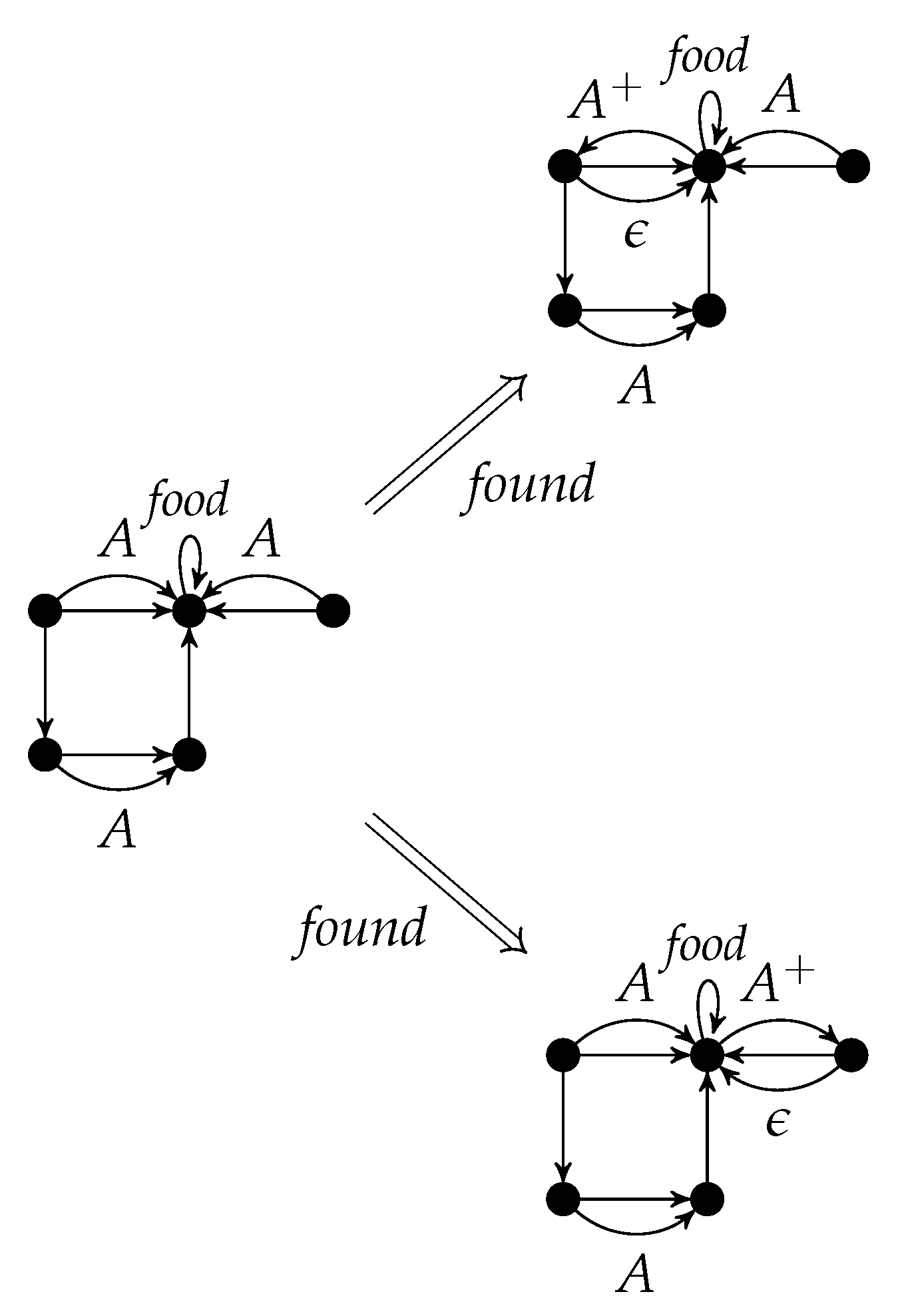
Figure 3 shows two applications of
found.
An application of
r to
G w.r.t. the graph morphism
g is denoted by
. It is called a
direct derivation from
G to
H. The subscript
r may be omitted if it is clear from the context. The sequential composition of direct derivations
(
) is called a
derivation from
G to
H. As usual, the derivation from
G to
H can also be denoted by
where
, or just by
. The string
is the
application sequence of the derivation.
Figure 4 shows a derivation with application sequence
.
Instead of applying to the left upper A-edge and then to the right upper one, one can interchange the order which yields the same result with a different intermediate graph.
In the following, the class of all rules (with and without positive context) is denoted by .
2.3. Parallel Rule Application
Let
for
. Then the
parallel rule is given by the disjoint unions of the components.
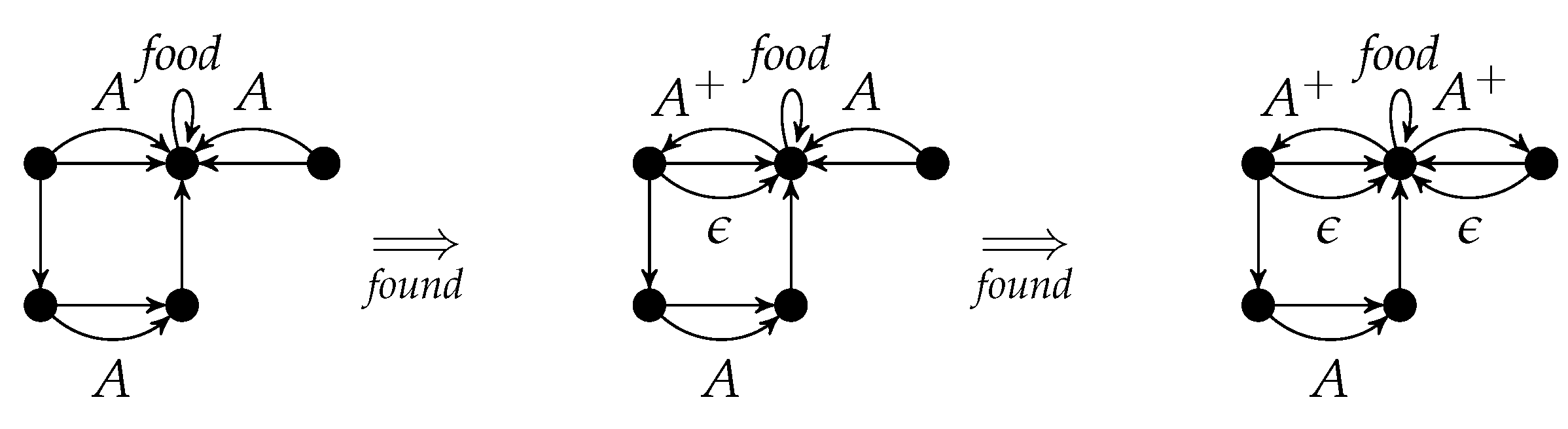
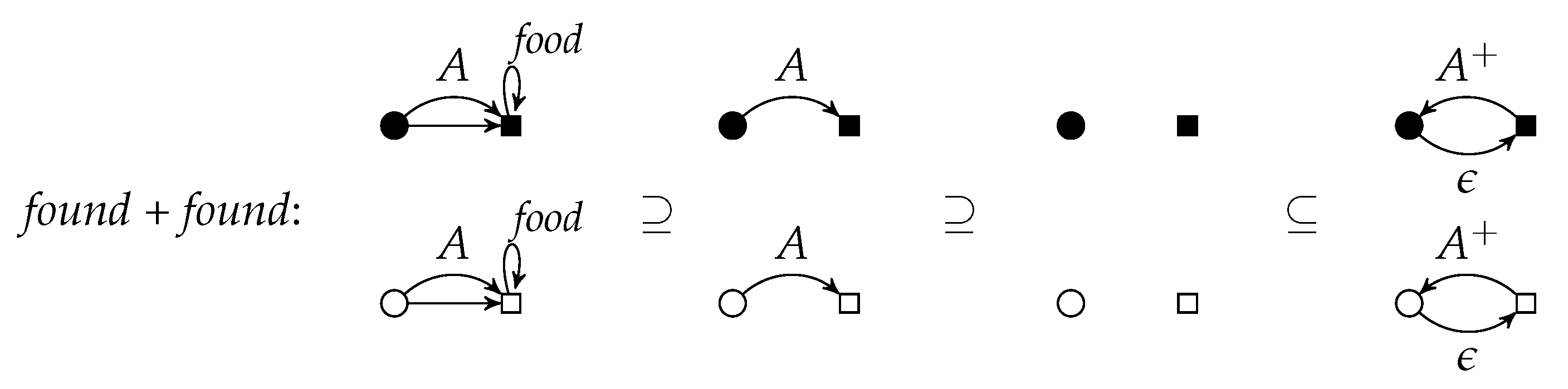
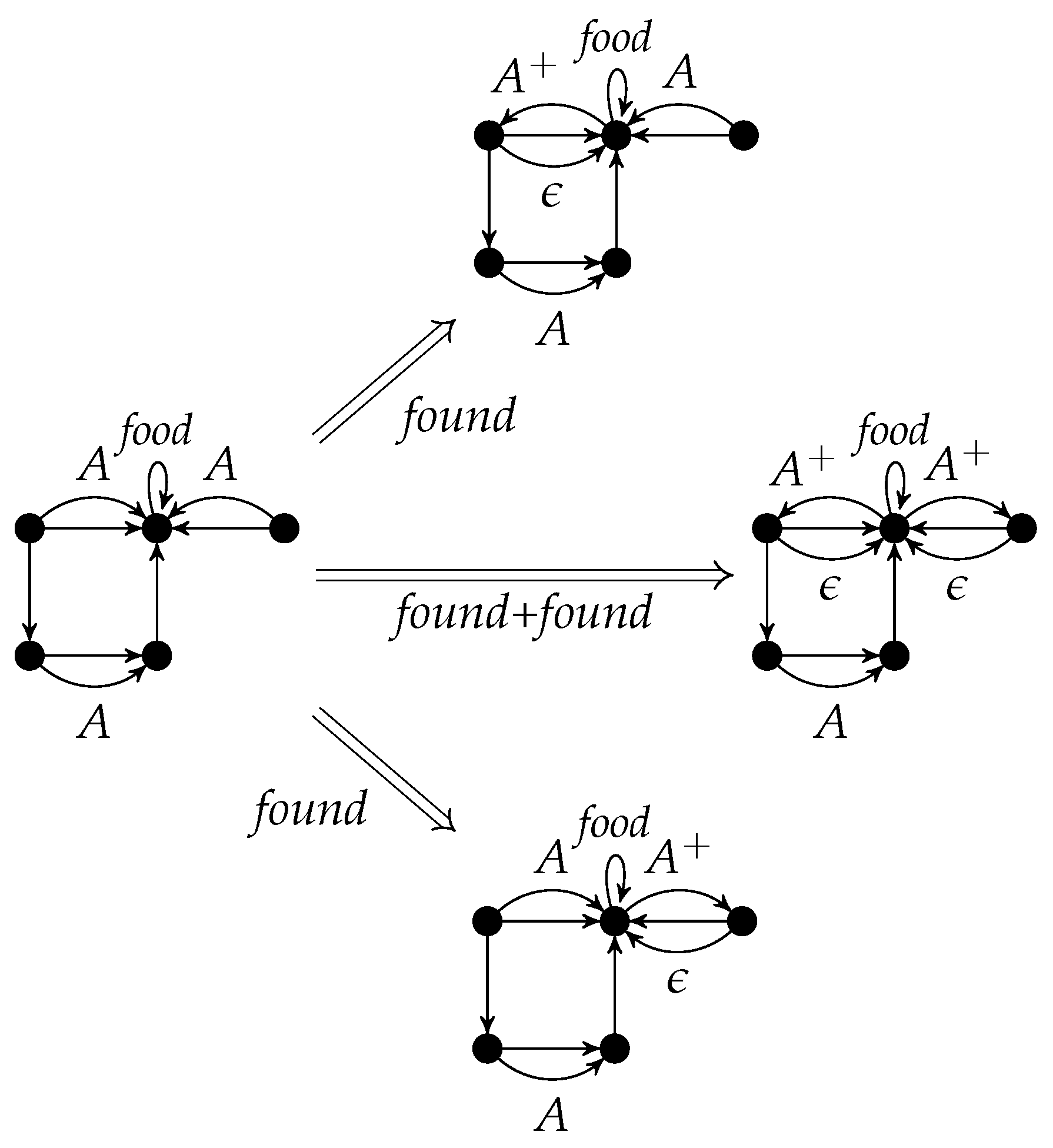
Figure 5 shows the parallel rule
found +
found. It can be applied to the left graph of
Figure 4, if the
A-edges are not identified (otherwise, the identification condition would be violated). The result is equal to the right graph of
Figure 4 (see also
Figure 6).
Let and be two rules and let and be two direct derivations w.r.t. the morphisms and . Then the direct derivations are parallel independent if the corresponding matches intersect in gluing items only, i.e., and .
The application of parallel rules and parallel independence are closely related as is shown by the well-known Paralllelization Theorem (see, e.g., [
16,
17] and Chapter 2 of [
15]). This result is the basis of the simultaneous actions of members of graph-transformational swarms as introduced in the next section.
Fact 1 (Parallelization Theorem). For , let and let be the corresponding parallel rule. Then the following hold.
Let be a direct derivation w.r.t. . Then there are direct derivations with the matching morphisms that are pairwise parallel independent where the morphism denotes the restriction of g to . for and .
Let for be direct derivations w.r.t. . Let each two of them be parallel independent. Then there is a direct derivation w.r.t. defined by for .
The theorem still holds for an infinite family with .
According to the Parallelization Theorem, the rule components of
found+
found in
Figure 6 can be applied separately to the left graph and are parallel independent. Conversely, these two parallel independent applications of
found can be executed in parallel.
2.4. Control Conditions and Graph Class Expressions
Control conditions can reduce the nondeterminism of rule application. In more detail, each control condition C is defined over a finite set P of rules and specifies a set of derivations. The class of all control conditions is denoted by . Control conditions can be composed by the operator & with for all .
A typical control condition is a priority relation > on a set P of rules meaning that a rule can only be applied if no other rule with higher priority is applicable. Another often used control condition is a regular expression over P. By definition, the constants , and are regular expressions and the composites , and are regular expressions if , , e are regular expressions. A derivation obeys a regular expression e if the application sequence of the derivation belongs to the language of e. In other words, allows a derivation if an initial section is allowed by and the remaining section by ; allows a derivation if or allows it; allows a derivation if it is a sequence of sub-derivations each allowed by e. The expression requires that r is applied; allows any derivation of length 0; forbids any derivation. Alternatively to , is used. It requests that r is applied as long as possible and not arbitrarily often.
All these examples of control conditions and their satisfaction apply not only to derivations over
P but also to derivations of the form
with
and
if
is an application sequence in the case of regular expressions or if, in the case of priorities for all
,
implies
for all
applicable to
.
Graph class expressions restrict the class to subclasses, i.e., each graph class expression X specifies a set . The class of all graph class expressions is denoted by . Typical examples of graph class expressions are graph properties like with or with where is the projection to the i-th component for . Moreover, each graph is a graph class expression with . We also use and for as graph class expressions. contains all graphs with a subgraph in . for some graph operator op contains all graphs obtained by the application of the operator to graphs in . Explicit examples of such operators are nest-looping and -looping. Applied to , the first operator adds one -loop to some node, and the second operator adds an arbitrary number of -loops. Graph class expressions can be composed by the operator with for all . Further graph class expressions are introduced where needed.
2.5. Graph Transformation Units
In the following we introduce a special case of graph transformation units, which is suitable for our purposes.
A graph transformation unit is a pair where is a set of rules, and is a control condition over P. The semantics of consists of all derivations allowed by C.
A unit is related to a unit if is obtained from by relabeling. For a mapping , the relabeling of is the unit where the relabeling replaces each occurring in the components and of by The set of units related to is denoted by
Each set of rules induces a graph transformation unit specified by where allows all derivations. For with we write for short.
3. Graph-Transformational Swarms
In this section, we introduce graph-transformational swarms and their computations. The swarm members act simultaneously in a common environment represented by a graph. All the members of a swarm may be of the same kind or of different kinds to distinguish between different roles members may play. The number of members of each kind is given by the size of the kind. To increase the flexibility of this notion, we also allow multidimensional swarms by means of size vectors. In this case, the number of members of the respective kind is the product of the size components. Given a size vector , the index vectors with for are used to identify the members of the swarms, where and . While a kind is specified as a graph transformation unit, the members of a kind are modeled as units related to the unit of this kind making sure in this way that all members of some kind are alike. A swarm computation starts with an initial environment and consists of iterated rule applications requiring massive parallelism meaning that each member of the swarm applies one of its rules in every step. In other words, each member acts sequentially according to its specification while all together are always busy. The choice of rules depends on their applicability and the control condition of the members. In some cases, a more restricted way of computation is reasonable. Hence, we allow to provide a swarm with an additional cooperation condition. Finally, a swarm may have a goal given by a graph class expression like the initial graphs are specified by such an expression. A computation is considered to be successful if an environment is reached that meets the goal.
Definition 1 (swarm). A swarm is a system where I is a graph class expression specifying the set of initial environments, K is a finite set of graph transformation units, called kinds, s associates a size vector with each kind where denotes the dimension of the kind k, m associates a family of members with each kind with for all , c is a control condition called cooperation condition, and g is a graph class expression specifying the goal. For and some , .
A swarm may be represented schematically as in
Figure 7 where
and
for
.
Definition 2 (swarm computation).
A swarm computation is a derivationsuch that , with a rule of for each , and , and c and the control conditions of all members are satisfied. For the satisfaction of the control condition of a unit, confer the definition for parallel derivations in Section 2.4. That all members must provide a rule to a computational step, is a strong requirement because graph transformation rules may not be applicable. In particular, if no rule of a swarm member is applicable to some environment, no further computational step would be possible and the inability of a single member stops the whole swarm. To avoid this global effect of a local situation, we assume that each member has the empty rule in addition to its other rules. The empty rule gets the lowest priority. In this way, each member can always act and is no longer able to terminate the computation of the swarm. In this context, the empty rule is called sleeping rule. It can always be applied, is always parallel independent with each other rule application, but does not produce any effect. Hence, there is no difference between the application of the empty rule and no application even within a parallel step.
To enhance the feasibility of the swarm concept, we allow also unbounded sizes, denoted by
or
. In this case, we allow only computations where in each step all but a finite number of rules are empty. An example of a swarm with unbounded size is the swarm version of a cellular automaton in
Section 5.
The concept of graph-transformational swarms provides a formal framework for the study of swarm computation. In many swarm approaches, the environments of the swarms are either chosen as graphs explicitly or can easily be represented by graphs. And because rules are widely and successfully used as the core of computation, graph transformation combining rules and graphs is a natural candidate for the formalization of swarm computation. The graph-transformational approach offers some advantages:
Graphs and rules are mathematically well-understood and quite intuitive syntactic means to model algorithmic processes. Moreover, the additional use of control and cooperation conditions as well as graph-class expressions allows very flexible forms of regulation.
Derivations as sequences of rule applications provide an operational semantics that is precise and reflects the computational intentions in a proper way.
Based on the formally defined derivation steps and the lengths of derivations, the approach provides a proof-by-induction principle that allows one to prove properties of swarm computations like termination, correctness, efficiency, etc.
In the area of graph transformation, one encounters several tools for the simulation, model checking and SAT-solving of graph transformation systems that can be adapted to graph-transformational swarms.
And maybe most important, the Parallelization Theorem establishes a systematic and reliable handling of massive parallelism. In several swarm approaches, the simultaneous actions of swarm members are organized in a very simplistic way by avoiding any kind of conflict or are required, but not always guaranteed (cf. e.g., [
18]). In contrast to that, the simultaneous actions of members of graph-transformational swarms is assured whenever the member rules are applicable and pairwise independent. Both can be checked locally and much more efficiently than the applicability of the corresponding parallel rule.
In the next three sections, we make an attempt to demonstrate the stated advantages by modeling three typical approaches to swarm computation.
4. A Simple Ant Colony
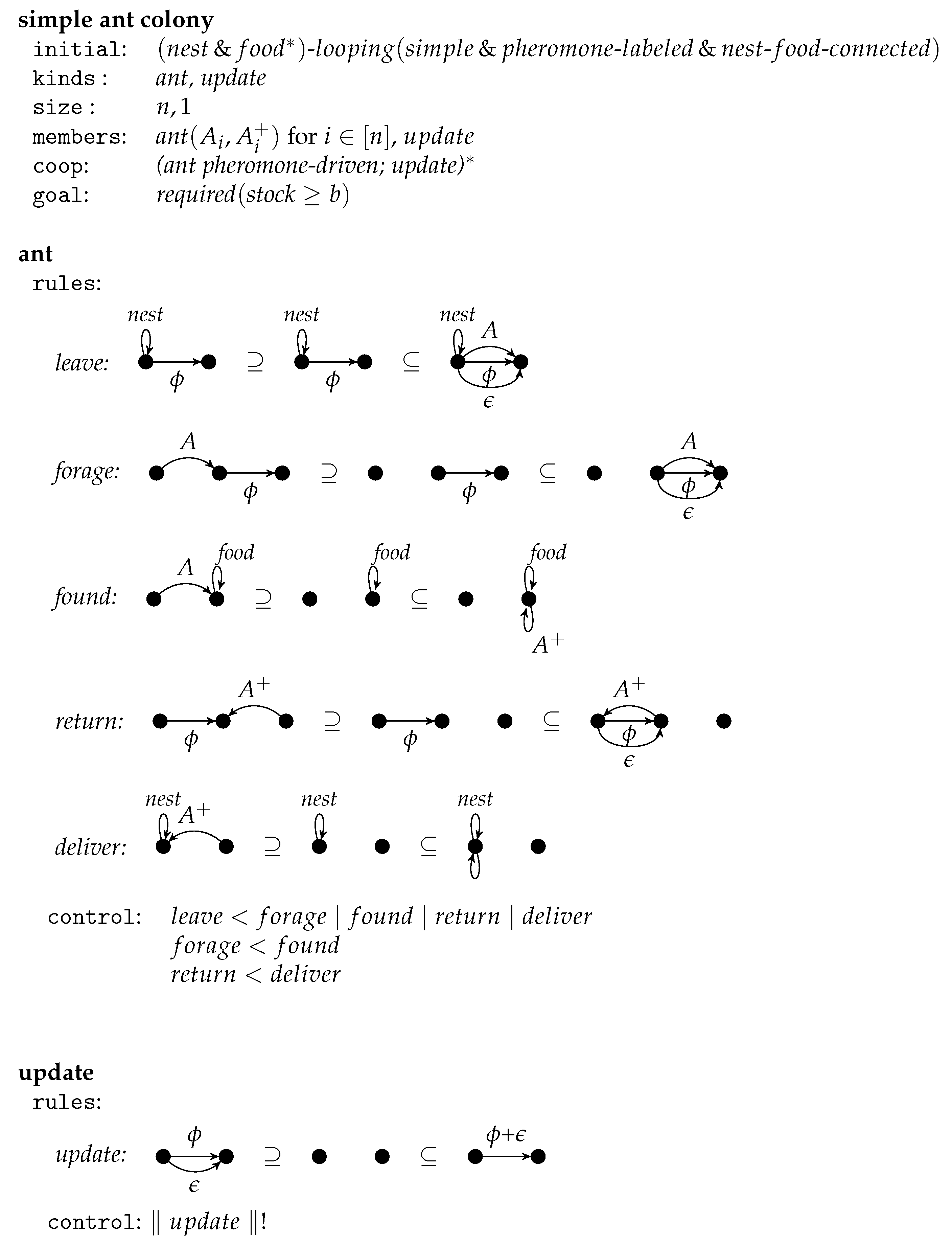
In this section, we illustrate the notion of graph-transformational swarms by modeling an ant colony the ants of which forage for food by mean of a simple pheromone mechanism. The sample graph-transformational swarm is presented in
Figure 8.
The swarm consists of some ants all of the same kind. They act in directed graphs with a nest-loop and some -loops. The node with the -loop has some further unlabeled loops that represent the actual food stock. All other initial edges are labeled by a positive integer representing a pheromone rate. We assume --connectedness meaning that the paths from the -looped node to some -looped node visit all nodes. Moreover, we assume that the underlying environment graph is simple meaning that there are no parallel pheromone-labeled edges. This class of graphs is denoted by ---. During swarm computations further edges appear and disappear.
The kind defines the potential activities of an ant by means of five rules and some priorities. It can the nest by placing an A-edge and an -labeled edge in parallel to a pheromone-labeled edge with the -looped node as source. Then it can forage for food by walking through the graph passing one pheromone-labeled edge per step and placing a parallel -edge. The label A refers to the ant, and is an integer to be added to the pheromone value. If an ant reaches a -node, then the rule is applied changing the label A into and indicating in this way that the ant takes food. In this state, it moves back using the rule until it can which adds a food unit to the stock. Note that the returning ants pass edges from target to source so that the same paths are used as for foraging. Moreover, an ant leaves the amount of pheromone along the return paths too. The pheromone values of the passed edges are not updated immediately, but in the next computational step. This allows several ants to pass the same edge in the same step. The control condition requests some priorities. An ant can only leave the nest if it cannot do anything else, i.e., if neither the label A nor is around. In other words, it leaves the nest at the beginning and after each delivery. Moreover, foraging for food stops whenever food is found. And moving back stops whenever the nest is reached. Further control is provided by the labels and A. As long as A is present, only the rules and may be applied. As long as is present, only and may be applicable. The application of turns a foraging phase into a returning phase that ends with .
Due to the --connectivity of the environmental graph, an ant can always act. If the A-edge points to a -looped node, then rule can and must be applied. Otherwise the A-edge has a target with another outgoing edge so that can be applied. If there is an -loop, then can be applied. To match the left-hand side of the rule in this case, its -edge must be mapped to the -loop. This is possible because matches are not assumed to be isomorphic images. If there is an -edge pointing to the -looped node, then can and must be applied. Otherwise, the -edge points to a node with an incoming edge so that can be applied. If all other fail, is allowed and possible.
The members of kind are obtained by relabeling A and by and resp. for where n is the chosen size of the ant colony. All other labels are kept. As all rule applications remove only edges with labels and , all rule applications are pairwise parallel independent if they concern different labels. In other words, the maximal parallel computation steps can be performed whenever an applicable rule is chosen for each ant. But there is one restriction given by the cooperation condition. It requires that ants act pheromone-driven meaning that the number of ants that pass an edge corresponds to the pheromone value of the edge. More precisely, let l be an ant that can pass the edges with pheromone values in the next step, then is used with the probability where the parameter can be chosen in a suitable way. The larger is, the more the effect of the pheromone values is intensified in the heuristic choice.
The cooperation condition requires that after each action of the ants an of the pheromone values takes place. The only member equals the kind and provides a single rule that adds to each pheromone-labeled edge for each parallel -labeled edge. The control condition requires that the -rule is applied with maximal parallelism as long as possible. The applications of the -rules are parallel independent if they update different pheromone-labeled edges. Therefore, needs m steps where m is the maximum number of parallel -edges.
Finally, the goal specifies graphs where the stock, i.e., the number of extra loops at the -looped node, exceeds a given bound b that can be chosen freely.
From the description of this swarm, it is clear how the computations look like. The ants act in parallel each applying one of its five rules according to applicability and priority. In the first step, all ants leave the nest. Later in the computations, all five types of rules may occur simultaneously. After each ants action step, an update takes place. The alternation between ant action and update can go on for ever, but can be stopped if the stock is large enough. Will this event occur eventually? We assume that the initial graphs are --connected so that there are paths from the nest to each -labeled node in particular. The ants use those paths with some probability depending on the pheromone values. Consequently, the ants come back to the nest after they found food with some probability so that the stock increases with some probability if the computation runs long enough and the number of ants is large enough. This can be guaranteed by assuming in addition that the initial environments are finite and cycle-free because then every ant finds food and returns to the nest eventually. The pheromone mechanism favors short paths before long ones. The fastest way to increase the stock is by running a shortest path from to and back. Short paths get some extra pheromone earlier than long ones so that they will be used in the further computation with even higher probability. This reasoning shows that there is a correlation between the length of paths and the number of computation steps needed to fill the stock.
Because this is a very first example of graph-transformational swarms, we have kept it simple. In particular, the kind could be designed in a more sophisticated way by adding evaporation rules. Moreover, the only member could be replaced by -members that are related to the pheromone-labeled edges so that the pheromone updating is also in the style of swarms.
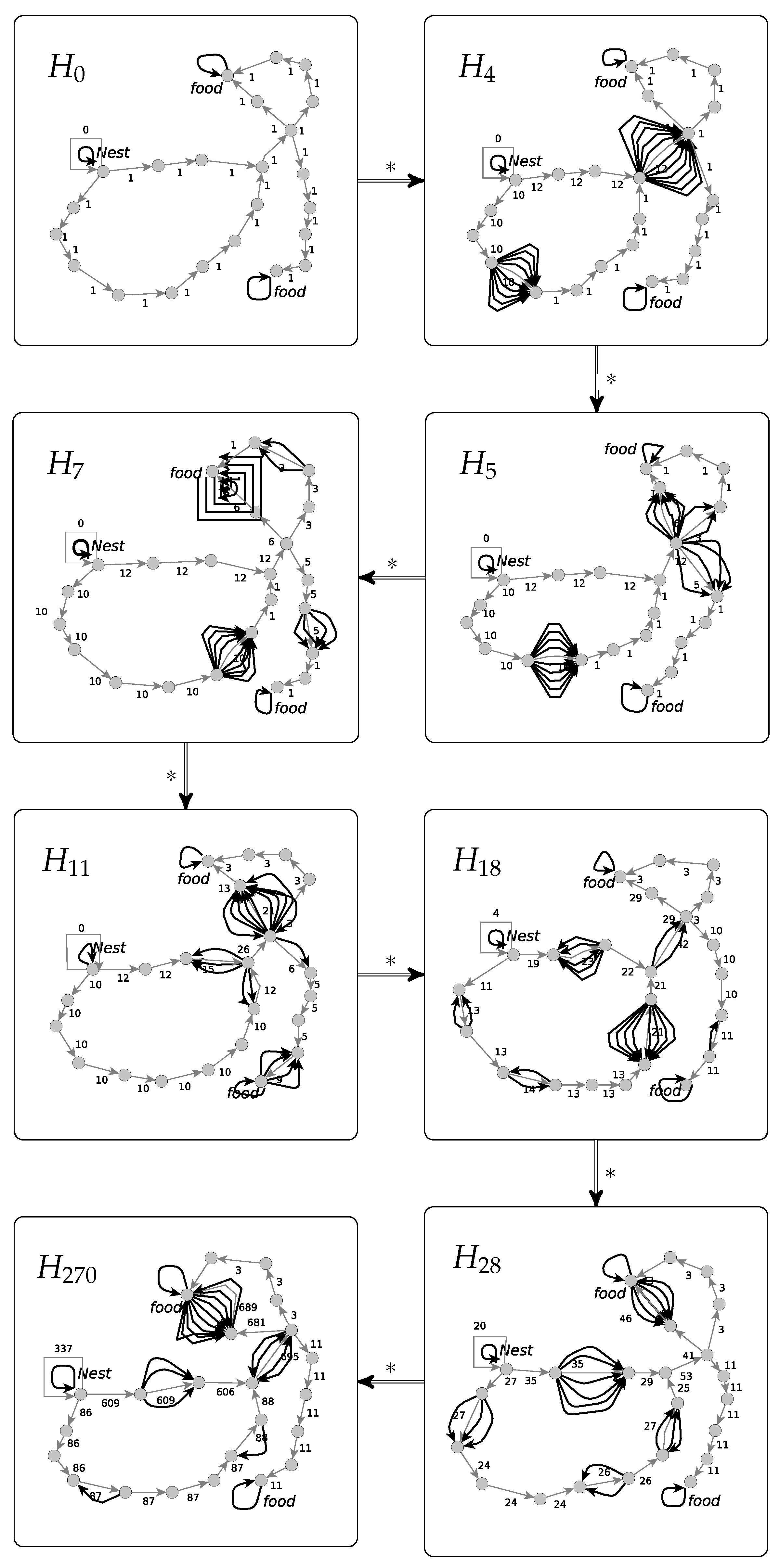
We have implemented the
simple ant colony swarm in the graph transformation tool GrGen.NET [
19]. An experimental computation with a swarm of 20 ants is documented in
Figure 9. For a better visualization, we omit the labels of the ants and replace the loops representing the food stock by a single loop labeled with the number of food units. The initial graph
has 23 nodes including a node with a
-loop and two nodes with
-loops. The initial pheromone values of all edges correspond to
. In the probability function, we use
. The seven further displayed graphs
for
are the graphs after the
i-th step of the ants and the following update each. The graph
represents the resulting graph after four
-steps. More precisely, in the first
step all ants leave the nest, however the swarm is split in two groups from almost the same size 9 and 11. This is due to the
-
action of ants and the equal initial pheromone values. Afterwards all ants apply their
-rules three times. The edges visited from each group can be easily recognized in
. Since their initial values are augmented by the underlying group’s number of members. The graph
results after the 5th
-step. One can see how all members go forward applying their forage rules again. However the group of 11 members splits in three subgroups when arriving in the node, say
u, with three outgoing edges. In the 7th
-step which generates
, a group of 5 ants find the
-node, say
, while all other ants forage further. In the 11th
-step, 11 ants have found food and are returning to the nest. The other members still forage.
displays the results of the 18th
-step. The first ants have delivered 4 units of food, in addition one can see that the path between
u and
starts slowly to be preferred. In
the ants have performed already 28 steps, and 20 units of food are delivered. The path between
u and
is frequently walked through meanwhile.
displays the graph after 270
-steps with 337 food units. Based on the pheromone values, one can see that ants prefer the shortest path between the
- and one of the
-nodes. The computation may be terminated whenever the chosen bound of the food stock is reached.
Our ant colony model is meant to exemplify how the features of graph-transformational swarms look like and work. How such models can be turned into applications that solve concrete optimization problems can be seen in [
11,
12].
5. Cellular Automata
Cellular automata are computational devices with massive parallelism known for many decades see, e.g., [
20,
21,
22,
23,
24]. They are also considered as typical representatives of swarm computation [
2]. In this section, we embed cellular automata into the framework of graph-transformational swarms.
A cellular automaton is a network of cells where each cell has got certain neighbor cells. A configuration is given by a mapping that associates a local state with each cell. A current configuration can change into a follow-up configuration by the simultaneous changes of all local states. The local transitions are specified by an underlying finite automaton where the local states of the neighbor cells are the inputs. If the network is infinite, one assumes a particular sleeping state that cannot change if all input states of neighbor cells are also sleeping. Consequently, all follow-up configurations have only a finite number of cells that are not sleeping if one starts with such a configuration.
To keep the technicalities simple, we consider 2-dimensional cellular automata the cells of which are the unit squares in the Euclidean plane
![Entropy 23 00453 i001 Entropy 23 00453 i001]()
for all
and can be identified by their left lower corner. The neighborhood is defined by a vector
where the neighbor cells of
are given by the translations
If one chooses the local states as colors, a cell with a local state can be represented by filling the area of the cell with the corresponding color. Accordingly, the underlying finite automaton is specified by a finite set of colors, say
COLOR, and its transition
Without loss of generality, we assume
and use it as sleeping state, i.e.,
Under these assumptions, a configuration is a mapping
and the follow-up configuration
of
S is defined by
If one starts with a configuration which has only a finite number of cells the colors of which are not white, then only these cells and those that have them as neighbors may change the colors. Therefore, the follow-up configuration has again only a finite number of cells with other colors than white. Consequently, the simultaneous change of colors of all cells can be computed. Moreover there is always a finite area of the Euclidean plane that contains all changing cells. In other words, a sequence of successive follow-up configurations can be depicted as a sequence of pictures by filling the cells with their colors.
Example 1. The following instance of a cellular automaton may illustrate the concept. It is called has two colors, and the neighborhood vector is meaning that each cell has the cell to its left and the next upper cell as neighbors.
The transition of changes white into black if exactly one neighbor is black, i.e., with and otherwise.
If one starts with the configuration with and otherwise, then one gets the configuration in Figure 10 after 50 steps. Starting with a single black cell, iterates the Sierpinski gadget (cf., e.g., [25]). Cellular automata can be considered as graph-transformational swarms. Let
be a cellular automaton with the neighborhood vector
the set of colors
COLOR and the transition function
Then a configuration
can be represented by a graph
with the cells as nodes, with an unlabeled edge from each cell to each of its neighbors and two loops at each cell where one loop is labeled with the color of the cell and the other loop with the coordinates of the cell. The set of all these graphs is denoted by
.
If the color of a cell
changes, i.e.,
then the following rule with positive context
![Entropy 23 00453 i002 Entropy 23 00453 i002]()
can be applied to the node
in
provided that
and
for
Due to the loops that identify the nodes, the matching is unique and the matches of the left-hand sides of each two of such applicable rules do not overlap. Consequently, all those applicable rules can be applied in parallel yielding
where
is the follow-up configuration of
This remains true if the (empty) sleeping rule is applied to each other node because it is always applicable, is always independent of each other rule application and does not change the result. In other words, the derivation step
is a swarm computation step if the rules above belong to members of a swarm which can be defined as follows:
![Entropy 23 00453 i003 Entropy 23 00453 i003]()
where the kind and the members are units induced by the sets of rules
containing all rules above for
and the transition
d. Every member
is obtained from the kind
by translating all points in the plane by
which is a special relabeling. Conversely, a computation step
in
changes a
c-loop into a
-loop at the node with the
-loop if and only if, for
, the neighbor with the
-loop has also a
-loop. All other c-loops are kept. This means that
. Summarizing, each cellular automaton can be transformed into a graph-transformational swarm such that the following correctness result holds.
Theorem 1. Let be a cellular automaton with neighborhood vector N and let be the corresponding graph-transformational swarm. Then there is a transition from S to in if and only if in .
Therefore, cellular automata behave exactly as their swarm versions up to the representation of configurations as graphs. We have considered cellular automata over the 2-dimensional space . It is not difficult to see that all our constructions also work for the d-dimensional space in a similar way. One may even replace the quadratic cells by triangular or hexagonal cells.
6. Particle Swarm Optimization
Particle swarm optimization is one of the major approaches to swarm intelligence one encounters in the literature in various variants (see, e.g., [
26,
27,
28,
29,
30]) In this section, we model a discrete version of particle swarm optimization in the framework of graph-transformational swarms.
A particle swarm acts in the Euclidean space for some dimension The space is provided with a fitness function and a neighborhood (where denotes the power set of some set A swarm consists of n particles each of which carries the following information at each time : a position a velocity a personal best (position) and a best neighbor (position)
The initial positions and initial velocities are chosen randomly. The initial personal bests coincide with the initial positions, i.e., In all steps, the best neighbor is the position of a particle j in the neighborhood of with maximum fitness, i.e., for all The positions, velocities and personal bests at time are given by the following formulas using the positions, velocities and personal bests at time t:
if and otherwise.
Here
and
are two pregiven bounds,
and
are vectors with randomly chosen components between 0 and
and
respectively and ⊗ is the componentwise product. A velocity represents a direction and a speed so that a particle moves in this direction with this speed from step to step where the velocity is adapted in such a way that the particle moves partly in the direction of the personal best and partly in the direction of the best neighbor. It is assumed that each particle is a neighbor of itself to guarantee that the best neighbor always exists. The goal is that one of the particles reaches a position the fitness of which meets or exceeds a given bound. In the literature, one can find a long list of examples of particle swarms which run successfully for a variety of optimization problems see, e.g., [
28,
29].
A simple way to discretize particle swarms is to assume that all position and velocity components and all randomly chosen scalars are integers. This discrete version of particle swarms can be transformed into the framework of graph-transformational swarms. Let
be such a discrete particle swarm with the fitness function
the neighborhood
the bounds
the goal value
and
n particles. Then the corresponding graph-transformational swarm is given in
Figure 11.
The initial environment graph is called
and has all points
in the
d-dimensional Euclidean plane with integer coordinates as nodes. There is an unlabeled edge
for
with the source
x and the target
y whenever
Furthermore, each
has two loops
and
where
x is source and target. The label of
is also
the label of
is
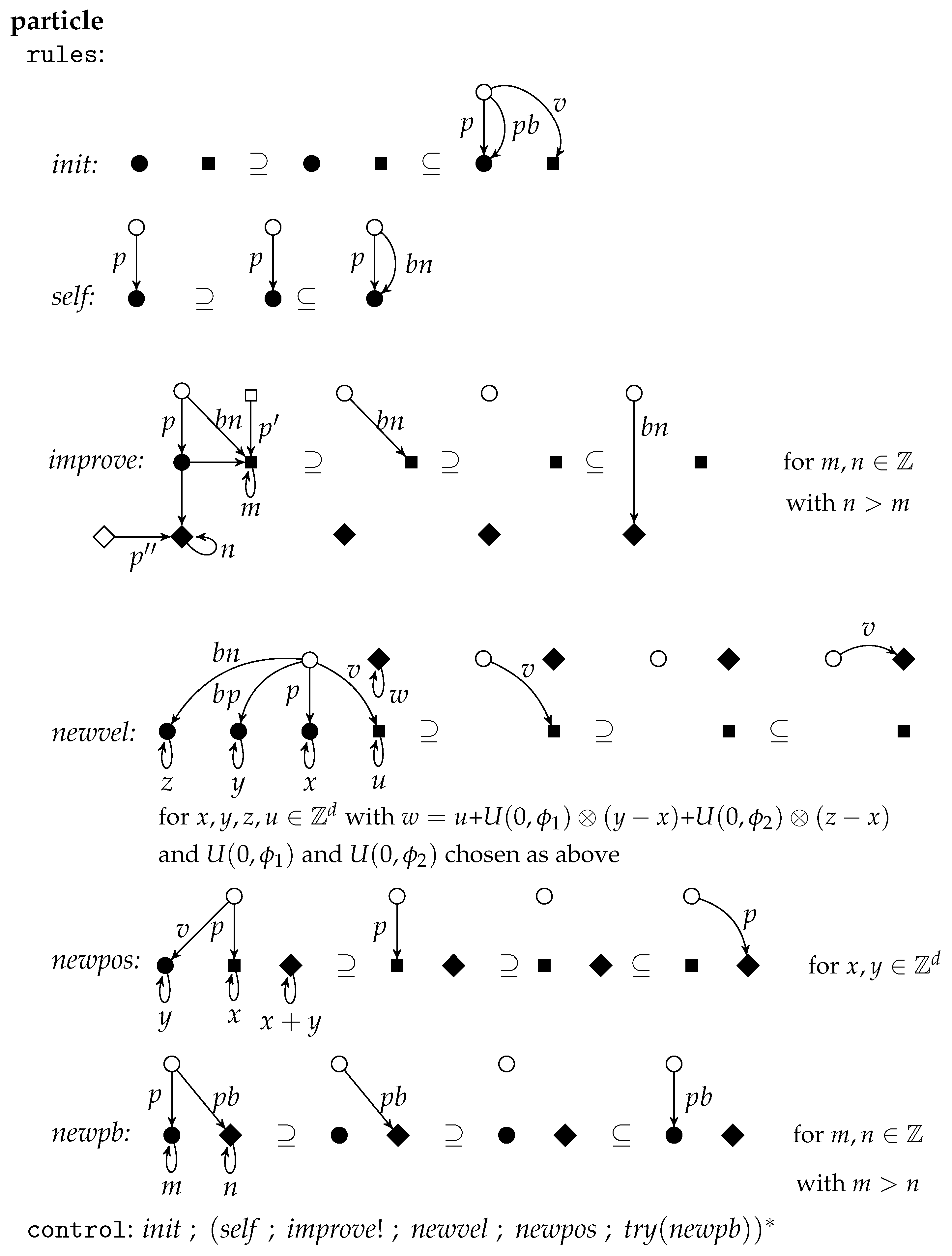
All particles are of the same kind specified by the unit
particle in
Figure 12. (For technical simplicity, we assume
).
The member for is obtained by indexing and with All other labels are kept variable with in particular. Due to the control condition, the rule init is applied first and then never again. It chooses two points x and y, generates a new node (representing a particle) and two edges from this node to x labeled with p and respectively and an edge to y labeled with v choosing randomly an initial position, which is also the personal best, and an initial velocity. As nothing is removed, each two applications of init are parallel independent such that all particles can be initialized simultaneously. Afterwards, a sequence of rule applications is iterated starting with self followed by improve as long as possible. The application of self takes the current position as best neighbor by adding a -edge parallel to the p-edge. The rule improve can be applied if one can find a particle in the neighborhood with a better fitness. Applied as long as possible, the -edge points to the current best neighbor.
If now newvel and then newpos are applied, then the velocity and position of a particle are changed using the formulas above by redirecting the v-edge and p-edge accordingly. If the new position has a better fitness than the former personal best, then the rule newpb can be applied to update the personal best. The control condition requires that is applied if possible.
The rules self can be applied to all particles in parallel as again nothing is removed. Two applications of improve for different particles are parallel independent as only the different -edges are redirected. Therefore, the improvements can be done in parallel provided that at most one improve-rule per particle is applied. The cooperation condition requires that the applications of newvel are synchronized, which means that they are done in parallel after all improvements are performed. Each two applications of newvel for different particles are parallel independent as only different edges are redirected. Because of the same reason, all particles can get a new position by applying the newpos-rules in parallel. And analogously the newpb-rules can be applied in parallel afterwards as far as they are applicable at all. The cooperation condition requires that self is synchronized, which means that in the next round all applications of self start simultaneously. The goal requires that one of the particles reach a position the fitness of which meets or exceeds the bound value b.
The rules , , and describe how the attributes of a particle can be changed by redirecting the respective edges where the positive context (placed left-most) provides the parameters that must be considered in each case.
By definition, a run of a particle swarm is determined by the choices of and for and the vectors and for The family of quadruples may be seen as the swarm state at time Such a state can be transformed into a graph that has space as subgraph and, for each , an additional node i as well as four new edges of the form
![Entropy 23 00453 i004 Entropy 23 00453 i004]()
Consider, on the other hand, the computation of using the same choices as the run Then the considerations of this section show that, for each , the graph is computed after all improve-steps in round t through the iteration in the control condition. This proves the following correctness result.
Theorem 2. Let PS be a discrete particle swarm and the corresponding graph- transformational swarm. Then there is a one-to-one correspondence between the runs in PS and the computations in .
While particle swarm optimization is usually defined over a continuous space, we have transformed discrete versions of particle swarms into graph-transformational swarms because of the following reasons.
In the framework of graph transformation, the usual underlying structures are finite graphs or infinite discrete graph in exceptional cases. But all the concepts employed in the paper work for arbitrary sets of nodes and edges including the set of real numbers, the Euclidean space of some dimension or other continuous domains. Nevertheless, we have decided to consider a discrete version of particle swarm optimization as we want to demonstrate the potential of the usual graph transformation rather than to introduce a new kind of graph transformation. Nevertheless, the latter may be an interesting topic of future research.
Moreover, implementations of particle swarm models are always discretized. As long as the abstract models are continuous, testing is the only way to validate an implementation against the model. A discrete abstract model between a continuous model and the implementation may allow to prove general properties and to improve the trustworthiness of system development in this way.
In the literature, one encounters applications of particle swarm optimization to solve discrete problems (see, e.g., [
30,
31,
32,
33]). In such a case, a discrete abstract model seems to be appropriate. The particles correspond to problem solutions and the velocity and position updates, as introduced above, are redefined to be applicable to the discrete space. The graph-transformational model
above can also be adapted in the same way to solve discrete problems. In this case
and the operators in the rule
should be adapted to the corresponding domains. Despite those changes all other components can be used unchanged
7. Conclusions
In this paper, we have introduced a graph-transformational approach to swarm computation providing formal methods for the modeling of swarms and the analysis of their correctness and efficiency. The concept exploits graph transformation units and the massive parallelism of rule applications.
As a first example, an ant colony with a simple pheromone-driven cooperation is modeled to illustrate the basic features of graph-transformational swarms. Our main results show that two other major approaches to swarm computation, cellular automata and particle swarms, can be embedded into the graph-transformational framework in a natural way.
The aim of this paper has been to advocate the syntactic and semantic concepts of graph-transformational swarms as a unifying framework for swarm modeling and analysis. To shed more light on the significance and usefulness of our approach, it would be of great interest to demonstrate that it does not only work on the abstract conceptual level, but also on the level of concrete real-world applications. To deliver convincing examples of this kind, quite some further work is needed and is a matter of future research. As first small steps in this direction, we refer to three papers where we consider potential applications concerning the solution of practical problems in cloud-based engineering systems [
34] and in dynamic logistic networks with decentralized processing and control in [
35] as well as of the routing problem of the automated guided vehicles in [
36].
Future studies should provide further correct transformations from models with massive parallelism like ant colony optimization with more sophisticated pheromone-based computation, L-systems and DNA-computing into graph-transformational swarms. The hope is that graph-transformational swarms can serve as a common formal framework for a wide spectrum of swarm approaches.
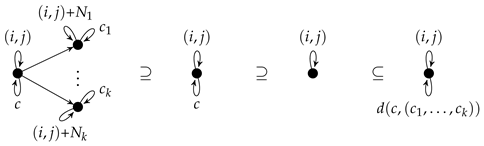 can be applied to the node in provided that and for Due to the loops that identify the nodes, the matching is unique and the matches of the left-hand sides of each two of such applicable rules do not overlap. Consequently, all those applicable rules can be applied in parallel yielding where is the follow-up configuration of This remains true if the (empty) sleeping rule is applied to each other node because it is always applicable, is always independent of each other rule application and does not change the result. In other words, the derivation step is a swarm computation step if the rules above belong to members of a swarm which can be defined as follows:
can be applied to the node in provided that and for Due to the loops that identify the nodes, the matching is unique and the matches of the left-hand sides of each two of such applicable rules do not overlap. Consequently, all those applicable rules can be applied in parallel yielding where is the follow-up configuration of This remains true if the (empty) sleeping rule is applied to each other node because it is always applicable, is always independent of each other rule application and does not change the result. In other words, the derivation step is a swarm computation step if the rules above belong to members of a swarm which can be defined as follows:
 where the kind and the members are units induced by the sets of rules containing all rules above for and the transition d. Every member is obtained from the kind by translating all points in the plane by which is a special relabeling. Conversely, a computation step in changes a c-loop into a -loop at the node with the -loop if and only if, for , the neighbor with the -loop has also a -loop. All other c-loops are kept. This means that . Summarizing, each cellular automaton can be transformed into a graph-transformational swarm such that the following correctness result holds.
where the kind and the members are units induced by the sets of rules containing all rules above for and the transition d. Every member is obtained from the kind by translating all points in the plane by which is a special relabeling. Conversely, a computation step in changes a c-loop into a -loop at the node with the -loop if and only if, for , the neighbor with the -loop has also a -loop. All other c-loops are kept. This means that . Summarizing, each cellular automaton can be transformed into a graph-transformational swarm such that the following correctness result holds.