BFF: Bayesian, Fiducial, and Frequentist Analysis of Cognitive Engagement among Cognitively Impaired Older Adults
Abstract
1. Introduction
1.1. Physical and Mental Health
1.2. Stress
1.3. Frequentist Paradigm
1.4. Bayesian Paradigm
1.5. Fiducial Paradigm
1.6. Present Study
2. Materials and Methods
2.1. Participants
2.2. Measures
Cognitive Engagement and Cardiovascular Monitoring
2.3. Procedure
3. Analysis
3.1. Data Preparation
3.2. Modeling
| Level 1 (within-person, t): |
| SBP-Rti = ß0ti + ß1ti(Tertile) + rti |
| Level 2 (between-person, i): |
| ß0i = γ10 + γ01(SBP baseline) + γ02(Cognition) + γ03(Physical health challenges) + u0i |
| ß1i = γ10 + γ11(Cognition) + γ12(Physical Health Challenges) |
4. Results
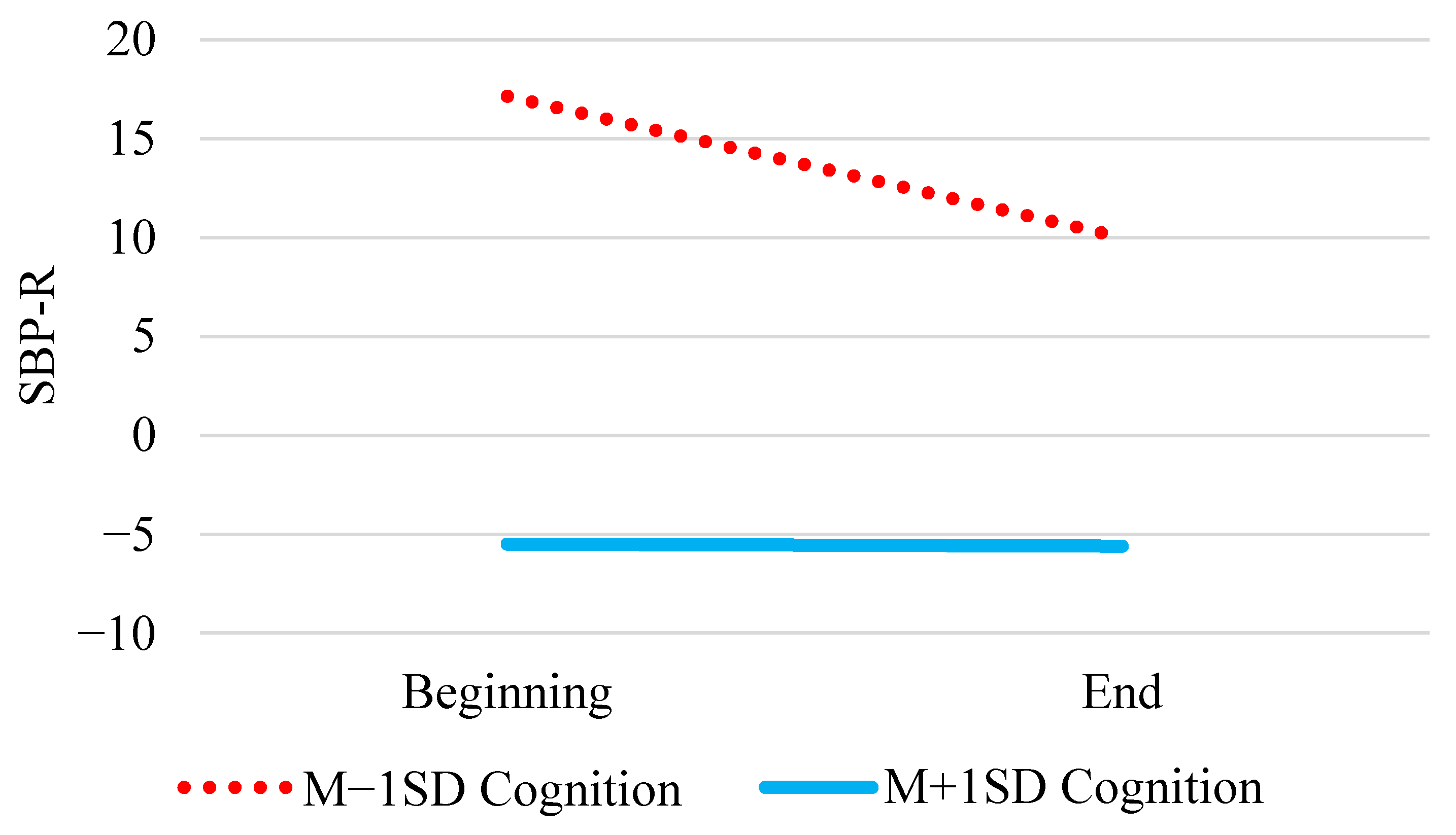
4.1. Frequentist Results
4.2. Bayesian Results
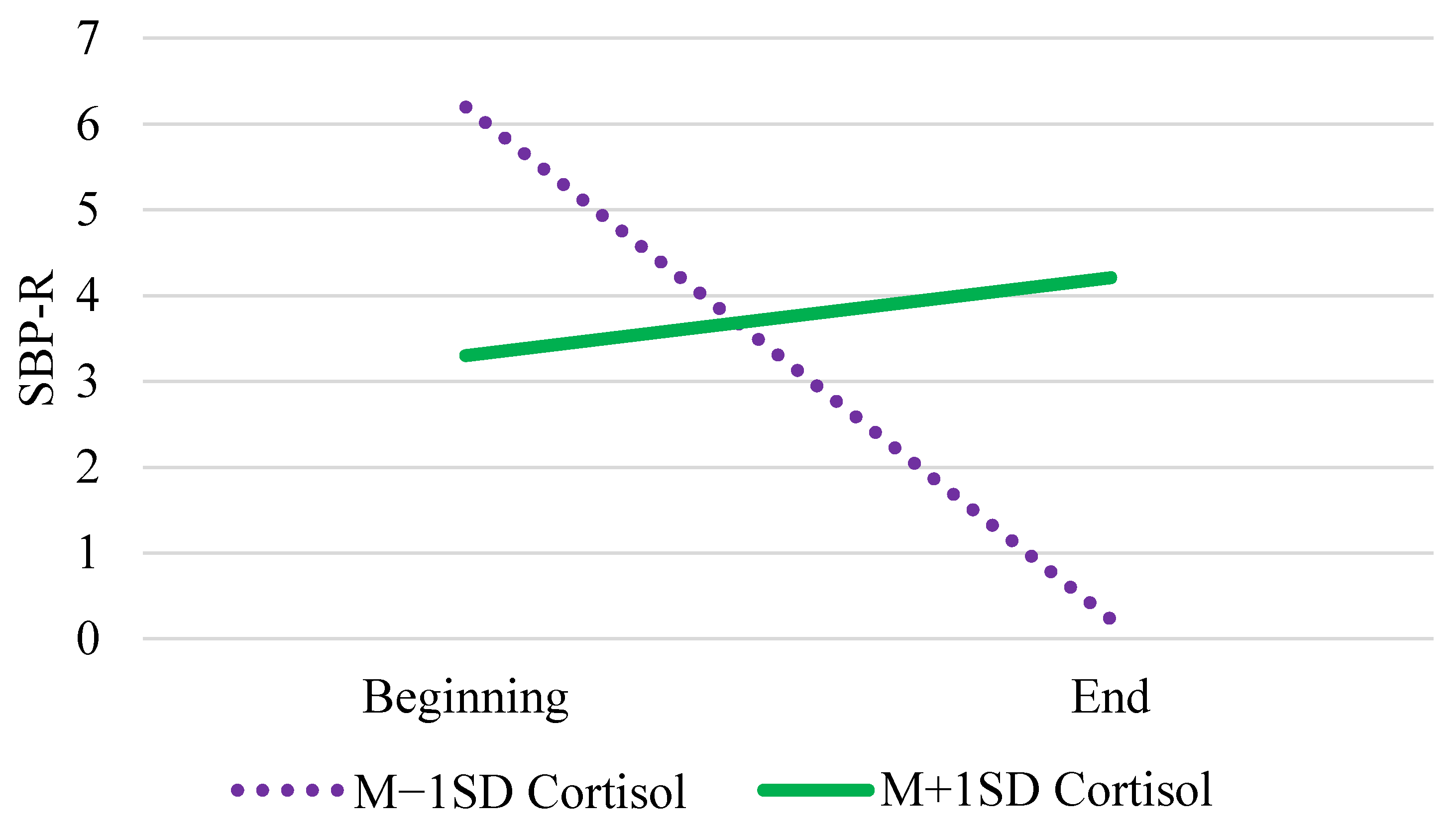
4.3. Fiducial Results
5. Discussion
5.1. Findings That Converge across the Paradigms
5.2. Findings that Diverge across the Paradigms
5.3. Limitations and Future Directions
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Additional Participant Information
Appendix A.2. Additional Measures Information
Appendix A.2.1. Physical Health Challenges
Appendix A.2.2. Mental Health Challenges
Appendix A.2.3. Cortisol
Appendix A.2.4. Cognitive Ability Assessment
Appendix A.3. Additional Procedure Information
References
- Hess, T.M. Selective engagement of cognitive resources: Motivational influences on older adults’ cognitive functioning. Perspect. Psychol. Sci. 2014, 9, 388–407. [Google Scholar] [CrossRef]
- Echegoyen, I.; López-Sanz, D.; Martínez, J.H.; Maestú, F.; Buldú, J.M. Permutation entropy and statistical complexity in Mild Cognitive Impairment and Alzheimer’s Disease: An analysis based on frequency bands. Entropy 2020, 22, 116. [Google Scholar] [CrossRef]
- Hess, T.M.; Growney, C.M.; O’Brien, E.L.; Neupert, S.D.; Sherwood, A. The role of cognitive costs, attitudes about aging, and intrinsic motivation in predicting engagement in everyday activities. Psychol. Aging 2018, 33, 953–964. [Google Scholar] [CrossRef]
- Hess, T.M.; Growney, C.M.; Lothary, A.F. Motivation moderates the impact of aging stereotypes on effort expenditure. Psychol. Aging 2019, 34, 56–67. [Google Scholar] [CrossRef]
- Ennis, G.E.; Hess, T.M.; Smith, B.T. The impact of age and motivation on cognitive effort: Implications for cognitive engagement in older adulthood. Psychol. Aging 2013, 28, 495–504. [Google Scholar] [CrossRef]
- Hess, T.M.; Ennis, G.E. Age differences in the effort and cost associated with cognitive activity. J. Gerontol. Ser. B Psychol. Sci. Soc. Sci. 2012, 67, 447–455. [Google Scholar] [CrossRef]
- Hess, T.M.; O’Brien, E.L.; Growney, C.M. Blood pressure as a biomarker method in lifespan developmental psychology. In Oxford Research Encyclopedia of Psychology; Knight, B., Ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar] [CrossRef]
- Gendolla, G.H.E.; Richter, M. Cardiovascular reactivity during performance under social observation: The moderating role of task difficulty. Int. J. Psychophysiol. 2006, 62, 185–192. [Google Scholar] [CrossRef]
- Uchino, B.N.; Birmingham, W.; Berg, C.A. Are older adults less or more physiologically reactive? A meta-analysis of age-related differences in cardiovascular reactivity to laboratory tasks. J. Gerontol. Ser. B Psychol. Sci. Soc. Sci. 2010, 65, 154–162. [Google Scholar] [CrossRef]
- Charles, S.T. Strength and vulnerability integration: A model of emotional well-being across adulthood. Psychol. Bull. 2010, 136, 1068–1091. [Google Scholar] [CrossRef]
- Obrist, P.A. Cardiovascular Psychophysiology: A Perspective; Plenum: New York, NY, USA, 1981. [Google Scholar] [CrossRef]
- Queen, T.L.; Hess, T.M. Linkages between resources, motivation, and engagement in everyday activities. Motiv. Sci. 2018, 4, 26–38. [Google Scholar] [CrossRef]
- Barnett, J.H.; Blackwell, A.; Auvinen, J.; Taivalantti, M.; Timonen, M.; Jarvelin, M.; Veijola, J. Mental health versus physical health as determinants of cognition in midlife. Alzheimers Dement. J. Alzheimers Assoc. 2015, 11, P281. [Google Scholar] [CrossRef]
- Bourassa, K.J.; Memel, M.; Woolverton, C.; Sbarra, D.A. Social participation predicts cognitive functioning in aging adults over time: Comparisons with physical health, depression, and physical activity. Aging Ment. Health 2017, 21, 133–146. [Google Scholar] [CrossRef] [PubMed]
- Hess, T.M.; Emery, L.; Neupert, S.D. Longitudinal relationships between resources, motivation, and functioning. J. Gerontol. Ser. B Psychol. Sci. Soc. Sci. 2012, 67, 299–308. [Google Scholar] [CrossRef] [PubMed]
- McEwen, B.S. The neurobiology of stress: From serendipity to clinical relevance. Brain Res. 2000, 886, 172–189. [Google Scholar] [CrossRef]
- Calvo, M.G.; Gutierrez-Garcia, A. Cognition and stress. In Stress: Concepts, Cognition, Emotion, and Behavior; Academic Press: Cambridge, MA, USA, 2016; pp. 139–144. [Google Scholar] [CrossRef]
- Stalder, T.; Kirschbaum, C. Analysis of cortisol in hair—State of the art and future directions. Brain Behav. Immun. 2012, 26, 1019–1029. [Google Scholar] [CrossRef]
- Wright, K.D.; Hickman, R.; Laudenslager, M.L. Hair Cortisol Analysis: A Promising Biomarker of HPA Activation in Older Adults. Gerontologist 2015, 55 (Suppl. 1), S140–S145. [Google Scholar] [CrossRef]
- Lakens, D.; McLatchi, N.; Isager, P.M.; Scheel, A.M.; Dienes, Z. Improving inferences about null effects with Bayes Factors and Equivalence Tests. J. Gerontol. Psychol. Sci. 2020, 75, 45–57. [Google Scholar] [CrossRef]
- Neupert, S.D.; Hannig, J. BFF: Bayesian, Fiducial, Frequentist analysis of age effects in daily diary data. J. Gerontol. Psychol. Sci. 2020, 75, 67–79. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Lazar, N.A. The ASA’s statement on p-values: Context, process, and purpose. Am. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef]
- Smith, B.T.; Hess, T.M. The impact of motivation and task difficulty on resource engagement: Differential influences on cardiovascular responses of young and older adults. Motiv. Sci. 2015, 1, 22–36. [Google Scholar] [CrossRef]
- Hess, T.M.; Lothary, A.F.; O’Brien, E.L.; Growney, C.M.; DeLaRosa, J. Predictors of engagement in young and older adults: The role of specific activity experience. Psychol. Aging 2020. [Google Scholar] [CrossRef]
- Edwards, W.; Lindman, H.; Savage, L.J. Bayesian statistical inference for psychological research. Psychol. Rev. 1963, 70, 193–242. [Google Scholar] [CrossRef]
- Franck, C.T.; Gramacy, R.B. Assessing Bayes factor surfaces using interactive visualization and computer surrogate modeling. arXiv 2018, arXiv:1809.05580. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Bickel, D.R. Bayesian revision of a prior given prior-data conflict, expert opinion, or a similar insight: A large-deviation approach. Statistics 2018, 52, 552–570. [Google Scholar] [CrossRef]
- Evans, M.; Guo, Y. Measuring and controlling bias for some Bayesian inferences and the relation to frequentist criteria. Entropy 2021, 23, 190. [Google Scholar] [CrossRef]
- Evans, M.; Moshonov, H. Checking for prior-data conflict. Bayesian Anal. 2006, 1, 893–914. [Google Scholar] [CrossRef]
- Mutsvari, T.; Tytgat, D.; Walley, R. Addressing potential prior-data conflict when using informative priors in proof-of-concept studies. Pharm. Stat. 2016, 15, 28–36. [Google Scholar] [CrossRef]
- Fisher, R.A. The concepts of inverse probability and fiducial probability referring to unknown parameters. Proc. R. Soc. Lond. Ser. A 1933, 139, 343–348. [Google Scholar]
- Zabell, S.L. RA Fisher and Fiducial Argument. Stat. Sci. 1992, 7, 369–387. [Google Scholar]
- Hannig, J. On generalized fiducial inference. Stat. Sin. 2009, 19, 491–544. [Google Scholar]
- Hannig, J.; Iyer, H.; Lai, R.C.S.; Lee, T.C.M. Generalized Fiducial Inference: A review and new results. J. Am. Stat. Assoc. 2016, 111, 1346–1361. [Google Scholar] [CrossRef]
- Cisewski, J.; Hannig, J. Generalized Fiducial Inference for normal linear mixed models. Ann. Stat. 2012, 40, 2102–2127. [Google Scholar] [CrossRef]
- Cui, Y.; Hannig, J. Nonparametric generalized fiducial inference for survival functions under censoring with discussion and rejoinder by the authors. Biometrika 2019, 106, 501–551. [Google Scholar] [CrossRef]
- Katzman, R.; Brown, T.; Fuld, P.; Peck, A.; Schechter, R.; Schimmel, H. Validation of a short Orientation-Memory-Concentration Test of cognitive impairment. Am. J. Psychiatry 1983, 140, 734–739. [Google Scholar] [CrossRef]
- SAS Institute. SAS/ACCESS 9.4 Interface to ADABAS: Reference; SAS Institute Inc.: Cary, NC, USA, 2013. [Google Scholar]
- Raudenbush, S.W.; Bryk, A.S. Hierarchical Linear Models; Sage: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Bayarri, M.J.; Berger, J.O.; Forte, A.; García-Donato, G. Criteria for Bayesian model choice with application to variable selection. Ann. Stat. 2012, 40, 1550–1577. [Google Scholar] [CrossRef]
- Zellner, A.; Siow, A. Posterior odds ratios for selected regression hypotheses. Trab. Estad. Investig. Oper. 1980, 31, 585–603. [Google Scholar] [CrossRef]
- Rouder, J.N.; Morey, R.D.; Speckman, P.L.; Province, J.M. Default Bayes factors for ANOVA designs. J. Math. Psychol. 2012, 56, 356–374. [Google Scholar] [CrossRef]
- Jarosz, A.F.; Wiley, J. What are the odds? A practical guide to computing and reporting Bayes factors. J. Probl. Solving 2014, 7, 2. [Google Scholar] [CrossRef]
- Baskurt, Z.; Evans, M. Hypothesis assessment and inequalities for Bayes factors and relative belief ratios. Bayesian Anal. 2013, 8, 569–590. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef]
- Morey, R.D.; Rouder, J.N. BayesFactor: Computation of Bayes Factors for Common Designs. R Package Version 0.9.12-4.2. 2018. Available online: https://CRAN.R-project.org/package=BayesFactor (accessed on 1 August 2020).
- Stan Development Team. RStan: The R Interface to Stan. R Package Version 2.21.2. 2020. Available online: http://mc-stan.org/ (accessed on 1 August 2020).
- Moffat, S.D.; Yang, A.; Resnick, S.M.; Diamond, M.P.; Ferrucci, L. Longitudinal change in cortisol levels across the adult life span. J. Gerontol. Ser. A 2020, 75, 394–400. [Google Scholar] [CrossRef] [PubMed]
- Aminzadeh, F.; Byszewski, A.; Molnar, F.J.; Eisner, M. Emotional impact of dementia diagnosis: Exploring persons with dementia and caregivers’ perspectives. Aging Mental Health 2007, 11, 281–290. [Google Scholar] [CrossRef]
- Peavy, G.M.; Salmon, D.P.; Jacobson, M.W.; Hervey, A.; Gamst, A.C.; Wolfson, T.; Patterson, T.L.; Goldman, S.; Mills, P.J.; Khandrika, S.; et al. Effects of chronic stress on memory decline in cognitively normal and mildly impaired older adults. Am. J. Psychiatry 2009, 166, 1384–1391. [Google Scholar] [CrossRef]
- Arend, M.G.; Schäfer, T. Statistical power in two-level models: A tutorial based on Monte Carlo simulation. Psychol. Methods 2019, 24, 1–19. [Google Scholar] [CrossRef]
- Alù, F.; Miraglia, F.; Orticoni, A.; Judica, E.; Cotelli, M.; Rossini, P.M.; Vecchio, F. Approximate entropy of brain network in the study of hemispheric differences. Entropy 2020, 22, 1220. [Google Scholar] [CrossRef]
- Ware, J.E., Jr. SF-36 Health Survey. In The Use of Psychological Testing for Treatment Planning and Outcomes Assessment; Maruish, M.E., Ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 1993; pp. 1227–1246. [Google Scholar]
- Sheikh, J.I.; Yesavage, J.A. Geriatric Depression Scale (GDS): Recent evidence and development of a shorter version. In Clinical Gerontology: A Guide to Assessment and Intervention; The Haworth Press: New York, NY, USA, 1986; pp. 165–173. [Google Scholar] [CrossRef]
- Stalder, T.; Steudte-Schmiedgen, S.; Alexander, N.; Klucken, T.; Vater, A.; Wichmann, S.; Kirschbaum, C.; Miller, R. Stress-related and basic determinants of hair cortisol in humans: A meta-analysis. Psychoneuroendocrinology 2017, 77, 261–274. [Google Scholar] [CrossRef]
- Prince, M.; Acosta, D.; Ferri, C.P.; Guerra, M.; Huang, Y.; Jacob, K.S.; Llibre Rodriguez, J.J.; Salas, A.; Sosa, A.L.; Williams, J.D.; et al. A brief dementia screener suitable for use by non-specialists in resource poor settings—The cross-cultural derivation and validation of the brief Community Screening Instrument for Dementia. Int. J. Geriatr. Psychiatry 2011, 26, 899–907. [Google Scholar] [CrossRef]
- Weir, D.R.; Langa, K.M.; Ryan, L.H. Harmonized Cognitive Assessment Protocol (HCAP): Study Protocol Summary. 2016. Available online: http://hrsonline.isr.umich.edu/index.php?p=shoavail&iyear=ZU (accessed on 2 January 2019).
- Wechsler, D. Wechsler Adult Intelligence Scale; Psychological Corporation: New York, NY, USA, 1997. [Google Scholar]
- Jersild, A.T. Mental set and shift. Arch. Psychol. 1927, 14, 81. [Google Scholar]
- Hull, R.; Martin, R.C.; Beier, M.E.; Lane, D.; Hamilton, A.C. Executive function in older adults: A structural equation modeling approach. Neuropsychology 2008, 22, 508–522. [Google Scholar] [CrossRef] [PubMed]
- Pulopulos, M.M.; Hidalgo, V.; Almela, M.; Puig-Perez, S.; Villada, C.; Salvador, A. Hair cortisol and cognitive performance in healthy older people. Psychoneuroendocrinology 2014, 4, 100–111. [Google Scholar] [CrossRef] [PubMed]
| Variables | M | SD |
|---|---|---|
| SBP-R | 4.41 | 11.56 |
| SBP at baseline | 130.92 | 21.31 |
| Cognition Factor | −0.03 | 0.90 |
| Recall (HCAP) | 3.90 | 1.88 |
| Serial Subtraction (HCAP) | 3.56 | 1.80 |
| CSI-D | 7.80 | 1.38 |
| Letter-Number Sequencing | 8.42 | 3.04 |
| Digit-Symbol Substitution | 46.30 | 15.71 |
| Plus-Minus Task | 69.64 | 74.22 |
| Stroop Task | 36.30 | 24.01 |
| Short Blessed | 8.58 | 4.45 |
| Mental Health Challenges | 0.01 | 0.68 |
| Geriatric Depression Scale | 0.89 | 1.44 |
| SF-36 Mental | 48.36 | 11.54 |
| Physical Health Challenges | −0.04 | 0.67 |
| Number of chronic conditions | 3.58 | 2.18 |
| SF-36 Physical | 46.51 | 6.47 |
| Cortisol (log) | 2.35 | 1.47 |
| Variable | Parameter | Frequentist Estimates | GFI Estimates | 95% GFI CI |
|---|---|---|---|---|
| Model 1 | ||||
| Intercept | γ00 | 5.82 (3.65) | 5.83 (3.87) | (−1.92, 13.30) |
| Tertile | γ10 | −0.33 * (0.15) | −0.33 (0.15) | (−0.64, −0.03) |
| SBP at baseline | γ01 | 0.22 ***(0.06) | 0.22 (0.07) | (0.09, 0.35) |
| Cognition | γ02 | −11.82 (2.57) | −11.98 (3.16) | (−18.28, −6.11) |
| Physical health challenges | γ03 | −6.59 * (2.57) | −6.53 (2.60) | (−11.65, −1.48) |
| Tertile × Cognition | γ11 | 0.32 * (0.16) | 0.32 (0.16) | (0.01, 0.64) |
| Tertile × Physical Health | γ12 | 0.13 (0.22) | 0.13 (0.21) | (−0.29, 0.56) |
| Between-person variance | τ00 | 318.9 (17.86) | 356.37 | (160.57, 720.52) |
| Within-person variance | σ2 | 121.5 (11.02) | 122.02 | (105.97, 140.45) |
| Model 2 | ||||
| Intercept | γ00 | 5.34 (5.42) | 5.31 (5.71) | (−5.89, 16.70) |
| Tertile | γ10 | −0.31 * (0.14) | −0.31 (0.14) | (−0.58, −0.04) |
| SBP at baseline | γ01 | 0.22 *** (0.06) | 0.22 (0.06) | (0.10, 0.33) |
| Cognition | γ02 | −23.33 *** (2.68) | −23.27 (3.17) | (−29.33, −16.99) |
| Mental health challenges | γ03 | −23.57 *** (3.13) | −23.58 (3.35) | (−30.08, −16.96) |
| Tertile × Cognition | γ11 | 0.36 * (0.15) | 0.36 (0.15) | (0.07, 0.66) |
| Tertile × Mental Health | γ12 | 0.15 (0.20) | 0.15 (0.20) | (−0.25, 0.53) |
| Between-person variance | τ00 | 742.2 (27.24) | 808.12 | (384.35, 1542.38) |
| Within-person variance | σ2 | 103.1 (10.15) | 103.76 | (90.12, 119.77) |
| Model 3 | ||||
| Intercept | γ00 | 4.74 (3.38) | 4.76 (3.54) | (−2.19, 11.89) |
| Tertile | γ10 | −0.23 (0.15) | −0.23 (0.15) | (−0.53, 0.06) |
| SBP at baseline | γ01 | 0.21 *** (0.05) | 0.22 (0.06) | (0.11, 0.33) |
| Cognition | γ02 | −10.12 ***(2.32) | −10.20 (3.16) | (−15.62, −4.99) |
| Cortisol | γ03 | −1.08 (1.16) | −1.07 (1.20) | (−3.40, 1.25) |
| Tertile × Cognition | γ11 | 0.38 * (0.16) | 0.38 (0.16) | (0.06, 0.69) |
| Tertile × Cortisol | γ12 | 0.22 * (0.10) | 0.22 (0.10) | (0.01, 0.42) |
| Between-person variance | τ00 | 260.2 (16.13) | 289.03 | (135.09, 576.38) |
| Within-person variance | σ2 | 121.5 (11.02) | 122.02 | (106.42, 139.90) |
| Model 4 | ||||
| Intercept | γ00 | −11.56 (17.21) | −12.14 (20.26) | (−52.43, 27.09) |
| Tertile | γ10 | −0.37 * (0.19) | −0.37 (0.19) | (−0.75, 0.004) |
| SBP at baseline | γ01 | 0.74 *** (0.06) | 0.75 (0.06) | (0.62, 0.87) |
| Cognition | γ02 | −15.99 *** (3.01) | −16.02 (3.04) | (−22.02, −0.10) |
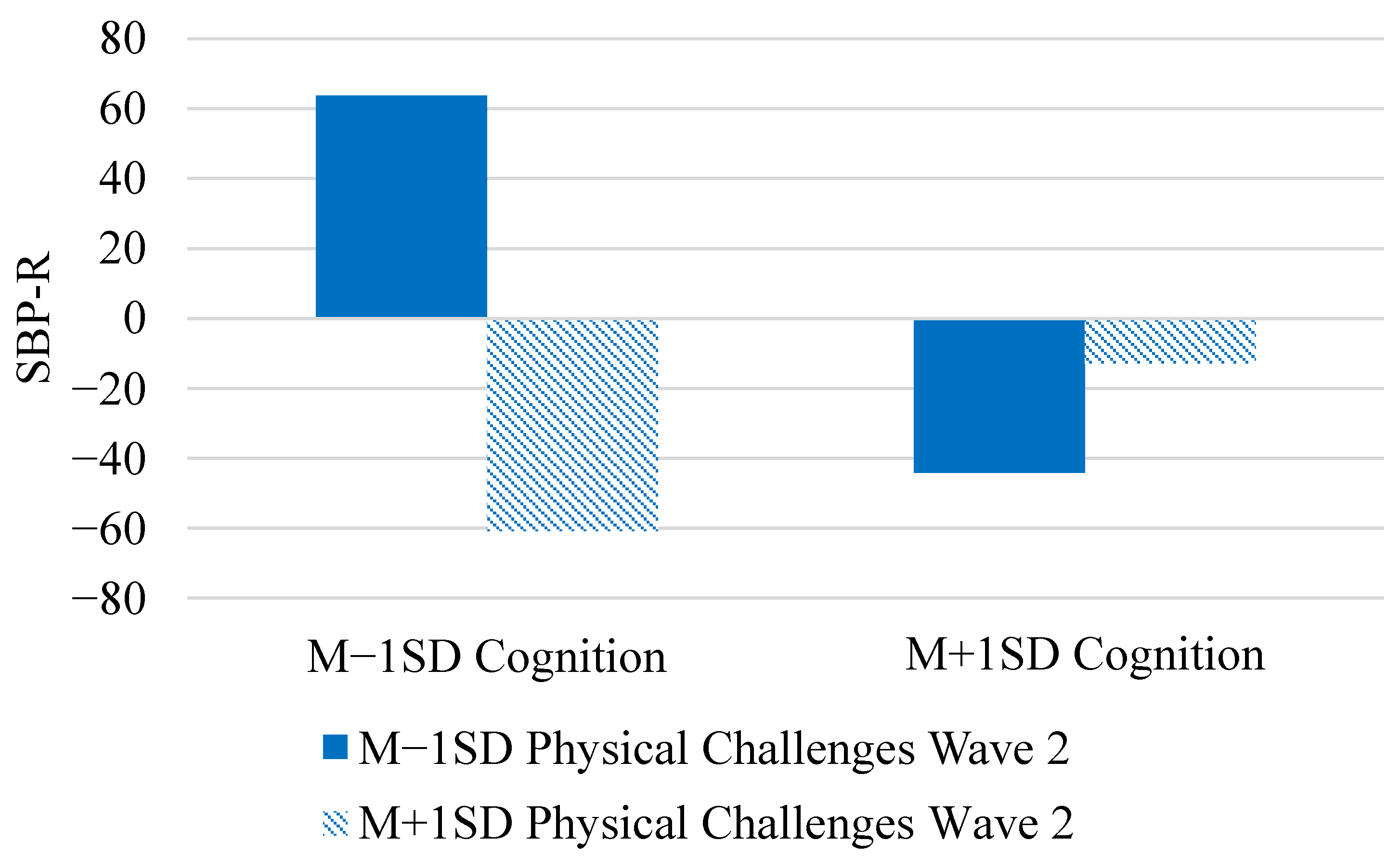
| Physical challenges Wave 1 | γ03 | 13.00 (35.49) | 13.39 (42.37) | (−67.28, 96.14) |
| Physical challenges Wave 2 | γ04 | −28.45 (29.14) | −29.09 (34.88) | (−96.27, 36.09) |
| Tertile × Cognition | γ11 | 0.04 (0.24) | 0.04 (0.24) | (−0.43, 0.51) |
| Tertile × Physical Wave 2 | γ12 | 0.02 (0.24) | 0.02 (0.24) | (−0.44, 0.49) |
| Cognition × Phys. Wave 2 | γ05 | 51.37 *** (4.38) | 51.39 (4.46) | (42.60, 60.15) |
| Tertile × Cog. × Phys. w2 | γ13 | 0.40 (0.30) | 0.40 (0.30) | (−0.19, 0.99) |
| Between-person variance | τ00 | 2603.9 (51.03) | 3482.92 | (1127.96, 9974.09) |
| Within-person variance | σ2 | 100.3 (10.02) | 101.26 | (84.28, 121.27) |
| Model 5 | ||||
| Intercept | γ00 | −1.68 (6.14) | −1.74 (7.13) | (−16.20, 12.70) |
| Tertile | γ10 | −0.31 (0.25) | −0.31 (0.25) | (−0.81, 0.50) |
| SBP at baseline | γ01 | 0.35 *** (0.07) | 0.35 (0.08) | (0.20, 0.87) |
| Cognition | γ02 | −14.02 ** (4.26) | −14.08 (4.53) | (−23.19, −5.21) |
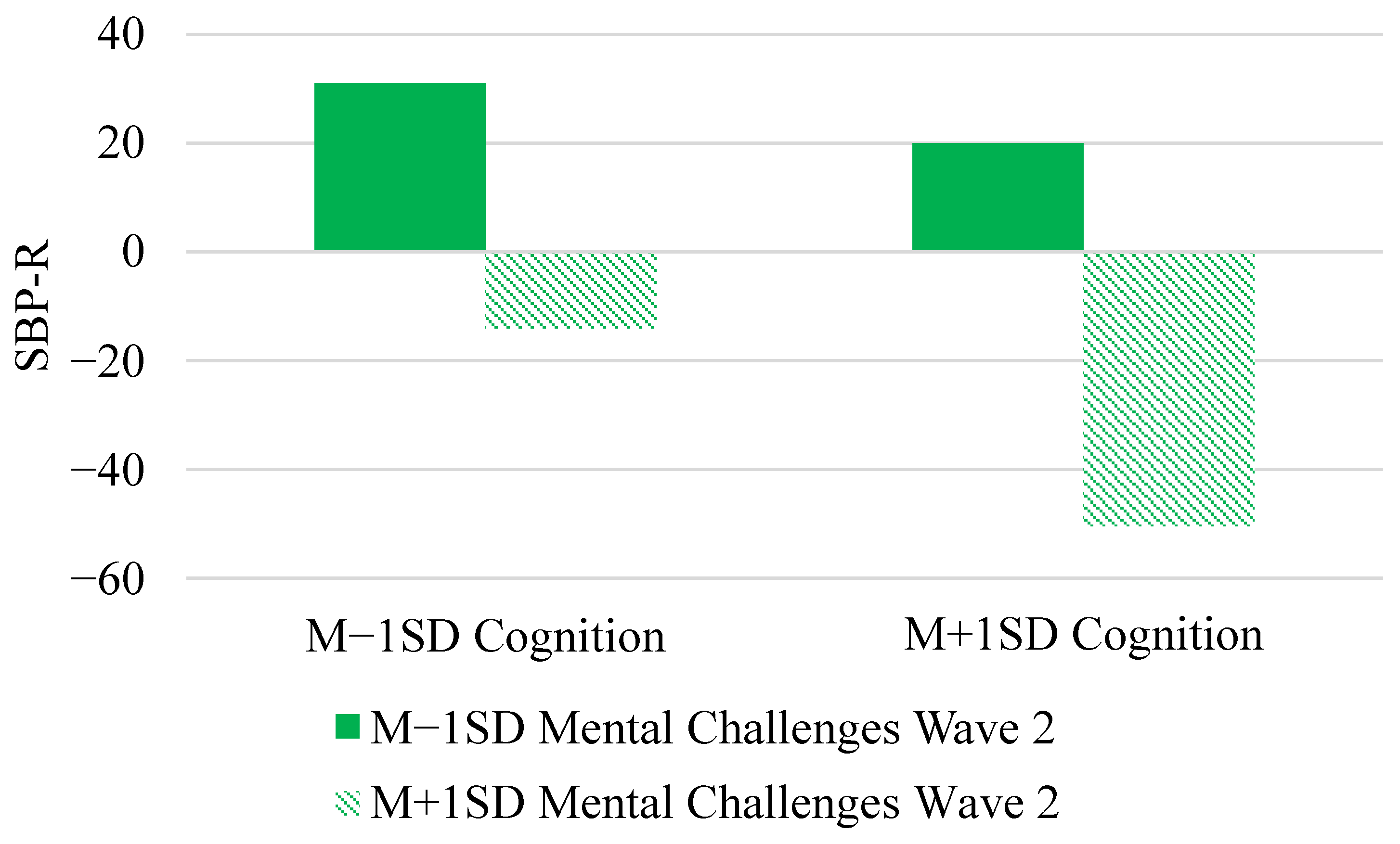
| Mental challenges Wave 1 | γ03 | 48.08 * (19.32) | 47.43 (22.18) | (4.2887, 91.98) |
| Mental challenges Wave 2 | γ04 | −35.44 * (14.73) | −34.94 (16.78) | (−69.057, −2.80) |
| Tertile × Cognition | γ11 | 0.14 (0.31) | 0.14 (0.31) | (−0.46, 0.74) |
| Tertile × Mental Wave 2 | γ12 | −0.04 (0.30) | −0.05 (0.30) | (−0.64, 0.55) |
| Cognition × Ment.Wave 2 | γ05 | −7.55 * (3.65) | −7.55 (3.70) | (−14.63, −0.22) |
| Tertile × Cog. × Ment. w2 | γ13 | 0.21 (0.34) | 0.21 (0.34) | (−0.47, 0.89) |
| Between-person variance | τ00 | 371.2 (19.27) | 501.73 | (146.46, 1464.99) |
| Within-person variance | σ2 | 176.5 (13.28) | 178.25 | (148.90, 212.98) |
| Model 6 | ||||
| Intercept | γ00 | −5.79 (9.29) | −5.86 (10.35) | (−26.25, 14.53) |
| Tertile | γ10 | 0.22 (0.25) | 0.23 (0.25) | (−0.26, 0.72) |
| SBP at baseline | γ01 | 0.43 *** (0.06) | 0.44 (0.07) | (0.31, 0.57) |
| Cognition | γ02 | −11.31 *** (3.10) | −11.29 (3.18) | (−17.66, −5.11) |
| Cortisol Wave 1 | γ03 | −8.59 (8.64) | −8.43 (9.62) | (−28.48, 10.68) |
| Coritsol Wave 2 | γ04 | −6.09 (10.87) | −6.34 (12.07) | (−30.29, 17.62) |
| Tertile × Cognition | γ11 | −0.02 (0.25) | −0.02 (0.25) | (−0.51, 0.48) |
| Tertile × Cortisol Wave 2 | γ12 | 0.79 * (0.34) | 0.80 (0.34) | (0.13, 1.46) |
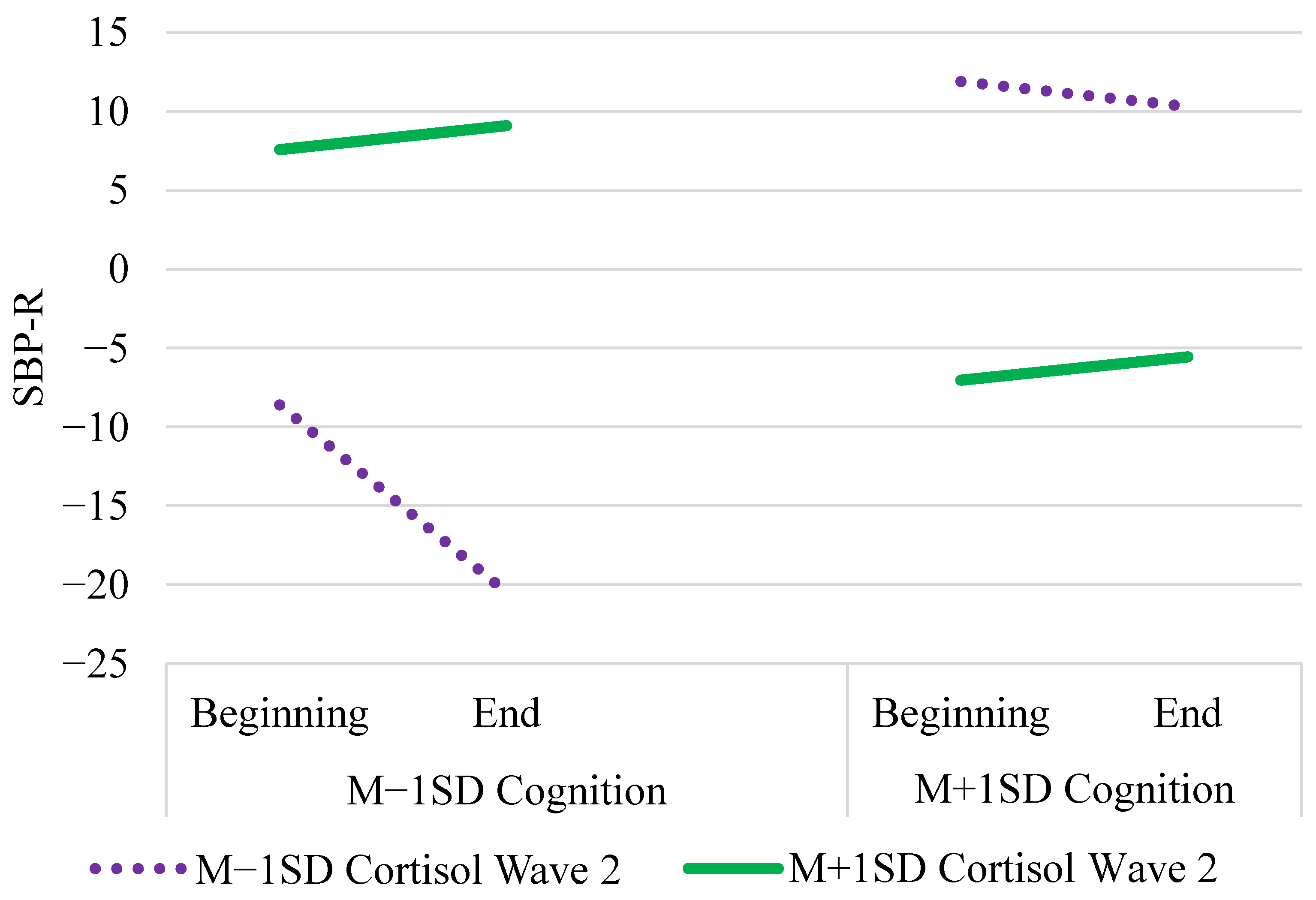
| Cognition × Cort. Wave 2 | γ05 | 24.10 *** (3.95) | 24.32 (4.10) | (16.33, 32.35) |
| Tertile × Cog. × Cort. w2 | γ13 | −0.83 * (0.38) | −0.84 (0.38) | (−1.58, −0.09) |
| Between-person variance | τ00 | 928.7 (30.47) | 1146.28 | (429.03, 2817.93) |
| Within-person variance | σ2 | 132.5 (11.51) | 133.46 | (113.88, 156.87) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neupert, S.D.; Growney, C.M.; Zhu, X.; Sorensen, J.K.; Smith, E.L.; Hannig, J. BFF: Bayesian, Fiducial, and Frequentist Analysis of Cognitive Engagement among Cognitively Impaired Older Adults. Entropy 2021, 23, 428. https://doi.org/10.3390/e23040428
Neupert SD, Growney CM, Zhu X, Sorensen JK, Smith EL, Hannig J. BFF: Bayesian, Fiducial, and Frequentist Analysis of Cognitive Engagement among Cognitively Impaired Older Adults. Entropy. 2021; 23(4):428. https://doi.org/10.3390/e23040428
Chicago/Turabian StyleNeupert, Shevaun D., Claire M. Growney, Xianghe Zhu, Julia K. Sorensen, Emily L. Smith, and Jan Hannig. 2021. "BFF: Bayesian, Fiducial, and Frequentist Analysis of Cognitive Engagement among Cognitively Impaired Older Adults" Entropy 23, no. 4: 428. https://doi.org/10.3390/e23040428
APA StyleNeupert, S. D., Growney, C. M., Zhu, X., Sorensen, J. K., Smith, E. L., & Hannig, J. (2021). BFF: Bayesian, Fiducial, and Frequentist Analysis of Cognitive Engagement among Cognitively Impaired Older Adults. Entropy, 23(4), 428. https://doi.org/10.3390/e23040428






