1. Introduction
Due to the well-known many-body problem, electron transport in nanoscale devices must be modeled as an open quantum system [
1]. The contacts, cables, atoms, electromagnetic radiation, etc. are commonly considered part of the environment. The effect of this environment on the dynamics of the simulated degrees of freedom, i.e., the electrons in the active region, can be recovered using some type of perturbative approximation. There are different formalisms in the literature to deal with such
environmental perturbation (Green’s functions [
2,
3,
4], density matrix [
5,
6], Wigner distribution function [
7,
8,
9,
10,
11], Kubo formalism [
12], Pauli quantum Master equation [
13,
14], pure states [
15,
16], etc). In this work, we analyze the possibility of modeling the quantum nature of such simulated degrees of freedom with single-particle time-dependent pure states and their
environmental perturbation as a transition between such single-particle time-dependent pure states.
In particular, we are interested in modeling the collision of an electron with a phonon or/and photon in an active region with tunneling barriers, i.e., in a scenario where the energy and momentum operators do not commute. The path to achieve this goal requires first the answer to the following question:
Is it possible to model an open system in terms of single-particle pure states?. Once this conceptual question is answered, the next practical question that needs to be addressed is the following:
How do we select the single-particle pure states before and after the collision? In this paper, we answer both questions. It will be shown that the alternative Bohmian formulation of quantum transport [
17] provides a rigorous and versatile tool to describe collisions in open quantum systems in terms of single-particle time-dependent pure wave functions. This work is part of a long-term research project for the development of a general-purpose nanoelectronic device simulator, the so-called BITLLES simulator [
18], using Bohmian trajectories.
The structure of the paper is the following. In
Section 2, the answer to the first question about using single-particle pure states for open systems is provided from the Bohmian description of quantum phenomena. In
Section 3, we provide an exact model for matter–light interaction in a closed system. Some simulation results are reported for different conditions of the total energy and a final discussion on the interaction between active region and environment to extend this description to an open system is provided. In
Section 4, the practical implementation of the transition between pre-selected and post-selected states is discussed. This transition is performed for two different models: model A deals with energy conservation, and model B deals with momentum conservation. In
Section 5 these two models, computed in a flat potential and in an arbitrary potential, are compared. Our conclusions are summarized in
Section 6.
2. Is It Possible to Model an Open System in Terms of Single-Particle Pure States?
As we have stated, the active region of an electron device is, strictly speaking, an open quantum system interacting with the contacts, atoms in thermal motion, radiation, etc. As a consequence, in principle, one is not allowed to describe the electron in the active region in terms of pure states, but one has to rely on the use of the reduced density matrix.
Most approaches to open systems revolve around the reduced density matrix built by tracing out the degrees of freedom of the environment [
1]. The ability to describe open systems with pure states can be partially justified when dealing with Markovian systems. In a pragmatical definition of Markovianity [
19], the correlations between system and environment decay in a time scale that is much smaller than the observation (or relevant) time interval of the system. Thus, it can be assumed that every time we observe the system, it is defined by a pure state. For Markovian evolutions, the Lindblad master equation [
20] for the reduced density matrix is a standard simulation tool. In addition, in Markovian scenarios where the off-diagonal terms of the reduced density matrix become irrelevant, a quantum master equation can be implemented, dealing with transitions between pure states [
13,
14].
In fact, it is possible to develop stochastic Schrödinger equations to unravel the reduced density matrix in terms of a pure-state solution for either Markovian or non-Markovian systems. The pure-state solution of stochastic Schrödinger equations can be interpreted as the state of the Markovian system while the environment is under (continuous) observation. However, such a physical interpretation cannot be given to the solutions of the stochastic Schrödinger equations for non-Markovian systems [
21,
22,
23,
24,
25,
26,
27,
28,
29,
30], where pure states can provide the correct one-time ensemble value but cannot be used to compute time correlations.
Therefore, for general non-Markovian quantum processes, when we are interested in a time-resolved description of the electron device performance, it is not possible to define the open system in terms of orthodox pure states. As described in [
31] and explained below, a proper solution for treating electrons in non-Markovian open systems as single-particle pure states comes from the Bohmian formalism.
To explain how the Bohmian theory allows for a general description of a many-body quantum system in terms of wave functions, we consider a simplified scenario with only two degrees of freedom: one degree of freedom
x belonging to the system plus one degree of freedom
y belonging to the environment. Thus, the pure state in the position representation solution of the unitary Schrödinger equation is
. For each experiment, labelled by
j, a Bohmian quantum state is defined by
plus two well-defined trajectories,
in the
x-physical space and
in the
y-physical space. The role of the many-body wavefunction
is guiding each trajectory
with a velocity that reads [
17,
32,
33]
where
is the current density with
the mass of the
x-particle, and where
is the phase of the wave function written in polar form
. Analogous definitions are possible for the
trajectory. By construction, the two positions
in different
experiments are distributed (obeying quantum equilibrium [
32,
33]) at any time as
The identity in (
2) requires
. Numerically, we only require a large enough
W to reproduce ensemble values given by the Born law in agreement with the orthodox theory. From a computational point of view, to ensure that (
2) is satisfied at any time
t, we only have to select the initial position
at time
according to the distribution
.
The Bohmian theory opens the possibility to deal with a wave function of a subsystem through the concept of Bohmian conditional wave function (BCWF) [
33,
34]. The BCWF is defined for the
x-degree of freedom during the
j-th experiment as
We emphasize that
provides a rigorous (Bohmian) definition of a single-particle wave function for an open system [
32] that still includes the correlations with the other degrees of freedom
y. Notice that the reason why the BCWF has a relevant role in Bohmian theory is because the trajectory
is equivalently guided by
or by
. In other words, the velocity
in (
1) can be equivalently computed from the BCWF as
where
,
, and
is the angle of the BCWF in polar form
. Notice that we have not performed any approximation about the Markovianity of the quantum system in the definition of the BCWF. Thus, at the conceptual level, we conclude that any quantum open system can be analyzed in terms of single-particle pure states (i.e., BCWF) using the Bohmian formalism. This is a well-known result [
31] and provides a definitive positive answer to the initial question:
Is it possible to model open system in terms of single-particle pure states? Yes. Notice that the BCWF
will be a time-dependent function either because
is a time-dependent function or because the trajectory
is moving.
Let us discuss now a more realistic scenario with
N electrons inside the active region with degrees of freedom
that we want to simulate explicitly (for simplicity, each electron is assumed to be defined in a 1D space). There are, however,
M environmental degrees of freedom
that we do not want to simulate explicitly. The new many-body wave function of such a scenario is
, which is numerically inaccessible. We define
as the set of all Bohmian trajectories of the system except
for the
i-particle in the
j-experiment. Notice that we are dealing now with a superindex
j indicating the experiment and subindex
i indicating each particle in a given experiment. We also define
as the set of all trajectories of the environment for the
j-experiment. Then, the set of equations of motion of the resulting
N single-electron BCWF
inside the active region can be written as follows:
The effective single-particle potential
is
where
is an external potential acting only on the system degrees of freedom
,
is the Coulomb potential between
and the rest of particles at fixed positions
and
, and
and
are potentials responsible for the remaining of quantum correlations between the degrees of freedom of the system and the environment [
31]. A mandatory clarification is needed here. Are the set of BCWFs in (
5) solving the many-body problem? No. If you want to use the coupled system of equations of motion of the
N BCWF in (
5) to describe a given experiment, first, you have to solve the Poisson (Gauss) equation to find
and
explicitly and, second, you have to know the exact solution of the many-body wave function
to find
and
for all electrons [
31]. The last step is numerically inaccessible. The merit of the system of equations in (
5) is showing that such a type of solution to the many-body function exists and that we can look for educated guesses on the shape of
and
to provide reasonable approximations. Notice that a similar procedure is followed in Density Functional Theory: it shows a method to rewrite the many-body wave function in terms of single-particle wave functions, but the procedure requires knowledge of the exchange-correlation functional, which is only known once the many-body wave function is known. See further details and an explanation on
and
in [
18,
31,
32,
33,
35,
36].
To better appreciate the details of this simulation technique for electron devices, we notice that the total current
at time
t for the
j-experiment, after solving the set of BCWF from (
5) with the appropriate approximations for
and
, can be defined from the Bohmian trajectories with the help of a quantum version of the Ramo–Shockley–Pellegrini theorem [
37] as follows:
where
L is the distance between the two (metallic) contacts that define the active region,
e is the electron charge (with sign), and
is the Bohmian velocity of the
ith electron inside the active region in the
j-experiment. Notice that the
observables are computed from the trajectories (not from the BCWF) and that they are linked to a particular experiment
j (which can be understood as a single configuration of the environment). The different possible values of
,
and
for the same (
preparation of the) many-body wave function
introduce the inherent quantum randomness in any experiment. As such, if one is interested in ensemble average values, one can repeat the calculation for all environment configurations
and particle distributions
and
. Typically, in electronics, this ensemble average of the current
over many experiments
is interesting in evaluating DC values of the electrical current under ergodic assumptions. In the laboratory, however, a large time-average of the current
in a single
j-experiment is usually performed. If one is interested in noise or time-correlations of the current at different times,
and
, then the access to the individual experiment offered by the BCWF is very relevant.
Finally, we mention which are the computational advantages of this simulation framework. It is a microscopic description of the transport in the sense that it provides an individual description for each electron inside the active region. It provides a rigorous estimation (a part from the approximations for
and
) to the quantum dynamics of electrons in the active region (open quantum system) for Markovian and non-Markovian systems. It is a versatile approach in the sense that it can simulate many different scenarios, from steady-state DC to transient and AC, including fluctuations of the current (noise). Notice that
in (
7) includes the particle and displacement current, even at THz frequencies, when multi-time measurements are implicit. In this sense, we argue that the amount of information that this simulator framework can provide in the quantum regime is comparable to the predicting capabilities of the traditional Monte Carlo solution of the Boltzmann transport equation [
38] in the semi-classical regime.
4. Implementation of the Transition from Pre- to Post-Selected BCWF
In this section, we describe practical issues on how such types of transitions between initial and final states can be implemented in a transport simulator for real electron devices based on Bohmian mechanics.
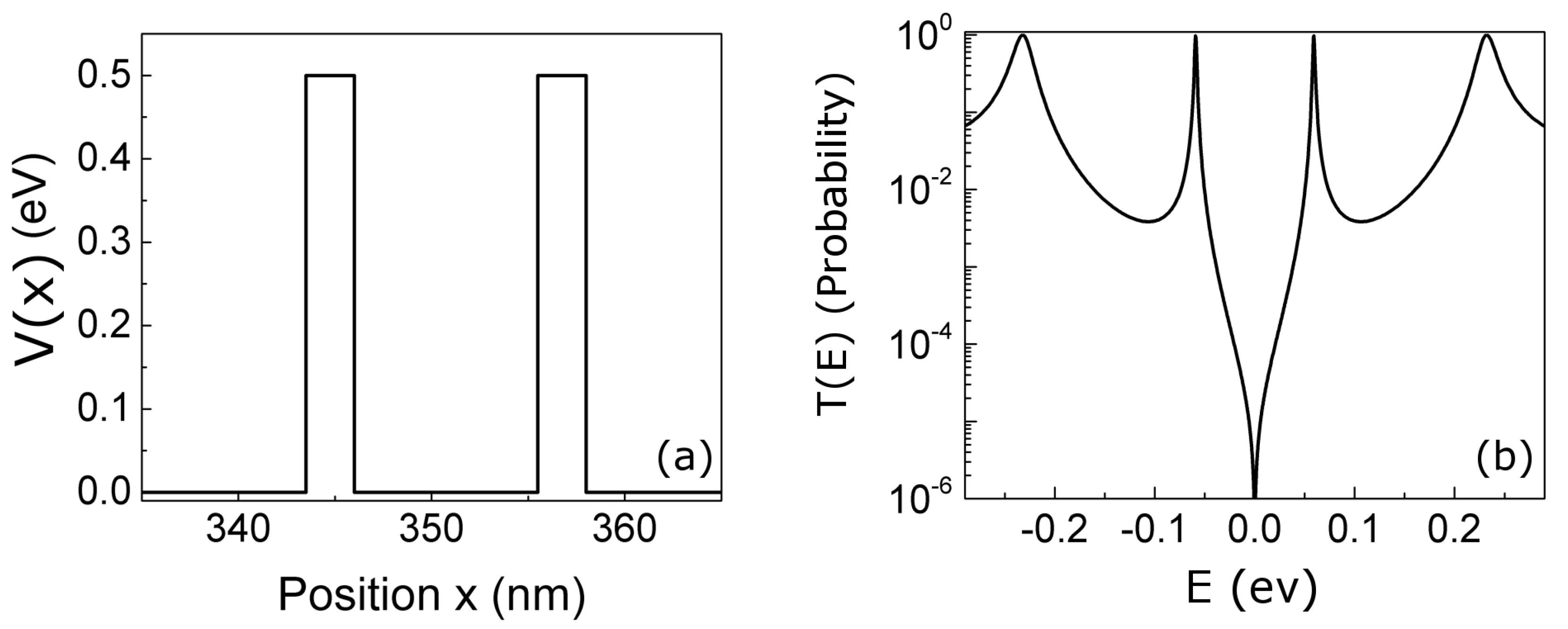
To implement the transition from pre- to post-selected BCWF, a definition of the initial and the final states is needed. Although the contacts do not allow us to perfectly prepare the wave description of electron, we can have some reasonable arguments to anticipate some of its properties. One option could be to deal with Hamiltonian eigenstates, which extend to infinite in both sides (left and right) of the device. Although these infinitely extended states are useful tools to model (steady-state) DC transport properties of quantum devices, they are less useful in describing other device performances, for example, the fluctuations of the electrical current due to the partition noise in a tunneling barrier. The initial electron, after impinging with the barrier, is either located to the left (reflection) or to the right (transmission) of a barrier but not on both sides of it. Such randomness (transmission or reflection) translates into current fluctuations. To model such fluctuations, a localized wave function seems appropriate to model electrons. However, the wave function cannot have a very narrow localization in position since the Heisenberg uncertainty principle would lead to extremely large momentum and energy uncertainties (larger than thermal energies). Thus, a definition of an electron, deep inside the contact, as a Gaussian wave packet with well-defined central position and central energy seems reasonable. We add that such a limited spatial extension of the electron wave function can be related to the coherence length of the sample.
In classical mechanics, an electron with a well-defined energy is compatible with an electron with a well-defined momentum. However, this is not the case for quantum electrons. As a general rule, two properties can be simultaneously well-defined if their operators commute. In our case, the energy (linked to the Hamiltonian operator
) and the momentum (linked to the momentum operator
) can be simultaneously defined when
. In the position representation, knowing that the Hamiltonian operator is the sum of the kinetic energy operator
, which obviously commutes with
, plus the potential energy operator
, momentum and energy are well-defined properties when
Thus, only when dealing with flat potentials we can assume that a wave packet with a reasonable well-defined energy has also a reasonable well-defined momentum. This restriction seems relevant to transport models developed in phase-space (the Wigner distribution function), where information on only momenta and positions are available.
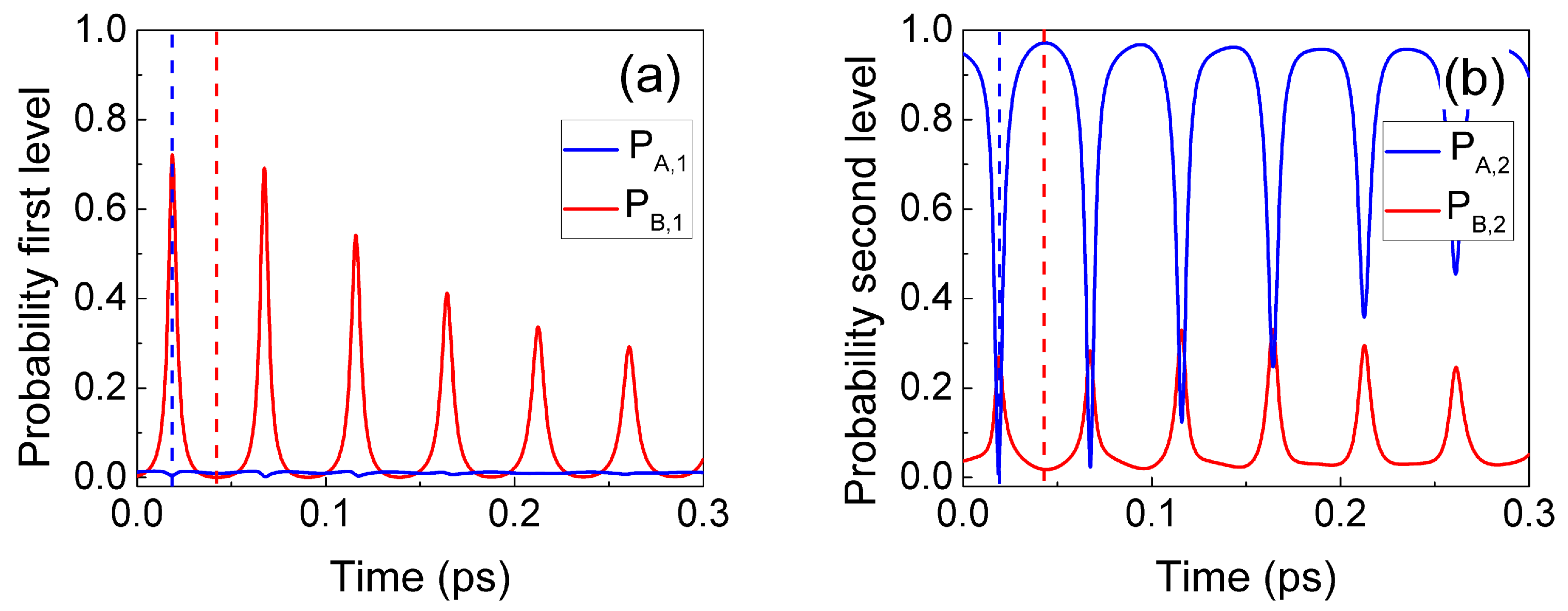
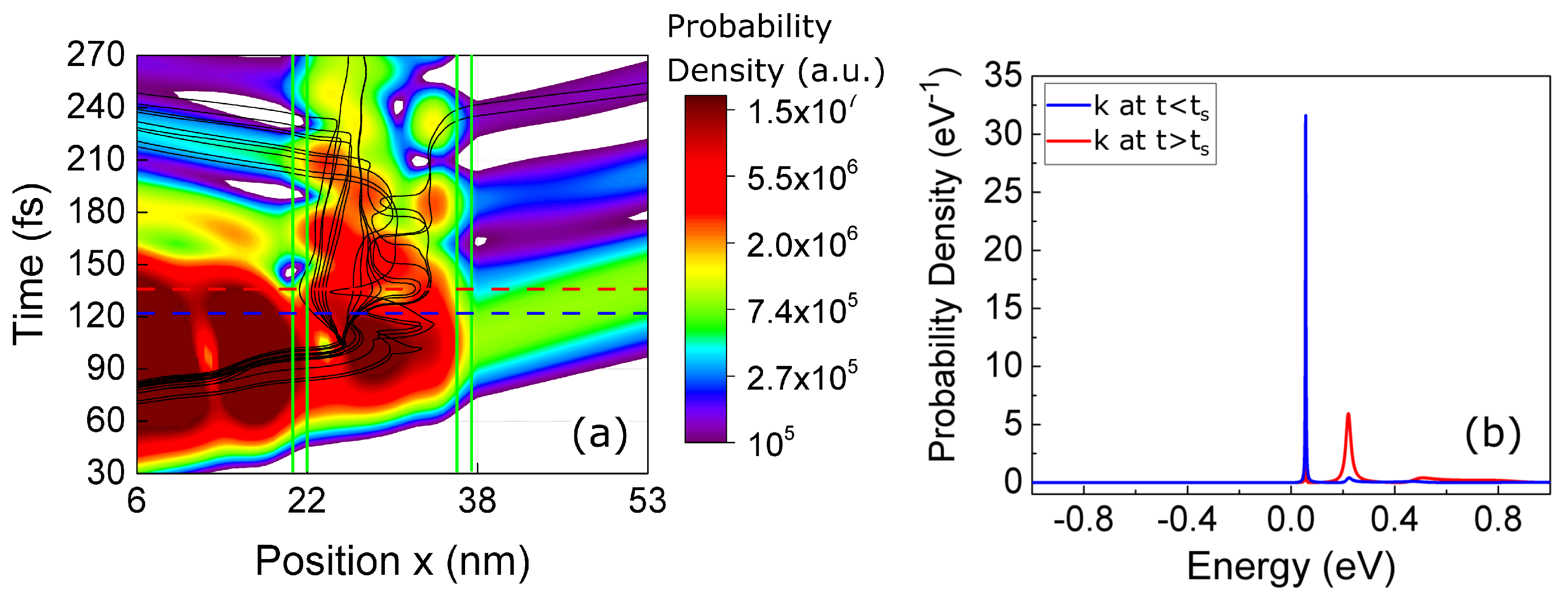
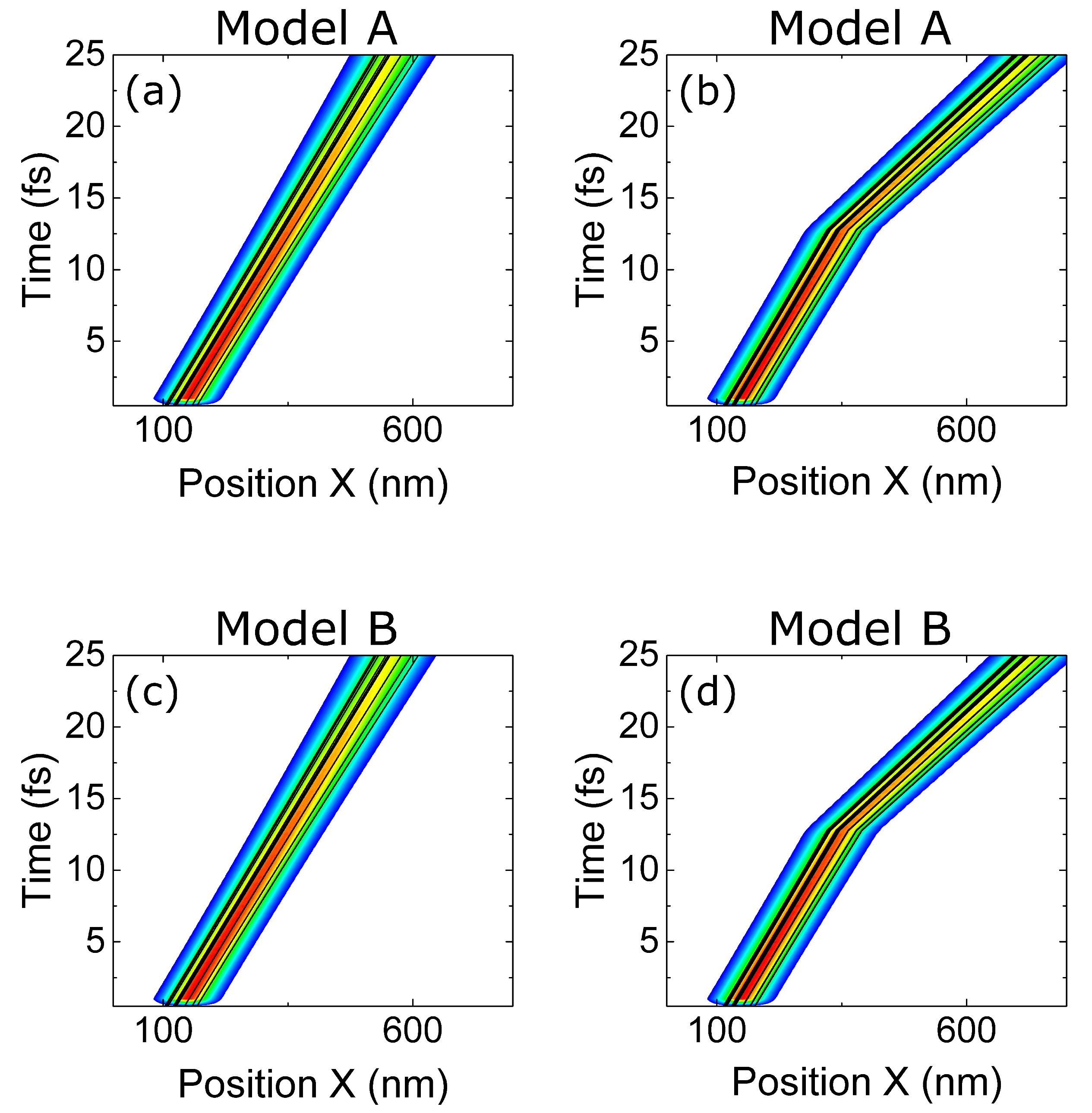
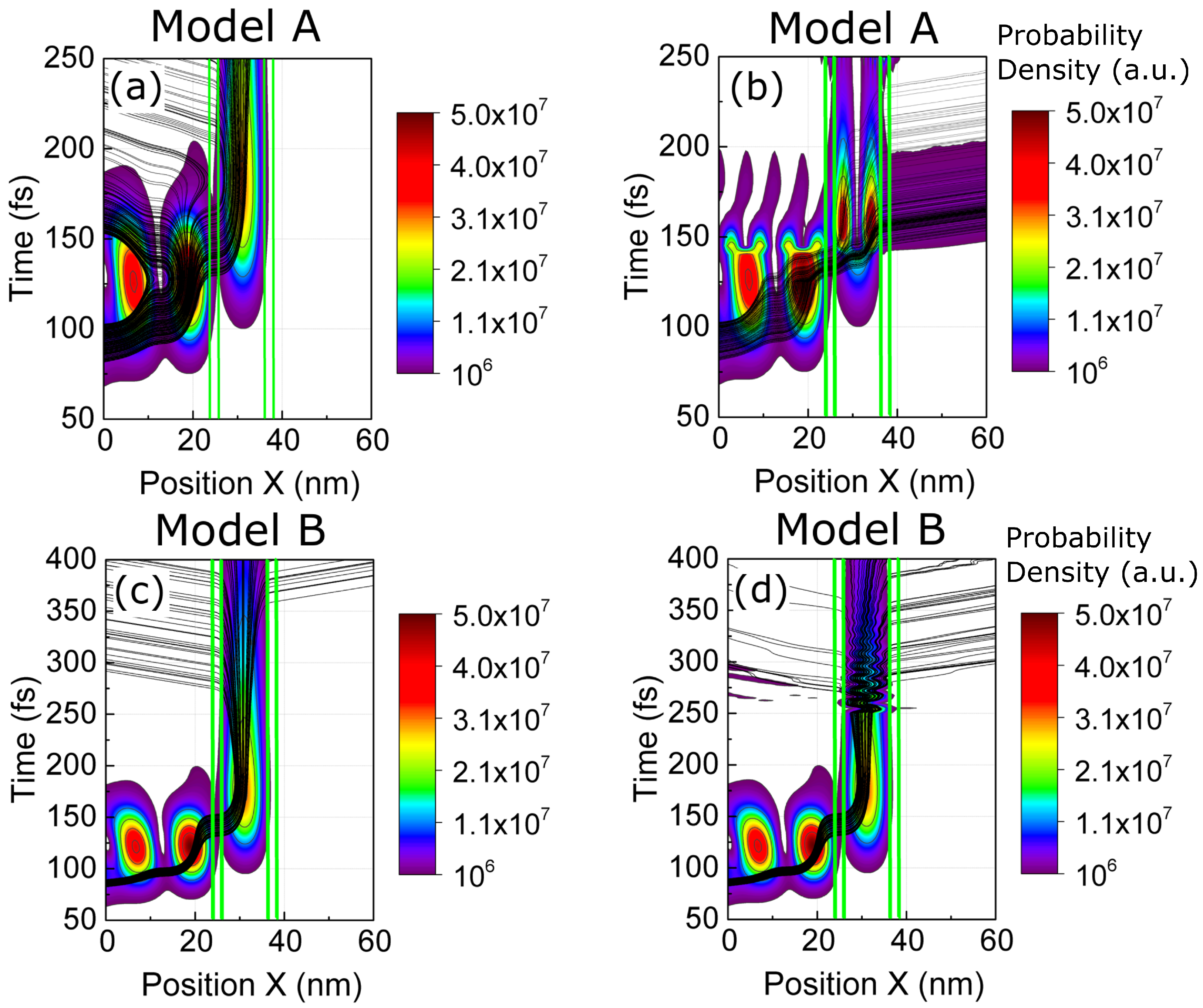
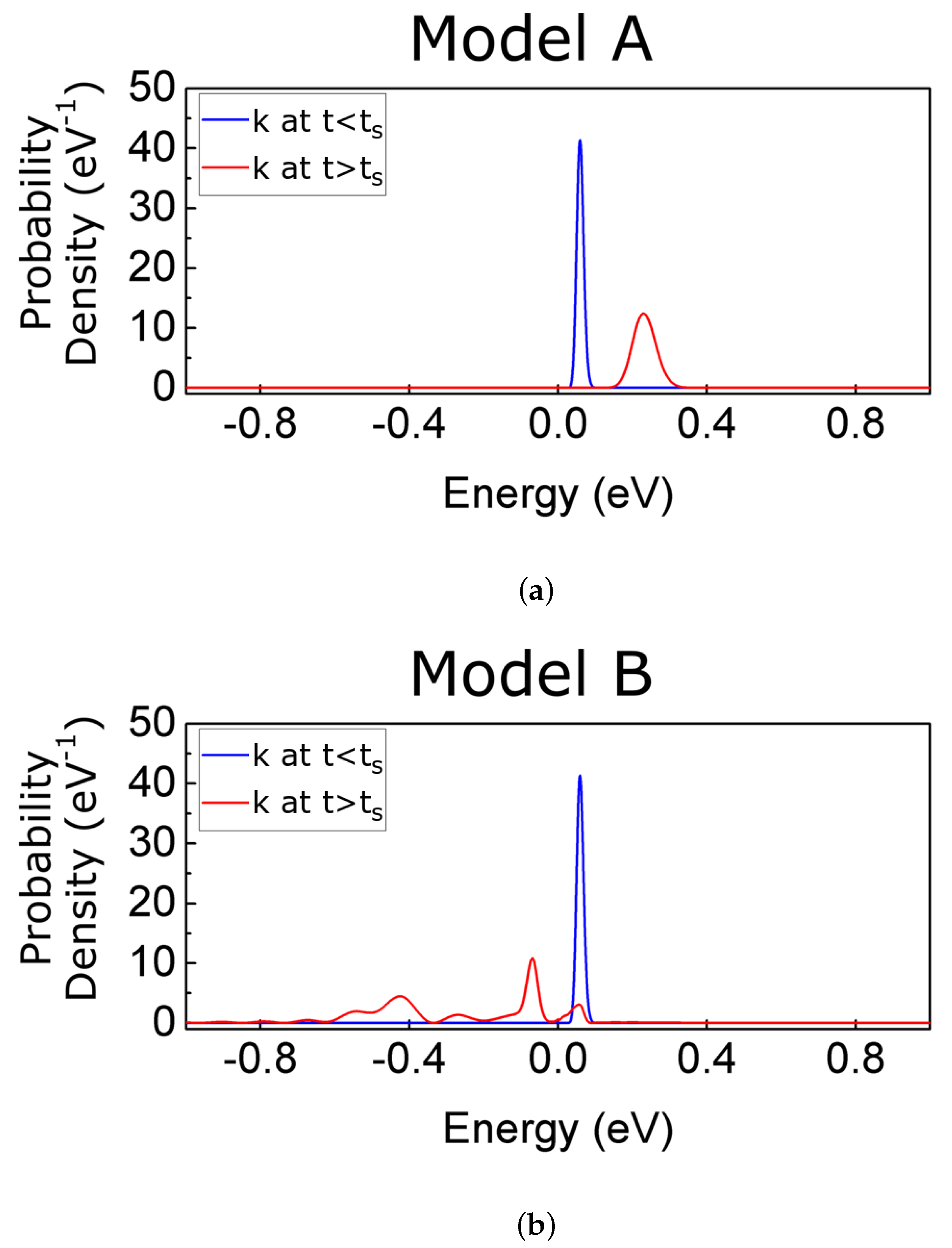
In the next two subsections, we discuss the implementation of the transition from a pre- to a post-selected BCWF when using well-defined energies (model A) or momenta (model B). In
Section 5, we compare the numerical results of these two different implementations.
4.1. Model A: Change in the Central Energy
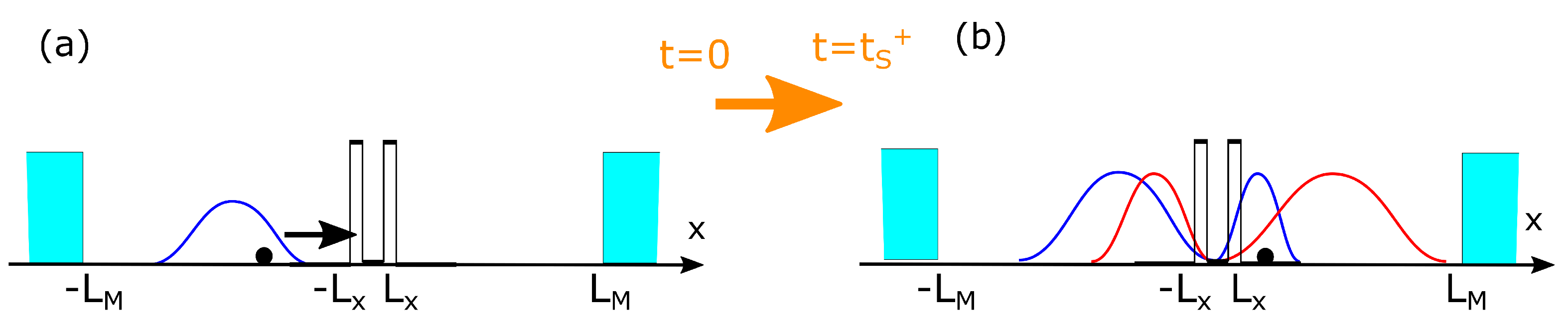
We consider an electron defined by a single-particle BCWF that, at time
, undergoes a scattering event. We define
as the time just before and
as the time just after the scattering event. For simplicity, we consider
, but we have seen in
Section 3 that such a transition between initial and final BCWFs takes a finite time because, from a conceptual point of view, it has to guarantee the continuity of the BCWF in space and time. The initial and final BCWFs are
and
, which satisfy
, with
the energy of a photon. Within the energy representation, the wave packet can be decomposed into a superposition of Hamiltonian eigenstates
of the electron
in (
8) as
with
. The central energy
is
which can be increased to obtain the new central energy at
as
where we have defined
. Thus, the new wavepacket after the collision is
This transition corresponds to the absorption of energy by the electron. Emission can be identically modeled by using
. If required, the
technical discontinuity between
and
can be solved by assuming that the change in energy is produced in a finite time interval
, with
being the time step of the simulation. Then, at each time step of the simulation, the change in the wave packet central energy is
. A
continuous change in both energy and wave packet will be obtained as far as
. This continuous evolution of the BCWF can be represented as a Schrödinger-like equation, as explained in [
31].
4.2. Model B: Change in Central Momentum
In Reference [
34], we explain how a change in momentum
in a wave packet in free space can be performed with a unitary Schrödinger equation. That algorithm can be understood as a pre- and a post-selection of the initial BCWF,
, and of the final BCWF,
, respectively. At time
, the BCWF can be written as a supersposition of momentum eigenstates
(which are a basis of the electron in the
x space) as
with
. The central momentum
is
which can be increased to get the new central momentum
at
as
where we have defined
. In this particular scenario, we know the explicit shape of the momentum eigenstates,
, so that
With the condition
, it can be easily found the unitary equation satisfied by the BCWF. If we define
as the wave function solution of the following Schrödinger equation,
, with initial condition at
given by
, then the solution
for
is identical to the following Schrödinger equation,
, for the original
and with its original initial condition for
. Finally, a single equation for
valid for all times is simply
where
is a Heaviside function equal to 1 for
and zero otherwise. Thus, a description of the evolution of the wave function
during the collision process can be made from a unitary Schrödringer equation, where the momentum operator
is changed for the new momentum operator
, as indicated in [
34]. Notice that the probability presence of the scattered wave packet satisfies
because only a global phase
is added.
It is quite easy to see from (
4) that the Bohmian velocity of the electron after the collision computed from
is just the old velocity computed from
plus
,
The collision increases the velocity of the electron by the same amount that we add in (
30). Unfortunately, as discussed at the beginning of the section, a global mechanism of scattering valid for scenarios with potential barriers requires dealing with a change in the energy as presented in model A (not with change of the momentum as presented in this model B).