Time-Reversibility, Causality and Compression-Complexity
Abstract
1. Introduction
2. Methods
2.1. Effort-to-Compress
2.2. Compression-Complexity Causality
2.3. A Novel Temporal Asymmetry Measure
2.3.1. Theoretical Underpinnings of ETC
- : the given sequence Y as it is;
- : transformed Y, once the most frequently occurring pair in Y has been substituted with another symbol, i.e., the sequence after the first iteration of the ETC algorithm;
- : transformed sequence after iterations of the ETC algorithm, where, at each iteration, the most frequently occurring pair in that sequence is being substituted by a new symbol;
- : transformed sequence Y after n iterations, where no more iterations after this are possible, and hence n is the ETC value;
- : most frequently occurring pair in . In other words, it is the first most dominant shortest pattern (of length 2);
- : most frequently occurring pair in . In other words, it is the second most dominant shortest pattern (of length 2 in , but may be of length 2 or 3 in the original sequence, Y);
- : most frequently occurring pair in ;
- : most frequently occurring pair in . It is the most dominant shortest pattern.
2.3.2. Compressive Potential
2.3.3. Compressive-Potential-Based Temporal Asymmetry Measure
3. Results
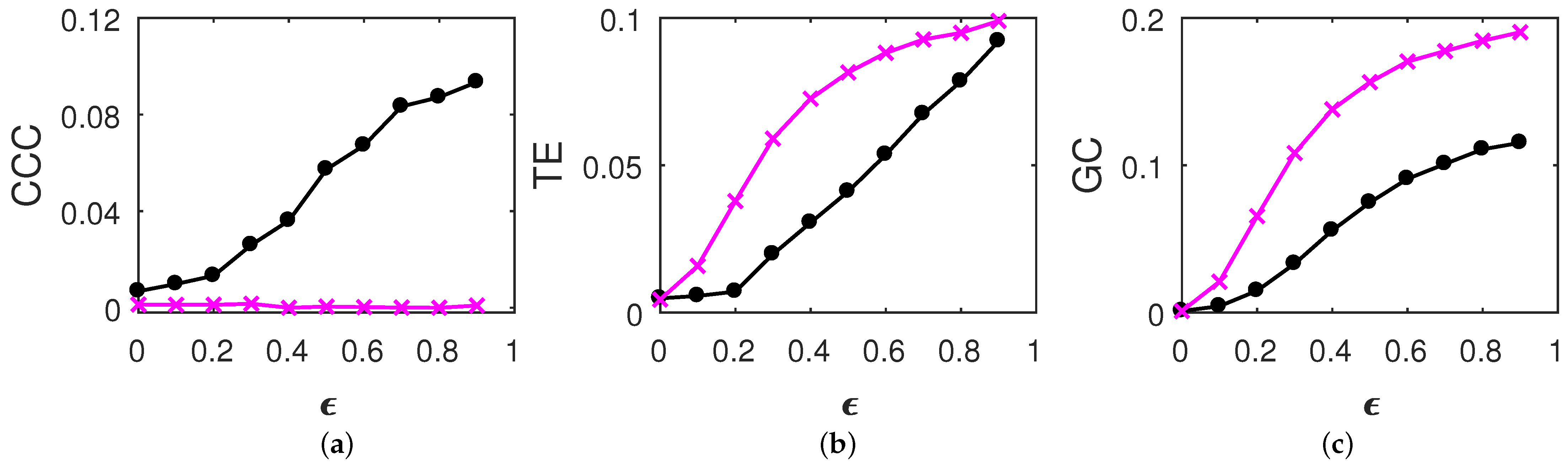
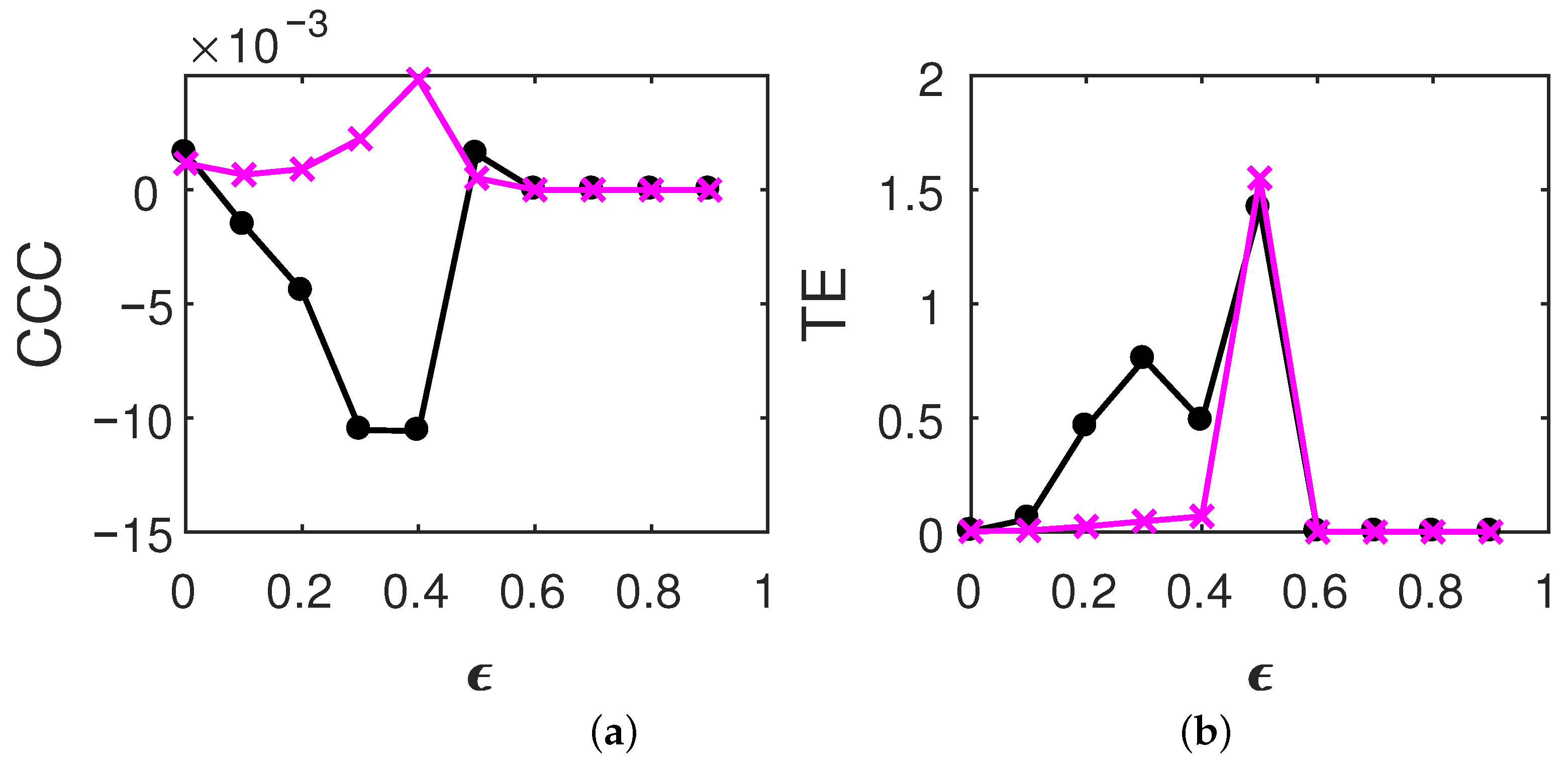
3.1. Causality between Coupled, Time-Reversed Processes
3.2. Detection of Temporal Reversibility
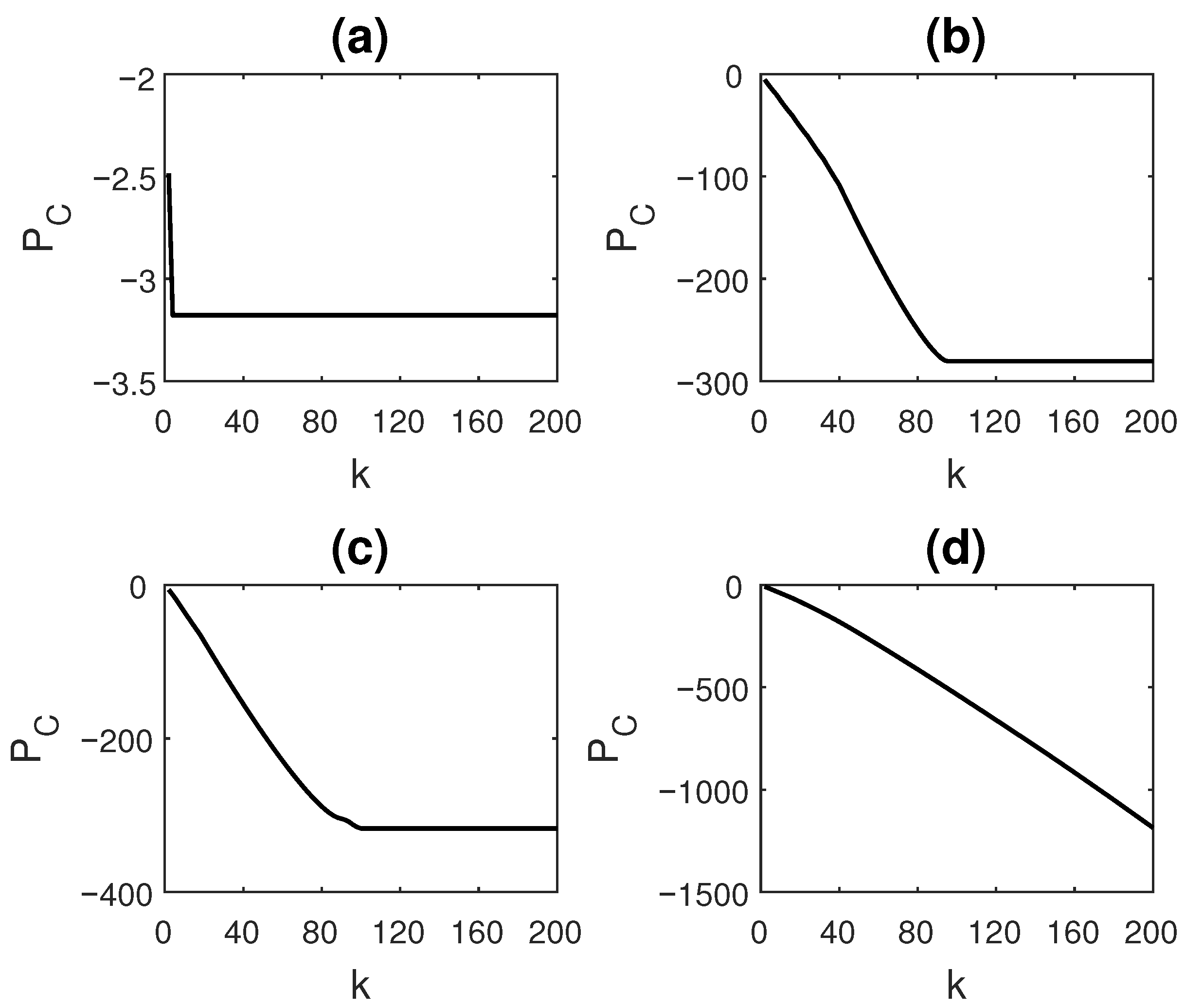
3.2.1. Example Cases to Demonstrate the Performance of Compressive Potential
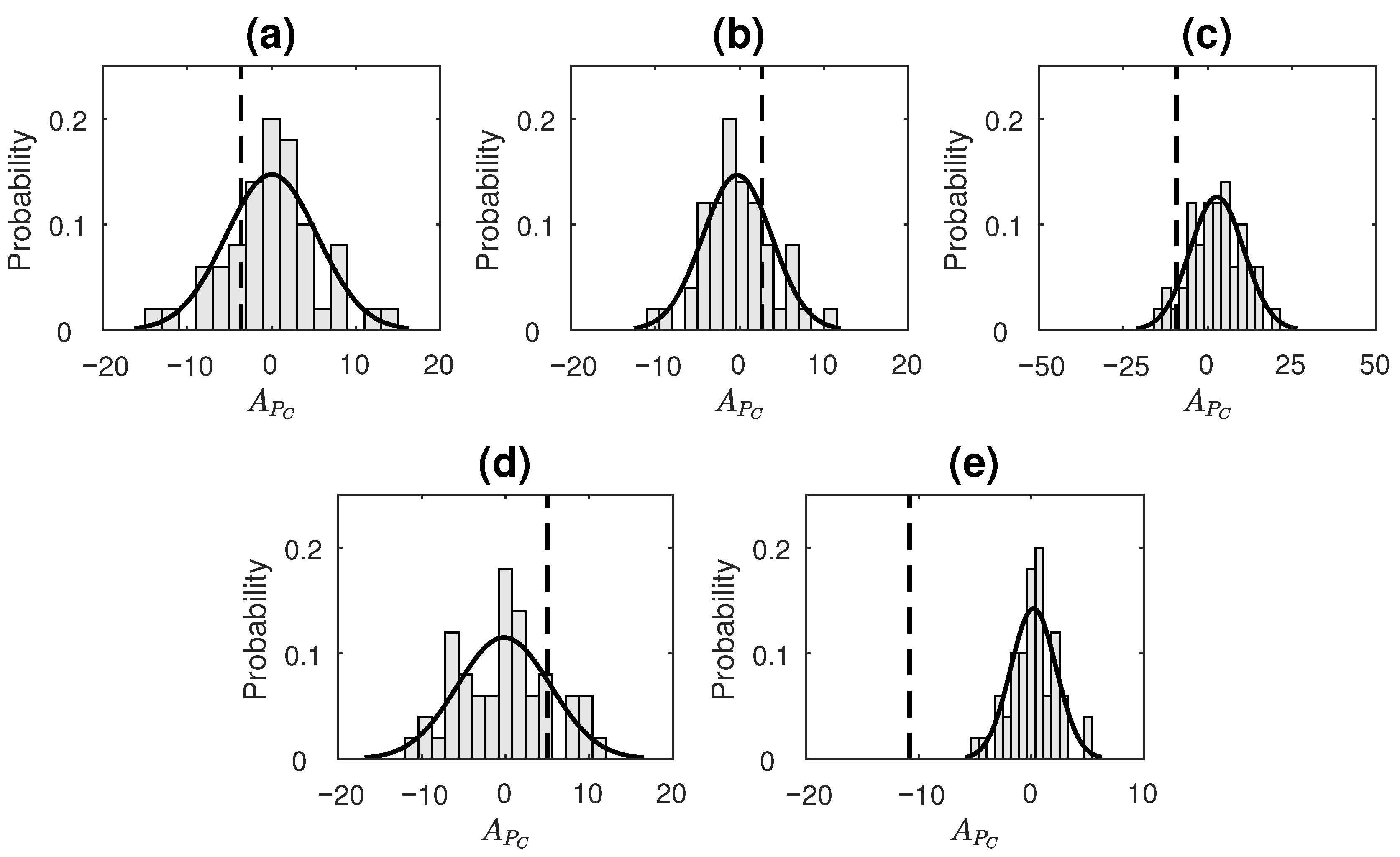
3.2.2. Performance of Compressive-Potential-Based Temporal Asymmetry Measure on Simulations
- Linear Gaussian Process (LGP), that is, Gaussian noise with distribution ;
- Autoregressive process of second order, AR(2)where t is the time index and is Gaussian white noise, ;
- Static nonlinear transformation of a first order Gaussian process, STAR(1)where is Gaussian white noise, .
- Self-Exciting Threshold AR (SETAR(2;2,2)) process with two regimes, each one with second-order delayswhere is Gaussian white noise, ;
- Chaotic tent-map process
3.2.3. Performance of Compressive-Potential-Based Temporal Asymmetry Measure on Real Data
- Sunspot numbersTime series analysis of sunspot numbers is an active area of research. Sunspots are regions of reduced surface temperature on the Sun’s surface that appear as spots darker than the surrounding areas. They are caused by concentrations of magnetic field flux that inhibit convection. These numbers are important in the study of the solar system as well as the activities of the sun. Monthly and annual data of sunspot activity are typically known to be nonlinear, non-Gaussian and non-stationary with characteristics of chaotic sequences [63,64,65], and, hence, these are treated as irreversible.The sunspot numbers used in this study were obtained from the SILSO website (www.sidc.be/silso/datafiles; accessed on 24 February 2021) as monthly mean measurements (Sunspot data from the World Data Center SILSO, Royal Observatory of Belgium, Brussels). This dataset consists of monthly data recorded starting from January, 1749. It currently comprises data from 3265 months of observation, recorded up to January, 2021. The entire dataset, comprising these 3265 datapoints, was used in our analysis. A subset of this dataset, starting from the beginning of the year 1920 to the end of year 2020, is depicted in Figure 5.
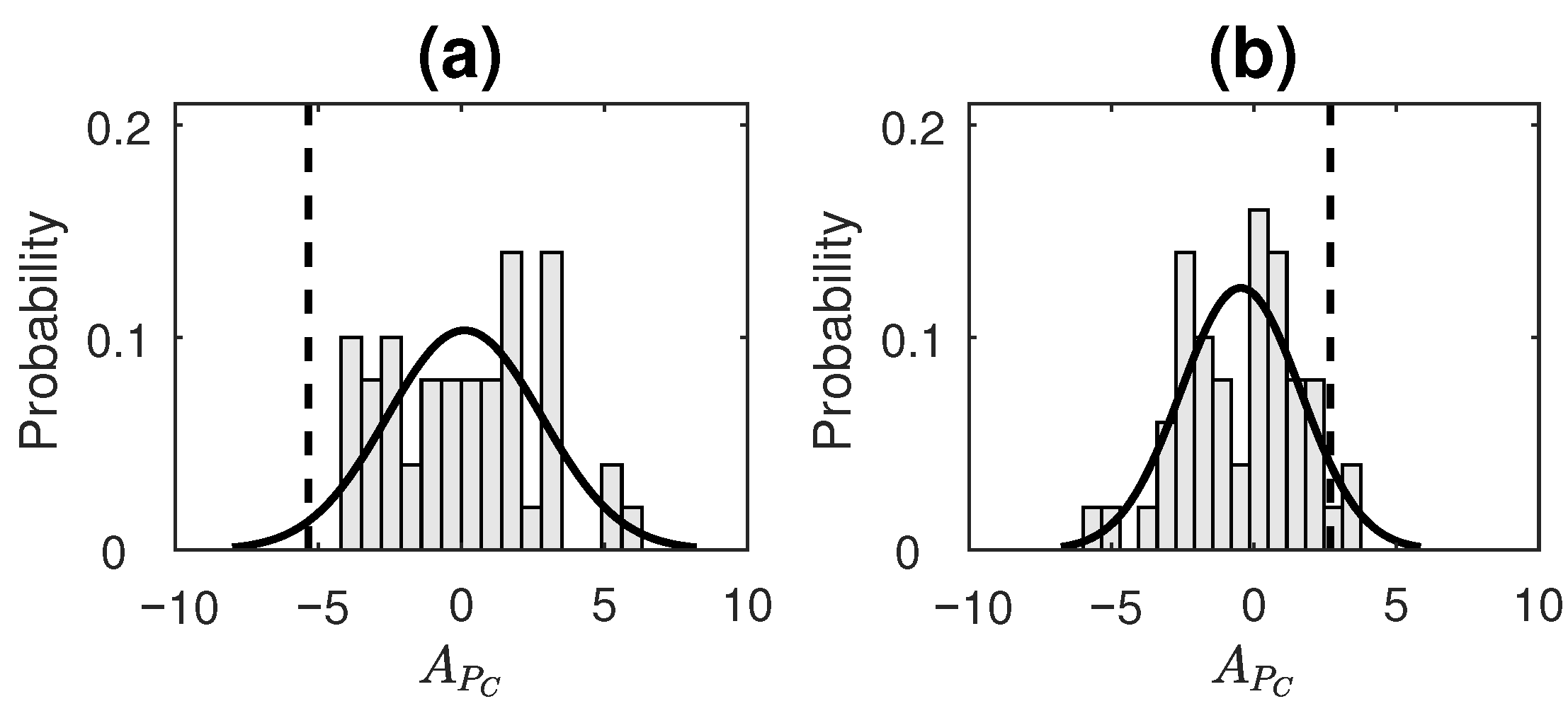
- Digits of the transcendental numberThe decimal expansion of number is known to be non-repeating (transcendental irrational number). Furthermore, it is widely believed that is a normal number (though proof has remained elusive till date). A number is said to be normal (in base b) if, for every positive integer N, all possible strings of length N have a frequency of occurrence . Equivalently, we can say that a normal number does not prefer a set of patterns in its expansion over others, and, thus, every possible pattern occurs equally often. A recent work by Peter Trueb [66] analyzed the first trillion decimal digits of and found that frequencies of sequences of lengths one, two and three are consistent with the hypothesis of being a normal number in base-10 and base-16. We claim that this would mean that normal numbers are essentially reversible, since the reversed order of the digits would not change the frequency of occurrence in any way (else it would fail to be normal). We consider the decimal expansion () of up to a 1000 digits and check its reversibility using our proposed measure.For the computation of value for 1. and 2., the time-series taken were symbolized using four bins. The number of bins taken here were fewer compared to that taken for simulated data in order to allow for more patterns to repeat (and, hence, an appropriate computation of ETC to take place) in a shorter length of available data. The parameters for the measure were set as . In order to assess the statistical significance of the obtained for each process taken, surrogate data testing was done by generating a surrogate ensemble of 50 realizations in the same manner as for simulated data (discussed in Section 3.2.2). Figure 6 displays the distribution of values of surrogate data, as well as a dotted line showing where the value of the original time series lies for real datasets 1 and 2. distribution of surrogates for both the processes was found to satisfy normality based on the Anderson–Darling test. For Sunspot numbers, the null hypothesis (of reversibility) was rejected with p-value = 0.04 (Figure 6a). On the other hand, for digits of , the null hypothesis was not rejected with p-value = 0.13 (Figure 6b). Hence, the sunspot numbers time-series was correctly determined as being irreversible and digits of were correctly determined as being time-reversible based on the performance of .
- Heart period variabilityThe last set of data taken was of heart interbeat intervals from young and elderly healthy human subjects. This dataset was obtained from “Physionet: Fantasia database” [67] and was originally acquired for the study in [68]. In the study, twenty young (21–34 years old) and twenty elderly (68–85 years old) subjects underwent 120 min of continuous supine resting while watching the movie Fantasia (Disney, 1940) in order to help maintain wakefulness. During this time, continuous ECG data were recorded and digitized by sampling at 250 Hz. The heartbeats were annotated using an automated arrhythmia detection algorithm and the beat annotations were later verified by visual inspection. The occurrence of each "R" peak was noted, and the time series consisting of the time difference between successive peaks was generated. This process was repeated for each of the participants.The interbeat interval variations in the heart are characterized by an asymmetric behavior under time reversal. This is because the heart decelerates faster than it accelerates, thus resulting in heart period variability asymmetry (HPVA) [69,70]. In previous studies, the HPVA has been assessed by the use of different measures applied to the difference between two successive heart period values. These studies include [11,13,14,71]. Furthermore, it has been shown that the HPVA is influenced by pathological conditions such as heart failure [14,72] and mental disorders [73,74], as well as aging [11,75]. In particular, HPVA is found to reduce with aging [11,75].In the analysis here, we estimated the values of for each of the young and old subjects by using time series obtained by subtracting successive values of heart periods (or RR intervals) taken from the Physionet Fantasia database. The first 2500 observations of heart period were taken from each subject. The number of bins used to obtain the symbolic sequence were set to four, and the parameters for estimation of were set to . Since the can attain both positive and negative values, and a higher magnitude of the measure implies higher asymmetry, the absolute values of obtained from young and old subjects were compared. The mean and standard deviation of absolute for young subjects were found to be 27.96 and 32.99, respectively, and the mean and standard deviation of absolute for elderly subjects were found to be 11.59 and 15.82, respectively. Further, the Mann–Whitney U (single tailed) test was done to check if the magnitude of values estimated from young subjects were significantly greater than the magnitude of values estimated from elderly subjects. The null hypothesis, , was that the median of the magnitude of values obtained from the young population was less than or equal to the median of the magnitude of values obtained from the old population. was considered statistically significant. It was found that was rejected in favour of the alternate hypothesis, with the p value being equal to 0.0168. This suggested that the HPV of younger subjects was more irreversible or asymmetric as compared to that of older subjects. This result is in line with the findings of existing studies.
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ETC | Effort-to-Compress |
| CCC | Compression-Complexity Causality |
| Compressive potential | |
| Compressive potential based temporal asymmetry measure | |
| GC | Granger Causality |
| TE | Transfer Entropy |
| CMI | Conditional Mutual Information |
| CCM | Convergent Cross Mapping |
| PI | Predictability Index |
| KLD | Kullback Leibler Divergence |
| AR | Autoregressive |
| LGP | Linear Gaussian Process |
| STAR | Static nonlinear transformation of a first order Gaussian process |
| SETAR | Self-Exciting Threshold AR |
| IAAFT | Iterative Amplitude Adjusted Fourier Transform |
| HP | Heart Period |
| HPV | Heart Period Variability |
| HPVA | Heart Period Variability Asymmetry |
| SAP | Systolic Arterial Pressure |
References
- Lamb, J.S.; Roberts, J.A. Time-reversal symmetry in dynamical systems: A survey. Physica D 1998, 112, 1–39. [Google Scholar] [CrossRef]
- Prigogine, I.; Antoniou, I. Laws of nature and time symmetry breaking. Ann. N. Y. Acad. Sci. 1999, 879, 8–28. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P.; Ciliberto, S.; Garnier, N.; Joubaud, S.; Petrosyan, A. Entropy production and time asymmetry in nonequilibrium fluctuations. Phys. Rev. Lett. 2007, 98, 150601. [Google Scholar] [CrossRef] [PubMed]
- Puglisi, A.; Villamaina, D. Irreversible effects of memory. EPL 2009, 88, 30004. [Google Scholar] [CrossRef]
- Grenfell, B.T.; Kleckzkowski, A.; Ellner, S.; Bolker, B. Measles as a case study in nonlinear forecasting and chaos. Philos. Trans. R. Soc. A 1994, 348, 515–530. [Google Scholar]
- Stone, L.; Landan, G.; May, R.M. Detecting time’s arrow: A method for identifying nonlinearity and deterministic chaos in time-series data. Proc. Royal Soc. 1996, 263, 1509–1513. [Google Scholar]
- Paluš, M. Nonlinearity in normal human EEG: Cycles, temporal asymmetry, nonstationarity and randomness, not chaos. Biol. Cybern. 1996, 75, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Van der Heyden, M.; Diks, C.; Pijn, J.; Velis, D. Time reversibility of intracranial human EEG recordings in mesial temporal lobe epilepsy. Phys. Lett. A 1996, 216, 283–288. [Google Scholar] [CrossRef]
- Pijn, J.P.M.; Velis, D.N.; van der Heyden, M.J.; DeGoede, J.; van Veelen, C.W.; da Silva, F.H.L. Nonlinear dynamics of epileptic seizures on basis of intracranial EEG recordings. Brain Topogr. 1997, 9, 249–270. [Google Scholar] [CrossRef]
- Schindler, K.; Rummel, C.; Andrzejak, R.G.; Goodfellow, M.; Zubler, F.; Abela, E.; Wiest, R.; Pollo, C.; Steimer, A.; Gast, H. Ictal time-irreversible intracranial EEG signals as markers of the epileptogenic zone. Clin. Neurophysiol. 2016, 127, 3051–3058. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Broken asymmetry of the human heartbeat: Loss of time irreversibility in aging and disease. Phys. Rev. Lett. 2005, 95, 198102. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Casali, K.R.; Casali, A.G.; Gnecchi-Ruscone, T.; Tobaldini, E.; Montano, N.; Lange, S.; Geue, D.; Cysarz, D.; Van Leeuwen, P. Temporal asymmetries of short-term heart period variability are linked to autonomic regulation. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2008, 295, R550–R557. [Google Scholar] [CrossRef] [PubMed]
- Casali, K.R.; Casali, A.G.; Montano, N.; Irigoyen, M.C.; Macagnan, F.; Guzzetti, S.; Porta, A. Multiple testing strategy for the detection of temporal irreversibility in stationary time series. Phys. Rev. E 2008, 77, 066204. [Google Scholar] [CrossRef]
- Porta, A.; D’addio, G.; Bassani, T.; Maestri, R.; Pinna, G.D. Assessment of cardiovascular regulation through irreversibility analysis of heart period variability: A 24 hours Holter study in healthy and chronic heart failure populations. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2009, 367, 1359–1375. [Google Scholar] [CrossRef]
- Pomeau, Y. Symétrie des fluctuations dans le renversement du temps. J. Phys. 1982, 43, 859–867. [Google Scholar] [CrossRef]
- Ramsey, J.B.; Rothman, P. Characterization of the Time Irreversibility of Economic Time Series: Estimators and Test Statistics; Technical Report; New York University: New York, NY, USA, 1988. [Google Scholar]
- De Lima, P.J. On the robustness of nonlinearity tests to moment condition failure. J. Econom. 1997, 76, 251–280. [Google Scholar] [CrossRef]
- Diks, C.; Van Houwelingen, J.; Takens, F.; DeGoede, J. Reversibility as a criterion for discriminating time series. Phys. Lett. A 1995, 201, 221–228. [Google Scholar] [CrossRef]
- Martínez, J.H.; Herrera-Diestra, J.L.; Chavez, M. Detection of time reversibility in time series by ordinal patterns analysis. Chaos 2018, 28, 123111. [Google Scholar] [CrossRef] [PubMed]
- Donges, J.F.; Donner, R.V.; Kurths, J. Testing time series irreversibility using complex network methods. EPL 2013, 102, 10004. [Google Scholar] [CrossRef]
- Flanagan, R.; Lacasa, L. Irreversibility of financial time series: A graph-theoretical approach. Phys. Lett. A 2016, 380, 1689–1697. [Google Scholar] [CrossRef]
- Li, J.; Shang, P. Time irreversibility of financial time series based on higher moments and multiscale Kullback–Leibler divergence. Physica A 2018, 502, 248–255. [Google Scholar] [CrossRef]
- Weiss, G. Time-reversibility of linear stochastic processes. J. Appl. Probab. 1975, 12, 831–836. [Google Scholar] [CrossRef]
- Lawrance, A. Directionality and reversibility in time series. Int. Stat. Rev. 1991, 59, 67–79. [Google Scholar] [CrossRef]
- Daw, C.; Finney, C.; Kennel, M. Symbolic approach for measuring temporal “irreversibility”. Phys. Rev. E 2000, 62, 1912. [Google Scholar] [CrossRef]
- Kennel, M.B. Testing time symmetry in time series using data compression dictionaries. Phys. Rev. E 2004, 69, 056208. [Google Scholar] [CrossRef]
- Kawai, R.; Parrondo, J.M.; Van den Broeck, C. Dissipation: The phase-space perspective. Phys. Rev. Lett. 2007, 98, 080602. [Google Scholar] [CrossRef] [PubMed]
- Parrondo, J.M.; Van den Broeck, C.; Kawai, R. Entropy production and the arrow of time. New J. Phys. 2009, 11, 073008. [Google Scholar] [CrossRef]
- Roldán, É.; Parrondo, J.M. Estimating dissipation from single stationary trajectories. Phys. Rev. Lett. 2010, 105, 150607. [Google Scholar] [CrossRef]
- Roldán, É.; Parrondo, J.M. Entropy production and Kullback-Leibler divergence between stationary trajectories of discrete systems. Phys. Rev. E 2012, 85, 031129. [Google Scholar] [CrossRef] [PubMed]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 2000, 44, 261. [Google Scholar] [CrossRef]
- Granger, C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Paluš, M.; Krakovská, A.; Jakubík, J.; Chvosteková, M. Causality, dynamical systems and the arrow of time. Chaos 2018, 28, 075307. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Paluš, M.; Komárek, V.; Hrnčíř, Z.; Štěrbová, K. Synchronization as adjustment of information rates: Detection from bivariate time series. Phys. Rev. E 2001, 63, 046211. [Google Scholar] [CrossRef] [PubMed]
- Krakovská, A.; Hanzely, F. Testing for causality in reconstructed state spaces by an optimized mixed prediction method. Phys. Rev. E 2016, 94, 052203. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Nagaraj, N.; Balasubramanian, K. Three Perspectives on Complexity: Entropy, compression, subsymmetry. Eur. Phys. J. Spec. Topics 2017, 226, 3251–3272. [Google Scholar] [CrossRef]
- Nagaraj, N.; Balasubramanian, K. Dynamical complexity of short and noisy time series. EPJ 2017, 226, 2191–2204. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Nagaraj, N.; Balasubramanian, K.; Dey, S. A new complexity measure for time series analysis and classification. EPJ 2013, 222, 847–860. [Google Scholar] [CrossRef]
- Nagaraj, N.; Balasubramanian, K. Measuring Complexity of Chaotic Systems with Cybernetics Applications. In Handbook of Research on Applied Cybernetics and Systems Science; Saha, S., Mandal, A., Narasimhamurthy, A., Sangam, S., Sarasvathi, V., Eds.; IGI Global: Hershey, PA, USA, 2017; pp. 301–334. [Google Scholar]
- Balasubramanian, K.; Nagaraj, N. Aging and cardiovascular complexity: Effect of the length of RR tachograms. PeerJ 2016, 4, e2755. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, C.; Overholt, D.; Eldridge, A. Shaping the behaviour of feedback instruments with complexity-controlled gain dynamics. In Proceedings of the 20th International Conference on New Interfaces for Musical Expression, Birmingham, UK, 21–25 July 2020; pp. 343–348. [Google Scholar]
- SY, P.; Nagaraj, N. Causal Discovery using Compression-Complexity Measures. arXiv 2020, arXiv:2010.09336. [Google Scholar]
- Kathpalia, A.; Nagaraj, N. Data-based intervention approach for Complexity-Causality measure. PeerJ Comput. Sci. 2019, 5, e196. [Google Scholar] [CrossRef]
- Kathpalia, A.; Nagaraj, N. Measuring Causality: The Science of Cause and Effect. arXiv 2019, arXiv:1910.08750. [Google Scholar]
- Budhathoki, K.; Vreeken, J. Origo: Causal inference by compression. Knowl. Inf. Syst. 2018, 56, 285–307. [Google Scholar] [CrossRef]
- Ebeling, W.; Jiménez-Montaño, M.A. On grammars, complexity, and information measures of biological macromolecules. Math. Biosci. 1980, 52, 53–71. [Google Scholar] [CrossRef]
- Larsson, N.J.; Moffat, A. Off-line dictionary-based compression. Proc. IEEE 2000, 88, 1722–1732. [Google Scholar] [CrossRef]
- Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect; Basic Books: New York, NY, USA, 2018. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication, Part I, Part II. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Barnett, L.; Seth, A.K. The MVGC multivariate Granger causality toolbox: A new approach to Granger-causal inference. J. Neurosci. Methods 2014, 223, 50–68. [Google Scholar] [CrossRef]
- Montalto, A.; Faes, L.; Marinazzo, D. MuTE: A MATLAB toolbox to compare established and novel estimators of the multivariate transfer entropy. PLoS ONE 2014, 9, e109462. [Google Scholar]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.R.; Gudmundsson, G.; Lindgren, G.; Bondesson, L.; Harsaae, E.; Laake, P.; Juselius, K.; Lauritzen, S.L. Statistical analysis of time series: Some recent developments [with discussion and reply]. Scand. J. Stat. 1981, 8, 93–115. [Google Scholar]
- Hallin, M.; Lefevre, C.; Puri, M.L. On time-reversibility and the uniqueness of moving average representations for non-Gaussian stationary time series. Biometrika 1988, 75, 170–171. [Google Scholar] [CrossRef]
- Bauer, S.; Schölkopf, B.; Peters, J. The arrow of time in multivariate time series. In International Conference on Machine Learning; PMLR: New York, NY, USA, 2016; pp. 2043–2051. [Google Scholar]
- Tong, H. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Petruccelli, J.D. A comparison of tests for SETAR-type non-linearity in time series. J. Forecast. 1990, 9, 25–36. [Google Scholar] [CrossRef]
- Rothman, P. The comparative power of the TR test against simple threshold models. J. Appl. Econom. 1992, 7, S187–S195. [Google Scholar] [CrossRef]
- Mundt, M.D.; Maguire, W.B.; Chase, R.R. Chaos in the sunspot cycle: Analysis and prediction. J. Geophys. Res-Space Phys. 1991, 96, 1705–1716. [Google Scholar] [CrossRef]
- Jiang, C.; Song, F. Sunspot Forecasting by Using Chaotic Time-series Analysis and NARX Network. JCP 2011, 6, 1424–1429. [Google Scholar] [CrossRef]
- Hanslmeier, A.; Brajša, R. The chaotic solar cycle-I. Analysis of cosmogenic-data. Astron. Astrophys. 2010, 509, A5. [Google Scholar] [CrossRef]
- Trueb, P. Digit statistics of the first 22.4 trillion decimal digits of Pi. arXiv 2016, arXiv:1612.00489. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Iyengar, N.; Peng, C.; Morin, R.; Goldberger, A.L.; Lipsitz, L.A. Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1996, 271, R1078–R1084. [Google Scholar] [CrossRef]
- Guzik, P.; Piskorski, J.; Krauze, T.; Wykretowicz, A.; Wysocki, H. Heart rate asymmetry by Poincaré plots of RR intervals. Biomed. Tech. 2006. [Google Scholar] [CrossRef]
- Porta, A.; Guzzetti, S.; Montano, N.; Gnecchi-Ruscone, T.; Furlan, R.; Malliani, A. Time reversibility in short-term heart period variability. In Proceedings of the 2006 Computers in Cardiology, Valencia, Spain, 17–20 September 2006; pp. 77–80. [Google Scholar]
- Piskorski, J.; Guzik, P. Geometry of the Poincaré plot of RR intervals and its asymmetry in healthy adults. Physiol. Meas. 2007, 28, 287. [Google Scholar] [CrossRef]
- Ricca-Mallada, R.; Migliaro, E.R.; Piskorski, J.; Guzik, P. Exercise training slows down heart rate and improves deceleration and acceleration capacity in patients with heart failure. J. Electrocardiol. 2012, 45, 214–219. [Google Scholar] [CrossRef]
- Tonhajzerova, I.; Ondrejka, I.; Chladekova, L.; Farsky, I.; Visnovcova, Z.; Calkovska, A.; Jurko, A.; Javorka, M. Heart rate time irreversibility is impaired in adolescent major depression. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2012, 39, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Tonhajzerová, I.; Ondrejka, I.; Farskỳ, I.; Višňovcová, Z.; Mešt’aník, M.; Javorka, M.; Jurko, A., Jr.; Čalkovská, A. Attention deficit/hyperactivity disorder (ADHD) is associated with altered heart rate asymmetry. Physiol. Res. 2014, 63, S509–S519. [Google Scholar] [CrossRef] [PubMed]
- De Maria, B.; Bari, V.; Cairo, B.; Vaini, E.; Martins de Abreu, R.; Perseguini, N.M.; Milan-Mattos, J.; Rehder-Santos, P.; Minatel, V.; Catai, A.M.; et al. Cardiac baroreflex hysteresis is one of the determinants of the heart period variability asymmetry. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2019, 317, R539–R551. [Google Scholar] [CrossRef]
- Paluš, M.; Vejmelka, M. Directionality of coupling from bivariate time series: How to avoid false causalities and missed connections. Phys. Rev. E 2007, 75, 056211. [Google Scholar] [CrossRef]
- Ziv, J.; Merhav, N. A measure of relative entropy between individual sequences with application to universal classification. IEEE Trans. Inf. Theory 1993, 39, 1270–1279. [Google Scholar] [CrossRef]
- Bertinieri, G.; Di Rienzo, M.; Cavallazzi, A.; Ferrari, A.; Pedotti, A.; Mancia, G. A new approach to analysis of the arterial baroreflex. J. Hypertens. Suppl. Off. J. Int. Soc. Hypertens. 1985, 3, S79–S81. [Google Scholar]
- Porta, A.; Baselli, G.; Rimoldi, O.; Malliani, A.; Pagani, M. Assessing baroreflex gain from spontaneous variability in conscious dogs: Role of causality and respiration. Am. J. Physiol.-Heart Circul. Physiol. 2000, 279, H2558–H2567. [Google Scholar] [CrossRef]
- Porta, A.; Bari, V.; Bassani, T.; Marchi, A.; Pistuddi, V.; Ranucci, M. Model-based causal closed-loop approach to the estimate of baroreflex sensitivity during propofol anesthesia in patients undergoing coronary artery bypass graft. J. Appl. Physiol. 2013, 115, 1032–1042. [Google Scholar] [CrossRef] [PubMed]
- Hunt, B.E.; Farquhar, W.B. Nonlinearities and asymmetries of the human cardiovagal baroreflex. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2005, 288, R1339–R1346. [Google Scholar] [CrossRef]
- De Maria, B.; Bari, V.; Ranucci, M.; Pistuddi, V.; Ranuzzi, G.; Takahashi, A.C.; Catai, A.M.; Dalla Vecchia, L.; Cerutti, S.; Porta, A. Separating arterial pressure increases and decreases in assessing cardiac baroreflex sensitivity via sequence and bivariate phase-rectified signal averaging techniques. Med. Biol. Eng. Comput. 2018, 56, 1241–1252. [Google Scholar] [CrossRef] [PubMed]
- De Maria, B.; Bari, V.; Cairo, B.; Vaini, E.; Esler, M.; Lambert, E.; Baumert, M.; Cerutti, S.; Dalla Vecchia, L.; Porta, A. Characterization of the asymmetry of the cardiac and sympathetic arms of the baroreflex from spontaneous variability during incremental head-up tilt. Front. Physiol. 2019, 10, 342. [Google Scholar] [CrossRef] [PubMed]

| Time Series | Composed of | ETC |
|---|---|---|
| Repeating periodic sequence: | 3 | |
| Repeating periodic sequence: | 95 | |
| Repeating partly periodic partly random sequence: | ||
| followed by 100 random numbers uniformly chosen from between 1 and 20 | 100 | |
| Uniformly randomly distributed real numbers in the range (0,1) | 4110 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kathpalia, A.; Nagaraj, N. Time-Reversibility, Causality and Compression-Complexity. Entropy 2021, 23, 327. https://doi.org/10.3390/e23030327
Kathpalia A, Nagaraj N. Time-Reversibility, Causality and Compression-Complexity. Entropy. 2021; 23(3):327. https://doi.org/10.3390/e23030327
Chicago/Turabian StyleKathpalia, Aditi, and Nithin Nagaraj. 2021. "Time-Reversibility, Causality and Compression-Complexity" Entropy 23, no. 3: 327. https://doi.org/10.3390/e23030327
APA StyleKathpalia, A., & Nagaraj, N. (2021). Time-Reversibility, Causality and Compression-Complexity. Entropy, 23(3), 327. https://doi.org/10.3390/e23030327







