Development of Econophysics: A Biased Account and Perspective from Kolkata
Abstract
:1. Introduction
2. What Attracted You to Econophysics?
3. Major Achievements and Publications of the ‘Kolkata School’
3.1. Traveling Salesman Problem and Simulated (Classical & Quantum) Annealing
3.2. Social Inequality Measure and Kolkata Index
3.3. Kinetic Exchange Model of Income and Wealth Distributions
3.4. Statistics of the Kolkata Paise Restaurant Problems
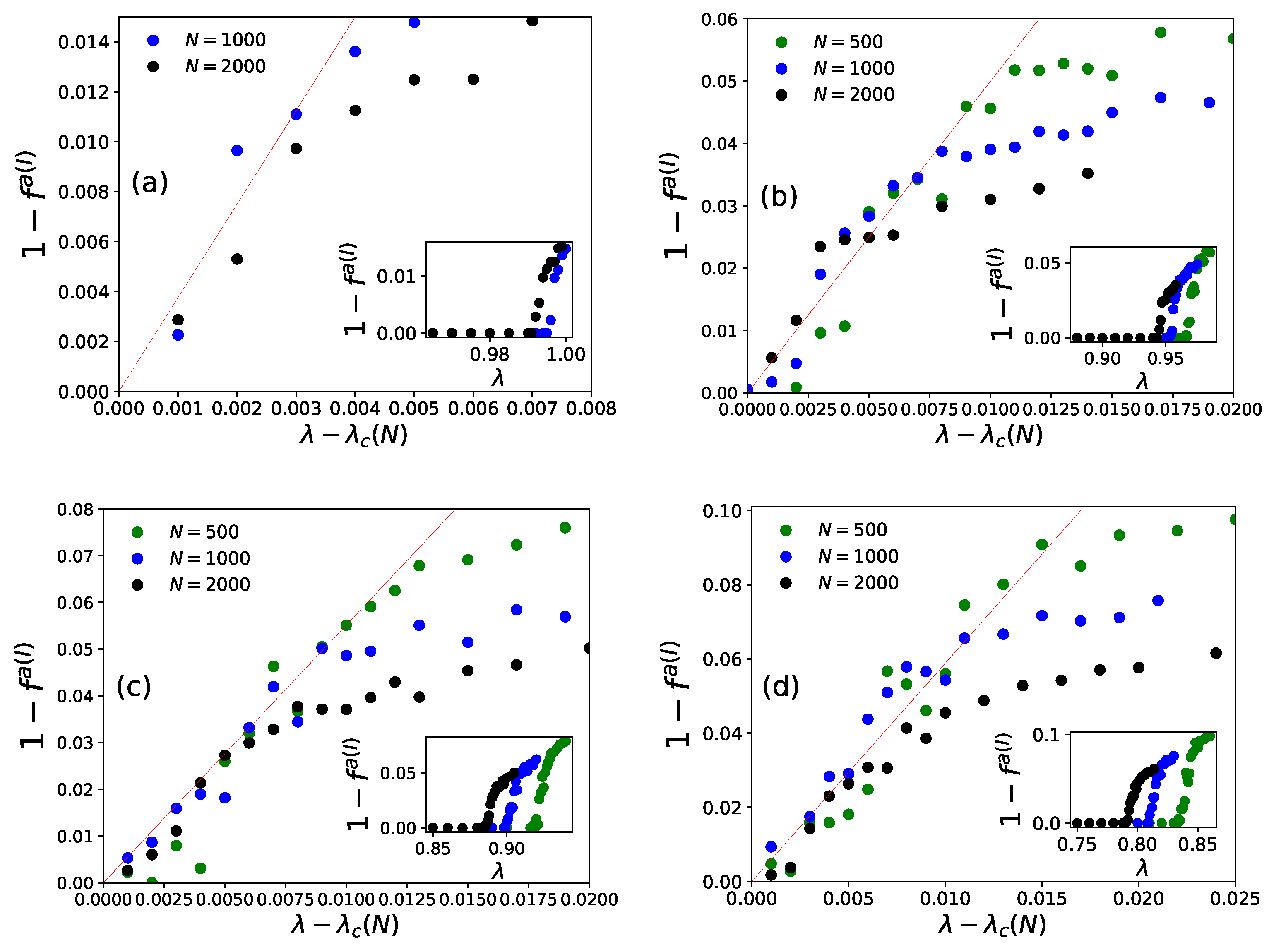
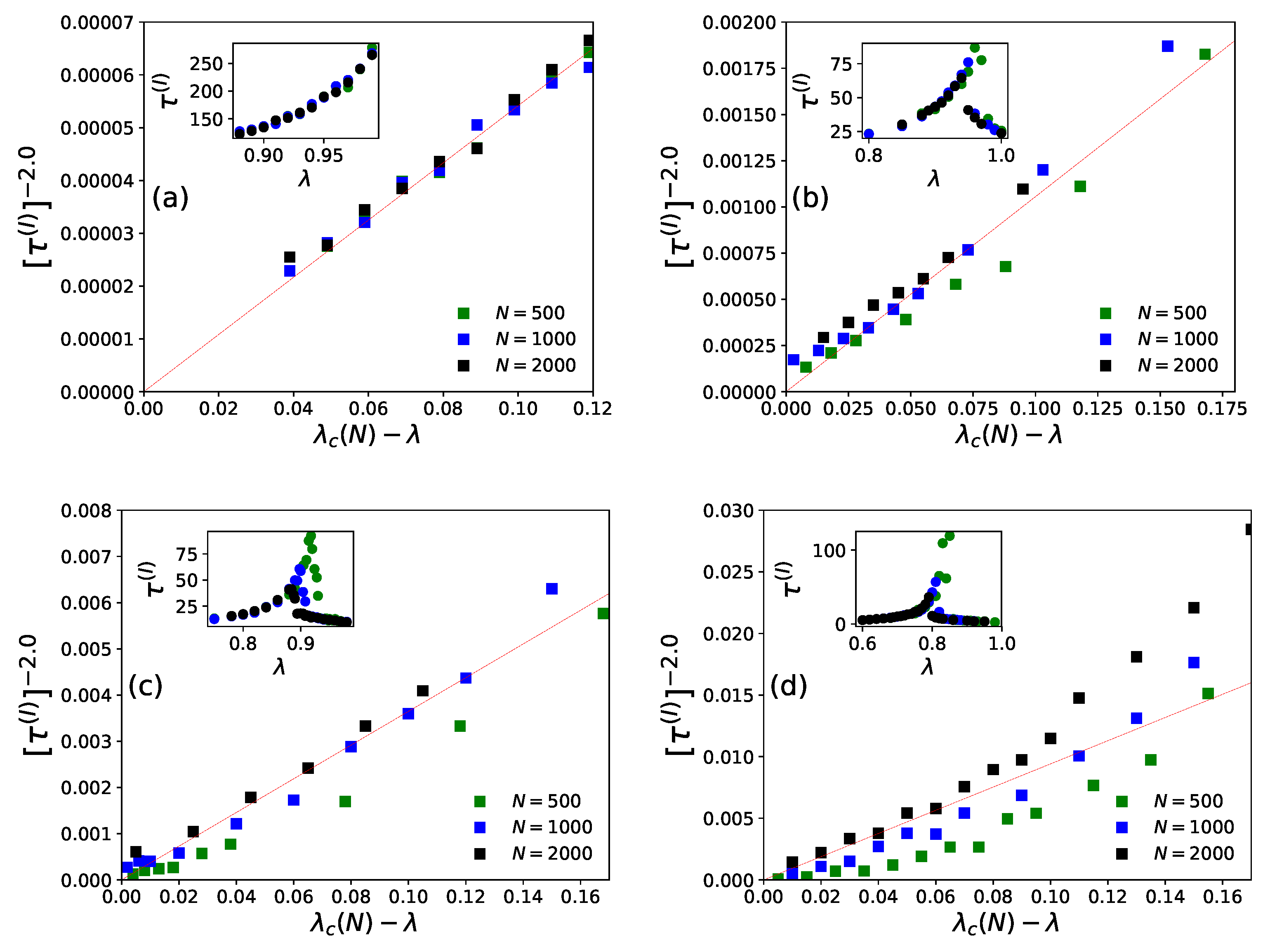
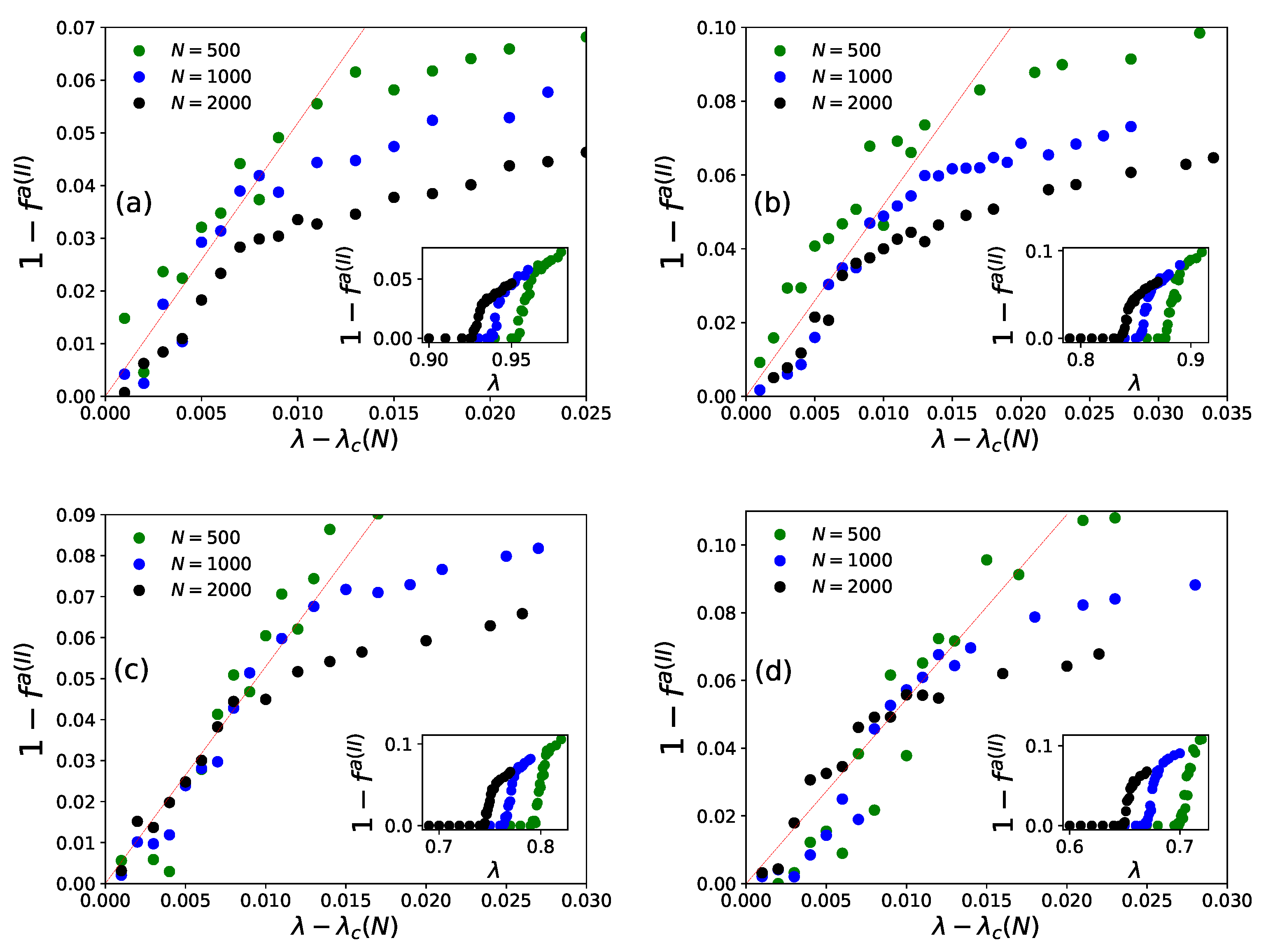
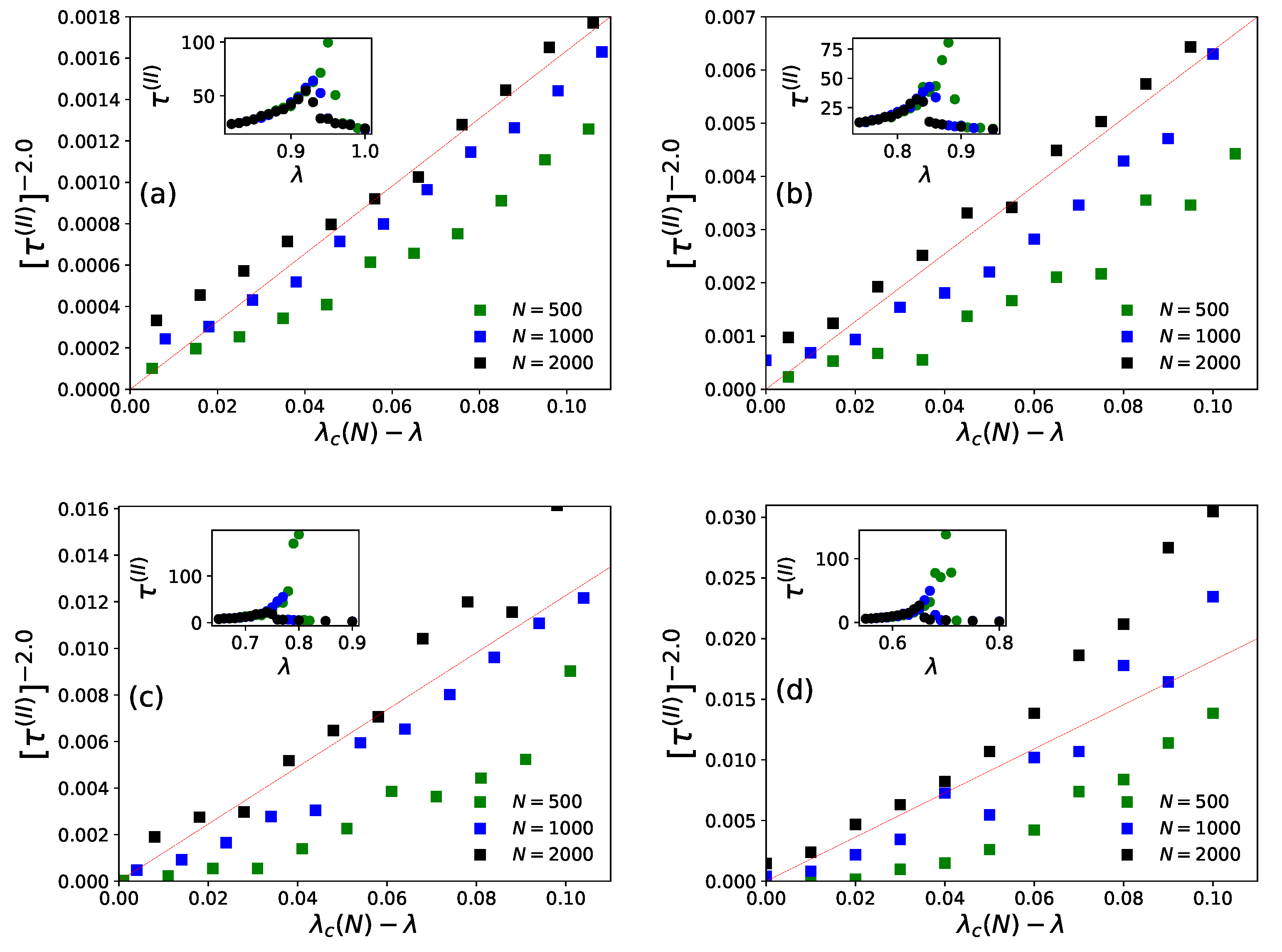
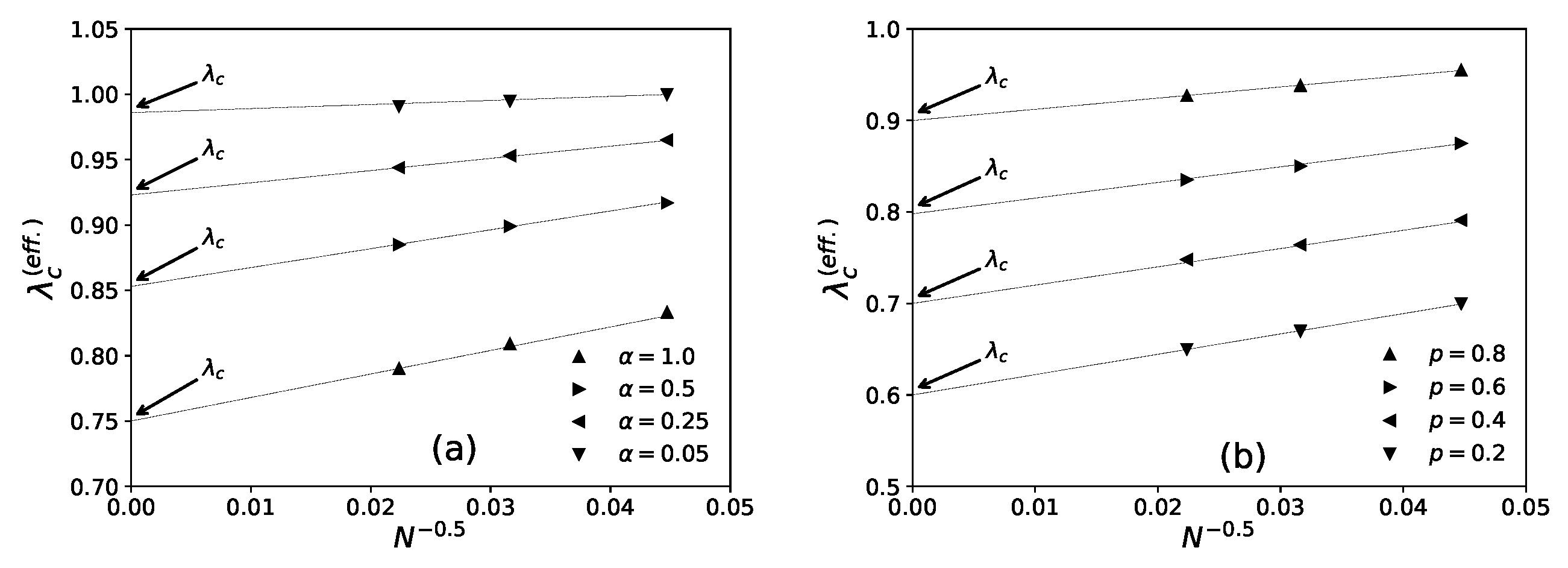
4. Some New Results for Statistics of the KPR Problem
4.1. Numerical Results
4.2. Summary
5. Future of Econophysics: Some Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gangopadhyay, K. Interview with Eugene H. Stanley. IIM Kozhikode Soc. Manag. Rev. 2013, 2, 73–78. [Google Scholar] [CrossRef]
- Rosser, J.B., Jr. Econophysics. In New Palgrave Dictionary of Economics; Durlauf, S.N., Blume, L.E., Eds.; Palgrave Macmillan: London, UK, 2008; Volume 2, pp. 729–732. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Galam, S.; Gefen, Y.; Shapir, Y. Sociophysics: A mean behavior model for the process of strike. J. Mathe. Sociol. Scimago 2000, 9, 1–13. [Google Scholar]
- Galam, S. Sociophysics: A Physicist’s Modeling of Psycho-Political Phenomena; Springer: New York, NY, USA, 2012. [Google Scholar]
- Chakrabarti, B.K. Econophysics as conceived by Meghnad Saha. Sci. Cult. Indian Sci. News Assoc. 2018, 84, 365–369. [Google Scholar]
- Saha, M.N.; Srivastava, B.N. A Treatise on Heat; Indian Press: Allahabad, India, 1931; p. 105. [Google Scholar]
- Dragulescu, A.; Yakovenko, V.M. Statistical mechanics of money. Eur. Phys. J. B-Condens. Matter Complex Syst. 2000, 17, 723–729. [Google Scholar] [CrossRef] [Green Version]
- Chakraborti, A.; Chakrabarti, B.K. Statistical mechanics of money: How saving propensity affects its distribution. Eur. Phys. J. B-Condens. Matter Complex Syst. 2000, 17, 167–170. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, A.; Chakrabarti, B.K.; Manna, S.S. Pareto law in a kinetic model of market with random saving propensity. Phys. A Stat. Mech. Appl. 2004, 335, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, B.K.; Marjit, S. Self-organisation and complexity in simple model systems: Game of life and economics. Indian J. Phys. IACS 1995, 69B, 681–698. [Google Scholar]
- Stanley, H.E.; Afanasyev, V.; Amaral, L.A.N.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Leschhorn, H.; Maass, P.; Mantegna, R.N.; Peng, C.-K. Anomalous fluctuations in the dynamics of complex systems: From DNA and physiology to econophysics. Phys. A Stat. Mech. Appl. 1996, 224, 302–321. [Google Scholar] [CrossRef]
- Chakrabarti, B.K. Econophysics. In Encyclopedia of Philosophy and the Social Sciences; Kaldis, B., Ed.; Sage: Thousand Oaks, CA, USA, 2013; Volume 1, pp. 229–230. [Google Scholar]
- Chakrabarti, B.K. Can economics afford not to become natural science? Eur. Phys. J. Spec. Top. 2016, 225, 3121–3125. [Google Scholar] [CrossRef] [Green Version]
- Epstein, B. Social Ontology. In The Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2018; Available online: https://plato.stanford.edu/entries/social-ontology/ (accessed on 8 January 2021).
- Whitehead, A.N.; Russell, B. Principia Mathematica; Cambridge University Press: Cambridge, UK, 1910; Volume I. [Google Scholar]
- Whitehead, A.N.; Russell, B. Principia Mathematica; Cambridge University Press: Cambridge, UK, 1912; Volume II. [Google Scholar]
- Whitehead, A.N.; Russell, B. Principia Mathematica; Cambridge University Press: Cambridge, UK, 1913; Volume III. [Google Scholar]
- Challet, D.; Marsili, M.; Zhang, Y.-C. Minority Games: Interacting Agents in Financial Markets; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Chakrabarti, B.K.; Chatterjee, A.; Ghosh, A.; Mukherjee, S.; Tamir, B. Econophysics of the Kolkata Restaurant Problem and Related Games: Classical and Quantum Strategies for Multi-Agent, Multi-Choice Repetitive Games; Springer: Cham, The Netherland, 2017. [Google Scholar]
- Mantegna, R.N. Lévy walks and enhanced diffusion in Milan stock exchange. Phys. A Stat. Mech. Appl. 1991, 179, 232–242. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Das, A.; Chakrabarti, B.K. Colloquium: Quantum annealing and analog quantum computation. Rev. Modern Phys. 2008, 80, 1061–1081. [Google Scholar] [CrossRef] [Green Version]
- Santoro, G.E.; Tosatti, E. Optimization using quantum mechanics: Quantum annealing through adiabatic evolution. J. Phys. A Math. Gener. 2006, 39, R393–R431. [Google Scholar] [CrossRef]
- Chakrabarti, B.K. Econophys-Kolkata: A short story. In Econophysics of Wealth Distributions; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Milan, Italiy, 2005; pp. 225–228. [Google Scholar]
- Sen, P.; Chakrabarti, B.K. Travelling salesman problem on dilute lattices: Visit to a fraction of cities. J. Phys. 1989, 50, 255–261. [Google Scholar] [CrossRef]
- Sen, P.; Chakrabarti, B.K. Sociophysics: An Introduction; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Yakovenko, V.M.; Rosser, J.B., Jr. Colloquium: Statistical mechanics of money, wealth, and income. Rev. Modern Phys. 2009, 81, 1703. [Google Scholar] [CrossRef] [Green Version]
- Orman, A.J.; Williams, H.P. A survey of different integer programming formulations of the travelling salesman problem. Optim. Econom. Financ. Anal. 2006, 9, 93–108. [Google Scholar]
- Rasmussen, R. TSP in Spreadsheets–a Guided Tour. Int. Rev. Econom. Educ. 2011, 10, 94–116. [Google Scholar] [CrossRef]
- Percus, A.G.; Martin, O.C. Finite size and dimensional dependence in the Euclidean traveling salesman problem. Phys. Rev. Lett. 1996, 76, 1188–1191. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Chatterjee, A.; Chakraborti, A.; Chakrabarti, B.K. Econophysics: An Introduction; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Beardwood, J.; Halton, J.H.; Hammersley, J.M. The shortest path through many points. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge Press: Cambridge, UK, 1959; Volume 55, pp. 299–327. [Google Scholar] [CrossRef]
- Chakrabarti, B.K. Directed travelling salesman problem. J. Phys. A Math. Gen. 1986, 19, 1273–1275. [Google Scholar] [CrossRef]
- Dhar, D.; Barma, M.; Chakrabarti, B.K.; Taraphder, A. The travelling salesman problem on a randomly diluted lattice. J. Phys. A Math. Gen. 1987, 20, 5289–5298. [Google Scholar] [CrossRef]
- Ghosh, M.; Manna, S.S.; Chakrabarti, B.K. The travelling salesman problem on a dilute lattice: A simulated annealing study. J. Phys. A Math. Gen. 1988, 21, 1483–1486. [Google Scholar] [CrossRef]
- Chakraborti, A.; Chakrabarti, B.K. The travelling salesman problem on randomly diluted lattices: Results for small-size systems. Eur. Phys. J. B-Condens. Matter Complex Syst. 2000, 16, 677–680. [Google Scholar] [CrossRef] [Green Version]
- Bonomi, E.; Lutton, J.-L. The N-city travelling salesman problem: Statistical mechanics and the Metropolis algorithm. SIAM Rev. 1984, 26, 551–568. [Google Scholar] [CrossRef]
- Zhou, A.-H.; Zhu, L.-P.; Hu, B.; Deng, S.; Song, Y.; Qiu, H.; Pan, S. Traveling-salesman-problem algorithm based on simulated annealing and gene-expression programming. Information 2019, 10, 7. [Google Scholar] [CrossRef] [Green Version]
- Ray, P.; Chakrabarti, B.K.; Chakrabarti, A. Sherrington-Kirkpatrick model in a transverse field: Absence of replica symmetry breaking due to quantum fluctuations. Phys. Rev. B 1989, 39, 11828–11832. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.W.; Amin, M.H.S.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A.J.; Johansson, J.; Bunyk, P. Quantum annealing with manufactured spins. Nature 2011, 473, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Chakrabarti, B.K. Multivariable optimization: Quantum annealing and computation. Eur. Phys. J. Spec. Top. 2015, 224, 17–24. [Google Scholar] [CrossRef]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Huang, Z. An Improved Noise Quantum Annealing Method for TSP. Int. J. Theor. Phys. 2020, 59, 3737–3755. [Google Scholar] [CrossRef]
- Tanaka, S.; Tamura, R.; Chakrabarti, B.K. Quantum Spin Glasses, Annealing and Computation; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Albash, T.; Lidar, D.A. Adiabatic quantum computation. Rev. Modern Phys. 2018, 90, 015002. [Google Scholar] [CrossRef] [Green Version]
- Gini, C. Measurement of inequality of incomes. Econ. J. 1921, 31, 124–126. [Google Scholar] [CrossRef]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Ghosh, A.; Chattopadhyay, N.; Chakrabarti, B.K. Inequality in societies, academic institutions and science journals: Gini and k-indices. Phys. A Stat. Mech. Appl. 2014, 410, 30–34. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Chatterjee, A.; Inoue, J.; Chakrabarti, B.K. Inequality measures in kinetic exchange models of wealth distributions. Phys. A Stat. Mech. Appl. 2016, 451, 465–474. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, A.; Ghosh, A.; Chakrabarti, B.K. Socio-economic inequality: Relationship between Gini and Kolkata indices. Phys. A Stat. Mech. Appl. 2017, 466, 583–595. [Google Scholar] [CrossRef] [Green Version]
- Sinha, A.; Chakrabarti, B.K. Inequality in death from social conflicts: A Gini & Kolkata indices-based study. Phys. A Stat. Mech. Appl. 2019, 527, 121185. [Google Scholar]
- Banerjee, S.; Chakrabarti, B.K.; Mitra, M.; Mutuswami, S. On the Kolkata index as a measure of income inequality. Phys. A Stat. Mech. Appl. 2020, 545, 123178. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Chakrabarti, B.K.; Mitra, M.; Mutuswami, S. Social Inequality Measures: The Kolkata index in comparison with other measures. Front. Phys. 2020, 8, 562182. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Pareto_principle (accessed on 28 January 2021).
- Hirsch, J.E. An index to quantify an individual’s scientific research output. Proc. Natl. Acad. Sci. USA 2005, 102, 16569–16572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subramanian, S. More tricks with the Lorenz curve. Econ. Bull. 2015, 35, 580–589. [Google Scholar]
- Sahasranaman, A.; Jensen, H.J. Spread of Covid-19 in urban neighbourhoods and slums of the developing world. arXiv 2020, arXiv:2010.06958. [Google Scholar]
- Fisher, M.E. Renormalization group theory: Its basis and formulation in statistical physics. Rev. Modern Phys. 1998, 70, 653–681. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Universal behavior in nonlinear systems. Phys. D Nonlinear Phenom. 1983, 7, 16–39. [Google Scholar] [CrossRef]
- Chatterjee, A.; Yarlagadda, S.; Chakrabarti, B.K. Econophysics of Wealth Distributions; Springer: Milano, Italiy, 2005. [Google Scholar]
- Chatterjee, A.; Chakrabarti, B.K. Kinetic exchange models for income and wealth distributions. Eur. Phys. J. B 2007, 60, 135–149. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, B.K.; Chakraborti, A.; Chakravarty, S.R.; Chatterjee, A. Econophysics of Income and Wealth Distributions; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Chakrabarti, A.S.; Chakrabarti, B.K. Microeconomics of the ideal gas like market models. Phys. A Stat. Mech. Appl. 2009, 388, 4151–4158. [Google Scholar] [CrossRef] [Green Version]
- Quevedo, D.S.; Quimbay, C.J. Non-conservative kinetic model of wealth exchange with saving of production. Eur. Phys. J. B 2020, 93, 186. [Google Scholar] [CrossRef]
- Pareschi, L.; Toscani, G. Interacting Multiagent Systems: Kinetic Equations and Monte Carlo Methods; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Ribeiro, M.B. Income Distribution Dynamics of Economic Systems: An Econophysical Approach; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Chakraborti, A. Distributions of money in model markets of economy. Int. J. Modern Phys. C World Sci. 2002, 13, 1315–1321. [Google Scholar] [CrossRef] [Green Version]
- Boghosian, B.M. Is Inequality Inevitable? Sci. Am. 2019, 321, 70–77. [Google Scholar] [CrossRef]
- Iglesias, J.R. How simple regulations can greatly reduce inequality. arXiv 2010, arXiv:1007.0461. [Google Scholar]
- Ghosh, A.; Basu, U.; Chakraborti, A.; Chakrabarti, B.K. Threshold-induced phase transition in kinetic exchange models. Phys. Rev. E 2011, 83, 061130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chakrabarti, A.S.; Chakrabarti, B.K.; Chatterjee, A.; Mitra, M. The Kolkata Paise Restaurant problem and resource utilization. Phys. A Stat. Mech. Appl. 2009, 388, 2420–2426. [Google Scholar] [CrossRef] [Green Version]
- Chakraborti, A.; Challet, D.; Chatterjee, A.; Marsili, M.; Zhang, Y.-C.; Chakrabarti, B.K. Statistical mechanics of competitive resource allocation using agent-based models. Phys. Rep. 2015, 552, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Chatterjee, A.; Mitra, M.; Chakrabarti, B.K. Statistics of the kolkata paise restaurant problem. New J. Phys. 2010, 12, 075033. [Google Scholar] [CrossRef]
- Sharif, P.; Heydari, H. Quantum solution to a three player Kolkata restaurant problem using entangled qutrits. arXiv 2011, arXiv:1111.1962. [Google Scholar]
- Sharif, P.; Heydari, H. An introduction to multi-player, multi-choice quantum games: Quantum minority games & kolkata restaurant problems. In Econophysics of Systemic Risk and Network Dynamics; Abergel, F., Ed.; Springer: Milano, Italy, 2013; pp. 217–236. [Google Scholar]
- Ghosh, D.; Chakrabarti, A.S. Emergence of distributed coordination in the Kolkata paise restaurant problem with finite information. Phys. A Stat. Mech. Appl. 2017, 483, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, P.; Mitra, M.; Mukherjee, K. The economics of the Kolkata Paise Restaurant problem. Sci. Cult. Indian Sci. News Assoc. 2018, 84, 26–30. [Google Scholar]
- Sharma, K.; Anamika; Chakrabarti, A.S.; Chakraborti, A.; Chakravarty, S. The Saga of KPR: Theoretical and experimental developments. Sci. Cult. Indian Sci. News Assoc. 2018, 84, 31–36. [Google Scholar]
- Tamir, B. Econophysics and the Kolkata Paise Restaurant Problem: More is different. Sci. Cult. Indian Sci. News Assoc. 2018, 84, 37–47. [Google Scholar]
- Sinha, A.; Chakrabarti, B.K. Phase transition in the Kolkata Paise Restaurant problem. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 083116. [Google Scholar] [CrossRef] [PubMed]
- Park, T.; Saad, W. Kolkata paise restaurant game for resource allocation in the Internet of Things. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, IEEE Xplore, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1774–1778. [Google Scholar]
- Martin, L. Extending Kolkata Paise Restaurant Problem to Dynamic Matching in Mobility Markets. Jr. Manag. Sci. 2019, 4, 1–34. [Google Scholar]
- Martin, L.; Karaenke, P. The Vehicle for Hire Problem: A Generalized Kolkata Paise Restaurant Problem. In Workshop on Information Technology and Systems; Technical University of Munich: Seoul, Korea, 2017. [Google Scholar]
- Ghosh, A.; Chakrabarti, A.S.; Chakrabarti, B.K. Kolkata Paise Restaurant problem in some uniform learning strategy limits. In Econophysics and Economics of Games, Social Choices and Quantitative Techniques; Springer: Berlin, Germany, 2010; pp. 3–9. [Google Scholar]
- Ghosh, A.; De Martino, D.; Chatterjee, A.; Marsili, M.; Chakrabarti, B.K. Phase transitions in crowd dynamics of resource allocation. Phys. Rev. E 2012, 85, 021116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghosh, A.; Chatterjee, A.; Chakrabarti, A.S.; Chakrabarti, B.K. Zipf’s law in city size from a resource utilization model. Phys. Rev. E 2014, 90, 042815. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, B.K. Kolkata restaurant problem as a generalised el farol bar problem. In Econophysics of Markets and Business Networks; Springer: Milan, Italy, 2007; pp. 239–246. [Google Scholar]
- Allais, M. Economics as a Science. Cah. Vilfredo Pareto 1968, 6, 5–24. Available online: https://www.jstor.org/stable/40368894?seq=1 (accessed on 28 January 2021).
- Frey, B.S. Economics As a Science of Human Behaviour: Towards a New Social Science Paradigm, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Solow, R.M. How did economics get that way and what way did it get? Daedalus 1997, 126, 39–58. [Google Scholar] [CrossRef]
- Colander, D. New millennium economics: How did it get this way, and what way is it? J. Econ. Perspect. 2000, 14, 121–132. [Google Scholar] [CrossRef] [Green Version]
- Venkatasubramanian, V. How Much Inequality Is Fair? Mathematical Principles of a Moral, Optimal, and Stable Capitalist Society; Columbia University Press: New York, NY, USA, 2017. [Google Scholar]
- Leiden University. Econophysics e-Prospectuses for 2012–2013, 2020–2021. Available online: https://studiegids.universiteitleiden.nl/en/courses/34804/econophysics or https://studiegids.universiteitleiden.nl/courses/99643/econophysics (accessed on 28 January 2021).
- Dash, K.C. The Story of Econophysics; Cambridge Scholars Publishing: Newcastle Upon Tyne, UK, 2019. [Google Scholar]
- Shubik, M.; Smith, E. The Guidance of an Enterprise Economy; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Jovanovic, F.; Schinckus, C. Econophysics and Financial Economics: An Emerging Dialogue; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Richmond, P.; Mimkes, J.; Hutzler, S. Econophysics and Physical Economics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Slanina, F. Essentials of Econophysics Modelling; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Aoyama, H.; Fujiwara, Y.; Ikeda, Y.; Iyetomi, H.; Souma, W. Macro-Econophysics: New Studies on Economic Networks and Synchronization; Cambridge University Press: Delhi, India; Cambridge, UK, 2017. [Google Scholar]
- Schinckus, C. When Physics Became Undisciplined An Essay on Econophysics; University of Cambridge: Cambridge, UK, 2018; Available online: https://www.repository.cam.ac.uk/bitstream/handle/1810/279683/Chris_Thesis_FINAL.pdf?sequence=5&isAllowed=y (accessed on 28 January 2021).
- Chakrabarti, B.K. International Center for Social Complexity, Econophysics and Sociophysics Studies: A Proposal. In New Perspectives and Challenges in Econophysics and Sociophysics; New Economic Windows Series; Abergel, F., Ed.; Springer: Cham, The Newtherland, 2019; pp. 259–267. [Google Scholar]
- Helbing, D.; Balietti, S.; Bishop, S.; Lukowicz, P. Understanding, creating, and managing complex techno-socio-economic systems: Challenges and perspectives (Visioneer White Papers). Eur. Phys. J. Spec. Top. 2011, 195, 165–186. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A. Econophysics Research in India in the last two Decades. IIM Kozhikode Soc. Manag. Rev. 2013, 2, 135–146. [Google Scholar] [CrossRef] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakrabarti, B.K.; Sinha, A. Development of Econophysics: A Biased Account and Perspective from Kolkata. Entropy 2021, 23, 254. https://doi.org/10.3390/e23020254
Chakrabarti BK, Sinha A. Development of Econophysics: A Biased Account and Perspective from Kolkata. Entropy. 2021; 23(2):254. https://doi.org/10.3390/e23020254
Chicago/Turabian StyleChakrabarti, Bikas K., and Antika Sinha. 2021. "Development of Econophysics: A Biased Account and Perspective from Kolkata" Entropy 23, no. 2: 254. https://doi.org/10.3390/e23020254
APA StyleChakrabarti, B. K., & Sinha, A. (2021). Development of Econophysics: A Biased Account and Perspective from Kolkata. Entropy, 23(2), 254. https://doi.org/10.3390/e23020254





