1. Introduction
Fractal groups are groups acting on self-similar objects in a self-similar way. The term “fractal group” was used for the first time in [
1] and then appeared in [
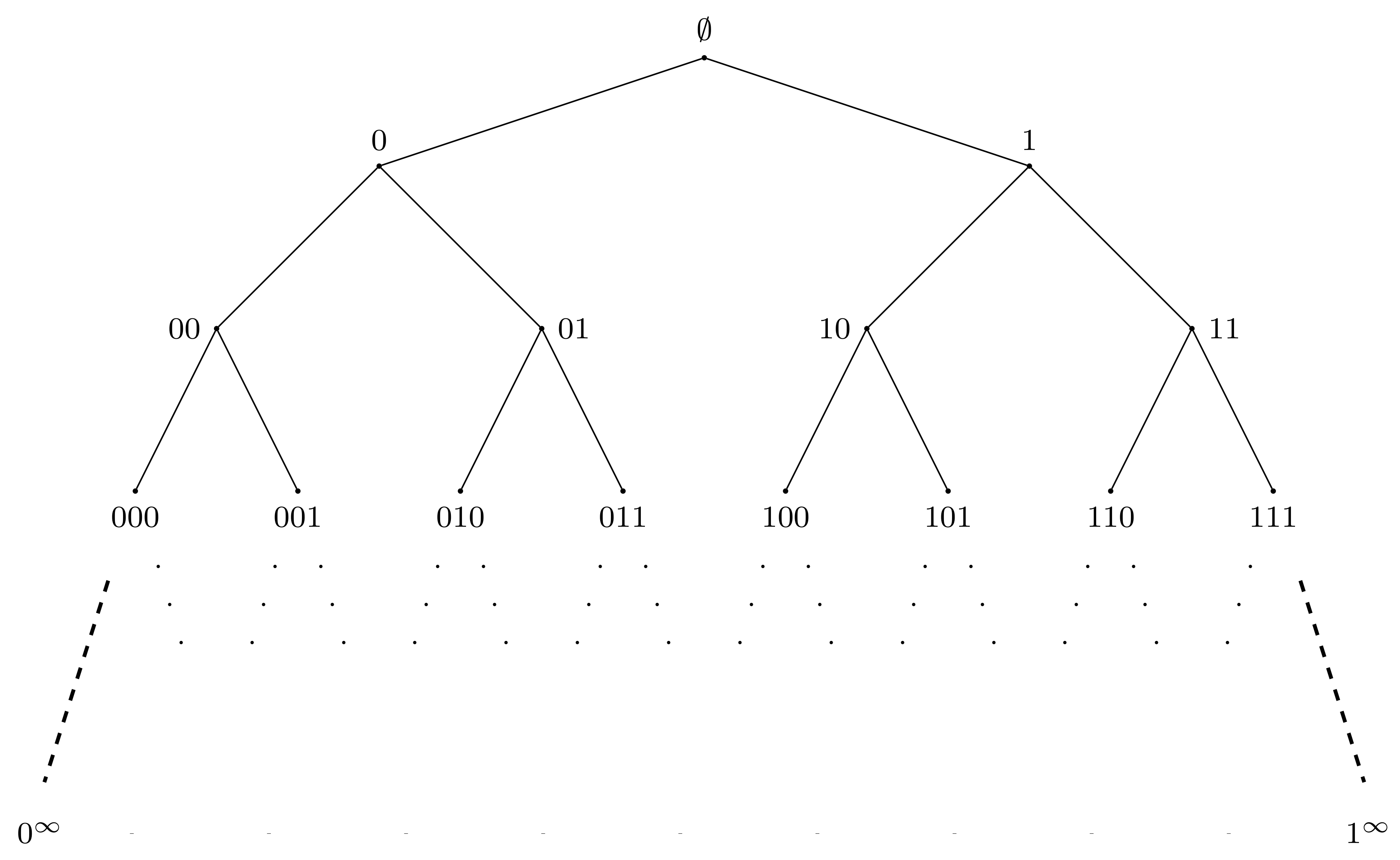
2]. Although there is no rigorous definition of a fractal group (like there is no rigorous definition of a fractal set), there is a definition of a self-similar group (see Definition 1). Self-similar groups act by automorphisms on regular rooted trees (like a binary rooted tree shown in
Figure 1). Such trees are among the most natural and often used self-similar objects. The properties of self-similar groups and their structure resemble the self-similarity properties of the trees and their boundaries. The nicest examples come from finite Mealy type automata, like automata presented by
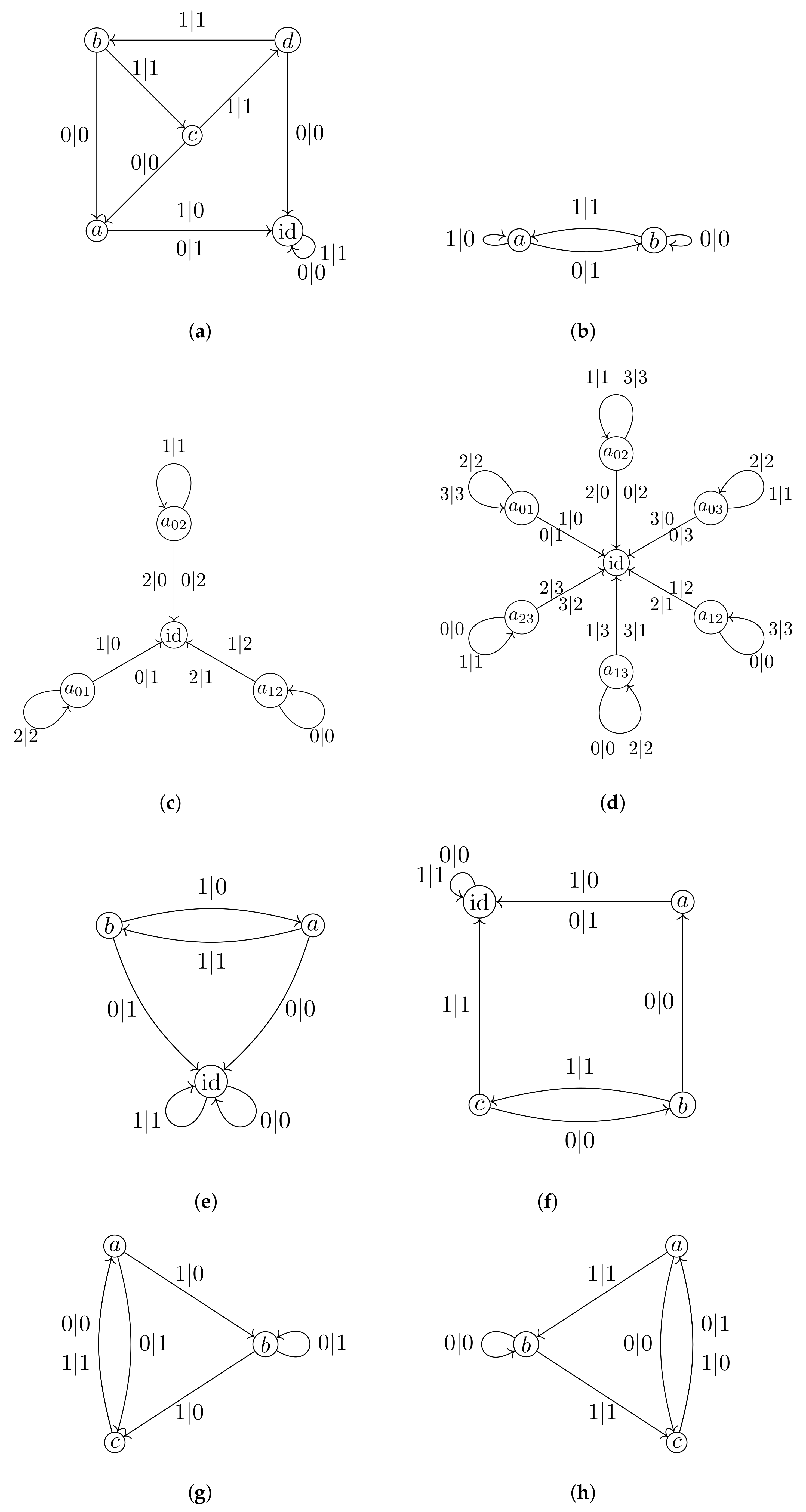
Figure 2.
Moreover, there are several ways to associate geometric objects of fractal type with a self-similar group. This includes limits of Schreier graphs [
1,
3,
4,
5,
6], limit spaces and limit solenoids of Nekrashevych [
7,
8,
9,
10], quasi-crystals [
11], Julia sets [
1,
12], etc.
Self-similar groups were used to solve several outstanding problems in different areas of mathematics. They provide an elegant contribution to the general Burnside problem [
13], to the J. Milnor problem on growth [
14,
15], to the von Neumann - Day problem on non-elementary amenability [
15,
16], to the Atiyah problem in
-Betti numbers [
17], etc. Self-similar groups have applications in many areas of mathematics such as dynamical systems, operator algebras, random walks, spectral theory of groups and graphs, geometry and topology, computer science, and many more (see the surveys [
2,
4,
11,
18,
19,
20,
21,
22] and the monograph [
12]).
Multi-dimensional rational maps appear in the study of spectral properties of graphs and unitary representations of groups (including representations of Koopman type). The spectral theory of such objects is closely related to the theory of joint spectrum of a pencil of operators in a Hilbert (or more generally in a Banach) space and is implicitly considered in [
1] and explicitly outlined in [
23].
There is some mystery regarding how multi-dimensional rational maps appear in the context of self-similar groups. There are basic examples like the first group
of intermediate growth from [
13,
14], the groups called “Lamplighter”, “Hanoi”, “Basilica”, Spinal Groups, GGS-groups, etc. The indicated classes of groups produce a large family of such maps, part of which is presented by examples (
1)–(
2) and (
5)–(
11).
These maps are very special and quite degenerate as claimed by N. Sibony and M. Lyubich, respectively. Nevertheless, they are interesting and useful, as, on the one hand, they are responsible for the associated spectral problems, on the other hand, they give a lot of material for people working in dynamics, being quite different from the maps that were considered before.
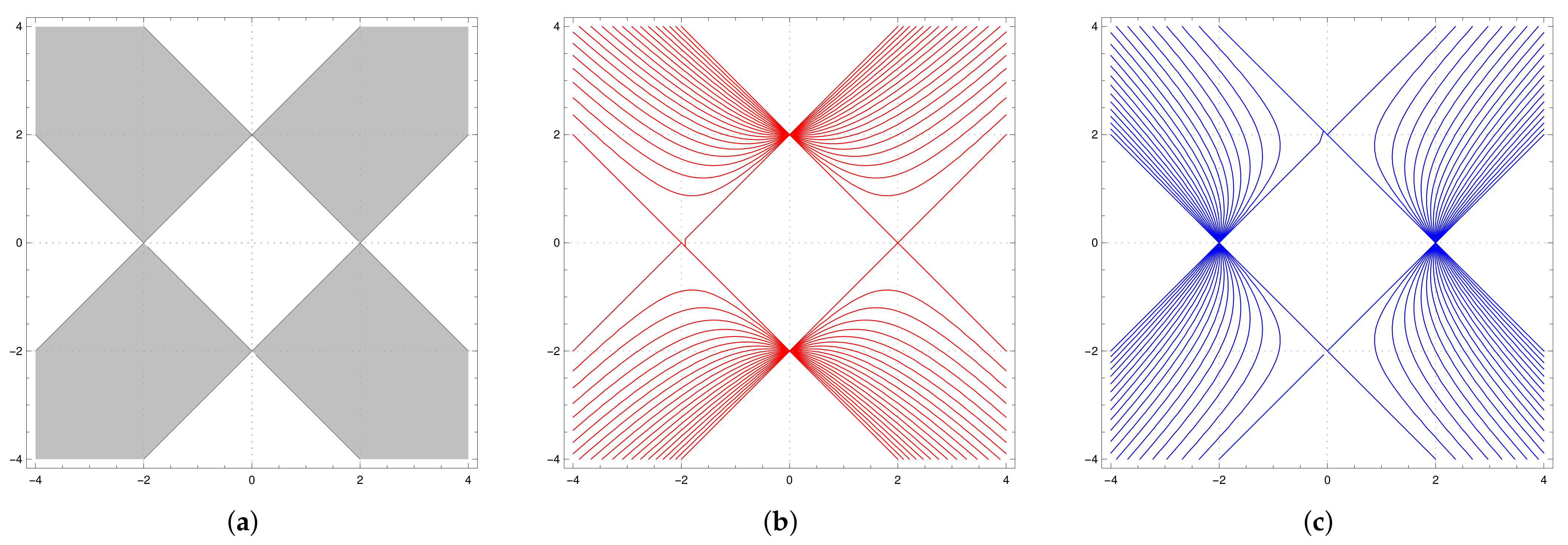
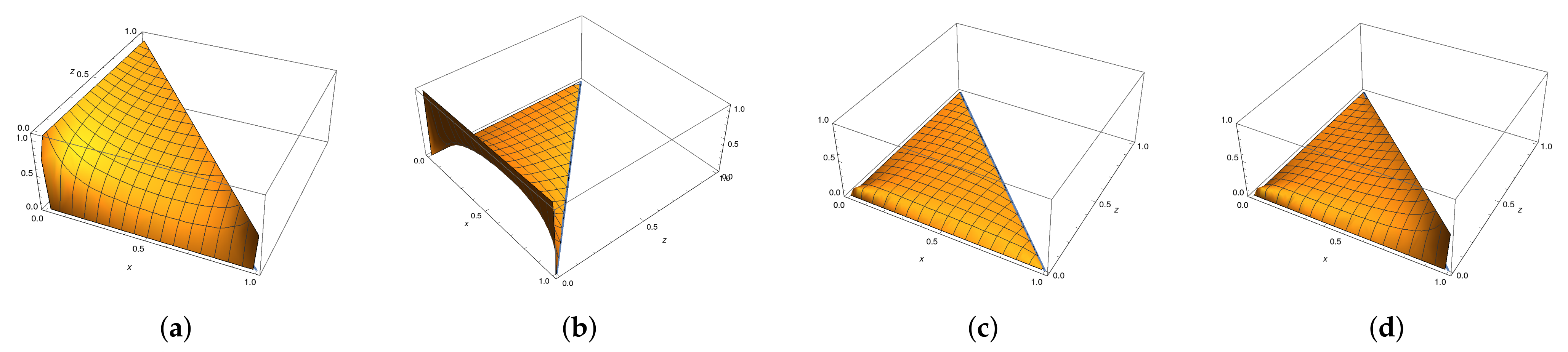
Some of them demonstrate features of integrability, which means that they semiconjugate to lower-dimensional maps, while the others do not seem to have integrability features and their dynamics (at least on an experimental level) demonstrate the chaotic behavior presented, for instance, by
Figure 3.
The phenomenon of integrability, discovered in the basic examples including the groups
, Lamplighter, and Hanoi, is thoroughly investigated by M-B. Dang, M. Lyubich and the first author in [
24]. For examples of intermediate complexity, the criterion found in [
24] based on the fractionality of the dynamical degree shows non-integrability; for instance, this is the case for the Basilica map (
9). More complicated cases of maps, like the Basilica map, or higher-dimensional
-maps given by (
5) and (
6) still wait for their resolution. An interesting phenomenon discovered in [
25] is the relation of self-similar groups with quasi-crystals and random Schrödinger operators.
This article surveys and explores the use of self-similar groups in the dynamics of multi-dimensional rational maps and provides a panorama of ideas, methods, and applications of fractal groups.
3. Self-Similar Groups
Self-similar groups arise from actions on d-regular rooted trees (for ), while self-similar (operator) algebras arise from d-similarities on an infinite dimensional Hilbert space H, where is an isomorphism.
Let us begin with the definition of a self-similar group. Let
be an alphabet,
be the set of finite words (including the empty word ∅) ordered lexiographically (assuming
), and let
be a
d-regular rooted tree with the set of vertices
V identified with
and set of edges
. The
Figure 1 shows the binary rooted tree when
. Usually we will omit the index
d in
. The root vertex corresponds to the empty word.
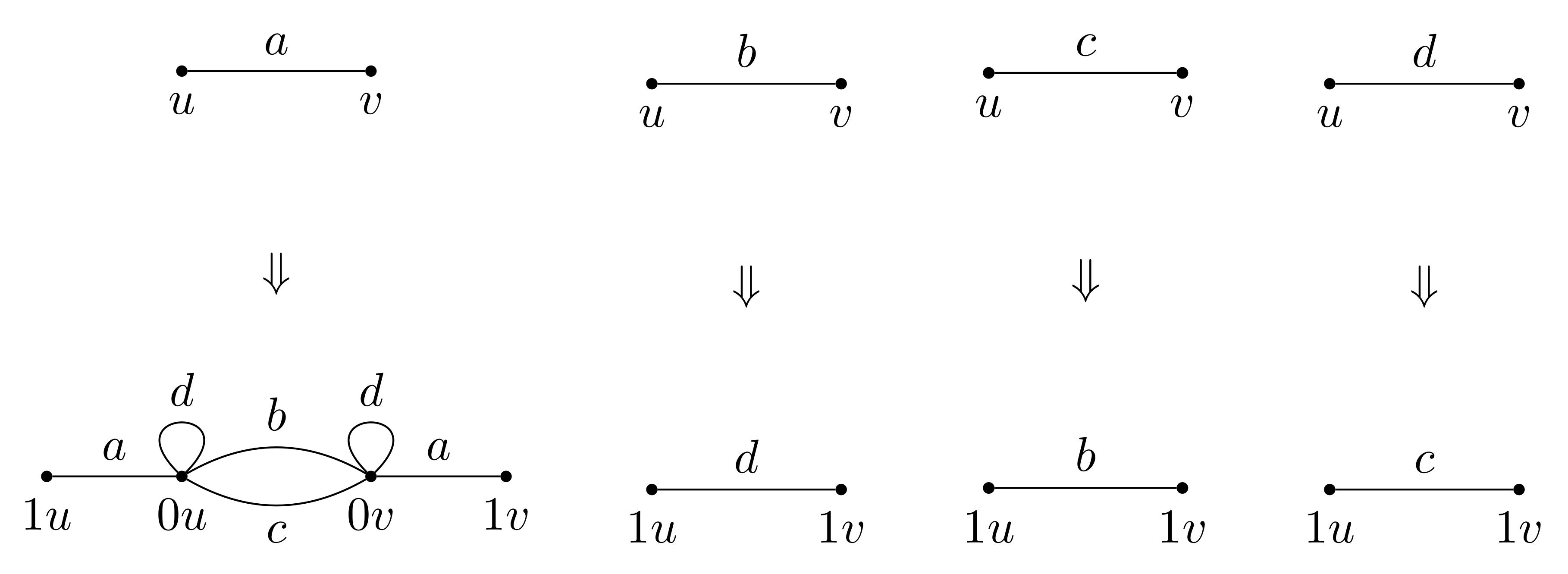
From a geometric point of view, the boundary of the tree T consists of infinite paths (without back tracking) joining the root vertex with infinity. It can be identified with the set of infinite words (sequences) of symbols from X and equipped with the Tychonoff product topology which makes it homeomorphic to a Cantor set. Let be the group of automorphisms of T (i.e., of bijections on V that preserve the tree structure). The cardinality of is and this group supplied with a natural topology is a profinite group (i.e., compact totally disconnected topological group, or a projective limit of group of automorphisms of finite groups , where is the finite subtree of T from the root until the n-th level, for ).
Symmetric group ( of permutations on naturally acts on X and on V by , for and . That is, a permutation permutes vertices of the first level according to its action on X and no further action below first level. For let be the subtree of T with the root at v.
For each
, the subtree
is naturally isomorphic to
T and the corresponding isomorphisms
constitute a canonical system of self-similarities of
T. Any automorphism
can be described by a permutation
showing how
g acts on the first level and a
d-tuple of automorphisms
of trees
showing how
g acts below the first level. As
this leads to the isomorphism
where ⋊ denotes the operation of semidirect product (recall that if
N is a normal subgroup in a group
G,
H is a subgroup in
G,
, and
, then
). Another interpretation of the isomorphism (
12) is
where
denotes the permutational wreath product [
4,
12]. According to (
12), for
,
Relations of this sort are called wreath recursions and elements are called sections.
If denotes the n-th level of the tree, then every preserves the level , for . Thus the maximum possible transitivity of a group is the level transitivity.
Definition 1. A group G acting on a tree by automorphism is said to be self-similar if for all the section coming from wreath recursion (14) belongs to G after identification of (on which acts) with T using identifications . An alternative way to define self-similar groups is via Mealy automata (also known as the transducers or the sequential machines. See [
39,
40] for more applications of automata).
A non-initial Mealy automaton
consists of a finite alphabet
, a set
Q of states, a transition function
, and an output function
. Selecting a state
as initial, produces the initial automaton
. The functions
and
naturally extends to
and
via inductive definitions
for all
. Thus the initial automaton
determines the maps
which we will denote also by
(or sometimes even by
q). Moreover,
induces an endomorphism of the tree
via identification of
V with
. The automaton
is said to be finite if
.
The initial automaton
can be schematically viewed as the sequential machine (or the transducer) shown in
Figure 8. At the zero moment
, the automaton
is in the initial state
, reads the symbol
, produces the output
, and moves to the state
. Then
continues to operate with input symbols in the same fashion until reading the last symbol
.
An automaton of this type is called a synchronous automaton. Asychronous automata can also be defined and used in group theory and coding as explained in [
4,
41].
An automaton
is invertible if for any
, the map
is a bijection, i.e.,
is an element
of the symmetric group
. Invertibility of
implies that for any
the initial automaton
induces an automorphism of the tree
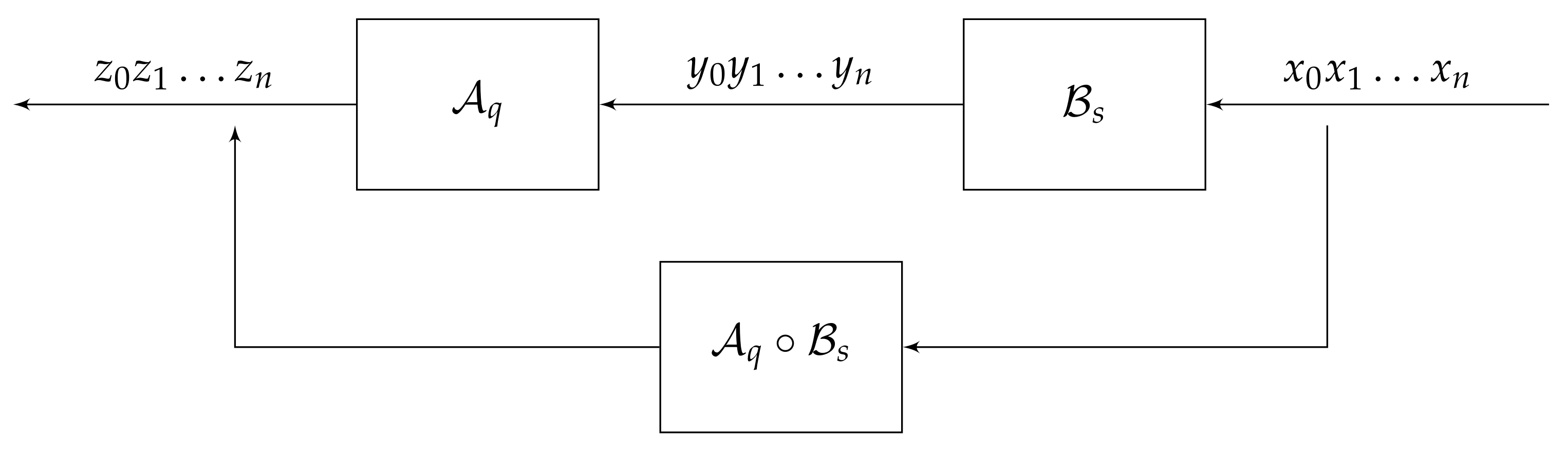
. The compositions
of maps
, where
is another automaton over the same alphabet, is the map determined by the automaton
with the set of states
and the transition and output functions determined by
in the obvious way (see
Figure 9). If
is an invertible automaton, then for any
, the inverse map also is determined by an automaton, which will be denoted by
.
The above discussion shows that for each
, we have a semigroup
of finite initial automata over the alphabet on
m letters. We can also define a group
of finite invertible initial automata. The group
naturally embeds in
. These groups are quite complicated, contain many remarkable subgroups, and depend on
m. At the same time in the asynchronous case there is only one (up to isomorphisms) group, introduced in [
4], called the group of rational homeomorphisms of a Cantor set. This group, for instance, contains famous R. Thompson’s groups
and
V. In fact, the elements in
and
are classes of equivalence of automata, usually presented by the minimal automaton. The classical algorithm of minimization of automata solves the word problem in
and
.
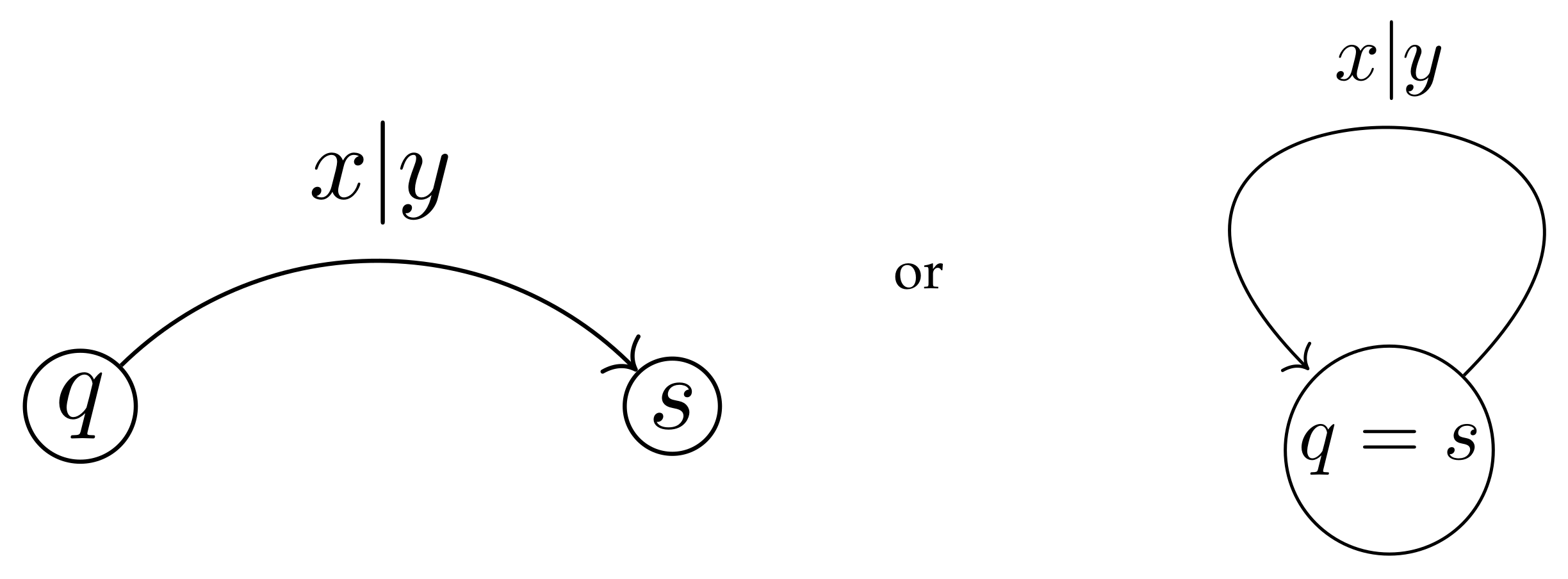
A convenient way to present finite automata is by diagrams, of the type shown on
Figure 2. The nodes (vertices) of a such diagram correspond to the states of
, each state
has
outgoing edges of the form shown in
Figure 10, indicating that if current state is
q and the input symbol is
x, then the next state will be
s and the output will be
y. This way we describe the transition and the output functions simultaneously.
If
is an invertible automaton, then we define
and
, the semigroup and the group generated by
;
is the semigroup generated by initial automata
and
is the group generated by
.
The group
acts on
by automorphisms and for each
the wreath recursion (
14) becomes
Therefore the groups generated by the states of the invertible automaton are self-similar.
The opposite is also true, any self-similar group can be realized as
for some invertible automaton, only the automaton could be infinite. Self-similar groups generated by finite automata, called fractal groups (see [
2]), constitute an interesting class of groups. Study of fractal groups in many cases leads to study of fractal objects, as explained for instance in [
2,
12,
22].
4. Self-Similar Algebras
The definition of self-similar algebras resembles the definition of self-similar groups. It is based on the important property of infinite dimensional Hilbert space
H to be isomorphic to the direct sum of
d (for
copies of it. A
d-fold similarity of
H is an isomorphism
There are many such isomorphisms and they are in a natural bijection with the *-representations of the Cuntz algebra
as observed in [
20]. The Cuntz algebra is given by the presentation
by generators and relations that we will call Cuntz relations.
Theorem 2 (Proposition 3.1 from [
20])
. The relation putting into correspondence to a *-representation of into the -algebra of bounded operators on a separable infinite dimensional Hibert space H, the map , where are generators of , is a bijection between the set of representations of on H and the set of d-fold self-similarities.The inverse of this bijection puts into correspondence to a d-similarity the *-representation of given by , forwhere ξ in the right hand side is at the k-th coordinate of . A natural example of a
d-similarity comes from the
d-regular rooted tree
T and its boundary
supplied by uniform Bernoulli measure
. That is,
, where
and
is the uniform distribution on
X. Then
decomposes as
where
is the subtree of
T with the root at the vertex
x of the first level and
. Then
via the isomorphism given by the operator
,
Another example associated with the self-similar subgroup
would be to consider a countable self-similar subset
, i.e., a subset
W such that
. Such a set can be obtained by including the orbit
,
into the set
W that is self-similar closure of
. Then
and
is isomorphic to
via the isomorphism
given by
Let
G be a self-similar group acting on the
d-regular tree
,
, and
be a
d-fold similarity. The unitary representation
of
G on
H is said to be self-similar with respect to
if for all
and for all
where
is the operator defined by (
18), the element
h is the section
of
g at the vertex
x of the first level, and
, for each
.
The meaning of the relation (
19) comes from the wreath recursion (
14) and its generalization represented by the relation
Examples of self-similar representations are the Koopman representation of G in (that is, for ) and permutational representations in given by the action of G on the self-similar subset .
The papers [
7,
20,
42] introduce and discuss a number of self-similar operator algebras associated with self-similar groups. They are denoted by
and if
is the algebra obtained by the completion of the group algebra
with respect to a self-similar representation
, then there are natural surjective homomorphisms
The definition of
involves a general theory of Cuntz-Pimsner
-algebras, which was developed in [
43].
Study of the algebra
is based on the matrix recursions. A matrix recursion on an associative algebra
A is a homomorphism
where
is the algebra of
matrices with entries in
A.
Wreath recursions (
14) associated with a self-similar representation
of a self-similar group
G naturally lead to a matrix recursion
for the group algebra
. Define
on group elements
by
where
and extended to the group algebra
and its closure
linearly.
In terms of the associated representation
of the Cuntz algebra we have the relations
where
, and
are generators of
from presentation (
17).
Example 1. In the case of the group , given by presentation (3), acting on via the automaton in Figure 2a, the recursions for the Koopman representation are,where 1 stands for the identity operator. Here (and henceforth), we abuse the notation and write g in place of , for any group element g. Example 2. In the case of the Basilica group , the recursions for the Koopman representation are, The minimal self-similar algebra
is defined using the algebra generated by permutational representation in
for an arbitrary self-similar subset
spanned by the orbit of any
G-regular point [
20]. A point
is
G-regular if
or
for all
for some neighborhood
of
. Points that are not
G-regular are called
G-singular. In the case of
,
-singular points constitute the orbit
. The set of
G-regular points is co-meager (i.e., an intersection of a countable family of open dense sets). This notion was introduced in [
4] and now play an important role in numerous studies.
Another example of a self-similar algebra is
generated by Koopman representation
on
. The representation
is the sum of finite dimensional representations and
is residually finite dimensional [
1,
18,
44]. The algebra
has a natural self-similar trace
, i.e., a trace that satisfies
for
, where
.
This trace was used in [
30] to compute the spectral measure associated with the Laplace operator on the Lamplighter group. The range of values of
for
is
[
19].
A group
G is said to be just-infinite if
G is infinite and every proper quotient of
G is finite. An algebra
is just-infinite dimensional if it is infinite dimensional but every proper quotient is finite dimensional. Infinite simple groups and infinite dimensional simple
-algebras are examples of such objects. Infinite cyclic group
, infinite dihedral group
, and
are examples of just-infinite groups. There is a natural partition of the class of just-infinite groups into the class of just-infinite branch groups, hereditary just-infinite groups, and near-simple groups [
45]. The proof of this result uses a result of J. Wilson from [
46]. Roughly speaking, a branch group is a group acting in a branch way on some spherically homogeneous rooted tree
, given by a sequence
(where,
for all
n) of integers (the integer
is called the branching number for vertices of
n-th level). The group
is an example of a just-infinite branch group and the algebra
, which sometimes (following S. Sidki [
47]) is called the “thin” algebra, is just-infinite dimensional [
48].
Problem 1. Is the -algebra , generated by Koopman representation of in , just-infinite dimensional?
There is also a natural partition of separable just-infinite dimensional
-algebras into three subclasses by the structure of its space of primitive ideals which can be of one of the types
,
, where type
means a singleton and corresponds to the case of simple
-algebras, the type
,
corresponds to an essential extension of a simple
-algebra by a finite dimensional
-algebra with
n-simple summands, and in the
case the algebras are residually finite dimensional. If
happens to be just-infinite dimensional, this would be a good addendum to the examples presented in [
49], where the above trichotomy for
-algebras is proven.
Given G, a self-similar group acting on , , the associated universal Cuntz-Pimsner -algebra , denoted as , is defined as the universal -algebra generated by G and satisfying the following relations:
Relations of G,
for and if for all (i.e., if and is a section).
A self-similar group
G is said to be contracting if there exists a finite set
such that for all
, there exists
with
for all words
of length greater than
. The smallest set
having this property is called the nucleus. Examples of contracting groups are the adding machine
given by the relation
, where
is a cyclic permutation of
X, group
, Basilica, Hanoi groups, and
. The Lamplighter group
presented by the automaton in
Figure 2b as well as the examples given by automata from
Figure 2g,h are not contracting.
The contracting property of the group is a tool used to prove subexponentiality of the growth. But not all contracting groups grow subexponentially. For instance, Basilica is contracting but has exponential growth. For a contracting group G with the nucleus , the Cuntz-Pimsner algebra has the following presentation by generators and relations:
- 1.
Cuntz relations,
- 2.
relations for ,
- 3.
relations
, when
and relations
for
[
7].
Thus, for contracting groups, the algebra is finitely presented.
The nucleus of the group
is
hence
is given by the presentation
For contracting level transitive groups with the property that for every element
g of the nucleus the interior of the set of fixed points of
g is closed, all self-similar completions of
are isomorphic, and the isomorphisms
hold. This condition holds for Basilica but does not hold for the group
and one of the groups
,
from [
15], presented by the sequence
(and studied by A. Erschler [
50]). In the latter case
. It is unclear at the moment if for
we have the equality
.
Representations and characters of self-similar groups of branch type are considered in [
51,
52]. On self-similarity, operators, and dynamics see also [
53].
6. Graphs of Algebraic Origin and Their Growth
A graph consists of a set V of vertices and a set E of edges. The edges are presented by the map (here denotes the set of non negative integers), where represents the number of edges connecting the vertex u to the vertex v. If , then the edges are loops. So what we call a graph in graph theory usually is called a directed multi-graph or an oriented multi-graph. Depending on the situation, graph can be non-oriented (if the edges are independent of the orientation, i.e., and edges and are identified) and labeled (if edges are colored by elements of a certain alphabet). We only consider connected locally finite graphs (the later means that each vertex is incident to a finite number of edges). The degree of the vertex u is the number of edges incident to it (where each edge from or to u contributes 1 to the degree and each loop contributes 2 to the degree). A graph is of uniformly bounded degree if there is a constant C such that for all , and is a regular graph if all vertices have the same degree.
There is a rich source of examples of graphs coming from groups. Namely, given a marked group
(i.e., a group
G with a generating set
A, usually we assume that
and therefore the group is finitely generated), one defines the directed graph
with
and
, where
g is the origin and
is the end of the edge
. This is the left Cayley graph. Similarly, one can define the right Cayley graph
, and there is a natural isomorphism
. Left and right Cayley graphs are vertex transitive, i.e., the group
of automorphisms acts transitively on the set of vertices (right translations by elements of
G on
induce automorphisms of
). When speaking about Cayley graph, we usually keep in mind the left Cayley graph. Depending on the situation, Cayley graphs are considered as labeled graphs (the edge
has label
a), or unlabeled (if labels do not play a role). Cayley graphs can also be converted into undirected graphs by identification of pairs
of mutually inverse pairs of edges. The examples of Cayley graphs are presented in
Figure 11. Non-oriented Cayley graph of
is
d-regular with
, where
is the set of generators whose order is two (involutions).
A Schreier graph
is determined by a triple
, where as before
A is a system of generators of
G and
H is a subgroup of
G. In this case
is a set of left cosets (for the left version of definition) and
. Again, one can consider a right version of the definition, oriented or non-oriented, labeled or unlabeled versions of the Schreier graph [
61,
62,
63].
Cayley graph
is isomorphic to the Schreier graph
when
is the trivial subgroup. Non-oriented Schreier graphs are also
d-regular with
d given by the same expression as above, but in contrast with Cayley graphs, they may have a trivial group of automorphism. Examples of Schreier graphs are presented in the
Figure 12.
We have the following chains of classes of graphs:
In fact the class of
d-regular graphs of even degree
coincides with the class of Schreier graphs of the free group
of rank
m (for finite graphs this was observed by Cross [
64] and for the general case see [
65] and Theorem 6.1 in [
19]). For an odd degree, the situation is slightly more complicated, but there is clear understanding on which of them are Schreier graphs [
66].
Schreier graphs have much more applications in mathematics being able to provide a geometrical-combinatorial representation of many objects and situations. In particular, they are used to approximate fractals, Julia sets, study the dynamics of groups of iterated monodromy, Hanoi Tower Game on d pegs for , etc.
Growth function of a graph
with distinguished vertex
is the function
where
is the combinatorial distance given by the length of a shortest path connecting two vertices
u and
v. Its rate of growth when
, defines the rate of growth of the graph at infinity (if
is an infinite graph). It does not depend on the choice of
(in case of connected graphs), and is bounded by the exponential function
when
is of uniformly bounded degree
.
The growth of Schreier graph can be of power function
,
type, even with irrational
[
1], of the type
[
32], and of many other unusual types of growth.
On the other hand, the growth of a Cayley graph (or what is the same the growth of the corresponding group) is much more restrictive. It is known that if it is of the power type
, then
is a positive integer (in which case the group is said to be of polynomial growth) and the group is virtually nilpotent (i.e., contains nilpotent subgroup of finite index) [
67]. The Cayley graphs of virtually solvable groups or of linear groups (i.e., groups presented by matrices over a field) either have polynomial or exponential growth [
68,
69,
70,
71]. The question about existence of groups of intermediate growth was raised by J. Milnor [
72] and got the answer in [
14,
15] using the group
.
The Cayley graph of the group of intermediate growth
is presented by
Figure 11c. The group
is a representative of an uncountable family of groups
,
, mostly consisting of groups of intermediate growth [
15] (definition is given by (
41) and (
42)). Moreover, there are uncountably many of different rates of growth in this family, where by the rate (or degree) of growth of a group
G we mean the dilatational equivalence class of
(two functions
are equivalent,
, if there is
C such that
and
). This gives the first family of cardinality
of continuum of finitely generated groups with pairwise non quasi-isometric Cayley graphs. As shown in [
73,
74], for any
,
where
is
and
is the (unique) positive root of the polynomial
. In [
75] the group
is used to show that for each
such that
, there is a group with growth equivalent to
.
Surprisingly, so far there is no example of a group with super-polynomial growth but slower than the growth of
. There is a conjecture [
76] that there is a gap in the scale of growth degrees of finitely generated groups between polynomial growth and growth of the partition function
(i.e., if
, then
G is virtually nilpotent and hence has a polynomial growth). The conjecture has been confirmed to be true for the class of groups approximated by nilpotent groups. More on the gap conjecture for group growth and other asymptotic characteristics of groups see [
21,
77].
Problem 2. Is there a finitely generated group with super polynomial growth smaller than the growth of the group ?
7. Space of Groups and Graphs and Approximation
A pair
where
G is a group and
is an ordered system of (not necessarily distinct) generators is said to be a marked group. There is a natural topology in the space
of
m-generated marked groups introduced in [
15]. Similarly, there is a natural topology in the space
of marked Schreier graphs associated with marked triples
(a marked graph is a graph with distinguished vertex viewed as the origin). For every
, the spaces
and
are totally disconnected compact metrizable spaces whose structure is closely related to various topics of groups theory and dynamics. For instance the closure
of
in
consists of a Cantor set
and a countable set
of isolated points accumulating to
and consisting of virtually metabelian groups containing a direct product of copies of the Lamplighter group
[
15,
78] as a subgroup of finite index. The closure of
is described in [
79] and has a more complicated structure. More on spaces
and
see [
18,
80,
81].
One of the fundamental questions about these spaces is finding the Cantor-Bendixson rank (for the definition see [
82]) characterized by the first ordinal when taking of Cantor-Bendixson derivative does not change the space.
A more general notion than Schreier graph is the notion of orbital graph. Given an action of marked group on the space X, one can build a graph with the set of vertices and the set of edges . Connected components of this graph are Schreier graphs , , where is the stabilizer of point and is the set of representatives of orbits. If action is transitive, then orbit graph is a Schreier graph.
Given a level transitive action of marked group
by automorphisms on a
d-regular rooted tree
T, one can consider the covering sequence
of graphs where
is orbital graph for action on
n-th level of the tree and
covers
. Additionally, for every point
(the boundary of
T) one can associate a Schreier graph
built on the orbit
of
(
). If
is a vertex of level
n that belongs to the path representing
, then
(the limit is taken in the topology of the space of marked Schreier graphs). The relation (
23) allows an approximation of infinite graphs by finite graphs that leads also to the approximation of their spectra as shortly explained in the next section.
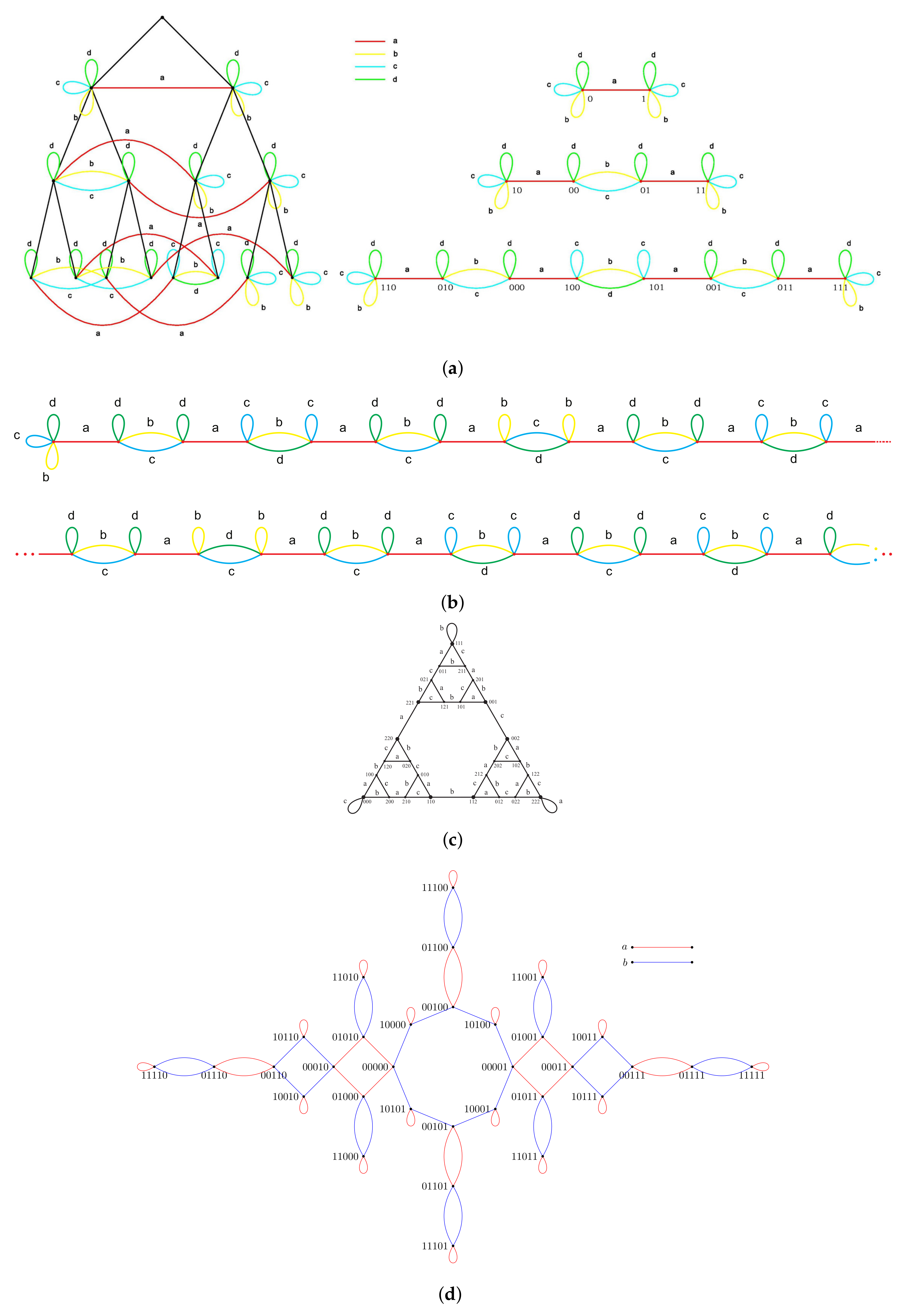
The example of
and
associated with the group
is given by
Figure 12a,b. In this example
can be obtained from
by substitution rule given by
Figure 13 that mimics the substitution
used in presentation (
3).
Similar property holds for associated with the overgroup and and graphs associated with and if instead of a single substitution, to use three substitutions and iterate them accordingly to “oracle” .
The correspondence
gives a map from
to
with the image
. The set of vertices
of
is the orbit
and
acts on
by changing the root vertex
. The graphs
are one-ended and are isolated points in
and also in the closure
in
. Deletion of them from
gives the set
which is a union of
and the countable set
consisting of the limit points of
that do not belong to
. The set
consists of pairs
, where
is one of the three graphs given by
Figure 14 (where,
is any cyclic permutation of
), and v is an arbitrary vertex of
[
5].
Now
X also is homeomorphic to a Cantor set,
acts on
X and the action is minimal and uniquely ergodic and the map
extends to a continuous factor map
which is one-to-one except in a countable set of points, where it is three-to-one [
5].
8. Spectra of Groups and Graphs
Let
be a
d-regular (non-oriented) graph. The Markov operator
M acts on the Hilbert space
(which we denote by
) and is defined as
where
and
is the adjacency relation. The operator
where
I is the identity operator is called the discrete Laplace operator. Operators
M and
L can be defined also for non-regular graphs as it is done for instance in [
83,
84]. The Markov operator
M is a self-adjoint operator with the norm
and the spectrum
. The name “Markov” comes from the fact that
M is the Markov operator associated with the random walk on
in which a transition
occurs with probability
, if
u and
v are adjacent vertices. Random walks on graphs are special case of Markov chains.
A graph
of uniformly bounded degree is called amenable if
(
). Such definition comes from the analogy with von-Neumann – Bogolyubov theory of amenable groups, i.e., groups with invariant mean [
85]. By Kesten’s criterion [
86], amenable groups can be characterized as groups for which the spectral radius
is equal to one, where
is the probability of return to identity element in
n steps of the simple random walk on the Cayley graph.
By a spectrum of a graph (or a group), we mean the spectrum of
M. A more general concept is used when graph is
weighted, in the sense that a weight function
on edges is given and the “weighted Markov” operator
is defined in
as
A special case of such situation is given by a marked group
(i.e., group
G together with its generating set
A) and symmetric probability distribution
on
:
, for all
and
. Then Markov operator
acts as
and
is the operator associated with a random walk on the (left) Cayley graph
, where transition
holds with probability
.
The case of uniform distribution on (i.e., of a simple random walk) is called isotropic case, while non-uniform distribution corresponds to the anisotropic case.
Basic questions about spectra of infinite graphs are:
What is the shape (up to homeomorphism) of ?
What can be said about spectral measures associated with functions , in particular, with delta functions , ?
As usual in mathematical physics, the gaps in the spectrum, discrete and singular continuous parts of the spectrum are of special interest. Also an important case is when graph has a subgroup of the group of automorphisms acting on the set of vertices freely and co-compactly (i.e., with finitely many orbits). The case of vertex transitive graphs and especially of the Cayley graph is of special interest and is related to many topics in abstract harmonic analysis, operator algebras, asymptotic group theory and theory of random walks. Among open problems, let us mention the following.
Problem 3. Can the spectrum of a Cayley graph of a finitely generated group be a Cantor set? (i.e., homeomorphic to a Cantor set). The problem is open in both isotropic and anisotropic cases.
Problem 4. Can a torsion free group have a gap in spectrum?
If the answer to the last question is affirmative, then this would give a counterexample to the Kadison-Kaplanski conjecture on idempotents.
Spectral theory of graphs of algebraic origin is a part of spectral theory of convolution operators in or given by elements of a group algebra or matrices with entries in and is closely related to many problems on -invariants, including -Betti numbers, Novikov-Slubin invariants, etc.
The state of art of the above problem is roughly as follows. Spectra of Euclidean grids (lattices
,
) and of their perturbations is a classical subject based on the use of Bloch-Floquet theory, representation theory of abelian groups and classical methods. The main facts include finiteness of the number of gaps in spectrum, band structure of the spectrum, absence of singular continuous spectrum, finiteness (and in many cases) absence of the discrete part in the spectrum [
87].
Another important case is trees and tree like graphs, such as, the Cayley graphs of free groups and free product of finite groups. For these groups the use of representation theory is limited but somehow possible, the structure of the spectrum is similar to the case of graphs with co-compact
-action, although the methods are quite different, see [
86,
88,
89,
90,
91,
92,
93,
94,
95,
96,
97].
One more important case constitute graphs associated with classical and non-classical self-similar fractals or self-similar groups [
1,
98,
99]. In particular, in [
1] it is shown that
Theorem 3. Spectrum of the Schreier graph of self-similar group can be a Cantor set or a Cantor set and a countable set of isolated points accumulated to it.
Recall that in
Section 7, for a group acting on rooted tree
T, we introduced a sequence
of finite graphs and family
of infinite graphs. In the next result
is a Markov operator associated with
and
is the Koopman representation.
Theorem 4. Let G be a group acting on rooted tree T and, where. Then,
- 1.
- 2.
If the action is level transitive and G is amenable, thendoes not depend on the pointand is equal to Σ.
- 3.
The limitof counting measures(summation is taken with multiplicities) exists. It is called the density of states.
This result is a combination of observations made in [
3,
100]. In fact, the relation (24) and the fact about the existence of limit hold not only for elements
of the group algebra (i.e., after normalization corresponding to a simple random walk, i.e., isotropic case) but for arbitrary self-adjoint element of the group algebra.
In [
26], the following result related to Theorem 4 is proved.
Theorem 5. Let be a measure space and a group G act by transformations preserving the class of measure μ (i.e., for all ). Let be the Koopman representation: and π be groupoid representation. Then for any ,μ-almost surely ( is the orbital graph on ) and if the action is amenable (i.e., partition on orbits is hyperfinite) then in (26) we have equality μ-almost surely instead of inclusion. For definition of groupoid representation, we direct reader to [
26]. Amenable actions are discussed in [
82,
101].
The idea of approximation of groups in the situation of group action was explored by A. Stepin and A. Vershik in the 1970s [
102]. Now the corresponding group property is called local embeddability into finite group (LEF). This is a weaker form of the classical residual finiteness of groups. For instance, topological full groups [
103] mentioned in
Section 12 are LEF.
Approximation of Ising model in infinite residually finite groups by Ising models on finite quotients is suggested in [
104]. The Ising model on self-similar Schreier graphs by finite approximations was studied in [
105] and the dimer model on these graphs was studied in [
106].
A recent result of B. Simanek and R. Grigorchuk [
31] shows that,
Theorem 6. There are Cayley graphs with infinitely many gaps in the spectrum.
It is a direct consequence of the next theorem.
Theorem 7 ([
31])
. Let be the lamplighter group . There is a system of generators of such that the convolution operation in determined by the element of the group algebra where , has pure point spectrum. Moreover,- 1.
if , the eigenvalues of densely pack the interval .
- 2.
If , the eigenvalues of form a countable set that densely packs the interval and also has an accumulation point .
- 3.
The spectral measure of the operator is discrete and is given bywhere is the degree k Chebyshev polynomial of the second kind.
Observe that if is an integer, then the spectrum of the Cayley graph of built using the system of generators with coincides with the spectrum of and hence has infinitely many gaps. This is the first example of a Cayley graph with infinitely many gaps in the spectrum.
In the case when
, this result was obtained by A. Zuk and R. Grigorchuk [
30] and used in [
17] to answer a question of M. Atiyah and to give a counterexample to a version of the strong Atiyah conjecture known in 2001. This was done by constructing a 7-dimensional closed Reimannian manifold with third
-Betti number
. For more on spectra of Lamplighter type groups and their finite approximations see [
107,
108].
The Schreier spectrum of the Hanoi Tower group
is a Cantor set and a countable set of isolated points accumulating to it (see
Figure 6) as follows from the following result.
Theorem 8 ([
32])
. The n-th level spectrum (), as a set, has points and is equal toThe multiplicity of the level n eigenvalues in , is and the multiplicity of the eigenvalues in , is , where and . Moreover, the Schreier spectrum of (i.e., ) is equal toIt consists of a set of isolated points and its set of accumulation points . The set is a Cantor set and is the Julia set of the polynomial f. The density of states is discrete and concentrated on the set . Its mass at each point of is , . Grabowski and Virag [
109,
110] observed that the Lamplighter group has a system of generators such that the spectral measure is purely singular continuous measure. An infinite family of Schreier graphs with a non-trivial singular continuous part of the spectral measure is constructed in [
111,
112].
9. Schur Complements
Schur complement is a useful tool in linear algebra, networks, differential operators, applied mathematics, etc. [
113]
Let
H be a Hilbert space (finite or infinite dimensional) decomposed into a direct sum
,
,
. Let
be a bounded operator and
be a matrix representation of
M by block matrices corresponding to this decomposition. Thus
Two partially defined maps
and
are defined by,
for any
. Note that
is defined when
D is invertible, and
is defined when
A is invertible. Maps
are said to be the Schur complements and the following fact holds.
Theorem 9 ([
20])
. Suppose D is invertible. Then M is invertible if and only if is invertible andwhere . A similar statement holds for
. The above expression for
is called Frobenius formula. In the case
, the determinant
of matrix
M satisfies
and the latter relation is attributed to Schur.
There is nothing special in decomposition of
H into a direct sum of two subspaces. If
and
for
and
, where
, then we are back in the case
. By change of the order of the summands (putting
on the first place) one can define the
i-th Schur complement
, for each
.
If
and
is a
d-similarity, then
, where
is the image of the generator
of the Cuntz algebra
under the representation
associated with
(as explained in
Section 4). Therefore, for each
, one can define
the semigroup generated by the Schur transformations
,
with the operation of composition. We will call
the Schur semigroup. For a general element of this semigroup, we get the following expression,
(see Corollary 5.4 in [
20]).
The Schur semigroup
consists of partially defined transformations on the infinite dimensional space
. There are examples of finite dimensional subspaces
invariant with respect to
, where the restrictions of Schur complements to
L generates a semigroup of rational transformations on
L. An example of this sort is the case of 3-dimensional subspace in
, for
, where
T is the binary tree and
is the uniform Bernoulli measure. It comes from the group
and
L, the space generated by three operators
, where
is the Koopman representation and
I is the identity operator. If
where
, then in coordinates
, the Schur complements
are given by
and the semigroup
generated by them is isomorphic to the semigroup
generated by maps (
1), (
2) (as (
27), (
28) are homogeneous realizations of
). Study of properties of the semigroups
and its restriction on finite dimensional invariant subspaces is a challenging problem.
10. Self-Similar Random Walks Coming from Self-Similar Groups and the Münchhausen Trick
Let
G be a self-similar group acting on
and
(where
denotes the simplex of probability measures on
G) be a probability measure whose support generates
G (we call such
non-degenerate). Using
one can define a (left) random walk that begins at
and transition
holds with probability
. Study of random walks on groups is a large area initiated by H. Kesten [
86] (see [
114,
115,
116,
117,
118,
119,
120] for more on random walks on groups and trees). The main topics of study in random walks are: the asymptotic behavior of the return probabilities
when
, the rate of escape, the entropy, the Liouville property and the spectral properties of the Markov operator
M acting in
by
as was discussed in
Section 8. The case when the measure
is symmetric (i.e.,
) is of special interest as in this case
M is self-adjoint.
A remarkable progress in the theory of random walks on groups was made by L. Bartholdi and B. Virag. They showed that the self-similarity of a group can be converted into a self-similarity of a random walk on the group and used it for proving the amenability of the group. In such a way it was shown that the Basilica is amenable [
121]. The idea of Bartholdi and Virag was developed by V. Kaimanovich in terms of entropy and interpreted as a kind of mathematical implementation of the legendary “Münchhausen trick” [
122].
Let us briefly describe the idea of the self-similarity of random walks. Recall, that a self-similar group is determined by the Mealy invertible automaton, or equivalently, by the wreath recursion (
14) coming from the embedding
.
If
is a random element of
G at the moment
associated with the random walk determined by
, then
Let
be the stabilizer of
. The index
is finite and hence the random walk hits
H with probability 1. Denote by
the distribution on
H given by the probability of the first hit:
where
is the probability of hitting
H at the element
h for the first time at time
n.
Now let us construct transformations
,
on the space of bounded operators
in a Hilbert space
when a
d-similarity
is fixed. Let
as before be the
i-th Schur complement
associated with
,
be the map in
, given by
(where,
I is the identity operator). We define
, so if
where
A is an operator acting on the first copy of
H in
, then
In the case when
M is the Markov operator of the random walk on
G determined by the measure
μ, this leads to the analogous map on simplex
which we denote by
. The measure
is called the
i-th probabilistic Schur complement.
Theorem 10 ([
20,
122])
. Let be the i-th projection map (where and is the section of h at vertex i of the first level) and let be the image of under . Then In the most interesting cases, the group
G acts level transitively (in particular, transitively on the first level) and its action of the first level
is a free transitive action of some subgroup
, for instance of
(the latter always holds in the case of binary tree as
). In this case for each
,
(where
is the stabilizer of the first level of
T), there is a random sequence of hitting times
of the subgroup
H so that
in (
29) and
Moreover, the random process
is a random walk on
G determined by the measure
,
. We call
the section (or the projection) of
at vertex
i.
The maps
have the property that they enlarge the
weight of the identity element and hence cannot have fixed points. Now let us resolve this difficulty by following [
122] (see also [
20]). A measure
on a self-similar group is said to be self-similar (or self-affine) at position
if for some
where
is the delta mass at the identity element. Observe that
is self-similar at position
i if and only if it is a fixed point of the map
Thus
is a modification of
: we delete from the measure
the mass at the identity element and normalize. Note that
is defined everywhere, except
. We can extend it by assigning
, which makes
a continuous map
for the weak topology on
. We are interested in non-degenerate fixed points because of the following theorem:
Theorem 11. If a self-similar group G has a non-degenerate symmetric self-similar probability measure, then
(where is the n-th convolution of μ determining the distribution of random walk at time n). Hence the group G is amenable in this case.
In
Section 14 we provide an example of self-similar measure in the case of the group
.
11. Can One Hear the Shape of a Group?
One of interesting directions of studies in spectral theory of graphs is finding of iso-spectral but not isomorphic graphs. It is inspired by the famous question of M. Kac, “Can you hear the shape of a drum” [
123]. It attracted a lot of attention of researchers, and after several preliminary results, starting with the result of J. Milnor [
124], the negative answer was given in 1992 by C. Gordon, D. Webb and S. Walpert, who constructed a pair of plane regions that have different shapes but identical eigenvalues [
125]. The regions are concave polygons, their construction uses group theoretical result of T. Sunada [
126].
In 1993, A. Valete [
127] raised the following question; “Can one hear the shape of a group?”, which means “Does the spectrum of the Cayley graph determines it up to isometry?”. The answer is immediate, and is
no as the spectra of all grids
,
are the same, namely the interval
. Still the question has some interest. The paper [
128] shows that the answer is
no in a very strong sense.
Theorem 12 - 1.
Let be a family of groups of intermediate growth between polynomial and exponential. Then for each the spectrum of the Cayley graph is the union - 2.
Moreover, for each that is not eventually constant sequence the group has uncountably many covering amenable groups (i.e., there is a surjective homomorphism ) generated by such that the spectrum of the Cayley graphs is the same set .
The proof uses the Hulanicki theorem [
129] on characterization of amenable groups in terms of weak containment of the trivial representation in the regular representation, and a weak Hulanicki type theorem for covering graphs. More examples of this sort are in [
130]. The above theorem is for the isotropic case. In the anisotrophic case by the result of D. Lenz, T. Nagnibeda and first author [
11,
29], we know only that
contains a Cantor subset of the Lebesgue measure 0, which is a spectrum of a random Schrödinger operator, whose potential is ruled by the substitutional dynamical system generated by the substitution
used in presentation (
3).
In the case of a vertex transitive graph, in particular Cayley graph, a natural choice of a spectral measure is the spectral measure associated with delta function for . The moments of this measure are the probabilities of return.
Problem 5. Does the spectral measure ν determine Cayley graph of an infinite finitely generated group up to isometry?
12. Substitutional and Schreier Dynamical System
Given an alphabet
and a substitution
, assuming that for some distinguished symbol
,
a is a prefix of
, we can consider the sequence of iterates
where application of
to a word
means the replacement of each symbol
in
A by
. If we denote
, then
is a prefix of
and there is a natural limit
This limit
is an infinite word over
A and the words
are prefixes of
. Also
is a fixed point of
:
. Using
, we can now define subshifts of the full shifts
and
(where
T is a shift map in the space of sequences). Let us do this for the bilateral shift.
Let . Equivalently, consists of words that appear as a subword of some (and hence in all ).
Now let be the set of sequences that are unions of words from , where . In other words, if and only if for all , there exist , such that the subword of belongs to . Obviously, is shift invariant closed subset of . The dynamical system with the shift map T restricted to is a substitutional dynamical system generated by .
The most important case is when such system is minimal, i.e., for each the orbit is dense in . For instance, this is the case when the substitution is primitive, which means that there exists K such that for each the symbol occur in the word .
By Krylov-Bogolyubov theorem, the system has at least one T-invariant probability measure and the invariant ergodic measures (i.e., extreme points of the simplex of T-invariant probability measures) are of special interest. Another important case is when the system is uniquely ergodic, i.e., there is only one invariant probability measure (necessarily ergodic).
A subshift
is called linearly repetitive (LR) if there exists a constant
C such that any word
occurs in any word
of length
. This is a stronger condition than minimality. The following result goes back to M. Boshernitzan [
131] (see also [
132]).
Theorem 13. Let be a linearly repetitive subshift. Then, the subshift is uniquely ergodic.
Here, it is not necessary for the subshift to be generated by a substitution. It is known that subshifts associated with primitive substitutions are linearly repetitive [
133,
134]. Theorem 1 of [
135] shows that linear repetitivity in fact holds for subshifts associated to any substitution provided minimality holds. Unique ergodicity is then a direct consequence of linear repetitivity due to Theorem 13.
The classical example of a substitutional system is the Thue-Morse system determined by the substitution
over binary alphabet [
40].
Following [
11,
25,
29] we consider the substitution
over alphabet
and system
generated by it. Despite
not being primitive, the system
satisfies the linear repetivity property (in fact the same system can be generated by a primitive substitution
).
An additional property of the fixed point
is that it is a Toeplitz sequence. i.e., for each entry
of
there is period
such that all entries with indices of the form
contain the same symbol
. In our case the periods have the form
. More on combinatorial properties of
and associated system see [
29].
Our interest in the substitution and the associated subshift comes from following four facts:
For any minimal action
of a group
G on a Cantor set
X, one can define a topological full group (TFG in short)
as a group consisting of homeomorphisms
that locally act as elements of
G. If
G is the infinite cyclic group generated by a minimal homeomorphism of a Cantor set, the TFG is an invariant of the Cantor minimal system up to the flip conjugacy [
136] and its commutator
is a simple group. Moreover,
is finitely generated if the system is conjugate to a minimal subshift over a finite alphabet. It was conjectured by K. Medynets and the first author, and proved by K. Juschenko and N. Monod [
137] that if
, then
is amenable. Thus TFGs are a rich source of non-elementary amenable groups, and satisfy many unusual properties [
103,
138]. N. Matte Bon observed that
embeds into
, where
is the substitution from (
3) [
139]. A similar result holds for overgroup
.
Study of substitutional dynamical systems and more generally of aperiodic order is a rich area of mathematics (see [
140,
141] and references there for instance). A special attention is paid to the classical substitutions like Thue-Morse, Arshon [
142], and Rudin-Shapiro substitutions.
Problem 6. For which primitive substitutions τ, the TFG , contains a subgroup of intermediate growth? contains a subgroup of Burnside type (i.e., finitely generated infinite torsion group)? In particular, does the classical substitutions listed above have such properties?
Given a Schreier graph
, one can consider the action of
G on
(i.e., on the set of marked graphs where
) and extend it to the action on the closure
in
. This is called in [
19] a Schreier dynamical system. Study of such systems is closely related to the study of invariant random subgroups. In important cases, such systems allows to recover the original action
if
,
is an orbital graph. In particular, this holds if the action is extremely non-free (i.e., stabilizers
of different points
are distinct). The action of
and any group of branch type is extremely non-free. More on this is in [
19].
13. Computation of Schur Maps for and
Recall the matrix recursions between generators of
(see (
22)),
Let
be an element of the group algebra
. By using (
22), we identify,
First we will calculate the first Schur complement
, which is defined when
is invertible. Since the group generated by
is isomorphic to
(via the identification
with
, respectively), by a direct calculation, we obtain that
D is invertible if and only if
and if the condition in (
33) is satisfied, then
is given by,
Therefore,
This leads to the map
given in (
6).
Now we will calculate the second Schur complement
which is defined when
is invertible. Since the group generated by
is isomorphic to
(via the identification
with
, respectively), by a direct calculation, we obtain that
A is invertible if and only if
and if the condition in (
34) is satisfied, then
is given by,
Therefore,
This leads to the map
given in (
5).
Now consider the case where
. Note that
fixes second, third and fourth coordinates and so we may restrict the map to first and fifth coordinates. Therefore we get
map
By the change of coordinates
, we obtain
F given in (
1).
Now note that second, third and fourth coordinates of
are the same and are equal to
. By re-normalization (i.e., multiplying by
) we obtain a map which fixes second, third and fourth coordinates. So we may restrict the map to first and fifth coordinates and get
map
By the change of coordinates
, we obtain
G given in (
2).
Now consider the overgroup
, where
satisfy matrix recursions given by (
35) and
a is a generator of
. We have
,
,
and hence
is a subgroup of
. It will be convenient to consider
as a group generated by eight elements
, where
satisfies the matrix recursion in (
35).
is a subgroup of
and so
is a subalgebra of
. So we can use (
22) as the matrix recursions of
. Let
. By using (
35) and (
22), we obtain the matrix recursion of
M as,
We can calculate first and second Schur complements
, and the multi-dimensional maps
associated with them as we did for the case of
. These maps are nine-dimensional and are given by
where
16. Random Model and Concluding Remarks
As explained above, the spectral problem associated with groups and their Schreier graphs in many important examples could be converted into study of invariant sets and dynamical properties of multi-dimensional rational maps. Some of these maps, like (
1), (
2), (
7), (
8) demonstrate strong integrability features explored in [
1,
3,
32,
33]. The roots of their integrability are comprehensively investigated in [
24]. The examples given by (
5), (
6), (
9), (
10), (
11), (
37) are much more complicated. They have an invariant set of fractal nature, and computer simulations demonstrate their chaotic behavior, shown by dynamical pictures given by
Figure 3 and
Figure 7.
The families of groups
(and many other similar families can be created) can be viewed as a random group if
is supplied with a shift invariant probability measure (for instance, Bernoulli or more generally Markov measure). The first step in this direction is publication [
143] where it is shown that for any ergodic shift invariant probability measure satisfying a mild extra condition (all Bernoulli measures satisfy it), there is a constant
such that the growth function
is bounded by
.
More general model would be to supply the space
of finitely generated groups or any of its subspaces
with a measure
(finite, or infinite, invariant or quasi-invariant with respect to any reasonable group or semigroup of transformations of the space) and study the typical properties of groups with respect to
. The system
(where
T denotes the shift) is just one example of this sort. As suggested in [
18], it would be wonderful if one could supply the space
with a measure that is invariant (or at least quasi-invariant) with respect to the group of finitary Nielsen transformations defined over infinite alphabet
.
Additionally to the randomness of groups, one can associate with each particular group a random family of Schreier graphs, like the family
,
for a group
using the uniform Bernoulli measure on the boundary (other choices for
are also possible, especially if
G is generated by automorphisms of polynomial activity [
26,
144,
145]). Putting all this together, it leads to study of random graphs associated with random groups (or equivalently, of random invariant subgroups in random groups).
Finally, even if we fix a group, say
,
and a Schreier graph
,
, study of spectral properties of this graph is related to the study of iterations
of maps given by (
44) as was mentioned above.
Recall a classical construction of skew product in dynamical systems. Given two spaces
, the measure
preserving transformation
, and for any
the measure
preserving transformation
, under the assumption that the map
,
is measurable, one can consider the map
,
, which preserves the measure
. Natural conditions imply that
Q is ergodic if
S and
,
are ergodic. If for
, we put
then the random ergodic theorem of Halmos–Kakutani [
146,
147] states that for
,
almost surely the averages
converge
almost surely to some function
. In the simplest case when
and
is given by a probability vector
,
,
,
, we have
m transformations
of
X. The semigroup generated by them typically is a free semigroup and if
are invertible in a typical case, the group
is a free group of rank
m.
The question of whether the pointwise ergodic theorem of Birkhoff holds for actions of a free group was raised by V. Arnold and A. Krylov [
148] and answered affirmatively by the first author in [
149]. A similar theorem is proven for the action of a free semigroup [
150]. The proofs are based on the use of the skew product when
S is the Bernoulli shift on
and
is a uniform Bernoulli measure on
. In fact these ergodic theorems hold for stationary measures.
By a different method, a similar result for the free group actions was obtained by A. Nevo and E. Stein [
151]. The method from [
149,
150] was used by A. Bufetov to get ergodic theorems for a large class of hyperbolic groups [
152]. Ergodic theorem for action of non-commutative groups became popular [
153,
154], but the case of semigroup action is harder and not so many results are known, especially in the case of stationary measure.
In fact, the product measure
in the construction of the skew product is invariant if and only if the measure
is
-stationary, which means the equality
In the case of
,
, it means that
(i.e., the
-average of images of
under transformations
is equal to
). The skew product approach for non-commutative transformations leads to a not well-investigated notion of entropy [
155,
156]. It would be interesting to compare this approach with the approach of L. Bowen for the definition of entropy of free group action [
157,
158].
Going back to the transformations
given by (
44), we could try to apply the idea of skew product to them and investigate the random model. Random dynamical model in the context of holomorphic dynamics is successfully considered in [
159] where stationary measures also play an important role. Each of these maps (as well as any map from the 2-parametric family
) is semiconjugate to the Chebyshev map and has families of
horizontal and
vertical hyperbolas similar to the case of the map
F given by
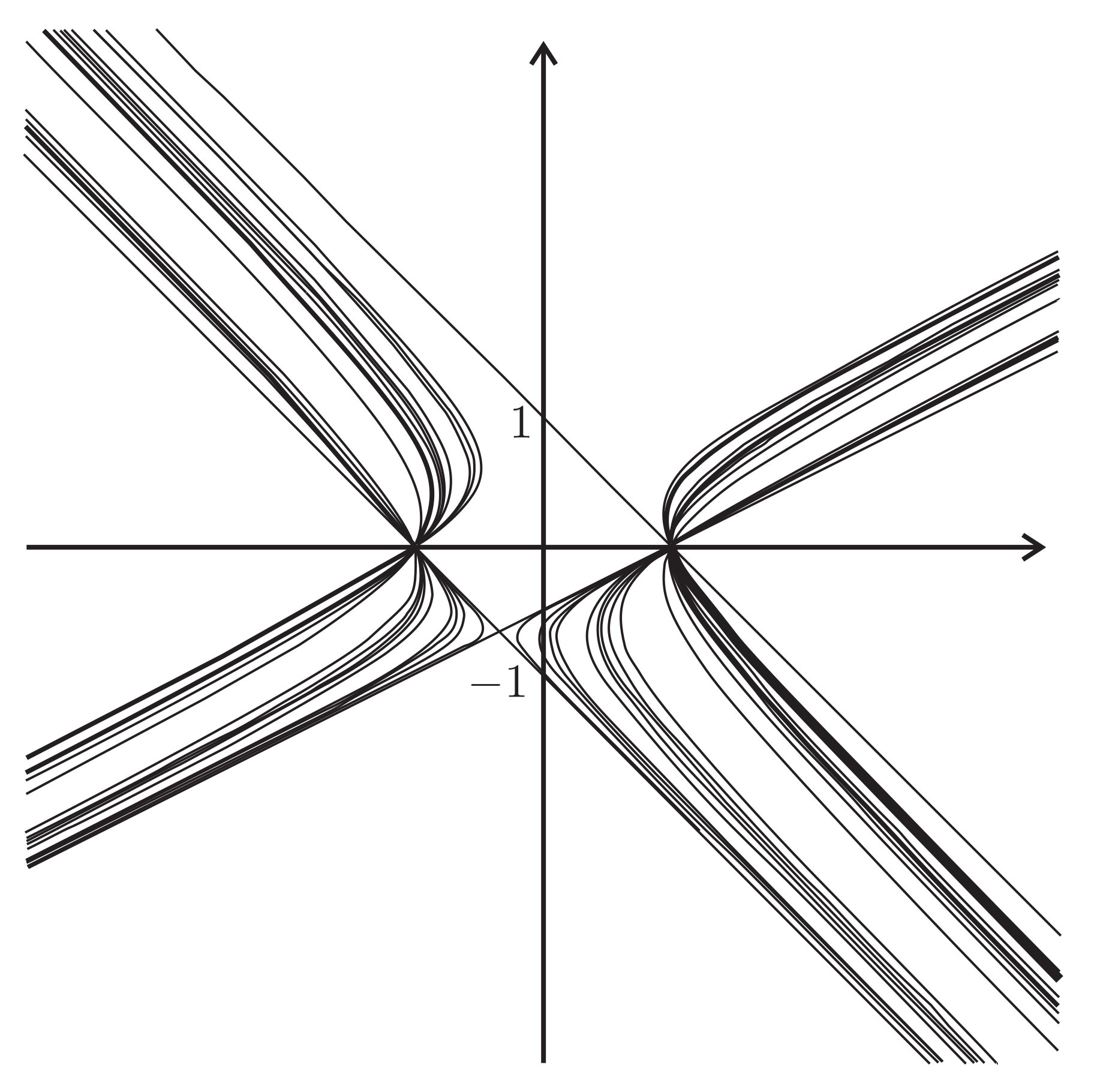
Figure 4. But when parameters
(the coefficients of
) are not equal, even in the case of periodic sequence
(in which case the group
is just our main
hero), the iterations
demonstrate chaotic dynamics presented by
Figure 3a. Still, it is possible that more chaos could appear if additionally,
is chaotic itself. Study of these systems and other topics discussed above is challenging and promising.
The notion of amenable group was introduced by J. von Neumann [
160] for discrete groups and by N. Bogolyubov [
161] for general topological groups. The concept of amenability entered many areas of mathematics [
85,
162,
163,
164,
165,
166,
167]. Groups of intermediate growth and topological full groups remarkably extended the knowledge about the class
of amenable groups [
15,
16,
137]. There are many characterizations of amenability: via existence of left invariant mean (LIM), existence of Fölner sets, Kesten’s probability criterion, hyperfiniteness [
82], co-growth [
168], etc.
From dynamical point of view, an important approach is due to Bogolyubov [
161]; if a topological group
G with left invariant mean acts continuously on a compact set
X, then there is a
G-invariant probability measure
on
X (this is a far reaching generalization of the famous Krylov-Bogolyubov theorem). In fact, such property characterizes amenability.
Amenability was mentioned in this article several times. We are going to conclude with open questions related to the considered maps
and the conjugates
of
F. Even though invariant measures seem not to play an important role in the study of dynamical properties of multi-dimensional rational maps (where the harmonic measure or measures of maximal entropy like the Mané-Lyubich measure dominate), we could be interested in existence of invariant or stationary measures supported on invariant subsets of maps coming from Schur complements, as it was discussed above. This could include the whole Schur semigroup
defined in
Section 9, its subsemigroups, or semigroups involving some relatives of these maps (like the map
H given by (
4)). The concrete questions are:
Problem 8. - 1.
Is the semigroup amenable from the left or right?
- 2.
Is there a probability measure on the cross , shown by Figure 5a, invariant with respect to the above semigroup?
By the last part of Theorem 4, we know that each horizontal slice of the cross possesses a probability measure that is the density of states for the corresponding Markov operator. Integrating it along the vertical direction we get a measure on which is somehow related to both maps F and G. Is it related to the semigroup ? is the simplest example of the Schur type semigroup. One can consider other semigroups of interest, for instance, or even semigroup generated by the maps for , and look for invariant or stationary measures.
The example of semigroup
is interesting because of the relations
,
. By J. Ritt’s result [
169], it is known that in the case of the relation of the type
for maps
given by polynomials in one variable, all its solutions can be described explicitly. In the paper [
170], it is proved that for polynomials
P and
Q, if there exists a point
in the complex Riemann sphere
such that the intersection of the forward orbits of
with respect to
P and
Q is an infinite set, then there are natural numbers
such that
. The result of C. Cabrera and P. Makienko [
171] generalizes this to the rational maps and includes in the statement the amenability properties of the semigroup
.
In the case of maps , we know that the semigroup is rationally semiconjugate to the commutative (and hence amenable) semigroup . Whether is amenable itself is an open question included in the Problem 8.
A very interesting question is the question about the dynamical properties of maps
given by (
45). They are conjugate to the maps of the form
via
and further simplification seems to be impossible. At the same time, maps
are conjugated to
F by
The dynamical picture for those that are outside the 2-parametric family
is presented by
Figure 16 and is quite different of those dynamical pictures presented by
Figure 3.
It is not clear at the moment if the maps presented in (
46) describe the joint spectrum of a pencil of operators associated with fractal groups. But the family (
46) itself could have interest for multi-dimensional dynamics and deserves to be carefully investigated, including semigroups generated by
in various combinations of the choice of generating set.