Entropy Pair Functional Theory: Direct Entropy Evaluation Spanning Phase Transitions
Abstract
1. Introduction
2. Free Energy Properties
3. Excess Entropy Pair Density Functional
4. Developing Approximations to the Entropy Functional
4.1. Kirkwood Entropy
- Due to a normalization problem it does not go to the correct limit at high temperature [49].
- It underestimates the entropy just above melting.
- It grossly underestimates the entropy below melting; it gives for the crystal.
4.2. Modified Kirkwood Entropy Applied to Fluid Pair Correlation Functions
4.3. Kirkwood Entropy Applied to Crystal Pair Correlation Functions
4.4. Connection to the Harmonic Crystal
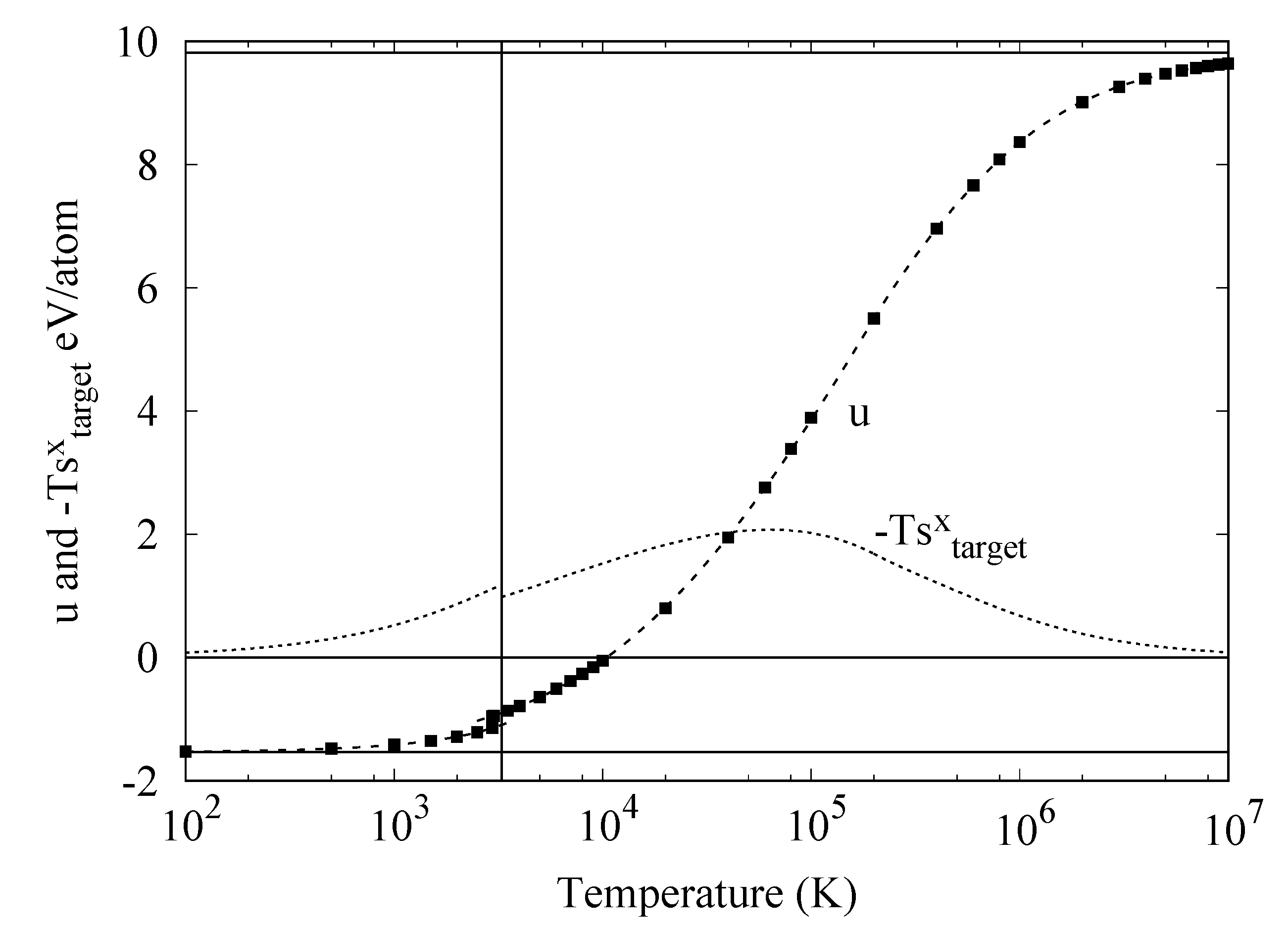
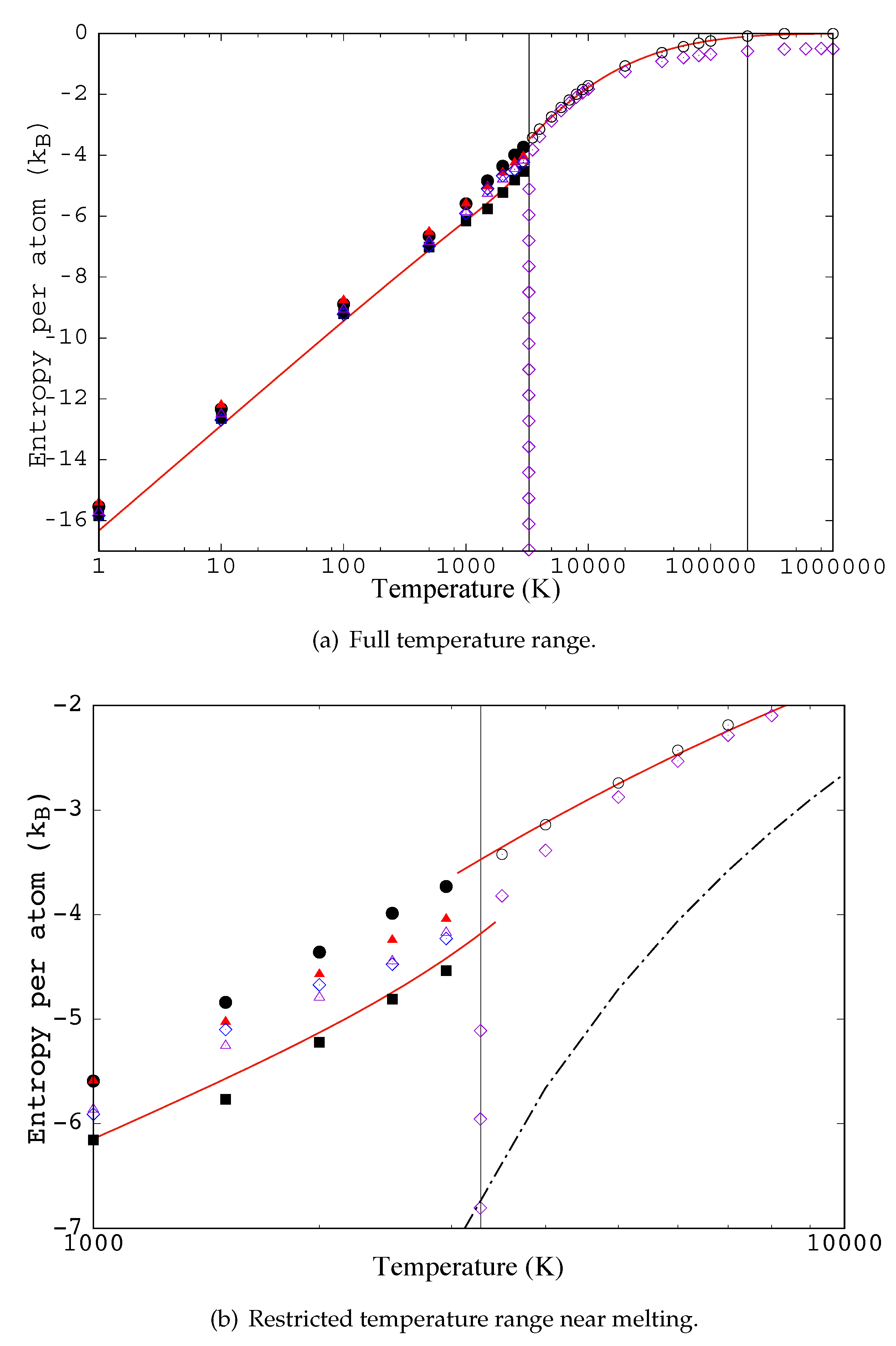
4.5. Comparison of Selected Functionals with the Target Entropy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Universal Functionals
Appendix B. Stationarity and the Unique Potential
- Both and are known;
- Only is known;
- Only is known.
Appendix C. Mapping Atomic Coordinates to Atom List
Appendix D. Inclusion of Many-Body Effects
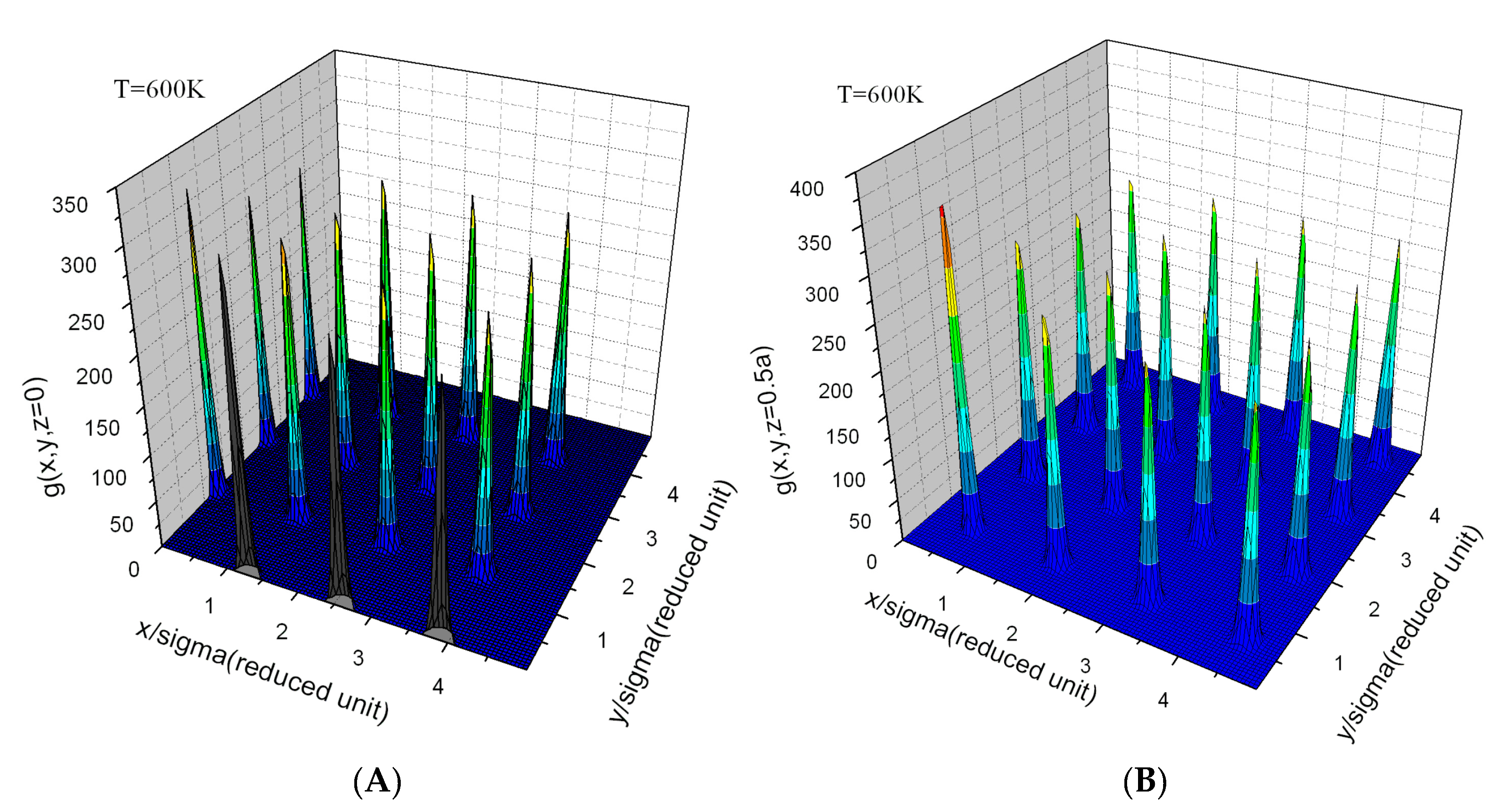
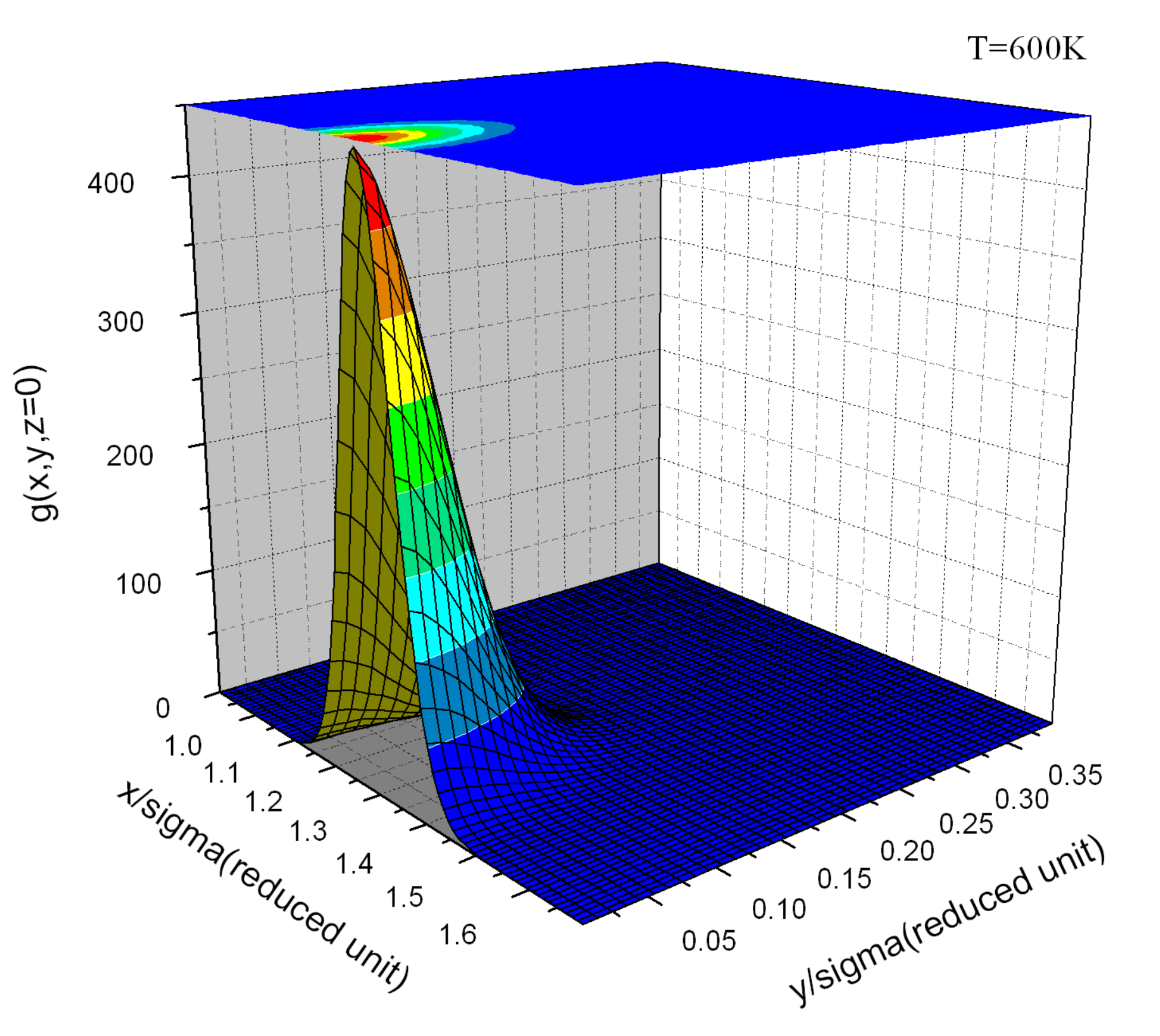
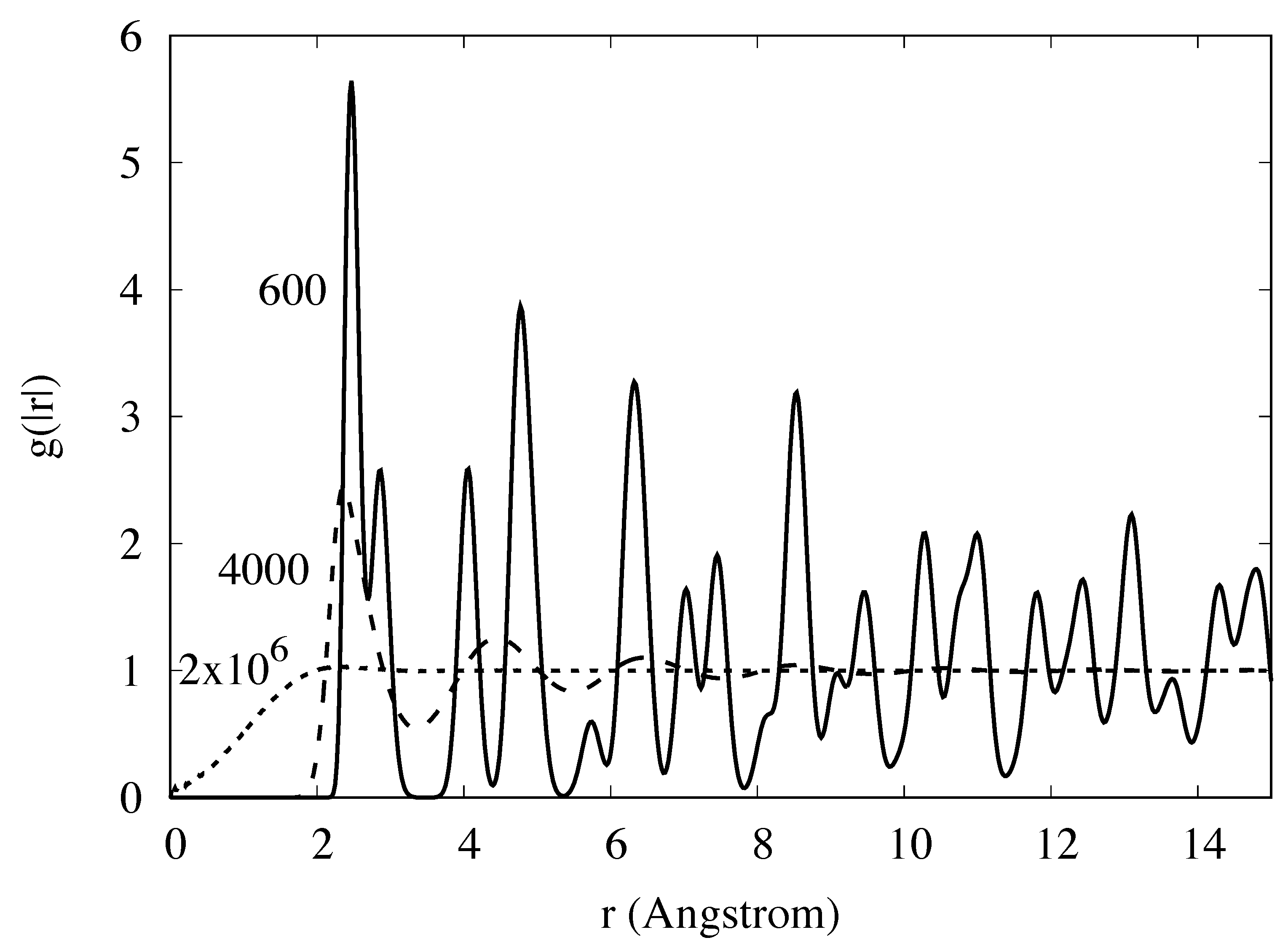
Appendix E. Simulation Results and Target Entropy from Johnson Potential
Appendix F. Classical Debye Approximation of ϵ
References and Notes
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300. [Google Scholar] [CrossRef]
- McDonnell, M.T.; Greeley, D.A.; Kit, K.M.; Keffer, D.K. Molecular Dynamics Simulations of Hydration Effects on Solvation, Diffusivity, and Permeability in Chitosan/Chitin Films. J. Phys. Chem. B 2016, 120, 8997. [Google Scholar] [CrossRef] [PubMed]
- Haskins, J.B.; Lawson, J.W. Finite temperature properties of NiTi from first principles simulations: Structure, mechanics, and thermodynamics. J. Appl. Phys. 2017, 121, 205103. [Google Scholar] [CrossRef]
- Moriarty, J.A.; Haskins, J.B. Efficient wide-range calculation of free energies in solids and liquids using reversible-scaling molecular dynamics. Phys. Rev. B 2014, 90, 054113. [Google Scholar] [CrossRef]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. Entropy Driven Stabilization of Energetically Unstable Crystal Structures Explained from First Principles Theory. Phys. Rev. Lett. 2008, 100, 095901. [Google Scholar] [CrossRef] [PubMed]
- Volcadlo, L.; Alfe, D. Ab initio melting curve of the fcc phase of aluminum. Phys. Rev. B 2002, 65, 214105. [Google Scholar] [CrossRef]
- Xiang, S.; Xi, F.; Bi, Y.; Xu, J.; Geng, H.; Cai, L.; Jing, F.; Liu, J. Ab initio thermodynamics beyond the quasiharmonic approximation: W as a prototype. Phys. Rev. B 2010, 81, 014301. [Google Scholar] [CrossRef]
- Grabowski, B.; Ismer, L.; Hickel, T.; Neugebauer, J. Ab initio up to the melting point: Anharmonicity and vacancies in aluminum. Phys. Rev. B 2009, 79, 134106. [Google Scholar] [CrossRef]
- Cazorla, C.; Alfe, D.; Gillan, M.J. Constraints on the phase diagram of molybdenum from first-principles free-energy calculations. Phys. Rev. B 2012, 85, 064113. [Google Scholar] [CrossRef]
- Van de Walle, A.; Ceder, G. First-principles computation of the vibrational entropy of ordered and disordered Pd3V. Phys. Rev B 2000, 61, 5972. [Google Scholar] [CrossRef]
- Asker, C.; Belonoshko, A.B.; Mikhaylushkin, A.S.; Abrikosov, I.A. Melting curve of tantalum from first principles. Phys. Rev. B 2008, 77, 220102. [Google Scholar] [CrossRef]
- Feng, R.; Liaw, P.K.; Gao, M.; Widom, M. First-principles prediction of high-entropy-alloy stability. NPJ Comp. Mater. 2017, 3, 50. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Direct entropy calculation from computer simulation of liquids. Phys. Rev. A 1989, 40, 3817. [Google Scholar] [CrossRef] [PubMed]
- Green, H.S. The Molecular Theory of Fluids; North-Holland: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Wallace, D.C. Correlation entropy in a classical liquid. J. Chem. Phys. 1987, 87, 4. [Google Scholar] [CrossRef]
- Widom, M.; Gao, M. First Principles Calculation of the Entropy of Liquid Aluminum. Entropy 2019, 21, 131. [Google Scholar] [CrossRef] [PubMed]
- Baranyai, A.; Evans, D.J. Three-particle contribution to the configurational entropy of simple fluids. Phys. Rev. A 1990, 42, 849. [Google Scholar] [CrossRef]
- Kikuchi, R.; Brush, S.G. Improvement of the Cluster Variation Method. J. Chem. Phys. 1967, 47, 195. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic: London, UK, 1986. [Google Scholar]
- There are two definitions of the in J.P. Hansen and I.R. McDonald, Theory of Simple Liquids; we use the definition introduced in their discussion of n-particle densities.
- Ken, D.A. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Cryst. 2001, 34, 172. [Google Scholar] [CrossRef]
- Johnson, R.A. Interstitials and Vacancies in α. Iron. Phys Rev. 1964, 134A, 1329, Johnson designed this potential to model BCC Fe with point defects. [Google Scholar]
- Henderson, R.L. A uniqueness theorem for fluid pair correlation functions. Phys. Lett. 1974, 49A, 197. [Google Scholar] [CrossRef]
- Nicholson, D.C.M.; Barabash, R.I.; Ice, G.E.; Sparks, C.J.; Robertson, J.L.; Wolverton, C. Relationship between pair and higher-order correlations in solid solutions and other Ising systems. J. Phys. Condens. Matt. 2005, 18, 11585. [Google Scholar] [CrossRef]
- Evans, R. The Nature of Liquid-Vapor Interface and Other Topics in the Statistical Mechanics of Non-Uniform Classical Fluids. Adv. Phys. 1979, 28, 143. [Google Scholar] [CrossRef]
- Lin, S.-C.; Martius, G.; Oettel, M. Analytical classical density functionals from an equation learning network featured. J. Chem. Phys. 2020, 152, 021102. [Google Scholar] [CrossRef]
- Bharadwaj, A.S.; Singh, S.L.; Singh, Y. Correlation functions in liquids and crystals: Free energy functional and liquid—Crystal transition. Phys. Rev. E 2013, 88, 022112. [Google Scholar] [CrossRef]
- Lutsko, J.F.; Lam, J. Classical density functional theory, unconstrained crystallization, and polymorphic behavior. Phys. Rev. E 2018, 98, 012604. [Google Scholar] [CrossRef]
- Evans, R.; Oettel, M.; Roth, R.; Kahl, G. New developments in classical density functional theory. J. Phys. Condens. Matter 2016, 28, 240401. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Gao, C.Y.; Nicholson, D.M.; Keffer, D.J.; Edwards, B.J. A multiscale modeling demonstration based on the pair correlation function. J. Non-Newton. Fluid Mech. 2008, 152, 140. [Google Scholar] [CrossRef]
- The constant term maintains consistency with the notation of Hansen.
- Mermin, N.D. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. A 1965, 137, 1441. [Google Scholar] [CrossRef]
- Ishihara, A. The Gibbs-Bogoliubov inequality. J. Phys. A Math. Gen. 1968, 1, 539. [Google Scholar] [CrossRef]
- Morris, J.R.; Ho, K.M. Calculating Accurate Free Energies of Solids Directly from Simulations. Phys. Rev. Lett. 1995, 74, 940. [Google Scholar] [CrossRef] [PubMed]
- Levy, M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Gao, M.; Widom, M. Information entropy of liquid metals. J. Phys. Chem. B 2018, 122, 3550. [Google Scholar] [CrossRef] [PubMed]
- This form is the natural generalization of Equation (1) in a macroscopically inhomogeneous system. We apply it here for inhomogeneity at the atomic level.
- Nettleton, R.E.; Green, M.S. Expression in Terms of Molecular Distribution Functions for the Entropy Density in an Infinite System. J. Chem Phys. 1958, 29, 1365. [Google Scholar] [CrossRef]
- Raveché, H.J. Entropy and Molecular Correlation Functions in Open Systems. I. Derivation. J. Chem. Phys. 1971, 55, 2242. [Google Scholar] [CrossRef]
- Sanchez-Castro, C.R.; Aidun, J.B.; Straub, G.K.; Wills, J.M.; Wallace, D.C. Temperature dependence of pair correlations and correlation entropy in a fluid. Phys. Rev. E 1994, 50, 2014. [Google Scholar] [CrossRef]
- Yvon, J. Correlations and Entropy in Classical Statistical Mechanics; Pergamon: Oxford, UK, 1969. [Google Scholar]
- For crystals we are actually referring to the relative probability.
- We continued the expression for the Johnson potential, VJ(r) to r = 0 where it is finite VJ(r = 0) = 57.851 eV.
- Expansions for the entropy in terms of correlation functions naturally generate approximate functionals, Sx[g], through maximization over higher order correlations for a fixed pair correlation.
- Terms limR→∞ ∫Rdr(−1) = 0, were added to accelerate convergence in system size [15].
- Baranyai et al. renormalized g by 1−1/N in the Kirkwood entropy to obtained an entropy with the correct high temperature limit (the change from Kirkwood is a constant upward shift by ).
- Levashov, V.A.; Billinge, S.J.L.; Thorpe, M.F. Density fluctuations and the pair correlation function. Phys. Rev. B 2005, 72, 024111. [Google Scholar] [CrossRef]
- q0 = 3.1430157 × 10−10, q1 = −2.9458269, q2 = 2.0263929.
- Jeong, I.-K.; Heffner, R.H.; Graf, M.J.; Billinge, S.J.L. Lattice dynamics and correlated atomic motion from the atomic pair distribution function. Phys Rev. 2003, 67, 104301. [Google Scholar] [CrossRef]
- Chung, J.S.; Thorpe, M.F. Local atomic structure of semiconductor alloys using pair distribution functions. Phys. Rev. B 1997, 55, 1545. [Google Scholar] [CrossRef]
- Gaussians of width λi in shells of coordination number Zi at distance di give gs(|r|)=∑i = 1,∞(exp( − exp( ). Zi and di are known; λi is used to fit gs. It varies slowly with di and reaches a limit, λ∞, at large di.
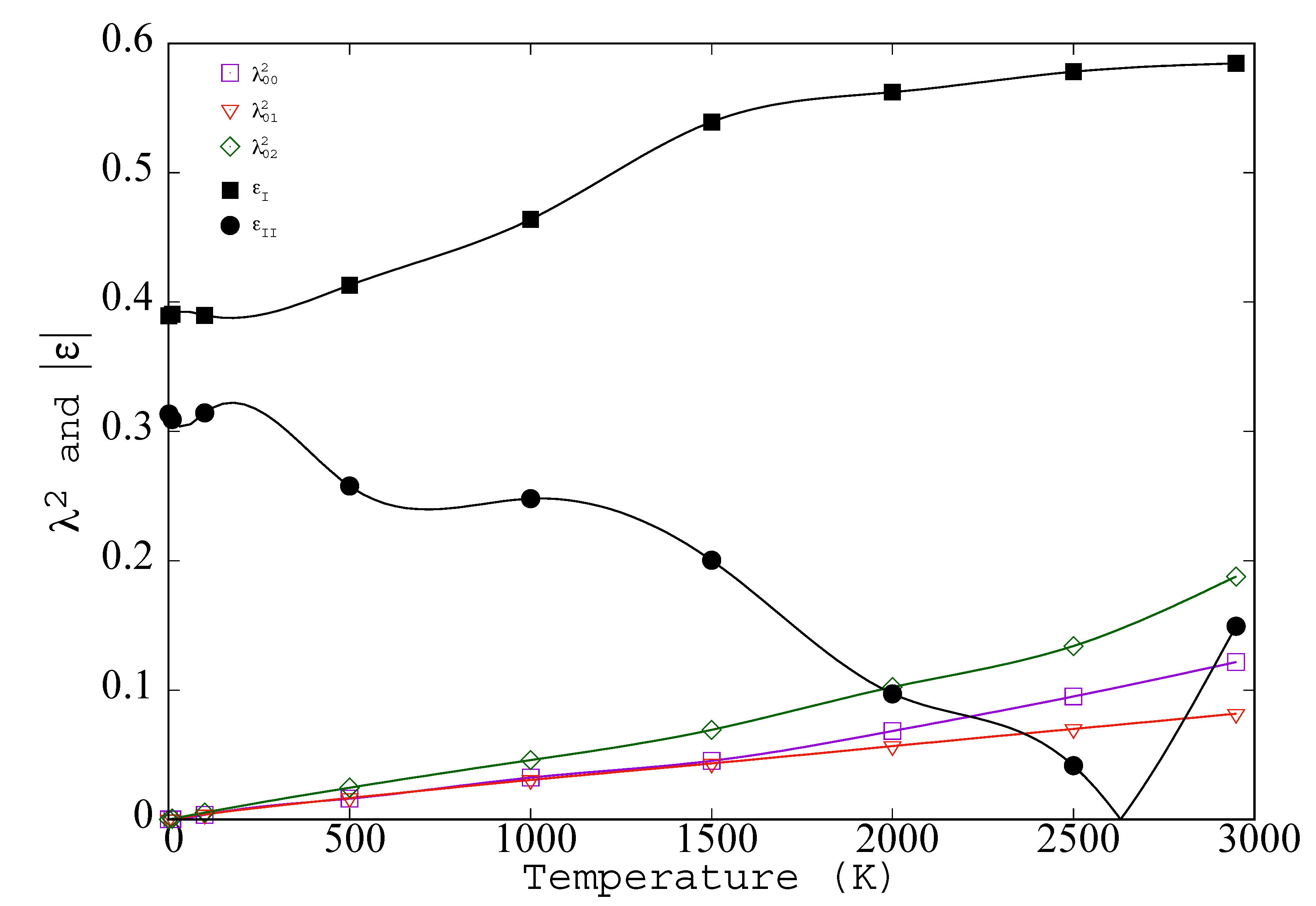
- The row index indicates neighbor position along the chain; it usually differs from the neighbor index in the lattice, however, λ1 = λ01.
- For a periodic system the entropy per site is modified from the result in [35] by subtracting one.
- The amplitudes of harmonic oscillations are assumed to be small compared to the lattice constant.
- Hu, G.Y.; O’Connell, R.F. Analytical inversion of symmetric tridiagonal matrices. J. Phys. A Math. Gen. 1996, 29, 1511–1513. [Google Scholar] [CrossRef]
- Lawson, A.C. Physics of the Lindemann melting rule. Philos. Mag. 2009, 89, 1757. [Google Scholar] [CrossRef]
- In Figure 4 the temperature range extends to the melting point, but it is interesting to speculate on possible definitions of λ that would extent to fluid phases. Introduction of a time scale, e.g., caging time, bond breaking time, or Maxwell time, would keep all λs finite above Tm. Another possible way to explore higher temperatures would be through application of a weak constraining point potential, v(1)(xi) that maintains all < xi >. The constraining potential should be chosen to be as weak as possible (for simplicity, its average should be zero); so as to minimize the magnitude of the change in potential energy. Such a constraining potential would preserve the crystal or glass beyond Lindemann’s Melting Criteria.
- Hohenberg, P.; Kohn, W. Density Functional Theory. Phys. Rev. B 1964, 136, 864. [Google Scholar] [CrossRef]
- Available online: http://www.psicode.org/psi4manual/master/dft_byfunctional.html (accessed on 19 December 2020).
- Ebner, C.; Saam, W.F.; Stroud, D. Density-functional theory of classical systems. Phys. Rev. A 1976, 14, 2264. [Google Scholar] [CrossRef]
- Yang, A.J.M.; Fleming, P.D.; Gibbs, J.H. Molecular theory of surface tension. J. Chem. Phys. 1976, 64, 3732. [Google Scholar] [CrossRef]
- Alster, E.; Elder, K.R.; Hoyt, J.J.; Voorhies, P.W. Phase-field-crystal model for ordered crystals. Phys. Rev. E 2017, 95, 022105. [Google Scholar] [CrossRef]
- Gonis, A.; Schulthess, T.C.; van Ek, J.; Turchi, P.E.A. A General Minimum Principle for Correlated Densities in Quantum Many-Particle Systems. Phys. Rev. Lett. 1996, 77, 2981. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, 1133. [Google Scholar] [CrossRef]
- Mei, J.; Davenport, J.W. Free-energy calculations and the melting point of Al. Phys. Rev. B 1992, 46, 21. [Google Scholar] [CrossRef]
- Morris, J.R.; Wang, C.Z.; Ho, K.M.; Chan, C.T. Melting line of aluminum from simulations of coexisting phases. Phys. Rev. B 1994, 49, 3109. [Google Scholar] [CrossRef]
- u0 = −1.53668082, u1 = 1.29259986 × 10−4, u2 = 3.80113908×10−9, u3 = 6.42748403 × 10−13, ut = 5.49984834, = 1.22230246 × 10−5, al = −(Tt + 2 ∗ bllt + 3cl + 4 ∗ dl), bl = 3.43822354, cl = −0.25383558, dl = 0.00647393, T0 = 1.75670976 × 106, Tt = 200000K, lt = lnTt, a = 9.816186, b = 0.11488535, c = −9.70656689 × 10−3, d = 4.30442613 × 10−4, and e = −7.28071000 × 10−6.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicholson, D.M.; Gao, C.Y.; McDonnell, M.T.; Sluss, C.C.; Keffer, D.J. Entropy Pair Functional Theory: Direct Entropy Evaluation Spanning Phase Transitions. Entropy 2021, 23, 234. https://doi.org/10.3390/e23020234
Nicholson DM, Gao CY, McDonnell MT, Sluss CC, Keffer DJ. Entropy Pair Functional Theory: Direct Entropy Evaluation Spanning Phase Transitions. Entropy. 2021; 23(2):234. https://doi.org/10.3390/e23020234
Chicago/Turabian StyleNicholson, Donald M., C. Y. Gao, Marshall T. McDonnell, Clifton C. Sluss, and David J. Keffer. 2021. "Entropy Pair Functional Theory: Direct Entropy Evaluation Spanning Phase Transitions" Entropy 23, no. 2: 234. https://doi.org/10.3390/e23020234
APA StyleNicholson, D. M., Gao, C. Y., McDonnell, M. T., Sluss, C. C., & Keffer, D. J. (2021). Entropy Pair Functional Theory: Direct Entropy Evaluation Spanning Phase Transitions. Entropy, 23(2), 234. https://doi.org/10.3390/e23020234





