Theory of Non-Equilibrium Heat Transport in Anharmonic Multiprobe Systems at High Temperatures
Abstract
:1. Introduction
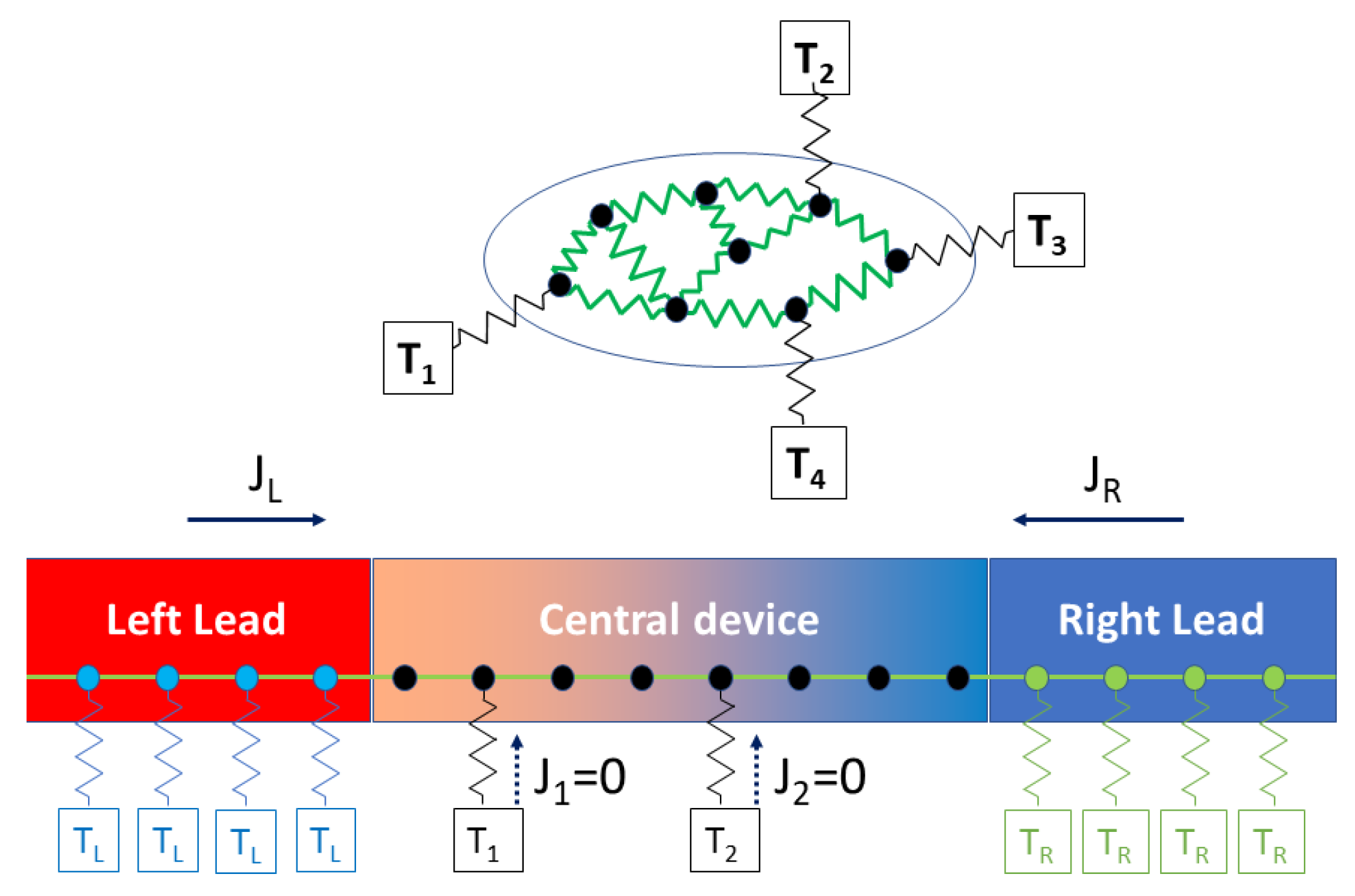
2. Dynamics
3. Physical Observables
3.1. Entropy Generation Rate
3.2. Heat Current
4. Constraints
5. Thermal Expansion
6. Force Constant Renormalization
7. Displacement-Noise Correlations
8. Displacement Autocorrelations
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| D | Device |
| DC | Direct Current |
| DFT | Density Functional Theory |
| FC | Force Constant |
| GF | Green’s Function |
| MD | Molecular Dynamics |
| NEMD | Non-Equilibrium Molecular Dynamics |
| NEMF | Non-Equilibrium Mean-Field |
Appendix A. Calculation of Time Averages
Appendix B. Change of Position Variables Due to Thermal Expansion
Appendix B.1. Thermal Expansion
Appendix B.2. The New Force Constants
Appendix B.3. New Equations of Motion
Appendix C. Explicit Form of the Correlation Functions including the Atomic and Cartesian Indices
Appendix C.1. Lead Self-Energies σ α and Escape Rates Γ α
Appendix C.2. Noise Autocorrelation Functions
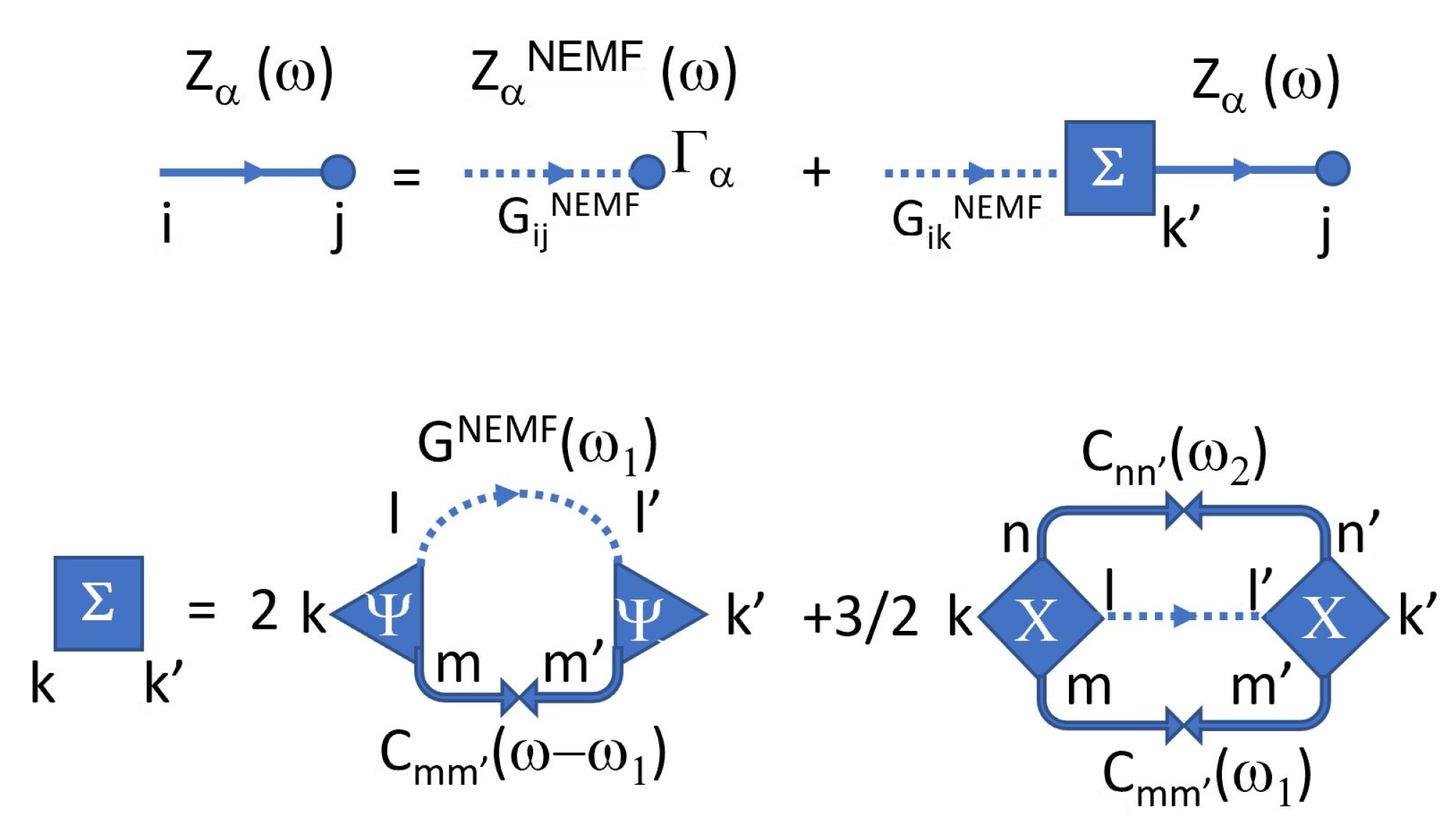
Appendix C.3. Noise-Displacement Correlations Z α
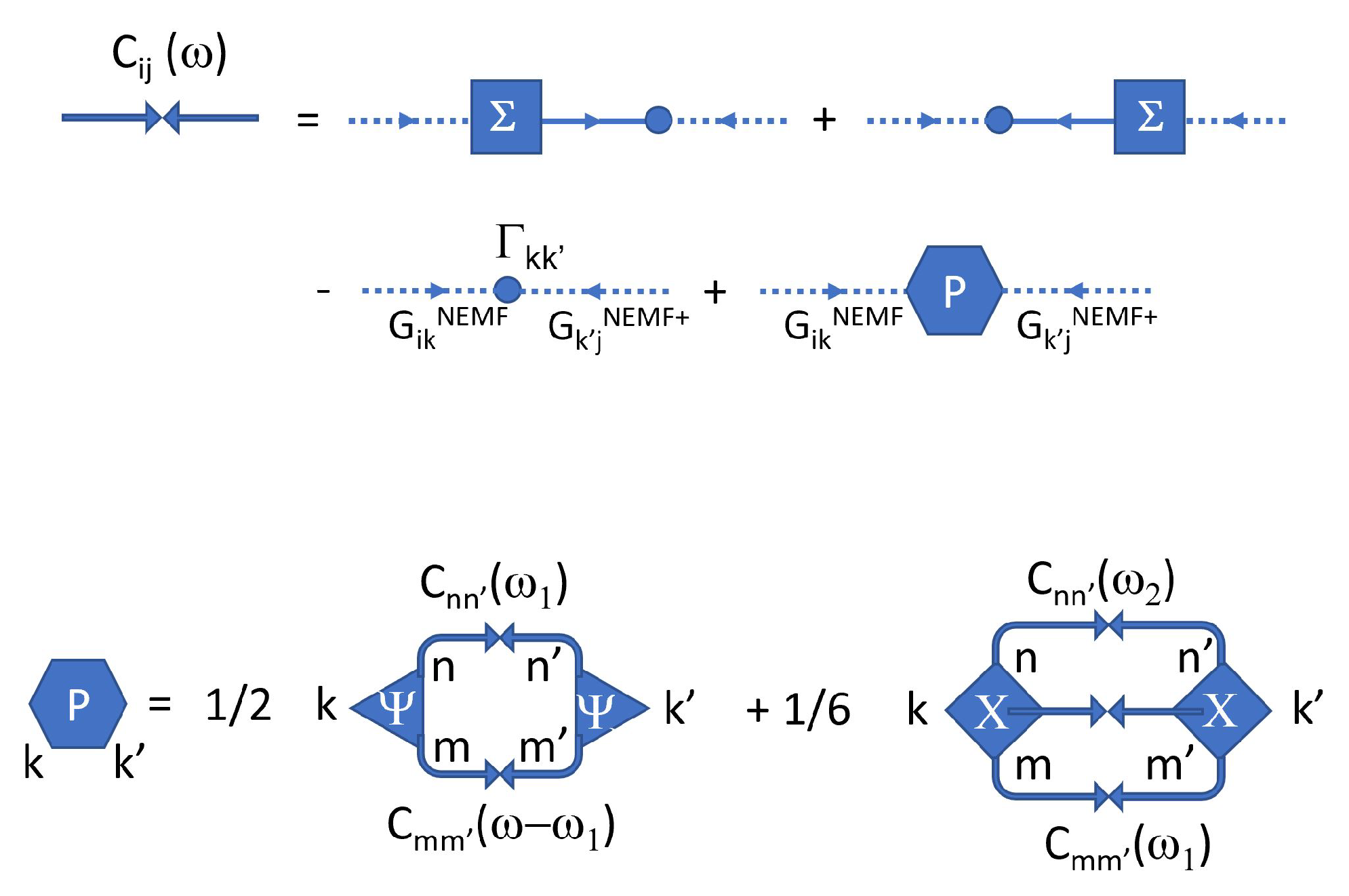
Appendix C.4. Displacement Autocorrelations C(ω)
Appendix D. Statement and Proof of the Novikov–Furutsu–Donsker (NFD) Relation
Appendix E. Heat Current within the Harmonic Approximation
References
- Caroli, C.; Combescot, R.; Lederer, D.; Nozieres, P.; Saint-James, D. A direct calculation of the tunnelling current. II. Free electron description. J. Phys. C Solid State Phys. 1971, 4, 2598–2610. [Google Scholar] [CrossRef]
- Meir, Y.; Wingreen, N.S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 1992, 68, 2512–2515. [Google Scholar] [CrossRef]
- Pastawski, H.M. Classical and quantum transport from generalized Landauer-Büttiker equations. Phys. Rev. B 1991, 44, 6329–6339. [Google Scholar] [CrossRef]
- Mingo, N. Anharmonic phonon flow through molecular-sized junctions. Phys. Rev. B 2006, 74, 125402. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Zeng, N. Nonequilibrium Green’s function approach to mesoscopic thermal transport. Phys. Rev. B 2006, 74, 033408. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Tian, Z. Rigorous formalism of anharmonic atomistic Green’s function for three-dimensional interfaces. Phys. Rev. B 2020, 101, 041301. [Google Scholar] [CrossRef]
- Guo, Y.; Bescond, M.; Zhang, Z.; Luisier, M.; Nomura, M.; Volz, S. Quantum mechanical modeling of anharmonic phonon-phonon scattering in nanostructures. Phys. Rev. B 2020, 102, 195412. [Google Scholar] [CrossRef]
- Luisier, M. Atomistic modeling of anharmonic phonon-phonon scattering in nanowires. Phys. Rev. B 2012, 86, 245407. [Google Scholar] [CrossRef] [Green Version]
- Polanco, C.A. Nonequilibrium Green’s functions (NEGF) in vibrational energy transport: A topical review. Nanoscale Microscale Thermophys. Eng. 2021, 25, 1–24. [Google Scholar] [CrossRef]
- Sääskilahti, K.; Oksanen, J.; Tulkki, J. Thermal balance and quantum heat transport in nanostructures thermalized by local Langevin heat baths. Phys. Rev. E 2013, 88, 012128. [Google Scholar] [CrossRef] [Green Version]
- Bolsterli, M.; Rich, M.; Visscher, W.M. Simulation of Nonharmonic Interactions in a Crystal by Self-Consistent Reservoirs. Phys. Rev. A 1970, 1, 1086–1088. [Google Scholar] [CrossRef]
- Feng, T.; Zhong, Y.; Shi, J.; Ruan, X. Unexpected high inelastic phonon transport across solid-solid interface: Modal nonequilibrium molecular dynamics simulations and Landauer analysis. Phys. Rev. B 2019, 99, 045301. [Google Scholar] [CrossRef] [Green Version]
- Le, N.Q.; Polanco, C.A.; Rastgarkafshgarkolaei, R.; Zhang, J.; Ghosh, A.W.; Norris, P.M. Effects of bulk and interfacial anharmonicity on thermal conductance at solid/solid interfaces. Phys. Rev. B 2017, 95, 245417. [Google Scholar] [CrossRef] [Green Version]
- Sääskilahti, K.; Oksanen, J.; Tulkki, J.; Volz, S. Role of anharmonic phonon scattering in the spectrally decomposed thermal conductance at planar interfaces. Phys. Rev. B 2014, 90, 134312. [Google Scholar] [CrossRef] [Green Version]
- Chalopin, Y.; Esfarjani, K.; Henry, A.; Volz, S.; Chen, G. Thermal interface conductance in Si/Ge superlattices by equilibrium molecular dynamics. Phys. Rev. B 2012, 85, 195302. [Google Scholar] [CrossRef]
- Chalopin, Y.; Volz, S. A microscopic formulation of the phonon transmission at the nanoscale. Appl. Phys. Lett. 2013, 103, 051602. [Google Scholar] [CrossRef]
- Lemons, D.S.; Gythiel, A. Paul Langevin’s 1908 paper “On the Theory of Brownian Motion” [“Sur la théorie du mouvement brownien,” C. R. Acad. Sci. (Paris) 146, 530–533 (1908)]. Am. J. Phys. 1997, 65, 1079–1081. [Google Scholar] [CrossRef]
- Tian, Z.; Esfarjani, K.; Chen, G. Green’s function studies of phonon transport across Si/Ge superlattices. Phys. Rev. B-Condens. Matter Mater. Phys. 2014, 89, 235307. [Google Scholar] [CrossRef] [Green Version]
- Rahimi Tabar, M. Analysis and Data-Based Reconstruction of Complex Nonlinear Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Esfarjani, K.; Stokes, H.T. Method to extract anharmonic force constants from first principles calculations. Phys. Rev. B 2008, 77, 144112. [Google Scholar] [CrossRef] [Green Version]
- Tadano, T.; Gohda, Y.; Tsuneyuki, S. Anharmonic force constants extracted from first-principles molecular dynamics: Applications to heat transfer simulations. J. Phys. Condens. Matter 2014, 26, 225402. [Google Scholar] [CrossRef]
- Dhar, A.; Roy, D. Heat transport in harmonic lattices. J. Stat. Phys. 2006, 125, 805–824. [Google Scholar] [CrossRef] [Green Version]
- Donsker, M.; Lions, J. Fréchet-Volterra variational equations, boundary value problems, and function space integrals. Acta Math. 1962, 108, 147–228. [Google Scholar] [CrossRef]
- Furutsu, K. On the Statistical Theory of Electromagnetic Waves in a Fluctuating Medium (II) Mathematical Basis of the Analogies to Quantum Field Theory; US Government Printing Office: Washington, DC, USA, 1964.
- Novikov, E.A. Functionals and the random-force method in turbulence theory. Sov. Phys. JETP 1965, 20, 1290–1294. [Google Scholar]
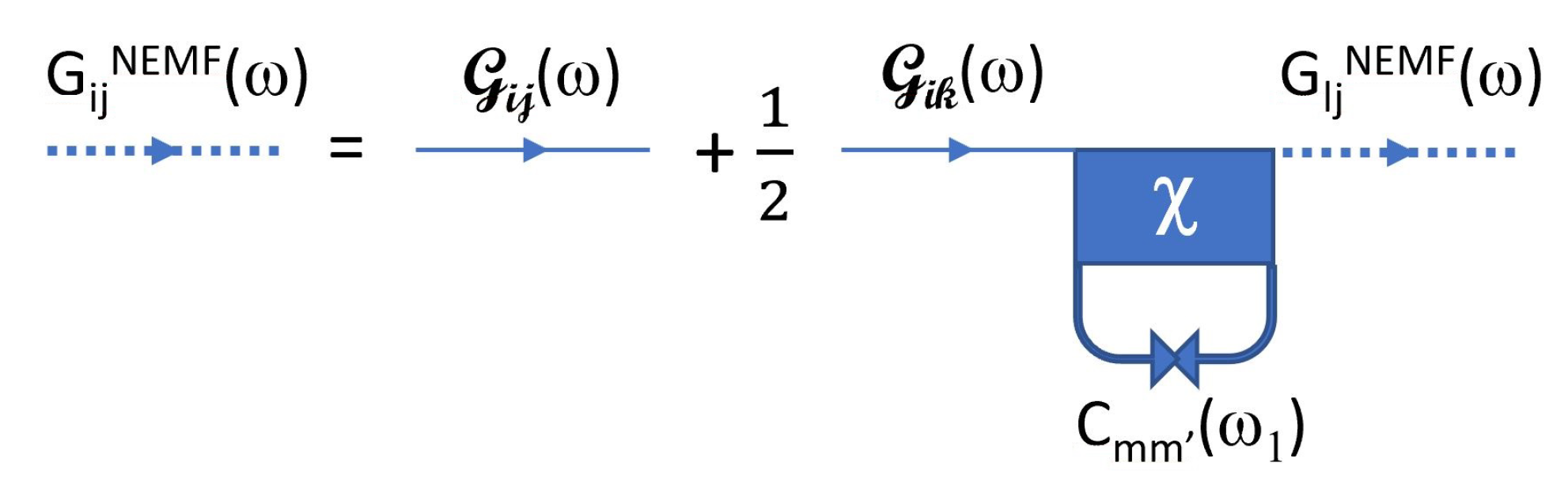
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esfarjani, K. Theory of Non-Equilibrium Heat Transport in Anharmonic Multiprobe Systems at High Temperatures. Entropy 2021, 23, 1630. https://doi.org/10.3390/e23121630
Esfarjani K. Theory of Non-Equilibrium Heat Transport in Anharmonic Multiprobe Systems at High Temperatures. Entropy. 2021; 23(12):1630. https://doi.org/10.3390/e23121630
Chicago/Turabian StyleEsfarjani, Keivan. 2021. "Theory of Non-Equilibrium Heat Transport in Anharmonic Multiprobe Systems at High Temperatures" Entropy 23, no. 12: 1630. https://doi.org/10.3390/e23121630
APA StyleEsfarjani, K. (2021). Theory of Non-Equilibrium Heat Transport in Anharmonic Multiprobe Systems at High Temperatures. Entropy, 23(12), 1630. https://doi.org/10.3390/e23121630





