Entropy-Based Temporal Downscaling of Precipitation as Tool for Sediment Delivery Ratio Assessment
Abstract
:1. Introduction
2. Materials and Methods
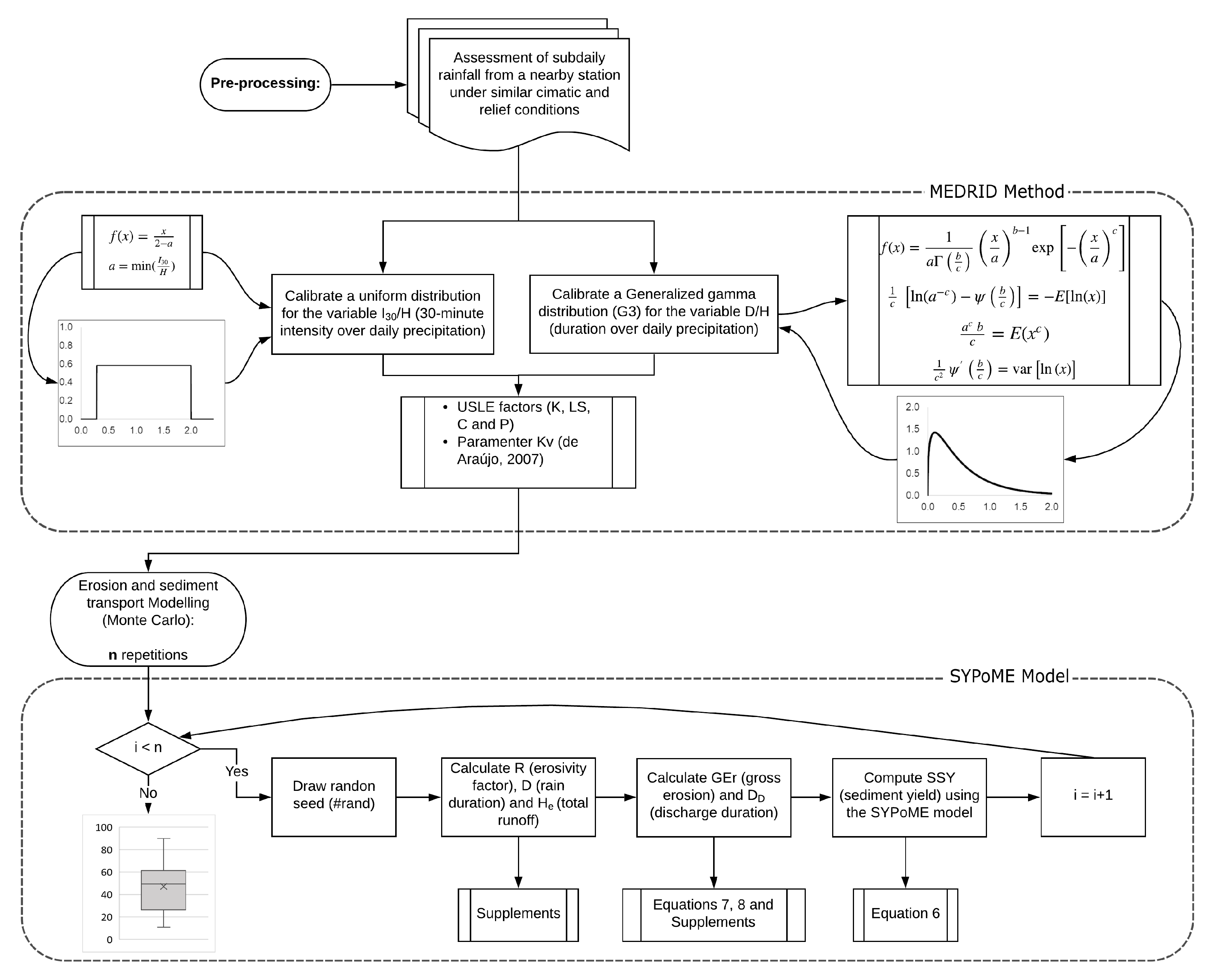
2.1. Maximum Entropy Distribution of Rainfall Intensity and Duration—MEDRID Method
Other Literature Approach
2.2. Sediment Yield-PoME—SYPOME Method
2.3. Monte Carlo and MEDRID-SYPoME Coupling
2.4. Gross Erosion and Siltation Assessment
2.5. Study Area
3. Results
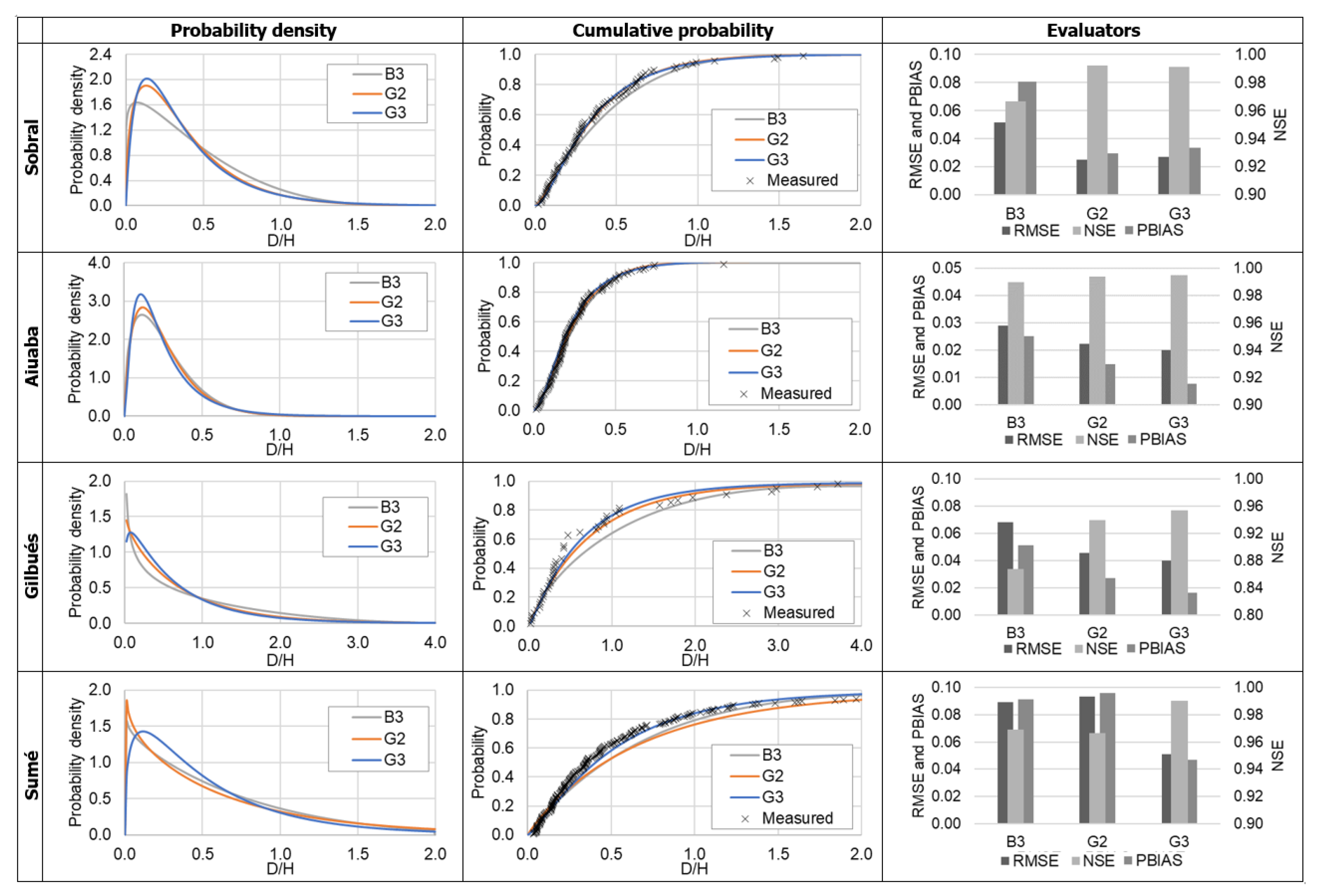
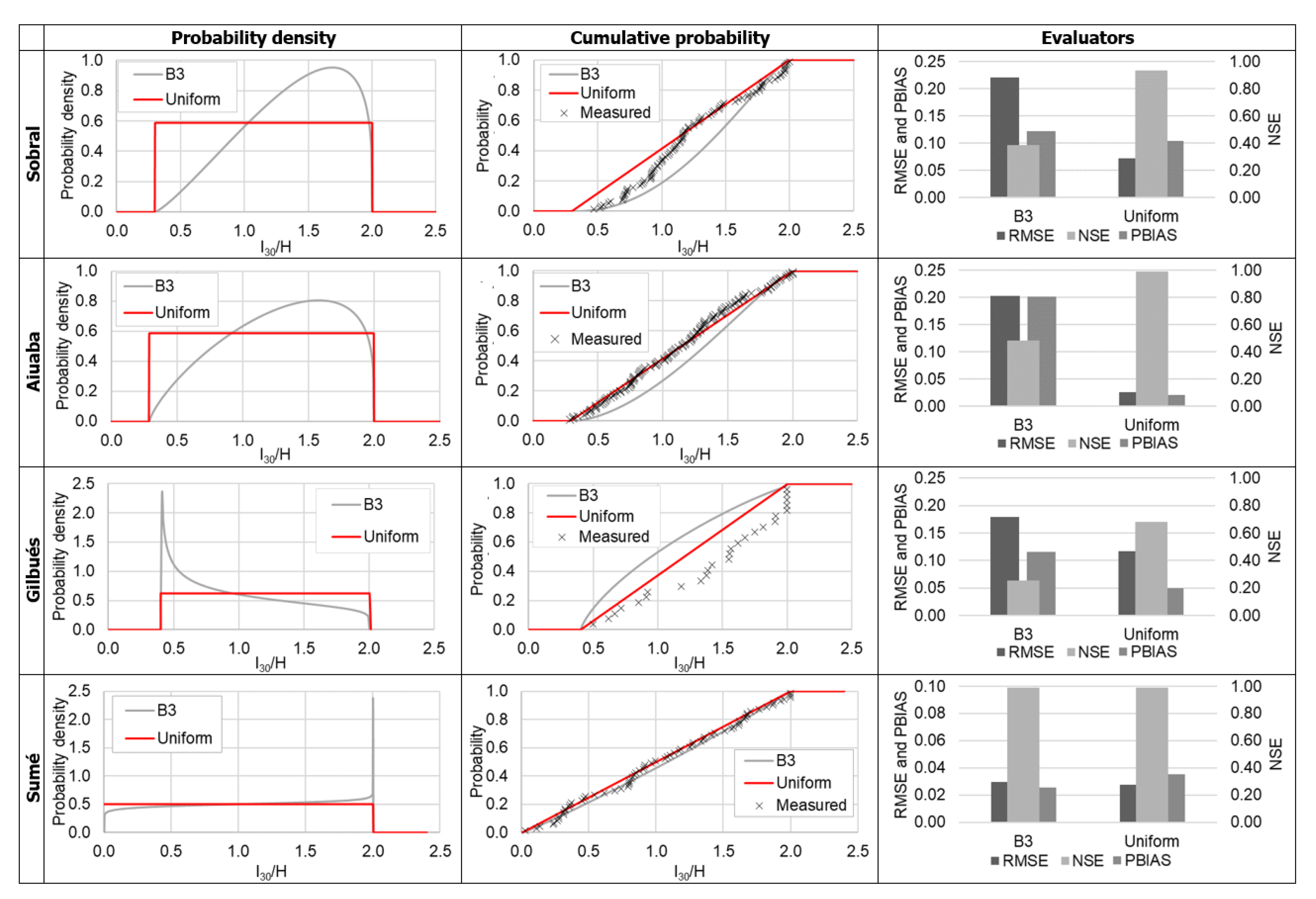
3.1. Probability Distribution Functions—MEDRID
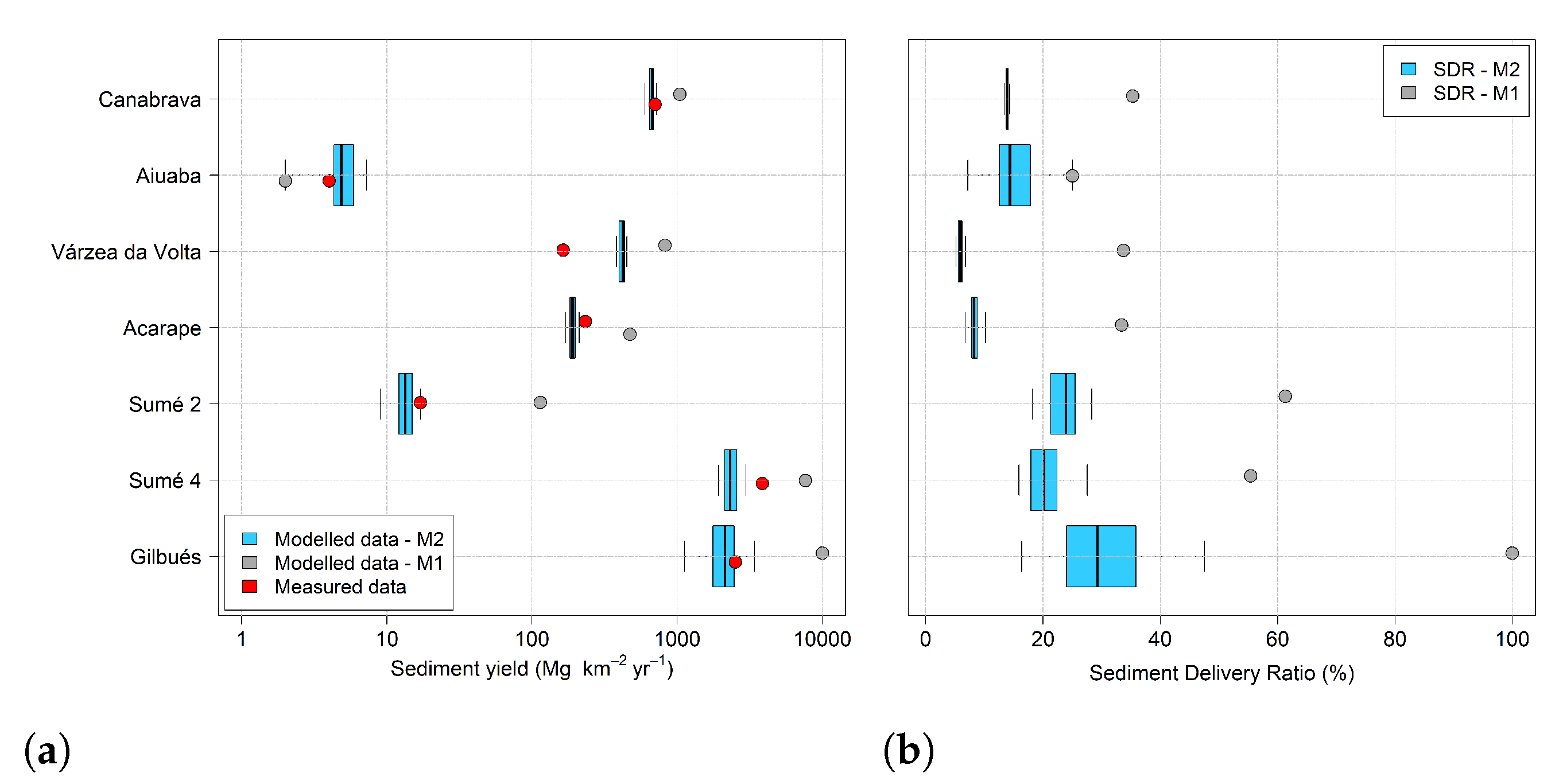
3.2. Sediment Yield Modeling
4. Discussion
4.1. Probability Distribution Functions—MEDRID
4.2. Sediment Yield Modeling
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FAO. Global Symposium on Soil Erosion, 15–17 May 2019, FAO, Rome. Outcome Document; Food and Agriculture Organization of the United Nations: Rome, Italy, 2019; p. 28. [Google Scholar]
- Nearing, M.A. Expected Climate Change Impacts on Soil Erosion Rates. J. Soil Water Conserv. 2004, 59, 43–50. [Google Scholar]
- Panagos, P.; Ballabio, C.; Meusburger, K.; Spinoni, J.; Alewell, C.; Borrelli, P. Towards estimates of future rainfall erosivity in Europe based on REDES and WorldClim datasets. J. Hydrol. 2017, 548, 251–262. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; van der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [Green Version]
- Coelho, C.; Heim, B.; Foerster, S.; Brosinsky, A.; de Araújo, J.C. In situ and satellite observation of CDOM and chlorophyll-a dynamics in small water surface reservoirs in the brazilian semiarid region. Water 2017, 9, 913. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Peng, H.; Xie, B.; Liu, C.; Nie, X.; Wang, D.; Huang, M.; Xiao, H.; Shi, L.; Zhang, X.; et al. Dissolved organic matter in surface runoff in the Loess Plateau of China: The role of rainfall events and land-use. Hydrol. Process. 2020, 34, 1446–1459. [Google Scholar] [CrossRef]
- Sivakumar, M.V.K.; Das, H.P.; Brunini, O. Impacts of Present and Future Climate Variability and Change on Agriculture and Forestry in the Arid and Semi-Arid Tropics; Springer: Dordrecht, The Netherlands, 2005; pp. 31–72. [Google Scholar] [CrossRef]
- Huang, J.; Ji, M.; Xie, Y.; Wang, S.; He, Y.; Ran, J. Global semi-arid climate change over last 60 years. Clim. Dyn. 2015, 46, 1131–1150. [Google Scholar] [CrossRef] [Green Version]
- Sanyal, J.; Densmore, A.L.; Carbonneau, P. Analysing the effect of land-use/cover changes at sub-catchment levels on downstream flood peaks: A semi-distributed modelling approach with sparse data. CATENA 2014, 118, 28–40. [Google Scholar] [CrossRef] [Green Version]
- Worqlul, A.W.; Yen, H.; Collick, A.S.; Tilahun, S.A.; Langan, S.; Steenhuis, T.S. Evaluation of CFSR, TMPA 3B42 and ground-based rainfall data as input for hydrological models, in data-scarce regions: The upper Blue Nile Basin, Ethiopia. CATENA 2017, 152, 242–251. [Google Scholar] [CrossRef]
- Rezende de Souza, G.; Merwade, V.; Coutinho de Oliveira, L.F.; Ribeiro Viola, M.; de Sá Farias, M. Regional flood frequency analysis and uncertainties: Maximum streamflow estimates in ungauged basins in the region of Lavras, MG, Brazil. CATENA 2021, 197, 104970. [Google Scholar] [CrossRef]
- Srinivasan, V.; Galvão, C. Bacia Experimental de Sumé: Descrição e Dados Coletados; UFCG/CNPq: Paraíba, Brazil, 2003. [Google Scholar]
- Shrestha, N.K.; Allataifeh, N.; Rudra, R.; Daggupati, P.; Goel, P.K.; Dickinson, T. Identifying threshold storm events and quantifying potential impacts of climate change on sediment yield in a small upland agricultural watershed of Ontario. Hydrol. Process. 2019, 33, 920–931. [Google Scholar] [CrossRef]
- Sidorchuk, A. Geomorphology A third generation erosion model: The combination of probabilistic and deterministic components. Geomorphology 2009, 110, 2–10. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic modeling: Progress and future directions. Geosci. Lett. 2018, 5. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and Probability Concepts in Hydraulics. J. Hydraul. Eng. 1987, 113, 583–599. [Google Scholar] [CrossRef]
- Singh, V.P.; Chowdhury, P.K. On Fitting Gamma Distrubution to Synthetic Runoff Hydrographs. Hydrol. Res. 1985, 16, 177–192. [Google Scholar] [CrossRef]
- Sterling, M.; Knight, D. An attempt at using the entropy approach to predict the transverse distribution of boundary shear stress in open channel flow. Stoch. Environ. Res. Risk Assess. (SERRA) 2002, 16, 127–142. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic Synthesis Using Entropy Theory: Review. J. Hydrol. Eng. 2011, 16, 421–433. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Two-Dimensional Velocity Distribution in Open Channels Using the Tsallis Entropy. J. Hydrol. Eng. 2013, 18, 331–339. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Xiong, F. An entropy-based generalized gamma distribution for flood frequency analysis. Entropy 2017, 19, 239. [Google Scholar] [CrossRef] [Green Version]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Two-dimensional distribution of streamwise velocity in open channel flow using maximum entropy principle: Incorporation of additional constraints based on conservation laws. Comput. Methods Appl. Mech. Eng. 2020, 361, 112738. [Google Scholar] [CrossRef]
- de Araújo, J.C. Entropy-based equation to assess hillslope sediment production. Earth Surf. Process. Landforms 2007, 32, 2005–2018. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Chapman, T.G.; Doran, D.G. Problems of rainfall-runoff modelling in arid and semiarid regions. Hydrol. Sci. J. 1988, 33, 379–400. [Google Scholar] [CrossRef]
- ANA. Rede Hidrometeorológica Nacional. Available online: http://www.snirh.gov.br/hidroweb/ (accessed on 12 October 2019).
- NOAA. NCDC/NOAA Land-Based Datasets and Products. Available online: https://www.ncei.noaa.gov/products/land-based-station (accessed on 10 May 2019).
- Baldassarre, G.D.; Castellarin, A.; Brath, A. Relationships between statistics of rainfall extremes and mean annual precipitation: An application for design-storm estimation in northern central Italy. Hydrol. Earth Syst. Sci. 2006, 10, 589–601. [Google Scholar] [CrossRef] [Green Version]
- Medeiros, P.H.A.; de Araújo, J.C. Temporal variability of rainfall in a semiarid environment in Brazil and its effect on sediment transport processes. J. Soils Sediments 2014, 1216–1223. [Google Scholar] [CrossRef]
- Cadier, E. Hidrologia das Pequenas Bacias do Nordeste Semi-árido: Transposição Hidrológica; Number 31 in Hidrologia, Sudene. 1994; p. 448. Available online: https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers12-05/010031008.pdf (accessed on 20 November 2021).
- Andrade, E.M.; Guerreiro, M.J.S.; Palácio, H.A.Q.; Campos, D.A. Ecohydrology in a Brazilian tropical dry forest: Thinned vegetation impact on hydrological functions and ecosystem services. J. Hydrol. Reg. Stud. 2020, 27, 100649. [Google Scholar] [CrossRef]
- de Figueiredo, J.V.; de Araújo, J.C.; Medeiros, P.H.A.; Costa, A.C. Runoff initiation in a preserved semiarid Caatinga small watershed, Northeastern Brazil. Hydrol. Process. 2016, 30, 2390–2400. [Google Scholar] [CrossRef]
- Gaiser, T.; Krol, M.; Frischkorn, H.; de Araujo, J.C. (Eds.) Global Change and Regional Impacts; Springer: Berlin/Heidelberg, Germany, 2003; p. 422. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A.; Camargo, H.; Riveros, M.P.; Pabló, A.D. Two Contrasting Severe Seasonal Extremes in Tropical South America in 2012: Flood in Amazonia and Drought in Northeast Brazil. J. Clim. 2013, 26, 9137–9154. [Google Scholar] [CrossRef]
- Montenegro, S.; Ragab, R. Impact of possible climate and land use changes in the semi arid regions: A case study from North Eastern Brazil. J. Hydrol. 2012, 434–435, 55–68. [Google Scholar] [CrossRef]
- Mamede, G.; Araujo, N.A.; Schneider, C.; de Araujo, J.C.; Herrmann, H.J. Overspill Avalanching in a Dense Reservoir Network. Proc. Natl. Acad. Sci. USA 2012, 109, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kullback, S. Information Theory and Statistics; Dover: New York, NY, USA, 1978; p. 409. [Google Scholar]
- Fedotov, A.; Harremoes, P.; Topsoe, F. Refinements of Pinsker’s inequality. IEEE Trans. Inf. Theory 2003, 49, 1491–1498. [Google Scholar] [CrossRef]
- Maner, S.B. Factors affecting sediment delivery rates in the red hills physiographic area. Trans. Am. Geophys. Union 1958, 39, 669. [Google Scholar] [CrossRef]
- Sharda, V.N.; Ojasvi, P.R. A revised soil erosion budget for India: Role of reservoir sedimentation and land-use protection measures. Earth Surf. Process. Landforms 2016, 41, 2007–2023. [Google Scholar] [CrossRef]
- Llena, M.; Batalla, R.; Smith, M.; Vericat, D. Do badlands (always) control sediment yield? Evidence from a small intermittent catchment. CATENA 2021, 198, 105015. [Google Scholar] [CrossRef]
- Royall, D.; Kennedy, L. Historical erosion and sedimentation in two small watersheds of the southern Blue Ridge Mountains, North Carolina, USA. CATENA 2016, 143, 174–186. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.K.; Singh, P.K.; Tyagi, J.; Sharma, G.; Jethoo, A.S. Rainstorm-generatedsediment yield model based on soil moisture proxies (SMP). Hydrol. Process. 2020, 34, 3448–3463. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Science and Education Administration, US Department of Agriculture: Washington, DC, USA, 1978.
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy-based Parameter Estimation in Hydrology; Springer Science: Dordrecht, The Netherland, 1998; p. 365. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una lgge di distribuzione. Inst. Ital. Attuari Giorn. 1933, 4, 83–91. [Google Scholar]
- Smirnov, N.V. Estimate of deviation between empirical distribution functions in two independent samples. Bull. Mosc. Univ. 1939, 2, 3–16. [Google Scholar]
- de Araújo, J.C. Entropy-based equation to assess sediment yield: Application to ungauged basins. In Proceedings of the IASWS 2017 Symposium, Taormina, Italy, 17–22 June 2017; pp. 2005–2018. [Google Scholar]
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. WAter Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Bagarello, V.; Ferro, V.; Pampalone, V. A comprehensive analysis of Universal Soil Loss Equation-based models at the Sparacia experimental area. Hydrol. Process. 2020, 34, 1545–1557. [Google Scholar] [CrossRef]
- Brune, G.M. Trap efficiency of reservoirs. Eos Trans. Am. Geophys. Union 1953, 34, 407–418. [Google Scholar] [CrossRef]
- Simplício, A.A.F.; Costa, C.A.G.; Navarro-Hevia, J.; Araújo, J.C. Erosion at hillslope and micro-basin scales in the Gilbués Desertification Region, North-eastern Brazil. Land Degrad. Dev. 2020. [Google Scholar] [CrossRef]
- Miles, L.; Newton, A.C.; DeFries, R.S.; Ravilious, C.; May, I.; Blyth, S.; Kapos, V.; Gordon, J.E. A global overview of the conservation status of tropical dry forests. J. Biogeogr. 2006, 33, 491–505. [Google Scholar] [CrossRef]
- Silva, A.C.; Souza, A.F. Aridity drives plant biogeographical sub regions in the Caatinga, the largest tropical dry forest and woodland block in South America. PLoS ONE 2018, 13, e0196130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tomasella, J.; Vieira, R.M.S.P.; Barbosa, A.A.; Rodriguez, D.A.; de Oliveira Santana, M.; Sestini, M.F. Desertification trends in the Northeast of Brazil over the period 2000–2016. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 197–206. [Google Scholar] [CrossRef]
- Morris, G.L.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs, and Watersheds for Sustainable Use; McGraw-Hill Book Co.: New York, NY, USA, 1998. [Google Scholar]
- FUNCEME. Foundation of Meteorology and Water Resources of Ceará, Daily total precipitation. Available online: http://www.funceme.br/?page_id=2694 (accessed on 14 June 2019).
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Berndtsson, R.; Ojha, C.S.P.; Mishra, S.K. Suitability of Gamma, Chi-square, Weibull, and Beta distributions as synthetic unit hydrographs. J. Hydrol. 2007, 334, 28–38. [Google Scholar] [CrossRef]
- Brigandì, G.; Aronica, G.T. Generation of sub-hourly rainfall events through a point stochastic rainfall model. Geosciences 2019, 9, 226. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Villalobos, C.; Neelin, J.D. Why Do Precipitation Intensities Tend to Follow Gamma Distributions? J. Atmos. Sci. 2019, 76, 3611–3631. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of Entropy Concept in Open-Channel Flow Study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Silva Filho, A.V.d.; de Araújo, J.C.; Raabe, A. Trade-off between number of constraints and primary-statement robustness in entropy models: The case of the open-channel velocity field. An. Acad. Bras. CiÊNcias 2020, 92. [Google Scholar] [CrossRef] [PubMed]
- Avila, H.F.; Avila, B.D. Spatial and temporal estimation of the erosivity factor R based on daily rainfall data for the department of Atlántico, Colombia. Ing. Investig. 2015, 35, 23–29. [Google Scholar] [CrossRef]
- Alencar, P.H.L.; de Araújo, J.C.; dos Santos Teixeira, A. Physically based model for gully simulation: Application to the Brazilian semiarid region. Hydrol. Earth Syst. Sci. 2020, 24, 4239–4255. [Google Scholar] [CrossRef]
- Dash, C.J.; Das, N.K.; Adhikary, P.P. Rainfall erosivity and erosivity density in Eastern Ghats Highland of east India. Nat. Hazards 2019, 97, 727–746. [Google Scholar] [CrossRef]
- Risse, L.M.; Nearing, M.A.; Laflen, J.M.; Nicks, A.D. Error Assessment in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1993, 57, 825–833. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Bennett, S.J.; Wells, R.R. Gully erosion processes, disciplinary fragmentation, and technological innovation. Earth Surf. Process. Landformsbeschuldigung 2019, 44, 46–53. [Google Scholar] [CrossRef] [Green Version]


| Equation | B3 | G2 | G3 | |
|---|---|---|---|---|
| Constraints | i. | |||
| ii. | ||||
| iii. | ||||
| System | i. | |||
| ii. | ||||
| iii. | ||||
| Basin | Area (km2) | Control System | Land Use | Location | Catchment Position | Bathymetry | Time Series | Automatic Weather Station | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Position | Recording | ||||||||||||
| Lon | Lat | First a | Second | Lon | Lat | Start | End | |||||||
| Canabrava | 2.9 | Reservoir | Agriculture and open range cattle raising | Ceará | 39.56 W | 6.97 S | 1944 | 2000 | 57 | Aiuaba | 40.22 W | 6.69 S | 2004 | 2014 |
| Aiuaba | 11.53 | Reservoir | Conservation area with native vegetation (Caatinga) | Ceará | 40.24 W | 6.65 S | 2003 | 2009 | 7 | Aiuaba | 40.22 W | 6.69 S | 2004 | 2014 |
| Várzea da Volta | 155 | Reservoir | Agriculture and open range cattle raising | Ceará | 40.62 W | 3.50 S | 1917 | 1997 | 81 | Sobral | 40.36 W | 3.69 S | 2017 | 2019 |
| Acarape | 208 | Reservoir | Agriculture and open range cattle raising | Ceará | 38.69 W | 4.20 S | 1924 | 1999 | 74 | Sobral | 40.36 W | 3.69 S | 2017 | 2019 |
| Sumé 2 | 0.0107 | Sediment load | Experimental area—preserved vegetation | Paraíba | 36.88 W | 7.67 S | - | 10 | Sumé | 36.88 W | 7.67 S | 1982 | 1991 | |
| Sumé 4 | 0.0048 | Sediment load | Experimental area—degraded land without vegetation | Paraíba | 36.9 W | 7.66 S | - | 10 | Sumé | 36.88 W | 7.67 S | 1982 | 1991 | |
| Gilbués | 0.0004 | Check dam | Abandoned land under desertification process without vegetation | Piauí | 45.34 W | 9.88 S | 2018 | 2019 | 1 | Gilbués | 45.34 W | 9.88 S | 2018 | 2019 |
| B3 | G2 | G3 | |||||
|---|---|---|---|---|---|---|---|
| a | b | a | b | a | b | c | |
| Sobral | 1.124 | 4.316 | 0.250 | 1.525 | 0.066 | 2.114 | 0.678 |
| Aiuaba | 1.584 | 10.686 | 0.138 | 1.855 | 0.004 | 3.306 | 0.488 |
| Gilbués | 0.696 | 2.691 | 0.777 | 0.953 | 0.390 | 2.099 | 0.812 |
| Sumé | 0.955 | 5.398 | 0.740 | 0.911 | 0.269 | 1.410 | 0.818 |
| (a) Symmetric Divergence | ||||
|---|---|---|---|---|
| Sobral | Aiuaba | Gilbués | Sumé | |
| Sobral | 0 | 0.198 | 1.210 | 0.097 |
| Aiuaba | 0.198 | 0 | 2.494 | 0.536 |
| Gilbués | 1.210 | 2.494 | 0 | 0594 |
| Sumé | 0.097 | 0.536 | 0.594 | 0 |
| (b) Kolmogorov–Smirnov Distance | ||||
| Sobral | Aiuaba | Gilbués | Sumé | |
| Sobral | 0 | 0.242 | 0.550 | 0.152 |
| Aiuaba | 0.242 | 0 | 0.719 | 0.365 |
| Gilbués | 0.550 | 0.719 | 0 | 0.404 |
| Sumé | 0.152 | 0.365 | 0.404 | 0 |
| Basin | Sediment yield | SDR | ||||||
|---|---|---|---|---|---|---|---|---|
| (Mg km−2 yr−1 ) | (%) | |||||||
| CV | CI | CV | CI | |||||
| Canabrava | 664.5 | 24.9 | 4% | 12.5 | 13.9 | 0.2 | 1.4% | 1.04 |
| Aiuaba | 5.0 | 1.2 | 25% | 0.6 | 14.8 | 4.2 | 28.4% | 2.12 |
| Várzea da Volta | 418.2 | 20.2 | 5% | 10.1 | 5.9 | 0.4 | 7.3% | 0.22 |
| Acarape | 189.5 | 9.1 | 5% | 3.1 | 8.3 | 0.7 | 8.1% | 0.23 |
| Sumé 2 | 13.1 | 1.8 | 14% | 0.9 | 23.5 | 2.6 | 11.1% | 1.32 |
| Sumé 4 | 2345.6 | 264.1 | 11% | 132.9 | 20.4 | 3.0 | 14.6% | 1.50 |
| Gilbués | 2141.7 | 540.5 | 25% | 272.0 | 29.7 | 8.9 | 29.9% | 4.47 |
| Name | Brune Coefficient | Sediment Yield (Mg km−2 yr−1) | Relative Error (%) | |||
|---|---|---|---|---|---|---|
| Measured | Modeled | Modeled | Modeled | Modeled | ||
| M1 | M2 | M1 | M2 | |||
| Canabrava | 0.98 | 704 | 1042 | 664 | 48.0% | −5.6% |
| Aiuaba | 1.00 | 4 | 2 | 5 | −50.0% | 27.5% |
| Várzea da Volta | 0.95 | 164 | 824 | 418 | 402.3% | 155.1% |
| Acarape | 0.98 | 233 | 473 | 191 | 102.9% | −18.1% |
| Sumé 2 | 1.00 | 17 | 114 | 13 | 570.6% | −21.8% |
| Sumé 4 | 1.00 | 3857 | 7644 | 2314 | 98.2% | −40.0% |
| Gilbués | 1.00 | 2518 | 10305 | 2142 | 309.3% | −14.9% |
| NSE | −4.49 | 0.96 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alencar, P.H.L.; Paton, E.N.; de Araújo, J.C. Entropy-Based Temporal Downscaling of Precipitation as Tool for Sediment Delivery Ratio Assessment. Entropy 2021, 23, 1615. https://doi.org/10.3390/e23121615
Alencar PHL, Paton EN, de Araújo JC. Entropy-Based Temporal Downscaling of Precipitation as Tool for Sediment Delivery Ratio Assessment. Entropy. 2021; 23(12):1615. https://doi.org/10.3390/e23121615
Chicago/Turabian StyleAlencar, Pedro Henrique Lima, Eva Nora Paton, and José Carlos de Araújo. 2021. "Entropy-Based Temporal Downscaling of Precipitation as Tool for Sediment Delivery Ratio Assessment" Entropy 23, no. 12: 1615. https://doi.org/10.3390/e23121615
APA StyleAlencar, P. H. L., Paton, E. N., & de Araújo, J. C. (2021). Entropy-Based Temporal Downscaling of Precipitation as Tool for Sediment Delivery Ratio Assessment. Entropy, 23(12), 1615. https://doi.org/10.3390/e23121615







