Fixed-Time Synchronization Control of Delayed Dynamical Complex Networks
Abstract
:1. Introduction
2. Preliminaries
3. Fixed-Time Synchronization
3.1. Discontinuous State Feedback Control
3.2. Adaptive State Control
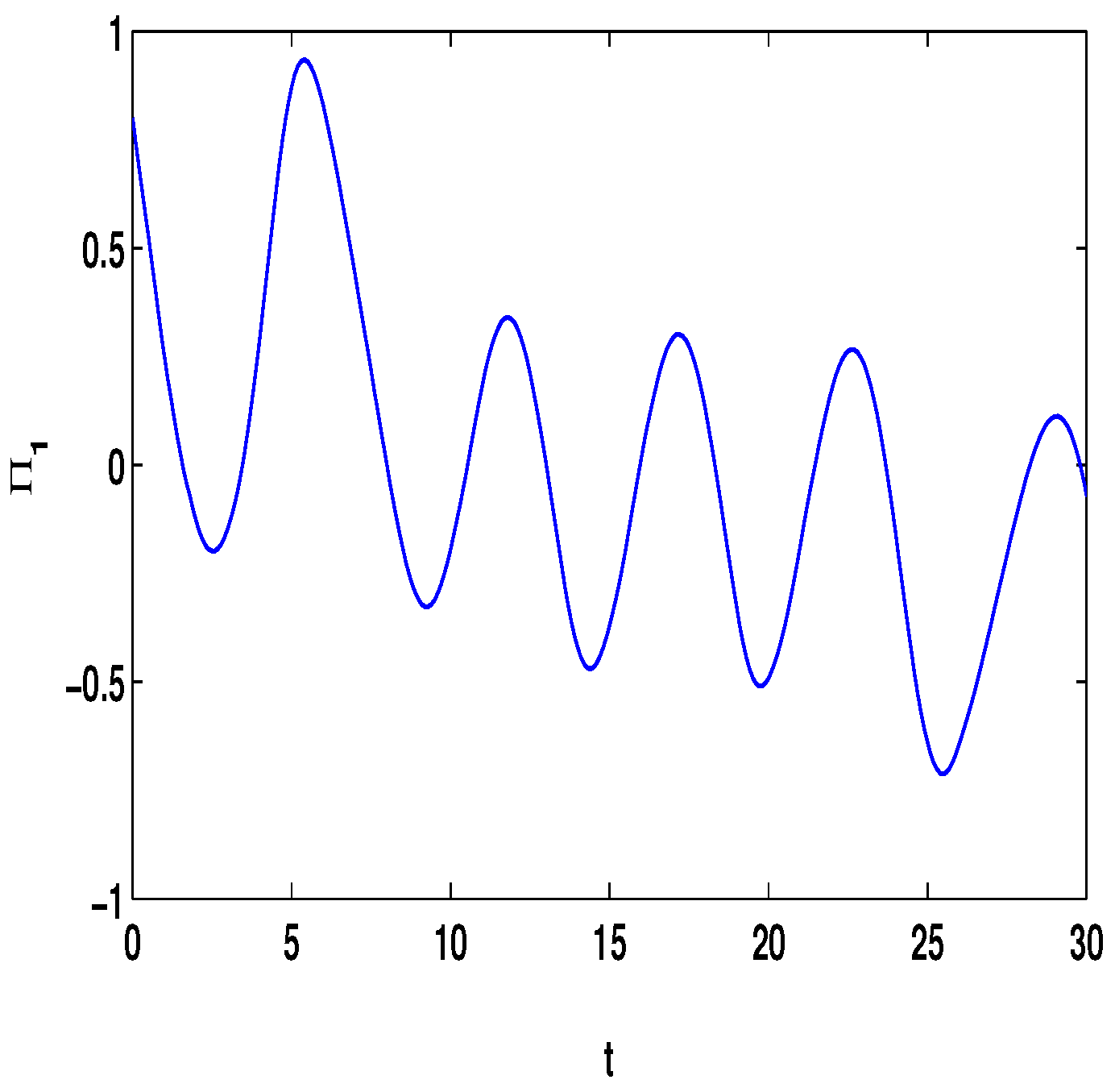
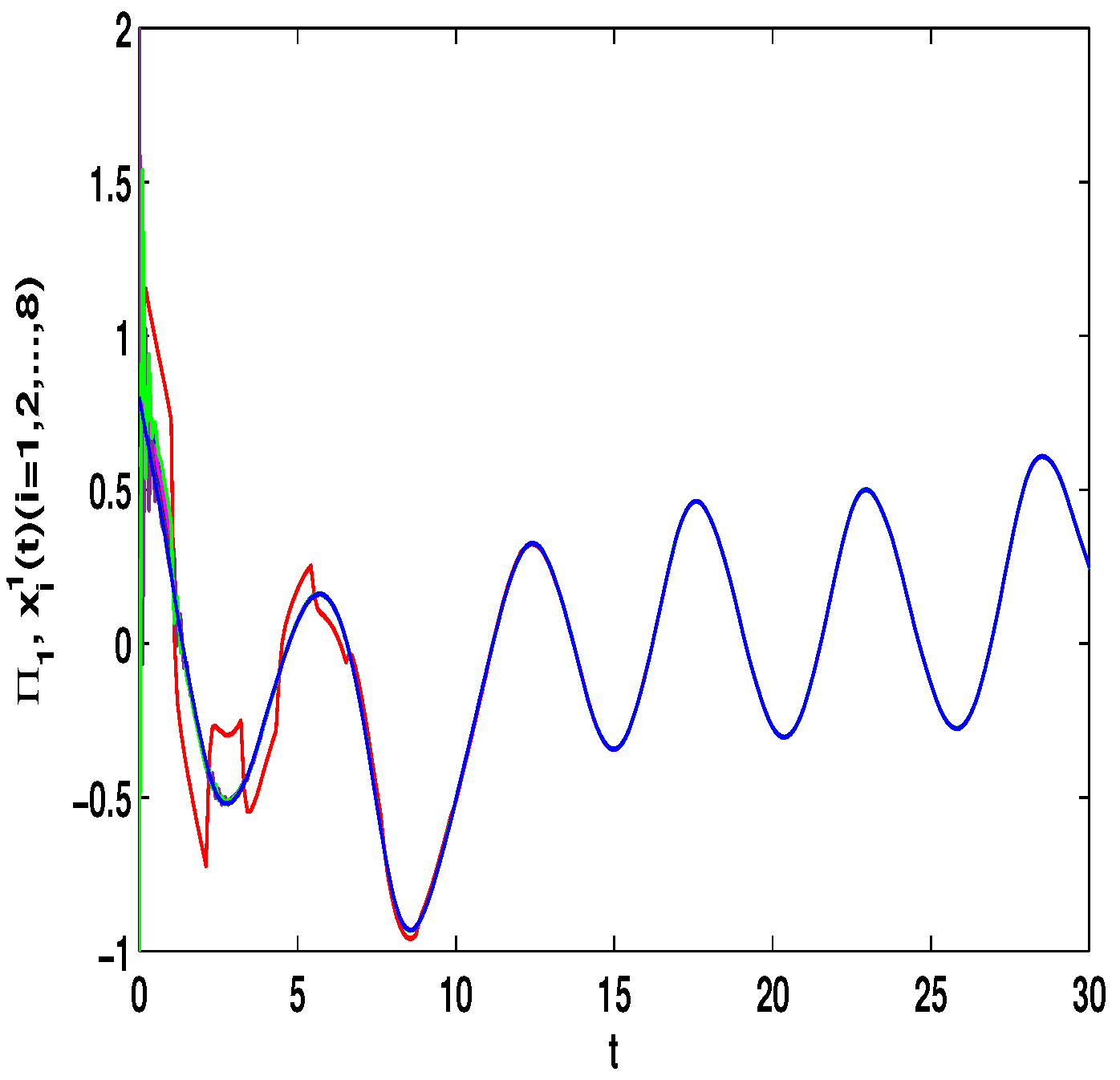
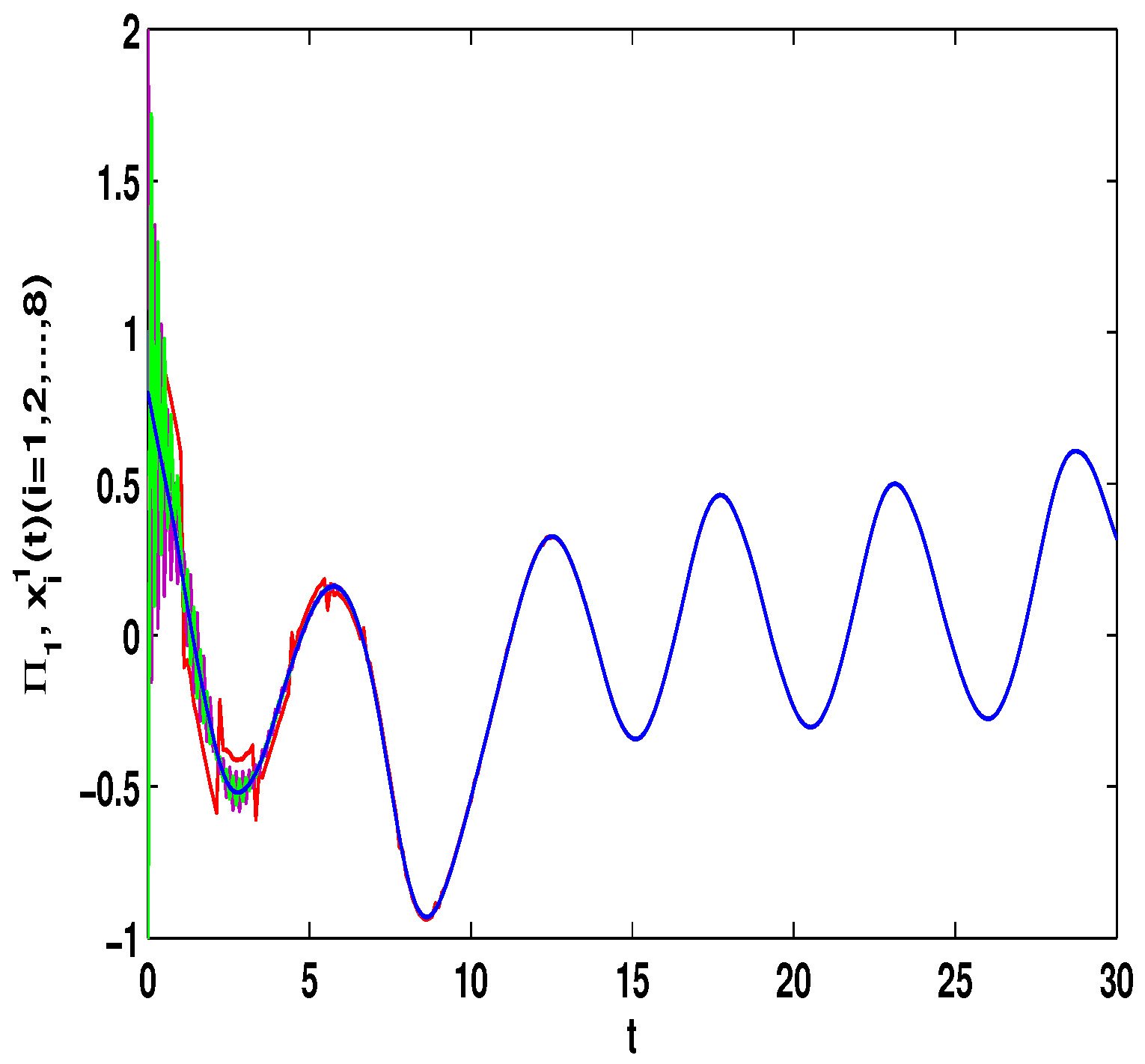
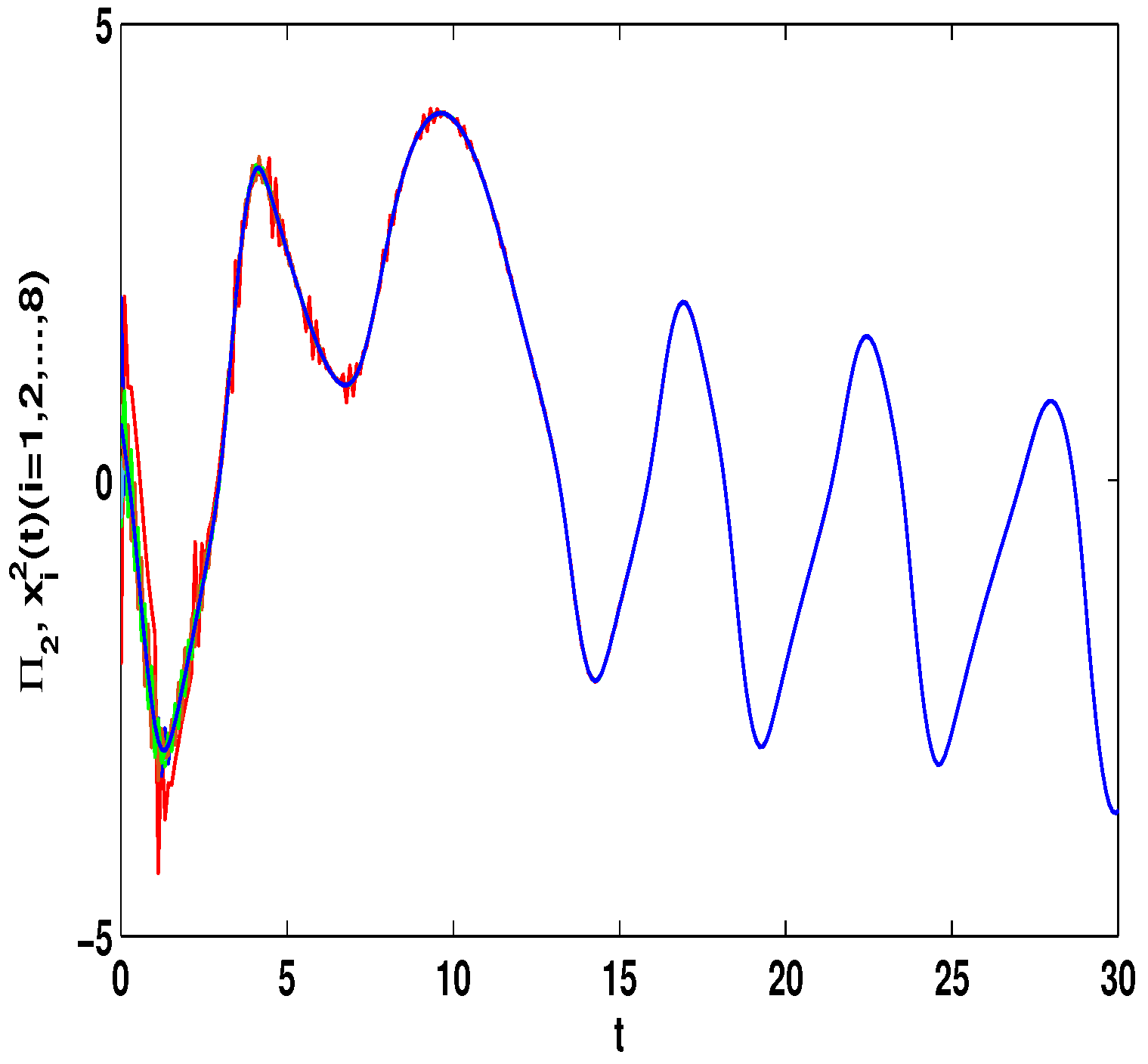
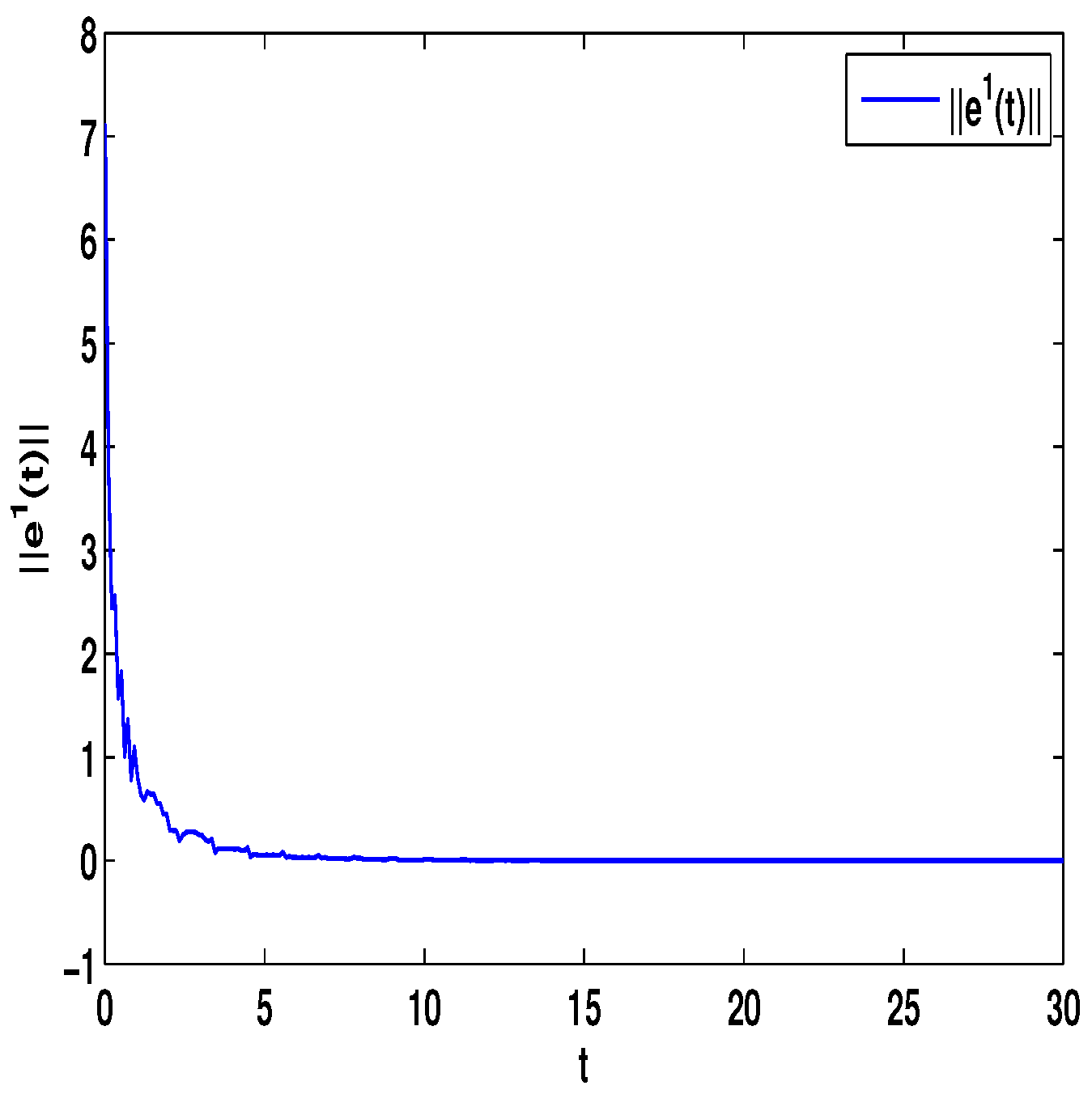
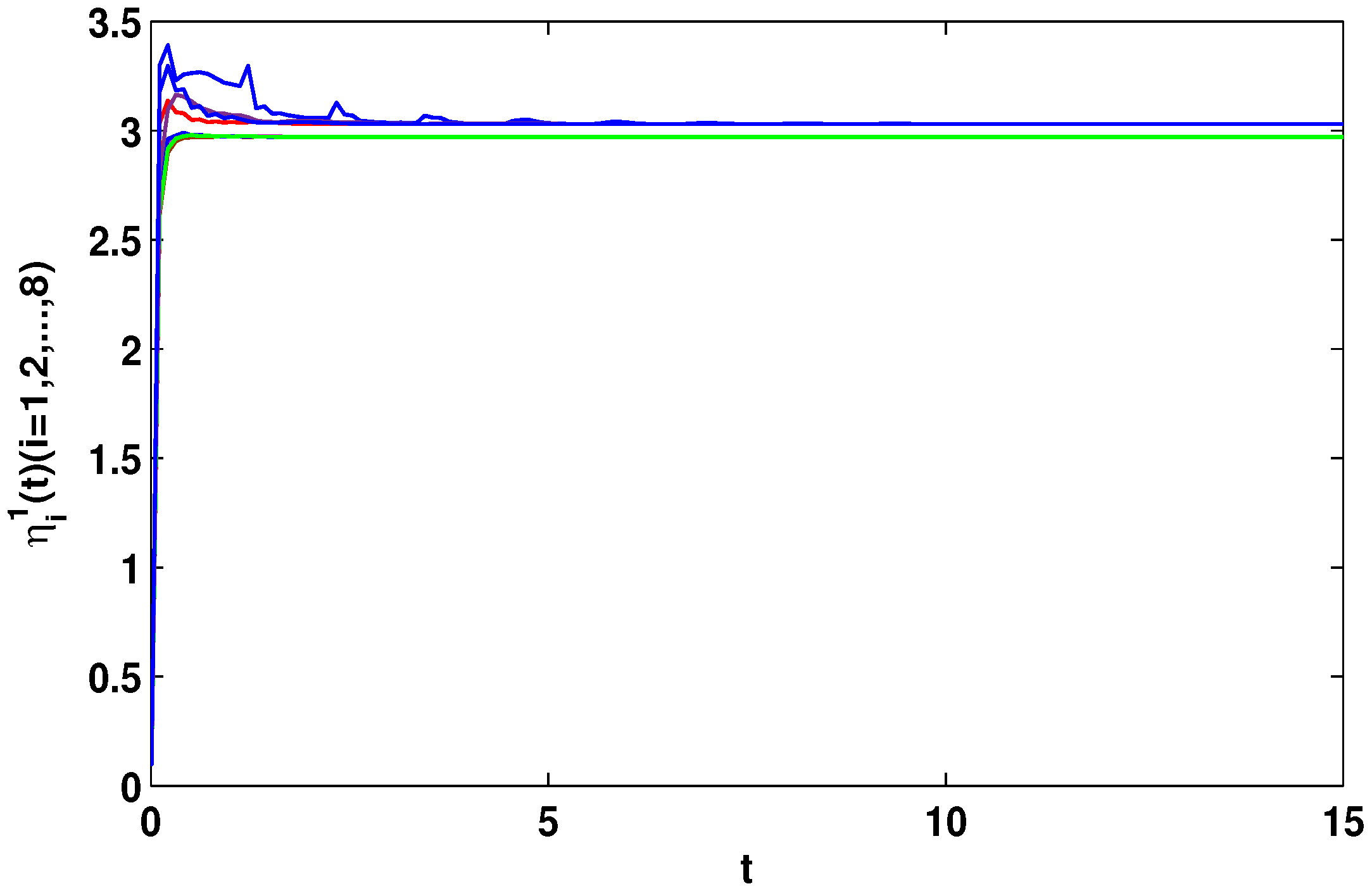
4. Numerical Simulations
4.1. Discontinuous Feedback Control
4.2. Adaptive State Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MASs | Complex networks model |
| FONMASs | Delayed complex networks model |
| SMC | Feedback control and adaptive control |
References
- Chua, L.; Roska, T. Cellular Neural Networks and Visual Computing: Foundation and Applications; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Zhang, X.; Zhou, Y.; Wang, J.; Lu, X. Personal interest attention graph neural networks for session-based recommendation. Entropy 2021, 23, 1500. [Google Scholar] [CrossRef] [PubMed]
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. On power-law relationships of the Interact topology. Comput. Commun. Rev. 1999, 29, 29–51. [Google Scholar] [CrossRef]
- Cardillo, A.; Scellato, S.; Latora, V.; Porta, S. Structural properties of planar graph of urban street patterns. Phys. Rev. E 2006, 73, 066107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M. Scientific collaboration networks I: Network construction and fundamental results. Phys. Rev. E 2001, 64, 016131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guelzim, N.; Bottani, S.; Bourgine, P. Topological and causal structure of the yeast transcriptional regulatory network. Nat. Genet. 2002, 31, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Yang, C.; Ferrigno, G.; Momi, E. Improved human-robot collaborative control of redundant robot for teleoperated minimally invasive surgery. IEEE Robot. Autom. Lett. 2019, 4, 1447–1453. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Ovur, S.; Li, Z.; Marzullo, A.; Song, R. Multi-sensor guided hand gestures recognition for teleoperated robot using recurrent neural network. IEEE Robot. Autom. Lett. 2021, 6, 6039–6045. [Google Scholar] [CrossRef]
- Qi, W.; Su, H.; Aliverti, A. A smartphone-based adaptive recognition and real-time monitoring system for human activities. IEEE Trans. Hum.-Mach. Syst. 2020, 50, 414–423. [Google Scholar] [CrossRef]
- Ruan, X.; Ma, L.; Zhang, Y.; Wang, Q.; Gao, X. Dissection of the complex transcription and metabolism regulation networks associated with maize resistance to ustilago maydis. Entropy 2021, 12, 1789. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.; Stewart, I. Coupled oscillators and biological synchronization. Sci. Am. 1993, 269, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Gray, C. Synchronous oscillations in neuronal systems: Mechanisms and functions. J. Comput. Neurosci. 1994, 1, 11–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Chen, L. Synchronizing genetic oscillators by signaling molecules. J. Biol. Rhythm. 2005, 20, 257–269. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; He, H.; Jiang, H. Edge-based adaptive distributed method for synchronization of intermittently coupled spatiotemporal networks. IEEE Trans. Autom. Control 2021. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, H.; Hu, C.; Yu, Z.; Li, Z. Pinning synchronization of complex delayed dynamical networks via generalized intermittent adaptive control strategy. Int. J. Robust Nonlinear Control 2020, 30, 421–442. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, H.; Hu, C. Synchronization of hybrid-coupled delayed dynamical networks via aperiodically intermittent pinning control. J. Frankl. Inst. 2016, 353, 2722–2742. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.; Peng, H.; Yang, Y. Adaptive synchronization of memristor-based BAM neural networks with mixed delays. Appl. Math. Comput. 2018, 322, 100–110. [Google Scholar] [CrossRef]
- Li, J.; Jiang, H.; Hu, C.; Alsaedi, A. Finite/fixed-time synchronization control of coupled memristive neural networks. J. Frankl. Inst. 2019, 356, 9928–9952. [Google Scholar] [CrossRef]
- Ji, G.; Hu, C.; Yu, J.; Jiang, H. Finite-time and fixed-time synchronization of discontinuous complex networks: A unified control framework design. J. Frankl. Inst. 2018, 355, 4665–4685. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, H.; Hu, C. Aperiodically intermittent strategy for finite-time synchronization of delayed neural networks. Neurocomputing 2018, 310, 1–9. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, H.; Hu, C. Finite-time synchronization of delayed dynamical networks via aperiodically intermittent control. J. Frankl. Inst. 2017, 354, 5374–5397. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Wan, P.; Sun, D.; Zhao, M. Finite-time and fixed-time anti-synchronization of Markovian neural networks with stochastic disturbances via switching control. Neural Netw. 2020, 123, 1–11. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Huang, T.; Ouyang, D. Fixed-time stability and stabilization of impulsive dynamical systems. J. Frankl. Inst. 2017, 354, 8626–8644. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Li, C.; Li, Z.; Yang, X. Fixed-time synchronization criteria for complex networks via quantized pinning control. ISA Trans. 2019, 91, 151–156. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Yu, J.; Jiang, H.; Wen, S. Fixed-time synchronization of coupled memristive complex-valued neural networks. Chaos Solitons Fractals 2021, 148, 110993. [Google Scholar] [CrossRef]
- Hu, C.; Jiang, H. Special functions-based fixed-time estimation and stabilization for dynamic systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 99, 1–12. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, H. Global synchronization in fixed time for semi-Markovian switching complex dynamical networks with hybrid couplings and time-varying delays. Nonlinear Dyn. 2019, 95, 2031–2062. [Google Scholar] [CrossRef]
- Cao, J.; Li, R. Fixed-time synchronization of delayed memristor-based recurrent neural networks. Sci. China Inf. Sci. 2017, 03, 032201. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.; Peng, H.; Yang, Y. Fixed-time synchronization of inertial memristor-based neural networks with discrete delay. Neural Netw. 2019, 109, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zeng, Z.; Hu, J.; Wang, X. Controller design for global fixed-time synchronization of delayed neural networks with discontinuous activations. Neural Netw. 2017, 87, 122–131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C.; He, H.; Jiang, H. Fixed/preassigned-time synchronization of complex networks via improving fixed-time stability. IEEE Trans. Cybern. 2021, 51, 2882–2892. [Google Scholar] [CrossRef]
- Hu, C.; Jiang, H. Pinning synchronization for directed networks with node balance via adaptive intermittent control. Nonlinear Dyn. 2015, 80, 295–307. [Google Scholar] [CrossRef]
- Liu, M.; Yu, Z.; Jiang, H.; Hu, C. Synchronization of complex networks with coupled and self-feedback delays via aperiodically intermittent strategy. Asian J. Control 2017, 19, 2062–2075. [Google Scholar] [CrossRef]
- Gong, S.; Guo, Z.; Wen, S.; Huang, T. Finite-time and fixed-time synchronization of coupled memristive neural networks with time delay. IEEE Trans. Cybern. 2021, 51, 2944–2955. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Lu, B.; Li, Z.; Jiang, H.; Hu, C. Fixed-Time Synchronization Control of Delayed Dynamical Complex Networks. Entropy 2021, 23, 1610. https://doi.org/10.3390/e23121610
Liu M, Lu B, Li Z, Jiang H, Hu C. Fixed-Time Synchronization Control of Delayed Dynamical Complex Networks. Entropy. 2021; 23(12):1610. https://doi.org/10.3390/e23121610
Chicago/Turabian StyleLiu, Mei, Binglong Lu, Zhanfeng Li, Haijun Jiang, and Cheng Hu. 2021. "Fixed-Time Synchronization Control of Delayed Dynamical Complex Networks" Entropy 23, no. 12: 1610. https://doi.org/10.3390/e23121610
APA StyleLiu, M., Lu, B., Li, Z., Jiang, H., & Hu, C. (2021). Fixed-Time Synchronization Control of Delayed Dynamical Complex Networks. Entropy, 23(12), 1610. https://doi.org/10.3390/e23121610





