Einstein-Podolsky-Rosen Steering for Mixed Entangled Coherent States
Abstract
1. Introduction
2. Steering, Bell Nonlocality, and Quantum Entanglement
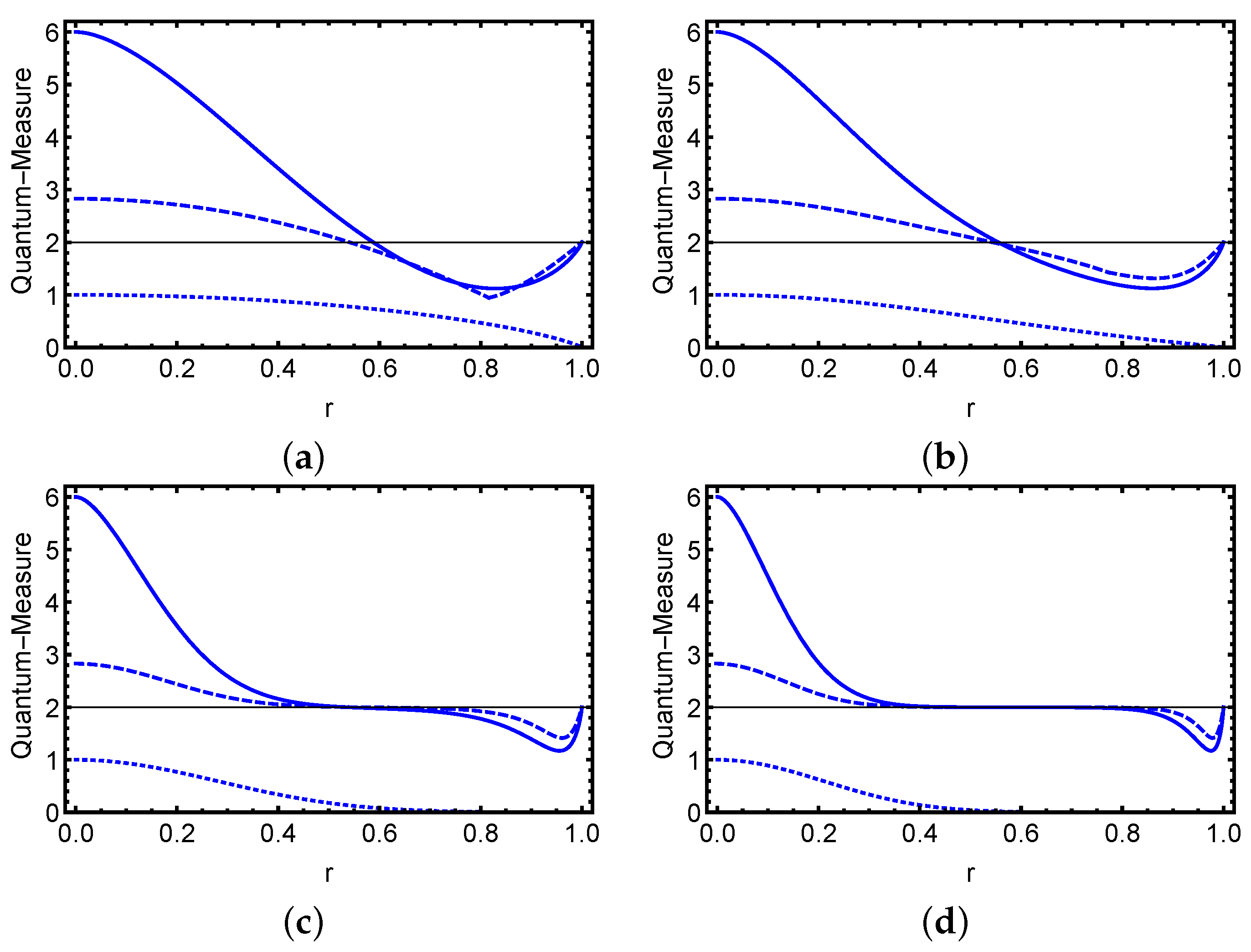
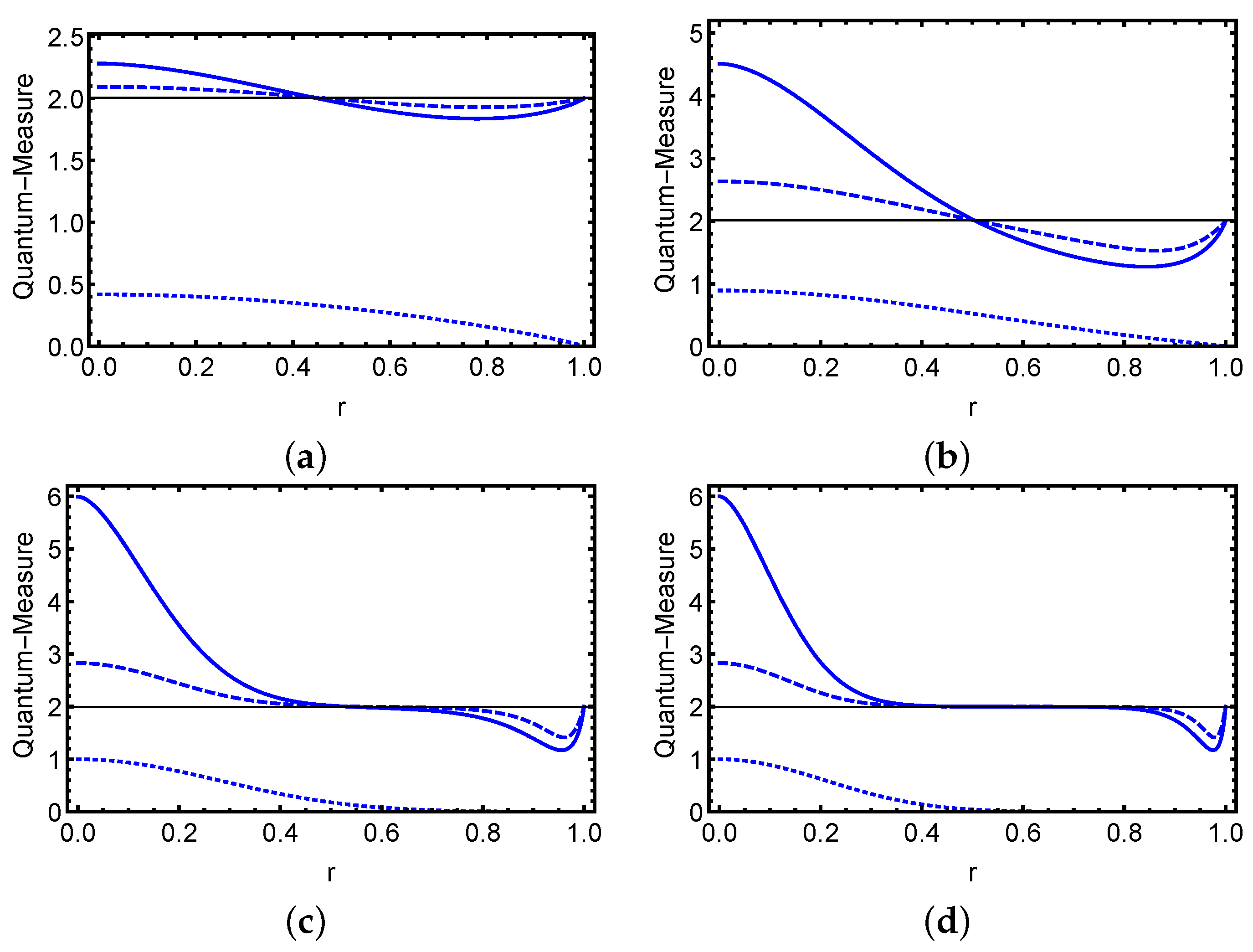
3. Physical System and Dynamics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nilsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Communication; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247. [Google Scholar] [CrossRef]
- Berrada, K. Quantum metrology with SU(1,1) coherent states in the presence of nonlinear phase shifts. Phys. Rev. A 2013, 88, 013817. [Google Scholar] [CrossRef]
- Zheng, S.B.; Guo, G.C. Efficient Scheme for Two-Atom Entanglement and Quantum Information Processing in Cavity QED. Phys. Rev. Lett. 2000, 85, 2392. [Google Scholar] [CrossRef] [PubMed]
- Castelano, L.K.; Fanchini, F.F.; Berrada, K. Open quantum system description of singlet-triplet qubits in quantum dots. Phys. Rev. B 2016, 94, 235433. [Google Scholar] [CrossRef]
- Berrada, K.; Eleuch, H. Noncommutative deformed cat states under decoherence. Phys. Rev. D 2019, 100, 016020. [Google Scholar] [CrossRef]
- Berrada, K. Quantum metrology with classical light states in non-Markovian lossy channels. J. Opt. Soc. Am. B. 2017, 34, 1912. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Schrödinger, E. Probability relations between separated systems. Math. Proc. Camb. Phil. Soc. 1936, 32, 446. [Google Scholar] [CrossRef]
- Wiseman, H.M.; Jones, S.J.; Doherty, A.C. Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox. Phys. Rev. Lett. 2007, 98, 140402. [Google Scholar] [CrossRef] [PubMed]
- Saunders, D.J.; Jones, S.J.; Wiseman, H.M.; Pryde, G.J. Experimental EPR-steering using Bell-local states. Nat. Phys. 2010, 6, 845. [Google Scholar] [CrossRef]
- Wollmann, S.; Walk, N.; Bennet, A.J.; Wiseman, H.M.; Pryde, G.J. Observation of Genuine One-Way Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2016, 116, 160403. [Google Scholar] [CrossRef] [PubMed]
- Gehring, T.; Händchen, V.; Duhme, J.; Furrer, F.; Franz, T.; Pacher, C.; Werner, R.F.; Schnabel, R. Implementation of continuous-variable quantum key. Nat. Commun. 2015, 6, 8795. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, B.; Ramelow, S.; Steinlechner, F.; Langford, N.K.; Brunner, N.; Wiseman, H.M.; Ursin, R.; Zeilinger, A. Loophole-free Einstein–Podolsky–Rosen experiment via quantum steering. New J. Phys. 2012, 14, 053030. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W. Quantum steering borders in three-qubit systems. Quant. Inf. Proc. 2017, 16, 175. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W.; Szczȩśniak, R. Quantum steering and entanglement in three-mode triangle Bose–Hubbard system. Quant. Inf. Proc. 2017, 16, 265. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W.; Peřina, J. Einstein-Podolsky-Rosen steering and coherence in the family of entangled three-qubit states. Phys. Rev. A 2018, 97, 042110. [Google Scholar] [CrossRef]
- Piani, M.; Watrous, J. Necessary and Sufficient Quantum Information Characterization of Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2015, 114, 060404. [Google Scholar] [CrossRef] [PubMed]
- Branciard, C.; Cavalcanti, E.G.; Walborn, S.P.; Scarani, V.; Wiseman, H.M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 2012, 85, 010301. [Google Scholar] [CrossRef]
- He, Q.; Rosales-Zárate, L.; Adesso, G.; Reid, M.D. Secure Continuous Variable Teleportation and Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2015, 115, 180502. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.J.; Wiseman, H.M.; Doherty, A.C. Entanglement, Einstein-Podolsky-Rosen correlations, Bell nonlocality, and steering. Phys. Rev. A 2007, 76, 052116. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Navascués, M.; Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2014, 112, 180404. [Google Scholar] [CrossRef] [PubMed]
- Walborn, S.P.; Salles, A.; Gomes, R.M.; Toscano, F.; Ribeiro, P.S. Revealing Hidden Einstein-Podolsky-Rosen Nonlocality. Phys. Rev. Lett. 2011, 106, 130402. [Google Scholar] [CrossRef] [PubMed]
- Zhen, Y.Z.; Zheng, Y.L.; Cao, W.F.; Li, L.; Chen, Z.B.; Liu, N.L.; Chen, K. Certifying Einstein-Podolsky-Rosen steering via the local uncertainty principle. Phys. Rev. A 2016, 93, 012108. [Google Scholar] [CrossRef]
- Bowles, J.; Vértesi, T.; Quintino, M.T.; Brunner, N. One-way Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2014, 112, 200402. [Google Scholar] [CrossRef]
- He, Q.-Y.; Reid, M.D. Genuine Multipartite Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2013, 111, 250403. [Google Scholar] [CrossRef] [PubMed]
- Cavalcanti, E.G.; Jones, S.J.; Wiseman, H.M.; Reid, M.D. Experimental criteria for steering and the Einstein-Podolsky-Rosen paradox. Phys. Rev. A 2009, 80, 032112. [Google Scholar] [CrossRef]
- Schneeloch, J.; Broadbent, C.J.; Walborn, S.P.; Cavalcanti, E.G.; Howell, J.C. Einstein-Podolsky-Rosen steering inequalities from entropic uncertainty relations. Phys. Rev. A 2013, 87, 062103. [Google Scholar] [CrossRef]
- Żukowski, M.; Dutta, A.; Yin, Z. Geometric Bell-like inequalities for steering. Phys. Rev. A 2015, 91, 032107. [Google Scholar] [CrossRef]
- Hofmann, H.F.; Takeuchi, S. Violation of local uncertainty relations as a signature of entanglement. Phys. Rev. A 2003, 68, 032103. [Google Scholar] [CrossRef]
- Hillery, M.; Zubairy, M.S. Entanglement Conditions for Two-Mode States. Phys. Rev. Lett. 2006, 96, 050503. [Google Scholar] [CrossRef] [PubMed]
- Gillet, J.; Bastin, T.; Agarwal, G.S. Multipartite entanglement criterion from uncertainty relations. Phys. Rev. A 2008, 78, 052317. [Google Scholar] [CrossRef]
- Berrada, K.; Eleuch, H.; Hassouni, Y. Asymptotic dynamics of quantum discord in open quantum systems. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 145503. [Google Scholar] [CrossRef]
- Maziero, J.; Werlang, T.; Fanchini, F.F.; Céleri, C.L.; Serra, R.M. System-reservoir dynamics of quantum and classical correlations. Phys. Rev. A 2010, 81, 022116. [Google Scholar] [CrossRef]
- Werlang, T.; Souza, S.; Fanchini, F.F.; Boas, C.V. Robustness of quantum discord to sudden death. Phys. Rev. A 2009, 80, 024103. [Google Scholar] [CrossRef]
- Fanchini, F.F.; Werlang, T.; Brasil, C.A.; Arruda, L.G.E.; Caldeira, A.O. Non-Markovian dynamics of quantum discord. Phys. Rev. A 2010, 81, 052107. [Google Scholar] [CrossRef]
- Huang, Z.M. Manipulating Einstein-Podolsky-Rosen steering by Quantum-Jump-Based feedback in dissipative environment. Int. J. Theor. Phys. 2018, 57, 3473. [Google Scholar] [CrossRef]
- Huang, Z. Feedback Control on Einstein-Podolsky-Rosen Steering of Dissipative System. Braz. J. Phys. 2019, 49, 215. [Google Scholar] [CrossRef]
- Sun, W.Y.; Wang, D.; Shi, J.-D.; Ye, L. Exploration quantum steering, nonlocality and entanglement of two-qubit X-state in structured reservoirs. Sci. Rep. 2017, 7, 39651. [Google Scholar] [CrossRef]
- Sun, W.-Y.; Wang, D.; Ye, L. How relativistic motion affects Einstein-Podolsky-Rosen steering. Laser Phys. Lett. 2017, 14, 095205. [Google Scholar] [CrossRef]
- Deng, X.; Liu, Y.; Wang, M.; Su, X.; Peng, K. Sudden death and revival of Gaussian Einstein–Podolsky–Rosen steering in noisy channels. npj Quantum Inf. 2021, 7, 65. [Google Scholar] [CrossRef]
- Sun, W.-Y.; Wang, D.; Ding, Z.-Y.; Ye, L. Recovering the lost steerability of quantum states within non-Markovian environments by utilizing quantum partially collapsing measurements. Laser Phys. Lett. 2017, 14, 12. [Google Scholar] [CrossRef]
- Cavalcanti, E.G.; He, Q.Y.; Reid, M.D.; Wiseman, H.M. Unified criteria for multipartite quantum nonlocality. Phys. Rev. A 2011, 84, 032115. [Google Scholar] [CrossRef]
- Costa, A.C.S.; Angelo, R.M. Quantification of Einstein-Podolsky-Rosen steering for two-qubit states. Phys. Rev. A 2016, 93, 020103. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M. Violating Bell inequality by mixed states: Necessary and sufficient condition. Phys. Lett. A 1995, 200, 340. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Ourjoumtsev, A.; Ferreyrol, F.; Tualle-Brouri, R.; Grangier, P. Preparation of non-local superpositions of quasi-classical light states. Nat. Phys. 2009, 5, 189. [Google Scholar]
- Eleuch, H.; Bennaceur, R. Nonlinear dissipation and the quantum noise of light in semiconductor microcavities. J. Opt. B Quantum Semiclass. Opt. 2004, 6, 189. [Google Scholar] [CrossRef]
- van Enk, S.J.; Hirota, O. Entangled coherent states: Teleportation and decoherence. Phys. Rev. A 2001, 64, 022313. [Google Scholar] [CrossRef]
- Sanders, B.C. Entangled coherent states. Phys. Rev. A 1992, 45, 6811. [Google Scholar] [CrossRef] [PubMed]
- Gerry, C.C. Generation of Schrödinger cats and entangled coherent states in the motion of a trapped ionby a dispersive interaction. Phys. Rev. A 1997, 55, 2478. [Google Scholar] [CrossRef]
- Solano, E.; Agarwal, G.S.; Walther, H. Strong-driving-assisted multipartite entanglement in cavity QED. Phys. Rev. Lett. 2003, 90, 027903. [Google Scholar] [CrossRef]
- Paternostro, M.; Kim, M.D. Generation of entangled coherent states via cross-phasemodulation in a double electromagnetically induced transparency regime. Phys. Rev. A 2003, 67, 023811. [Google Scholar] [CrossRef]
- Armour, A.D.; Blencowe, M.P.; Schwab, K.C. Entanglement and decoherence of a micromechanical resonator via coupling to a Cooper-Pair box. Phys. Rev. Lett. 2002, 88, 148301. [Google Scholar] [CrossRef]
- Bose, S.; Agarwal, G.S. Entangling pairs of nano-cantilevers, Cooper-pair boxes and mesoscopic teleportation. New J. Phys. 2006, 8, 34. [Google Scholar] [CrossRef]
- Wang, X. Quantum teleportation of entangled coherent states. Phys. Rev. A 2001, 64, 022302. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, M.S.; Lee, J. Quantum-information processing for a coherent superposition state via a mixedentangled coherent channel. Phys. Rev. A 2001, 64, 052308. [Google Scholar] [CrossRef]
- Fu, H.; Wang, X.; Solomon, A.I. Maximal entanglement of nonorthogonal states: Classification. Phys. Lett. A. 2001, 291, 73–76. [Google Scholar] [CrossRef][Green Version]
- Dodonov, V.V.; Malkin, I.A.; Man’ko, V.I. Even and odd coherent states and excitations of a singular oscillator. Physica 1974, 72, 597. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Khalek, S.; Berrada, K.; Algarni, M.; Eleuch, H. Einstein-Podolsky-Rosen Steering for Mixed Entangled Coherent States. Entropy 2021, 23, 1442. https://doi.org/10.3390/e23111442
Abdel-Khalek S, Berrada K, Algarni M, Eleuch H. Einstein-Podolsky-Rosen Steering for Mixed Entangled Coherent States. Entropy. 2021; 23(11):1442. https://doi.org/10.3390/e23111442
Chicago/Turabian StyleAbdel-Khalek, Sayed, Kamal Berrada, Mariam Algarni, and Hichem Eleuch. 2021. "Einstein-Podolsky-Rosen Steering for Mixed Entangled Coherent States" Entropy 23, no. 11: 1442. https://doi.org/10.3390/e23111442
APA StyleAbdel-Khalek, S., Berrada, K., Algarni, M., & Eleuch, H. (2021). Einstein-Podolsky-Rosen Steering for Mixed Entangled Coherent States. Entropy, 23(11), 1442. https://doi.org/10.3390/e23111442





