Anti-Quantum Lattice-Based Ring Signature Scheme and Applications in VANETs
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivation
1.3. Our Contribution
- (1)
- Combining lattice-based cryptography with a ring signature, we construct a secure lattice-based ring signature under the random oracle model. The proposed scheme satisfies unconditional anonymity and unforgeability. The unforgeability of the proposed ring signature scheme is reduced to the difficult assumption of the small integer solution (SIS) on the lattice.
- (2)
- Our scheme also provides a certain degree of unconditional anonymity for ring members and ensures signature unforgeability.
- (3)
- We give a detailed performance analysis and provide applications of our scheme in VANETs, and the results show that our scheme is significantly better than the ongoing schemes. Our scheme satisfies security requirements in VANETs.
1.4. Outline
2. Preliminaries
2.1. Notations
2.2. Lattices and Lattice Problems
2.3. Hard Problems for q-ary Lattices
2.4. Chameleon Hash Function
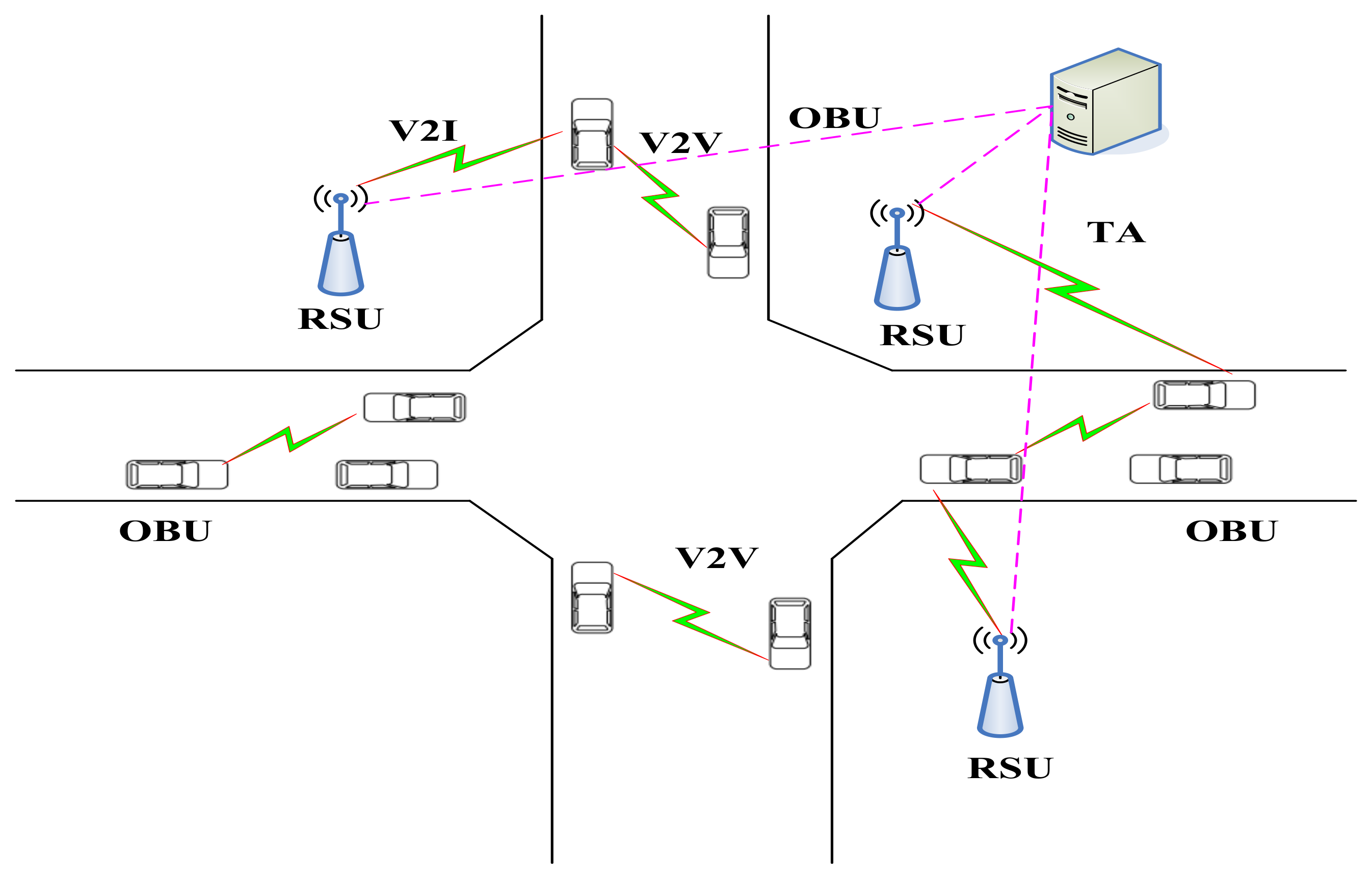
3. System Models
3.1. Basic Model
3.2. Threat Model
- (1)
- creates a group of public parameters , a ring , two secret keys (, and a message .
- (2)
- is permitted to make ring-signing queries and corruption queries. responds with as a ring-signing query. The signer of an index performs a corruption query. Finally, sends to .
- (3)
- requests a challenge to with the values ; calculates two challenge signatures.and ; responds to with , .
- (4)
- responds a guess and wins the game if .
- (1)
- creates a group of public parameters , a ring , two secret keys (, and a message .
- (2)
- is permitted to make ring-signing queries and corruption queries. responds with as a ring-signing query. The signer of an index performs a corruption query. Finally, sends to .
- (3)
- sends the result to the challenger, and is considered as successful if , where .
4. The Proposed Scheme Description
| Algorithm 1 KeyGen algorithm |
| Input: A security parameter Output: The public parameters 1: Let and be a prime number; 2: Define three sets , hash function , and nearly injective mapping ; 3: Set and such that ; 4: Set ; |
| 5: Output . |
- (1)
- For all , calculate , where .
- (2)
- Calculate and .
- (3)
- Pick a random bit ; calculate , where .
- (4)
- For , compute .
- (5)
- Publish .
| Algorithm 2 Ring-signing algorithm |
| Input: A message , a long-term key , public keys Output: The signature 1: Calculate , , where ; 2: Calculate and ; 3: For and , compute ; 4: Pick ; compute , where ; 5: Continue the next steps with probability , otherwise Restart; 6: Output . |
- (1)
- (2)
| Algorithm 3 Ring-verify algorithm |
| Input: The signature ; public keys Output: Accept or Reject 1: If , then continue; 2: else if , then continue; 3: else if , then continue; 4: else if , then Accept, else Reject; 5: Output Accept or Reject. |
5. Correctness and Security Analysis
5.1. Correctness
5.2. Security Analysis
- (1)
- For all , calculate , , where .
- (2)
- Calculate and .
- (3)
- Pick a random bit ; calculate , where .
- (4)
- For , compute .
- (5)
- Publish .
6. Performance Evaluation
6.1. Parameter Selection
6.2. Efficiency Analysis
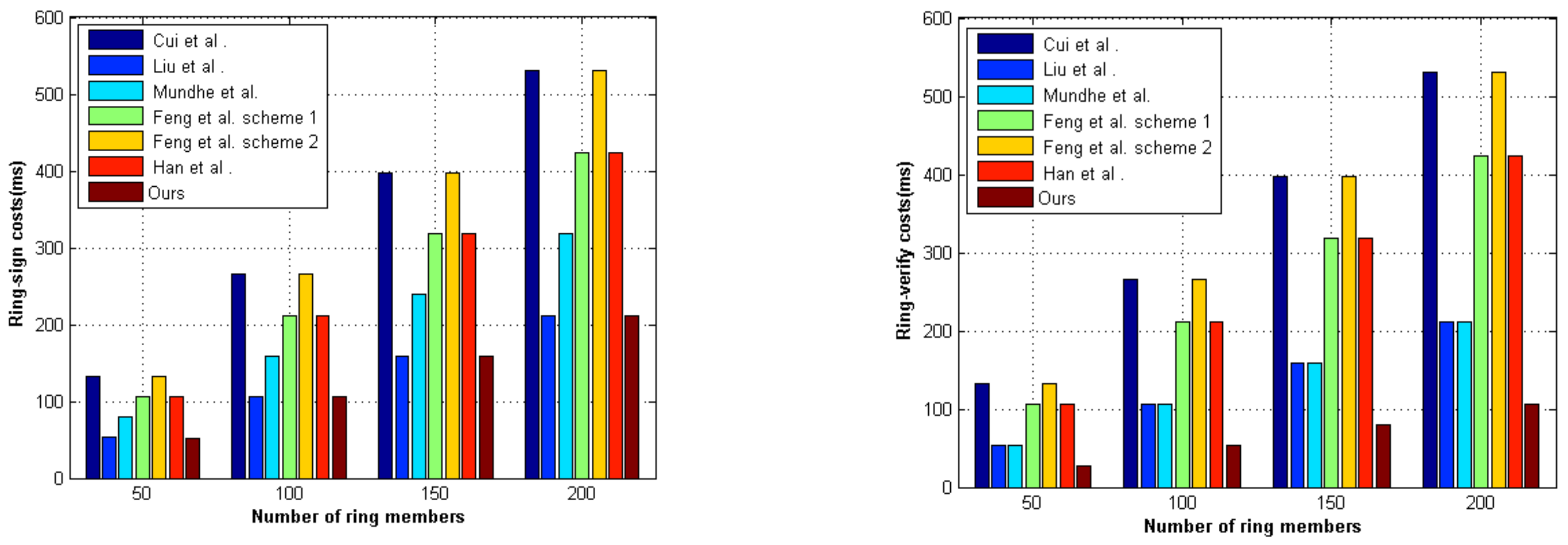
6.3. Performance Comparison
7. Sharper Ring Rignatures
- (1)
- Set and such that .
- (2)
- For all , calculate , where .
- (3)
- Calculate , where denotes high-order bits of .
- (4)
- Calculate .
- (5)
- Pick a random bit ; calculate , where .
- (6)
- For , compute .
- (7)
- Publish .
- (1)
- (2)
8. Applications in VANETs
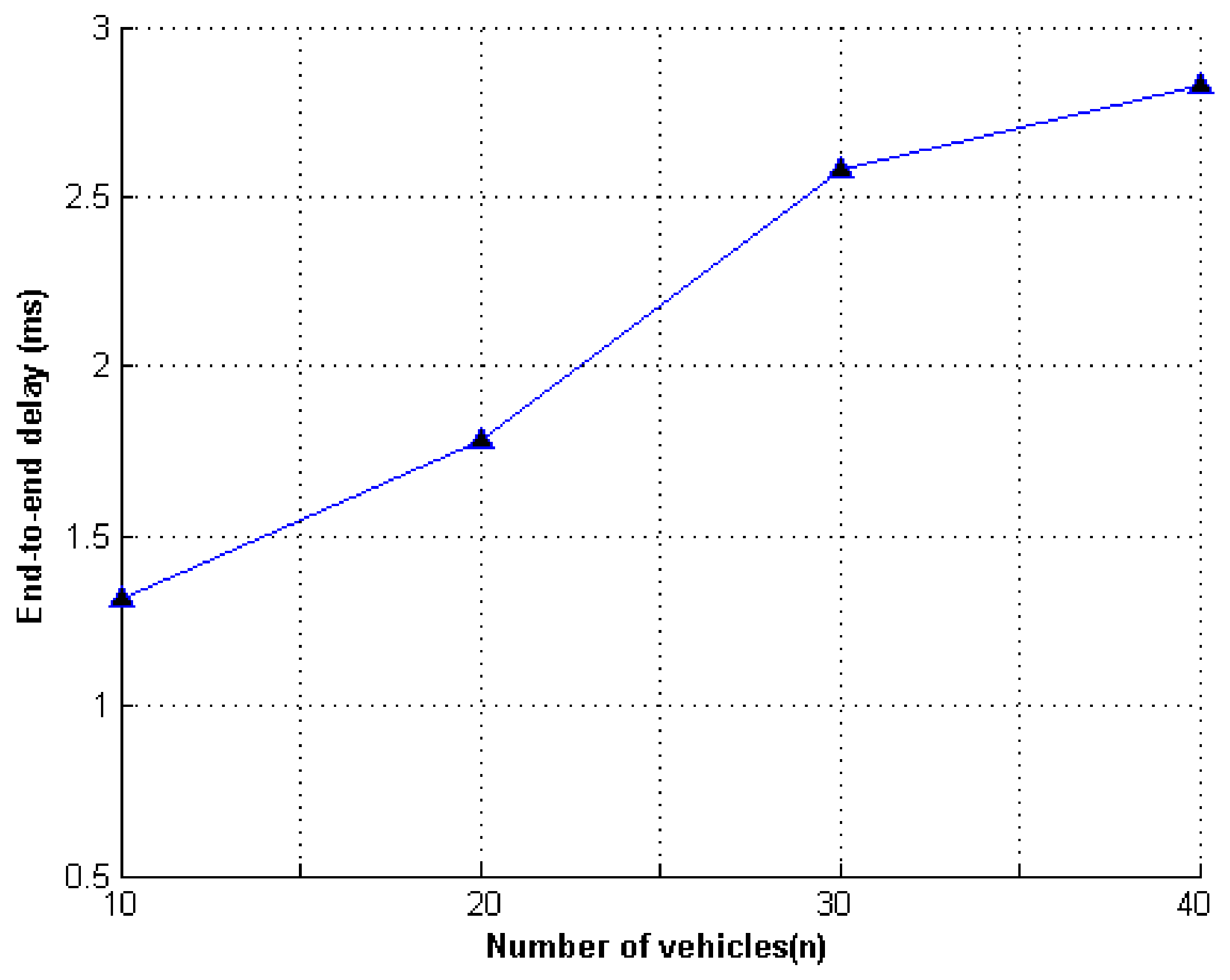
8.1. Experimental Simulation
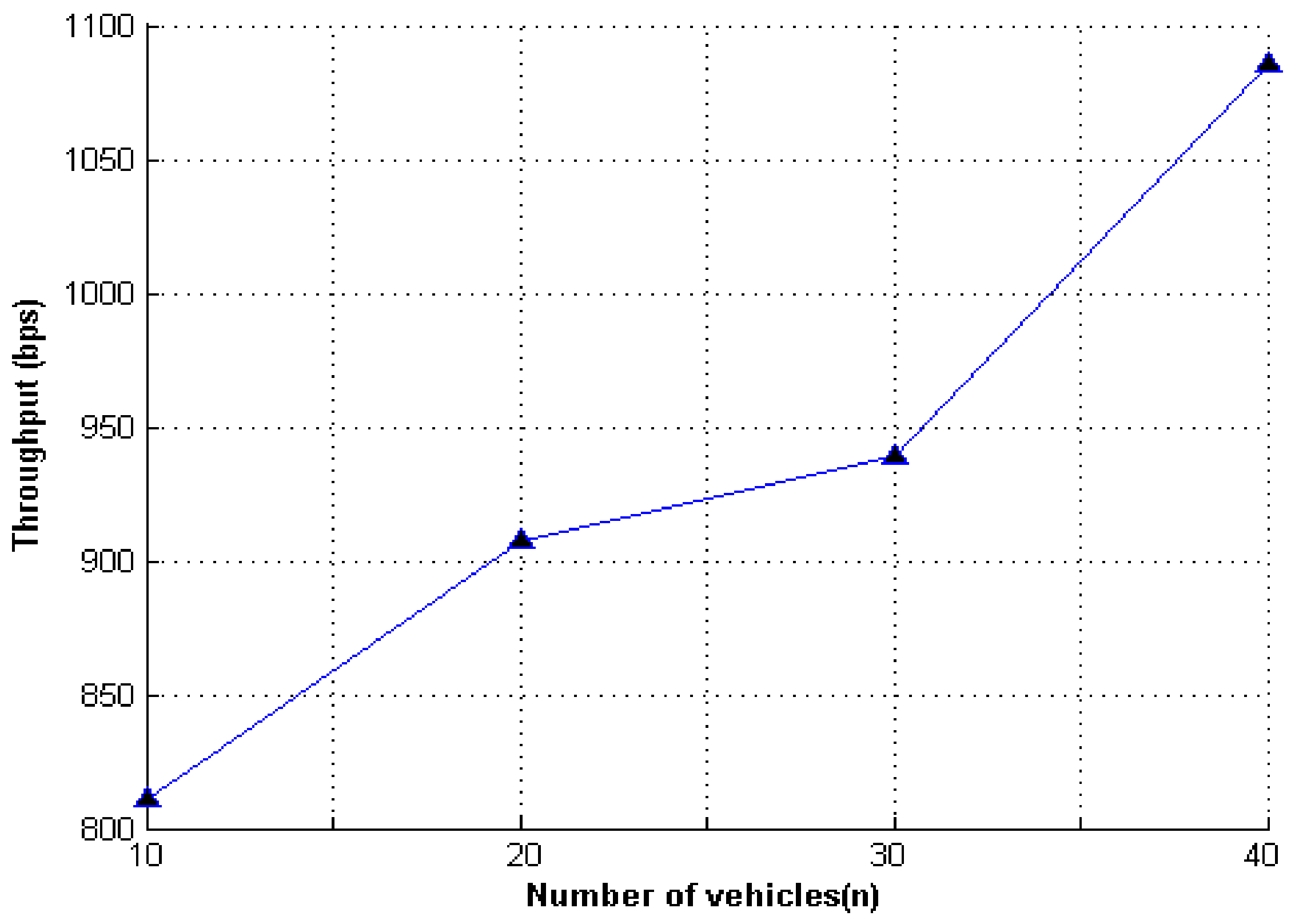
8.2. Simulation Results
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chaum, D.; Van Heyst, E. Group Signatures. In Eurocrypt; Cramer, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3494, pp. 457–473. [Google Scholar]
- Rivest, R.; Shamir, A.; Tauman, Y. How to Leak a Secret, Advances in Cryptology-ASIACRYPT 2001; Laboratory for Computer Science, Massachusetts Institute of Technology: Cambridge, MA, USA, 2001. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 10 September 2021).
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the 40th Annual ACM Symposium on Theory of Computing STOC’08, Victory, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]
- Buchmann, J.; Lindner, R.; Ruckert, M.; Schneider, M. Post-quantum cryptography: Lattice signatures, computing. Computing 2009, 86, 105–125. [Google Scholar] [CrossRef] [Green Version]
- Boyen, X. Lattice mixing and vanishing trapdoors: A framework for fully secure short signatures and more. In Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2010; pp. 499–517. [Google Scholar]
- Brakerski, Z.; Kalai, Y.T. A framework for efficient signatures, ring signatures and identity-based encryption in the standard model. IACR Cryptol. ePrint Arch. 2010, 2010, 86. [Google Scholar]
- Liu, J.K.; Au, M.H.; Susilo, W.; Zhou, J. Linkable ring signature with unconditional anonymity. IEEE Trans. Knowl. Data Eng. 2014, 26, 157–165. [Google Scholar] [CrossRef]
- Duan, J.; Gu, L.; Zheng, S. ARCT: An efficient aggregating ring confidential transaction protocol in blockchain. IEEE Access 2020, 8, 198118–198130. [Google Scholar] [CrossRef]
- Jia, H.; Tang, C.; Zhang, Y. Lattice-based logarithmic-size non-interactive deniable ring signatures. Entropy 2021, 23, 980. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Tang, D.; Yang, H.; Li, F. A public key encryption scheme based on a new variant of LWE with small cipher size. J. Syst. Archit. 2021, 117, 102165. [Google Scholar] [CrossRef]
- Xiang, X.Y.; Li, H.; Wang, M.Y.; Zhao, X.W. Efficient multi-party concurrent signature from lattices. Inf. Process. Lett. 2016, 116, 497–502. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, R. Lattice-based ring signature scheme under the random oracle model. Int. J. High-Perform. Comput. Netw. 2018, 11, 332–341. [Google Scholar] [CrossRef]
- Torres, A.; Steinfeld, R.; Sakzad, A.; Liu, J.K.; Kuchta, V.; Bhattacharjee, N.; Au, M.H.; Cheng, J. Post-quantum one-time linkable ring signature and application to ring confidential transactions in blockchain (lattice ringct v1.0). In Proceedings of the Australasian Conference on Information Security and Privacy, Wollongong, Australia, 11–13 July 2018; Volume 2018, p. 379. Available online: http://eprint.iacr.org/2018/379.pdf (accessed on 10 September 2021).
- Torres, W.A.; Kuchta, V.; Steinfeld, R.; Sakzad, A.; Liu, J.K.; Cheng, J. Lattice RingCT v2.0 with multiple input and multiple output wallets. IACR Cryptol. ePrint Arch. 2019, 2019, 569. [Google Scholar]
- Cui, Y.; Cao, L.; Zhang, X.; Zeng, G. Ring signature based on lattice and VANET privacy preservation. Chin. J. Comput. 2017, 40, 1–14. [Google Scholar]
- Liu, J.; Yu, Y.; Jia, J.; Wang, S.; Fan, P.; Wang, H.; Zhang, H. Lattice-based double-authentication-preventing ring signature for security and privacy in vehicular ad-hoc networks. Tsinghua Sci. Technol. 2019, 24, 575–584. [Google Scholar] [CrossRef]
- Esgin, M.F.; Steinfeld, R.; Sakzad, A.; Liu, J.K.; Liu, D. Short lattice-based one-out-of-many proofs and applications to ring signatures. In Applied Cryptography and Network Security—ACNS 2019; Springer: Cham, Germany, 2019; pp. 67–88. [Google Scholar]
- Groth, J.; Kohlweiss, M. One-out-of-many proofs: Or how to leak a secret and spend a coin. In Advances in Cryptology—EUROCRYPT 2015, Part II; Springer: Berlin/Heidelberg, Germany, 2015; pp. 253–280. [Google Scholar]
- Langlois, A.; Stehle, D. Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 2015, 75, 565–599. [Google Scholar] [CrossRef]
- Feng, H.; Liu, J.; Li, D.; Li, Y.-N.; Wu, Q. Traceable ring signatures: General framework and post-quantum security. Des. Codes Cryptogr. 2021, 89, 1111–1145. [Google Scholar] [CrossRef]
- Ajtai, M. Determinism versus non-determinism for linear time RAMs (extended abstract). In Proceedings of the 31st Annual ACM Symposium on Theory of Computing, Atlanta, GA, USA, 1–4 May 1999; ACM Press: New York City, NY, USA, 1999; pp. 632–641. [Google Scholar]
- Micciancio, D.; Regev, O. Worst-case to average-case reductions based on Gaussian measures. In Proceedings of the 45th Annual Symposium on Foundations of Computer Science, Rome, Italy, 17–19 October 2004; IEEE Computer Society Press: Piscataway, NJ, USA, 2004; pp. 372–381. [Google Scholar]
- Lyubashevsky, V. Lattice signatures without trapdoors. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, Y.; Liu, Y.; Guo, Y.; Zheng, S.; Wang, L. Adaptively secure efficient (H)IBE over ideal lattice with short parameters. Entropy 2020, 22, 1247. [Google Scholar] [CrossRef] [PubMed]
- Ducas, L.; Durmus, A.; Lepoint, T.; Lyubashevshy, V. Lattice signatures and bimodal gaussians. In Advances in Cryptology-CRYPTO 2013; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8042, pp. 40–56. [Google Scholar]
- Mundhe, P.; Yadav, V.K.; Verma, S.; Venkatesan, S. Efficient lattice-based ring signature for message authentication in VANETs. IEEE Syst. J. 2020, 14, 5463–5474. [Google Scholar] [CrossRef]
- Han, L.; Cao, S.; Yang, X.; Zhang, Z. Privacy protection of VANET based on traceable ring signature on ideal lattice. IEEE Access 2020, 8, 206581–206591. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Fang, Y. A conditional privacy protection scheme based on ring signcryption for vehicular Ad Hoc networks. IEEE Internet Things J. 2021, 8, 647–656. [Google Scholar] [CrossRef]
- Cao, J.; Yu, P.; Xiang, X.; Ma, M.; Li, H. Anti-quantum fast authentication and data transmission scheme for massive devices in 5G NB-IoT system. IEEE Internet Things J. 2019, 6, 9794–9805. [Google Scholar] [CrossRef]
- Secure Hash Standard. FIPS PUB 180-1, National Institute of Standards and Technology (NIST), U.S. Department of Commerce, April 1995. Available online: http://csrc.nist.gov/publications/fips/fips1802/fips180-2.pdf (accessed on 20 July 2018).

| Parameter | Description | Sample |
|---|---|---|
| Polynomial ring degree | 512 | |
| Large prime | ||
| Polynomial ring size | 6 | |
| Security parameter | 100 | |
| Hermite factor | 1.007 | |
| Random Oracle weight | 14 | |
| Correctness | 1.1 | |
| Rejection sampling | 45 | |
| Rejection sampling | 1.0027 | |
| Gaussian standard deviation | ||
| Rejection sampling | 1.0027 | |
| Gaussian standard deviation | ||
| Rejection sampling | 1.0027 | |
| Public key size | 4992 KB | |
| Secret key size | 4992 KB | |
| Signature size | 672 KB |
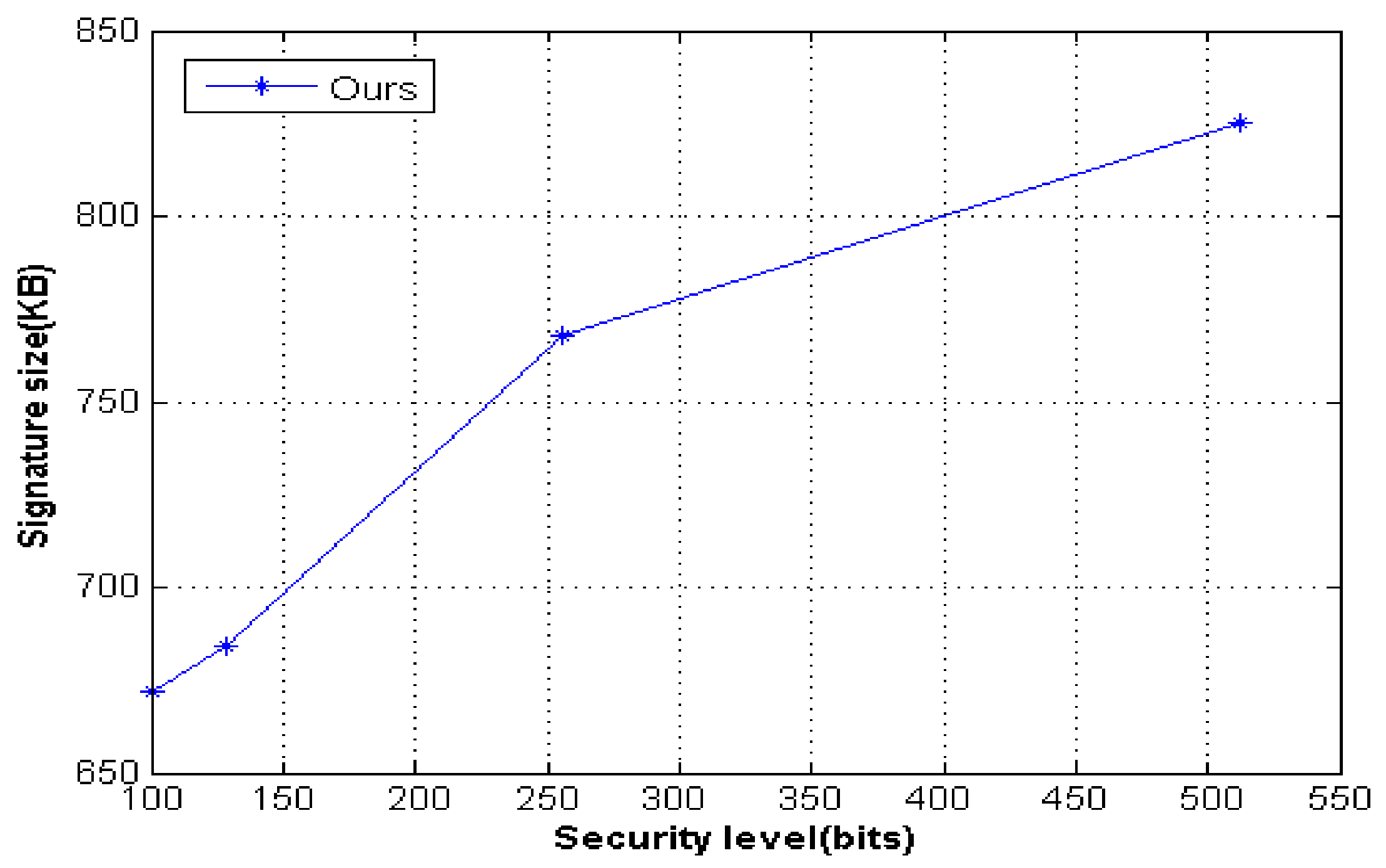
| Security Level (bits) | Signature Size (KB) |
|---|---|
| 100 | 672 |
| 128 | 684 |
| 256 | 768 |
| 512 | 825 |
| Schemes | Ring-Sign Costs | Ring-Verify Costs | Signature Length |
|---|---|---|---|
| Cui et al. [16] | |||
| Liu et al. [17] | |||
| Mundhe et al. [27] | |||
| Feng et al. [21] scheme 1 | |||
| Feng et al. [21] scheme 2 | |||
| Han et al. [28] | |||
| Ours |
| Schemes | Unconditional Anonymity | Strong Unforgeability | Message Integrity |
|---|---|---|---|
| Wang et al. [11] | No | Yes | Yes |
| Cui et al. [16] | No | No | Yes |
| Liu et al. [17] | No | No | Yes |
| Mundhe et al. [27] | Yes | No | Yes |
| Feng et al. [21] | No | No | Yes |
| Han et al. [28] | Yes | Yes | Yes |
| Cai et al. [29] | No | No | Yes |
| Ours | Yes | Yes | Yes |
| Parameter | Value |
|---|---|
| Speed of vehicle | 20 km/h |
| Transmission range | 100 m |
| Time interval | 2 s |
| MAC type | IEEE 802.11p |
| Number of lanes | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, C.; Xiang, X. Anti-Quantum Lattice-Based Ring Signature Scheme and Applications in VANETs. Entropy 2021, 23, 1364. https://doi.org/10.3390/e23101364
Jiao C, Xiang X. Anti-Quantum Lattice-Based Ring Signature Scheme and Applications in VANETs. Entropy. 2021; 23(10):1364. https://doi.org/10.3390/e23101364
Chicago/Turabian StyleJiao, Chunhong, and Xinyin Xiang. 2021. "Anti-Quantum Lattice-Based Ring Signature Scheme and Applications in VANETs" Entropy 23, no. 10: 1364. https://doi.org/10.3390/e23101364
APA StyleJiao, C., & Xiang, X. (2021). Anti-Quantum Lattice-Based Ring Signature Scheme and Applications in VANETs. Entropy, 23(10), 1364. https://doi.org/10.3390/e23101364




