3.1. Locally and Independently Generated Randomness
To discuss indeterminism in the framework of SR, and rephrase Rietdijk’s and Putnam’s argument, we introduce the concept of a True Random Number Generator (TRNG), by which we mean an abstract device that outputs genuinely random bits. Namely, before each bit is output, its value is not only unknown (epistemic uncertainty), but it actually has no determined value (ontic indeterminacy), even though there might be a probability distribution associated with the outcome to be realized (in principle, both at the epistemic and at the ontic level). More precisely, even having complete knowledge of (i) the
state—i.e., the values of all the variables that may influence the outcome of the TRNG (this can be, in principle, everything that lies in the past light-cone of the event associated to the generation of the bit)—and (ii) of the
dynamical laws that rule the evolution of each and every of the said variables, there is no way to predict with certainty which will be value of the bit output by the TRNG, not even in principle (see
Table 1).
This is what we mean by true randomness, which clearly entails indeterminism. In what follows, we will be concerned solely with the (ontic) indeterminacy that each bit has before it is output and acquires a definite value (on the contrary, we will not consider what dynamical laws—deterministic or otherwise—govern the evolution of the considered systems). This very concept can be expressed in terms of truth values of empirical propositions, such that the statement, e.g., “the value of the bit
j output by the TRNG at time
(in a certain reference frame) is
” has a definite truth value, either true or false, only after
, whereas it was (ontologically) indeterminate before, i.e., its truth value is neither true nor false (see also [
24]). (We refer to propositions (or statements) as
empirical because they are about the values taken by physical variables, i.e., outcomes of hypothetical experiments; however, in principle, we will not immediately disregard those statements that refer to indirectly empirically accessible quantities (e.g., a joint proposition about two outcomes of experiments conducted in spacelike separation), which instead would be meaningless to genuine empiricists because they are unverifiable). Note that this makes the law of the excluded middle of classical logic fail, so it relates the concept of indeterminacy to mathematical intuitionism (see [
11,
25]).
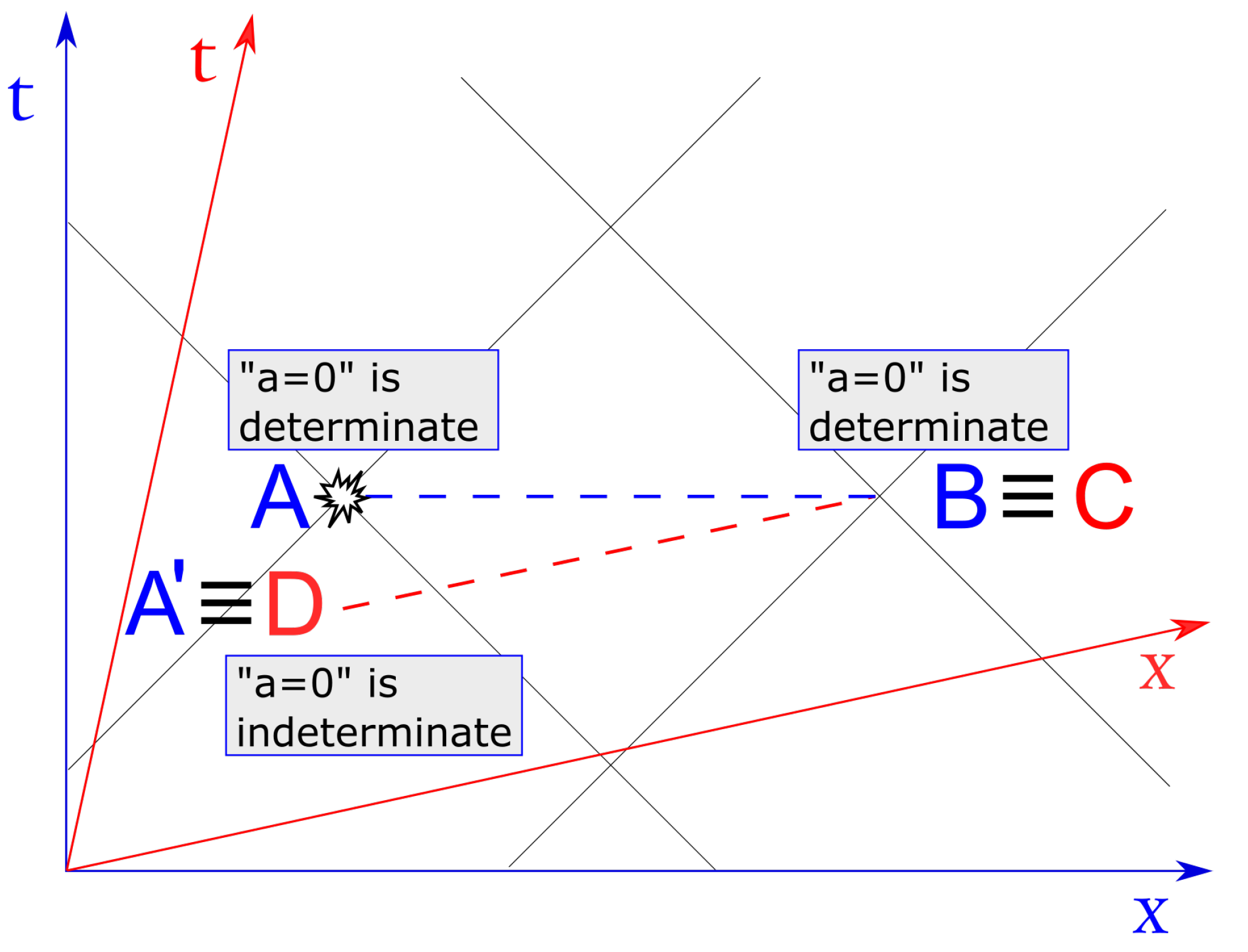
Turning now to SR, with reference to
Figure 1, let us consider four inertial observers—Alice, Bob, Charlie, and Debbie. Assume that Alice has a TRNG that outputs a fresh random bit every minute (locally in her inertial reference frame). Assume also that Bob, at rest in Alice’s frame, is located at a certain fixed distance from Alice, e.g., one minute away at light speed (one light-minute). Charlie and Debbie, at relative rest, move at a constant speed
v with respect to Alice’s and Bob’s frame. All parties know that Alice’s TRNG outputs a fresh random bit every minute in her frame, i.e., every
minutes in Charlie’s and Debbie’s reference frame. Moreover, the positions and velocity
v are tailored such that at 1:00 p.m. in both reference frames, Charlie’s position lies on Bob’s world-line (point
in
Figure 1), while Debbie’s position overlaps with Alice’s world-line (point
in
Figure 1).
Let us denote by the bit output by Alice’s TRNG at 1:00 p.m. in her reference frame. As explained above, by the very nature of a TRNG, at any time instant before 1:00 p.m., the proposition “” has no truth value for Alice (nor for any possible observer for that matter) but rather, is fundamentally indeterminate. Yet, at 1:00 p.m., Alice’s TRNG outputs a fresh bit that now becomes determined for Alice. Is the value of this bit determined for Bob as well? One may be tempted to answer in the positive (as in fact, Rietdijk and Putnam do), since the events happening at Alice’s and Bob’s locations, respectively, are simultaneous in their rest frames. Of course, Bob may not know the value of a because Alice may not have communicated it, or, more fundamentally, because Bob is spacelike separated from Alice; however, does the proposition “” have a truth value or is it indeterminate for Bob?
Since at 1:00 p.m., Bob and Charlie are next to each other—ideally they exactly overlap at the same location—it is plausible to assume that the proposition “” has the same truth value for both of them (since this is empirically testable, there is actually no room for any alternatives at the ontological level). Hence, let us assume it has a determinate truth value for Charlie as well. However, by applying the same reasoning as before, this implies that the proposition also has a truth value at all locations simultaneous to Charlie in his inertial frame, thus, it must be determinate for Debbie too. Yet, given the relative motion between the two reference frames, Debbie overlaps with Alice’s world line at the space-time point , where her TRNG has not yet outputted the bit. Hence, following this chain of inferences, “” had already a definite truth value before Alice’s TRNG outputs the bit a, which is a contradiction with the assumption of a TRNG. From this contradiction, Rietdijk and Putnam concluded that, in general, the structure of SR does not allow for indeterminate events.
The previous argument, however, relies on two assumptions that seem prima facie innocuous, which originate from an intuitive extension of classical concepts to a relativistic scenario. In fact, these assumptions are introduced to characterize what it means for two (or more) observers to share a determinate reality (in terms of truth values of propositions). Their assumptions can be made explicit as follows:
Local reality: Any two observers that locally overlap attribute the same truth values to empirical propositions (including the value “indeterminate”).
Present reality: Any two distant observers at relative rest attribute the same truth values (including the value “indeterminate”) to empirical propositions about present events (i.e., lying on the same plane of simultaneity in their rest frame).
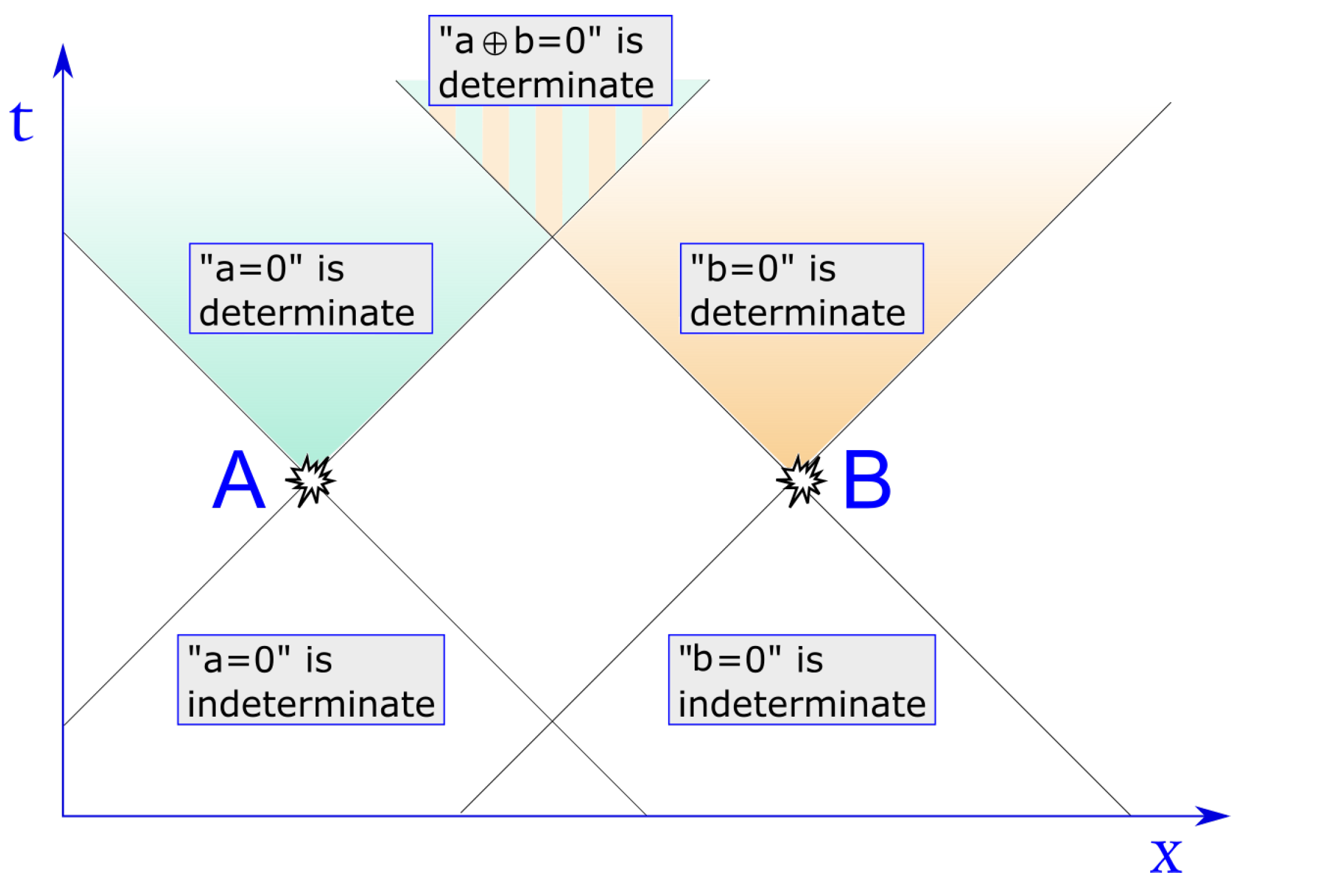
However, while the former of these assumptions may still be upheld in SR because any two observers can operationally verify the consistency of their attributed truth values locally, the latter assumption becomes questionable. Indeed, we maintain that the finiteness of the maximum speed of propagation of any piece of information renders also determinacy (i.e., the definiteness of the truth values of empirical statements), a property relative to specific regions of space-time. This can be seen by taking any binary function (e.g., the sum modulo 2) of the statements describing the outcomes of local physical processes taking place at distant locations (e.g., the output bits of two distant TRNG’s). Thus, it becomes a straightforward assumption that determinacy itself propagates in space at the maximal signal velocity, i.e., instantaneously in Newtonian physics, but at a finite speed (that of light) according to relativity. This is where Rietdijk and Putnam’s argument fails, in the assumption that truth values are always shared by observers lying on the same plane of simultaneity, even though this is not verifiable except for the region enclosed within the intersection of their future light-cones. Hence, in short, (in)determinacy is relative.
In our simple example, this means that at 1:00 p.m., the proposition “
” has no definite truth value for Bob, nor for Charlie, but it is for them still indeterminate, as it was for Alice before 1:00 p.m. It is only one minute later, i.e., at 1:01 p.m., that “
” acquires a definite truth value for Bob, though Bob may still not know this value. For instance, if Bob also holds a TRNG—here assumed to generate randomness locally and independently of Alice’s TRNG—which also outputs a fresh random bit, denoted by
b, every minute; then, the value of their sum modulo 2,
, is indeterminate everywhere until 30 s after 1:00 p.m. (in their common inertial frame), and the proposition “
” has no truth value, i.e., is indeterminate, until then (see
Figure 2).
The present rebuttal of Rietdijk’s and Putnam’s argument is in agreement with that put forward by Stein [
26], who also argued for the notion of indeterminacy relative to a space-time point and pointed out the inadequacy of what we have named
present reality. However, his argument differed from ours inasmuch as it was based on some anthropic considerations on the distance that light can travel within an interval of time that we can perceive as present. Moreover, our view of relative determinacy is also similar to that of Savitt, who—without directly addressing Rietdijk’s and Putnam’s argument—put forward the idea that “special relativistic transience is the successive occurrence of local
nows along a timelike curve.” [
27]. Further, Myrwold [
28] discussed the compatibility between relativity and the openness of future (indeterminacy) in the context of objective collapse models of quantum mechanics. Finally, Healey [
29] reached a similar conclusion to our relativity of (in)determinacy. However, he used a pragmatist view (which, in contrast to our position, takes probabilities to be relative to hypothetical agents in a specific physical situation, rather than objective propensities) to claim that the assignment of quantum states (and thus, the probabilistic predictions they entail) should be specified relative to different hypothetical observers located at distant space-time regions, in a relativistic scenario.
3.2. “Classical” Correlated Randomness
In the previous section, we argued that contrarily to a well-known philosophical argument, indeterminism and relativity remain compatible, insofar as the (in)determinacy of the values taken by physical variables, each measured by a distinct relativistic observer, is relative. So far, however, we have limited our analysis to the assumption that each TRNG generates random bits at its local position and independently from any other random generators. Yet, one can, in principle, envision a form of “classical” correlated randomness between two or more TRNG’s, which will help bridge the gap between the classical and the quantum case. (Here, by “classical” we mean without introducing the structure of quantum probabilities, but merely consider systems whose outcomes are correlated through randomness).
Let us thus consider once more two distant observers, Alice and Bob, each provided with a TRNG such that their respective bits
a and
b take one of their two possible values with equal probability, i.e.,
. However, when considered jointly, some correlations between the bits outputted by the two TRNGs may have been established. (We do not discuss possible physical mechanisms that may establish these kinds of correlations, but we assume that in principle these can exist). For example, although at the local level the values of the bits are random with uniform distribution, there could be a bias towards certain joint results. For instance, the cases when their values are the same could occur with a higher probability, e.g.,
. One can think that at the ontological level there is a physical property such as a (nonlocal) propensity—i.e., an objective tendency that quantifies the bias towards the possible realization of an indeterministic outcome—that accounts for the correlations between the two TRNGs. (This is inspired by the propensity interpretation of probability, which was introduced by Popper [
30]; see also [
5] for a recent application of this concept to indeterministic physics). Due to the spacelike separation between Alice and Bob, there exist inertial reference frames in which Alice’s TRNG generates a random bit, say
, before Bob’s one (which thus remains indeterminate in such reference frames). However, because of the correlations between TRNG’s, within the future light-cone of Alice, the propensity for Bob to find the outcome 0 is updated from
to
. On the other hand, in a reference frame in which the realization of a fresh bit by Bob’s TRNG comes first, it is the propensity for the outcome of Alice’s TRNG that is updated according to the established correlations. Note that the realization of a fresh bit by a local TRNG, say, on Alice’s side, does not directly affect the value of the bits generated on Bob’s side (otherwise, this could be used to signal). It is Alice’s propensity for the outcome of Bob’s TRNG that is updated, such that if she obtains
, within her future light-cone, the propensity associated with the statement
will change (to 3/4 in this case). In this way, when Alice’s bit becomes determinate, the propensity for the value of
b relative to Alice’s future light cone also becomes determinate, but not the value of
b. It is only within the intersection of the future light-cones of Alice and Bob that their outcomes unambiguously assume a definite value, which ought to comply with this nonlocal propensity.
The reader acquainted with quantum physics would have already noticed the similarity of this “classical” nonlocal randomness with quantum correlations. However, we wanted here to express a hypothetical property of indeterminacy that can be conceptually introduced independently of quantum theory (although we do observe it experimentally in quantum systems and not in classical ones). Before moving to the quantum case, we deem it useful to consider the so-called Popescu–Rohrlich (PR) boxes [
31], because, contrary to the indeterministic scenarios so far discussed (in terms of TRNG), they admit the choice of inputs that is crucial in the quantum case (i.e., the choice of the measurement basis). PR boxes are a theoretical model of an operational setup that displays the maximal amount of correlated (nonlocal) randomness, which, however, does not lead to instantaneous signaling (i.e., it respects the no-signaling conditions). In terms of correlations between two distant parties—which carry out local operations (i.e., they choose an input bit
x and
y, respectively) and measure an outcome of some not fully specified random process (indicated by the bits
a and
b, respectively)—the no-signaling conditions are given by the fact that the input choice (which, in turn, could be picked according to local and independent TRNGs) of one party cannot directly influence the outcome of the other one. PR boxes are a set of correlations
defined as follows: if the pair of inputs,
; then, the outputs are perfectly correlated, i.e.,
. Otherwise, if the input pair
, the outcomes are perfectly anticorrelated, i.e.,
. It is straightforward to show that these correlations respect the no-signaling conditions. Accordingly, if, for example,
and
, then the propensity
(i.e., in this case,
), where the superscript index indicates Alice’s future light-cone, but
everywhere else.
3.3. Quantum Correlated Randomness
In the previous sections, we have discussed different “classical” scenarios that bring together true randomness (i.e., indeterminism) and special relativity, reaching the conclusion that (in)determinacy is relative. Moreover, in the case of correlated randomness between two TRNGs, there are regions of space-time in which different inertial observers attribute, in general, different probabilities for measurement outcomes (corresponding to different objective propensities), and it is only in the overlap between their future light-cones that their predictions match (where they also become testable). However, it would be impossible to discuss indeterminism without addressing quantum physics, which not only is the most successful theory ever in terms of predictions, but also a theory that hints at the indeterministic nature of our world. Indeed, the violation of Bell’s inequalities [
32] has proven that if there is at least a random event in the universe, then there can be arbitrarily many of them [
33] (see also [
5] for a discussion), and even that classical trajectories of particles cannot exist predetermined (if one upholds locality) [
34]. Moreover, in a recent work, Dragan and Ekert showed that elementary special relativistic considerations can lead to quantum randomness [
35].
Hence, we now introduce quantum (nonlocal) correlations—that is, what happens if Alice’s and Bob’s TRNGs are entangled? Assume an initial maximally entangled state, say, the singlet
, where
and
are eigenstates of
, the first qbit is with Alice, and the second with Bob. When Alice measures her local qbit on an arbitrary basis, say, the
x-basis (recall that
has the same form in every basis), she obtains, for example, the outcome
, corresponding to the state
. While Bob’s local quantum state remains unchanged, Alice describes, after her measurement, the global state using the projection postulate, i.e., it becomes
. Symmetrically, however, Bob locally measures his qbit, which is still in the initial entangled state
, in the
y-basis, and obtains, say, outcome
, corresponding to
. By using the projection postulate, he updates the global state to
, while Alice’s state remains unchanged. Since Alice’s and Bob’s measurements are carried out in spacelike separation, there are inertial reference frames in which one measurement occurs before the other and vice versa, from which we conclude that there are certain regions of space-time in which the global quantum state as assigned by Alice and Bob differ. At the intersection of the respective future light-cones, however, the two bits acquire their value and the quantum state is reduced to
, which reconciles with the usual projection postulate. In the way here described, the state is well-defined at every point in space-time, but in every inertial frame there are regions of space-time where two different states are attributed to the two qbits. Notice that the probabilities of the two outcomes
a and
b are correlated, as is usual in quantum mechanics (if one performs local measurement in two bases that are not mutually unbiased): this is nonlocal randomness [
36], but the states change only locally.
Our view is similar to that of Aharonov and Albert, who, in a series of papers [
37,
38,
39], pointed out the inadequacy of the standard quantum state-vector description for multipartite systems in a relativistic scenario. We thus deem it worth rephrasing, in the language of the present paper, one of the examples given in Ref. [
38]. With reference to
Figure 3, let Alice, Bob, and Charlie be located at three distant locations and share a tripartite entangled W-state
, (normalization is omitted) which can be seen as the Fock representation of a single particle in a quantum superposition between the three different locations (entanglement with vacuum). In a certain reference frame, a measurement is performed on the first qbit at
, revealing that the particle is not located at Alice’s position (formally, this means to apply to Alice’s qbit the projector
). The global state thus is updated to
. A second measurement is then performed, at time
, on the second qbit, revealing that the particles are also not located at Bob’s location. This leaves the global state in
. Given the spacelike separation of these events, however, there exists another reference frame, in which the measurements occur in reversed order. In that frame, the initial state is the Lorentz-transformed of
, which we indicate by
. The first measurement happens at
and leads to the updated state
and then, after the second measurement at time
, to the final global state
. This shows that the intermediate states
and
, which describe the tripartite system in the period in between the two measurements in their respective reference frames, differ in a way that they are not the Lorenz-transformed of one another.
In conclusion, the examples here discussed show that at both the classical level (yet, assuming ontic indeterminacy and associated propensities) and in quantum mechanics, (in)determinacy is in general well-defined only with respect to specific space-time regions. In particular, in this section, we showed that different (global) quantum states pertain to two (or more) spacelike separated regions. It is only at the intersection of the future light-cones of the events that locally determine the truth value of a previously indeterminate empirical statement (i.e., the outcome of a measurement in quantum physics, or the generation of a bit in a TRNG in our previous scenarios) that the state becomes unique and reconciles with the standard quantum-state-update rule.