Preference Parameters for the Calculation of Thermal Conductivity by Multiparticle Collision Dynamics
Abstract
1. Introduction
2. Numerical Model
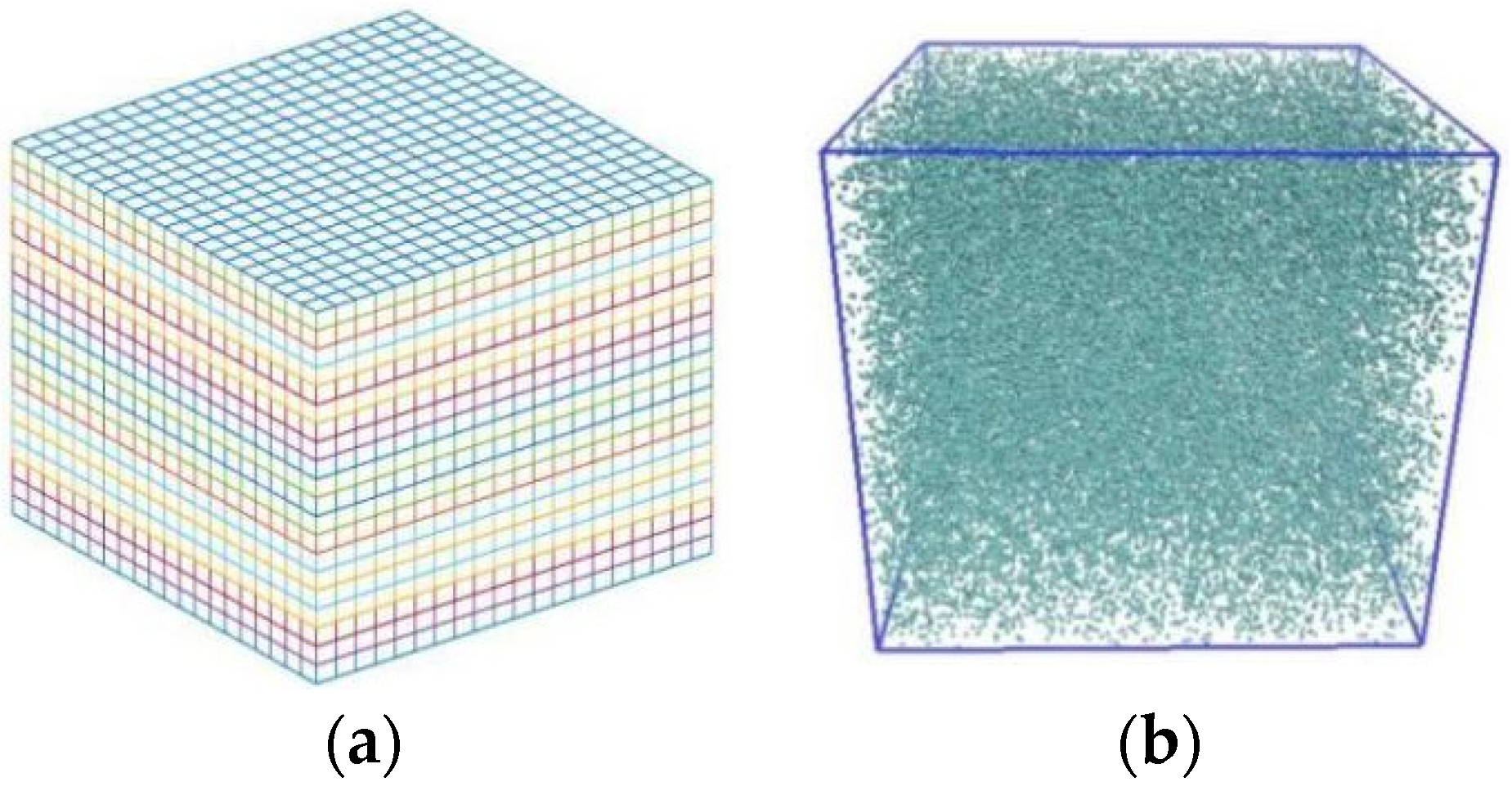
2.1. MPCD Implementation
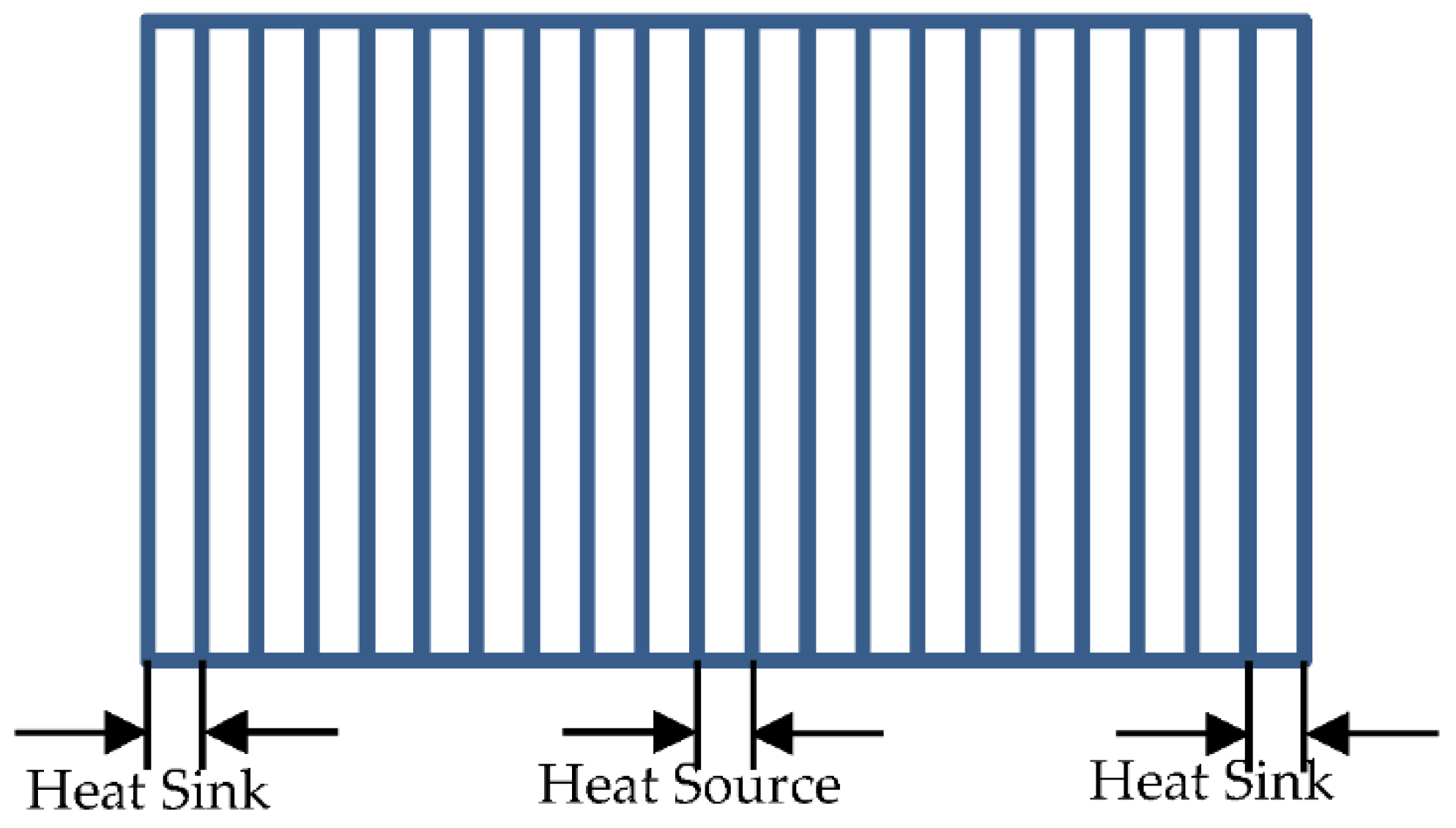
2.2. Calculation of Thermal Conductivity
2.3. Definition of Nondimensional Parameters
3. Analysis of Various Effect Factors
3.1. Effect of Time-Step and Coarse-Grained Mass
3.2. Effect of Bin Size
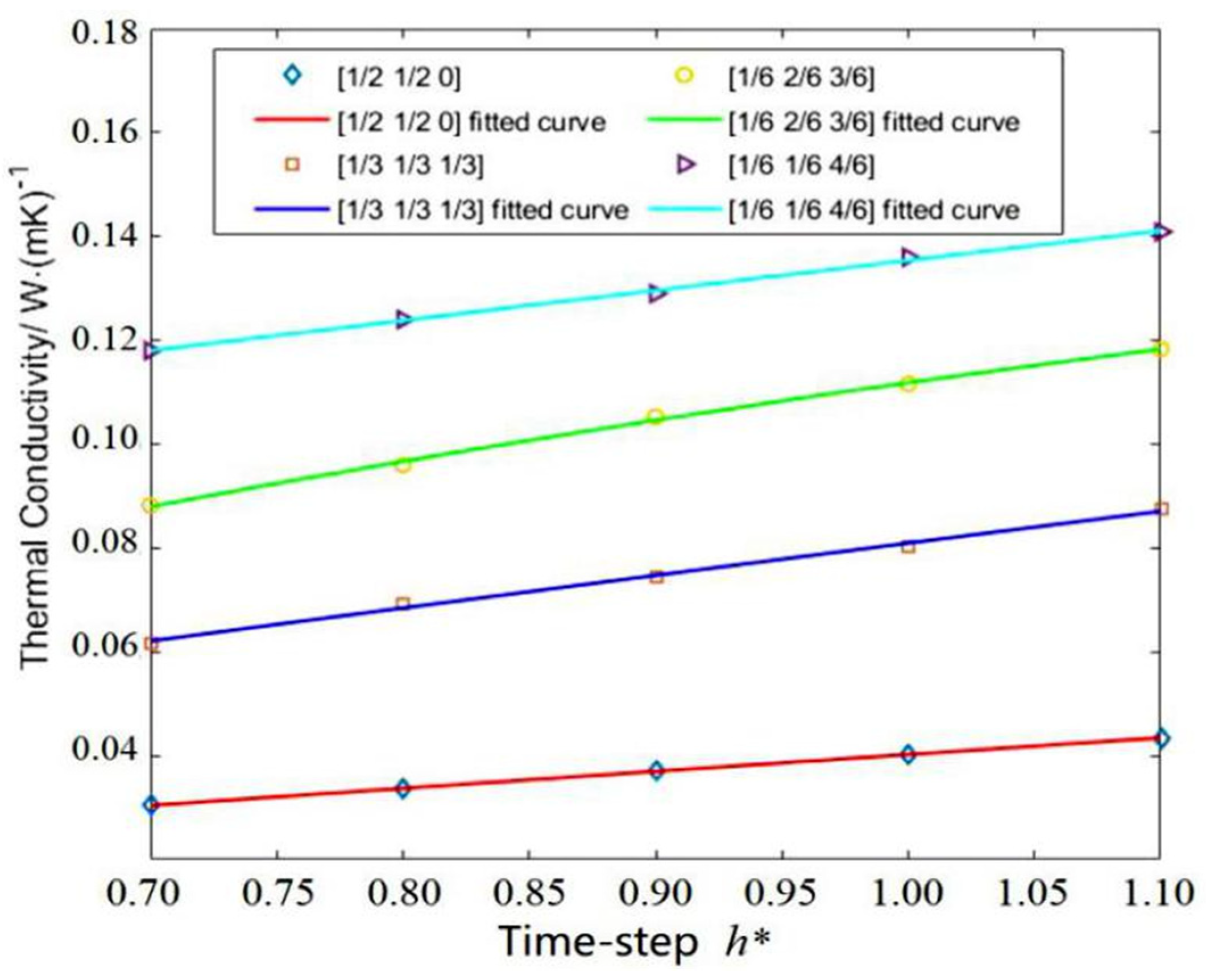
3.3. Effect of Rotation Angle
3.4. Effect of Temperature
4. Thermal Conductivity Calculations
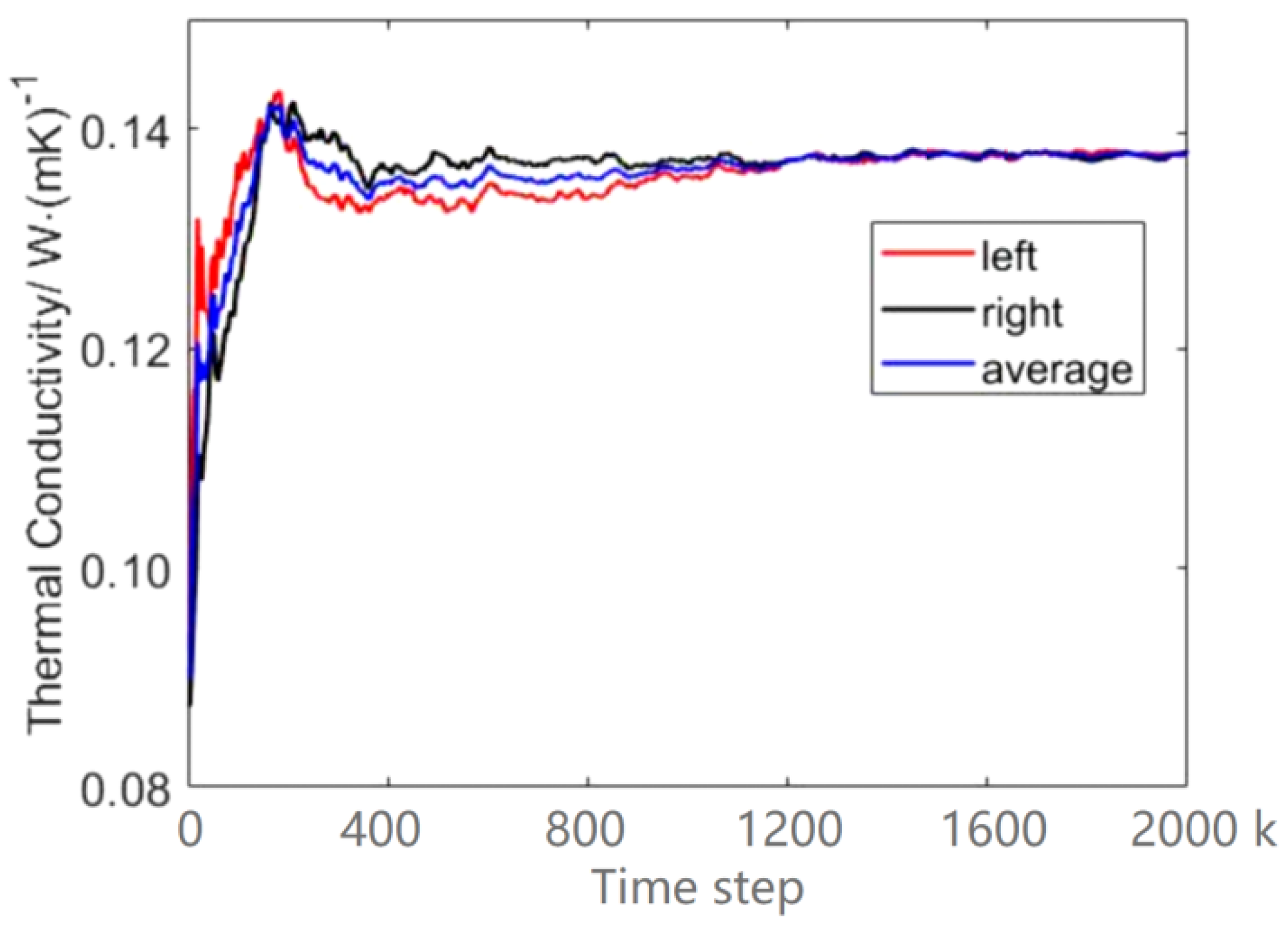
4.1. Thermal Conductivity of Ar
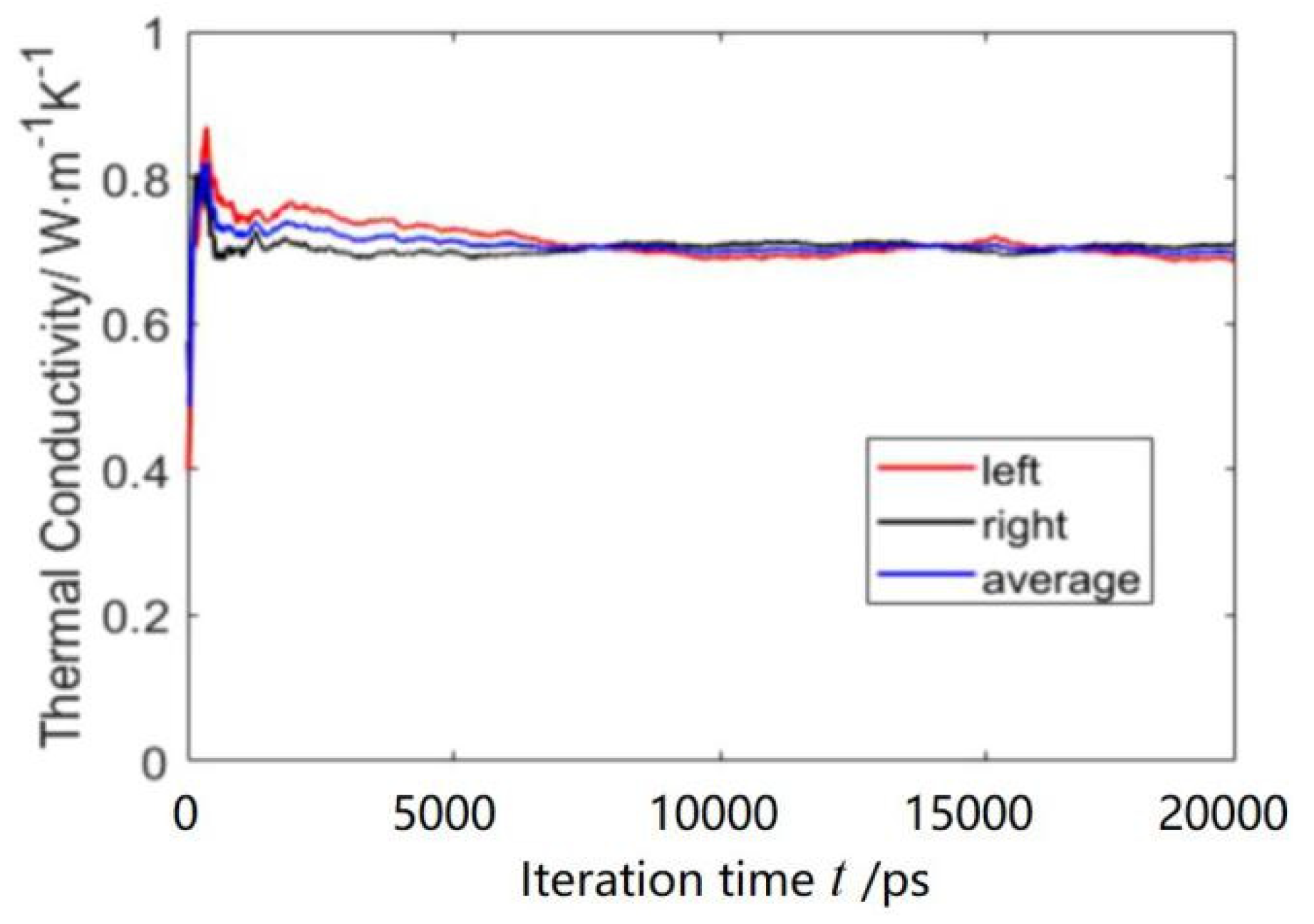
4.2. Thermal Conductivity of Water
4.3. Thermal Conductivity of Cu-Water Nanofluid
5. Conclusions
- (1)
- The method proposed is applicable as long as suitable MPCD parameters are selected. It is suitable for various systems, such as argon, water and nanofluids. The computational accuracy was ensured, and the deviations of argon, water and Cu-water nanofluid were 3.4%, 1.5% and 1.2%, respectively.
- (2)
- The combined rotation angle (90°, 180°, 270°) with a probability of (1/6, 1/6, 4/6) may be preferential for calculating the thermal conductivity. The reason could be the isotropy of the simulation system.
- (3)
- The adaptive time-steps were 1.0, 0.35 and 0.35 for argon, water and copper-water nanofluid respectively, because argon has a greater weight compared to water. The underlying mechanism may be the different interaction intensity between different particles. It can be interpreted by the different parameters, and , in L-J potential for different molecules.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Bin size |
| Stochastic rotation matrix | |
| e | Local energy |
| fcc | Lattice constant |
| Time-step | |
| j | Local momentum |
| k | Thermal conductivity |
| kB | Boltzmann constant |
| m | Mass of fluid particle |
| M | Mass of coarse-grained particle |
| N | Number of particles |
| Q | Heat flux |
| Position vector | |
| Thermostats | |
| Time | |
| T | Temperature |
| Velocity | |
| x | z-coordinate |
| Rotation angle | |
| Mean free path | |
| Average number density | |
| Scale parameter of L-J potential | |
| Well depth of L-J potential | |
| Superscript and subscript | |
| b | Solvents/fluid |
| i | ith particle |
| p | Solutes/particle |
| th cell |
References
- Vogelsang, R.; Hoheisel, C. Thermal conductivity of the Lennard-Jones liquid by Molecular Dynamics Calculations. J. Chem. Phys. 1987, 86, 6371–6375. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, Y.; Yang, M. Molecular dynamics simulation of thermal conductivity of Cu-Ar nanofluid using EAM potential for Cu-Cu Interactions. Appl. Phys. A Mater. Sci. Process. 2011, 103, 1001–1008. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q.; Hu, W. Aggregation structure and shermal conductivity of nanofluids. AIChE J. 2003, 49, 1038–1043. [Google Scholar] [CrossRef]
- Wang, R.J.; Qian, S.; Zhang, Z.Q. Investigation of the aggregation morphology of nanoparticle on the thermal conductivity of nanofluid by molecular dynamics simulations. Int. J. Heat Mass Transf. 2018, 127, 1138–1146. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Qian, S.; Wang, R.J.; Zhu, Z.F. Effect of aggregation morphology of nanoparticles on thermal conductivity of nanofluid. Acta Phys. Sin. 2019, 68, 054401. [Google Scholar]
- Marrink, S.J.; Risselada, H.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulation. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.A.; Rzepiela, A.J.; Vries, A.H.; Dijkhuizen, L.; Hünenberger, P.H.; Marrink, S.J. Martini coarse-grained force field: Extension to carbo-hydrates. J. Chem. Theory Comp. 2009, 5, 3195–3210. [Google Scholar] [CrossRef] [PubMed]
- He, C.Y.; Liu, X.J. Simulations studies of viscosity of Cu-H2O nanofluids based on coarse graining water molecules. Chin. J. Theory Appl. Mech. 2014, 46, 871–877. [Google Scholar]
- Malevanets, A.; Kapral, R. Mesoscopic model for solvent dynamics. J. Chem. Phys. 1999, 110, 8605–8617. [Google Scholar] [CrossRef]
- De Angelis, E.; Chinappi, M.; Graziani, G. Flow simulations with multi-particle collision dynamics. Meccanica 2012, 47, 2069–2077. [Google Scholar] [CrossRef]
- Elgeti, J.; Gompper, G. Emergence of metachronal waves in cilia arrays. Proc. Natl. Acad. Sci. USA 2013, 110, 4470–4475. [Google Scholar] [CrossRef]
- Babu, S.B.; Stark, H. Modeling the locomotion of the African trypanosome using multi-particle collision dynamics. New J. Phys. 2012, 14, 085012. [Google Scholar] [CrossRef]
- Yang, M.C.; Ripoll, M. Thermophoretically induced flow field around a colloidal particle. Soft Matter 2013, 9, 4661. [Google Scholar] [CrossRef]
- Burelbach, J.; Brückner, D.B.; Frenkel, D.; Eiser, E. Thermophoretic Forces on a Mesoscopic Scale. Soft Matter 2018, 14, 7446–7454. [Google Scholar] [CrossRef] [PubMed]
- José, R.F.; Diego, J.C.; Manuel, C.; Christos, N.L.; Emanuela, Z. Multi-particle collision dynamics for a coarse-grained model of soft colloids. J. Chem. Phys. 2019, 151, 074902. [Google Scholar]
- Zablotsky, D. Field effect in the viscosity of magnetic colloids studied by multi-particle collision dynamics. J. Magn. Magn. Mater. 2019, 474, 462–466. [Google Scholar] [CrossRef]
- Dahirel, V.; Zhao, X.D.; Couet, B.; Batôt, G.; Jardat, M. Hydrodynamic interactions between solutes in multiparticle collision dynamics. Phys. Rev. E 2018, 98, 053301. [Google Scholar] [CrossRef]
- Batot, G.; Dahirel, V.; Meriguet, G.; Louis, A.A.; Jardat, M. Dynamics of solutes with hydrodynamic interactions: Comparison between Brownian dynamics and stochastic rotation dynamics simulations. Phys. Rev. E 2013, 88, 043304. [Google Scholar] [CrossRef]
- Yamamoto, T.; Masaoka, N. Numerical simulation of star polymers under shear flow using a coupling method of multi-particle collision dynamics and molecular dynamics. Rheol. Acta 2015, 54, 139–147. [Google Scholar] [CrossRef]
- Laganapan, A.M.K.; Videcoq, A.; Bienia, M.; Ala-Nissila, T.; Bochicchio, D.; Ferrando, R. Computation of shear viscosity of colloidal suspensions by SRD-MD. J. Chem. Phys. 2015, 142, 144101. [Google Scholar] [CrossRef]
- Du, J.Y.; Su, Q.M.; Li, L.; Wang, R.J.; Zhu, Z.F. Evaluation of the morphology of aggregation and thermal conductivity of Cu-H2O nanofluid by MPCD-MD hybrid method. Int. Commun. Heat Mass Transf. 2021, 127, 105501. [Google Scholar] [CrossRef]
- Lüsebrink, D.; Yang, M.C.; Ripoll, M. Thermophoresis of colloids by mesoscale simulations. J. Phys. Condens. Matter 2012, 24, 284132. [Google Scholar] [CrossRef][Green Version]
- Howard, M.P.; Nikoubashman, A.; Palmer, J.C. Modeling hydrodynamic interactions in soft materials with multiparticle collision dynamics. Cur. Opin. Chem. Eng. 2019, 23, 34–43. [Google Scholar] [CrossRef]
- Wysocki, A.; Löwen, H. Effects of hydrodynamic interactions in binary colloidal mixtures driven oppositely by oscillatory external fields. J. Phys. Condens. Matter 2011, 23, 284117. [Google Scholar] [CrossRef]
- Pooley, C.M.; Yeomans, J.M. Kinetic Theory Derivation of the Transport Coefficients of Stochastic Rotation Dynamics. Phys. Chem. B 2005, 109, 6505. [Google Scholar] [CrossRef]
- Ihle, T.; Kroll, D.M. Stochastic rotation dynamics. II. Transport coefficients, numerics, and long-time tails. Phys. Rev. E 2003, 67, 066705. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, N.; Pooley, C.M.; Ryder, J.F.; Yeomans, J.M. Transport coefficients of a mesoscopic fluid dynamics model. J. Chem. Phys. 2008, 119, 6388–6395. [Google Scholar] [CrossRef]
- Lüsebrink, D.; Ripoll, M. Temperature inhomogeneities simulated with multiparticle collision dynamics. J. Chem. Phys. 2012, 136, 084106. [Google Scholar] [CrossRef] [PubMed]
- Ripoll, M.; Mussawisade, K.; Winkler, R.G.; Gompper, G. Dynamic regimes of fluids simulated by multiparticle collision dynamics. Phys. Rev. E 2005, 72, 016701. [Google Scholar] [CrossRef] [PubMed]
- Muhlbauer, S.; Strobl, S.; Poschel, T. Isotropic stochastic rotation dynamics. Phys. Rev. Fluids 2017, 12, 124204. [Google Scholar] [CrossRef]
- Yang, M.C.; Theers, M.; Hu, J.L.; Gompper, G.; Winkler, R.G.; Ripoll, M. Effect of angular momentum conservation on hydrodynamic simulations of colloids. Phys. Rev. E 2015, 92, 013301. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.C.; Varghese, A.; Gompper, G.; Winkler, R.G. Thermostat for nonequilibrium multiparticle collision dynamics simulations. Phys. Rev. E 2015, 91, 013310. [Google Scholar] [CrossRef]
- Götze, I.O.; Noguchi, H.; Gompper, G. Relevance of angular momentum conservation in mesoscale hydrodynamics simulations. Phys. Rev. E 2007, 76, 046705. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, H.; Gompper, G. Transport coefficients of off-lattice mesoscale-hydrodynamics simulation techniques. Phys. Rev. E 2008, 78, 016706. [Google Scholar] [CrossRef] [PubMed]
- Muller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082. [Google Scholar] [CrossRef]



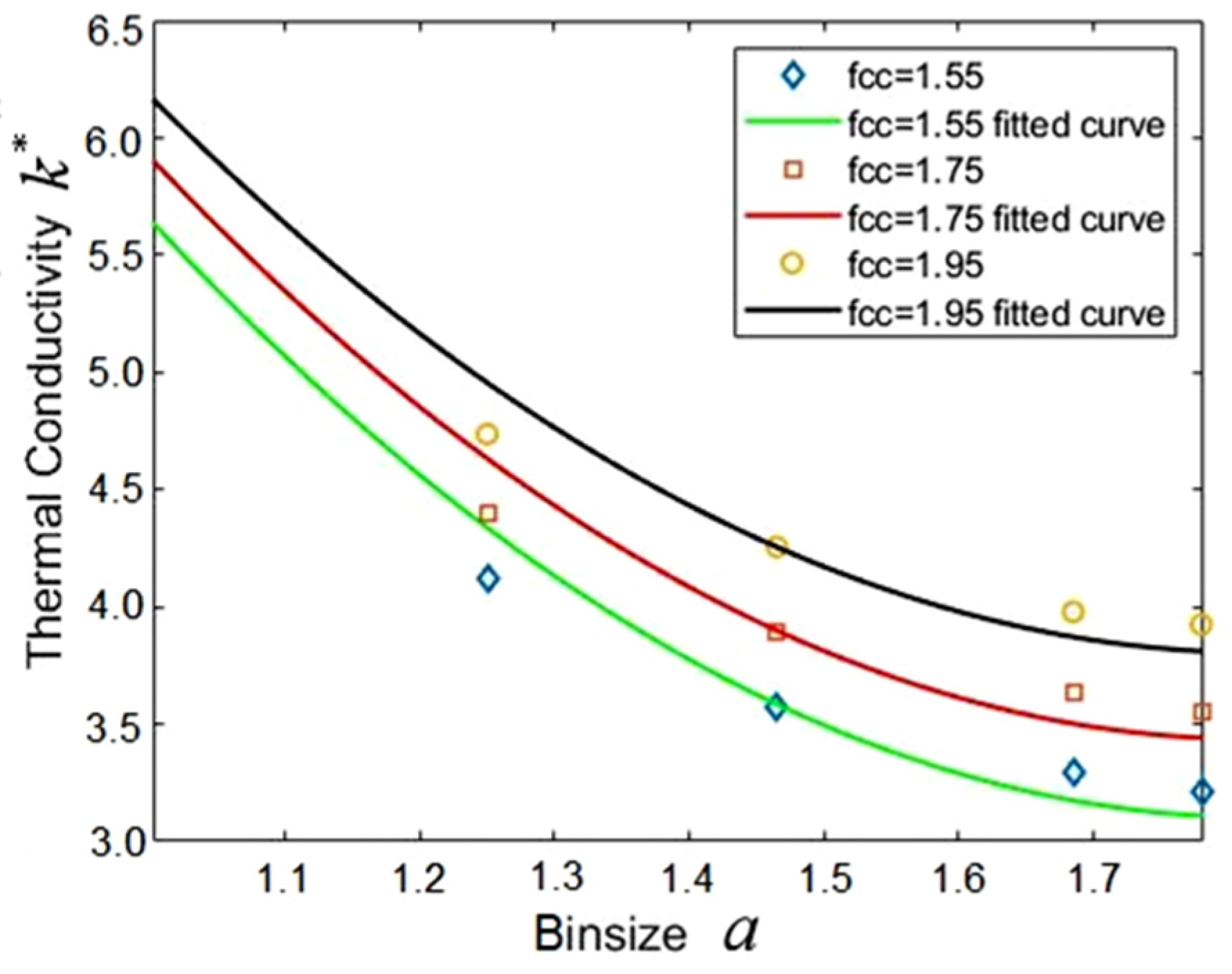
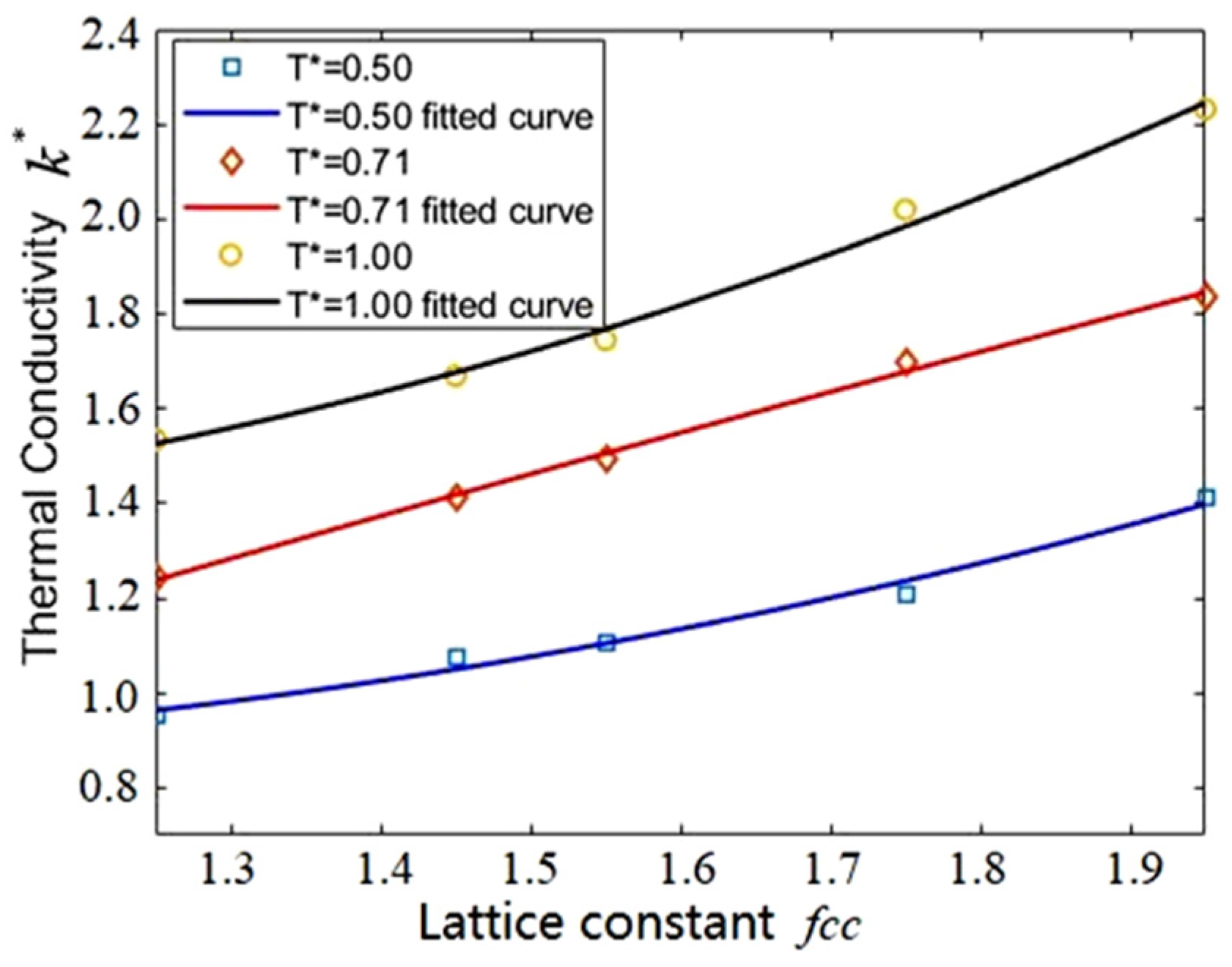

| Lattice Constant | fcc = 1.550 | |||||
| Bin size | 1.000 | 1.250 | 1.465 | 1.685 | 1.780 | 1.983 |
| Number density | 1.590 | 3.370 | 5.140 | 7.810 | 9.110 | 12.720 |
| Lattice Constant | fcc = 1.750 | |||||
| Bin size | 1.000 | 1.250 | 1.465 | 1.685 | 1.780 | 1.983 |
| Number density | 1.782 | 3.778 | 5.771 | 8.788 | 10.250 | 14.310 |
| Lattice Constant | fcc = 1.950 | |||||
| Bin size | 1.000 | 1.250 | 1.465 | 1.685 | 1.780 | 1.983 |
| Number density | 2.003 | 4.000 | 6.470 | 9.840 | 11.500 | 16.020 |
| Case Number | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |||||||
| CRA | 130° | 90° | 180° | 90° | 180° | 270° | 90° | 180° | 270° | 90° | 180° | 270° |
| Probability | 1 | 1/2 | 1/2 | 1/3 | 1/3 | 1/3 | 1/6 | 2/6 | 3/6 | 1/6 | 1/6 | 4/6 |
| TC | 3.1241 | 3.1548 | 3.1476 | 3.2304 | 3.2714 | |||||||
| Case Number | Case 6 | Case 7 | Case 8 | Case 9 | Case 10 | |||||||
| CRA | 135° | 90° | 270° | 90° | 270° | 360° | 90° | 270° | 360° | 90° | 270° | 360° |
| Probability | 1 | 1/2 | 1/2 | 1/3 | 1/3 | 1/3 | 1/6 | 2/6 | 3/6 | 1/6 | 1/6 | 4/6 |
| TC | 3.1453 | 3.2159 | 5.2538 | 7.0564 | 11.2008 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Zhang, Z.; Li, L.; Zhu, Z. Preference Parameters for the Calculation of Thermal Conductivity by Multiparticle Collision Dynamics. Entropy 2021, 23, 1325. https://doi.org/10.3390/e23101325
Wang R, Zhang Z, Li L, Zhu Z. Preference Parameters for the Calculation of Thermal Conductivity by Multiparticle Collision Dynamics. Entropy. 2021; 23(10):1325. https://doi.org/10.3390/e23101325
Chicago/Turabian StyleWang, Ruijin, Zhen Zhang, Long Li, and Zefei Zhu. 2021. "Preference Parameters for the Calculation of Thermal Conductivity by Multiparticle Collision Dynamics" Entropy 23, no. 10: 1325. https://doi.org/10.3390/e23101325
APA StyleWang, R., Zhang, Z., Li, L., & Zhu, Z. (2021). Preference Parameters for the Calculation of Thermal Conductivity by Multiparticle Collision Dynamics. Entropy, 23(10), 1325. https://doi.org/10.3390/e23101325







