Various Auto-Correlation Functions of m-Bit Random Numbers Generated from Chaotic Binary Sequences
Abstract
:1. Introduction
2. Auto-Correlation Functions of -Bit Random Sequences
2.1. Definition of Auto-Correlation Function
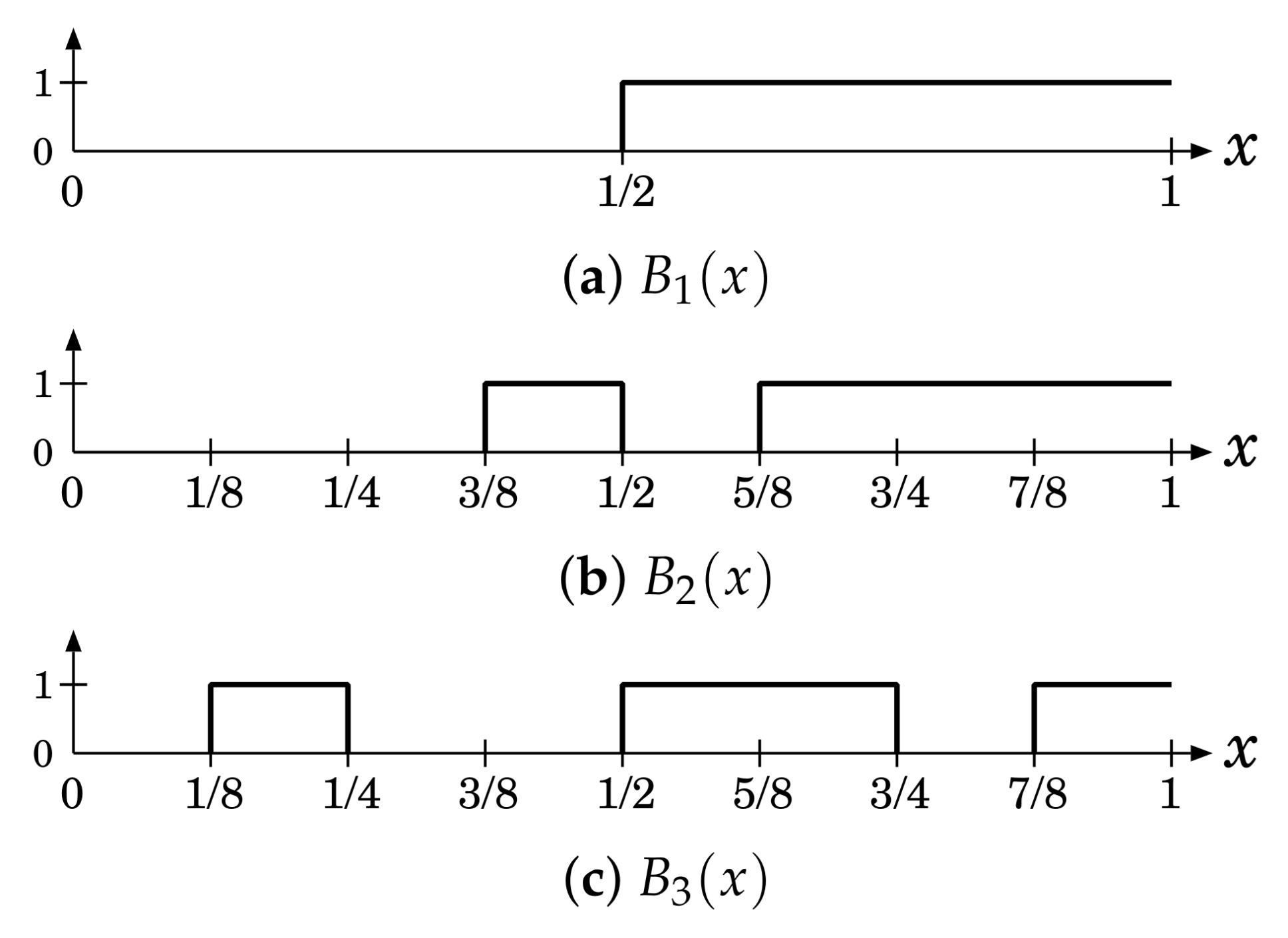
2.2. Generation of m-Bit Sequences from Binary Sequences
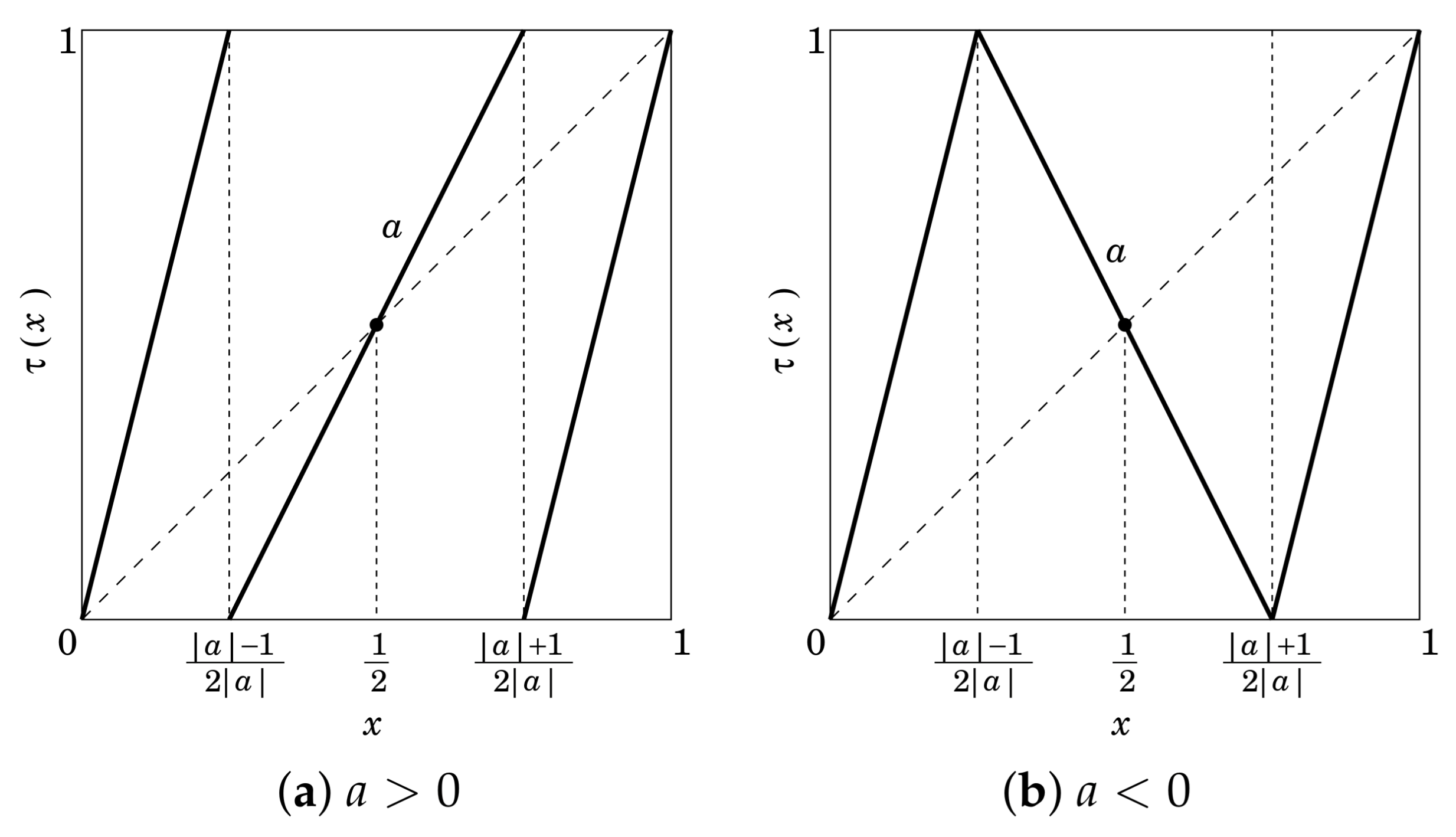
3. Chaotic Binary Sequences with Prescribed Auto-Correlations
4. Numerical Experiments
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kohda, T.; Tsuneda, A. Statistics of chaotic binary sequences. IEEE Trans. Inf. Theory 1997, 43, 104–112. [Google Scholar] [CrossRef]
- Kennedy, M.P.; Rovatti, R.; Setti, G. (Eds.) Chaotic Electronics in Telecommunications; CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Stojanovski, T.; Kocarev, L. Chaos-based random number generators—Part I: Analysis. IEEE Trans. Circuits Syst. I 2001, 48, 281–288. [Google Scholar] [CrossRef]
- Stojanovski, T.; Pihl, J.; Kocarev, L. Chaos-based random umber generators—Part II: Practical realization. IEEE Trans. Circuits Syst. I 2001, 48, 382–385. [Google Scholar] [CrossRef] [Green Version]
- Bernardini, R.; Cortelazzo, G. Tools for designing chaotic systems for secure random number generation. IEEE Trans. Circuits Syst. I 2001, 48, 552–564. [Google Scholar] [CrossRef]
- Gerosa, A.; Bernardini, R.; Pietri, S. A fully integrated chaotic system for the generation of truly random numbers. IEEE Trans. Circuits Syst. I 2001, 49, 993–1000. [Google Scholar] [CrossRef]
- Fort, A.; Cortigiani, F.; Rocchi, S.; Vignoli, V. Very high-speed true random noise generator. Analog. Integr. Circuits Signal Process. 2003, 34, 97–105. [Google Scholar] [CrossRef]
- Tsuneda, A. Design of binary sequences with tunable exponential autocorrelations and run statistics based on one-dimensional chaotic maps. IEEE Trans. Circuits Syst. I 2005, 52, 454–462. [Google Scholar] [CrossRef]
- Tsuneda, A.; Morikawa, K. A study on random bit sequences with prescribed auto-correlations by post-processing using linear feedback shift registers. In Proceedings of the 2013 European Conference on Circuit Theory and Design, Dresden, Germany, 8–12 September 2013. [Google Scholar]
- Cicek, I.; Pusane, A.E.; Dundar, G. A novel design method for discrete time chaos based true random number generators. Integration 2014, 47, 38–47. [Google Scholar] [CrossRef]
- Kyaw, T.N.N.; Tsuneda, A. Generation of chaos-based random bit sequences with prescribed auto-correlations by post-processing using linear feedback shift registers. Nonlinear Theory Its Appl. 2017, 8, 224–234. [Google Scholar] [CrossRef]
- Demir, K.; Ergün, S. An analysis of deterministic chaos as an entropy source for random number generators. Entropy 2018, 20, 957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. I 2019, 66, 2322–2335. [Google Scholar] [CrossRef] [Green Version]
- Tsuneda, A.; Shiraishi, H. A study on auto-correlation functions of quaternary random sequences generated from chaotic binary sequences. In Proceedings of the 2019 International Symposium on Nonlinear Theory and its Applications, Kuala Lumpur, Malaysia, 2–6 December 2019; pp. 165–168. [Google Scholar]
- Gentle, J.E. Random Number Generation and Monte-Carlo Method, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Yang, C.A.; Yao, K.; Umeno, K.; Biglieri, E. Using deterministic chaos for superefficient Monte-Carlo simulations. IEEE Circuits Syst. Mag. 2013, 13, 26–35. [Google Scholar] [CrossRef]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Boyarsky, A.; Góra, P. Laws of Chaos; Birkhäuser: Boston, MA, USA, 1997. [Google Scholar]

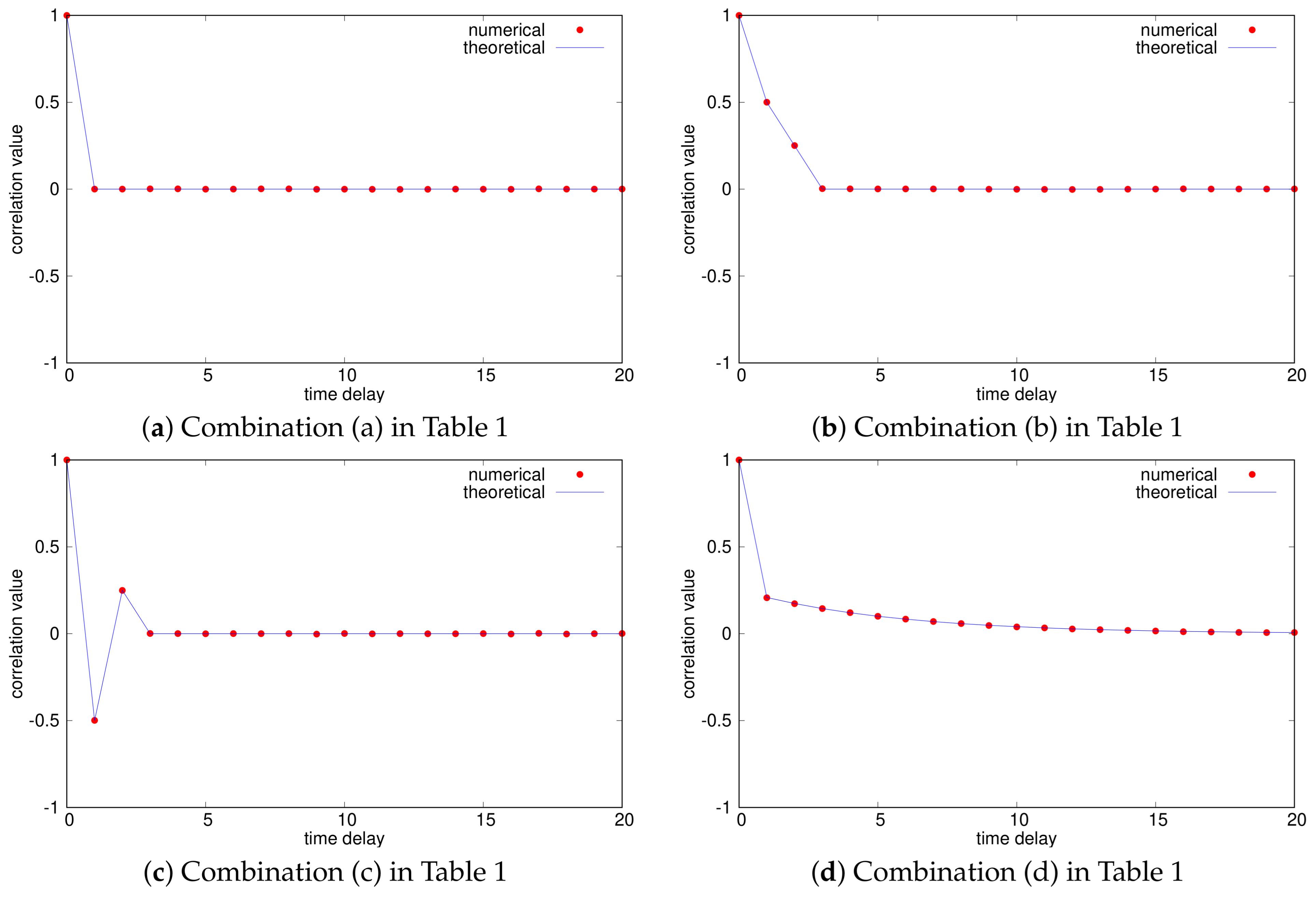
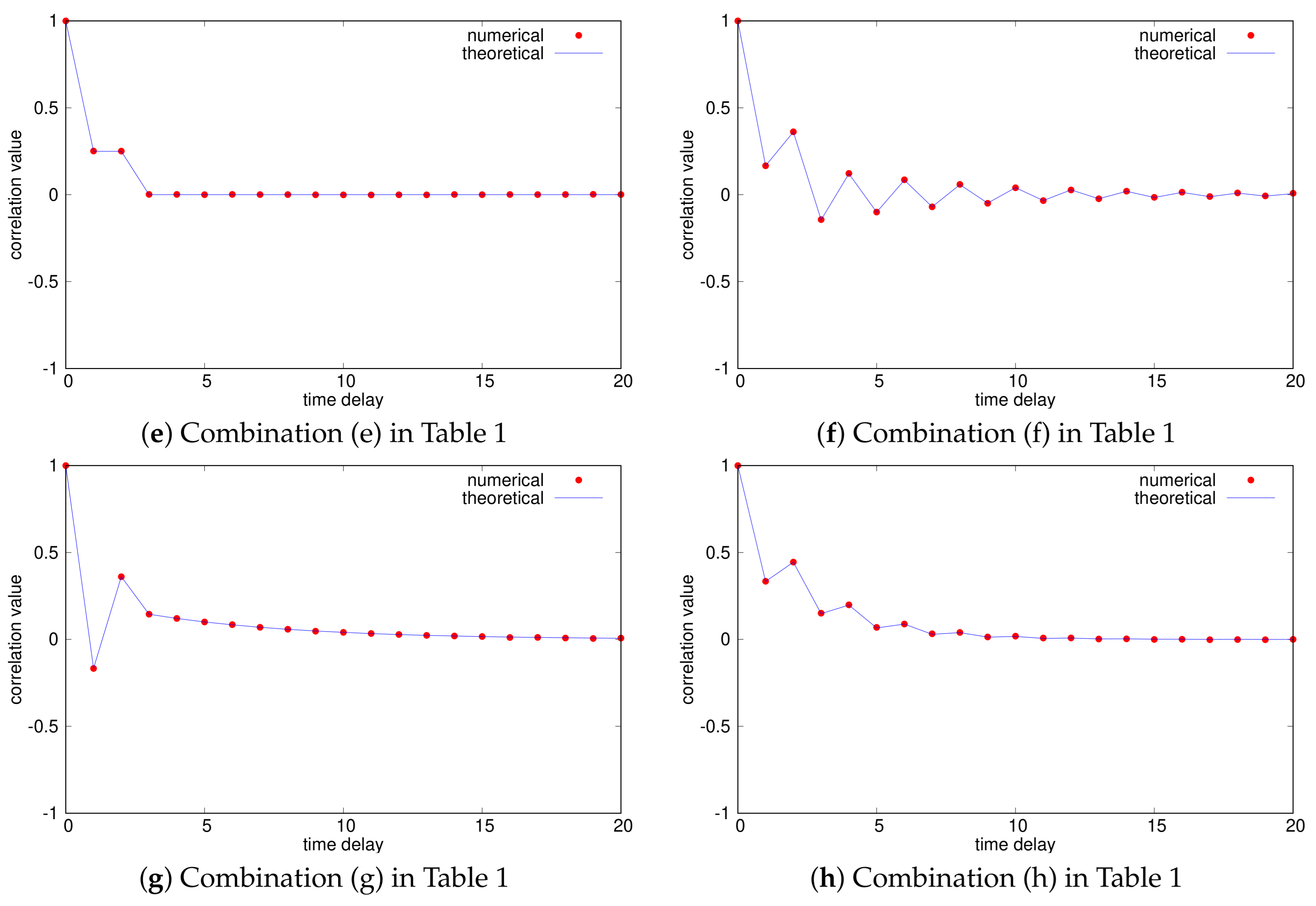
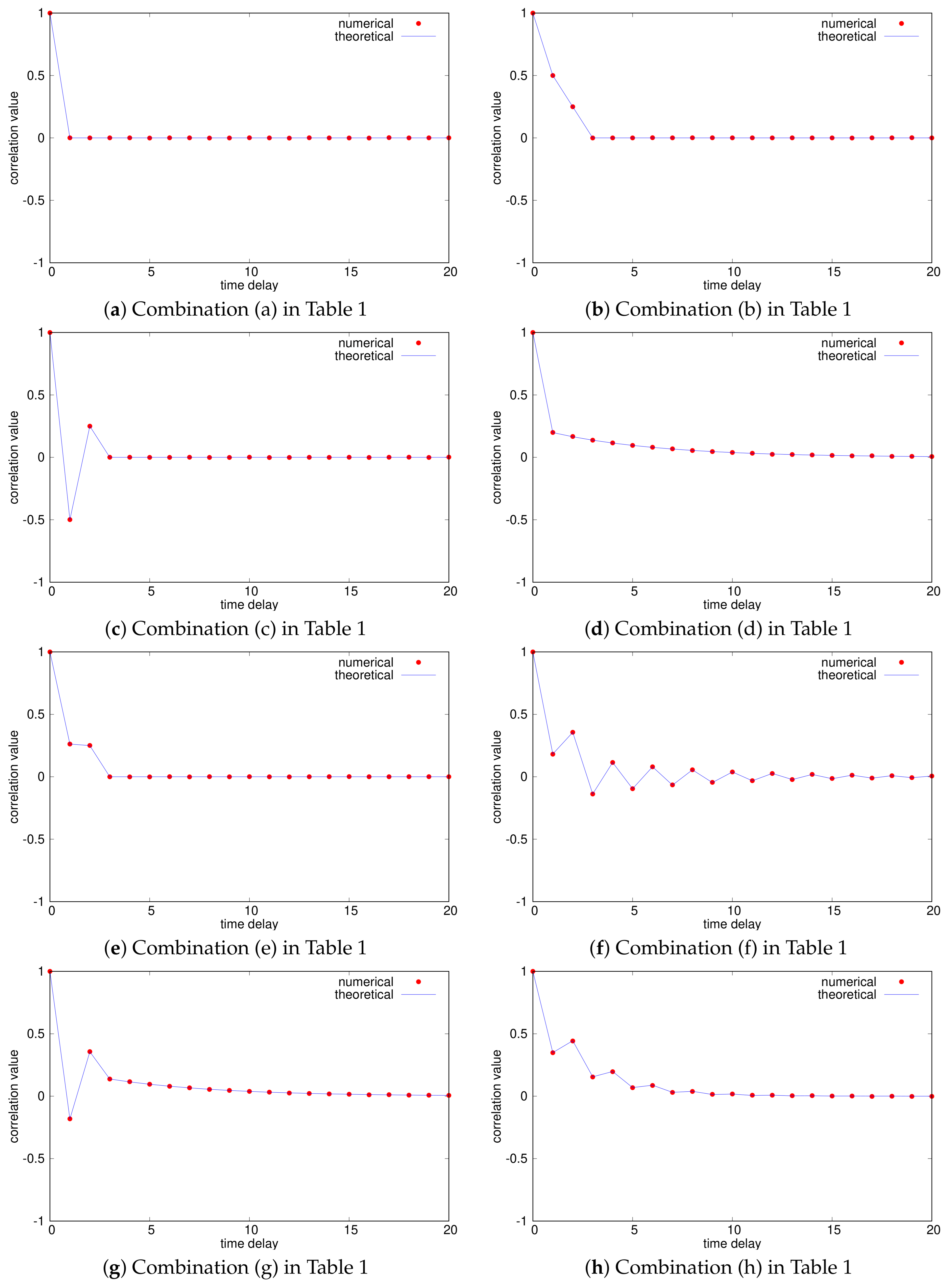
| (a) | ACF-1 | ACF-1 |
| (b) | ACF-2 | ACF-2 |
| (c) | ACF-3 | ACF-3 |
| (d) | ACF-1 | ACF-4 () |
| (e) | ACF-2 | ACF-3 |
| (f) | ACF-2 | ACF-4 () |
| (g) | ACF-3 | ACF-4 () |
| (h) | ACF-4 () | ACF-4 () |
| Value | Probability | |||||||
|---|---|---|---|---|---|---|---|---|
| (-ary Symbol) | (a) | (b) | (c) | (d) | (e) | (f) | (g) | (h) |
| 0 | 0.125601 | 0.125200 | 0.125324 | 0.124573 | 0.125290 | 0.124844 | 0.124969 | 0.125310 |
| 1 | 0.125116 | 0.125883 | 0.124778 | 0.125444 | 0.124755 | 0.125496 | 0.125057 | 0.125829 |
| 2 | 0.124546 | 0.125090 | 0.124958 | 0.125049 | 0.124806 | 0.125352 | 0.125063 | 0.126000 |
| 3 | 0.125041 | 0.124091 | 0.125284 | 0.125238 | 0.125413 | 0.124572 | 0.125255 | 0.124875 |
| 4 | 0.124809 | 0.125149 | 0.124792 | 0.124936 | 0.124826 | 0.125353 | 0.124540 | 0.124821 |
| 5 | 0.124954 | 0.125055 | 0.124779 | 0.124460 | 0.124802 | 0.124458 | 0.124847 | 0.124540 |
| 6 | 0.125100 | 0.124851 | 0.124749 | 0.124727 | 0.124901 | 0.124467 | 0.124713 | 0.124196 |
| 7 | 0.124833 | 0.124681 | 0.125336 | 0.125573 | 0.125207 | 0.125458 | 0.125556 | 0.124429 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuneda, A. Various Auto-Correlation Functions of m-Bit Random Numbers Generated from Chaotic Binary Sequences. Entropy 2021, 23, 1295. https://doi.org/10.3390/e23101295
Tsuneda A. Various Auto-Correlation Functions of m-Bit Random Numbers Generated from Chaotic Binary Sequences. Entropy. 2021; 23(10):1295. https://doi.org/10.3390/e23101295
Chicago/Turabian StyleTsuneda, Akio. 2021. "Various Auto-Correlation Functions of m-Bit Random Numbers Generated from Chaotic Binary Sequences" Entropy 23, no. 10: 1295. https://doi.org/10.3390/e23101295
APA StyleTsuneda, A. (2021). Various Auto-Correlation Functions of m-Bit Random Numbers Generated from Chaotic Binary Sequences. Entropy, 23(10), 1295. https://doi.org/10.3390/e23101295






