Variational Sparse Bayesian Learning for Estimation of Gaussian Mixture Distributed Wireless Channels
Abstract
1. Introduction
- The Gaussian mixture model as a powerful method for sparse parameter learning for wireless channels is introduced to the estimation problem of wireless channel parameters under the VSBL framework. The flexibility of GMM is capable of describing the statistical characteristics of both theoretical general channels and complex real-world channels.
- A new variational Bayesian inference scheme for the Gaussian mixture model (VB-GMM) is developed based on multiple channel observations. The corresponding graphical model is given, and the closed-form updates of the model variables are derived. By setting a pruning criterion on the sparsity priors, the joint estimation of channel parameters and model order is achieved with low complexity.
- The simulation results demonstrate that the performance of VB-GMM is superior to the existing algorithms in terms of the estimation error, the convergence rate, and the model order selection accuracy in most non-Gaussian channels.
2. System Model
2.1. Signal Model
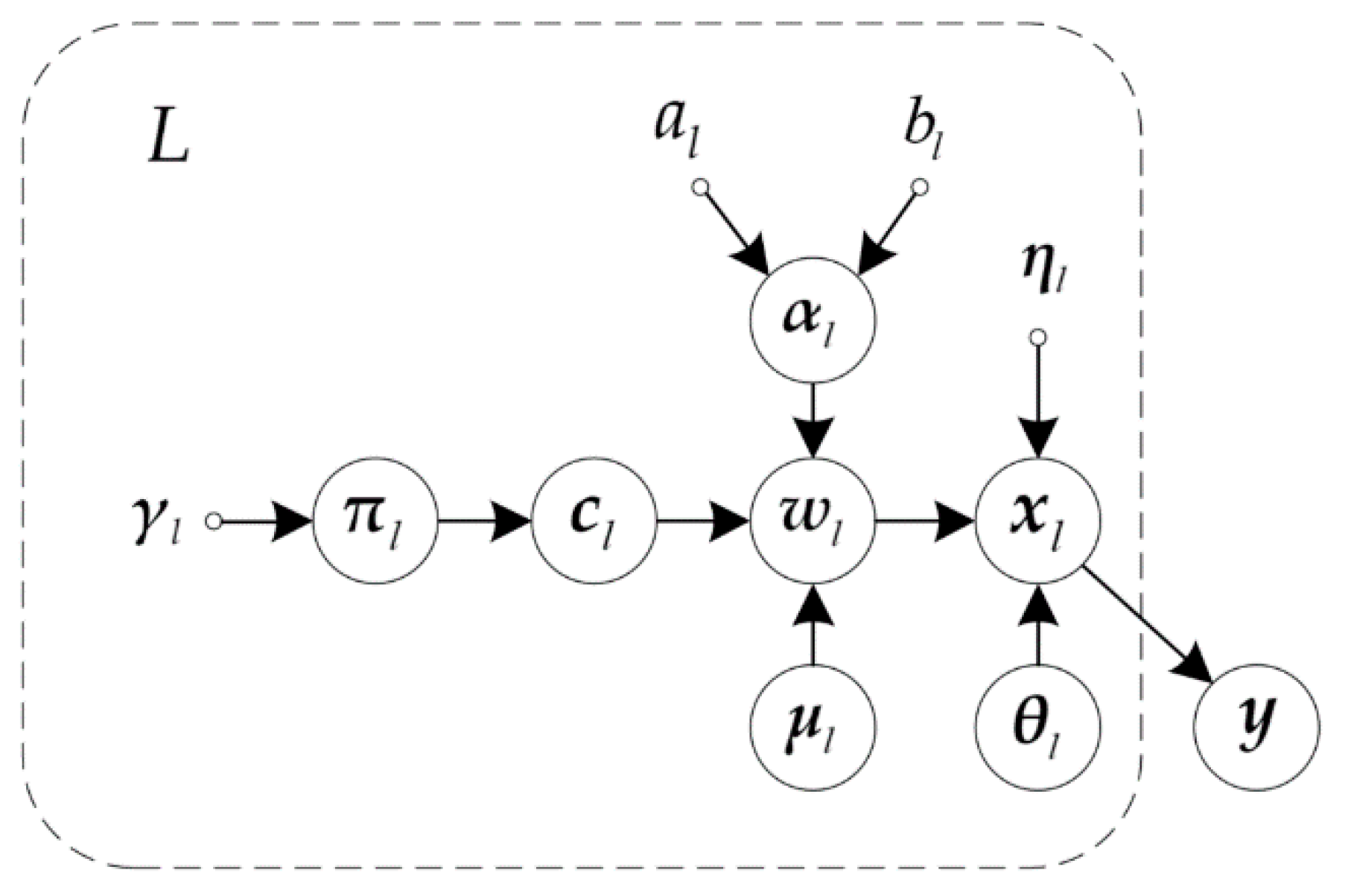
2.2. The GMM Model of Channel Coefficients
3. GMM-Based Variational Bayesian Learning
3.1. Variational Bayesian Inference
3.2. Update of the Estimation Expressions
- 1.
- 2.
- Estimation of: Evaluating (15) with (5) and (10), the VPD of takes the formin whichand represents the di-gamma function. Since is a 0–1 matrix with a discrete VPD, the posterior expectation of is .
- 3.
- Estimation of: From the graph the Markov blanket of is , thus
- 4.
- Estimation of: Similarly, evaluating (15) leads to . As mentioned above, the proxy PDF is defined as in order to obtain a point estimation. Therefore, we have
- 5.
- Estimation of: From the graphic model the Markov blanket of is and . Due to the gamma hyperprior and the nature of conjugate prior, the VPD also satisfies the Gamma distribution, i.e., with
- 6.
- Estimation of: The only variable related to is , thus, . By substituting (5) and (6) into (15) we obtainwhich indicates that the VPD also satisfies the Dirichlet distribution. The parameter of the VPD can be updated by
- 7.
- Estimation of: The Markov blanket of is , so that
3.3. Initialization Algorithm
| Algorithm 1: Initialization |
3.4. Pruning and Convergence Condition
3.5. Computational Complexity
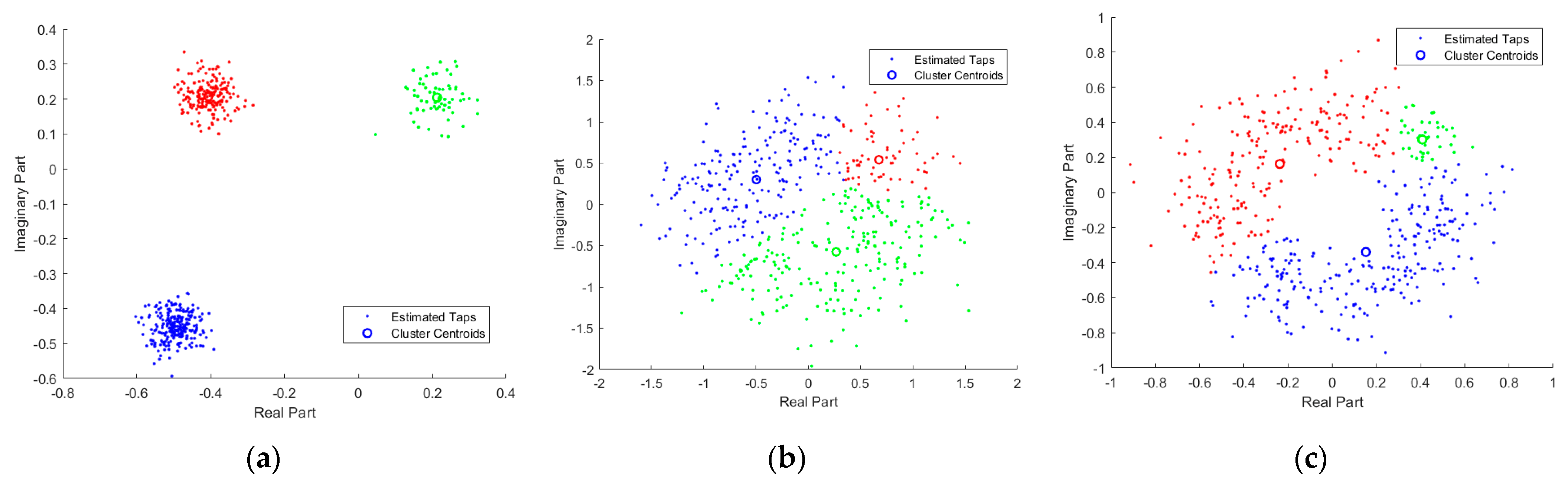
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Fleury, B.H.; Tschudin, M.; Heddergott, R.; Dahlhaus, D.; Pedersen, K.I. Channel parameter estimation in mobile radio envi-ronments using the SAGE algorithm. IEEE J. Sel. Areas Commun. 1999, 17, 434–450. [Google Scholar] [CrossRef]
- Liu, T.C.-K.; Kim, D.I.; Vaughan, R.G. A High-Resolution, Multi-Template Deconvolution Algorithm for Time-Domain UWB Channel Characterization. Can. J. Electr. Comput. Eng. 2007, 32, 1183–1186. [Google Scholar] [CrossRef]
- Lanterman, A.D. Schwarz, Wallace, and Rissanen: Intertwining themes in theories of model order estimation. Int. Stat. Rev. 2000, 69, 185–212. [Google Scholar] [CrossRef]
- Myung, J.I.; Navarro, D.J.; Pitt, M.A. Model selection by normalized maximum likelihood. J. Math. Psychol. 2006, 50, 167–179. [Google Scholar] [CrossRef]
- Shutin, D.; Fleury, B.H. Sparse Variational Bayesian SAGE Algorithm with Application to the Estimation of Multipath Wire-less Channels. IEEE Trans. Signal Process. 2011, 59, 3609–3623. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed Channel Sensing: A New Approach to Estimating Sparse Multipath Channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Thomas, B. Variational Sparse Bayesian Learning: Centralized and Distributed Processing. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2013. [Google Scholar]
- Badiu, M.; Hansen, T.L.; Fleury, B.H. Variational Bayesian Inference of Line Spectra. IEEE Trans. Signal Process. 2017, 65, 2247–2261. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Yuan, J.; Ng, D.W.K. A Simple Variational Bayes Detector for Orthogonal Time Frequency Space (OTFS) Modulation. IEEE Trans. Veh. Technol. 2020, 69, 7976–7980. [Google Scholar] [CrossRef]
- Hu, B.; Land, I.; Rasmussen, L.K.; Piton, R.; Fleury, B.H. A Divergence Minimization Approach to Joint Multiuser Decoding for Coded CDMA. IEEE J. Sel. Areas Commun. 2008, 26, 432–445. [Google Scholar]
- Zhong, K.; Wu, Y.; Li, S. Signal Detection for OFDM-Based Virtual MIMO Systems under Unknown Doubly Selective Chan-nels, Multiple Interferences and Phase Noises. IEEE Trans. Wirel. Commun. 2013, 12, 5309–5321. [Google Scholar] [CrossRef][Green Version]
- Bai, X.; Zhang, Y.; Zhou, F. High-Resolution Radar Imaging in Complex Environments Based on Bayesian Learning with Mixture Models. IEEE Trans. Geosci. Remote Sens. 2018, 57, 972–984. [Google Scholar] [CrossRef]
- Karseras, E.; Dai, W.; Dai, L.; Wang, Z. Fast variational Bayesian learning for channel estimation with prior statistical infor-mation. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 470–474. [Google Scholar]
- He, R.; Zhong, Z.; Ai, B.; Wang, G.; Ding, J.; Molisch, A.F. Measurements and Analysis of Propagation Channels in High-Speed Railway Viaducts. IEEE Trans. Wirel. Commun. 2012, 12, 794–805. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sen, I.; Xiong, W. The 5-GHz Airport Surface Area Channel—Part I: Measurement and Modeling Results for Large Airports. IEEE Trans. Veh. Technol. 2008, 57, 2014–2026. [Google Scholar] [CrossRef]
- Sen, I.; Matolak, D.W. The 5-GHz Airport Surface Area Channel—Part II: Measurement and Modeling Results for Small Airports. IEEE Trans. Veh. Technol. 2008, 57, 2027–2035. [Google Scholar] [CrossRef]
- Yu, J.; Chen, W.; Li, F.; Li, C.; Yang, K.; Liu, Y.; Chang, F. Channel Measurement and Modeling of the Small-Scale Fading Characteristics for Urban Inland River Environment. IEEE Trans. Wirel. Commun. 2020, 19, 3376–3389. [Google Scholar] [CrossRef]
- Tan, S.; Huang, K.; Shang, B. Sparse Bayesian Learning with joint noise robustness and signal sparsity. IET Signal Process. 2017, 11, 1104–1113. [Google Scholar] [CrossRef]
- Pedersen, N.L.; Manchon, C.N.; Shutin, D.; Fleury, B.H. Application of Bayesian Hierarchical Prior Modeling to Sparse Channel Estimation. IEEE Int. Conf. Commun. 2012, 3487–3492. [Google Scholar] [CrossRef]
- Tzikas, D.G.; Likas, A.C.; Galatsanos, N.P. The variational approximation for Bayesian inference. IEEE Signal Process. Mag. 2008, 25, 131–146. [Google Scholar] [CrossRef]
- Lee, W. Estimate of local average power of a mobile radio signal. IEEE Trans. Veh. Technol. 1985, 34, 22–27. [Google Scholar] [CrossRef]
- Fessler, J.A.; Hero, A.O. Space-alternating generalized expectation-maximization algorithm. IEEE Trans. Signal Process. 1994, 42, 2664–2677. [Google Scholar] [CrossRef]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian Compressive Sensing Using Laplace Priors. IEEE Trans. Image Process. 2009, 19, 53–63. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberger, Germany, 2006. [Google Scholar]
- McQueen, J.B. Some methods of classification and analysis in multivariate observations. In Proceedings of the Fifth Barkley Symposium on Mathematical Statistics and Probability; California University Press: Oakland, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Kusume, K.; Joham, M.; Utschick, W. MMSE block decision-feedback equalizer for spatial multiplexing with reduced com-plexity. In Proceedings of the IEEE Global Telecommunications Conference 2004, Dallas, TX, USA, 29 November–3 December 2004; Volume 4, pp. 2540–2544. [Google Scholar]
- Pakhira, M.K. A Linear Time-Complexity k-Means Algorithm Using Cluster Shifting. In Proceedings of the 2014 International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 14–16 November 2014; pp. 1047–1051. [Google Scholar]




| Procedure | VB-G | VB-GMM |
|---|---|---|
| Initialization | ||
| Variational inference |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Zhang, X.; Zhao, H.; Wei, J. Variational Sparse Bayesian Learning for Estimation of Gaussian Mixture Distributed Wireless Channels. Entropy 2021, 23, 1268. https://doi.org/10.3390/e23101268
Kong L, Zhang X, Zhao H, Wei J. Variational Sparse Bayesian Learning for Estimation of Gaussian Mixture Distributed Wireless Channels. Entropy. 2021; 23(10):1268. https://doi.org/10.3390/e23101268
Chicago/Turabian StyleKong, Lingjin, Xiaoying Zhang, Haitao Zhao, and Jibo Wei. 2021. "Variational Sparse Bayesian Learning for Estimation of Gaussian Mixture Distributed Wireless Channels" Entropy 23, no. 10: 1268. https://doi.org/10.3390/e23101268
APA StyleKong, L., Zhang, X., Zhao, H., & Wei, J. (2021). Variational Sparse Bayesian Learning for Estimation of Gaussian Mixture Distributed Wireless Channels. Entropy, 23(10), 1268. https://doi.org/10.3390/e23101268






