Discriminable Multi-Label Attribute Selection for Pre-Course Student Performance Prediction
Abstract
1. Introduction
- For the first time, we used the multi-label attribute selection method to transform the pre-class student performance prediction problem into a multi-label learning model, and then applied the attribute reduction method to scientifically streamline the characteristic information of the courses taken, along with mining the characteristics of the previous courses for the upcoming advanced or upper courses. The attributes of the curriculum were significant in studying academic early warning from a new perspective, from pre-class student performance prediction to subsequent courses;
- We perceived the task as a multi-label learning problem, which can fully uncover the correlation between the students’ previous course information and multiple target courses, so as to detect and screen out high-risk students in each course prior to the start of the course;
- We collected a new set of student performance prediction data, and proposed a novel multi-label attribute selection method, which improved the ability to express feature information of the previously completed courses.
2. Related Work
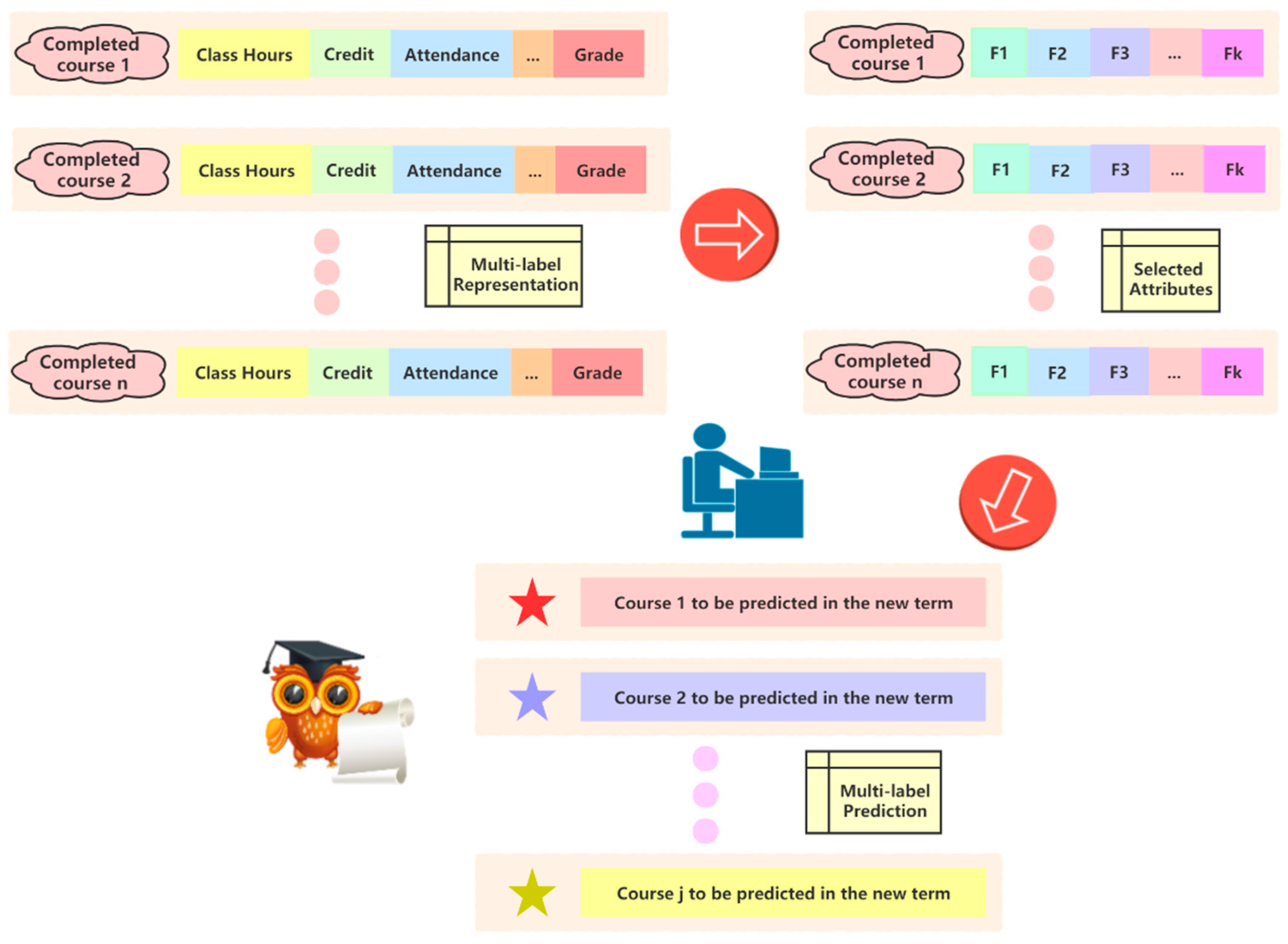
3. Methods
3.1. Multi-Label Learning
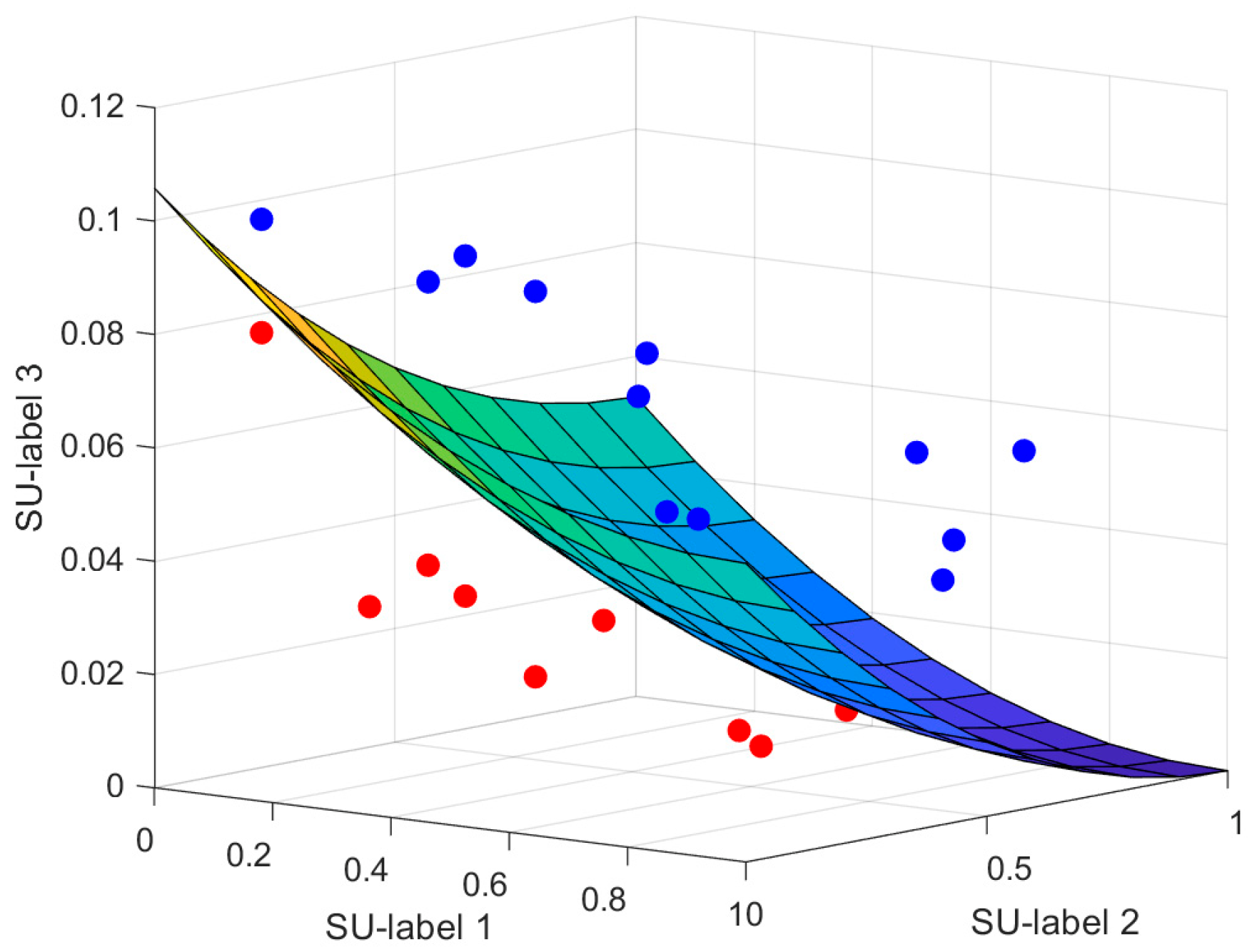
3.2. Multi-Label Attribute Selection
4. Results
4.1. Data Preparation
4.2. Evaluation Indicators
4.3. Experimental Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tomasevic, N.; Gvozdenovic, N.; Vranes, S. An overview and comparison of supervised data mining techniques for student exam performance prediction. Comput. Educ. 2019, 143, 103676. [Google Scholar] [CrossRef]
- Sweeney, M.; Rangwala, H.; Lester, J.; Johri, A. Next-term student performance prediction: A recommender systems approach. arXiv 2016, arXiv:1604.01840. [Google Scholar]
- Grayson, A.; Miller, H.; Clarke, D.D. Identifying barriers to help-seeking: A qualitative analysis of students preparedness to seek help from tutors. Br. J. Guid. Couns. 1998, 26, 237–253. [Google Scholar] [CrossRef]
- Sweeney, M.; Lester, J.; Rangwala, H. Next-term student grade prediction. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), New York City, NY, USA, 27 June–2 July 2015; pp. 970–975. [Google Scholar]
- Palacios, C.; Reyes-Suárez, J.; Bearzotti, L.; Leiva, V.; Marchant, C. Knowledge Discovery for Higher Education Student Retention Based on Data Mining: Machine Learning Algorithms and Case Study in Chile. Entropy 2021, 23, 485. [Google Scholar] [CrossRef] [PubMed]
- Adelman, C.; Daniel, B.; Berkovits, I. Postsecondary Attainment, Attendance, Curriculum, and Performance: Selected Results from the NELS: 88/2000 Postsecondary Education Transcript Study (PETS), 2000. ED Tabs. Educ. Technol. Soc. 2003. Available online: https://eric.ed.gov/?id=ED480959 (accessed on 10 September 2021).
- Huang, S.; Yang, J.; Fong, S.; Zhao, Q. Mining Prognosis Index of Brain Metastases Using Artificial Intelligence. Cancers 2019, 11, 1140. [Google Scholar] [CrossRef]
- Yang, J.; Fong, S.; Wang, H.; Hu, Q.; Lin, C.; Huang, S.; Shi, J.; Lan, K.; Tang, R.; Wu, Y.; et al. Artificial intelligence in ophthalmopathy and ultra-wide field image: A survey. Expert Syst. Appl. 2021, 182, 115068. [Google Scholar] [CrossRef]
- Yang, J.; Ji, Z.; Liu, S.; Jia, Q. Multi-objective optimization based on Pareto optimum in secondary cooling and EMS of Continuous casting. In Proceedings of the 2016 International Conference on Advanced Robotics and Mechatronics (ICARM), Macau, China, 18–20 August 2016; Institute of Electrical and Electronics Engineers (IEEE): Macau, China, 2016; pp. 283–287. [Google Scholar]
- Hu, Q.; Yang, J.; Qin, P.; Fong, S.; Guo, J. Could or could not of Grid-Loc: Grid BLE structure for indoor localisation system using machine learning. Serv. Oriented Comput. Appl. 2020, 14, 161–174. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, J.; Qin, P.; Fong, S. Towards a Context-Free Machine Universal Grammar (CF-MUG) in Natural Language Processing. IEEE Access 2020, 8, 165111–165129. [Google Scholar] [CrossRef]
- Hu, Q.; Qin, P.; Yang, J.; Fong, S. An enhanced particle swarm optimization with distribution fields appearance model for object tracking. Int. J. Wavelets Multiresolut. Inf. Process. 2020, 19, 2050065. [Google Scholar] [CrossRef]
- Chaiyanan, C.; Iramina, K.; Kaewkamnerdpong, B. Investigation on Identifying Implicit Learning Event from EEG Signal Using Multiscale Entropy and Artificial Bee Colony. Entropy 2021, 23, 617. [Google Scholar] [CrossRef]
- Sepasgozar, S.M. Digital Twin and Web-Based Virtual Gaming Technologies for Online Education: A Case of Construction Management and Engineering. Appl. Sci. 2020, 10, 4678. [Google Scholar] [CrossRef]
- Bernacki, M.L.; Chavez, M.M.; Uesbeck, P.M. Predicting Achievement and Providing Support before STEM Majors Begin to Fail. Comput. Educ. 2020, 158, 103999. [Google Scholar] [CrossRef]
- Marbouti, F.; Diefes-Dux, H.; Madhavan, K. Models for early prediction of at-risk students in a course using standards-based grading. Comput. Educ. 2016, 103, 1–15. [Google Scholar] [CrossRef]
- Meier, Y.; Xu, J.; Atan, O.; Van der Schaar, M. Predicting grades. IEEE Trans. Signal. Process. 2015, 64, 959–972. [Google Scholar] [CrossRef]
- Gedeon, T.; Turner, H. Explaining student grades predicted by a neural network. In Proceedings of the International Conference on Neural Networks, Nagoya, Japan, 5–29 October 1993; pp. 609–612. [Google Scholar]
- Acharya, A.; Sinha, D. Early Prediction of Students Performance using Machine Learning Techniques. Int. J. Comput. Appl. 2014, 107, 37–43. [Google Scholar] [CrossRef]
- Huang, S.; Fang, N. Predicting student academic performance in an engineering dynamics course: A comparison of four types of predictive mathematical models. Comput. Educ. 2013, 61, 133–145. [Google Scholar] [CrossRef]
- Asselman, A.; Khaldi, M.; Aammou, S. Evaluating the impact of prior required scaffolding items on the improvement of student performance prediction. Educ. Inf. Technol. 2020, 25, 3227–3249. [Google Scholar] [CrossRef]
- Ma, Y.; Cui, C.; Nie, X.; Yang, G.; Shaheed, K.; Yin, Y. Pre-course student performance prediction with multi-instance multi-label learning. Sci. China Inf. Sci. 2018, 62, 29101. [Google Scholar] [CrossRef]
- Tan, R.Z.; Wang, P.C.; Lim, W.H.; Ong, S.H.C.; Avnit, K. Early Prediction of Students Mathematics Performance. IEEE 2018, 651–656. [Google Scholar] [CrossRef]
- Li, Q.; Baker, R. The different relationships between engagement and outcomes across participant subgroups in Massive Open Online Courses. Comput. Educ. 2018, 127, 41–65. [Google Scholar] [CrossRef]
- Ren, Z.; Rangwala, H.; Johri, A. Predicting performance on MOOC assessments using multi-regression models. arXiv 2016, arXiv:1605.02269. [Google Scholar]
- Trivedi, S.; Pardos, Z.A.; Heffernan, N.T. Clustering Students to Generate an Ensemble to Improve Standard Test Score Predictions. In International Conference on Artificial Intelligence in Education; Springer: Berlin/Heidelberg, Germany, 2011; pp. 377–384. [Google Scholar] [CrossRef]
- Er, E. Identifying At-Risk Students Using Machine Learning Techniques: A Case Study with IS 100. Int. J. Mach. Learn. Comput. 2012, 2, 476–480. [Google Scholar] [CrossRef][Green Version]
- Hu, Y.-H.; Lo, C.-L.; Shih, S.-P. Developing early warning systems to predict students’ online learning performance. Comput. Hum. Behav. 2014, 36, 469–478. [Google Scholar] [CrossRef]
- Macfadyen, L.P.; Dawson, S. Mining LMS data to develop an “early warning system” for educators: A proof of concept. Comput. Educ. 2010, 5, 588–599. [Google Scholar] [CrossRef]
- Zafra, A.; Romero, C.; Ventura, S. Multiple instance learning for classifying students in learning management systems. Expert Syst. Appl. 2011, 38, 15020–15031. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Pierrakeas, C.; Pintelas, P.E. Preventing Student Dropout in Distance Learning Using Machine Learning Techniques. In International Conference on Knowledge-Based and Intelligent Information and Engineering Systems; Springer: Berlin, Germany, 2003; pp. 267–274. [Google Scholar]
- Xenos, M. Prediction and assessment of student behaviour in open and distance education in computers using Bayesian networks. Comput. Educ. 2004, 43, 345–359. [Google Scholar] [CrossRef]
- Wang, A.Y.; Newlin, M.H.; Tucker, T.L. A Discourse Analysis of Online Classroom Chats: Predictors of Cyber-Student Performance. Teach. Psychol. 2001, 28, 222–226. [Google Scholar] [CrossRef]
- Wang, A.Y.; Newlin, M.H. Predictors of performance in the virtual classroom: Identifying and helping at-risk cyber-students. J. Technol. Horiz. Educ. 2002, 29, 21. [Google Scholar]
- Lopez, M.I.; Luna, J.M.; Romero, C.; Ventura, S. Classification via clustering for predicting final marks based on student participation in forums. Int. Educ. Data Min. Soc. 2012. Available online: https://eric.ed.gov/?id=ED537221 (accessed on 10 September 2021).
- Conijn, R.; Van den Beemt, A.; Cuijpers, P. Predicting student performance in a blended MOOC. J. Comput. Assist. Learn. 2018, 34, 615–628. [Google Scholar] [CrossRef]
- Moscoso-Zea, O.; Saa, P.; Luján-Mora, S. Evaluation of algorithms to predict graduation rate in higher education institutions by applying educational data mining. Australas. J. Eng. Educ. 2019, 24, 4–13. [Google Scholar]
- Elayyan, S. The future of education according to the fourth industrial revolution. J. Educ. Technol. Online Learn. 2021, 4, 23–30. [Google Scholar]
- Ma, Y.; Cui, C.; Yu, J.; Guo, J.; Yang, G.; Yin, Y. Multi-task MIML learning for pre-course student performance prediction. Front. Comput. Sci. 2020, 14, 145313. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zhou, Z.-H. A review on multi-label learning algorithms. IEEE Trans. Knowl. Data Eng. 2013, 26, 1819–1837. [Google Scholar] [CrossRef]
- Boutell, M.R.; Luo, J.; Shen, X.; Brown, C.M. Learning multi-label scene classification. Pattern Recognit. 2004, 37, 1757–1771. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Zhou, Z.-H. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef]
- Kashef, S.; Nezamabadi-Pour, H. A label-specific multi-label feature selection algorithm based on the Pareto dominance concept. Pattern Recognit. 2018, 88, 654–667. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Yang, J.; Fong, S.; Li, T. Attribute Reduction Based on Multi-objective Decomposition-Ensemble Optimizer with Rough Set and Entropy. In 2019 International Conference on Data Mining Workshops (ICDMW); IEEE: Beijing, China, 2019; pp. 673–680. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Yin, J.; Tao, T.; Xu, J. A Multi-label feature selection algorithm based on multi-objective optimization. In 2015 International Joint Conference on Neural Networks (IJCNN); Killarney Convention Centre: Killarney, Ireland, 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Sun, X.-Y.; Guo, Y. A PSO-based multi-objective multi-label feature selection method in classification. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef]
- Yu, K.; Ding, W.; Wu, X. LOFS: A library of online streaming feature selection. Knowl. Based Syst. 2016, 113, 1–3. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Weng, W.; Zhang, J.; Chen, B.; Wu, S. Feature selection for multi-label learning with streaming label. Neurocomputing 2020, 387, 268–278. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Peña, J.M.; Robles, V. Feature selection for multi-label naive Bayes classification. Inf. Sci. 2009, 179, 3218–3229. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.-H. Multilabel dimensionality reduction via dependence maximization. ACM Trans. Knowl. Discov. Data 2010, 4, 1–21. [Google Scholar] [CrossRef]
- Lin, Y.; Li, Y.; Wang, C.; Chen, J. Attribute reduction for multi-label learning with fuzzy rough set. Knowl. Based Syst. 2018, 152, 51–61. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, Q.; Liu, J.; Chen, J.; Duan, J. Multi-label feature selection based on neighborhood mutual information. Appl. Soft Comput. 2016, 38, 244–256. [Google Scholar] [CrossRef]
- Spolaôr, N.; Cherman, E.A.; Monard, M.C.; Lee, H.D. ReliefF for multi-label feature selection. In Proceedings of the Brazilian Conference on Intelligent Systems, Fortaleza, Brazil, 19–24 October 2013; pp. 6–11. [Google Scholar]
- Lee, J.; Lim, H.; Kim, D.-W. Approximating mutual information for multi-label feature selection. Electron. Lett. 2012, 48, 929–930. [Google Scholar] [CrossRef]
- Jian, L.; Li, J.; Shu, K.; Liu, H. Multi-label informed feature selection. IJCAI 2016, 16, 1627–1633. [Google Scholar]


| Authors | Year | Features |
|---|---|---|
| Macfadyen and Dawson [29] | 2010 | Predictive modeling of students’ final grades using factors such as student discussion information, number of emails sent, and test completion. |
| Zafra et al. [30] | 2011 | Use of information such as quizzes, assignments, forums, etc., to predict whether a student will pass or fail the course. |
| Sweeny et al. [4] | 2015 | Predicting grades for the next semester based on information about students’ grades in completed courses. |
| Ren et al. [25] | 2016 | Applying data from MOOC server logs to predict learning outcomes. |
| Conijn et al. [36] | 2018 | Predicting student performance and discovering the potential for MOOC improvements. |
| Oswaldo et al. [37] | 2019 | Comparing different educational data mining (EDM) algorithms to discover research trends and patterns in graduation rate indicators. |
| Ma et al. [22] | 2020 | Multi-instance multi-label learning for pre-course student performance prediction. |
| Ma et al. [36] | 2020 | Multi-instance multi-label learning with multi-task learning for pre-course student performance prediction. |
| Data Sets | Instances | Features | Labels | Train | Test |
|---|---|---|---|---|---|
| CEE01 | 102 | 164 | 4 | 87 | 15 |
| CEE02 | 58 | 153 | 3 | 49 | 9 |
| CEE03 | 64 | 153 | 3 | 54 | 10 |
| CAE01 | 83 | 175 | 5 | 71 | 12 |
| CAE02 | 61 | 164 | 4 | 52 | 9 |
| CFE01 | 205 | 142 | 4 | 174 | 31 |
| CFE02 | 137 | 153 | 5 | 116 | 21 |
| CBC01 | 92 | 186 | 7 | 78 | 14 |
| CBC02 | 86 | 175 | 6 | 73 | 13 |
| CAL01 | 317 | 231 | 10 | 269 | 48 |
| Datasets | AMI [56] | RF-ML [55] | MFNMI [54] | MDDMproj [52] | MLFRS [53] | MLNB [51] | AMuL |
|---|---|---|---|---|---|---|---|
| CEE01 | 0.81 | 0.81 | 0.81 | 0.80 | 0.81 | 0.81 | 0.81 |
| CEE02 | 0.84 | 0.78 | 0.83 | 0.81 | 0.80 | 0.83 | 0.84 |
| CEE03 | 0.78 | 0.78 | 0.79 | 0.77 | 0.80 | 0.74 | 0.80 |
| CAE01 | 0.75 | 0.75 | 0.74 | 0.51 | 0.74 | 0.75 | 0.75 |
| CAE02 | 0.75 | 0.76 | 0.74 | 0.75 | 0.75 | 0.77 | 0.77 |
| CFE01 | 0.61 | 0.99 | 0.83 | 0.61 | 0.85 | 0.69 | 0.89 |
| CFE02 | 0.80 | 0.80 | 0.80 | 0.80 | 0.81 | 0.81 | 0.81 |
| CBC01 | 0.88 | 0.89 | 0.88 | 0.85 | 0.89 | 0.89 | 0.89 |
| CBC02 | 0.85 | 0.86 | 0.87 | 0.86 | 0.86 | 0.82 | 0.88 |
| CAL01 | 0.76 | 0.73 | 0.75 | 0.78 | 0.81 | 0.80 | 0.80 |
| Win/Draw/Loss | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 9/0/1 | 9/1/0 | - |
| Datasets | AMI [56] | RF-ML [55] | MFNMI [54] | MDDMproj [52] | MLFRS [53] | MLNB [51] | AMuL |
|---|---|---|---|---|---|---|---|
| CEE01 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 | 0.17 |
| CEE02 | 0.16 | 0.21 | 0.17 | 0.19 | 0.19 | 0.20 | 0.16 |
| CEE03 | 0.23 | 0.24 | 0.23 | 0.25 | 0.23 | 0.23 | 0.23 |
| CAE01 | 0.16 | 0.14 | 0.12 | 0.12 | 0.10 | 0.10 | 0.10 |
| CAE02 | 0.17 | 0.16 | 0.16 | 0.16 | 0.17 | 0.16 | 0.16 |
| CFE01 | 0.08 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 |
| CFE02 | 0.07 | 0.07 | 0.07 | 0.08 | 0.07 | 0.07 | 0.07 |
| CBC01 | 0.13 | 0.13 | 0.14 | 0.14 | 0.13 | 0.13 | 0.10 |
| CBC02 | 0.11 | 0.10 | 0.10 | 0.10 | 0.11 | 0.12 | 0.10 |
| CAL01 | 0.17 | 0.18 | 0.17 | 0.16 | 0.17 | 0.17 | 0.16 |
| Win/Draw/Loss | 10/0/0 | 10/0/0 | 10/0/0 | 10/0/0 | 9/0/1 | 9/1/0 | - |
| Datasets | AMI [56] | RF-ML [55] | MFNMI [54] | MDDMproj [52] | MLFRS [53] | MLNB [51] | AMuL |
|---|---|---|---|---|---|---|---|
| CEE01 | 0.072 | 0.069 | 0.065 | 0.064 | 0.061 | 0.057 | 0.057 |
| CEE02 | 0.060 | 0.064 | 0.066 | 0.067 | 0.059 | 0.063 | 0.057 |
| CEE03 | 0.055 | 0.060 | 0.052 | 0.062 | 0.064 | 0.058 | 0.052 |
| CAE01 | 0.075 | 0.072 | 0.078 | 0.064 | 0.076 | 0.074 | 0.066 |
| CAE02 | 0.083 | 0.083 | 0.087 | 0.086 | 0.078 | 0.079 | 0.078 |
| CFE01 | 0.044 | 0.045 | 0.048 | 0.048 | 0.056 | 0.043 | 0.050 |
| CFE02 | 0.049 | 0.054 | 0.052 | 0.047 | 0.058 | 0.049 | 0.046 |
| CBC01 | 0.036 | 0.026 | 0.031 | 0.035 | 0.033 | 0.029 | 0.028 |
| CBC02 | 0.041 | 0.045 | 0.035 | 0.047 | 0.035 | 0.040 | 0.034 |
| CAL01 | 0.088 | 0.074 | 0.081 | 0.070 | 0.076 | 0.082 | 0.070 |
| Win/Draw/Loss | 10/0/0 | 9/0/1 | 10/0/0 | 9/0/1 | 10/0/0 | 08/1/1 | - |
| Datasets | AMI [56] | RF-ML [55] | MFNMI [54] | MDDMproj [52] | MLFRS [53] | MLNB [51] | AMuL |
|---|---|---|---|---|---|---|---|
| CEE01 | 3.86 | 3.78 | 3.84 | 3.83 | 3.83 | 3.82 | 3.75 |
| CEE02 | 4.61 | 4.51 | 3.83 | 4.10 | 4.11 | 4.33 | 3.55 |
| CEE03 | 5.08 | 5.26 | 4.95 | 5.41 | 5.25 | 5.05 | 4.95 |
| CAE01 | 3.65 | 3.18 | 3.55 | 3.71 | 3.46 | 3.06 | 2.78 |
| CAE02 | 3.50 | 3.56 | 3.52 | 3.64 | 3.74 | 3.52 | 3.50 |
| CFE01 | 3.09 | 3.04 | 3.11 | 3.10 | 3.08 | 2.93 | 2.93 |
| CFE02 | 2.53 | 2.47 | 2.46 | 2.50 | 2.51 | 2.70 | 2.42 |
| CBC01 | 1.85 | 1.82 | 1.88 | 1.95 | 1.84 | 1.82 | 1.81 |
| CBC02 | 1.88 | 1.86 | 1.87 | 1.84 | 1.82 | 1.85 | 1.79 |
| CAL01 | 3.79 | 3.94 | 3.80 | 3.56 | 3.76 | 3.58 | 3.25 |
| Win/Draw/Loss | 10/0/0 | 10/0/0 | 9/0/1 | 10/0/0 | 10/0/0 | 9/1/0 | - |
| Datasets | AMI [56] | RF-ML [55] | MFNMI [54] | MDDMproj [52] | MLFRS [53] | MLNB [51] | AMuL |
|---|---|---|---|---|---|---|---|
| CEE01 | 0.36 | 0.34 | 0.33 | 0.32 | 0.30 | 0.29 | 0.28 |
| CEE02 | 0.30 | 0.32 | 0.33 | 0.33 | 0.30 | 0.32 | 0.29 |
| CEE03 | 0.27 | 0.30 | 0.26 | 0.31 | 0.32 | 0.29 | 0.26 |
| CAE01 | 0.38 | 0.36 | 0.39 | 0.32 | 0.38 | 0.37 | 0.33 |
| CAE02 | 0.41 | 0.42 | 0.44 | 0.43 | 0.39 | 0.38 | 0.39 |
| CFE01 | 0.22 | 0.23 | 0.24 | 0.24 | 0.28 | 0.22 | 0.25 |
| CFE02 | 0.25 | 0.27 | 0.26 | 0.24 | 0.29 | 0.25 | 0.23 |
| CBC01 | 0.18 | 0.13 | 0.15 | 0.17 | 0.17 | 0.15 | 0.19 |
| CBC02 | 0.20 | 0.22 | 0.18 | 0.24 | 0.18 | 0.20 | 0.17 |
| CAL01 | 0.44 | 0.27 | 0.41 | 0.35 | 0.38 | 0.41 | 0.35 |
| Win/Draw/Loss | 10/0/0 | 9/0/1 | 9/1/0 | 10/0/0 | 10/0/0 | 9/0/1 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Hu, S.; Wang, Q.; Fong, S. Discriminable Multi-Label Attribute Selection for Pre-Course Student Performance Prediction. Entropy 2021, 23, 1252. https://doi.org/10.3390/e23101252
Yang J, Hu S, Wang Q, Fong S. Discriminable Multi-Label Attribute Selection for Pre-Course Student Performance Prediction. Entropy. 2021; 23(10):1252. https://doi.org/10.3390/e23101252
Chicago/Turabian StyleYang, Jie, Shimin Hu, Qichao Wang, and Simon Fong. 2021. "Discriminable Multi-Label Attribute Selection for Pre-Course Student Performance Prediction" Entropy 23, no. 10: 1252. https://doi.org/10.3390/e23101252
APA StyleYang, J., Hu, S., Wang, Q., & Fong, S. (2021). Discriminable Multi-Label Attribute Selection for Pre-Course Student Performance Prediction. Entropy, 23(10), 1252. https://doi.org/10.3390/e23101252






