Connection between Inverse Engineering and Optimal Control in Shortcuts to Adiabaticity
Abstract
1. Introduction
2. Fast Cooling in Time-Varying Harmonic Traps
2.1. Model, Hamiltonian, and the Inverse Engineering Approach
2.2. Optimal Control Theory
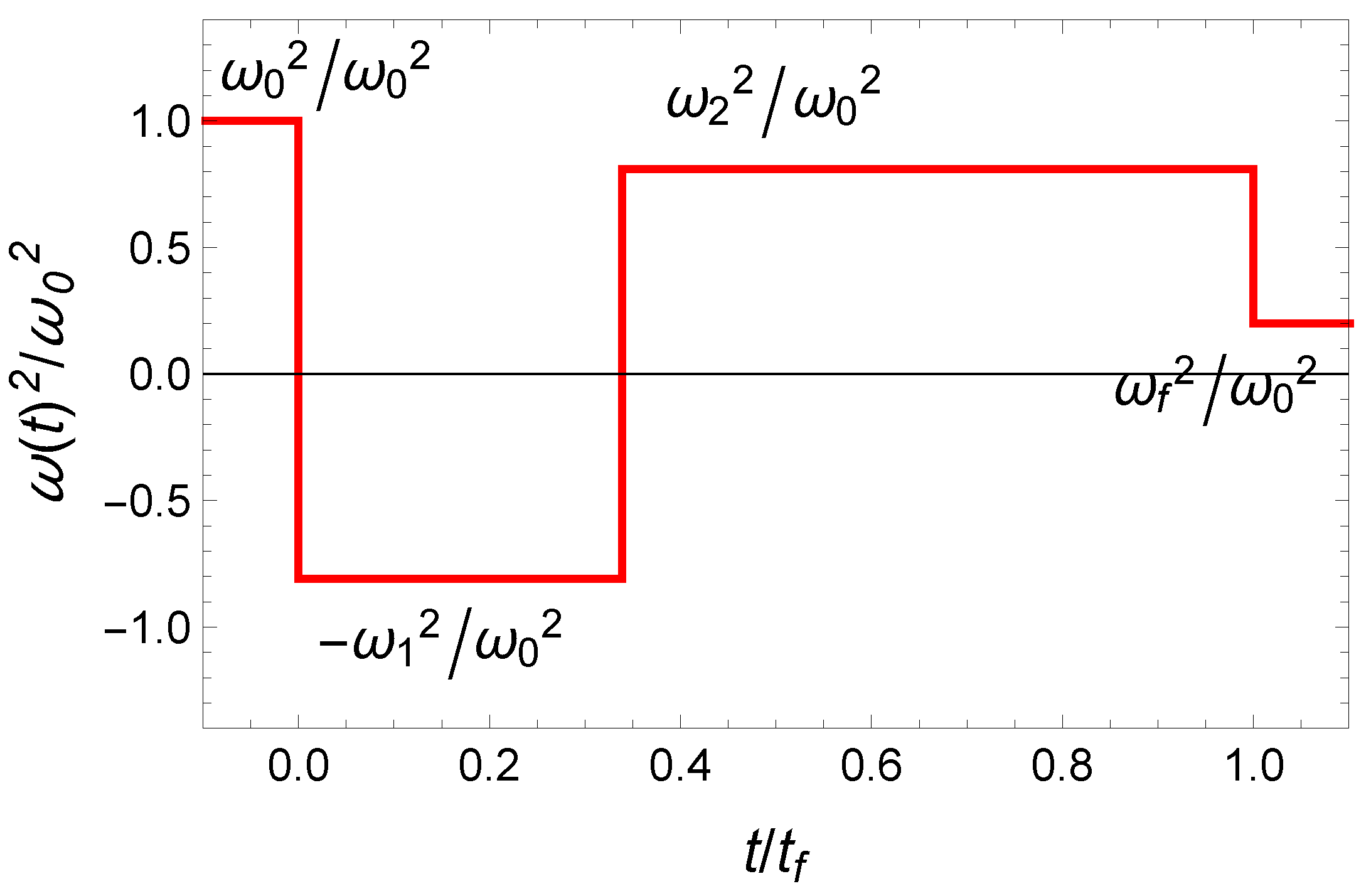
2.2.1. Time-Optimal Solution
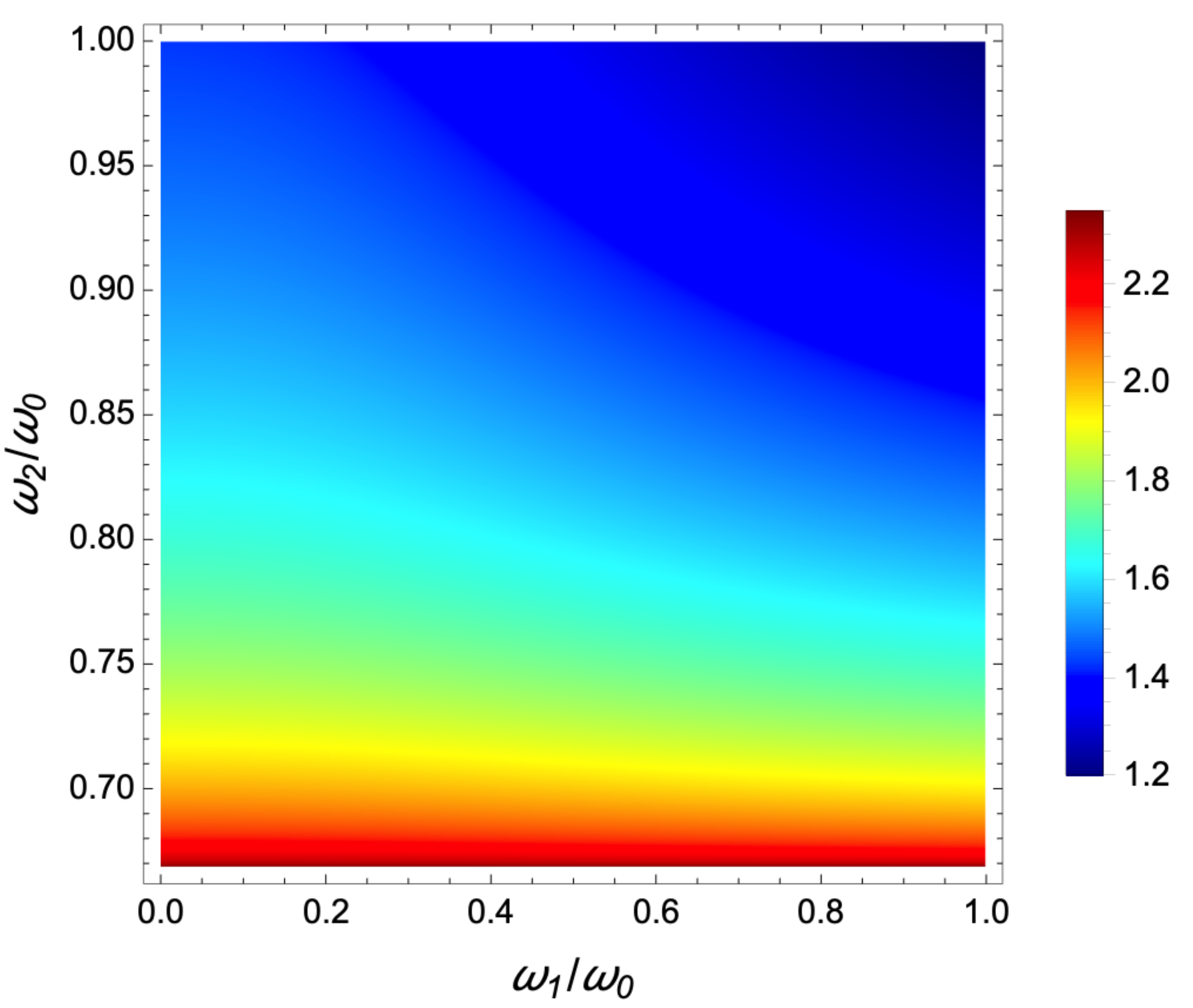
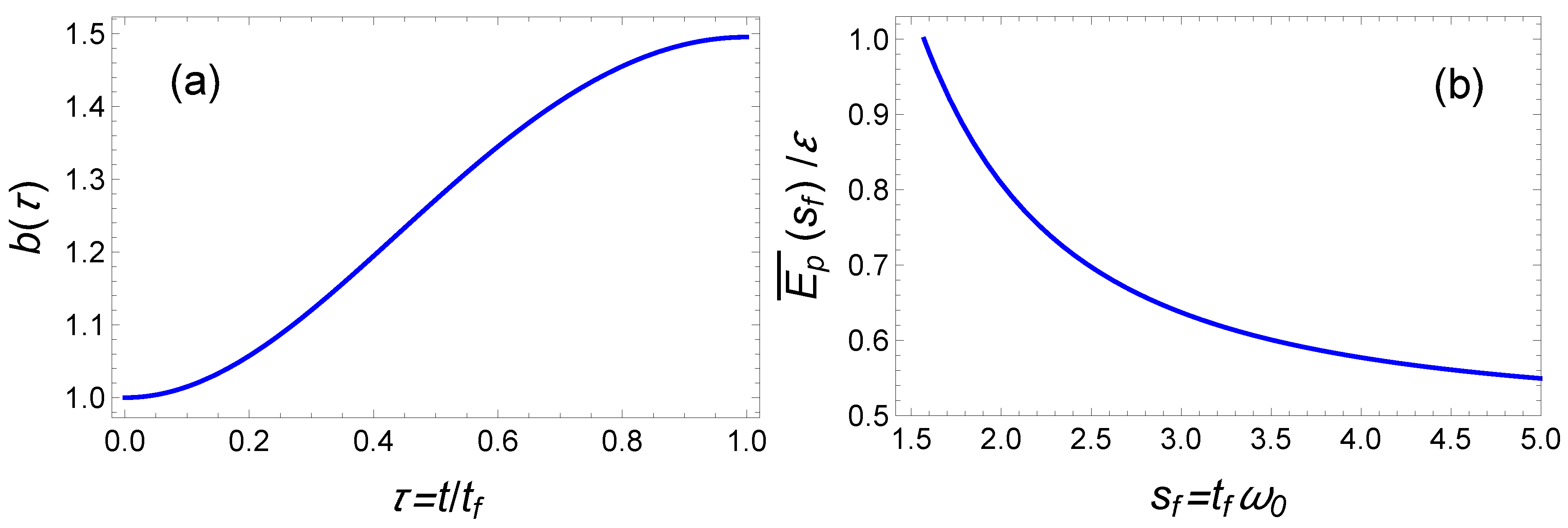
2.2.2. Time-Averaged Energy Minimization
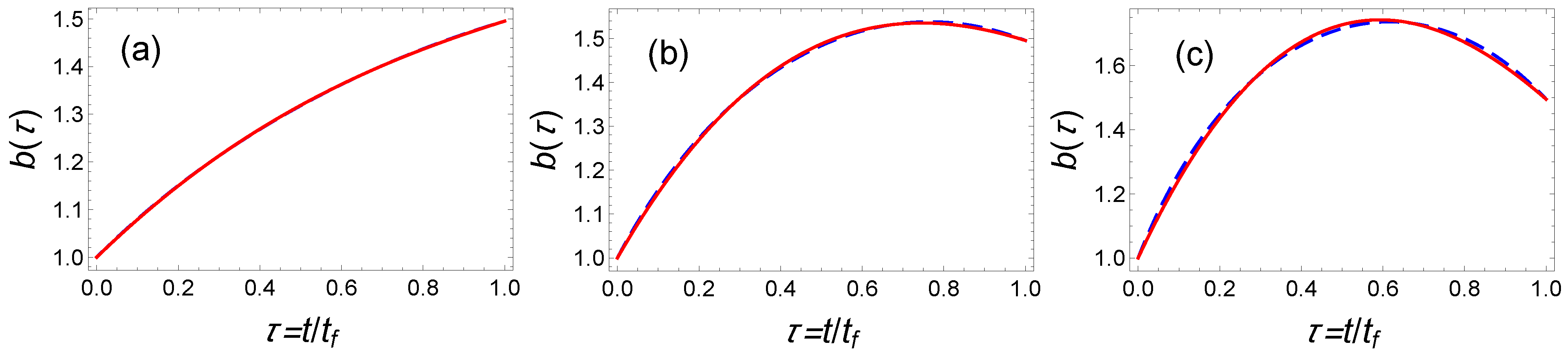
2.3. Comparison between IE and OCT
3. Fast Transport of Atoms in Moving Harmonic Traps
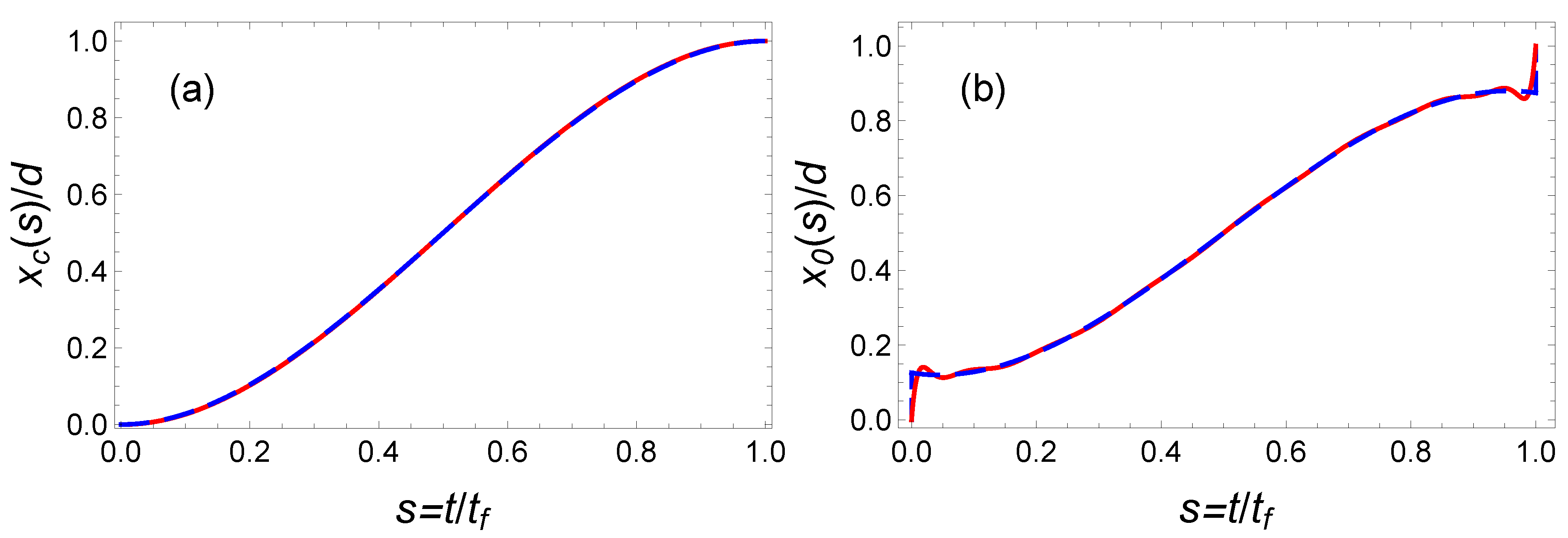
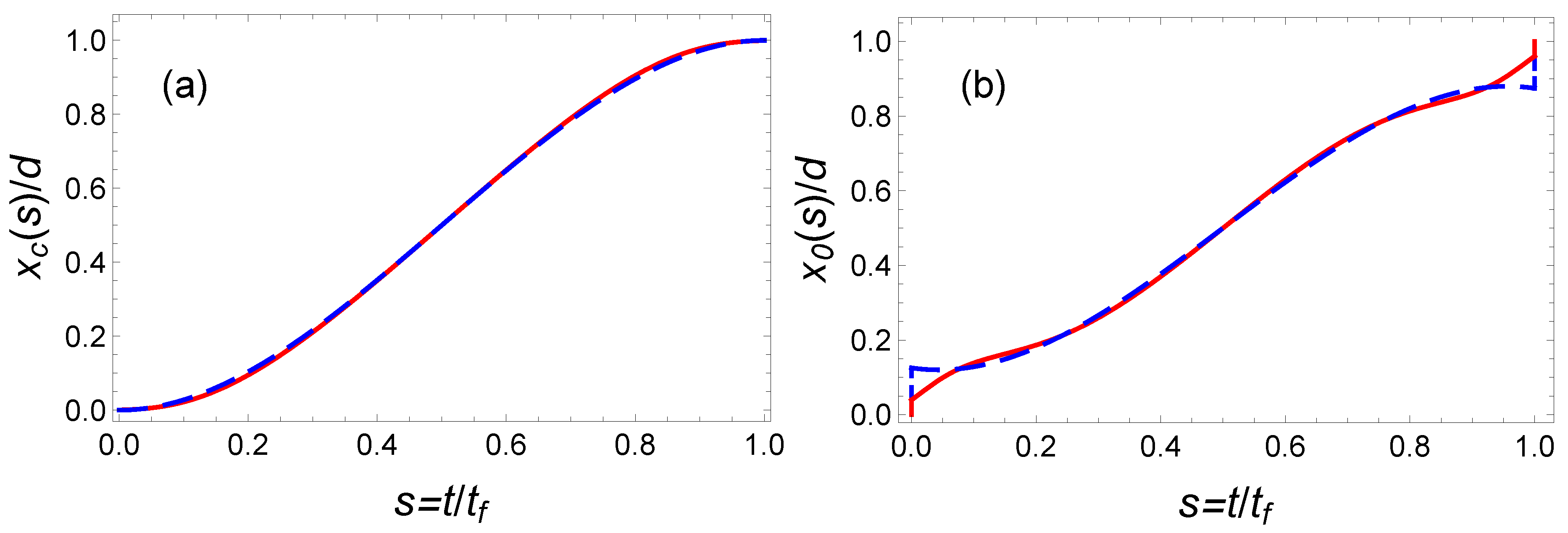
3.1. Classical and Quantum Inverse-Engineered Solutions
3.2. Optimal Control Theory
3.2.1. Time Minimization
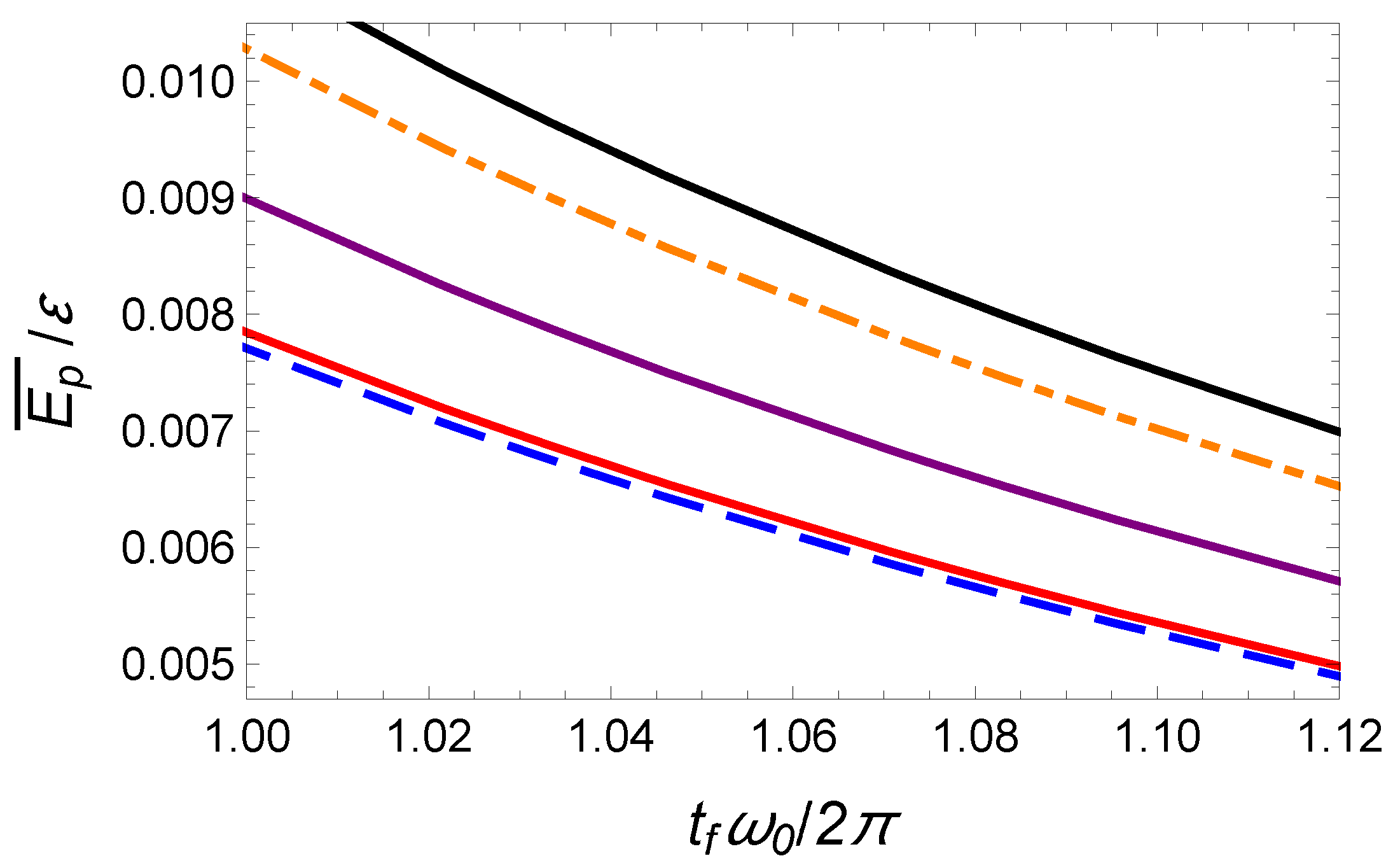
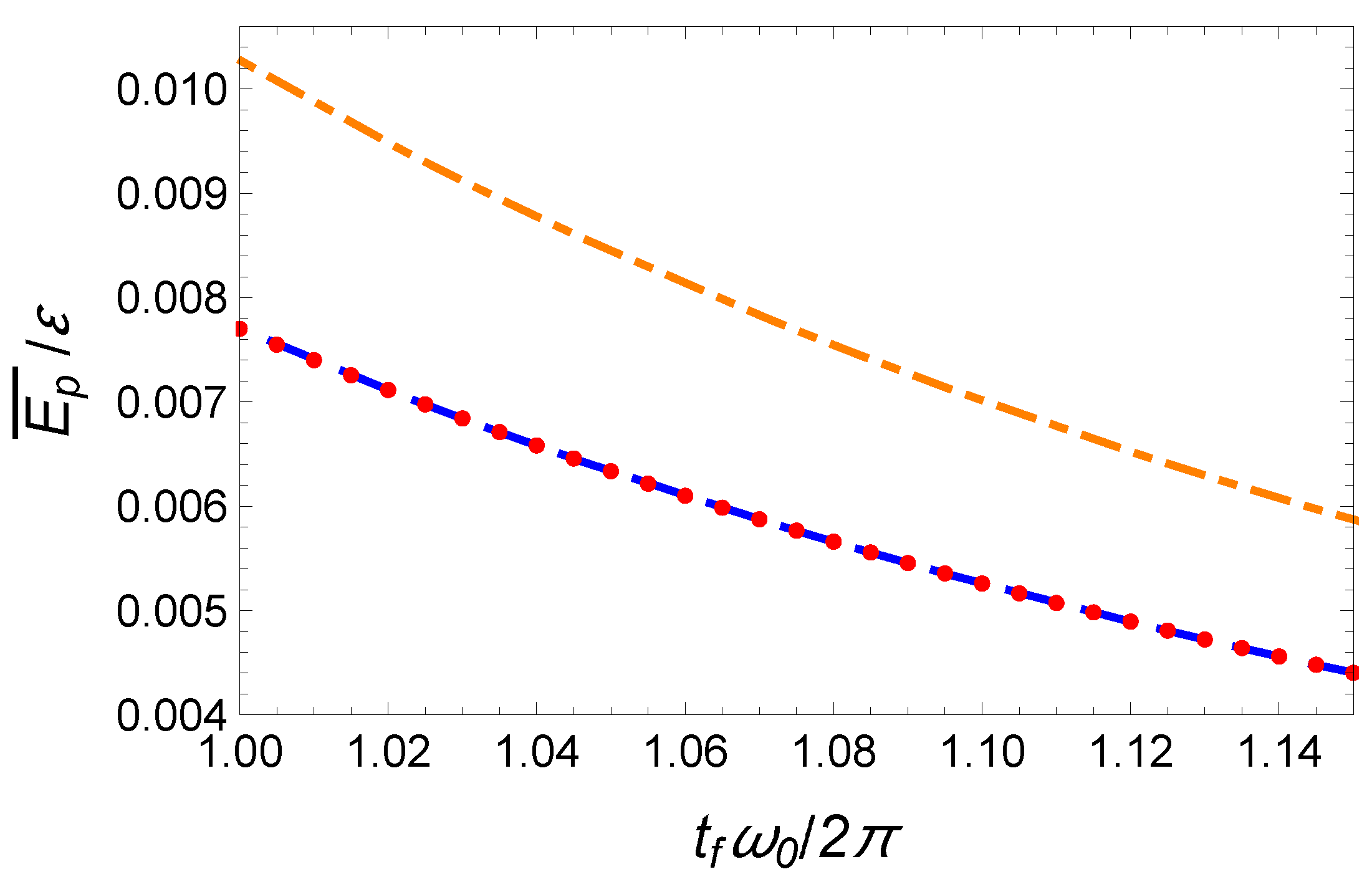
3.2.2. Mean Potential Energy Minimization
3.3. Comparison between IE and OCT
3.3.1. IE with Polynomial Ansatzs
3.3.2. IE with Hyperbolic Ansatz
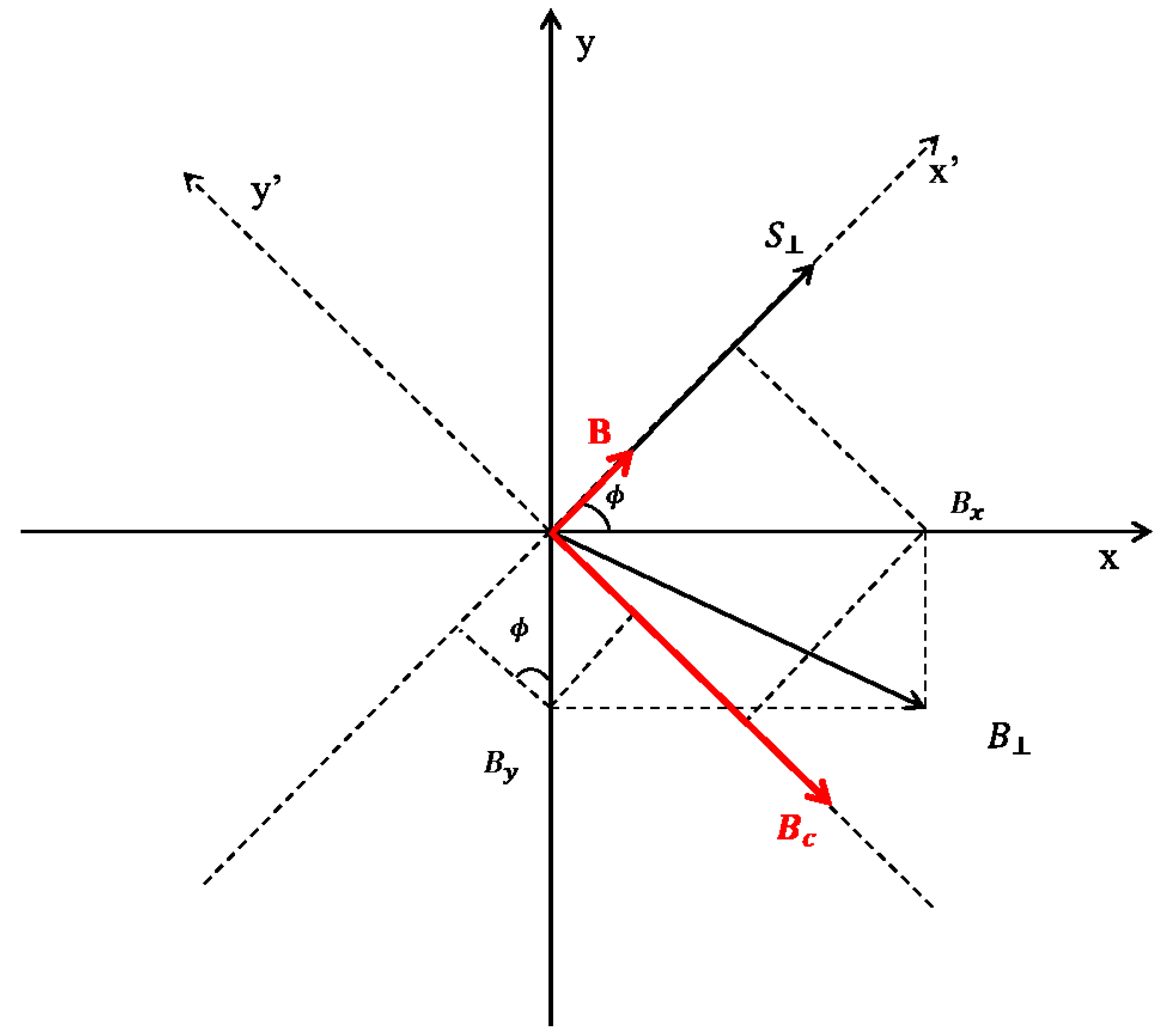
4. Spin Dynamics in the Presence of Dissipation
4.1. Energy Minimization by OCT
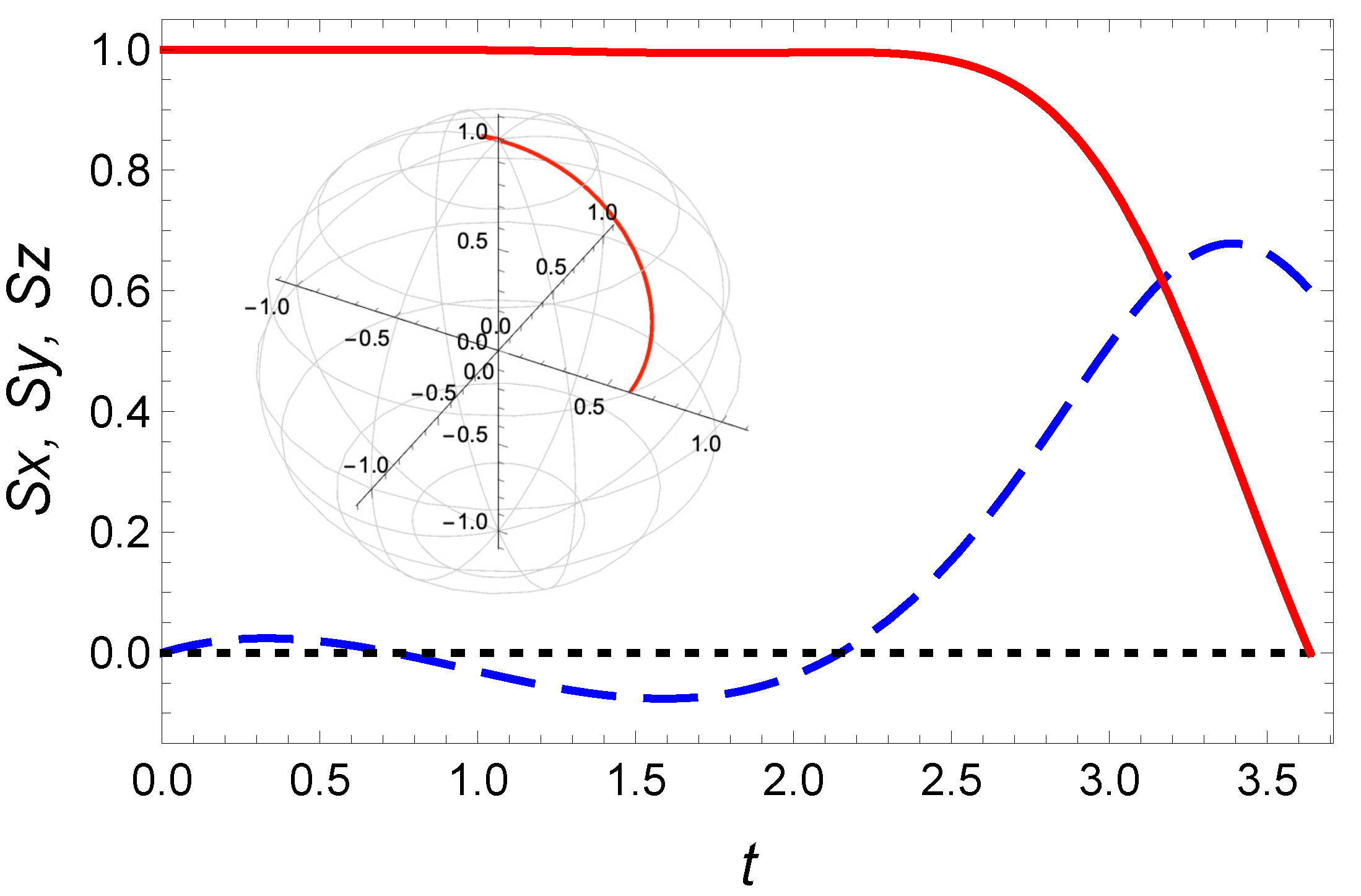
4.2. Case I: Reaching the Horizontal Plane of the Bloch Sphere
4.3. Case II: Spin Flip
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| STA | shortcuts to adiabaticity |
| IE | inverse engineering |
| OCT | optimal control theory |
References
- Torrontegui, E.; Ibánez, S.; Martínez-Garaot, S.; Modugno, M.; del Campo, A.; Guéry-Odelin, D.; Ruschhaupt, A.; Chen, X.; Muga, J.G. Shortcuts to adiabaticity. In Advances in Atomic, Molecular, and Optical Physics; Arimondo, E., Berman, P.R., Lin, C.C., Eds.; Academic Press: Cambridge, MA, USA, 2013; Volume 62, pp. 117–169. [Google Scholar]
- Guéry-Odelin, D.; Ruschhaupt, A.; Kiely, A.; Torrontegui, E.; Martínez-Garaot, S.; Muga, J.G. Shortcuts to adiabaticity: Concepts, methods, and applications. Rev. Mod. Phys. 2019, 91, 045001. [Google Scholar] [CrossRef]
- Guéry-Odelin, D.; Muga, J.G.; Ruiz-Montero, M.J.; Trizac, E. Nonequilibrium solutions of the boltzmann equation under the action of an external force. Phys. Rev. Lett. 2014, 112, 180602. [Google Scholar] [CrossRef] [PubMed]
- Martínez, I.A.; Petrosyan, A.; Guéry-Odelin, D.; Trizac, E.; Ciliberto, S. Engineered swift equilibration of a Brownian particle. Nat. Phys. 2016, 12, 843–846. [Google Scholar] [CrossRef]
- Chung, H.C.; Martínez-Garaot, S.; Chen, X.; Muga, J.G.; Tseng, S.Y. Shortcuts to adiabaticity in optical waveguides. EPL (Europhys. Lett.) 2019, 127, 34001. [Google Scholar] [CrossRef]
- Faure, S.; Ciliberto, S.; Trizac, E.; Guéry-Odelin, D. Shortcut to stationary regimes: A simple experimental demonstration. Am. J. Phys. 2019, 87, 125–129. [Google Scholar] [CrossRef]
- Jarzynski, C. Generating shortcuts to adiabaticity in quantum and classical dynamics. Phys. Rev. A 2013, 88, 040101. [Google Scholar] [CrossRef]
- Jarzynski, C.; Deffner, S.; Patra, A.; Subasi, Y. Fast forward to the classical adiabatic invariant. Phys. Rev. E 2017, 95, 032122. [Google Scholar] [CrossRef]
- Li, Y.; Wu, L.-A.; Wang, Z. Fast ground-state cooling of mechanical resonators with time-dependent optical cavities. Phys. Rev. A 2011, 83, 043804. [Google Scholar] [CrossRef]
- Masuda, S.; Nakamura, K. Fast-forward problem in quantum mechanics. Phys. Rev. A 2008, 78, 062108. [Google Scholar] [CrossRef]
- Masuda, S.; Nakamura, K. Fast-forward of adiabatic dynamics in quantum mechanics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1135–1154. [Google Scholar] [CrossRef]
- Demirplak, M.; Rice, S.A. Adiabatic population transfer with control fields. J. Phys. Chem. A 2003, 107, 9937–9945. [Google Scholar] [CrossRef]
- Demirplak, M.; Rice, S.A. Assisted adiabatic passage revisited. J. Phys. Chem. B 2005, 109, 6838–6844. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Transitionless quantum driving. J. Phys. A Math. Theor. 2009, 42, 365303. [Google Scholar] [CrossRef]
- Chen, X.; Lizuain, I.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J. Shortcut to adiabatic passage in two-and three-level atoms. Phys. Rev. Lett. 2010, 105, 123003. [Google Scholar] [CrossRef] [PubMed]
- Del Campo, A. Shortcuts to adiabaticity by counterdiabatic driving. Phys. Rev. Lett. 2013, 111, 100502. [Google Scholar] [CrossRef]
- Deffner, S.; Jarzynski, C.; del Campo, A. Classical and quantum shortcuts to adiabaticity for scale-invariant driving. Phys. Rev. X 2014, 4, 021013. [Google Scholar] [CrossRef]
- Chen, X.; Ruschhaupt, A.; Schmidt, S.; del Campo, A.; Guéry-Odelin, D.; Muga, J.G. Fast optimal frictionless atom cooling in harmonic traps: Shortcut to adiabaticity. Phys. Rev. Lett. 2010, 104, 063002. [Google Scholar] [CrossRef]
- Chen, X.; Torrontegui, E.; Muga, J.G. Lewis-Riesenfeld invariants and transitionless quantum driving. Phys. Rev. A 2011, 83, 062116. [Google Scholar] [CrossRef]
- Torrontegui, E.; Martínez-Garaot, S.; Ruschhaupt, A.; Muga, J.G. Shortcuts to adiabaticity: Fast-forward approach. Phys. Rev. A 2012, 86, 013601. [Google Scholar] [CrossRef]
- Ibáñez, S.; Chen, X.; Torrontegui, E.; Muga, J.G.; Ruschhaupt, A. Multiple Schrödinger pictures and dynamics in shortcuts to adiabaticity. Phys. Rev. Lett. 2012, 109, 100403. [Google Scholar] [CrossRef]
- Du, Y.-X.; Liang, Z.-T.; Li, Y.-C.; Yue, X.-X.; Lv, Q.-X.; Huang, W.; Chen, X.; Yan, H.; Zhu, S.-L. Experimental realization of stimulated Raman shortcut-to-adiabatic passage with cold atoms. Nat. Commun. 2016, 7, 12479. [Google Scholar] [CrossRef] [PubMed]
- Schaff, J.-F.; Song, X.-L.; Vignolo, P.; Labeyrie, G. Fast optimal transition between two equilibrium states. Phys. Rev. A 2010, 82, 033430. [Google Scholar] [CrossRef]
- Schaff, J.-F.; Song, X.-L.; Capuzzi, P.; Vignolo, P.; Labeyrie, G. Shortcut to adiabaticity for an interacting Bose-Einstein condensate. EPL (Europhys. Lett.) 2011, 93, 23001. [Google Scholar] [CrossRef]
- Zhang, J.; Shim, J.H.; Niemeyer, I.; Taniguchi, T.; Teraji, T.; Abe, H.; Onoda, S.; Yamamoto, T.; Ohshima, T.; Isoya, J. Experimental implementation of assisted quantum adiabatic passage in a single spin. Phys. Rev. Lett. 2013, 110, 240501. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.B.; Baksic, A.; Ribeiro, H.; Yale, C.G.; Heremans, F.J.; Jerger, P.C.; Auer, A.; Burkard, G.; Clerk, A.A.; Awschalom, D.D. Accelerated quantum control using superadiabatic dynamics in a solid-state lambda system. Nat. Phys. 2017, 13, 330–334. [Google Scholar] [CrossRef]
- Munuera-Javaloy, C.; Ban, Y.; Chen, X.; Casanova, J. Robust Detection of High-Frequency Signals at the Nanoscale. Phys. Rev. Appl. 2020, 14, 054054. [Google Scholar] [CrossRef]
- An, S.; Lv, D.; Del Campo, A.; Kim, K. Shortcuts to adiabaticity by counterdiabatic driving for trapped-ion displacement in phase space. Nat. Commun. 2016, 7, 12999. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Z.; Xiang, L.; Jia, Z.; Duan, P.; Cai, W.; Gong, Z.; Zong, Z.; Wu, M.; Wu, J. The experimental realization of high-fidelity ‘shortcut-to-adiabaticity’ quantum gates in a superconducting Xmon qubit. New J. Phys. 2018, 20, 065003. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Z.; Xiang, L.; Jia, Z.; Duan, P.; Zong, Z.; Sun, Z.; Dong, Z.; Wu, J.; Yin, Y. Experimental realization of a fast controlled-Z gate via a shortcut to adiabaticity. Phys. Rev. Appl. 2019, 11, 034030. [Google Scholar] [CrossRef]
- Vepsäläinen, A.; Danilin, S.; Paraoanu, G.S. Superadiabatic population transfer in a three-level superconducting circuit. Sci. Adv. 2019, 5, eaau5999. [Google Scholar] [CrossRef]
- Yan, T.; Liu, B.-J.; Xu, K.; Song, C.; Liu, S.; Zhang, Z.; Deng, H.; Yan, Z.; Rong, H.; Huang, K. Experimental realization of nonadiabatic shortcut to non-Abelian geometric gates. Phys. Rev. Lett. 2019, 122, 080501. [Google Scholar] [CrossRef]
- Glaser, S.J.; Boscain, U.; Calarco, T.; Koch, C.P.; Köckenberger, W.; Kosloff, R.; Kuprov, I.; Luy, B.; Schirmer, S.; Schulte-Herbrüggen, T. Training Schrödinger’s cat: Quantum optimal control. Eur. Phys. J. D 2015, 69, 1–24. [Google Scholar] [CrossRef]
- Assémat, E.; Attar, L.; Penouilh, M.-J.; Picquet, M.; Tabard, A.; Zhang, Y.; Glaser, S.; Sugny, D. Optimal control of the inversion of two spins in Nuclear Magnetic Resonance. Chem. Phys. 2012, 405, 71–75. [Google Scholar] [CrossRef]
- Henson, B.M.; Shin, D.K.; Thomas, K.F.; Ross, J.A.; Hush, M.R.; Hodgman, S.S.; Truscott, A.G. Approaching the adiabatic timescale with machine learning. Proc. Natl. Acad. Sci. USA 2018, 115, 13216–13221. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, J.J.W.H.; Pedersen, M.K.; Munch, M.; Haikka, P.; Jensen, J.H.; Planke, T.; Andreasen, M.G.; Gajdacz, M.; Mølmer, K.; Lieberoth, A. Exploring the quantum speed limit with computer games. Nature 2016, 532, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Sels, D. Stochastic gradient ascent outperforms gamers in the quantum moves game. Phys. Rev. A 2018, 97, 040302. [Google Scholar] [CrossRef]
- Ding, Y.; Ban, Y.; Martín-Guerrero, J.D.; Solano, E.; Casanova, J.; Chen, X. Breaking Adiabatic Quantum Control with Deep Learning. arXiv 2020, arXiv:2009.04297. [Google Scholar]
- Larocca, M.; Calzetta, E.; Wisniacki, D.A. Exploiting landscape geometry to enhance quantum optimal control. Phys. Rev. A 2020, 101, 023410. [Google Scholar] [CrossRef]
- Stefanatos, D.; Ruths, J.; Li, J.-S. Frictionless atom cooling in harmonic traps: A time-optimal approach. Phys. Rev. A 2010, 82, 063422. [Google Scholar] [CrossRef]
- Stefanatos, D.; Li, J.-S. Frictionless decompression in minimum time of Bose-Einstein condensates in the Thomas-Fermi regime. Phys. Rev. A 2012, 86, 063602. [Google Scholar] [CrossRef]
- Lu, X.-J.; Chen, X.; Alonso, J.; Muga, J. Fast transitionless expansions of Gaussian anharmonic traps for cold atoms: Bang-singular-bang control. Phys. Rev. A 2014, 89, 023627. [Google Scholar] [CrossRef]
- Chen, X.; Torrontegui, E.; Stefanatos, D.; Li, J.-S.; Muga, J. Optimal trajectories for efficient atomic transport without final excitation. Phys. Rev. A 2011, 84, 043415. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, X.; Guéry-Odelin, D. Fast and optimal transport of atoms with nonharmonic traps. Phys. Rev. A 2015, 92, 043410. [Google Scholar] [CrossRef]
- Zhang, Q.; Muga, J.G.; Guéry-Odelin, D.; Chen, X. Optimal shortcuts for atomic transport in anharmonic traps. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 125503. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Chen, X.; Alonso, D.; Muga, J. Optimally robust shortcuts to population inversion in two-level quantum systems. New J. Phys. 2012, 14, 093040. [Google Scholar] [CrossRef]
- Lu, X.-J.; Chen, X.; Ruschhaupt, A.; Alonso, D.; Guerin, S.; Muga, J.G. Fast and robust population transfer in two-level quantum systems with dephasing noise and/or systematic frequency errors. Phys. Rev. A 2013, 88, 033406. [Google Scholar] [CrossRef]
- Daems, D.; Ruschhaupt, A.; Sugny, D.; Guerin, S. Robust quantum control by a single-shot shaped pulse. Phys. Rev. Lett. 2013, 111, 050404. [Google Scholar] [CrossRef]
- Martikyan, V.; Guéry-Odelin, D.; Sugny, D. Comparison between optimal control and shortcut to adiabaticity protocols in a linear control system. Phys. Rev. A 2020, 101, 013423. [Google Scholar] [CrossRef]
- Guéry-Odelin, D.; Muga, J.G. Transport in a harmonic trap: Shortcuts to adiabaticity and robust protocols. Phys. Rev. A 2014, 90, 063425. [Google Scholar] [CrossRef]
- Martikyan, V.; Devra, A.; Guéry-Odelin, D.; Glaser, S.J.; Sugny, D. Robust control of an ensemble of springs: Application to ion cyclotron resonance and two-level quantum systems. Phys. Rev. A 2020, 102, 053104. [Google Scholar] [CrossRef]
- Choi, S.; Onofrio, R.; Sundaram, B. Optimized sympathetic cooling of atomic mixtures via fast adiabatic strategies. Phys. Rev. A 2011, 84, 051601. [Google Scholar] [CrossRef]
- Del Campo, A. Frictionless quantum quenches in ultracold gases: A quantum-dynamical microscope. Phys. Rev. A 2011, 84, 031606. [Google Scholar] [CrossRef]
- Deng, S.; Diao, P.; Yu, Q.; del Campo, A.; Wu, H. Shortcuts to adiabaticity in the strongly coupled regime: Nonadiabatic control of a unitary Fermi gas. Phys. Rev. A 2018, 97, 013628. [Google Scholar] [CrossRef]
- Rohringer, W.; Fischer, D.; Steiner, F.; Mazets, I.E.; Schmiedmayer, J.; Trupke, M. Non-equilibrium scale invariance and shortcuts to adiabaticity in a one-dimensional Bose gas. Sci. Rep. 2015, 5, 9820. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Muga, J.G. Transient energy excitation in shortcuts to adiabaticity for the time-dependent harmonic oscillator. Phys. Rev. A 2010, 82, 053403. [Google Scholar] [CrossRef]
- Hoffmann, K.; Salamon, P.; Rezek, Y.; Kosloff, R. Time-optimal controls for frictionless cooling in harmonic traps. EPL (Europhys. Lett.) 2011, 96, 60015. [Google Scholar] [CrossRef]
- Cui, Y.Y.; Chen, X.; Muga, J.G. Transient particle energies in shortcuts to adiabatic expansions of harmonic traps. J. Phys. Chem. A 2016, 120, 2962–2969. [Google Scholar] [CrossRef]
- Couvert, A.; Kawalec, T.; Reinaudi, G.; Guéry-Odelin, D. Optimal Transport of Ultracold Atoms in the Nonadiabatic Regime. EPL (Europhys. Lett.) 2008, 83, 13001. [Google Scholar] [CrossRef]
- Walther, A.; Ziesel, F.; Ruster, T.; Dawkins, S.T.; Ott, K.; Hettrich, M.; Singer, K.; Schmidt-Kaler, F.; Poschinger, U. Controlling Fast Transport of Cold Trapped Ions. Phys. Rev. Lett. 2012, 109, 080501. [Google Scholar] [CrossRef]
- Bowler, R.; Gaebler, J.; Lin, Y.; Tan, T.R.; Hanneke, D.; Jost, J.D.; Home, J.P.; Leibfried, D.; Wineland, D.J. Coherent Diabatic Ion Transport and Separation in a Multizone Trap Array. Phys. Rev. Lett. 2012, 109, 080502. [Google Scholar] [CrossRef]
- Torrontegui, E.; Ibáñez, S.; Chen, X.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J. Fast atomic transport without vibrational heating. Phys. Rev. A 2011, 83, 013415. [Google Scholar] [CrossRef]
- Torrontegui, E.; Chen, X.; Modugno, M.; Schmidt, S.; Ruschhaupt, A.; Muga, J. Fast transport of Bose-Einstein condensates. New J. Phys. 2012, 14, 013031. [Google Scholar] [CrossRef]
- Corgier, R.; Amri, S.; Herr, W.; Ahlers, H.; Rudolph, J.; Guéry-Odelin, D.; Rasel, E.M.; Charron, E.; Gaaloul, N. Fast manipulation of Bose?Einstein condensates with an atom chip. New J. Phys. 2018, 20, 055002. [Google Scholar] [CrossRef]
- Becker, D.; Lachmann, M.D.; Seidel, S.T.; Ahlers, H.; Dinkelaker, A.N.; Grosse, J.; Hellmig, O.; Müntinga, H.; Schkolnik, V.; Wendrich, T. Space-borne Bose-Einstein condensation for precision interferometry. Nature 2018, 562, 391–395. [Google Scholar] [CrossRef] [PubMed]
- Amri, S.; Corgier, R.; Sugny, D.; Rasel, E.M.; Gaaloul, N.; Charron, E. Optimal control of the transport of Bose-Einstein condensates with atom chips. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Dupont-Nivet, M.; Westbrook, C.I.; Schwartz, S. Contrast and phase-shift of a trapped atom interferometer using a thermal ensemble with internal state labelling. New J. Phys. 2016, 18, 113012. [Google Scholar] [CrossRef]
- Lu, X.-J.; Muga, J.G.; Chen, X.; Poschinger, U.; Schmidt-Kaler, F.; Ruschhaupt, A. Fast shuttling of a trapped ion in the presence of noise. Phys. Rev. A 2014, 89, 063414. [Google Scholar] [CrossRef]
- Lu, X.-J.; Ruschhaupt, A.; Muga, J.G. Fast shuttling of a particle under weak spring-constant noise of the moving trap. Phys. Rev. A 2018, 97, 053402. [Google Scholar] [CrossRef]
- Boscain, U.; Charlot, G.; Gauthier, J.-P.; Guérin, S.; Jauslin, H.-R. Optimal control in laser-induced population transfer for two-and three-level quantum systems. J. Math. Phys. 2002, 43, 2107–2132. [Google Scholar] [CrossRef]
- Van Damme, L.; Ansel, Q.; Glaser, S.; Sugny, D. Robust optimal control of two-level quantum systems. Phys. Rev. A 2017, 95, 063403. [Google Scholar] [CrossRef]
- Van Damme, L.; Ansel, Q.; Glaser, S.; Sugny, D. Time-optimal selective pulses of two uncoupled spin-1/2 particles. Phys. Rev. A 2018, 98, 043421. [Google Scholar] [CrossRef]
- Stefanatos, D. Optimal design of minimum-energy pulses for Bloch equations in the case of dominant transverse relaxation. Phys. Rev. A 2009, 80, 045401. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. Efficient generation of the triplet Bell state between coupled spins using transitionless quantum driving and optimal control. Phys. Rev. A 2019, 99, 022327. [Google Scholar] [CrossRef]
- Owrutsky, P.; Khaneja, N. Control of inhomogeneous ensembles on the Bloch sphere. Phys. Rev. A 2012, 86, 022315. [Google Scholar] [CrossRef]
- Lin, C.; Sels, D.; Wang, Y. Time-optimal control of a dissipative qubit. Phys. Rev. A 2020, 101, 022320. [Google Scholar] [CrossRef]
- Mortensen, H.L.; Sørensen, J.J.W.; Mølmer, K.; Sherson, J.F. Fast state transfer in a Λ-system: A shortcut-to-adiabaticity approach to robust and resource optimized control. New J. Phys. 2018, 20, 025009. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, X.; Guéry-Odelin, D. Reverse engineering protocols for controlling spin dynamics. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Yu, X.-T.; Zhang, Q.; Ban, Y.; Chen, X. Fast and robust control of two interacting spins. Phys. Rev. A 2018, 97, 062317. [Google Scholar] [CrossRef]
- Impens, F.; Guéry-Odelin, D. Fast quantum control in dissipative systems using dissipationless solutions. Sci. Rep. 2019, 9, 4048. [Google Scholar] [CrossRef]


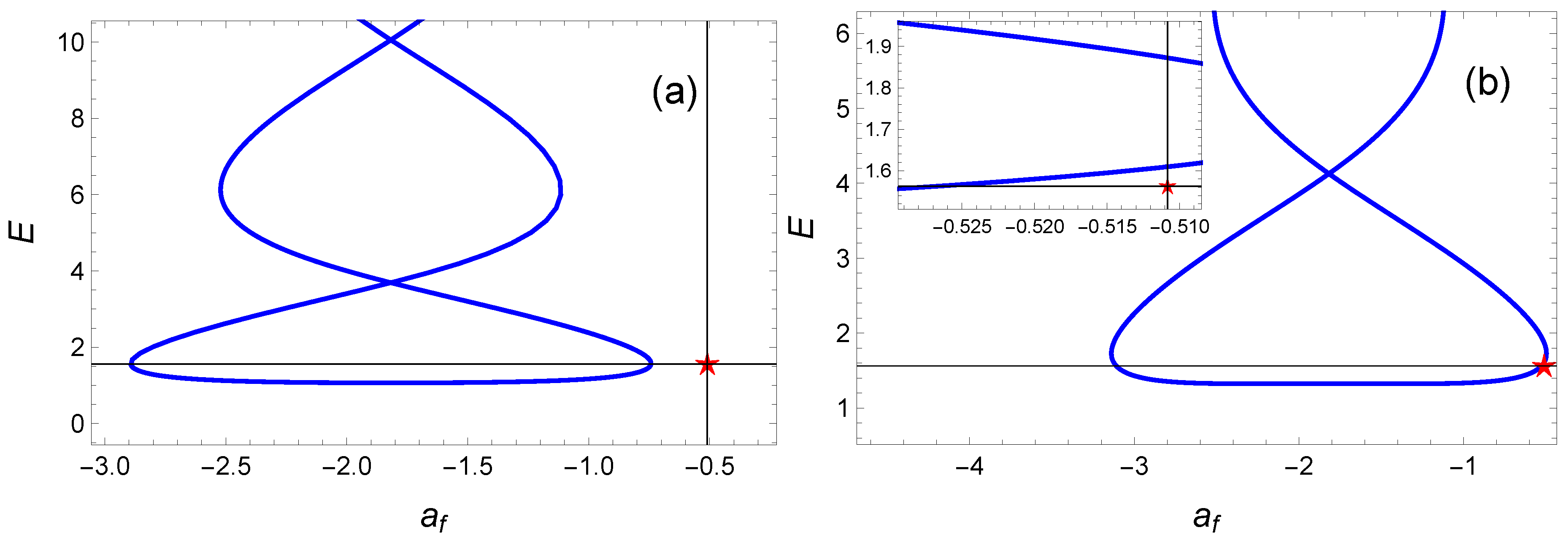



| 1.1 | −0.44893 | 0.10996 |
| −1.47741 | 0.34535 | |
| 4 | −2.86194 | 0.62841 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Chen, X.; Guéry-Odelin, D. Connection between Inverse Engineering and Optimal Control in Shortcuts to Adiabaticity. Entropy 2021, 23, 84. https://doi.org/10.3390/e23010084
Zhang Q, Chen X, Guéry-Odelin D. Connection between Inverse Engineering and Optimal Control in Shortcuts to Adiabaticity. Entropy. 2021; 23(1):84. https://doi.org/10.3390/e23010084
Chicago/Turabian StyleZhang, Qi, Xi Chen, and David Guéry-Odelin. 2021. "Connection between Inverse Engineering and Optimal Control in Shortcuts to Adiabaticity" Entropy 23, no. 1: 84. https://doi.org/10.3390/e23010084
APA StyleZhang, Q., Chen, X., & Guéry-Odelin, D. (2021). Connection between Inverse Engineering and Optimal Control in Shortcuts to Adiabaticity. Entropy, 23(1), 84. https://doi.org/10.3390/e23010084






