Second-Order Phase Transition in Counter-Rotating Taylor–Couette Flow Experiment
Abstract
1. Introduction
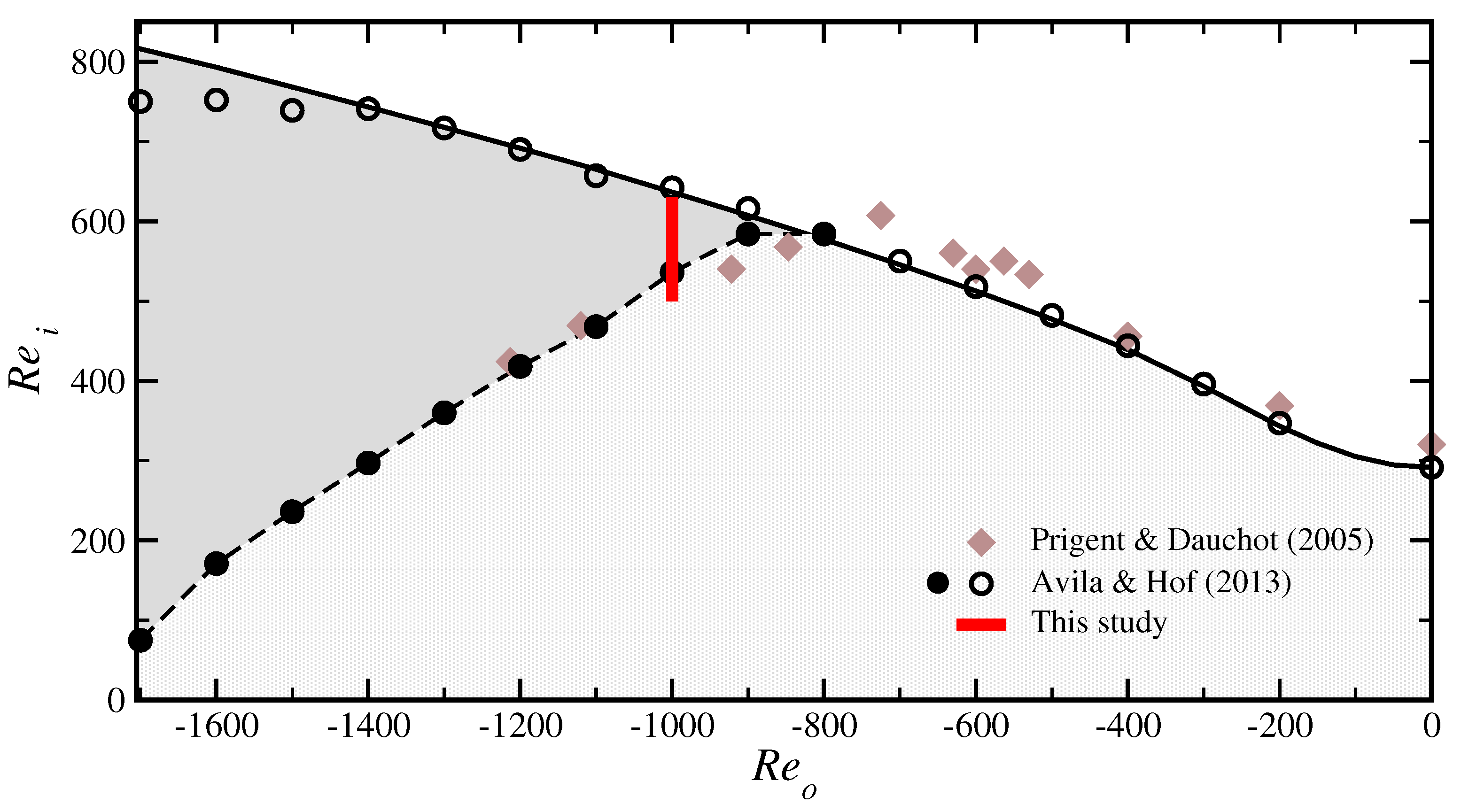
2. Experimental Methods
3. Results
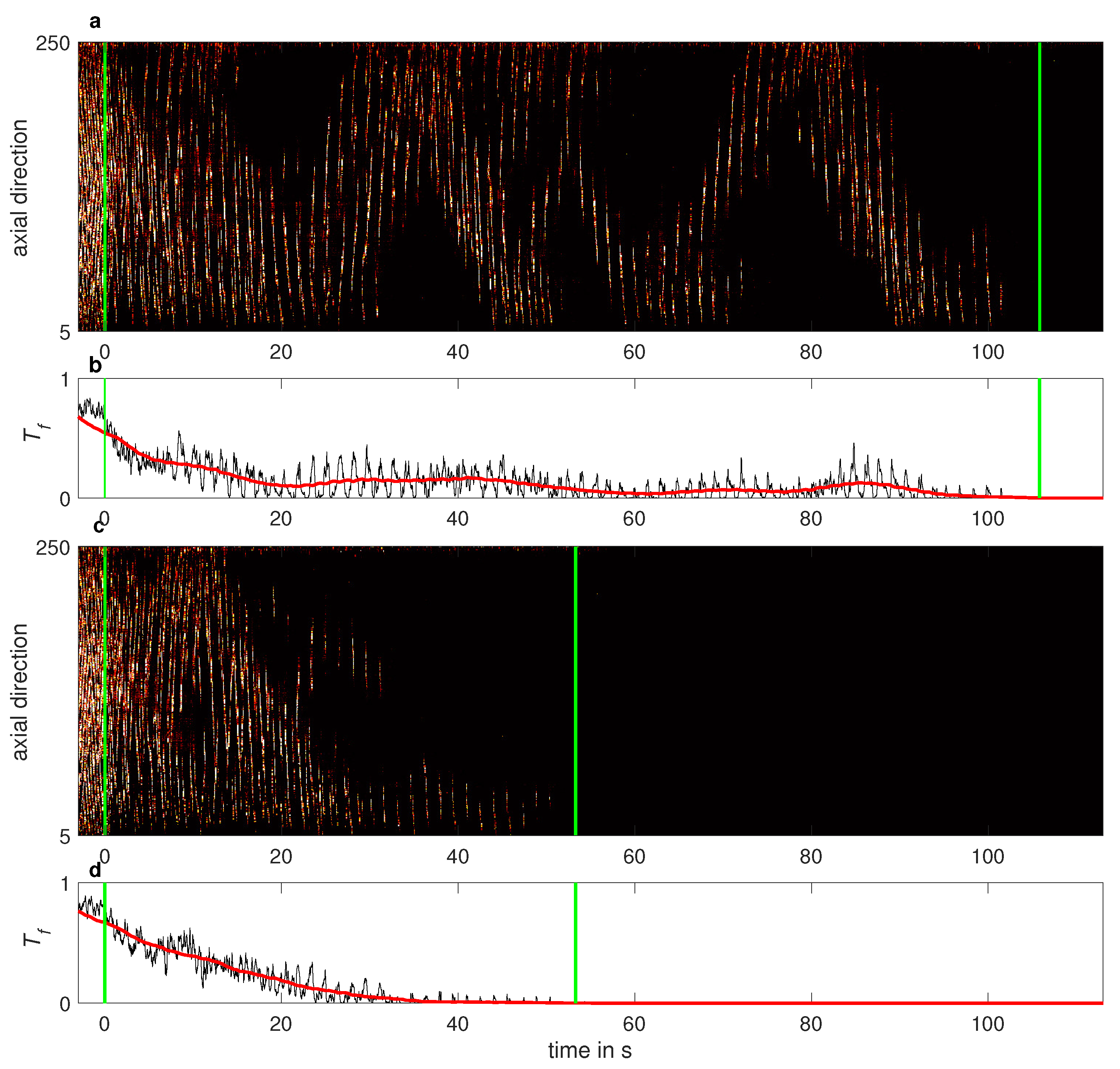
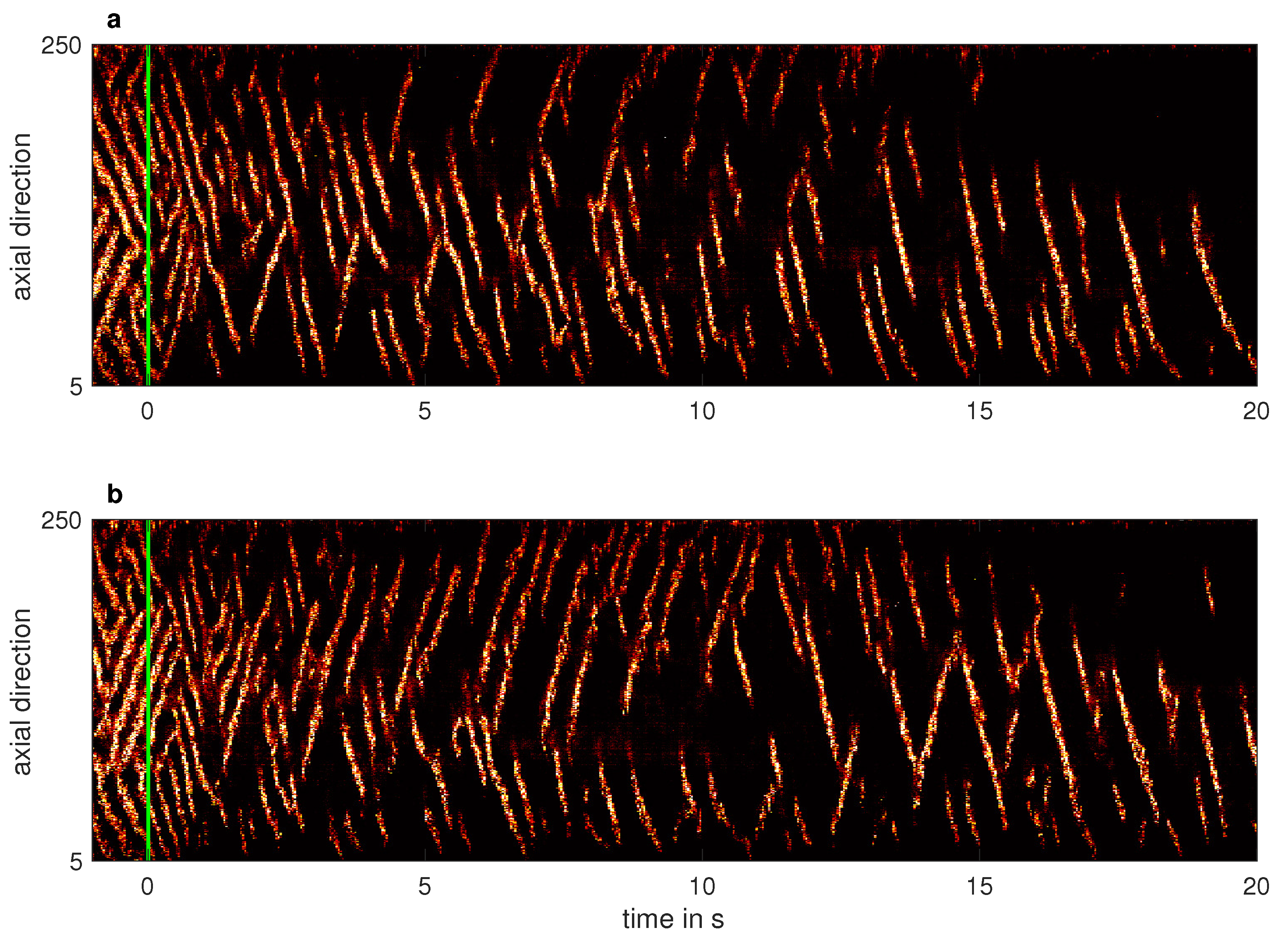
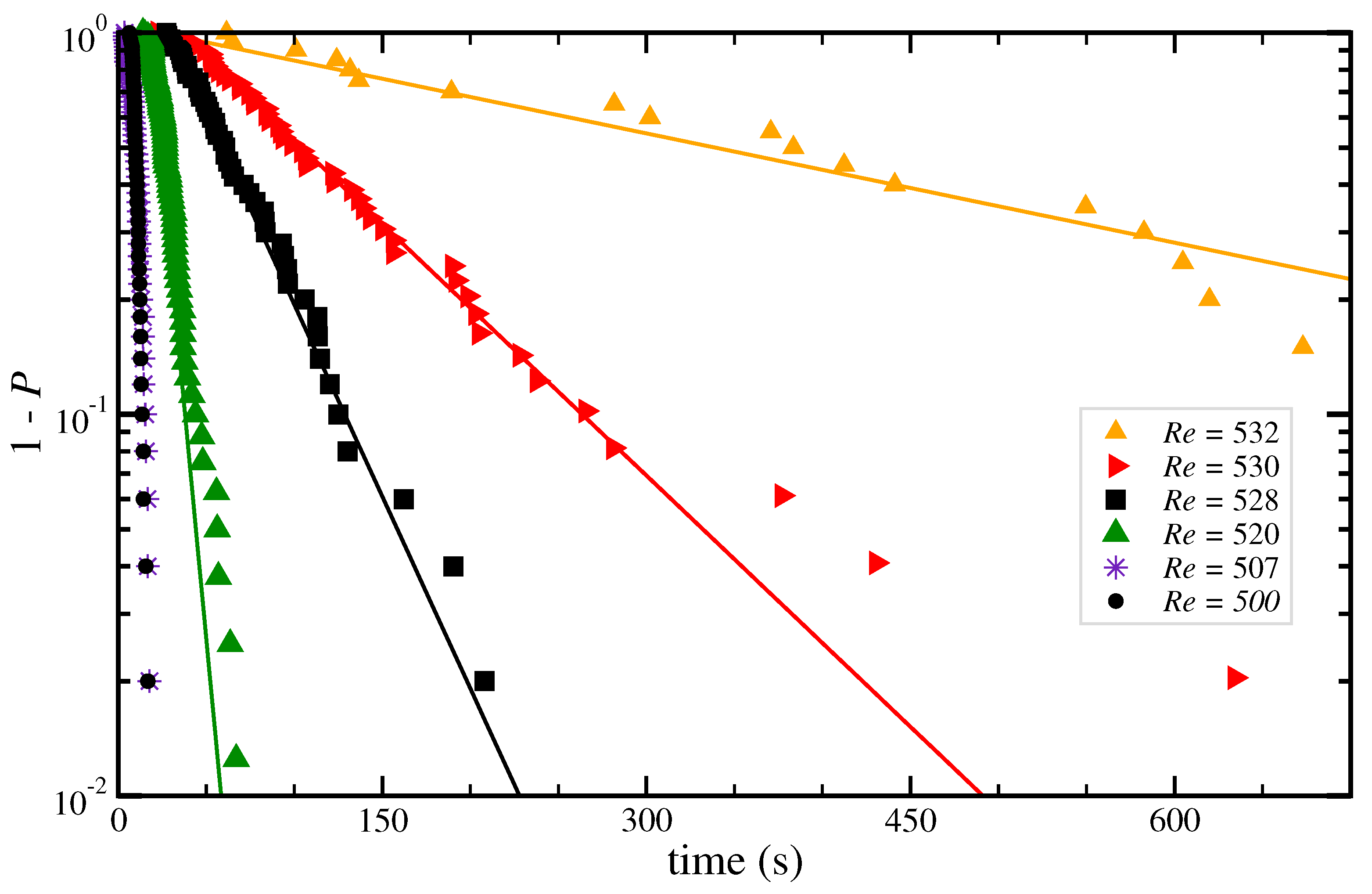
3.1. Lifetimes of Turbulent Stripes and Spots
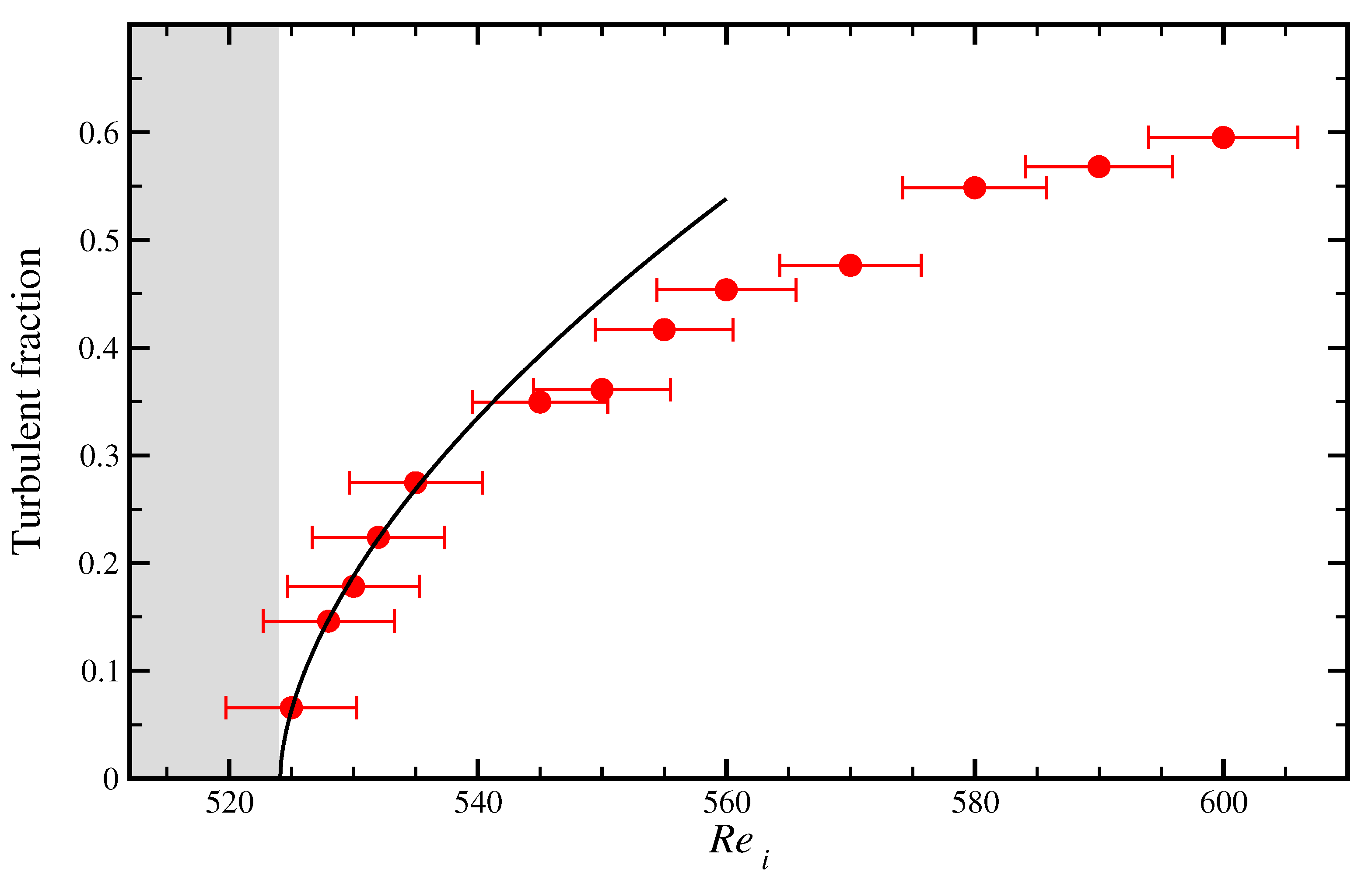
3.2. Second-Order Phase Transition
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 1883, 35, 84–99. [Google Scholar]
- Wygnanski, I.J.; Sokolov, M.; Friedman, D. On transition in a pipe. Part 2. The equilibrium puff. J. Fluid Mech. 1975, 69, 283–304. [Google Scholar] [CrossRef]
- Barkley, D. Simplifying the complexity of pipe flow. Phys. Rev. E 2011, 84, 016309. [Google Scholar] [CrossRef] [PubMed]
- Coles, D. Transition in circular Couette flow. J. Fluid Mech. 1965, 21, 385–425. [Google Scholar] [CrossRef]
- Prigent, A.; Grégoire, G.; Chaté, H.; Dauchot, O.; van Saarloos, W. Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 2002, 89, 14501. [Google Scholar] [CrossRef] [PubMed]
- Ishida, T.; Duguet, Y.; Tsukahara, T. Transitional structures in annular Poiseuille flow depending on radius ratio. J. Fluid Mech. 2016, 794. [Google Scholar] [CrossRef]
- Tuckerman, L.S.; Chantry, M.; Barkley, D. Patterns in Wall-Bounded Shear Flows. Annu. Rev. Fluid Mech. 2020, 52, 343–367. [Google Scholar] [CrossRef]
- Bottin, S.; Chaté, H. Statistical analysis of the transition to turbulence in plane Couette flow. Eur. Phys. J. B 1998, 6, 143–155. [Google Scholar] [CrossRef]
- Faisst, H.; Eckhardt, B. Sensitive dependence on initial conditions in transition to turbulence in pipe flow. J. Fluid Mech. 2004, 504, 343–352. [Google Scholar] [CrossRef]
- Peixinho, J.; Mullin, T. Decay of turbulence in pipe flow. Phys. Rev. Lett. 2006, 96, 094501. [Google Scholar] [CrossRef]
- Willis, A.P.; Kerswell, R.R. Critical behavior in the relaminarization of localized turbulence in pipe flow. Phys. Rev. Lett. 2007, 98, 014501. [Google Scholar] [CrossRef] [PubMed]
- Hof, B.; Westerweel, J.; Schneider, T.M.; Eckhardt, B. Finite lifetime of turbulence in shear flows. Nature 2006, 443, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Hof, B.; De Lozar, A.; Kuik, D.J.; Westerweel, J. Repeller or attractor? Selecting the dynamical model for the onset of turbulence in pipe flow. Phys. Rev. Lett. 2008, 101, 214501. [Google Scholar] [CrossRef] [PubMed]
- Avila, M.; Willis, A.P.; Hof, B. On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 2010, 646, 127. [Google Scholar] [CrossRef]
- Kuik, D.J.; Poelma, C.; Westerweel, J. Quantitative measurement of the lifetime of localized turbulence in pipe flow. J. Fluid Mech. 2010, 645, 529–539. [Google Scholar] [CrossRef]
- Borrero-Echeverry, D.; Schatz, M.F.; Tagg, R. Transient turbulence in Taylor-Couette flow. Phys. Rev. E 2010, 81, 025301. [Google Scholar] [CrossRef]
- Pomeau, Y. Front motion, metastability and subcritical bifurcations in hydrodynamics. Physica D 1986, 23, 3–11. [Google Scholar] [CrossRef]
- Kaneko, K. Spatiotemporal intermittency in coupled map lattices. Prog. Theor. Phys. 1985, 74, 1033–1044. [Google Scholar] [CrossRef]
- Kaneko, K. Supertransients, spatiotemporal intermittency and stability of fully developed spatiotemporal chaos. Phys. Lett. A 1990, 149, 105–112. [Google Scholar] [CrossRef]
- Chaté, H.; Manneville, P. Transition to turbulence via spatio-temporal intermittency. Phys. Rev. Lett. 1987, 58, 112–115. [Google Scholar] [CrossRef]
- Manneville, P. Spatiotemporal perspective on the decay of turbulence in wall-bounded flows. Phys. Rev. E 2009, 79, 25301. [Google Scholar] [CrossRef] [PubMed]
- Moxey, D.; Barkley, D. Distinct large-scale turbulent-laminar states in transitional pipe flow. Proc. Natl. Acad. Sci. USA 2010, 107, 8091. [Google Scholar] [CrossRef] [PubMed]
- Avila, K.; Moxey, D.; de Lozar, A.; Avila, M.; Barkley, D.; Hof, B. The onset of turbulence in pipe flow. Science 2011, 333, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 2000, 49, 815–958. [Google Scholar] [CrossRef]
- Mukund, V.; Hof, B. The critical point of the transition to turbulence in pipe flow. J. Fluid Mech. 2018, 839, 76–94. [Google Scholar] [CrossRef]
- Lemoult, G.; Shi, L.; Avila, K.; Jalikop, S.V.; Avila, M.; Hof, B. Directed percolation phase transition to sustained turbulence in Couette flow. Nat. Phys. 2016, 12, 254–258. [Google Scholar] [CrossRef]
- Duguet, Y.; Schlatter, P.; Henningson, D.S. Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 2010, 650, 119. [Google Scholar] [CrossRef]
- Chantry, M.; Tuckerman, L.S.; Barkley, D. Universal continuous transition to turbulence in a planar shear flow. JFM 2017, 824, R1. [Google Scholar] [CrossRef]
- Andereck, C.D.; Liu, S.S.; Swinney, H.L. Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 1986, 164, 155–183. [Google Scholar] [CrossRef]
- Meseguer, A.; Mellibovsky, F.; Avila, M.; Marques, F. Instability mechanisms and transition scenarios of spiral turbulence in Taylor-Couette flow. Phys. Rev. E 2009, 80, 046315. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Brauckmann, H.J.; Salewski, M.; Eckhardt, B. Momentum transport in Taylor–Couette flow with vanishing curvature. J. Fluid Mech. 2016, 790, 419–452. [Google Scholar] [CrossRef]
- Faisst, H.; Eckhardt, B. Transition from the Couette-Taylor system to the plane Couette system. Phys. Rev. E 2000, 61, 7227. [Google Scholar] [CrossRef] [PubMed]
- Deguchi, K. Linear instability in Rayleigh-stable Taylor-Couette flow. Phys. Rev. E 2017, 95, 021102. [Google Scholar] [CrossRef] [PubMed]
- Avila, K.; Hof, B. High-precision Taylor-Couette experiment to study subcritical transitions and the role of boundary conditions and size effects. Rev. Sci. Instrum. 2013, 84, 065106. [Google Scholar] [CrossRef]
- Prigent, A.; Dauchot, O. Transition to versus from turbulence in subcritical Couette flows. In IUTAM Symposium on Laminar-Turbulent Transition and Finite Amplitude Solutions; Springer: Dordrecht, The Netherlands, 2005; pp. 195–219. [Google Scholar]
- Prigent, A.; Grégoire, G.; Chaté, H.; Dauchot, O. Long-wavelength modulation of turbulent shear flows. Physica D 2003, 174, 100–113. [Google Scholar] [CrossRef]
- Shi, L.; Avila, M.; Hof, B. Scale invariance at the onset of turbulence in Couette flow. Phys. Rev. Lett. 2013, 110, 204502. [Google Scholar] [CrossRef]
- Ravelet, F.; Delfos, R.; Westerweel, J. Influence of global rotation and Reynolds number on the large-scale features of a turbulent Taylor–Couette flow. Phys. Fluids 2010, 22, 055103. [Google Scholar] [CrossRef]
- Paoletti, M.S.; Lathrop, D.P. Measurement of angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 2011, 106, 024501. [Google Scholar] [CrossRef]
- Van Gils, D.P.M.; Huisman, S.G.; Bruggert, G.W.; Sun, C.; Lohse, D. Torque scaling in turbulent Taylor-Couette flow with co-and counterrotating cylinders. Phys. Rev. Lett. 2011, 106, 24502. [Google Scholar] [CrossRef]
- Heise, M.; Hochstrate, K.; Abshagen, J.; Pfister, G. Spirals vortices in Taylor-Couette flow with rotating endwalls. Phys. Rev. E 2009, 80, 045301. [Google Scholar] [CrossRef]
- Schartman, E.; Ji, H.; Burin, M.J. Development of a Couette–Taylor flow device with active minimization of secondary circulation. Rev. Sci. Instrum. 2009, 80, 024501. [Google Scholar] [CrossRef] [PubMed]
- Lopez, J.M.; Avila, M. Boundary-layer turbulence in experiments on quasi-Keplerian flows. J. Fluid Mech. 2017, 817, 21–34. [Google Scholar] [CrossRef]
- Gomé, S.; Tuckerman, L.S.; Barkley, D. Statistical transition to turbulence in plane channel flow. Phys. Rev. Fluids 2020, 5, 083905. [Google Scholar] [CrossRef]
- Shimizu, M.; Manneville, P. Bifurcations to turbulence in transitional channel flow. Phys. Rev. Fluids 2019, 4, 113903. [Google Scholar] [CrossRef]

| Reference | System | Streamwise Length | Spanwise Length | Area |
|---|---|---|---|---|
| Bottin and Chatté [8] | pCf () | 190d | 35d | 6650 |
| Borrero et al. [16] | TCf () | 55d | 34d | 1870 |
| Lemoult et al. [26] | TCf () | 2750d | 8d | ——— |
| This work | TCf () | 311d | 263d | 81,793 |
| Duguet et al. [27] | pCf () | 400d | 178d | 71,200 |
| Shi et al. [26] | TCf () | 480d | 5d | ——— |
| Lemoult et al. [26] | TCf () | 960d | 5d | ——— |
| Chantry et al. [28] | Waleffe flow | 1280d | 1280d | 1,638,400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avila, K.; Hof, B. Second-Order Phase Transition in Counter-Rotating Taylor–Couette Flow Experiment. Entropy 2021, 23, 58. https://doi.org/10.3390/e23010058
Avila K, Hof B. Second-Order Phase Transition in Counter-Rotating Taylor–Couette Flow Experiment. Entropy. 2021; 23(1):58. https://doi.org/10.3390/e23010058
Chicago/Turabian StyleAvila, Kerstin, and Björn Hof. 2021. "Second-Order Phase Transition in Counter-Rotating Taylor–Couette Flow Experiment" Entropy 23, no. 1: 58. https://doi.org/10.3390/e23010058
APA StyleAvila, K., & Hof, B. (2021). Second-Order Phase Transition in Counter-Rotating Taylor–Couette Flow Experiment. Entropy, 23(1), 58. https://doi.org/10.3390/e23010058





