Cache-Aided General Linear Function Retrieval
Abstract
1. Introduction
1.1. Paper Organization
1.2. Notation Convention
2. System Model
- In the placement phase, the server pushes up to symbols into the local cache of each user, where , without knowing what the users will demand later. The cached content of user is denoted bywhere is the placement function for user k defined asis referred to as the cache (or memory) size. If each user directly copies symbols from the library into its cache, the cache placement is said to be uncoded.
- In the delivery phase, each user wants to retrieve linear combinations of all the symbols in the library, where .The demand of user is represented by the matrix , meaning user k aims to retrieveLet the collection of all demand matrices be . We assume that the server and all users know which is communicated on a separate channel, thus not impacting the downlink load next—see also Remark 4. ( Notice that differently from the cache-aided matrix multiplication problem in [14], where the matrix on the each side of the desired multiplication is one of the library files, in this paper each user desires where is known by all the users in the delivery phase and represents the vector of all symbols in the library.)According to all the users’ demand matrix , the server broadcasts the messagewhere is the encoding functionfor some . is referred to as the load.
- In order to achieve the load , we transmit one by one the elements of in (3). The main limitation of this unicast transmission scheme is the lack of multicast gain.
- In order to achieve we let each user recover all the symbols in the library. In the placement phase, each user caches the first symbols in the library. In the delivery phase, the server transmits all the remaining symbols. The main limitation of this scheme is that, if , the users do not need to recover all the symbols in the library in order to retrieve their desired function.
3. Main Result
- if where and , the following normalized load is achievable
- if where , the following normalized load is achievable
- We start by the achievable scheme for (20) with . We aim to design the cache placement such that each user caches a fraction of the file and the uncached part of file by this user is known by the remaining users. With this cache placement, the delivery consists of a single multicast message with multicasting gain . More precisely, the construction of the proposed scheme is as follows.ecalling that, in Remark 1 with , each user misses a fraction of each file and that missing fraction is known by the remaining users; with , the delivery consists of a single multicast message with multicasting gain that is the sum of each user’s missing fraction of the demanded file. In our context, this idea becomes the following scheme.Assume divides . We use here a Matlab-like notation for submatrices. The library is partitioned into equal length subfiles as followsuser caches ; the server delivers the multicast messagewhere represents the sub-matrix of including the columns with indices in . In X, each user knows all but the requested vectorsuch that user k can recover either of them. Thus an achieved normalized memory-load tradeoff is
- We then introduce the achievable scheme for (17) with . Assume now the users are portioned into g groups of users each, where . Let the users in the same group share the same cache content and recover all the linear combinations demanded by the users in the group. Then the normalized memory-load tradeoff is as in (25) but with replaced by with g and replaced by . Therefore, we get that the following normalized memory-load points are achievable
- The rest of the proof of Theorem 1 consists of a method to ‘interpolate’ among the points in (26), as explained in Appendix A. Unlike cache-aided scalar linear function retrieval in [7], the difficulty in the considered problem is that connecting two normalized memory-load points by a line segment is generally impossible. The main reason is that if we partition as and use a different cache placement strategy on each part, each demanded function is in the formthus it cannot be divided into two separate parts, where the first part only contains the linear combinations of and the second part only contains the linear combinations of . An example to highlight this limitation and our approach to overcome it is provided at the end of this section.
- is partitioned into two equal-length subfiles,, each of which hassymbols. We divide the 6 users into 2 groups whereand. We let users incacheand let users incache.
- is partitioned into three equal-length subfiles,, each of which hassymbols. We divide the 6 users into 3 groups, where, , and . We let users incacheand, let users in cache, and let users incacheand.
- For the first term in in (38), since the dimension of is and the sub-demand matrix is known by each user, we let user 1 directly recover , which contains symbols, and then compute . Similarly, we let users recover , and users recover . Thus in the delivery phase, the server transmitsfor a total of symbols, where users know and users know .
- For the second term in in (38), since the dimension of is and the sub-demand matrix is known by each user, user 1 needs to recover all symbols in . We denote since it is known by users . Hence, in order to let each user recover the first term in its desired sum, the server transmitsfor a total of symbols.
- In the first step, we let each user recover the first term of its demand . In this step, the server transmitswhich contains symbols.
- In the second step, we let each user recover the second term of its demand . In this step, the server transmitsfor a total of symbols. From the received multicast messages and its cache content, each user can recover , and then compute from .
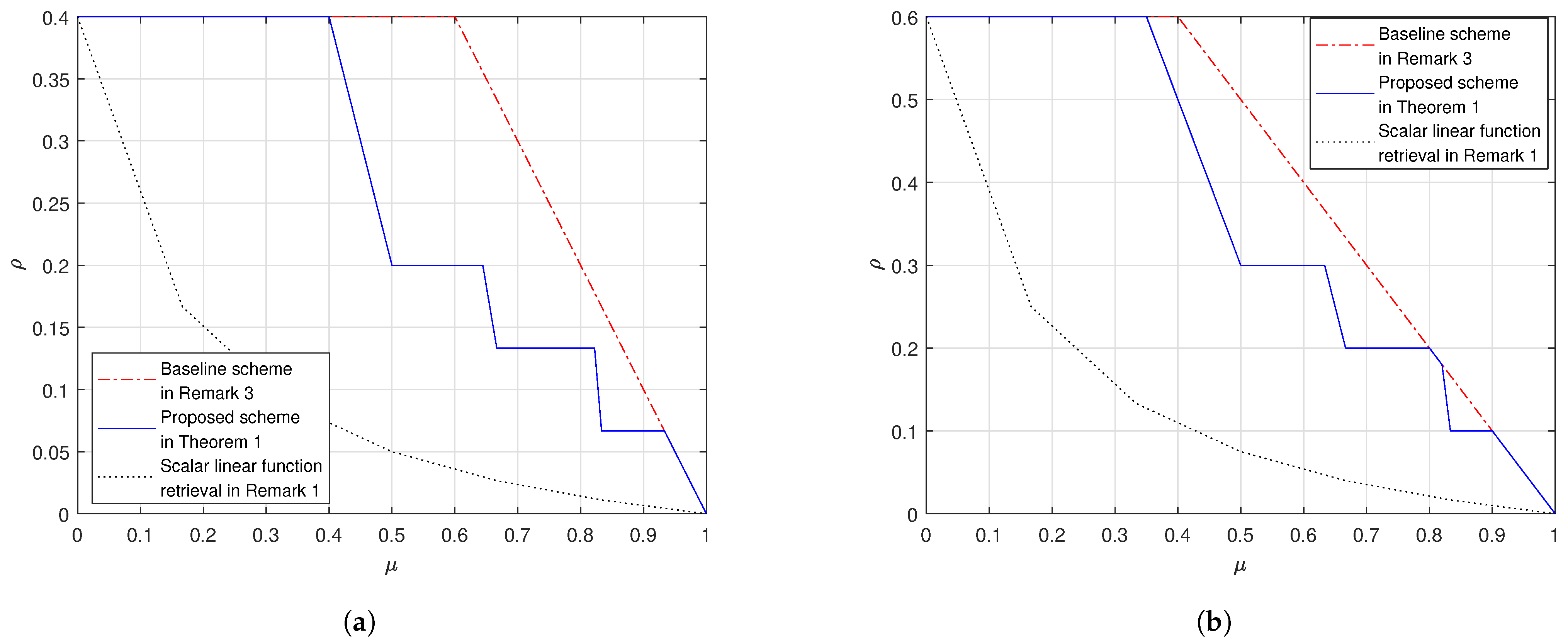
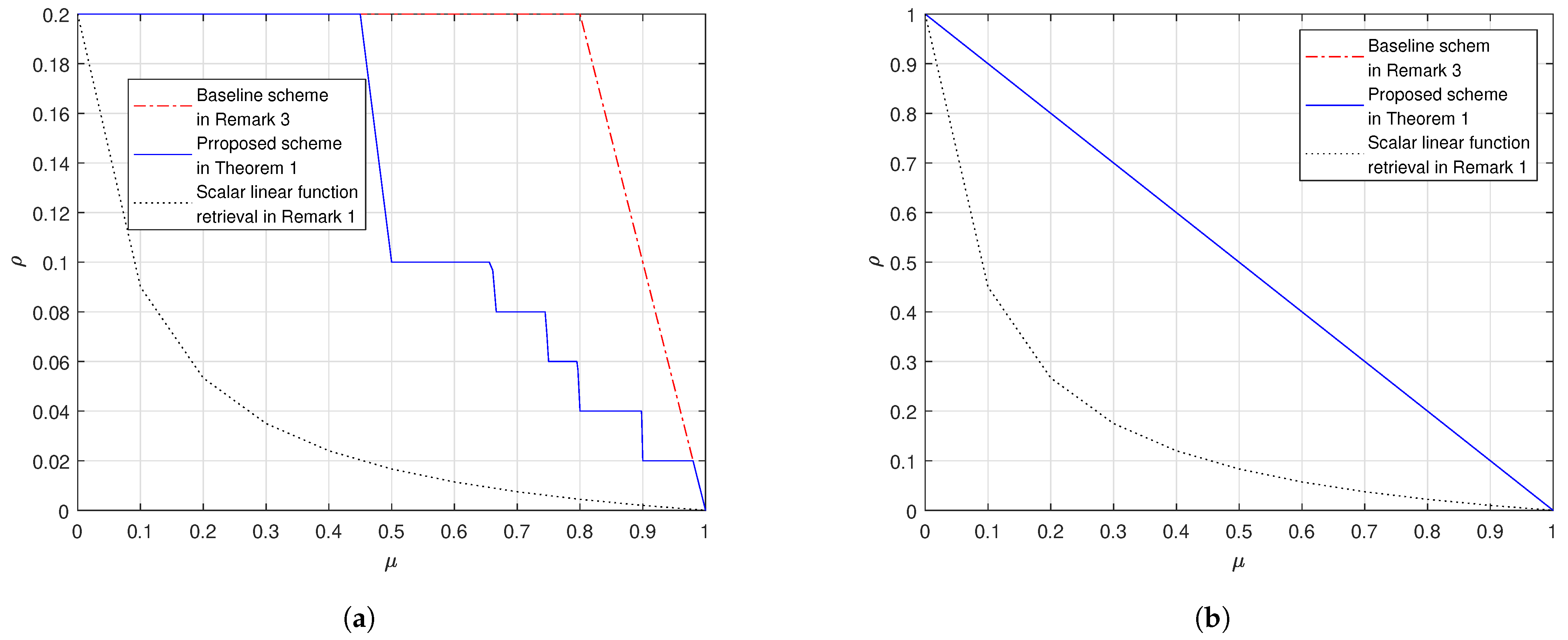
4. Numerical Evaluations
- In both settings our proposed scheme in Theorem 1 outperforms the baseline scheme, as proved in Remark 5.
- Fix and . When grows, the gap between the proposed scheme and the baseline scheme reduces. When , the proposed scheme and the baseline scheme have the same load; this is because at the corner points of the proposed scheme in (26) we achieve the load which is the same as the baseline scheme.
- In addition, we also plot the cache-aided scalar linear function retrieval scheme in (14), which only works for the case where the demand matrices are with the form in (12). This comparison shows that, if the demand matrices are structured, we can design caching schemes that leverage the special structure of the demands to achieve a load that is no larger than the load for the worst-case demands. Moreover, the more the structure the more the gain compared to in (17).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix A.1. and
Appendix A.2. and
Appendix A.3. Proof of (20)
- we directly use the caching scheme in (25) for the memory size with the achieved normalized load equal to .
- In this case, the number of symbols which are not cached by user is . Hence, we can let each user directly recover the uncached symbols with the achieved normalized load equal to .
Appendix B. Proof of Lemma A1
References
- Borst, S.; Gupta, V.; Walid, A. Distributed caching algorithms for content distribution networks. In Proceedings of the 2010 Proceedings IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1478–1486. [Google Scholar]
- Maddah-Ali, M.A.; Niesen, U. Fundamental Limits of Caching. IEEE Trans. Inf. Theory 2014, 60, 2856–2867. [Google Scholar] [CrossRef]
- Wan, K.; Tuninetti, D.; Piantanida, P. On the Optimality of Uncoded Cache Placement. In Proceedings of the IEEE Information Theory Workshop (ITW), Cambridge, UK, 11–14 September 2016. [Google Scholar]
- Wan, K.; Tuninetti, D.; Piantanida, P. An Index Coding Approach to Caching With Uncoded Cache Placement. IEEE Trans. Inf. Theory 2020, 2020. 66, 1318–1332. [Google Scholar] [CrossRef]
- Yu, Q; Maddah-Ali, M.A.; Avestimehr, S. The Exact Rate-Memory Tradeoff for Caching with Uncoded Prefetching. IEEE Trans. Inf. Theory 2018, 64, 1281–1296. [Google Scholar] [CrossRef]
- Yu, Q; Maddah-Ali, M.A.; Avestimehr, S. Characterizing the Rate-Memory Tradeoff in Cache Networks Within a Factor of 2. IEEE Trans. Inf. Theory 2019, 65, 647–663. [Google Scholar] [CrossRef]
- Wan, K.; Sun, H.; Ji, M.; Tuninetti, D.; Caire, G. On Optimal Load-Memory Tradeoff of Cache-Aided Scalar Linear Function Retrieval. arXiv 2020, arXiv:2001.03577. [Google Scholar]
- Wan, K.; Caire, G. On Coded Caching with Private Demands. IEEE Trans. Inf. Theory 2020. [Google Scholar] [CrossRef]
- Ji, M.; Caire, G.; Molisch, A.F. Fundamental Limits of Caching in Wireless D2D Networks. IEEE Trans. Inf. Theory 2016, 62, 849–869. [Google Scholar] [CrossRef]
- Yapar, C.; Wan, K.; Schaefer, R.F.; Caire, G. On the Optimality of D2D Coded Caching With Uncoded Cache Placement and One-Shot Delivery. IEEE Trans. Commun. 2019, 67, 8179–8192. [Google Scholar] [CrossRef]
- Yan, Q.; Tuninetti, D. Fundamental Limits of Caching for Demand Privacy against Colluding Users. arXiv 2020, arXiv:2008.03642. [Google Scholar]
- Yan, Q.; Tuninetti, D. Key Superposition Simultaneously Achieves Security and Privacy in Cache-Aided Linear Function Retrieval. arXiv 2020, arXiv:2009.06000. [Google Scholar]
- Shanmugam, K.; Ji, M.; Tulino, A.M.; Llorca, J.; Dimakis, A.G. Finite-Length Analysis of Caching-Aided Coded Multicasting. IEEE Trans. Inf. Theory 2016, 2016. 62, 5524–5537. [Google Scholar] [CrossRef]
- Wan, K.; Sun, H.; Ji, M.; Tuninetti, D.; Caire, G. Cache-Aided Matrix Multiplication Retrieval. arXiv 2020, arXiv:2007.00856. [Google Scholar]
- Bar-Yossef, Z.; Birk, Y.; Jayram, T.S.; Kol, T. Index Coding with Side Information. IEEE Trans. Inf. Theory 2011, 57, 1479–1494. [Google Scholar] [CrossRef]
- Lee, N.; Dimakis, A.G.; Heath, R.W. Index Coding with Coded Side-Information. IEEE Commun. Lett. 2015, 19, 319–322. [Google Scholar] [CrossRef]
- Jia, Z.; Jafar, S.A. Cross Subspace Alignment Codes for Coded Distributed Batch Computation. arXiv 2019, arXiv:1909.13873. [Google Scholar]
- Chang, W.; Tandon, R. On the Upload versus Download Cost for Secure and Private Matrix Multiplication. arXiv 2019, arXiv:1906.10684. [Google Scholar]
- Kakar, J.; Khristoforov, A.; Ebadifar, S.; Sezgin, A. Uplink-downlink tradeoff in secure distributed matrix multiplication. arXiv 2019, arXiv:1910.13849. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, K.; Sun, H.; Ji, M.; Tuninetti, D.; Caire, G. Cache-Aided General Linear Function Retrieval. Entropy 2021, 23, 25. https://doi.org/10.3390/e23010025
Wan K, Sun H, Ji M, Tuninetti D, Caire G. Cache-Aided General Linear Function Retrieval. Entropy. 2021; 23(1):25. https://doi.org/10.3390/e23010025
Chicago/Turabian StyleWan, Kai, Hua Sun, Mingyue Ji, Daniela Tuninetti, and Giuseppe Caire. 2021. "Cache-Aided General Linear Function Retrieval" Entropy 23, no. 1: 25. https://doi.org/10.3390/e23010025
APA StyleWan, K., Sun, H., Ji, M., Tuninetti, D., & Caire, G. (2021). Cache-Aided General Linear Function Retrieval. Entropy, 23(1), 25. https://doi.org/10.3390/e23010025








