Explainable AI: A Review of Machine Learning Interpretability Methods
Abstract
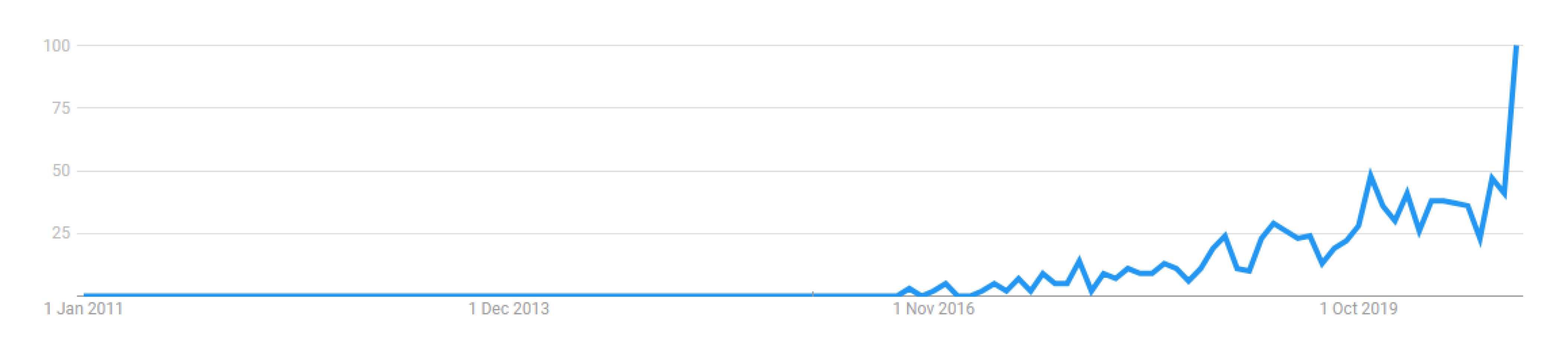
1. Introduction
The Contribution of this Survey
2. Fundamental Concepts and Background
2.1. Explainability and Interpretability
2.2. Evaluation of Machine Learning Interpretability
2.3. Related Work
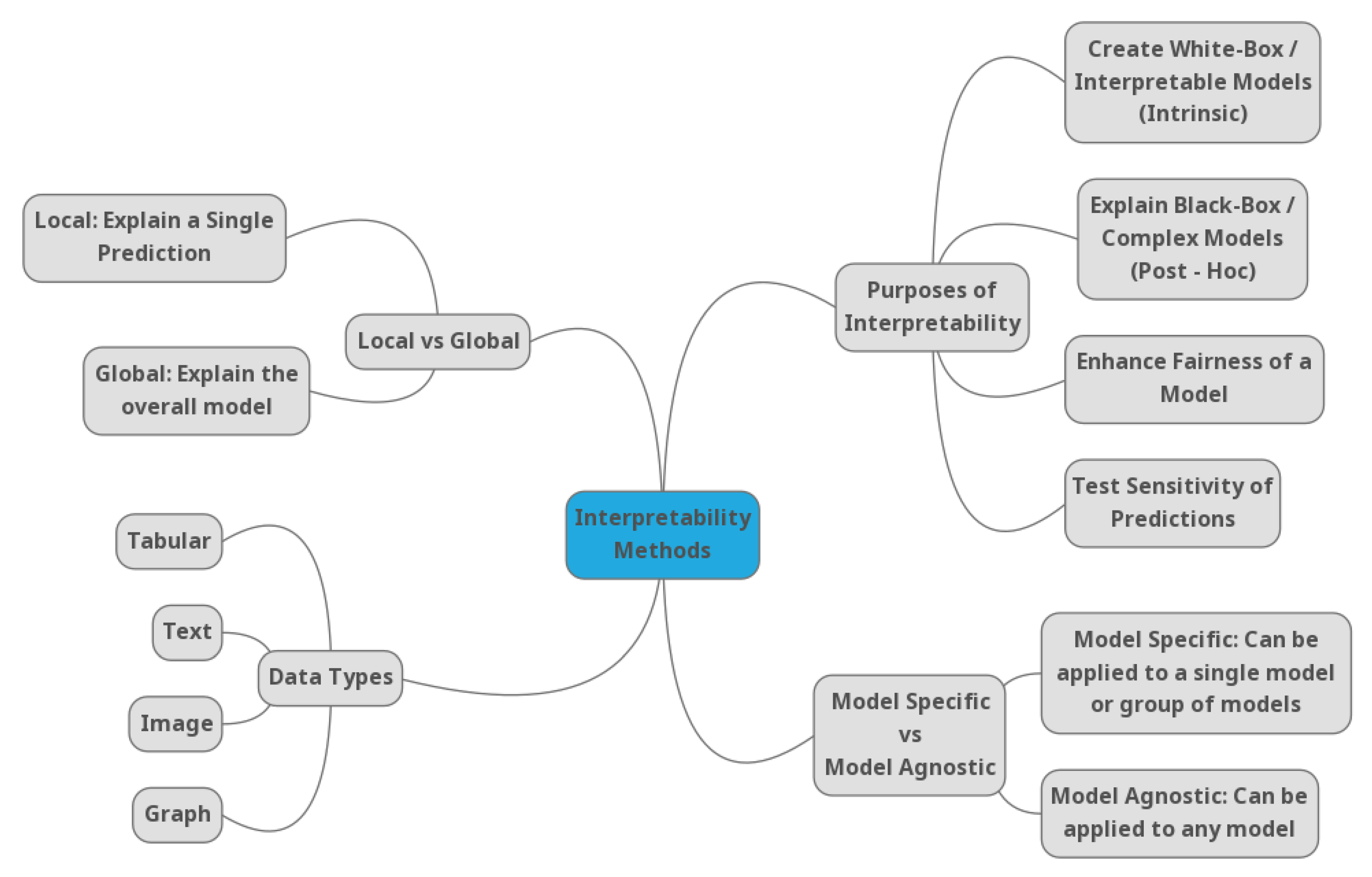
3. Different Scopes of Machine Learning Interpretability: A Taxonomy of Methods
3.1. Interpretability Methods to Explain Black-Box Models
3.1.1. Interpretability Methods to Explain Deep Learning Models
3.1.2. Interpretability Methods to Explain any Black-Box Model
3.2. Interpretability Methods to Create White-Box Models
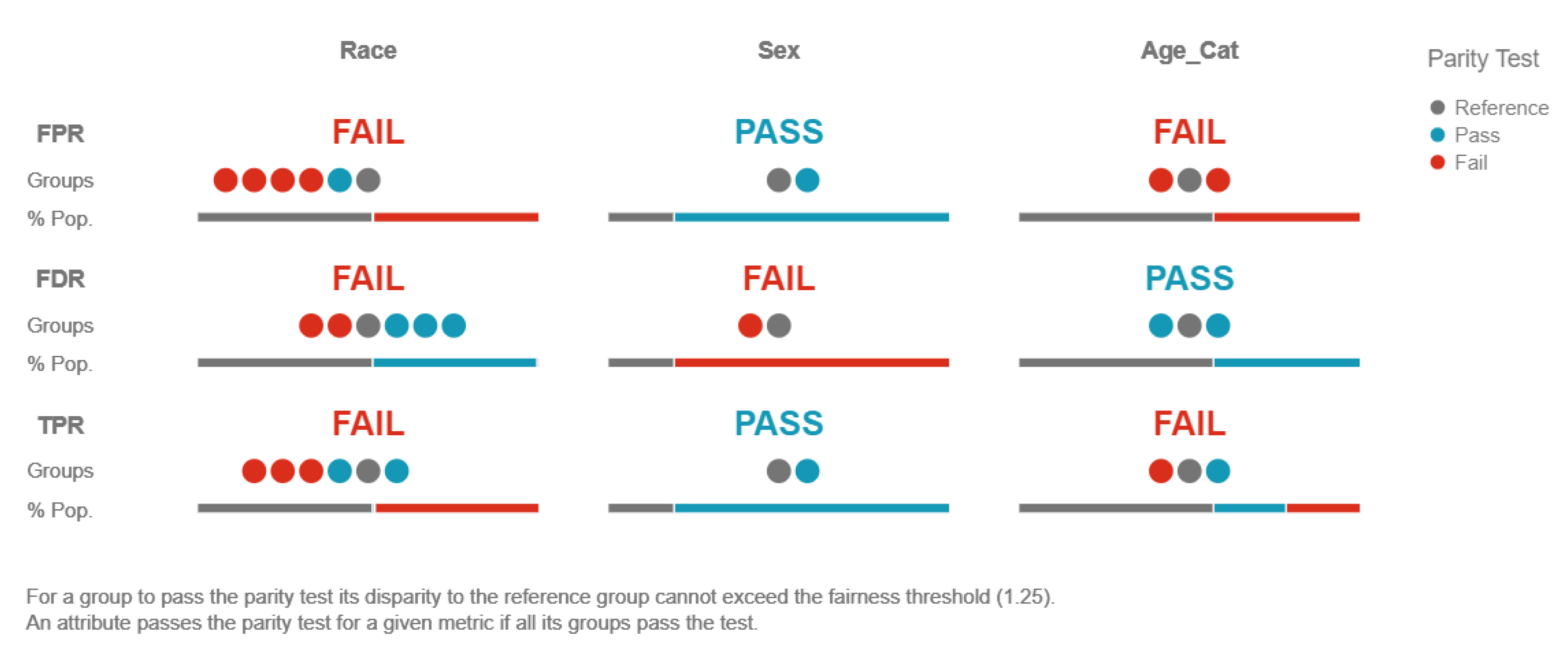
3.3. Interpretability Methods to Restrict Discrimination and Enhance Fairness in Machine Learning Models
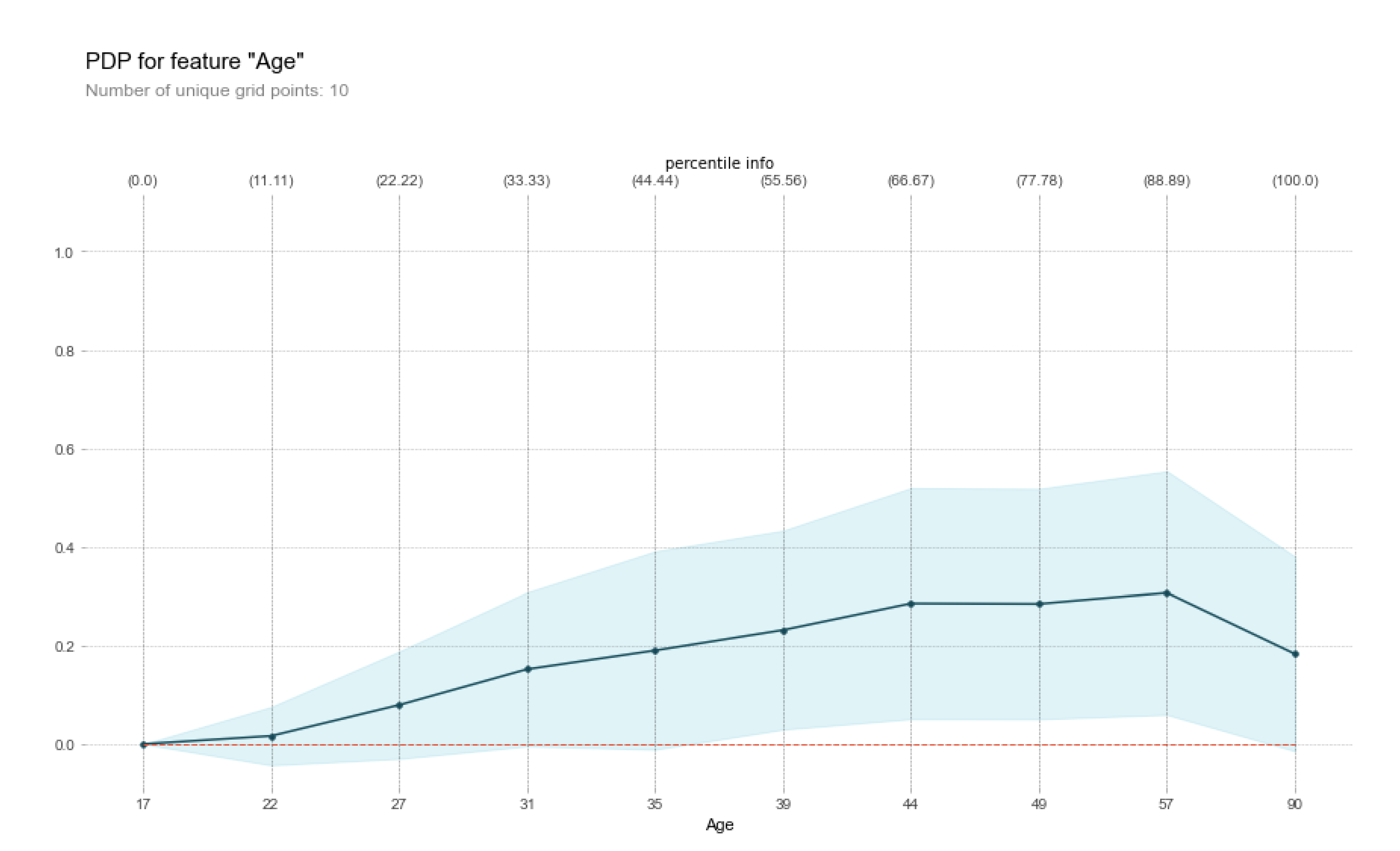
3.4. Interpretability Methods to Analyse the Sensitivity of Machine Learning Model Predictions
3.4.1. Traditional Sensitivity Analysis Methods
3.4.2. Adversarial Example-based Sensitivity Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| W | Whit-Box/Interpretable Models |
| PH | Post-Hoc |
| F | Fairness |
| S | Sensitivity |
| L | Local |
| G | Global |
| Agnostic | Model Agnostic |
| Specific | Model Specific |
| tab | Tabular Data |
| img | Image Data |
| txt | Text Data |
| graph | Graph Data |
Appendix A. Repository Links
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Khandani, A.E.; Kim, A.J.; Lo, A.W. Consumer credit-risk models via machine-learning algorithms. J. Bank. Financ. 2010, 34, 2767–2787. [Google Scholar] [CrossRef]
- Le, H.H.; Viviani, J.L. Predicting bank failure: An improvement by implementing a machine-learning approach to classical financial ratios. Res. Int. Bus. Financ. 2018, 44, 16–25. [Google Scholar] [CrossRef]
- Dua, S.; Acharya, U.R.; Dua, P. Machine Learning in Healthcare Informatics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 56. [Google Scholar]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Callahan, A.; Shah, N.H. Machine learning in healthcare. In Key Advances in Clinical Informatics; Elsevier: Amsterdam, The Netherlands, 2017; pp. 279–291. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–34. [Google Scholar]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 528. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Gunning, D.; Aha, D.W. DARPA’s Explainable Artificial Intelligence (XAI) Program. AI Magazine 2019, 40, 44–58. [Google Scholar] [CrossRef]
- Lipton, Z.C. The mythos of model interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Turin, Italy, 1–3 October 2018; pp. 80–89. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [PubMed]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2014, arXiv:1312.6034. [Google Scholar]
- Kümmerer, M.; Theis, L.; Bethge, M. Deep Gaze I: Boosting Saliency Prediction with Feature Maps Trained on ImageNet. arXiv 2014, arXiv:1411.1045. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Zhao, R.; Ouyang, W.; Li, H.; Wang, X. Saliency detection by multi-context deep learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1265–1274. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3319–3328. [Google Scholar]
- Roth, A.E. The Shapley Value: Essays in Honor of Lloyd S. Shapley; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning Important Features Through Propagating Activation Differences. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3145–3153. [Google Scholar]
- Mudrakarta, P.K.; Taly, A.; Sundararajan, M.; Dhamdhere, K. Did the Model Understand the Question? In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Melbourne, Australia, 15–20 July 2018; pp. 1896–1906. [Google Scholar]
- Springenberg, J.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for Simplicity: The All Convolutional Net. In Proceedings of the ICLR (Workshop Track), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 818–833. [Google Scholar]
- Zeiler, M.D.; Taylor, G.W.; Fergus, R. Adaptive deconvolutional networks for mid and high level feature learning. In Proceedings of the 2011 International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 2018–2025. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018. [Google Scholar] [CrossRef]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. SmoothGrad: Removing noise by adding noise. In Proceedings of the ICML Workshop on Visualization for Deep Learning, Sydney, Australia, 10 August 2017. [Google Scholar]
- Petsiuk, V.; Das, A.; Saenko, K. RISE: Randomized Input Sampling for Explanation of Black-box Models. In Proceedings of the British Machine Vision Conference 2018, BMVC 2018, Newcastle, UK, 3–6 September 2018; BMVA Press: Durham, UK, 2018; p. 151. [Google Scholar]
- Yosinski, J.; Clune, J.; Fuchs, T.; Lipson, H. Understanding neural networks through deep visualization. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.R. Explaining nonlinear classification decisions with deep taylor decomposition. Pattern Recognit. 2017, 65, 211–222. [Google Scholar] [CrossRef]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.; Wexler, J.; Viegas, F. Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (tcav). In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2668–2677. [Google Scholar]
- Lei, T.; Barzilay, R.; Jaakkola, T.S. Rationalizing Neural Predictions. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, EMNLP 2016, Austin, TX, USA, 1–4 November 2016; The Association for Computational Linguistics: Stroudsburg, PA, USA, 2016; pp. 107–117. [Google Scholar]
- Kindermans, P.J.; Schütt, K.T.; Alber, M.; Muller, K.; Erhan, D.; Kim, B.; Dähne, S. Learning how to explain neural networks: Patternnet and Patternattribution. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Garreau, D.; von Luxburg, U. Explaining the Explainer: A First Theoretical Analysis of LIME. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics, AISTATS 2020, Palermo, Sicily, Italy, 26–28 August 2020; Volume 108, pp. 1287–1296. [Google Scholar]
- Zafar, M.R.; Khan, N.M. DLIME: A deterministic local interpretable model-agnostic explanations approach for computer-aided diagnosis systems. arXiv 2019, arXiv:1906.10263. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Binder, A.; Montavon, G.; Lapuschkin, S.; Müller, K.; Samek, W. Layer-Wise Relevance Propagation for Neural Networks with Local Renormalization Layers. In Proceedings of the Artificial Neural Networks and Machine Learning—ICANN 2016—25th International Conference on Artificial Neural Networks, Barcelona, Spain, 6–9 September 2016; Proceedings, Part II; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2016; Volume 9887, pp. 63–71. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-precision model-agnostic explanations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Dhurandhar, A.; Chen, P.Y.; Luss, R.; Tu, C.C.; Ting, P.; Shanmugam, K.; Das, P. Explanations based on the missing: Towards contrastive explanations with pertinent negatives. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 592–603. [Google Scholar]
- Luss, R.; Chen, P.Y.; Dhurandhar, A.; Sattigeri, P.; Zhang, Y.; Shanmugam, K.; Tu, C.C. Generating contrastive explanations with monotonic attribute functions. arXiv 2019, arXiv:1905.12698. [Google Scholar]
- Wachter, S.; Mittelstadt, B.; Russell, C. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harv. JL Tech. 2017, 31, 841. [Google Scholar] [CrossRef]
- Van Looveren, A.; Klaise, J. Interpretable counterfactual explanations guided by prototypes. arXiv 2019, arXiv:1907.02584. [Google Scholar]
- Kim, B.; Khanna, R.; Koyejo, O.O. Examples are not enough, learn to criticize! criticism for interpretability. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2280–2288. [Google Scholar]
- Gurumoorthy, K.S.; Dhurandhar, A.; Cecchi, G.; Aggarwal, C. Efficient Data Representation by Selecting Prototypes with Importance Weights. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 260–269. [Google Scholar]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Chen, J.; Song, L.; Wainwright, M.J.; Jordan, M.I. Learning to Explain: An Information-Theoretic Perspective on Model Interpretation. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 882–891. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Staniak, M.; Biecek, P. Explanations of Model Predictions with live and breakDown Packages. R J. 2018, 10, 395. [Google Scholar] [CrossRef]
- Dhurandhar, A.; Shanmugam, K.; Luss, R.; Olsen, P.A. Improving simple models with confidence profiles. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 10296–10306. [Google Scholar]
- Ustun, B.; Rudin, C. Supersparse linear integer models for optimized medical scoring systems. Mach. Learn. 2016, 102, 349–391. [Google Scholar] [CrossRef]
- Caruana, R.; Lou, Y.; Gehrke, J.; Koch, P.; Sturm, M.; Elhadad, N. Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1721–1730. [Google Scholar]
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate intelligible models with pairwise interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Gold Coast, Australia, 14–17 April 2013; pp. 623–631. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized additive models: Some applications. J. Am. Stat. Assoc. 1987, 82, 371–386. [Google Scholar] [CrossRef]
- Dash, S.; Gunluk, O.; Wei, D. Boolean decision rules via column generation. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 4655–4665. [Google Scholar]
- Wei, D.; Dash, S.; Gao, T.; Gunluk, O. Generalized Linear Rule Models. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 6687–6696. [Google Scholar]
- McCullagh, P. Generalized Linear Models; Routledge: Abingdon, UK, 2018. [Google Scholar]
- Hind, M.; Wei, D.; Campbell, M.; Codella, N.C.; Dhurandhar, A.; Mojsilović, A.; Natesan Ramamurthy, K.; Varshney, K.R. TED: Teaching AI to explain its decisions. In Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, Honolulu, HI, USA, 27–28 January 2019; pp. 123–129. [Google Scholar]
- Feldman, M.; Friedler, S.A.; Moeller, J.; Scheidegger, C.; Venkatasubramanian, S. Certifying and removing disparate impact. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 259–268. [Google Scholar]
- Kamiran, F.; Calders, T. Data preprocessing techniques for classification without discrimination. Knowl. Inf. Syst. 2012, 33, 1–33. [Google Scholar] [CrossRef]
- Kamiran, F.; Calders, T. Classifying without discriminating. In Proceedings of the 2009 2nd International Conference on Computer, Control and Communication, Karachi, Pakistan, 17–18 February 2009; pp. 1–6. [Google Scholar]
- Calders, T.; Kamiran, F.; Pechenizkiy, M. Building classifiers with independency constraints. In Proceedings of the 2009 IEEE International Conference on Data Mining Workshops, Miami, FL, USA, 6 December 2009; pp. 13–18. [Google Scholar]
- Calmon, F.; Wei, D.; Vinzamuri, B.; Ramamurthy, K.N.; Varshney, K.R. Optimized pre-processing for discrimination prevention. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3992–4001. [Google Scholar]
- Zhang, B.H.; Lemoine, B.; Mitchell, M. Mitigating unwanted biases with adversarial learning. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–3 February 2018; pp. 335–340. [Google Scholar]
- Kamiran, F.; Karim, A.; Zhang, X. Decision theory for discrimination-aware classification. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 924–929. [Google Scholar]
- Liu, L.T.; Dean, S.; Rolf, E.; Simchowitz, M.; Hardt, M. Delayed Impact of Fair Machine Learning. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 3156–3164. [Google Scholar]
- Elzayn, H.; Jabbari, S.; Jung, C.; Kearns, M.; Neel, S.; Roth, A.; Schutzman, Z. Fair algorithms for learning in allocation problems. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 170–179. [Google Scholar]
- Ensign, D.; Friedler, S.A.; Neville, S.; Scheidegger, C.; Venkatasubramanian, S. Runaway Feedback Loops in Predictive Policing. In Proceedings of the Conference on Fairness, Accountability and Transparency, FAT 2018, New York, NY, USA, 23–24 February 2018; Volume 81, pp. 160–171. [Google Scholar]
- Hu, L.; Immorlica, N.; Vaughan, J.W. The disparate effects of strategic manipulation. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 259–268. [Google Scholar]
- Milli, S.; Miller, J.; Dragan, A.D.; Hardt, M. The social cost of strategic classification. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 230–239. [Google Scholar]
- Kusner, M.J.; Loftus, J.; Russell, C.; Silva, R. Counterfactual fairness. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4066–4076. [Google Scholar]
- Bolukbasi, T.; Chang, K.W.; Zou, J.Y.; Saligrama, V.; Kalai, A.T. Man is to computer programmer as woman is to homemaker? debiasing word embeddings. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 4349–4357. [Google Scholar]
- Zemel, R.; Wu, Y.; Swersky, K.; Pitassi, T.; Dwork, C. Learning fair representations. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 325–333. [Google Scholar]
- Calders, T.; Verwer, S. Three naive Bayes approaches for discrimination-free classification. Data Min. Knowl. Discov. 2010, 21, 277–292. [Google Scholar] [CrossRef]
- Dwork, C.; Hardt, M.; Pitassi, T.; Reingold, O.; Zemel, R. Fairness through awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; pp. 214–226. [Google Scholar]
- Grgic-Hlaca, N.; Zafar, M.B.; Gummadi, K.P.; Weller, A. Beyond Distributive Fairness in Algorithmic Decision Making: Feature Selection for Procedurally Fair Learning. In Proceedings of the AAAI, New Orleans, LA, USA, 2–7 February 2018; pp. 51–60. [Google Scholar]
- Joseph, M.; Kearns, M.; Morgenstern, J.H.; Roth, A. Fairness in learning: Classic and contextual bandits. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 325–333. [Google Scholar]
- Joseph, M.; Kearns, M.; Morgenstern, J.; Neel, S.; Roth, A. Meritocratic fairness for infinite and contextual bandits. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–3 February 2018; pp. 158–163. [Google Scholar]
- Hardt, M.; Price, E.; Srebro, N. Equality of opportunity in supervised learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3315–3323. [Google Scholar]
- Zafar, M.B.; Valera, I.; Gomez Rodriguez, M.; Gummadi, K.P. Fairness beyond disparate treatment & disparate impact: Learning classification without disparate mistreatment. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 1171–1180. [Google Scholar]
- Zafar, M.B.; Valera, I.; Rogriguez, M.G.; Gummadi, K.P. Fairness constraints: Mechanisms for fair classification. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 962–970. [Google Scholar]
- Agarwal, A.; Beygelzimer, A.; Dudík, M.; Langford, J.; Wallach, H.M. A Reductions Approach to Fair Classification. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 60–69. [Google Scholar]
- Kearns, M.; Neel, S.; Roth, A.; Wu, Z.S. Preventing fairness gerrymandering: Auditing and learning for subgroup fairness. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2564–2572. [Google Scholar]
- Pleiss, G.; Raghavan, M.; Wu, F.; Kleinberg, J.; Weinberger, K.Q. On fairness and calibration. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5680–5689. [Google Scholar]
- Celis, L.E.; Huang, L.; Keswani, V.; Vishnoi, N.K. Classification with fairness constraints: A meta-algorithm with provable guarantees. In Proceedings of the Conference on Fairness Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 319–328. [Google Scholar]
- Kamishima, T.; Akaho, S.; Asoh, H.; Sakuma, J. Fairness-aware classifier with prejudice remover regularizer. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2012; pp. 35–50. [Google Scholar]
- Zafar, M.B.; Valera, I.; Rodriguez, M.; Gummadi, K.; Weller, A. From parity to preference-based notions of fairness in classification. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 229–239. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Cukier, R.; Fortuin, C.; Shuler, K.E.; Petschek, A.; Schaibly, J. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Tarantola, S.; Gatelli, D.; Mara, T.A. Random balance designs for the estimation of first order global sensitivity indices. Reliab. Eng. Syst. Saf. 2006, 91, 717–727. [Google Scholar] [CrossRef]
- Plischke, E. An effective algorithm for computing global sensitivity indices (EASI). Reliab. Eng. Syst. Saf. 2010, 95, 354–360. [Google Scholar] [CrossRef]
- Tissot, J.Y.; Prieur, C. Bias correction for the estimation of sensitivity indices based on random balance designs. Reliab. Eng. Syst. Saf. 2012, 107, 205–213. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Plischke, E.; Borgonovo, E.; Smith, C.L. Global sensitivity measures from given data. Eur. J. Oper. Res. 2013, 226, 536–550. [Google Scholar] [CrossRef]
- Kucherenko, S. Derivative based global sensitivity measures and their link with global sensitivity indices. Math. Comput. Simul. 2009, 79, 3009–3017. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Goodfellow, I.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1765–1773. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrücken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9185–9193. [Google Scholar]
- Li, Y.; Li, L.; Wang, L.; Zhang, T.; Gong, B. NATTACK: Learning the Distributions of Adversarial Examples for an Improved Black-Box Attack on Deep Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 3866–3876. [Google Scholar]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (sp), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Papernot, N.; McDaniel, P.; Wu, X.; Jha, S.; Swami, A. Distillation as a defense to adversarial perturbations against deep neural networks. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 582–597. [Google Scholar]
- Carlini, N.; Katz, G.; Barrett, C.; Dill, D.L. Provably minimally-distorted adversarial examples. arXiv 2017, arXiv:1709.10207. [Google Scholar]
- Xiao, C.; Zhu, J.; Li, B.; He, W.; Liu, M.; Song, D. Spatially Transformed Adversarial Examples. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [Google Scholar] [CrossRef]
- Chen, P.Y.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.J. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017; pp. 15–26. [Google Scholar]
- Narodytska, N.; Kasiviswanathan, S. Simple black-box adversarial attacks on deep neural networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1310–1318. [Google Scholar]
- Chen, J.; Jordan, M.I.; Wainwright, M.J. Hopskipjumpattack: A query-efficient decision-based attack. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (sp), San Francisco, CA, USA, 18–21 May 2020; pp. 1277–1294. [Google Scholar]
- Liu, Y.; Chen, X.; Liu, C.; Song, D. Delving into Transferable Adversarial Examples and Black-box Attacks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Cisse, M.M.; Adi, Y.; Neverova, N.; Keshet, J. Houdini: Fooling Deep Structured Visual and Speech Recognition Models with Adversarial Examples. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 6977–6987. [Google Scholar]
- Chen, P.; Sharma, Y.; Zhang, H.; Yi, J.; Hsieh, C. EAD: Elastic-Net Attacks to Deep Neural Networks via Adversarial Examples. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018; AAAI Press: Palo Alto, CA, USA, 2018; pp. 10–17. [Google Scholar]
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, UAE, 2–6 April 2017; pp. 506–519. [Google Scholar]
- Brendel, W.; Rauber, J.; Bethge, M. Decision-Based Adversarial Attacks: Reliable Attacks Against Black-Box Machine Learning Models. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Brendel, W.; Rauber, J.; Kümmerer, M.; Ustyuzhaninov, I.; Bethge, M. Accurate, reliable and fast robustness evaluation. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Koh, P.W.; Liang, P. Understanding Black-box Predictions via Influence Functions. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1885–1894. [Google Scholar]
- Zügner, D.; Akbarnejad, A.; Günnemann, S. Adversarial attacks on neural networks for graph data. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2847–2856. [Google Scholar]
- Dai, H.; Li, H.; Tian, T.; Huang, X.; Wang, L.; Zhu, J.; Song, L. Adversarial Attack on Graph Structured Data. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1123–1132. [Google Scholar]
- Zügner, D.; Günnemann, S. Adversarial Attacks on Graph Neural Networks via Meta Learning. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Sharif, M.; Bhagavatula, S.; Bauer, L.; Reiter, M.K. Accessorize to a crime: Real and stealthy attacks on state-of-the-art face recognition. In Proceedings of the 2016 ACM Sigsac Conference on Computer And Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1528–1540. [Google Scholar]
- Hayes, J.; Danezis, G. Learning universal adversarial perturbations with generative models. In Proceedings of the 2018 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 24 May 2018; pp. 43–49. [Google Scholar]
- Schott, L.; Rauber, J.; Bethge, M.; Brendel, W. Towards the first adversarially robust neural network model on MNIST. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Rauber, J.; Bethge, M. Fast differentiable clipping-aware normalization and rescaling. arXiv 2020, arXiv:2007.07677. [Google Scholar]
- Huang, S.H.; Papernot, N.; Goodfellow, I.J.; Duan, Y.; Abbeel, P. Adversarial Attacks on Neural Network Policies. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Yang, P.; Chen, J.; Hsieh, C.J.; Wang, J.L.; Jordan, M.I. Greedy Attack and Gumbel Attack: Generating Adversarial Examples for Discrete Data. J. Mach. Learn. Res. 2020, 21, 1–36. [Google Scholar]
- Samanta, S.; Mehta, S. Towards crafting text adversarial samples. arXiv 2017, arXiv:1707.02812. [Google Scholar]
- Iyyer, M.; Wieting, J.; Gimpel, K.; Zettlemoyer, L. Adversarial Example Generation with Syntactically Controlled Paraphrase Networks. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2018, New Orleans, LA, USA, 1–6 June 2018; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; Volume 1, pp. 1875–1885. [Google Scholar]
- Miyato, T.; Dai, A.M.; Goodfellow, I.J. Adversarial Training Methods for Semi-Supervised Text Classification. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Ebrahimi, J.; Rao, A.; Lowd, D.; Dou, D. HotFlip: White-Box Adversarial Examples for Text Classification. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, ACL 2018, Melbourne, Australia, 15–20 July 2018; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; Volume 2, pp. 31–36. [Google Scholar] [CrossRef]
- Liang, B.; Li, H.; Su, M.; Bian, P.; Li, X.; Shi, W. Deep Text Classification Can be Fooled. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI 2018, Stockholm, Sweden, 13–19 July 2018; pp. 4208–4215. [Google Scholar]
- Jia, R.; Liang, P. Adversarial Examples for Evaluating Reading Comprehension Systems. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, EMNLP 2017, Copenhagen, Denmark, 9–11 September 2017; Association for Computational Linguistics: Stroudsburg, PA, USA, 2017; pp. 2021–2031. [Google Scholar]
- Alzantot, M.; Sharma, Y.; Elgohary, A.; Ho, B.J.; Srivastava, M.; Chang, K.W. Generating Natural Language Adversarial Examples. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 2890–2896. [Google Scholar]
- Kuleshov, V.; Thakoor, S.; Lau, T.; Ermon, S. Adversarial examples for natural language classification problems. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, X.; Jin, H.; He, K. Natural language adversarial attacks and defenses in word level. arXiv 2019, arXiv:1909.06723. [Google Scholar]
- Gao, J.; Lanchantin, J.; Soffa, M.L.; Qi, Y. Black-box generation of adversarial text sequences to evade deep learning classifiers. In Proceedings of the 2018 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 24 May 2018; pp. 50–56. [Google Scholar]
- Li, J.; Ji, S.; Du, T.; Li, B.; Wang, T. TextBugger: Generating Adversarial Text Against Real-world Applications. In Proceedings of the 26th Annual Network and Distributed System Security Symposium, NDSS 2019, San Diego, CA, USA, 24–27 February 2019; The Internet Society: Reston, VA, USA, 2019. [Google Scholar]
- Cheng, M.; Yi, J.; Chen, P.Y.; Zhang, H.; Hsieh, C.J. Seq2Sick: Evaluating the Robustness of Sequence-to-Sequence Models with Adversarial Examples. In Proceedings of the AAAI, New York, NY, USA, 7–12 February 2020; pp. 3601–3608. [Google Scholar]
- Feng, S.; Wallace, E.; Grissom, A., II; Iyyer, M.; Rodriguez, P.; Boyd-Graber, J. Pathologies of Neural Models Make Interpretations Difficult. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; Association for Computational Linguistics: Brussels, Belgium, 2018; pp. 3719–3728. [Google Scholar] [CrossRef]
- Ren, S.; Deng, Y.; He, K.; Che, W. Generating natural language adversarial examples through probability weighted word saliency. In Proceedings of the 57th Annual Meeting of the Association For Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 1085–1097. [Google Scholar]
- Jin, D.; Jin, Z.; Zhou, J.T.; Szolovits, P. Is BERT Really Robust? A Strong Baseline for Natural Language Attack on Text Classification and Entailment. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, the Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, the Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; AAAI Press: Palo Alto, CA, USA, 2020; pp. 8018–8025. [Google Scholar]
- Garg, S.; Ramakrishnan, G. BAE: BERT-based Adversarial Examples for Text Classification. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing, EMNLP 2020, Online, 16–20 November 2020; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 6174–6181. [Google Scholar]
- Li, L.; Ma, R.; Guo, Q.; Xue, X.; Qiu, X. BERT-ATTACK: Adversarial Attack Against BERT Using BERT. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing, EMNLP 2020, Online, 16–20 November 2020; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 6193–6202. [Google Scholar]
- Tan, S.; Joty, S.; Kan, M.Y.; Socher, R. It’s Morphin’ Time! Combating Linguistic Discrimination with Inflectional Perturbations. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 2920–2935. [Google Scholar] [CrossRef]
- Zang, Y.; Qi, F.; Yang, C.; Liu, Z.; Zhang, M.; Liu, Q.; Sun, M. Word-level textual adversarial attacking as combinatorial optimization. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 6066–6080. [Google Scholar]



| Ref | Tool | Category | Local vs. Global | Model Specific vs. Model Agnostic | Data Type | Citations/Year | Year |
|---|---|---|---|---|---|---|---|
| [32] | DeepExplain iNNvestigate tf-explain | PH | L | Specific | img | 1548.3 | 2014 |
| [35] | Grad-CAM tf-explain | PH | L | Specific | img | 797.8 | 2017 |
| [34] | CAM | PH | L | Specific | img | 607.8 | 2016 |
| [31] | iNNvestigate | PH | L | Specific | img | 365.3 | 2014 |
| [23] | DeepExplain iNNvestigate tf-explain | PH | L | Specific | img | 278.3 | 2013 |
| [27] | DeepExplain iNNvestigate Integrated Gradients tf-explain alibi Skater | PH | L | Specific | img txt tab | 247 | 2017 |
| [40] | Deep Visualization Toolbox | PH | L | Specific | img | 221.7 | 2015 |
| [37] | DeepExplain iNNvestigate The LRP Toolbox Skater | PH | L | Specific | img txt | 217.8 | 2015 |
| [29] | DeepExplain DeepLift iNNvestigate tf-explain Skater | PH | L | Specific | img | 211.5 | 2017 |
| [41] | iNNvestigate | PH | L | Specific | img | 131.5 | 2017 |
| [38] | iNNvestigate tf-explain | PH | L | Specific | img | 113.3 | 2017 |
| [42] | tcav | PH | L | Specific | img | 95 | 2018 |
| [43] | rationale | PH | L | Specific | txt | 81.4 | 2016 |
| [36] | Grad-CAM++ | PH | L | Specific | img | 81 | 2018 |
| [39] | RISE | PH | L | Specific | img | 43.3 | 2018 |
| [44] | iNNvestigate | PH | L | Specific | img | 41.8 | 2017 |
| Ref | Tool | Category | Local vs. Global | Model Specific vs. Model Agnostic | Data Type | Citations/Year | Year |
|---|---|---|---|---|---|---|---|
| [45] | lime Eli5 InterpretML AIX360 Skater | PH | L | Agnostic | img txt tab | 845.6 | 2016 |
| [59] | PDPbox InterpretML Skater | PH | G | Agnostic | tab | 589.2 | 2001 |
| [48] | shap alibi AIX360 InterpretML | PH | L & G | Agnostic | img txt tab | 504.5 | 2017 |
| [50] | alibi Anchor | PH | L | Agnostic | img txt tab | 158.3 | 2018 |
| [53] | alibi | PH | L | Agnostic | tab img | 124.5 | 2017 |
| [60] | PyCEbox | PH | L & G | Agnostic | tab | 53.3 | 2015 |
| [58] | L2X | PH | L | Agnostic | img txt tab | 50.3 | 2018 |
| [57] | Eli5 | PH | G | Agnostic | tab | 41.5 | 2010 |
| [51] | alibi AIX360 | PH | L | Agnostic | tab img | 34.3 | 2018 |
| [61] | Alibi | PH | G | Agnostic | tab | 23.2 | 2016 |
| [54] | alibi | PH | L | Agnostic | tab img | 17 | 2019 |
| [62] | pyBreakDown | PH | L | Agnostic | tab | 8.3 | 2018 |
| [62] | pyBreakDown | PH | G | Agnostic | tab | 8.3 | 2018 |
| [47] | DLIME | PH | L | Agnostic | img txt tab | 7.5 | 2019 |
| [56] | AIX360 | PH | L | Agnostic | tab | 7 | 2019 |
| [52] | AIX360 | PH | L | Agnostic | tab img | 3 | 2019 |
| Ref | Tool | Category | Local vs. Global | Model Specific vs. Model Agnostic | Data Type | Citations/Year | Year |
|---|---|---|---|---|---|---|---|
| [65] | InterpretML | W | G | Specific | tab | 129.5 | 2015 |
| [64] | Slim | W | G | Specific | tab | 35.2 | 2016 |
| [68] | AIX360 | W | G | Specific | tab | 12.3 | 2018 |
| [71] | AIX360 | W | L | Specific | tab | 12 | 2019 |
| [69] | AIX360 | W | G | Specific | tab | 5 | 2019 |
| Ref | Tool | Category | Local vs. Global | Model Specific vs. Model Agnostic | Data Type | Citations/Year | Year |
|---|---|---|---|---|---|---|---|
| [92] | equalized_odds_and_calibration fairlearn AIF360 | F | G | Agnostic | tab | 242.2 | 2016 |
| [85] | debiaswe | F | L | Specific | txt | 216.8 | 2016 |
| [88] | fairness | F | L | Agnostic | tab | 133.4 | 2012 |
| [72] | Aequitas AIF360 themis-ml | F | G | Agnostic | tab | 124.5 | 2015 |
| [93] | fair-classification | F | G | Agnostic | tab | 117.8 | 2017 |
| [84] | fairness-in-ml | F | L | Agnostic | tab | 115.5 | 2017 |
| [94] | fair-classification | F | G | Agnostic | tab | 110.8 | 2017 |
| [86] | AIF360 | F | L & G | Agnostic | tab | 94.6 | 2013 |
| [95] | fairlearn | F | G | Agnostic | tab | 94 | 2018 |
| [77] | AIF360 | F | L & G | Agnostic | tab | 92.3 | 2018 |
| [96] | AIF360 GerryFair | F | G | Agnostic | tab | 76 | 2018 |
| [97] | equalized_odds_and_calibration AIF360 | F | G | Agnostic | tab | 60 | 2017 |
| [76] | AIF360 | F | G | Agnostic | tab | 53.5 | 2017 |
| [79] | ML-fairness-gym | F | G | Agnostic | tab | 51.7 | 2018 |
| [81] | ML-fairness-gym | F | G | Agnostic | tab | 45.7 | 2018 |
| [87] | fairness-comparison | F | G | Specific | tab | 45 | 2010 |
| [73] | AIF360 | F | G | Agnostic | tab | 37.2 | 2012 |
| [98] | AIF360 | F | G | Agnostic | tab | 37 | 2019 |
| [99] | AIF360 | F | G | Agnostic | tab | 35.3 | 2012 |
| [100] | fair-classification | F | G | Agnostic | tab | 26.8 | 2017 |
| [83] | ML-fairness-gym | F | L | Specific | tab | 24 | 2019 |
| [82] | ML-fairness-gym | F | L | Specific | tab | 23 | 2019 |
| [89] | procedurally_fair_learning | F | G | Agnostic | tab | 22 | 2018 |
| [74] | themis-ml | F | L | Agnostic | tab | 19.6 | 2009 |
| [75] | AIF360 | F | L | Agnostic | tab | 17 | 2009 |
| [78] | AIF360 themis-ml | F | G | Agnostic | tab | 12.1 | 2012 |
| [80] | ML-fairness-gym | F | G | Specific | tab | 10.5 | 2019 |
| [91] | FairMachineLearning | F | L | Specific | tab | 3.8 | 2016 |
| Ref | Tool | Category | Local vs. Global | Model Specific vs. Model Agnostic | Data Type | Citations/Year | Year |
|---|---|---|---|---|---|---|---|
| [109] | SALib | S | G | Agnostic | tab | 400.8 | 2008 |
| [103] | SALib | S | G | Agnostic | tab | 160.2 | 2010 |
| [101] | SALib | S | G | Agnostic | tab | 152.4 | 2001 |
| [110] | SALib | S | G | Agnostic | tab | 117.6 | 1991 |
| [111] | SALib | S | G | Agnostic | tab | 101.5 | 2007 |
| [105] | SALib | S | G | Agnostic | tab | 87.5 | 1999 |
| [102] | SALib | S | G | Agnostic | tab | 76.2 | 2002 |
| [112] | SALib | S | G | Agnostic | tab | 50.2 | 2007 |
| [113] | SALib | S | G | Agnostic | tab | 29.9 | 2013 |
| [114] | SALib | S | G | Agnostic | tab | 29.1 | 2009 |
| [104] | SALib | S | G | Agnostic | tab | 21.6 | 1973 |
| [106] | SALib | S | G | Agnostic | tab | 16.5 | 2006 |
| [107] | SALib | S | G | Agnostic | tab | 9.2 | 2010 |
| [108] | SALib | S | G | Agnostic | tab | 6.3 | 2012 |
| Ref | Tool | Category | Local vs. Global | Model Specific vs. Model Agnostic | Data Type | Citations/Year | Year |
|---|---|---|---|---|---|---|---|
| [116] | cleverhans foolbox | S | L & G | Agnostic | img | 876.4 | 2014 |
| [115] | cleverhans foolbox | S | L & G | Agnostic | img | 727.4 | 2013 |
| [123] | cleverhans nn_robust_attacks | S | L & G | Agnostic | img | 716 | 2017 |
| [120] | cleverhans foolbox | S | L & G | Agnostic | img | 429 | 2016 |
| [127] | one-pixel-attack-keras | S | L & G | Agnostic | img | 409 | 2019 |
| [117] | cleverhans foolbox | S | L & G | Agnostic | img | 392 | 2016 |
| [119] | cleverhans foolbox | S | L & G | Agnostic | img | 381.2 | 2016 |
| [134] | cleverhans | S | L & G | Agnostic | img | 378.8 | 2017 |
| [137] | influence-release | S | L & G | Agnostic | img | 224 | 2017 |
| [121] | cleverhans | S | L & G | Agnostic | img | 181.7 | 2018 |
| [152] | adversarial-squad | S | L & G | Specific | txt | 162 | 2017 |
| [131] | transferability-advdnn-pub | S | L & G | Agnostic | img | 148.6 | 2016 |
| [141] | accessorize-to-a-crime | S | L & G | Agnostic | img | 141.6 | 2016 |
| [128] | ZOO-Attack | S | L & G | Agnostic | img | 129.8 | 2017 |
| [135] | foolbox boundary-attack | S | L & G | Agnostic | img | 99.5 | 2017 |
| [158] | TextAttack | S | L & G | Specific | txt | 83 | 2020 |
| [149] | adversarial_text adversarial_training adversarial_training_methods | S | L & G | Specific | txt | 70.8 | 2016 |
| [138] | nettack | S | L & G | Specific | graph data | 70.3 | 2018 |
| [153] | nlp_adversarial_examples | S | L & G | Agnostic | txt | 70.3 | 2018 |
| [148] | scpn | S | L & G | Agnostic | txt | 66.7 | 2018 |
| [126] | stAdv | S | L & G | Agnostic | img | 65.3 | 2018 |
| [133] | cleverhans | S | L & G | Agnostic | img | 64.3 | 2017 |
| [150] | WordAdver | S | L & G | Agnostic | txt | 63.5 | 2017 |
| [139] | graph_adversarial_attack | S | L & G | Specific | graph data | 55.3 | 2018 |
| [143] | foolbox AnalysisBySynthesis | S | L & G | Agnostic | img | 44.3 | 2018 |
| [140] | gnn-meta-attack | S | L & G | Specific | graph data | 42 | 2019 |
| [156] | TextAttack | S | L & G | Agnostic | txt | 41 | 2018 |
| [118] | universal | S | L & G | Agnostic | img | 34 | 2017 |
| [159] | TextAttack | S | L & G | Agnostic | txt | 31.7 | 2018 |
| [130] | HSJA | S | L & G | Agnostic | img | 31.5 | 2019 |
| [160] | TextAttack | S | L & G | Agnostic | txt | 29.5 | 2019 |
| [122] | Nattack | S | L & G | Agnostic | img | 29 | 2019 |
| [129] | foolbox | S | L & G | Agnostic | img | 26.8 | 2016 |
| [157] | TextAttack | S | L & G | Agnostic | txt | 26.7 | 2018 |
| [161] | TextAttack TextFooler | S | L & G | Specific | txt | 21 | 2019 |
| [125] | nn_robust_attacks | S | L & G | Agnostic | img | 11 | 2017 |
| [165] | TextAttack | S | L & G | Agnostic | txt | 10 | 2020 |
| [142] | UAN | S | L & G | Agnostic | img | 9.7 | 2018 |
| [154] | TextAttack | S | L & G | Agnostic | txt | 9.3 | 2018 |
| [136] | foolbox | S | L & G | Agnostic | img | 6.5 | 2019 |
| [155] | TextAttack | S | L & G | Agnostic | txt | 6.5 | 2019 |
| [163] | TextAttack | S | L & G | Specific | txt | 5 | 2020 |
| [164] | TextAttack | S | L & G | Agnostic | txt | 5 | 2020 |
| [162] | TextAttack | S | L & G | Specific | txt | 4 | 2020 |
| [144] | foolbox | S | L & G | Agnostic | img | 1.5 | 2019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2021, 23, 18. https://doi.org/10.3390/e23010018
Linardatos P, Papastefanopoulos V, Kotsiantis S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy. 2021; 23(1):18. https://doi.org/10.3390/e23010018
Chicago/Turabian StyleLinardatos, Pantelis, Vasilis Papastefanopoulos, and Sotiris Kotsiantis. 2021. "Explainable AI: A Review of Machine Learning Interpretability Methods" Entropy 23, no. 1: 18. https://doi.org/10.3390/e23010018
APA StyleLinardatos, P., Papastefanopoulos, V., & Kotsiantis, S. (2021). Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy, 23(1), 18. https://doi.org/10.3390/e23010018







