On Products of Random Matrices
Abstract
1. Introduction
2. Technical Tools
2.1. Partitions; Power Sums and Schur Functions; Hurwitz Numbers
2.2. Mixed Ensembles of Random Matrices
2.3. Integrals of Schur Functions and Integrals of Power Sums
3. Our Models. Products of Random Matrices We Choose
3.1. Preliminary. On the Products of Random Matrices
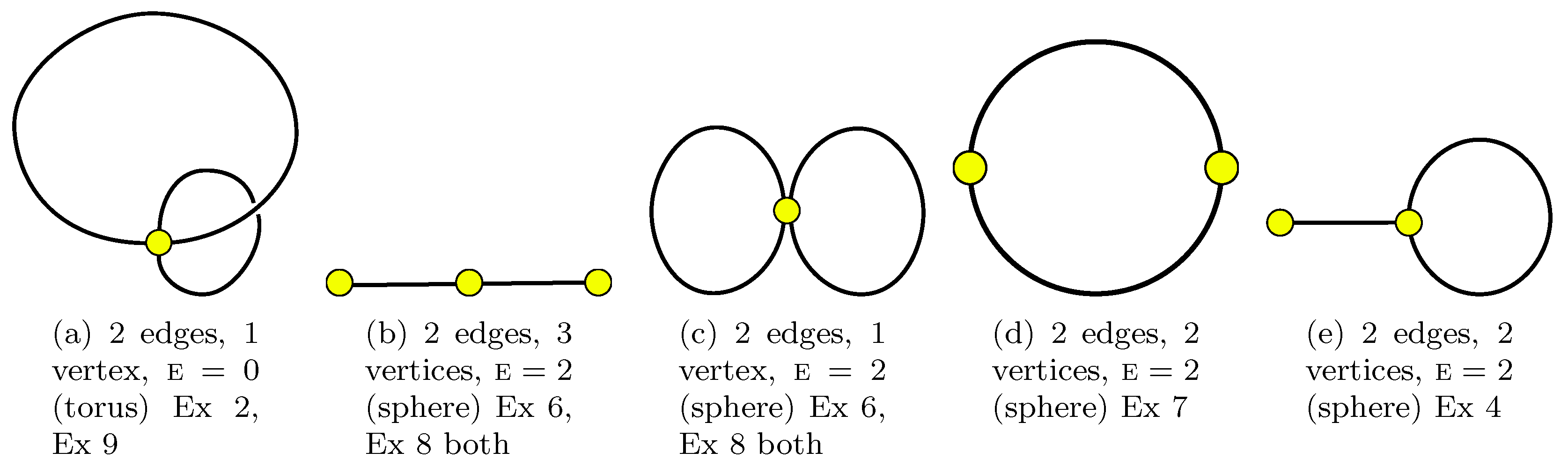
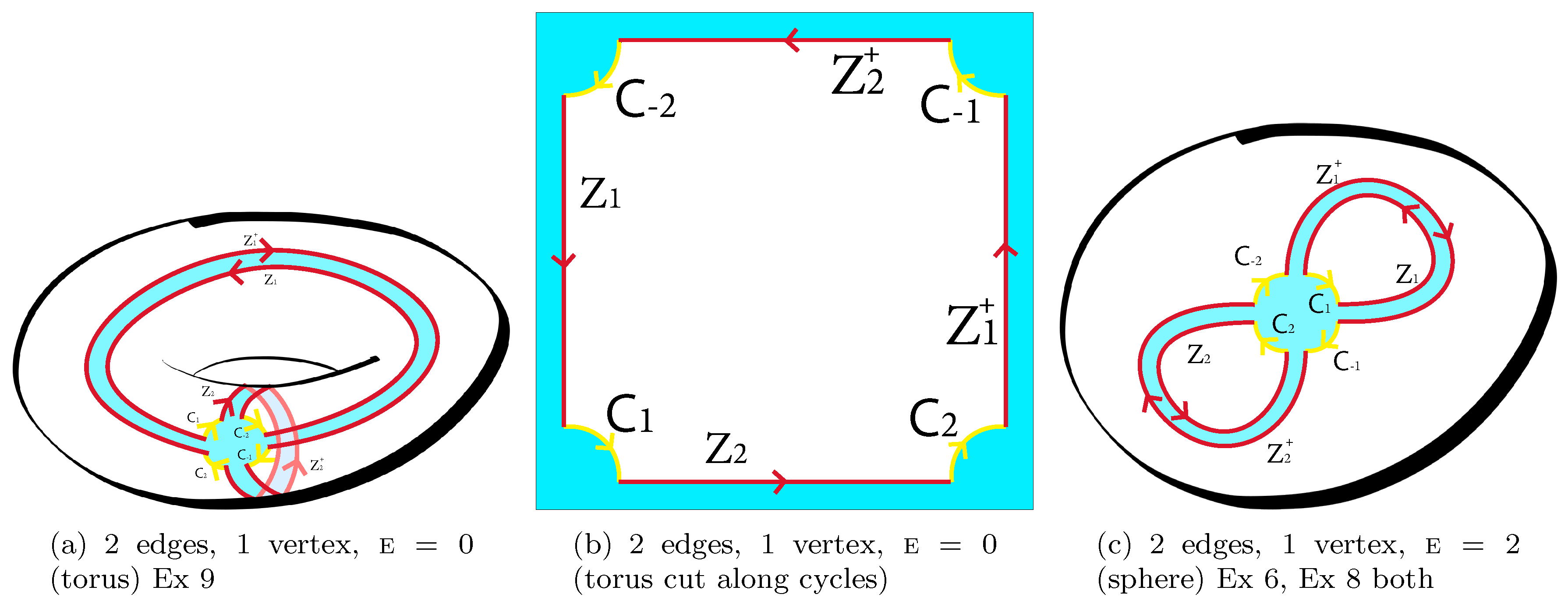
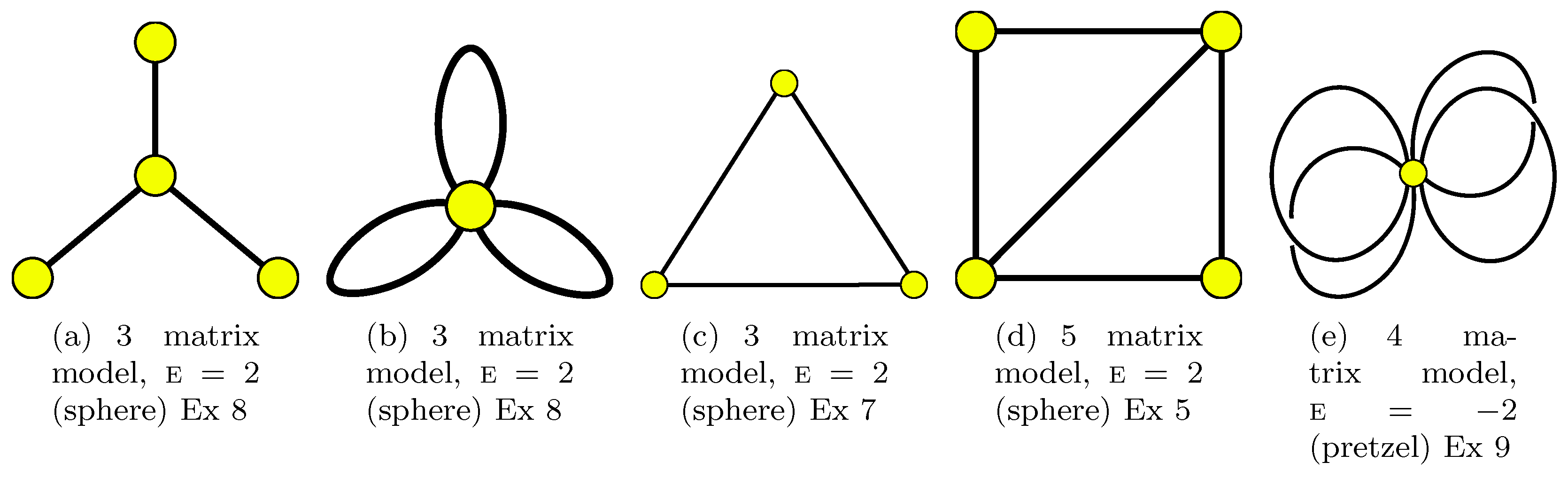
3.2. Models Obtained from Graphs (Geometrical View)
- The answer (i.e., the left-hand side of (52)) depends only on the spectrum of star monodromies
- The answer does not depend on how exactly in our model we distribute the matrices and to dress the source matrices—only two numbers and are important. For example, it does not matter, in the right-hand side of (52), whether we dress and or and .
3.3. Our Models. Algebraic View
4. Expectation Values of Matrix Products
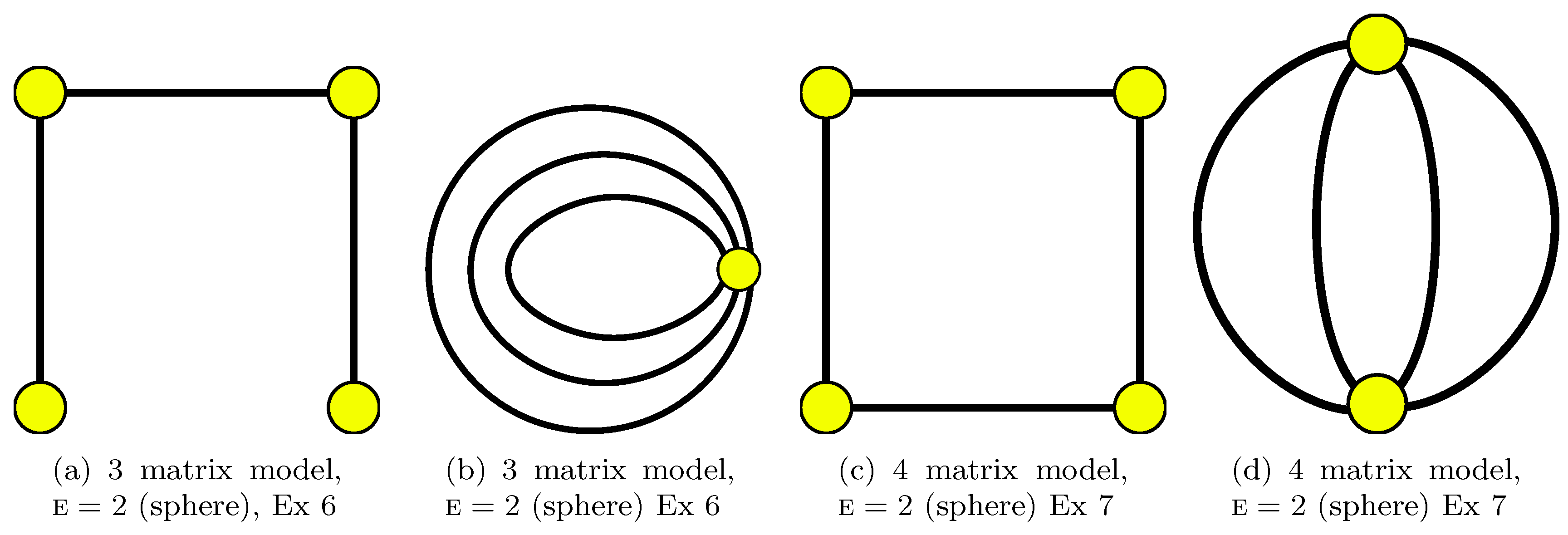
5. Examples of Matrix Models
- Dual sets ;
- The fraction of unitary matrices given by ;
- The set of functions ;
- The sets .
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Partitions and Schur Functions
Appendix B. Integrals over the Unitary Group
Appendix C. Geometrical Definition of Hurwitz Numbers
Appendix D. Combinatorial Definition of Hurwitz Numbers
Appendix E. Differential Operators
References
- Vilenkin, N.Y.; Klimyk, A.U. Representation of Lie Groups and Special Functions; Volume 3: Classical and Quantum Groups and Special Functions; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- t’Hooft, G. A planar diagram theory for strong interactions. Nucl. Phys. 1974, 72, 461–473. [Google Scholar]
- Itzykson, C.; Zuber, J.-B. The planar approximation. II. J. Math. Phys. 1980, 21, 411. [Google Scholar] [CrossRef]
- Kazakov, V.A.; Kostov, I.K.; Nekrasov, N. D-particles, Matrix Integrals and KP hierachy. Nucl. Phys. 1999, 557, 413–442. [Google Scholar] [CrossRef]
- Brezin, E.; Kazakov, V.A. Exactly solvable field theories of closed strings. Phys. Lett. 1990, B236, 144–150. [Google Scholar] [CrossRef]
- Gross, D.J.; Migdal, A.A. A nonperturbative treatment of two-dimensional quantum gravity. Nucl. Phys. B 1990, 340, 333–365. [Google Scholar] [CrossRef]
- Collins, B.; Nechita, I. Random matrix techniques in quantum information theory. J. Math. Phys. 2016, 57, 015215. [Google Scholar] [CrossRef]
- Preskill, J. Lecture Notes. Available online: http://www.theory.caltech.edu/~preskill/ph219/index.html#lecture (accessed on 3 August 2020).
- Tulino, A.M.; Verdu, S. Random Matrix Theory and Wireless Communications. Foundations and Trends in Communications and Information Theory; Now Publishers Inc.: Breda, The Netherlands, 2004; Volume 1. [Google Scholar]
- Akemann, G.; Ipsen, J.R.; Kieburg, M. Products of Rectangular Random Matrices: Singular Values and Progressive Scattering. Phys. Rev. E 2013, 88, 052118. [Google Scholar] [CrossRef]
- Akemann, G.; Checinski, T.; Kieburg, M. Spectral correlation functions of the sum of two independent complex Wishart matrices with unequal covariances. J. Phys. A Math. Theor. 2016, 49, 315201. [Google Scholar] [CrossRef]
- Akemann, G.; Strahov, E. Hard edge limit of the product of two strongly coupled random matrices. Nonlinearity 2016, 29, 3743. [Google Scholar] [CrossRef]
- Ipsen, J.R. Products of Independent Gaussian Random Matrices. arXiv 2015, arXiv:1510.06128. [Google Scholar]
- Strahov, E. Dynamical correlation functions for products of random matrices. arXiv 2015, arXiv:1505.02511. [Google Scholar] [CrossRef]
- Strahov, E. Differential equations for singular values of products of Ginibre random matrices. arXiv 2014, arXiv:1403.6368. [Google Scholar] [CrossRef]
- Ambjørn, J.; Chekhov, L. The matrix model for dessins d’enfants. arXiv 2014, arXiv:1404.4240. [Google Scholar]
- Kazakov, V.A.; Staudacher, M.; Wynter, T. Character Expansion Methods for Matrix Models of Dually Weighted Graphs. Commun. Math. Phys. 1996, 177, 451–468. [Google Scholar] [CrossRef]
- Kazakov, V.A.; Staudacher, M.; Wynter, T. Almost Flat Planar Diagrams. Commun. Math. Phys. 1996, 179, 235–256. [Google Scholar] [CrossRef]
- Kazakov, V.A.; Staudacher, M.; Wynter, T. Exact Solution of Discrete Two-Dimensional R2 Gravity. Nucl. Phys. 1996, B471, 309–333. [Google Scholar] [CrossRef]
- Kazakov, V.A. Solvable Matrix Models. arXiv 2000, arXiv:hep-th/0003064. [Google Scholar]
- Alexandrov, A. Matrix models for random partitions. Nucl. Phys. B 2011, 851, 620–650. [Google Scholar] [CrossRef]
- Ambjørn, J.; Chekhov, L.O. The matrix model for hypergeometric Hurwitz number. Theor. Math. Phys. 2014, 81, 1486–1498. [Google Scholar]
- Macdonald, I.G. Symmetric Functions and Hall Polynomials, 2nd ed.; Clarendon Press: Oxford, UK; New York, NY, USA, 1995. [Google Scholar]
- Orlov, A.Y.; Scherbin, D.M. Fermionic representation for basic hypergeometric functions related to Schur polynomials. arXiv 2000, arXiv:nlin/0001001. [Google Scholar]
- Orlov, A.Y.; Scherbin, D.M. Hypergeometric solutions of soliton equations. Theor. Math. Phys. 2001, 128, 906–926. [Google Scholar] [CrossRef]
- Orlov, A.Y. New solvable matrix integrals. Intern. J. Mod. Phys. 2004, 19 (Suppl. S2), 276–293. [Google Scholar] [CrossRef]
- Orlov, A.Y.; Shiota, T.; Takasaki, K. Pfaffian structures and certain solutions to BKP hierarchies I. Sums over partitions. arXiv 2012, arXiv:math-ph/12014518. [Google Scholar]
- Lando, S.K.; Zvonkin, A.K. Graphs on Surfaces and Their Applications; Encyclopaedia of Mathematical Sciences; Zagier, D., Ed.; Springer: New York, NY, USA, 2004; Volume 141. [Google Scholar]
- Okounkov, A.; Pandharipande, R. Gromov-Witten theory, Hurwitz theory and completed cycles. Ann. Math. 2006, 163, 517. [Google Scholar] [CrossRef]
- Dijkgraaf, R. Mirror Symmetry and Elliptic Curves, The Moduli Space of Curves; Dijkgraaf, R., Faber, C., van der Geer, G., Eds.; Progress in Mathematics; Birkhauser: Basel, Switzerland, 1995; Volume 129. [Google Scholar]
- Natanzon, S.M.; Orlov, A.Y. Hurwitz numbers from matrix integrals over Gaussian measure. arXiv 2020, arXiv:2002.00466. [Google Scholar]
- Natanzon, S.M.; Orlov, A.Y. Hurwitz numbers from Feynman diagrams. Theor. Math. Phys. 2020, 204, 1172–1199. [Google Scholar]
- Chekhov, L.O. The Harer-Zagier recursion for an irregular spectral curve. J. Geom. Phys. 2016, 110, 30–43. [Google Scholar] [CrossRef]
- Orlov, A.Y. Hurwitz numbers and products of random matrices. Theor. Math. Phys. 2017, 192, 1282–1323. [Google Scholar] [CrossRef]
- Orlov, A.Y. Links between quantum chaos and counting problems. In Geometric Methods in Physics XXXVI, Trends in Mathematics; Kielanowski, P., Odzijewicz, A., Previato, E., Eds.; Birkhauser: Cham, Switzerland, 2019; pp. 355–373. [Google Scholar]
- Adrianov, N.M.; Amburg, N.Y.; Dremov, V.A.; Kochetkov, Y.Y.; Kreines, E.M.; Levitskaya, Y.A.; Nasretdinova, V.F.; Shabat, G.B. Catalog of dessins d’enfants with ≤ 4 edges. J. Math. Sci. 2009, 158, 22–80. [Google Scholar] [CrossRef][Green Version]
- Natanzon, S.M.; Orlov, A.Y. Integals of tau functions. arXiv 2019, arXiv:1911.02003. [Google Scholar]
- Migdal, A.A. Recursion equations in gauge field theories. JETP 1975, 42, 413. [Google Scholar]
- Rusakov, B.Y. Loop avareges and partition functions in U(N) gauge theory on two-dimensional manifold. Mod. Phys. Lett. A 1990, 5, 693–703. [Google Scholar] [CrossRef]
- Witten, E. On Quantum Gauge Theories in Two Dimensions. Com. Math. Phys. 1991, 141, 153–209. [Google Scholar] [CrossRef]
- Olshanski, G.I. Yangians and universal enveloping algebras. J. Soviet Math. 1989, 47, 2466–2473. [Google Scholar] [CrossRef]
- Olshanski, G.I. Representations of infinite-dimensional classical groups, limits of envelopingalgebras, and Yangians. In Topics in Representation Theory; Kirillov, A.A., Ed.; Advances in Soviet Math; American Mathematical Society: Providence, RI, USA, 1991; pp. 1–66. [Google Scholar]
- Okounkov, A.; Olshanski, G. Shifted Schur functions. Algebra i Analiz 1998, 9, 73–146. [Google Scholar]
- Okounkov, A. Shifted Schur functions II. The binomial formulafor characters of classical groups and its applications. In American Mathematical Society Translations; v. 185, Kirillov’s Seminar on Representation Theory; American Mathematical Society: Providence, RI, USA, 1998; pp. 245–271. [Google Scholar]
- Okounkov, A. Quantum Immanants and Higher Capelli Identities; Transformation Groups, v. 1; Springer: Boston, MA, USA, 1996; pp. 99–126. [Google Scholar]
- Okounkov, A. Young Basis, Wick Formula, and Higher Capelli Identities. Internat. Math. Res. Not. 1996, 17, 817–839. [Google Scholar] [CrossRef]
- Vershik, A.M.; Okounkov, A.Y. A new approach to the representation theory of symmetric groups. II. J. Math. Sci. 2005, 131, 5471–5494. [Google Scholar] [CrossRef]
- Gerasimov, A.A.; Shatashvili, S.L. Two-dimensional Gauge Theory and Quantum Integrable Systems. arXiv 2007, arXiv:0711.1472. [Google Scholar]
- Rumanov, I. Classical integrability for beta ensembles and general Fokker-Plank equation. J. Math. Phys. 2015, 56, 013508. [Google Scholar] [CrossRef]
- Mironov, A.; Morozov, A.; Semenoff, G. Unitary Matrix Integrals in the Framework of he Generalized Kontsevich Model. Intern J. Mod. Phys. A 1996, 11, 5031–5080. [Google Scholar] [CrossRef]
- Jimbo, M.; Miwa, T. Solitons and Infinite Dimensional Lie Algebras. Publ. RIMS Kyoto Univ. 1983, 19, 943–1001. [Google Scholar] [CrossRef]
- Ueno, K.; Takasaki, K. Toda lattice hierarchy. Adv. Stud. Pure Math. 1984, 4, 1–95. [Google Scholar]
- Takasaki, K. Initial value problem for the Toda lattice hierarchy. Adv. Stud. Pure Math. 1984, 4, 139–163. [Google Scholar]
- Takebe, T. Representation Theoretical Meaning of Initial Value Problem for the Toda Lattice Hierarchy I. Lett. Math. Phys. 1991, 21, 77–84. [Google Scholar] [CrossRef]
- Takebe, T. Representation Theoretical Meaning of Initial Value Problem for the Toda Lattice Hierarchy II. Publ. RIMS Kyoto Univ. 1991, 27, 491–503. [Google Scholar] [CrossRef]
- Ekedahl, T.; Lando, S.; Shapiro, M.; Vainshtein, A. On Hurwitz numbers and Hodge integrals. Comptes Rendus de l’Académie des Sciences-Series I-Math. 1999, 146, 175–1180. [Google Scholar] [CrossRef]
- Okounkov, A. Toda equations for Hurwitz numbers. Math. Res. Lett. 2000, 7, 447–453. [Google Scholar] [CrossRef]
- Mednykh, A.D. Determination of the number of nonequivalent covering over a compact Riemann surface. Soviet Math. Dokl. 1978, 19, 318–320. [Google Scholar]
- Mednykh, A.D.; Pozdnyakova, G.G. The number of nonequivalent covering over a compact nonorientable surface. Sibirs. Mat. 1986, 27, 123–131. [Google Scholar] [CrossRef]
- Jones, G.A. Enumeration of Homomorphisms and Surface-Coverings. Q. J. Math. Oxford 1995, 46, 485–507. [Google Scholar] [CrossRef]
- Mironov, A.D.; Morozov, A.Y.; Natanzon, S.M. Complect set of cut-and-join operators in the Hurwitz-Kontsevich theory. Theor. Math. Phys. 2011, 166, 1–22. [Google Scholar] [CrossRef]
- Orlov, A.Y. Vertex Operator, ∂-Problem, Symmetries, Variational Identities and Hamiltonian Formalism for 2+ 1 Integrable Systems; Nonlinear and Turbulent Processes in Physics; World Scientific: Singapore, 1987. [Google Scholar]
- Mironov, A.; Morozov, A.; Natanzon, S. Algebra of differential operators associated with Young diagramms. J. Geom. Phys. 2012, 62, 148–155. [Google Scholar] [CrossRef]
- Perelomov, A.M.; Popov, V.S. Casimir operators for groups U(N) SU(N). Yadernaya Fizika 1966, 3, 924–931. [Google Scholar]
- Perelomov, A.M.; Popov, V.S. Casimir operators for classical groups. Doklady AN SSSR 1967, 174, 287–290. (In Russian) [Google Scholar]
- Perelomov, A.M.; Popov, V.S. Casimir operators for semisimple Lie groups. Izavestia AN SSSR 1968, 32, 1368–1390. [Google Scholar] [CrossRef]
- Zhelobenko, D.P. Compact Lie Groups and Their Representations; American Mathematical Soc.: Providence, RI, USA, 1973. [Google Scholar]
- Dubrovin, B.A. Symplectic field theory of a disk, quantum integrable systems, and Schur polynomials. arXiv 2016, arXiv:1407.5824. [Google Scholar] [CrossRef]
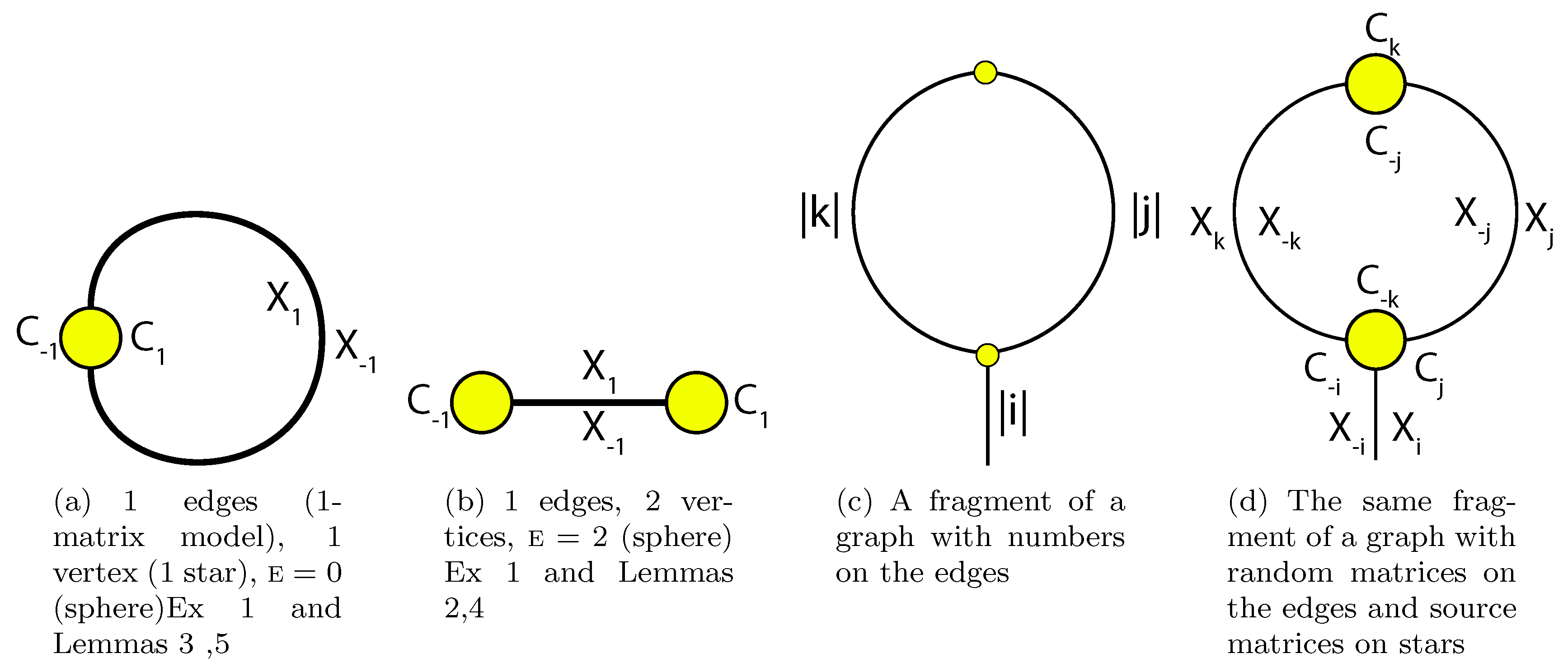
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amburg, N.; Orlov, A.; Vasiliev, D. On Products of Random Matrices. Entropy 2020, 22, 972. https://doi.org/10.3390/e22090972
Amburg N, Orlov A, Vasiliev D. On Products of Random Matrices. Entropy. 2020; 22(9):972. https://doi.org/10.3390/e22090972
Chicago/Turabian StyleAmburg, Natalia, Aleksander Orlov, and Dmitry Vasiliev. 2020. "On Products of Random Matrices" Entropy 22, no. 9: 972. https://doi.org/10.3390/e22090972
APA StyleAmburg, N., Orlov, A., & Vasiliev, D. (2020). On Products of Random Matrices. Entropy, 22(9), 972. https://doi.org/10.3390/e22090972




