1. Introduction
Entropy is a core concept in thermodynamics, which is a branch of physics, and explains “almost all known physical processes in the universe” [
1]. This concept (widely referred to as thermodynamic entropy) was first described by the German physicist Rudolf Clausius in the 1850s to discuss the change of unavailable energy during a spontaneous process [
2] then modeled by the Austrian physicist Ludwig Boltzmann [
3] using the famous Boltzmann equation (hence the term Boltzmann entropy). Entropy has been widely used to express the most remarkable law of classical physics [
4], the second law of thermodynamics, as follows, “the entropy of a closed system increases continuously and irrevocably toward a maximum” [
5]. In addition to its fundamental role in physics, it has found applications in diverse fields such as sustainability (e.g., Gao et al. [
6]), image processing (e.g., Sawant and Manoharan [
7]), urban planning (e.g., Fistola and La Rocca [
8]), and neurobiology (e.g., Blokh and Stambler [
9]).
The application of entropy has also been explored and discussed in landscape ecology (e.g., Forman and Godron [
10]; Jiang et al. [
11]; Naveh [
12]; O’Neill et al. [
13]; Wu and Loucks [
14]; Zurlini et al. [
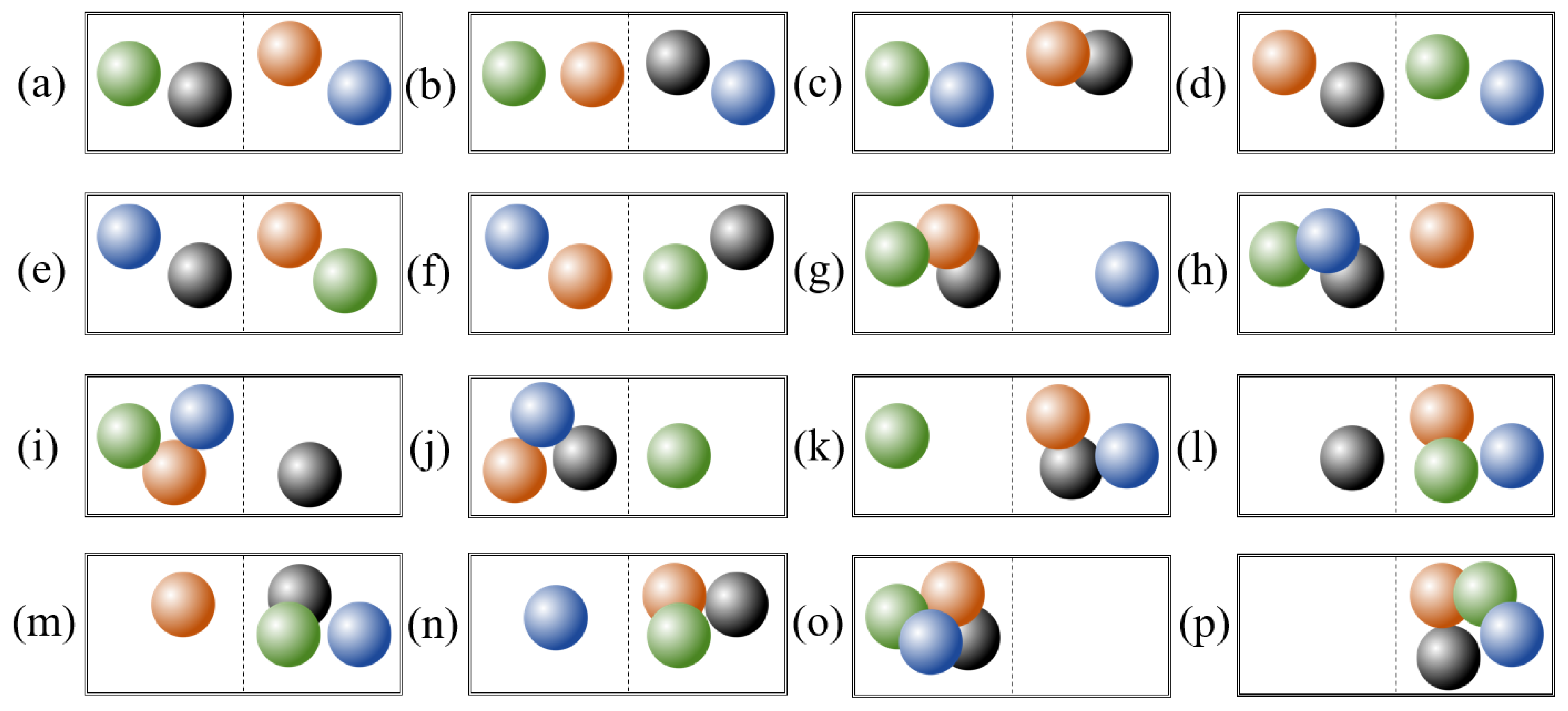
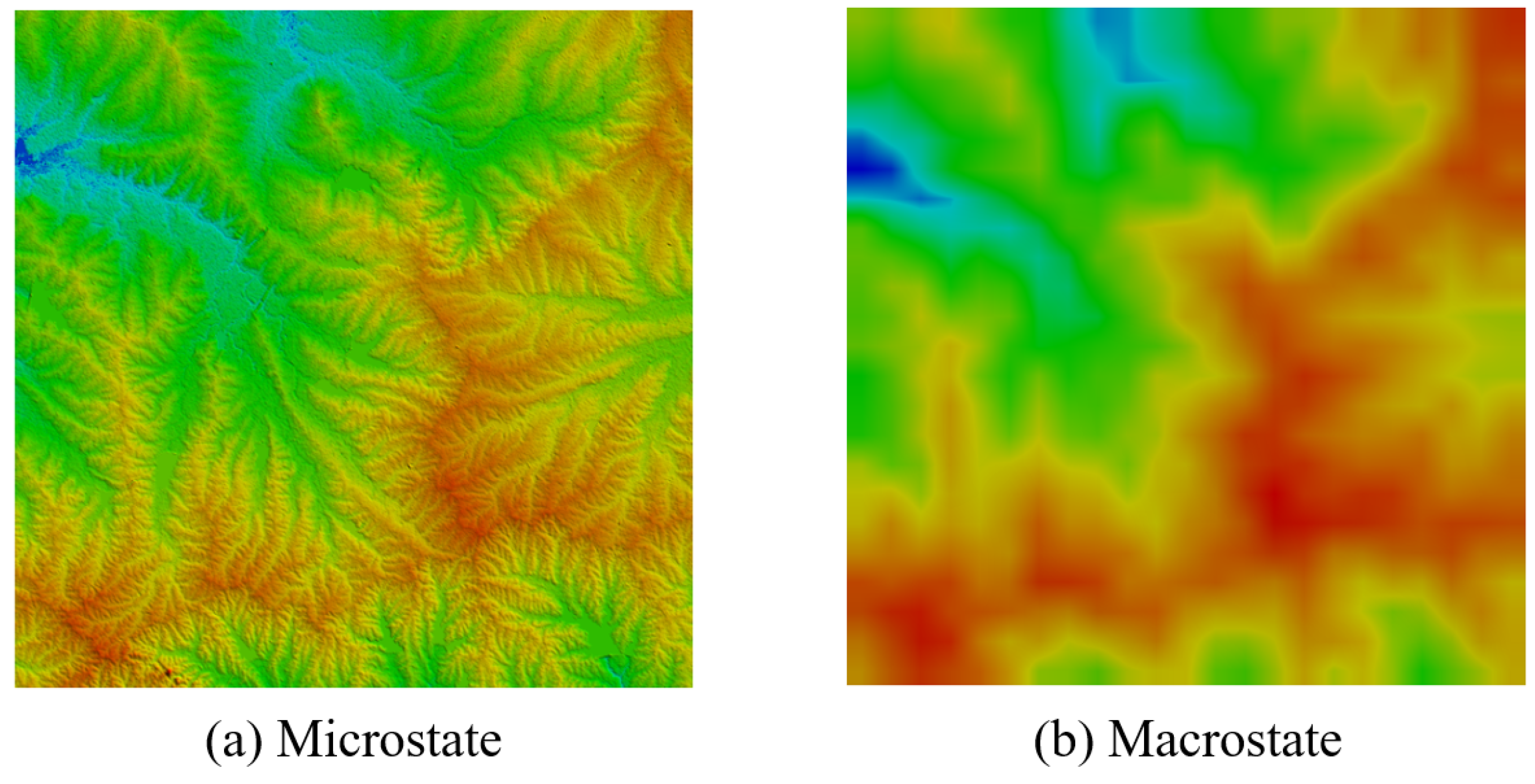
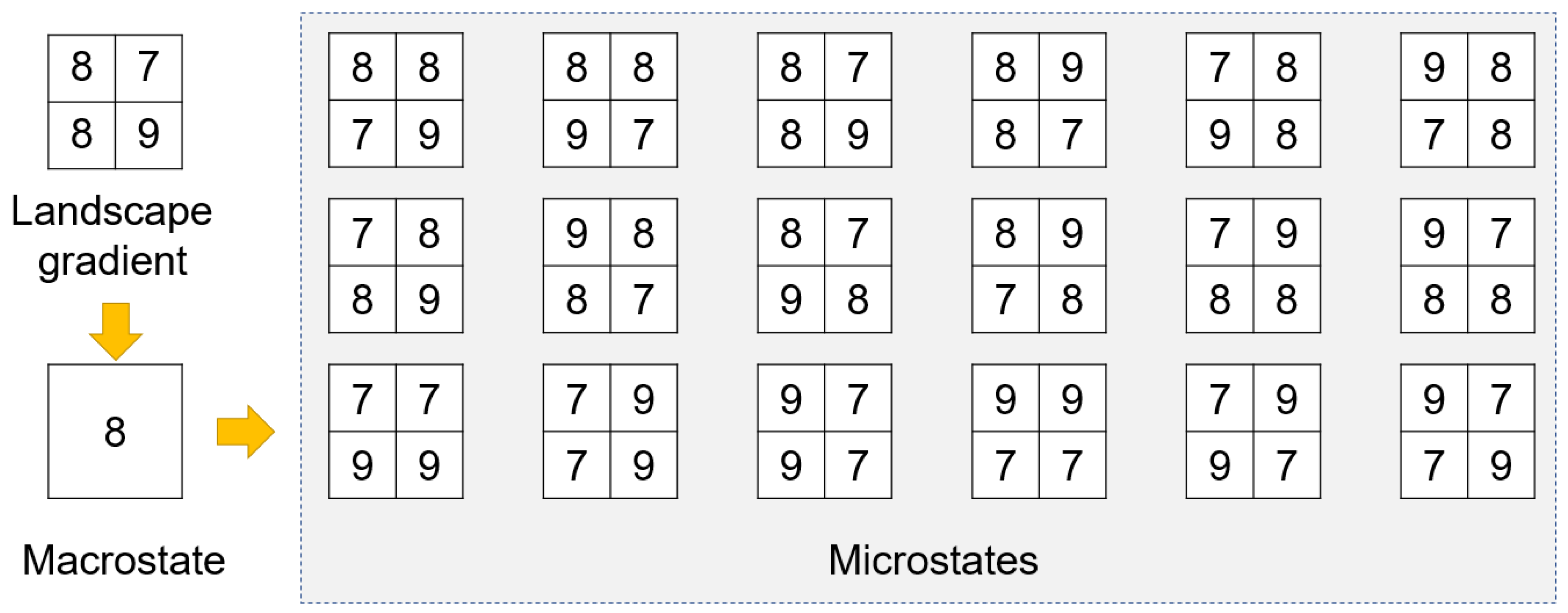
15]), for the following reason. Boltzmann entropy provides a statistical method to quantify unavailable energy based on the number of microstates in the macrostate of a thermodynamic system.
Accordingly, by specifying this number with a landscape pattern, one computes the Boltzmann entropy of a landscape pattern and establishes a relationship between the pattern and the energy of the landscape. Such a relationship allows for a deeper understanding of landscape dynamics based on thermodynamic insights, and it can be expected to “provide a theoretical context which could help clarify and unify a large portion of landscape ecology research” [
16]. However, the computation of Boltzmann entropy remained a problem in landscape ecology for a long time because researchers have no idea on “how to specify and measure the macrostate/microstate relations” (Bailey [
17], p. 151). Indeed, as confirmed by Vranken et al. [
18], “no thermodynamic entropy quantification methods have been proposed” (p. 61).
As a result, the use of Boltzmann entropy in landscape ecology has long limited to conceptual discussion, with Shannon entropy being used as an alternative in practical applications (e.g., Rocchini et al. [
19]; Díaz-Varela et al. [
20]). Shannon entropy (i.e., information entropy) was proposed by the American mathematician Claude Shannon [
21] to quantify the information content of a telegraph message and laid the foundation of information theory [
22,
23]. It has been widely considered as Boltzmann entropy in essence, and both entropies are used interchangeably (e.g., Lopez-Ruiz et al. [
24]; Mohajeri et al. [
25]). However, considerable criticisms are emerging about the equivalence between the two entropies. More recently, Vranken et al. [
18] concluded that Shannon entropy is “merely a formal parallelism” (p. 54) to Boltzmann entropy. They further observed that almost all applications of Shannon entropy to landscape ecology—including spatial heterogeneity, the unpredictability of pattern dynamics and, and pattern scale dependence—can be questionable in terms of thermodynamic basis. Such observations have drawn much attention and described as “astounding” by leading ecologists [
16].
Therefore, calls have been recently made for returning from Shannon entropy to Boltzmann entropy in spatial sciences [
26,
27] and landscape ecology in particular [
16,
18]. To apply Boltzmann entropy, the primary and most fundamental step is to compute the Boltzmann entropy of a landscape pattern. Note that this step is also the most difficult and had limited Boltzmann entropy to a conceptual level for centuries. Fortunately, this step has been taken in recent years. Specifically, methods have been developed for computing the Boltzmann entropy of a landscape pattern represented either using a patch-mosaic model [
28,
29,
30,
31] or a gradient model [
32,
33], according to a recent review [
34]. However, these methods are much more complicated than that of Shannon entropy in terms of the amount of computation, and they are challenging to implement in practice [
35]. Therefore, there is a need for software tools for conveniently computing the Boltzmann entropy of a landscape pattern.
This study aimed at presenting an R [
36] package,
belg, for conveniently computing the Boltzmann entropy of a landscape pattern represented using a gradient model, namely, a landscape gradient. The gradient model was focused for two reasons: First, the gradient model could be more universally [
37] because it “subsumes the patch-mosaic model as a special case” (McGarigal and Cushman [
38], p. 118). Second, software tools for the patch-mosaic model have been developed [
35]. It is expected that our package
belg, associated with existing tools, will make Boltzmann entropy easy-to-compute with all kinds of landscape patterns, facilitating a thermodynamic understanding of landscape dynamics for sustainable development.
3. Examples
3.1. Basic Example
The belg R package aims at calculating Boltzmann entropy values and it is well connected with existing R packages used to represent spatial raster data, including raster and stars. Except belg, the following examples also use raster to represent spatial raster data.
| library(belg) |
| library(raster) |
The
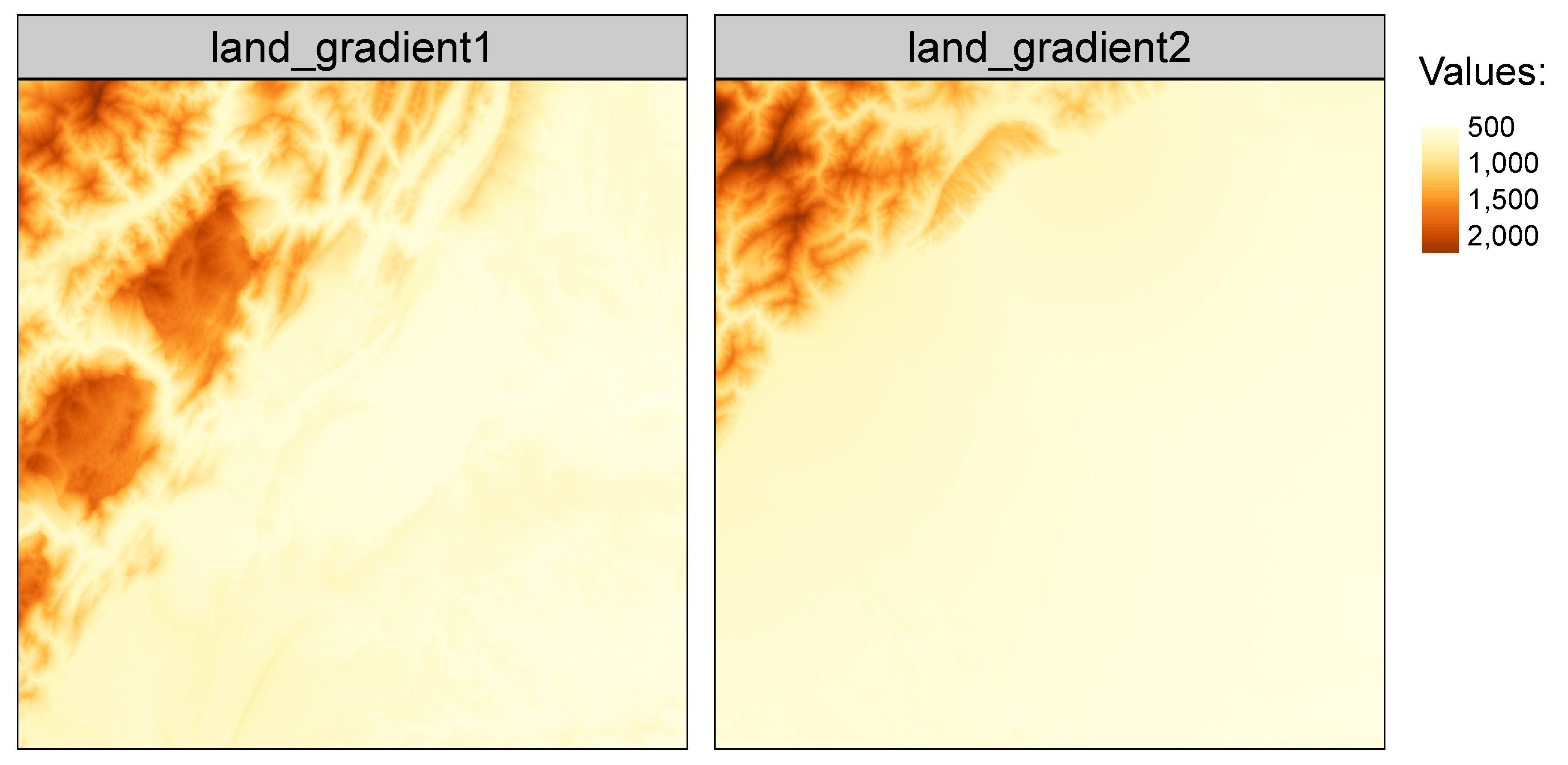
belg package has several build-in datasets allowing users to test its capabilities, including
land_gradient1 and
land_gradient2 (
Figure 7). Both datasets have 512 rows and columns (262,144 cells in total), where the first one represents a more diverse landscape gradient than the second one.
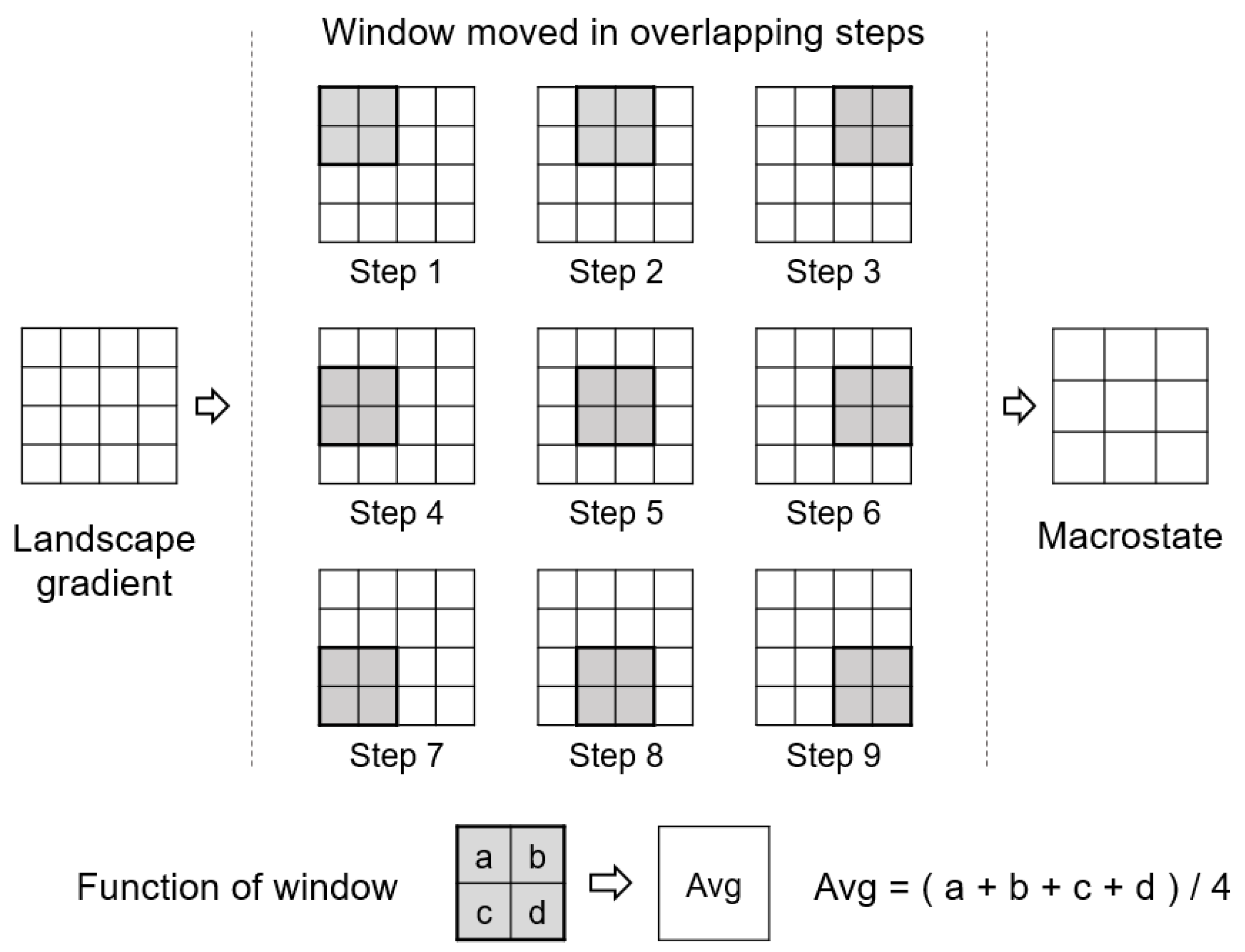
The get_boltzmann() function calculates the Boltzmann entropy of landscape gradients. It requires, at least, one argument with input data to work. Other arguments are set by default. This function uses the aggregation-based method (method = “aggregation”), values are scaled based on the proportion of missing values (na_adjust = TRUE), a logarithm of base 10 is used (base = “log10”), and absolute entropy is calculated (relative = FALSE).
| get_boltzmann(land_gradient1) |
| ## [1] 188772.5 |
| get_boltzmann(land_gradient2) |
| ## [1] 121875.2 |
The above results confirm the visual evaluation—the values Boltzmann entropy of the first landscape is distinctly larger than of the second landscape.
3.2. Example with Missing Values
The calculations using the belg package can be extended to many landscapes. The data/sample_rasters folder has eight GeoTIFF files containing digital elevation models for different areas. Each file has 64 rows and columns and a resolution of 90 m.
All files can be found using the dir() function, and subsequently read to R using the lapply() and raster() functions.
| sample_rasters_path = dir(“data/sample_rasters”, pattern = “.tif$”, full.names = TRUE) |
| sample_rasters = lapply(sample_rasters_path, raster) |
The original methods for calculating Boltzmann entropy for landscape gradients by Gao et al. [
32] and Gao and Li [
33] works only on rasters without missing values. To solve this problem, we specified how to perform two steps of Boltzmann entropy calculations, upscaling and downscaling, in cases of data with missing values. In terms of upscaling, the average is computed using cells with values. When all values are missing, then the
NA constant is returned. In downscaling, the number and positions of cells with missing values are preserved. More details about calculations for data with missing values are available in the package documentation at
https://r-spatialecology.github.io/belg/articles/belg1.html.
This modification makes it possible to calculate Boltzmann entropy for data with different degrees of missing values. However, it makes the results dependable on the number of missing cells. For example, removing 20% of cells from a relatively uniform landscape will result in a decrease in Boltzmann entropy of about 20%. Therefore, it makes it impossible to compare landscapes with different proportions of missing values correctly. The top row in
Figure 8 represents landscapes sorted by the values of Boltzmann entropy, calculated using the following code:
|
be_na = sapply(sample_rasters, get_boltzmann, na_adjust = FALSE) |
| be_na |
| ## [1] 1713.9065 1985.3938 3061.0793 2457.6999 2259.5122 3387.7103 2171.1460 |
| ## [8] 963.3178 |
This approach returns larger values for landscapes without missing values. For example, the fifth landscape visually seems to be less complex than the fourth one, but it has more non-missing cells and therefore larger value of Boltzmann entropy.
To allow for proper comparison of landscapes with different levels of missing values, the belg package allows for adjusting the results:
|
be_na_adj = sapply(sample_rasters, get_boltzmann, na_adjust = TRUE) |
| be_na_adj |
| ## [1] 3029.849 3330.128 3061.079 3768.903 2259.512 3387.710 3577.238 1345.754 |
When
na_adjust is set to
TRUE, then the initially calculated value of Boltzmann entropy is divided by the proportion (0–1) of cells without missing values. The adjusted values are presented in the bottom row in
Figure 8.
3.3. Example of a Larger Workflow
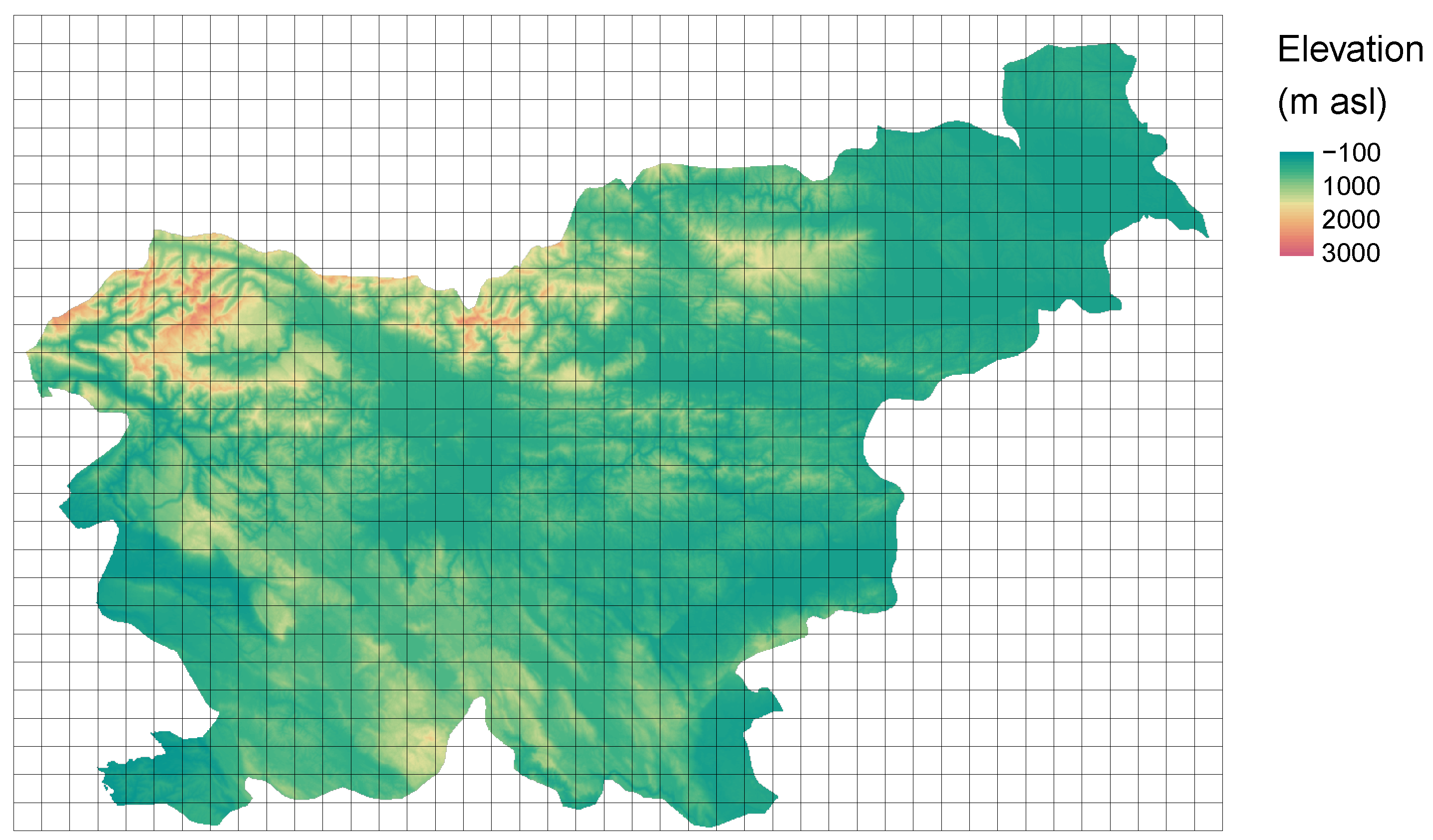
The
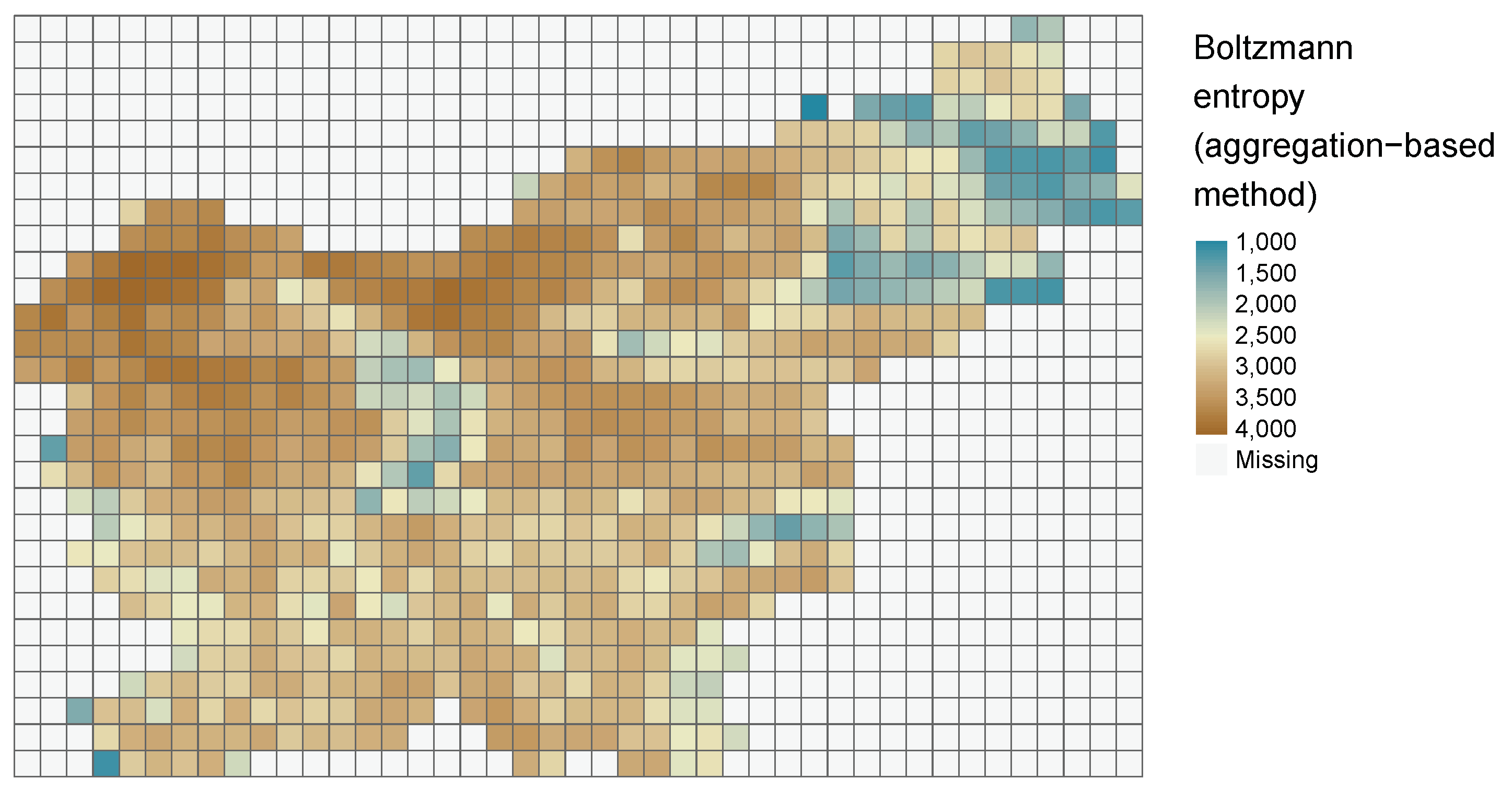
svn_dem.tif contains a digital elevation model of 90 m resolution for the whole country of Slovenia (
Figure 9).
|
svn_dem = raster(“data/svn_dem.tif”) |
The R language [
36] has extensive abilities for doing spatial data analyses, including data preparation, visualization, modeling, or communicating the results [
45]. Therefore, it is possible to integrate the
belg package into larger workflows. For example, users can create a polygonal grid using the
sf package [
46] and calculate Boltzmann entropy for a landscape in each grid cell.
The polygonal grid is created by extracting the bounding box of the elevation dataset, and specifying the new grid cell size in the st_make_grid() function.
|
svn_grid_geom = st_as_sfc(st_bbox(svn_dem)) |
|
svn_grid = st_make_grid(svn_grid_geom, cellsize = 5760) |
|
svn_grid = st_sf(id = seq_along(svn_grid), |
|
geom = svn_grid) |
Next, the following code can be used to calculate Boltzmann entropy for each polygonal grid cell. The loop subsets a landscape for each polygonal grid cell, checks if it has any values other than NA, calculates entropy value, and returns it in a new column results.
|
svn_grid$results = NA |
| for (i in seq_len(nrow(svn_grid))){ |
|
small_raster = crop(svn_dem, svn_grid[i, ]) |
|
if(!all(is.na(getValues(small_raster)))){ |
|
svn_grid$results[i] = get_boltzmann(small_raster) |
|
} |
|
} |
The output is a spatial object containing a column with calculated values of Boltzmann entropy.
| head(svn_grid) |
|
## Simple feature collection with 6 features and 2 fields |
|
## geometry type: POLYGON |
|
## dimension: XY |
|
## bbox: xmin: 371601.3 ymin: 31015.3 xmax: 406161.3 ymax: 36775.3 |
|
## CRS: +proj=tmerc +lat_0=0 +lon_0=15 +k=0.9999 +x_0=500000 +y_0=-5000000 ... |
|
## id geom results |
|
## 1 1 POLYGON ((371601.3 31015.3,... NA |
|
## 2 2 POLYGON ((377361.3 31015.3,... NA |
|
## 3 3 POLYGON ((383121.3 31015.3,... NA |
|
## 4 4 POLYGON ((388881.3 31015.3,... 1139.992 |
|
## 5 5 POLYGON ((394641.3 31015.3,... 2834.936 |
|
## 6 6 POLYGON ((400401.3 31015.3,... 3120.389 |
It can be visualized either using internal
sf function
plot() (
plot(svn_grid["results"])) or external packages such as
tmap [
47] (
Figure 10).
4. Discussion
In this paper, we introduced the
belg R package for computing Boltzmann entropy of landscape gradients. It implements two computational methods—hierarchy-based and aggregation-based—of Boltzmann entropy using an efficient C++ code. An R interface allows for connecting methods in this package with an abundance of existing R packages for spatial data preparation or visualization. The
belg package also expands the implemented methods by allowing calculations for rasters with missing values. We also presented three examples showing different aspects of the Boltzmann entropy calculations. Complete code and data to recreate all of the examples are available at
https://github.com/Nowosad/belg-examples.
The
belg package has a few limitations, however, they are mostly also the limitations of the implemented methods. It should be stressed that the absolute Boltzmann entropy calculated using the hierarchy-based method is not thermodynamically consistent [
33], meaning that the entropy calculated using this approach does not increase continuously toward a maximum. The relative Boltzmann entropy is thermodynamically consistent, however, it does not allow for comparison between two different landscape gradients [
32]. While the later proposed aggregation-based method is thermodynamically consistent, it only works on regular rasters with each dimension equal to
k to base 2 [
33].
The above limitations confirm that methods on how to derive Boltzmann entropy for spatial data are still an active area of research. Several concepts on how to compute the Boltzmann entropy on landscape patterns were proposed in recent years [
28,
29,
30,
31,
32,
33]. However, rarely the results of these methods were compiled and compared. Therefore, it is vital to have tools allowing to apply the previously mentioned methods on a diverse set of data. This not only could help to compare different methods underlining their strengths and limitations but above all, testing how well they represent lows of thermodynamics. Robust tools can also be used to evaluate relationships between proposed methods of computing Boltzmann entropy with existing measures based on Shannon entropy. It includes recently proposed conditional entropy, joint entropy, mutual information, and relative mutual information based on co-occurrence matrices [
23].
Future improvements of the software will be aimed at implementing newly proposed methods for calculating Boltzmann entropy of landscape gradients. Additionally, while existing R packages, such as
parallel and
future [
36,
48], can be used together with
belg to calculate Boltzmann entropy of many rasters in parallel, the package does not offer multi-core support for single raster images. Thus, it could be also worth adding parallel processing support for single large rasters. Finally, we look forward to the users’ comments and suggestions on potential changes and improvements in this package.