1. Introduction
The main advantages of the energy supplied through Solar Thermal Power Plants (STPPs) are its capacity, reliability and stability to the grid, which in turn allows the renewable electricity percentage to be also higher. However, when compared to the costs of solar photovoltaic electricity, the reduction in cost must still be very large for solar thermal electricity, to be competitive. One of the ways to achieve this is by increasing global conversion efficiency by coupling the solar field to a supercritical cycle. In this scheme, a reliable design of the heat exchanger between the solar field and the Brayton cycle is essential for the technical viability of these STPPs.
Within the SunShot program [
1], the U.S. Department of Energy (DOE) has identified three potential schemes for the next generation of STPPs, based on the Heat Transfer Fluid (HTF) in the receiver: molten salts, falling particles or gas phase. In all the schemes, the solar field is coupled to a supercritical carbon dioxide (sCO
2) cycle, achieving high thermo-electric conversion efficiency.
The scheme based on a molten salt central receiver coupled to a sCO
2 Brayton cycle is the most conventional one, as the molten salt systems are a state-of-art technology. Besides that, the Thermal Energy Storage (TES) associated, provides this scheme of a high capacity factor and a dispatchable electricity production [
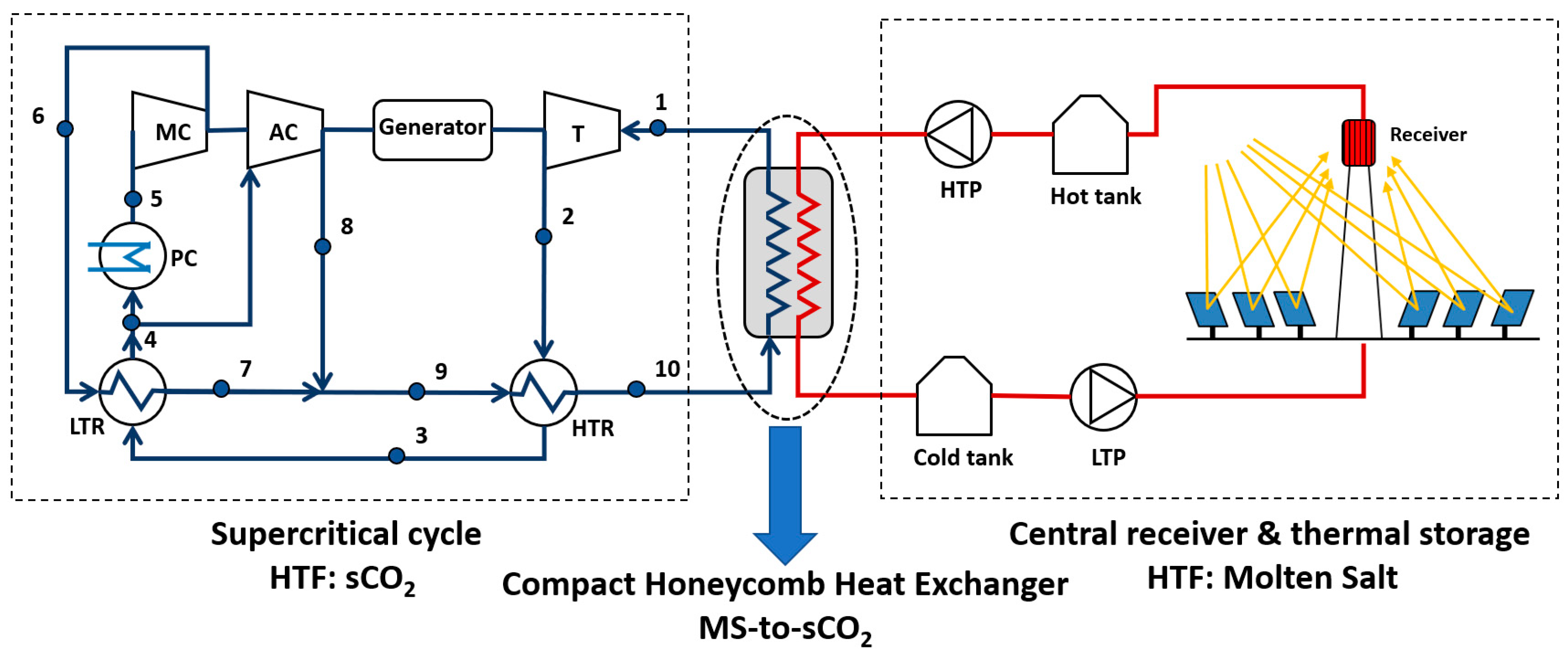
2]. This scheme is showed in
Figure 1.
Nevertheless, several challenges arise in this technology, like an efficient central receiver working at a temperature higher than 700 °C; a supercritical cycle that maximizes performance and minimizes cost, taking into account the peculiarities of the solar field to which it is coupled; and, between these two subsystems, a key element is the heat exchanger (HX) to transfer energy from the molten salt in the solar field to the CO2 in the Brayton cycle, the Source Heat Exchanger (SHX). This paper deals in depth with this last equipment, proposing a design that can overcome some of the technological difficulties of these type of HXs: the mechanical stress due to the high pressure of the supercritical phase; the need of improving the heat transfer of the supercritical fluid; and overall, the molten salt plugging in the microchannels of a Compact Heat Exchanger (CHX), as it will be explained below.
Supercritical CO
2 Brayton cycles have a very high efficiency, above 50%, even with dry-cooling [
3], so their integration in a STPP can yield to an overall performance increase. Wang et al. [
4] identified six possible supercritical cycles that can be integrated in a molten salt central receiver system with thermal storage: simple recovery cycle; recompression cycle; precompression cycle; intercooling cycle; partial-cooling cycle; and split expansion cycle. These cycles can be assessed according to different parameters, being the most important ones: the cycle efficiency; the complexity of the cycle compared to the most conventional one, the recompression cycle (represented in
Figure 1); and the CO
2 temperature increment in the source heat exchanger, as this value determines the molten salt volume in the solar field.
The intercooling cycle is the one with higher thermal efficiency when the thermal source temperature ranges from 600 °C to 800 °C, followed by the recompression cycle, that is also the simplest. Regarding the temperature difference in the source heat exchanger, the partial cooling layout is the one with the largest increment. In summary, three cycles can be identified to be the most suitable for coupling to a molten salt central receiver: recompression cycle, intercooling cycle and partial-cooling cycle [
4,
5]
The central receiver is usually a external-type with a surrounding heliostat field [
1], although the cavity-type is recommended in recent investigations when the working temperature is high [
2], because the radiation heat loss is lower compared to external receivers working at the same temperature. At last, the molten salt thermal storage consists of two tanks of molten salts, which have been sized to provide the nominal thermal power to the supercritical cycle for 6 h, with a charging time of 6 h.
This paper is focused in the heat exchanger between the solar field and the supercritical cycle, so a literature review on this heat exchanger is presented below.
There are several designs proposed in the literature for MS-to-CO2 heat exchangers, for both nuclear and solar applications, since both technologies use the scheme of a thermal source coupled to a supercritical CO2 cycle, as an alternative to increase performance.
The simplest design for this heat exchanger is a Shell and Tube Heat Exchanger (STHX), in which the CO
2 at supercritical pressure circulates inside the tubes, and the molten salt trough the shell. This HX is well suited in supercritical cycles in which the source thermal energy is supplied through the low pressure side of the layout (85 bar approximately), as the one presented in [
6]. Nevertheless, if a conventional supercritical cycle is used, the turbine inlet pressure should be limited to 200 bar, which constrains the cycle efficiency. There are several reasons that make the STHX not the most appropriate in conventional supercritical cycles: the great tube thickness due to the high pressure of the CO
2 yields to a limited heat transfer and performance [
7]; and, although the molten salt plugging does not occur in the shell, this fluid can be kept retained in the baffles and interstices of the HX, also yielding to a reduction in the heat transfer [
8,
9].
A more advanced design is the Printed Circuit Heat Exchanger (PCHE), which consists of plate sheets joined by diffusion-bonding, alternating hot-cold rows of semi-circular channels [
10,
11]. These microchannels withstand the high pressure of the CO
2 (180–300 bar, approximately), and they also improve the heat transfer of this fluid, as the convection coefficient and the hydraulic diameter are inversely related. Nevertheless, PCHEs have the drawback of the viscous molten salt plugging in the microchannels. This issue has been studied in several reports of both nuclear [
12] and solar [
13] power plants, but very few designs address this problem. The most recent designs of MS-to-CO
2 based on PCHE are focused on the heat transfer improvement by using airfoil fins in the microchannels [
14,
15,
16].
Only one design has been found in the bibliography that tries to solve the problem of the molten salt plugging in microchannels [
17]; the basic principle of this design is to face two plate sheets intended for molten salt, so that a circular channel is formed for this fluid, whereas the CO
2 still circulates through semi-circular channels. Although this design does not optimize the heat transfer, the plugging and corrosion problems of the MS are reduced; nevertheless, the channel dimension for the molten salt is still small.
To overcome the problems detailed in the two HX configurations described above, this work proposes and studies a new MS-to-CO
2 HX design. From the analysis of the state of the art, it is clear that it would be desirable to increase the ratio of heat transfer area compared to the volume of the HX, that is, the most suitable design is a Compact Heat Exchanger (CHX); the lower convection coefficient of the supercritical phase is compensated by the larger area to transfer the thermal energy. But, at the same time, the MS channel must be larger enough to avoid plugging. To meet both conditions, a small compact shell and tube design [
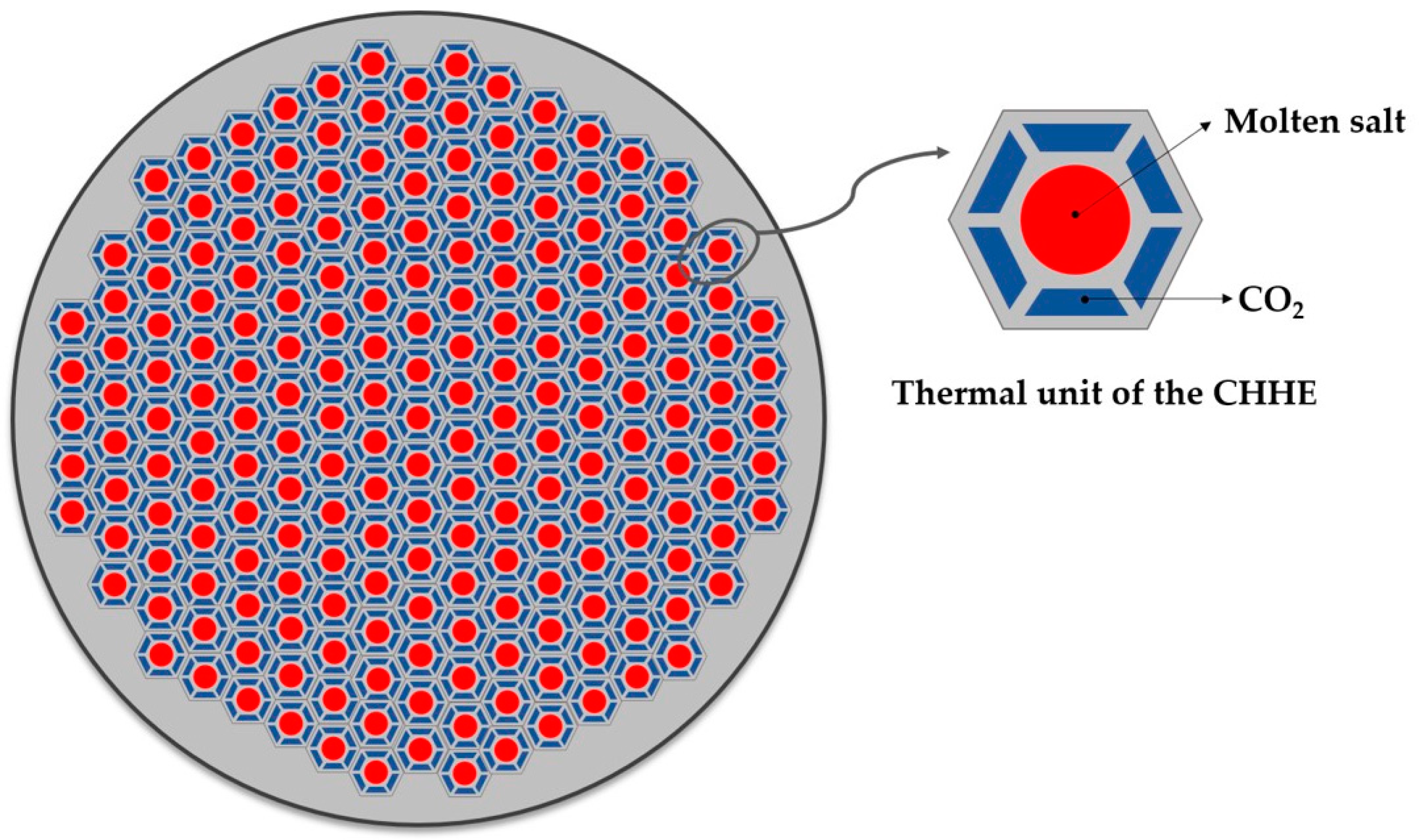
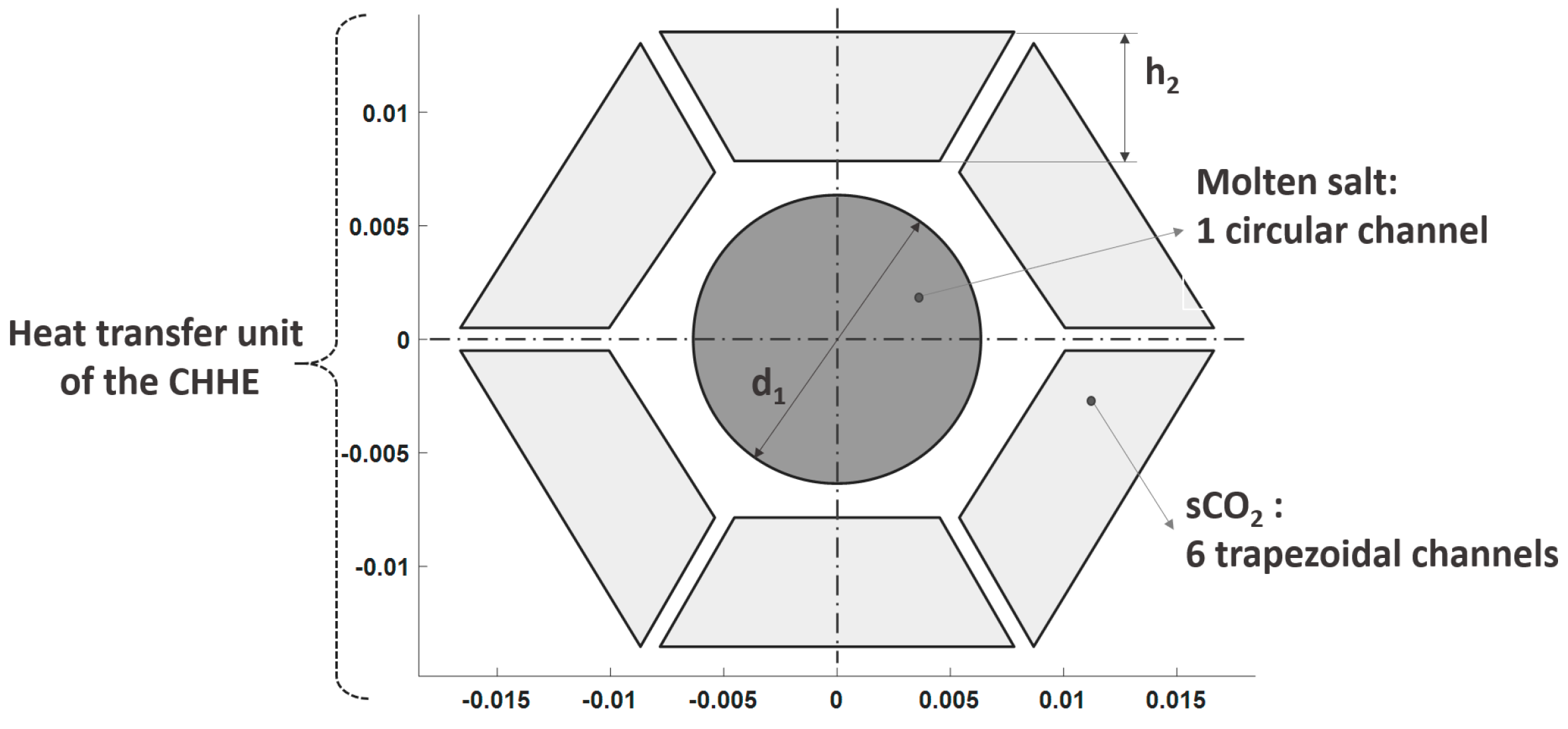
18] has been modified for the thermal duty and working pressure required by the supercritical cycle. The cross section of this design is a compact shell consisting of many thermal units like the one shown in
Figure 2. The MS goes through a circular duct that is surrounded by 6 trapezoidal ducts, through which the CO
2 circulates. Repetition of this unit gives the cross section of the shell a honeycomb-like appearance. Because of that, this HX will be referred as Compact Honeycomb Heat Exchanger (CHHE).
The thermo-mechanic model of this CHHE is explained in
Section 2; an optimization of this design is accomplished in
Section 3, by means of an exergy destruction minimization. As a result, the optimum working conditions of this design are set in
Section 4.
3. Optimization Procedure of the Heat Exchanger Based on the Exergy Destruction Minimization
The optimization of the CHHE proposed is based on the minimization of the exergy destruction, or entropy generation, in the heat exchanger. Assigning monetary values to these irreversibilities, this method allows to assess the cost of exergy destruction on each stream of the heat exchanger against its capital cost. Thus, the new objective function to be minimized is the Annual Total Cost (ATC), which takes into account the investment cost and the operation cost, including the irreversibilities in this last one.
In Equation (6),
CRF is the capital-recovery factor and
CELF is the constant-escalation levelization factor, both defined below;
CE is the cost per unit of exergy (
$/Wh), which has been taken as 0.00005
$/Wh, according to several references [
27,
28];
Y is the yearly operation time, calculated for a solar multiple equal to 2:
Y = 365*12 h;
CC is the investment cost of the CHHE; finally,
is the total exergy destruction due to the most important irreversibilities in the heat exchanger.
The capital-recovery factor (CRF) and the constant-escalation levelization factor (CELF) are calculated by means of Equations (7) and (8).
In the above equations,
ieff (%) is the weighted average capital cost, and
n (years) is the economic life o span period of the power plant; r
n is the nominal escalation rate, which represents the annual change in cost and includes the effects of both the real escalation rate
rr and the inflation
ri. The values of the parameters defined above are summarized in
Table 4.
The next two subsections are devoted to the calculation of the Exergy Destruction () and the Capital Cost (CC) of the Compact Honeycomb Heat Exchanger.
3.1. Accounting for the Exergy Destruction in the CHHE
Many researchers [
29,
30] have used the minimization of entropy generation, or exergy destruction, method to optimize the design of heat exchangers.
The causes of exergy destruction in a heat exchanger are: the finite temperature difference between hot and cold fluids, pressure drops on both fluids, and exergy losses associated to the non-adiabatic condition of a real heat exchanger, with a heat leakage with the environment; taking the limit of the system in the outer wall of the heat exchanger, these exergy losses constitute external irreversibilities to the heat exchanger.
In general, the total (internal and external) exergy destruction measured, normalized by the thermal power of the heat exchanger, is given by Equation (9).
These irreversibilities are calculated taking into account Gouy-Stodola Theorem [
31], obtaining the equations summarized in
Table 5, valid for ideal gas or incompressible liquid. For this exergy analysis, CO
2 and MS can be assimilated to ideal gas and incompressible liquid, respectively. Dead state temperature (
T0) has been taken as 298 K.
For the heat exchanger under study, the two main sources of exergy destruction are the finite temperature difference and the friction pressure drop on both sides, so these are the two irreversibilities that are going to be considered in the optimization procedure.
3.2. Capital Cost Estimation of the CHHE
The capital cost of the CHHE is estimated by means of a base cost,
CB, affected by three correction factors: pressure factor,
FP, material factor,
FM, and tube length correction factor,
FL [
32].
The base cost,
CB (
$), is calculated by Equation (12):
In Equation (12), is the heat transfer area of the CHHE.
The pressure factor, F
P, the material of construction factor,
FM, and the tube length correction factor,
FL, are given by Equations (13) and (14) and
Table 6, respectively:
In Equation (13), P (psia) is the working pressure; in Equation (14), is the heat transfer area of the CHHE, the constant a is equal to 9.6, and the constant b is equal to 0.06.
4. Results from the Optimization of the Compact Honeycomb Heat Exchanger
As said in
Section 2, the optimization procedure to minimize the objective function Annual Total Cost (Mio.
$) is done on the following parametrized thermal inputs: the temperature approach (TA
MS-CO2) between both streams, and the pressure drop of the supercritical phase (dP
CO2). TA
MS-CO2 ranges from 30 °C to 60 °C, whereas dP
CO2 ranges from 1.5 bar to 3.25 bar. These two parameters (pressure drop and temperature approach) have been considered in several optimization studies of heat exchangers, as they affect both the investment and the operation costs [
33,
34].
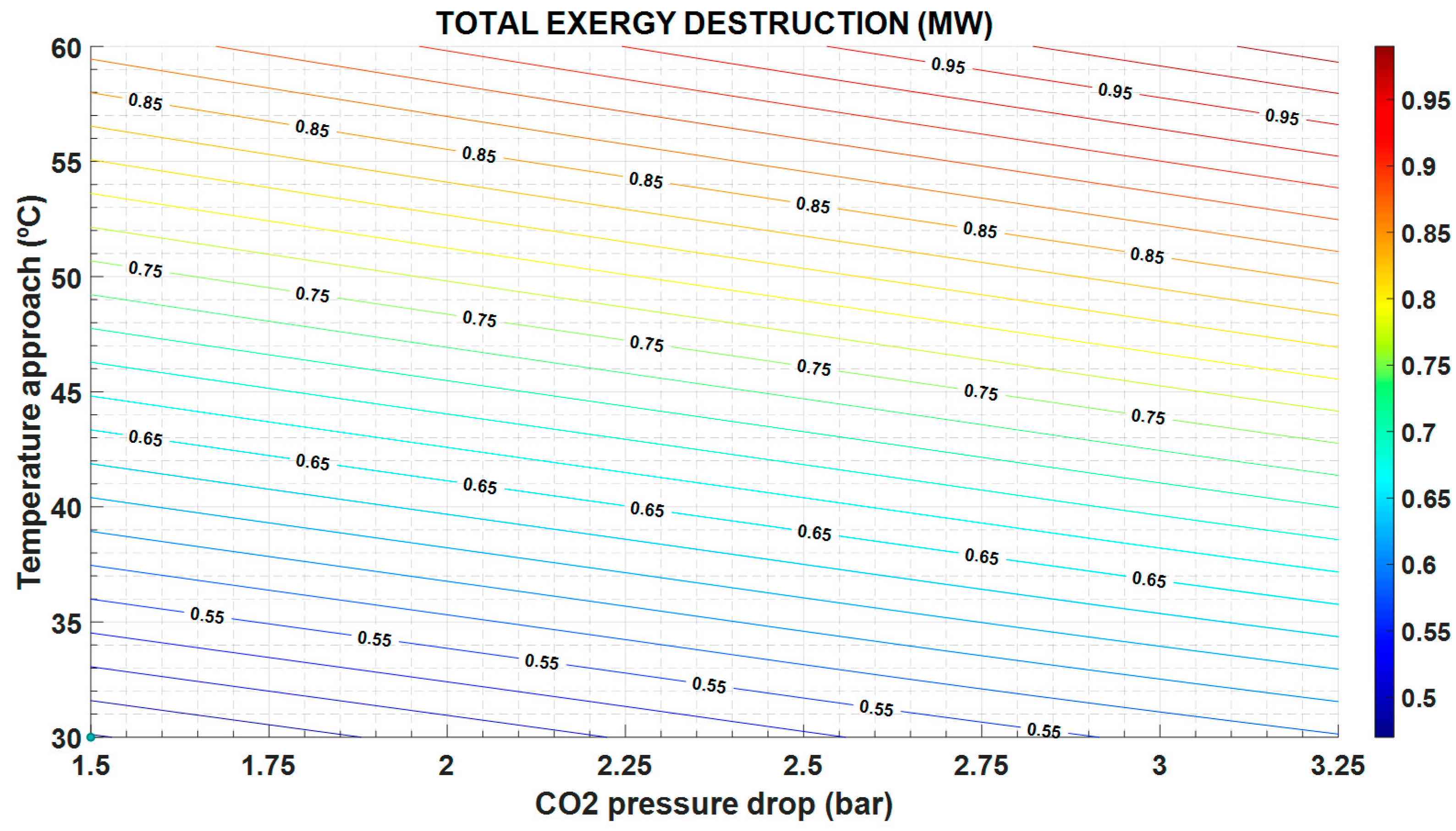
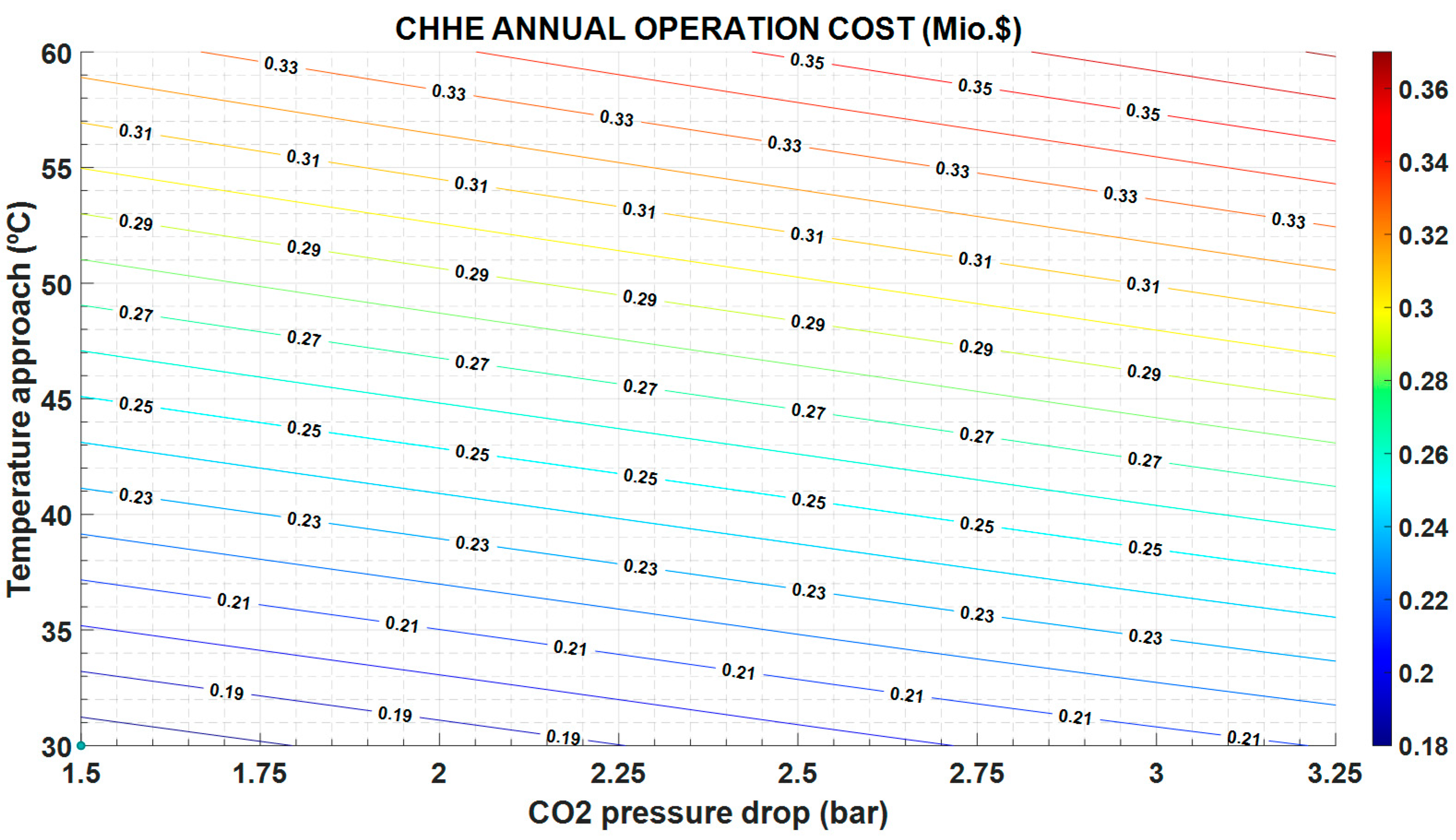
The greater the temperature approach, the higher the exergy destruction (
Figure 7) and the operation cost (
Figure 8), but the lower the capital cost because the heat exchange area is also lower (
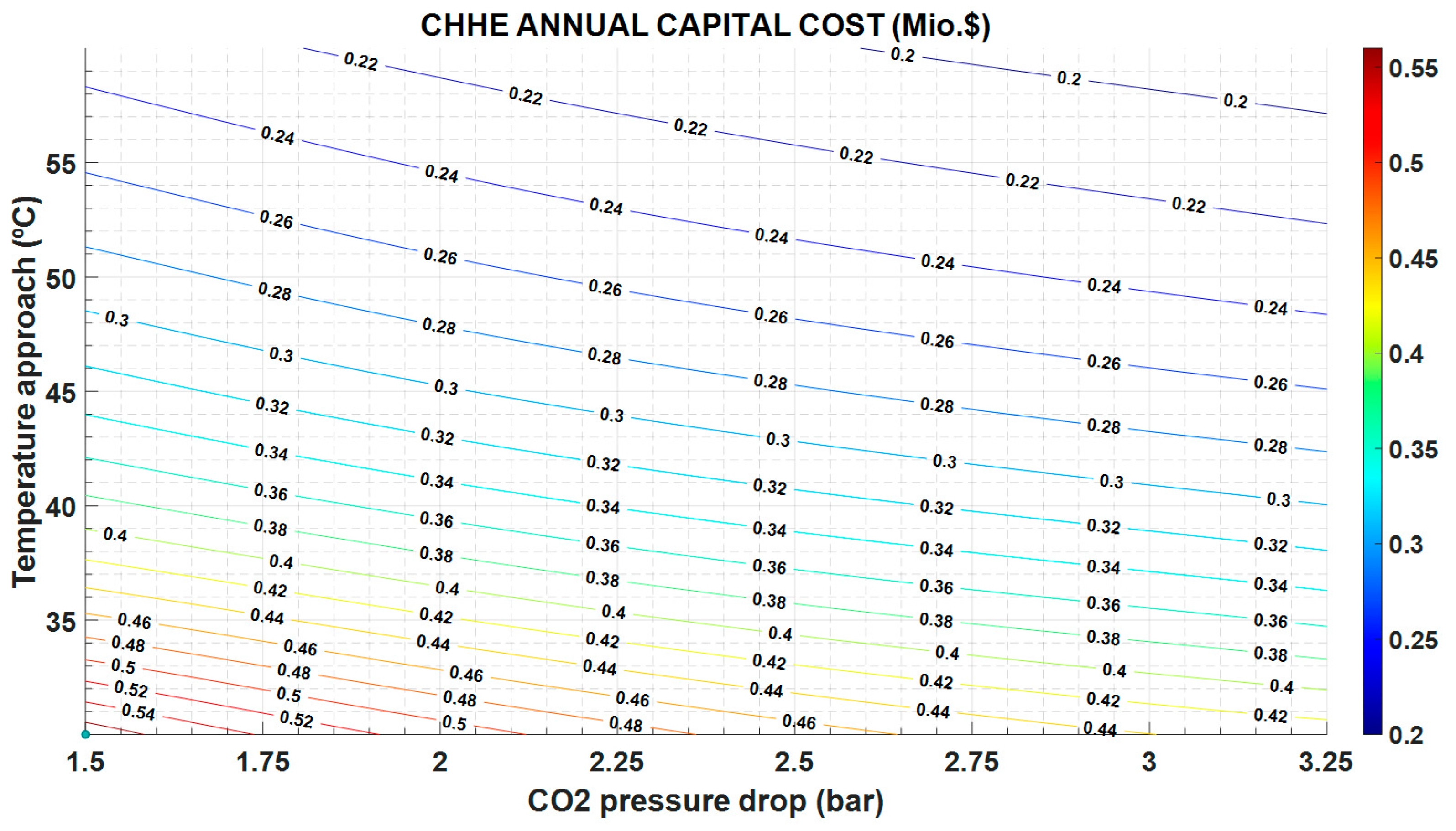
Figure 9).
In the same way, the exergy destruction increases as the pressure drop increases, following expression in
Table 5 and
Figure 7. Instead, the greater the pressure drop, the lower the heat exchange area and the investment cost (
Figure 9).
It is important to note that the exergy destruction increases with a greater pressure drop, since the entropy generation by friction also increases; and with the temperature difference between the two streams in the HX, as shown in the
Figure 7.
The exergy destruction influences both the operation and maintenance cost and the investment cost. As can be seen in
Figure 8, the operation and maintenance cost is proportional to the exergy destruction and follows the same variation: it increases with increasing exergy destruction. However, the investment cost in CHHE decreases as exergy destruction increases, as shown in
Figure 9; in this case, a cheaper CHEE (due to smaller dimensions) also exhibits a more limited performance.
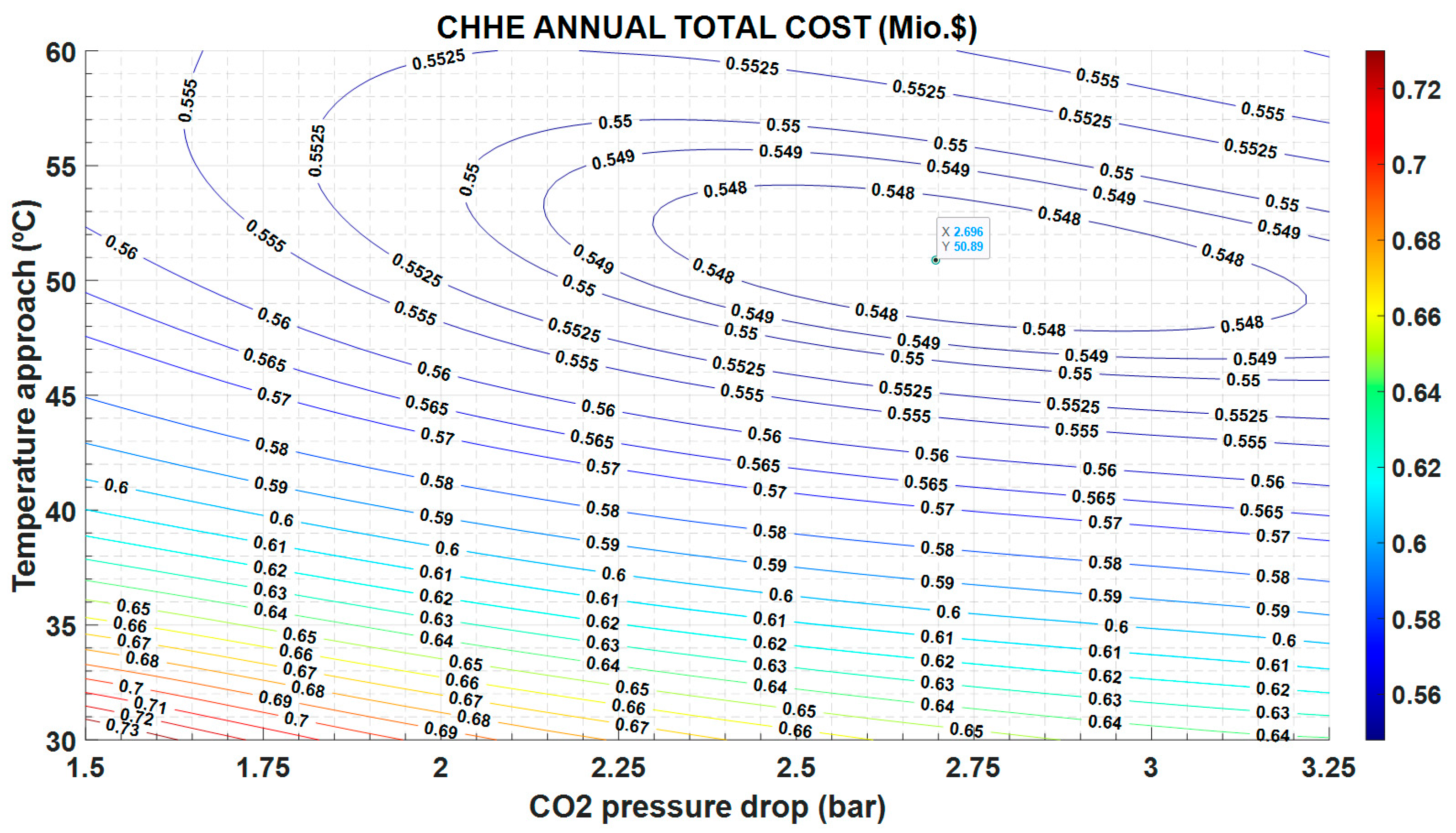
This different trend in O&M costs versus investment costs, yields to the minimum in the annual total cost observed in
Figure 10.
Figure 10 plots the results of the optimization, showing that there is a minimum value for the ATC equal to 0.547 Mio.
$, for 2.7 bar and 51 °C, approximately. These working conditions are very different of those reported in other type of HXs [
24], in which pressure drop is 0.5 bar, whereas the temperature difference is 10 °C, approximately. It must be taken into account that this source heat exchanger only works 12 h a day, as it is located in a STPP, so cost derived of the irreversibilities in the operation are less penalized than if the power plant works continuously.
5. Conclusions
This work presents a new design for the source heat exchanger between the molten salt in the solar field and the supercritical CO2 in a Brayton cycle. This heat exchanger is compact, so the heat transfer of the supercritical phase in enhanced; and, at the same time, the molten salt duct is large enough to avoid plugging problems. This last characteristic is the main advantage of this design compared to other designs presented in the bibliography, since it allows the technological viability of this type of STPP based on a MS solar field and a sCO2 cycle.
The structure best suited to the above requirements is the honeycomb: the thermal unit of this compact heat exchanger consists of a circular channel for the molten salt, surrounded by 6 trapezoidal channels for the CO2. The thermal model of this new Compact Honeycomb Heat Exchanger (CHHE) is implemented and explained.
It is important note that the objective of this design is not to attain the highest heat transfer performance, but the technical feasibility of the heat transfer between a supercritical fluid, at high pressure, and a viscous liquid, that can cause plugging in the small channels of a CHX.
An economic optimization of the CHHE is also accomplished. Previous to this optimization procedure the main sources of exergy destruction have been identified: the temperature approach between both streams and the pressure drop on both fluids. If an exergy cost is defined and assigned to these irreversibilities, they can be included as an operation cost, that can be compared to the initial investment cost. In this way, the objective function Annual Total Cost is minimized as a function of the two thermal inputs: TAMS-CO2 and dPCO2. Results show that there is a minimum for 2.7 bar and 51 °C, approximately. These values are higher than others reported in bibliography, probably because the operational cost are lower, as the operation period of this STTP is lower than that of a conventional power plant.
Other future works include a numerical CFD model to validate the analytical model described in this paper, and to show possible thermo-mechanical problems. A later objective would be to build a laboratory scale model to obtain empirical results.