Skyrmions and Spin Waves in Magneto–Ferroelectric Superlattices
Abstract
1. Introduction
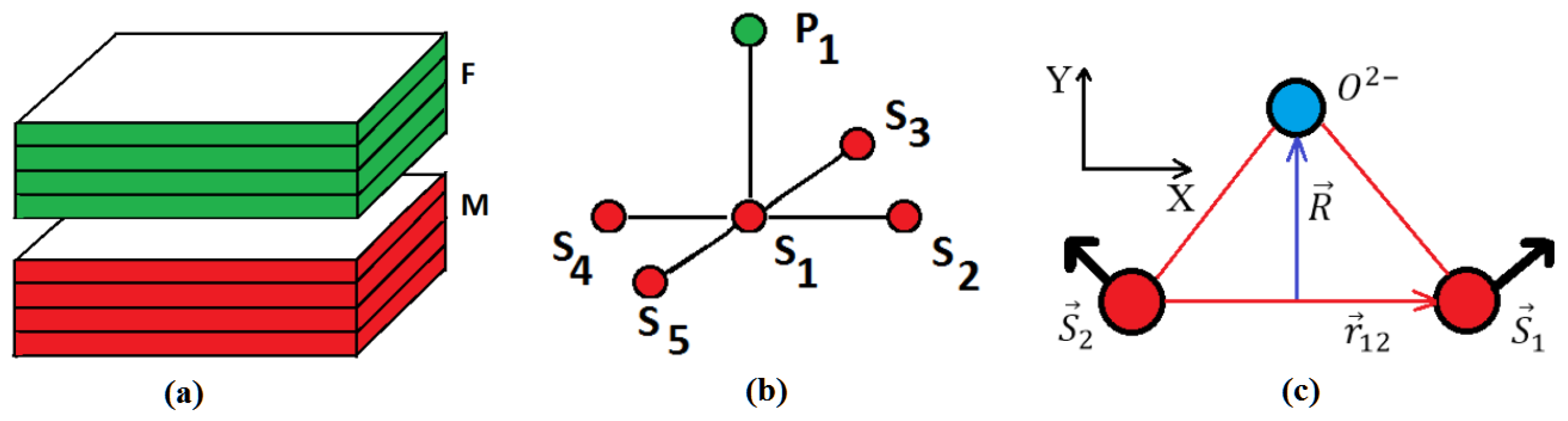
2. Model—Ground State
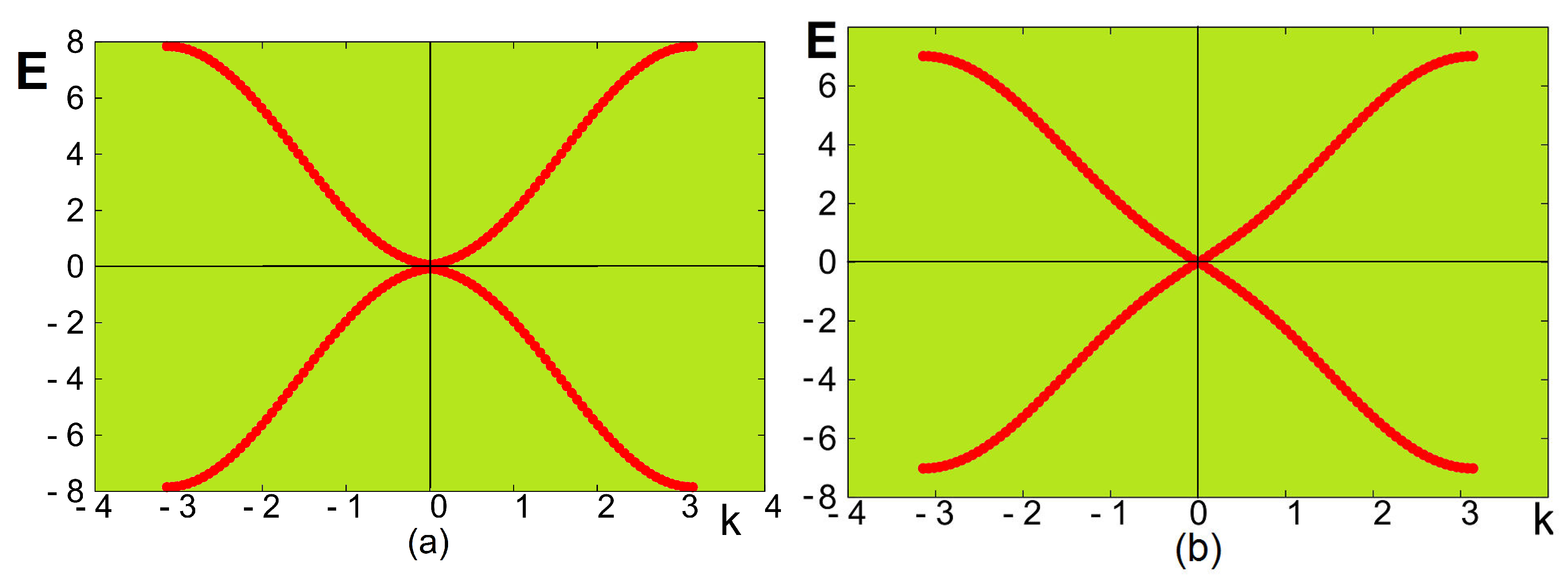
3. Spin Waves
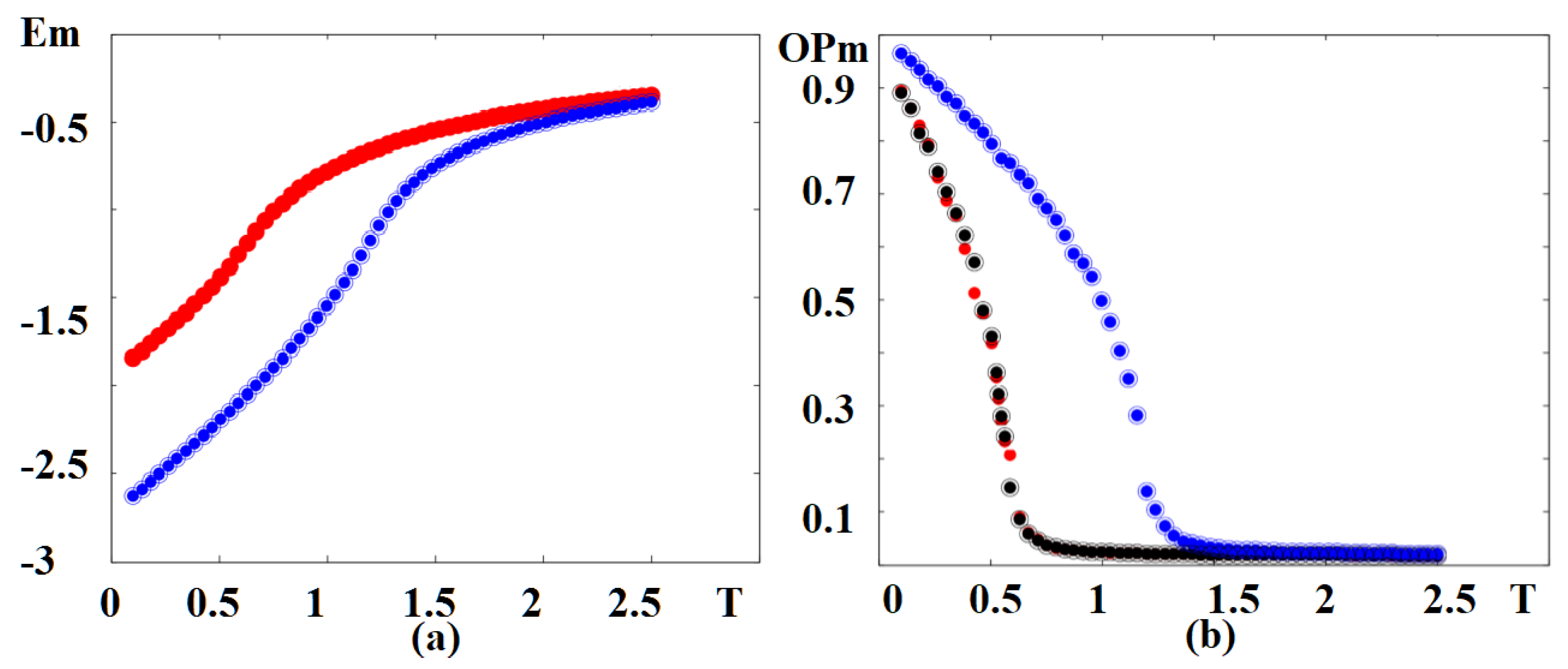
4. Phase Transition
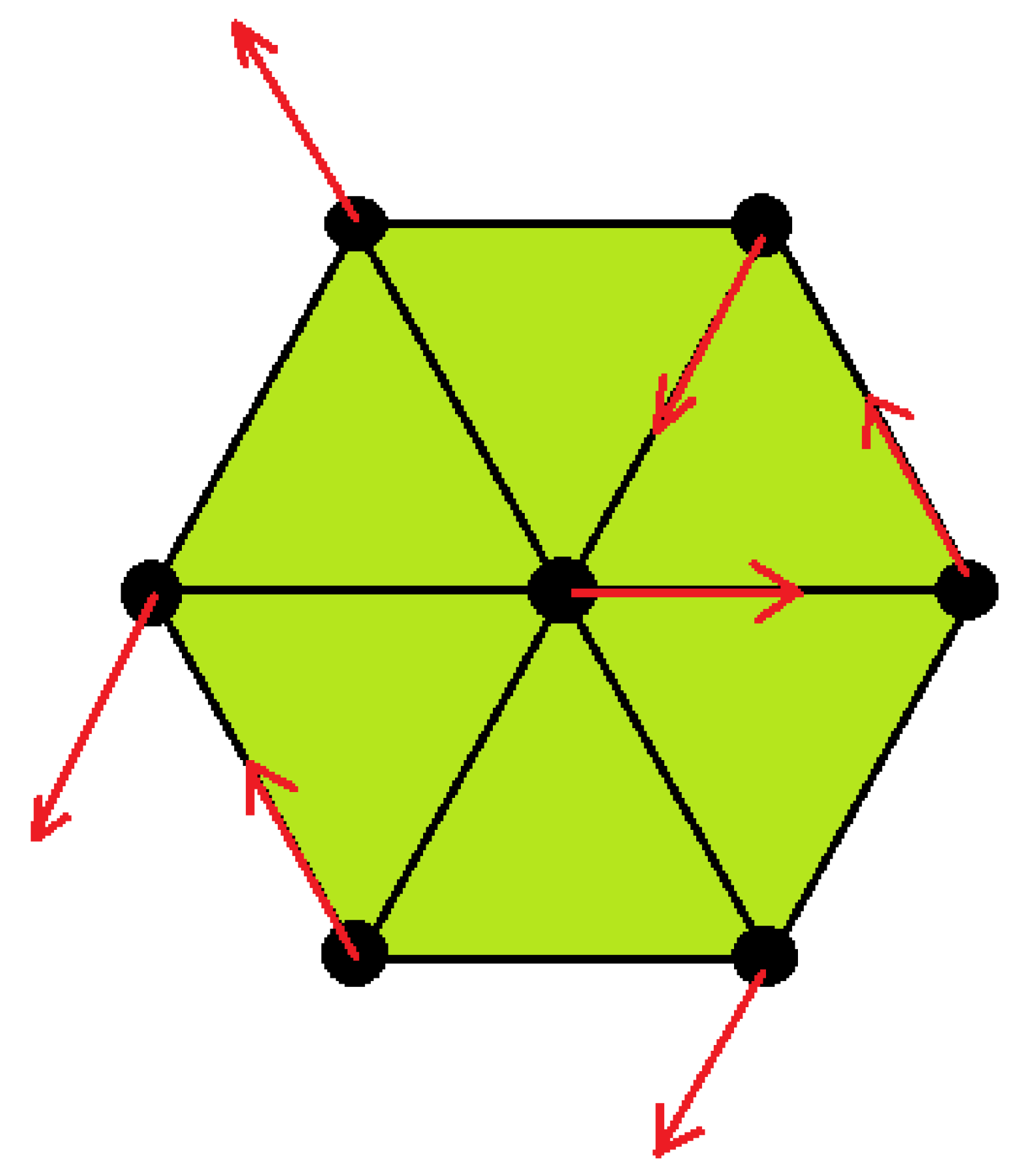
5. The Case of Triangular Lattice
5.1. Ground State in Zero Field
5.2. Ground State in an Applied Magnetic Field
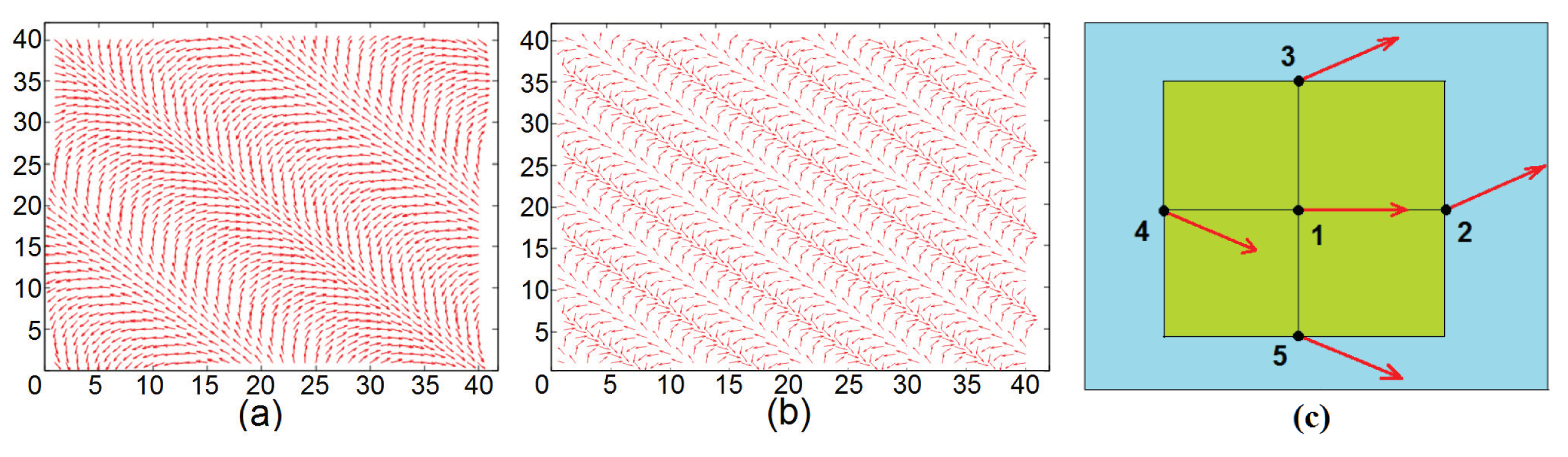
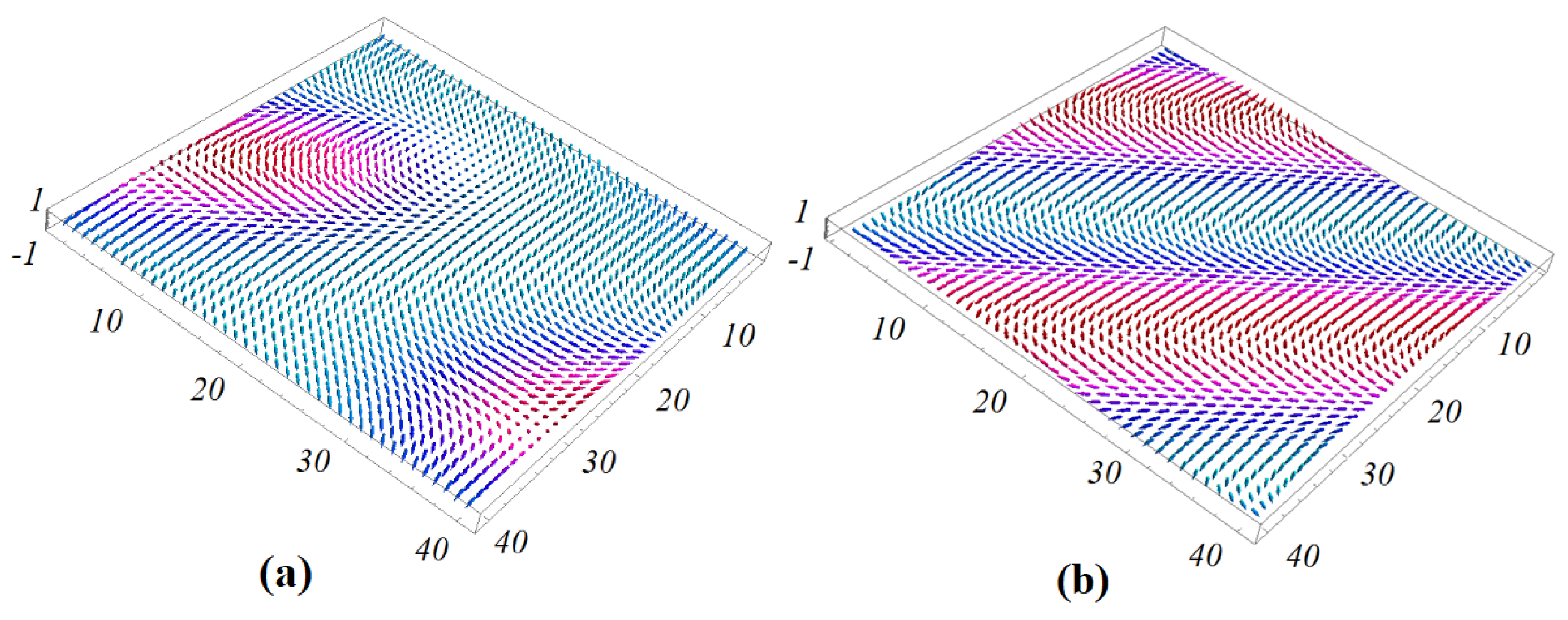
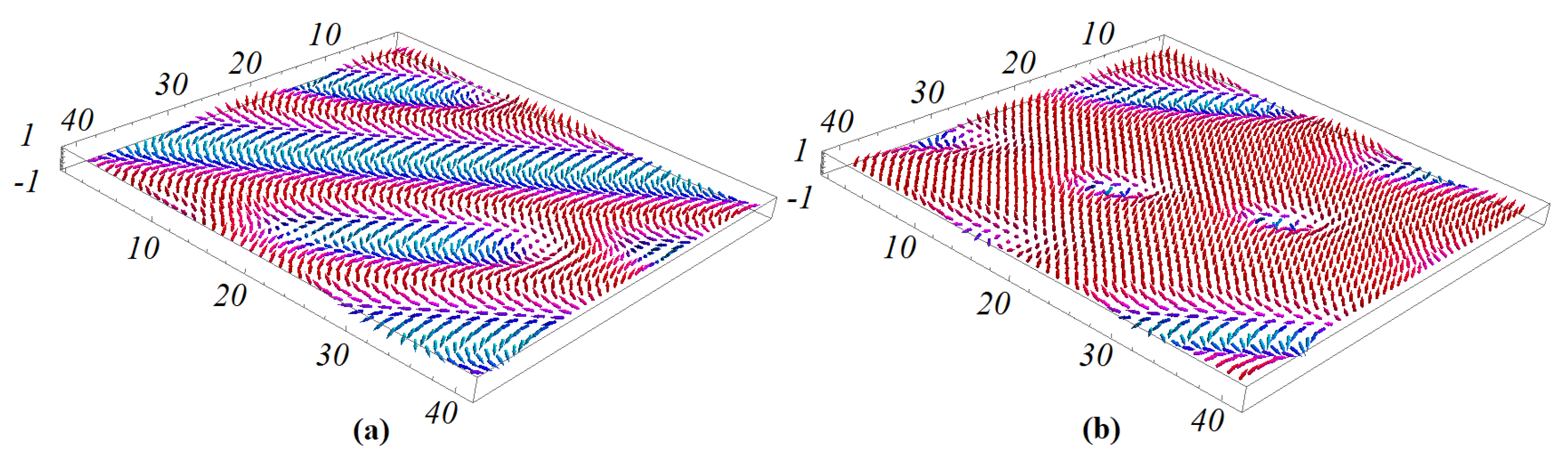
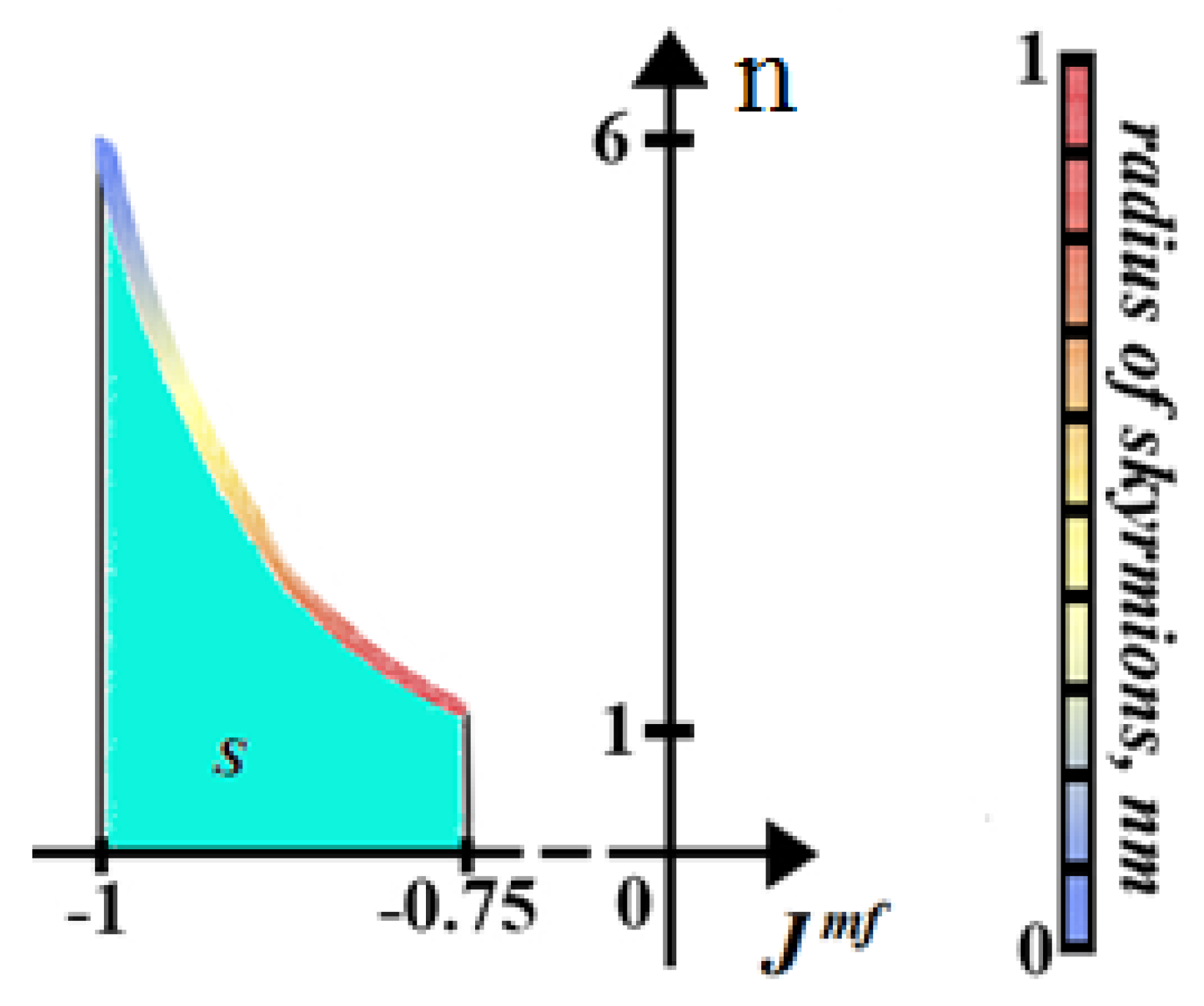
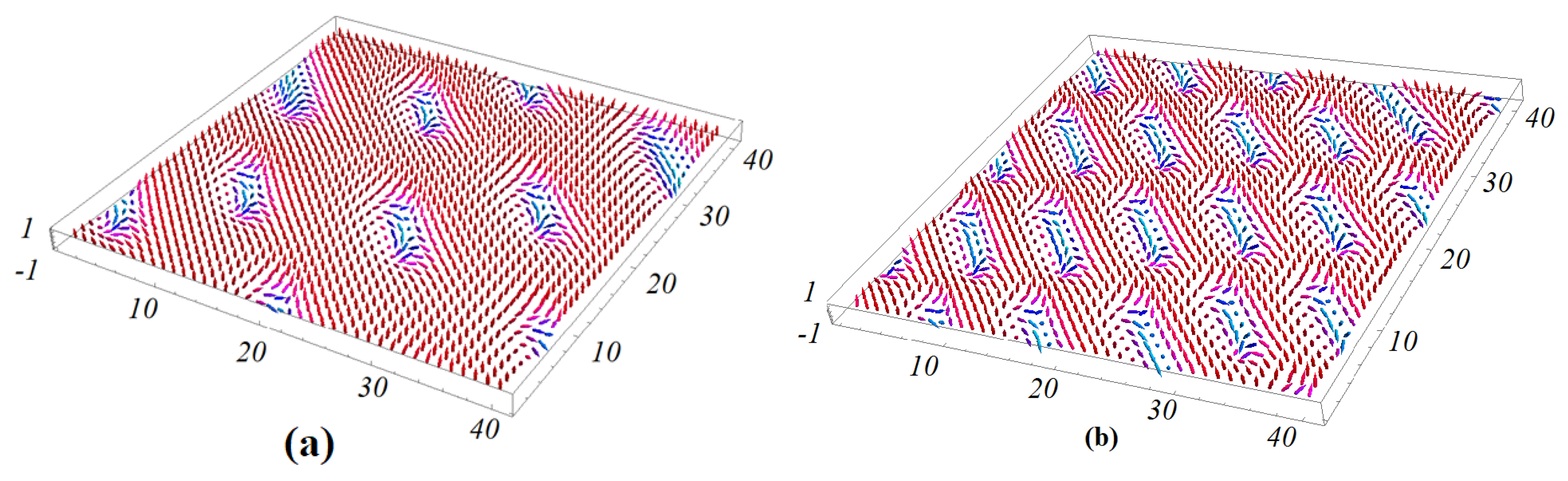
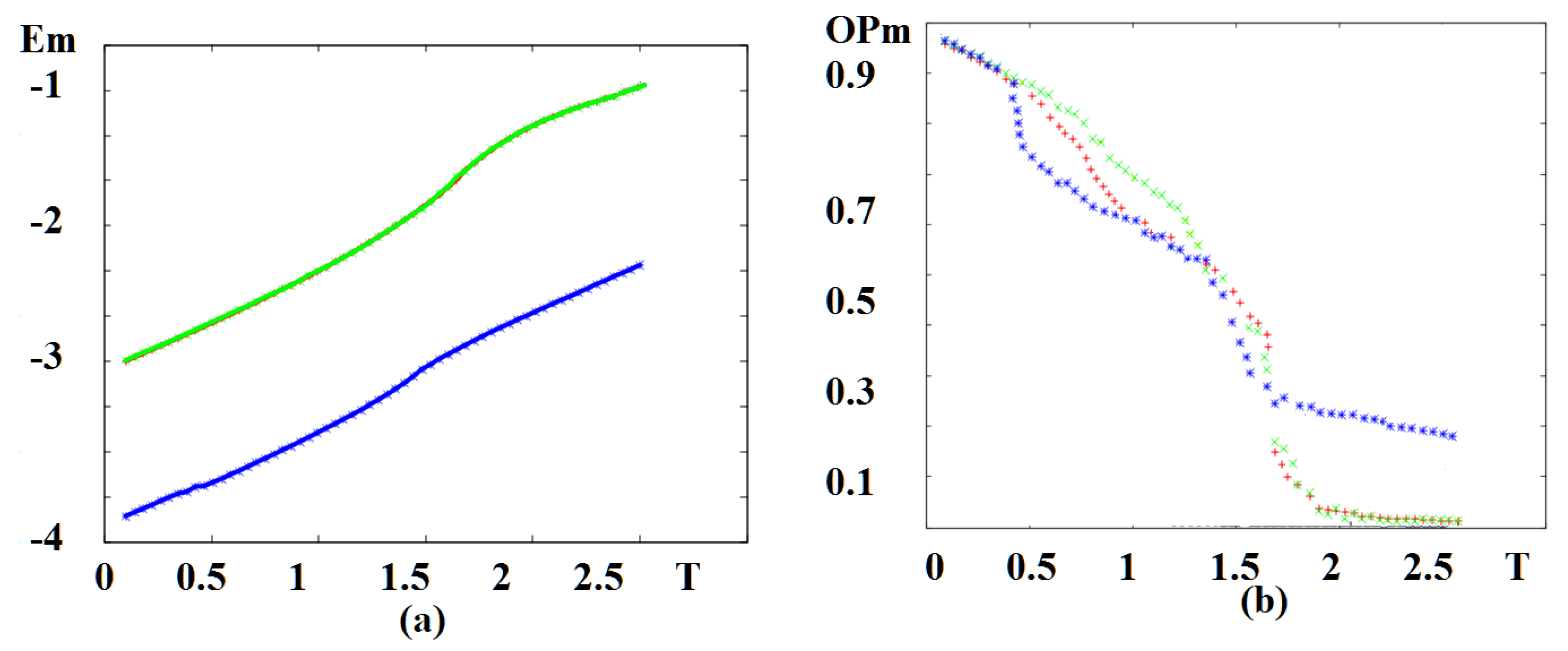
6. Monte Carlo Results for the Case of Triangular Lattice
7. Discussion on the Applicability of the Model
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kugler, M.; Shtrikman, S. Skyrmion crystals and their symmetries. Phys. Rev. D 1989, 40, 3421. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, M. Spin-Wave Modes and Their Intense Excitation Effects in Skyrmion Crystals. Phys. Rev. Lett. 2012, 108, 017601. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable vortices in magnetically ordered crystals. The mixed state of magnets. Z. Eksp. Teor. Fiz. 1989, 95, 178. [Google Scholar]
- Yu, X.; Onose, Y.; Kanazawa, N.; Park, J.; Han, J.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Yu, X.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; Von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; Von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636–639. [Google Scholar] [CrossRef]
- Rosch, A. Skyrmions: Moving with the current. Nat. Nanotechnol. 2013, 8, 160. [Google Scholar] [CrossRef]
- Liu, Z.; Ian, H. Ferromagnetic sublattices of antiferromagnetic skyrmion crystals formed in two-dimensional square lattices. Superlattices Microstruct. 2019, 126, 25–31. [Google Scholar] [CrossRef]
- Leonov, A.; Togawa, Y.; Monchesky, T.; Bogdanov, A.; Kishine, J.; Kousaka, Y.; Miyagawa, M.; Koyama, T.; Akimitsu, J.; Koyama, T.; et al. Chiral surface twists and skyrmion stability in nanolayers of cubic helimagnets. Phys. Rev. Lett. 2016, 117, 087202. [Google Scholar] [CrossRef]
- Moreau-Luchaire, C.; Moutafis, C.; Reyren, N.; Sampaio, J.; Vaz, C.A.F.; Van Horne, N.; Bouzehouane, K.; Garcia, K.; Deranlot, C.; Warnicke, P.; et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 2016, 11, 444–448. [Google Scholar] [CrossRef] [PubMed]
- Soumyanarayanan, A.; Raju, M.; Oyarce, A.G.; Tan, A.K.; Im, M.Y.; Petrović, A.P.; Ho, P.; Khoo, K.H.; Tran, M.; Gan, C.K.; et al. Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers. Nat. Mater. 2017, 16, 898–904. [Google Scholar] [CrossRef] [PubMed]
- Dupé, B.; Bihlmayer, G.; Böttcher, M.; Blügel, S.; Heinze, S. Engineering skyrmions in transition-metal multilayers for spintronics. Nat. Commun. 2016, 7, 11779. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Rosch, A.; Garst, M. Edge instabilities and skyrmion creation in magnetic layers. New J. Phys. 2016, 18, 065006. [Google Scholar] [CrossRef]
- Rosch, A. Spintronics: Electric control of skyrmions. Nat. Nanotechnol. 2017, 12, 103–104. [Google Scholar]
- Shen, L.; Xia, J.; Zhao, G.; Zhang, X.; Ezawa, M.; Tretiakov, O.A.; Liu, X.; Zhou, Y. Spin torque nano-oscillators based on antiferromagnetic skyrmions. Appl. Phys. Lett. 2019, 114, 042402. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Bessarab, P.; Yudin, D.; Gulevich, D.; Wadley, P.; Titov, M.; Tretiakov, O.A. Stability and lifetime of antiferromagnetic skyrmions. Phys. Rev. B 2019, 99, 140411. [Google Scholar] [CrossRef]
- Koshibae, W.; Kaneko, Y.; Iwasaki, J.; Kawasaki, M.; Tokura, Y.; Nagaosa, N. Memory functions of magnetic skyrmions. Jpn. J. Appl. Phys. 2015, 54, 053001. [Google Scholar] [CrossRef]
- Kang, W.; Huang, Y.; Zheng, C.; Lv, W.; Lei, N.; Zhang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Voltage controlled magnetic skyrmion motion for racetrack memory. Sci. Rep. 2016, 6, 23164. [Google Scholar] [CrossRef]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, J.; Zhou, Y.; Liu, X.; Zhang, H.; Ezawa, M. Skyrmion dynamics in a frustrated ferromagnetic film and current-induced helicity locking-unlocking transition. Nat. Commun. 2017, 8, 1717. [Google Scholar] [CrossRef] [PubMed]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Che, R.; Kong, L.; Zhao, X.; Jin, C.; Wang, C.; Yang, J.; Ning, W.; Li, W.; Jin, C.; et al. Edge-mediated skyrmion chain and its collective dynamics in a confined geometry. Nat. Commun. 2015, 6, 8504. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Upadhyaya, P.; Zhang, W.; Yu, G.; Jungfleisch, M.B.; Fradin, F.Y.; Pearson, J.E.; Tserkovnyak, Y.; Wang, K.L.; Heinonen, O.; et al. Blowing magnetic skyrmion bubbles. Science 2015, 349, 283–286. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A.; Monchesky, T.; Romming, N.; Kubetzka, A.; Bogdanov, A.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Woo, S.; Litzius, K.; Krüger, B.; Im, M.-Y.; Caretta, L.; Richter, K.; Mann, M.; Krone, A.; Reeve, R.M.; Weigand, M.; et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016, 15, 501–506. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Wang, X.; Jungfleisch, M.B.; Pearson, J.E.; Cheng, X.; Heinonen, O.; Wang, K.L.; et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162–169. [Google Scholar] [CrossRef]
- Litzius, K.; Lemesh, I.; Krüger, B.; Bassirian, P.; Caretta, L.; Richter, K.; Büttner, F.; Sato, K.; Tretiakov, O.A.; Förster, J.; et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 2017, 13, 170–175. [Google Scholar] [CrossRef]
- Woo, S.; Song, K.M.; Han, H.S.; Jung, M.S.; Im, M.Y.; Lee, K.S.; Song, K.S.; Fischer, P.; Hong, J.-I.; Choi, J.W.; et al. Spin-orbit torque-driven skyrmion dynamics revealed by time-resolved X-ray microscopy. Nat. Commun. 2017, 8, 15573. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Nahas, Y.; Prokhorenko, S.; Louis, L.; Gui, Z.; Kornev, I.; Bellaiche, L. Discovery of stable skyrmionic state in ferroelectric nanocomposites. Nat. Commun. 2015, 6, 8542. [Google Scholar] [CrossRef] [PubMed]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Rønnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor gav 4 s 8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed]
- Hog, S.E.; Bailly-Reyre, A.; Diep, H.T. Stability and phase transition of skyrmion crystals generated by Dzyaloshinskii-Moriya interaction. J. Magn. Magn. Mater. 2018, 455, 32–38. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, C.; Qin, Y.; Shen, S.; Li, Y.D.; Bewley, R.; Schneidewind, A.; Chen, G.; Zhao, J. Intertwined dipolar and multipolar order in the triangular-lattice magnet TmMgGaO4. Nat. Commun. 2019, 10, 1–7. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef]
- Oitmaa, J. Magnetic phases in the J1 − J2 Heisenberg antiferromagnet on the triangular lattice. Phys. Rev. B 2020, 101, 214422. [Google Scholar] [CrossRef]
- Chen, L.; Qu, D.W.; Li, H.; Chen, B.B.; Gong, S.S.; Von Delft, J.; Weichselbaum, A.; Li, W. Two-temperature scales in the triangular-lattice Heisenberg antiferromagnet. Phys. Rev. B 2019, 99, 140404. [Google Scholar] [CrossRef]
- Sharafullin, I.F.; Kharrasov, M.K.; Diep, H.T. Dzyaloshinskii-Moriya interaction in magnetoferroelectric superlattices: Spin waves and skyrmions. Phys. Rev. B 2019, 99, 214420. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, J.; Lofland, S.; Ma, Z.; Mohaddes-Ardabili, L.; Zhao, T.; Salamanca-Riba, L.G.; Shinde, S.V.; Ogale, S.B.; Bai, F.; et al. Multiferroic BaTiO3-CoFe2O4 nanostructures. Science 2004, 303, 661–663. [Google Scholar] [CrossRef]
- Bibes, M.; Barthélémy, A. Multiferroics: Towards a magnetoelectric memory. Nat. Mater. 2008, 7, 425–426. [Google Scholar] [CrossRef] [PubMed]
- Sergienko, I.A.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef]
- Sharafullin, I.F.; Diep, H.T. Skyrmion Crystals and Phase Transitions in Magneto-Ferroelectric Superlattices: Dzyaloshinskii-Moriya Interaction in a Frustrated J1 − J2 Model. Symmetry 2020, 12, 26. [Google Scholar] [CrossRef]
- Pinettes, C.; Diep, H.T. Phase transition and phase diagram of the J1 − J2 Heisenberg model on a simple cubic lattice. J. Appl. Phys. 1998, 83, 6317. [Google Scholar] [CrossRef]
- Hoang, D.-T.; Magnin, Y.; Diep, H.T. Spin resistivity in the frustrated J1 − J2 model. Mod. Phys. Lett. 2011, 25, 937–945. [Google Scholar] [CrossRef]
- Yang, H.; Chen, G.; Cotta, A.A.C.; N’ Diaye, A.T.; Nikolaev, S.A.; Soares, E.A.; Macedo, W.A.A.; Liu, K.; Schmid, A.K.; Fert, A.; et al. Significant Dzyaloshinskii-Moriya interaction at graphene-ferromagnet interfaces due to the Rashba effect. Nat. Mater. 2018, 17, 605–609. [Google Scholar] [CrossRef]
- Manchon, A.; Koo, H.C.; Nitta, J.; Frolov, S.; Duine, R. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 2015, 14, 871–882. [Google Scholar] [CrossRef]
- Diep, H.T. Quantum theory of helimagnetic thin films. Phys. Rev. B 2015, 91, 014436. [Google Scholar] [CrossRef]
- Hog, S.E.; Diep, H.T.; Puszkarski, H. Theory of magnons in spin systems with Dzyaloshinskii-Moriya interaction. J. Phys. Condens. Matter 2017, 29, 305001. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: London, UK, 2009. [Google Scholar]
- Mézard, M.; Parisi, M.; Virasoro, M. Spin Glass Theory and Beyond an Introduction to the Replica Method and Its Applications; World Scientific: Singapore, 1986. [Google Scholar]
- Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Skyrmion- Electronics: An Overview and Outlook. Proc. IEEE 2016, 104, 2040–2061. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Motohiko, E.M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Ezawa, M. A reversible conversion between a skyrmion and a domain-wall pair in junction geometry. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, Y.; Ezawa, M.; Zhao, G.P.; Zhao, W. Magnetic skyrmion transistor: Skyrmion motion in a voltage-gated nanotrack. Sci. Rep. 2015, 5, 11369. [Google Scholar] [CrossRef]
- Kim, J.S.; Jung, S.; Jung, M.H.; You, C.Y.; Swagten, H.J.M.; Koopmans, B. Voltage controlled propagating spin waves on a perpendicularly magnetized nanowire. arXiv 2014, arXiv:1401.6910. [Google Scholar]
- Shiota, Y.; Murakami, S.; Bonell, F.; Nozaki, T.; Shinjo, T.; Suzuki, Y. Quantitative evaluation of voltage-induced magnetic anisotropy change by magnetoresistance measurement. Appl. Phys. Express 2011, 4, 43005. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, W.; Zhang, X.; Zhou, Y.; Weisheng, Z.W. Magnetic skyrmion-based synaptic devices. Nanotechnology 2017, 28, 08LT02. [Google Scholar] [CrossRef]
- Li, S.; Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion- based artificial neuron device. Nanotechnology 2017, 28, 31LT01. [Google Scholar] [CrossRef]
- Pyatakov, A.; Sechin, D.; Sergeev, A.; Nikolaev, A.; Nikolaeva, E.; Logginov, A.; Zvezdin, A. Magnetically switched electric polarity of domain walls in iron garnet films. Europhys. Lett. 2011, 93, 17001. [Google Scholar] [CrossRef]
- Geprägs, S. Magnetoelectric Interactions in Multiferroic Thin Films and Composites. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2011. [Google Scholar]
- Chen, J.; Bai, Y.; Nie, C.; Zhao, S. Strong magnetoelectric effect of Bi4Ti3O12/Bi5Ti3FeO15 composite films. J. Alloys Compd. 2016, 663, 480–486. [Google Scholar] [CrossRef]
- Golovenchits, E.; Sanina, V. Magnetic and Magnetoelectric Dynamics in RMn2O5 (R = Gd and Eu) in Magnetoelectric Interaction Phenomena; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Jedrecy, N.; Von Bardeleben, H.J.; Badjeck, V.; Demaille, D.D.; Stanescu, D.; Magnan, H.; Barbier, A. Strong magnetoelectric coupling in multiferroic Co/BaTiO thin films. Phys. Rev. B 2013, 88, 121409. [Google Scholar] [CrossRef]
- Laletin, V.M.; Paddubnaya, N. Frequency and field dependence of magnetoelectric interactions in layered ferromagnetic transition metal-piezoelectric lead zirconate titanate. Appl. Phys. Lett. 2005, 87, 222507. [Google Scholar] [CrossRef]
- Srinivasan, G.; De Vreugd, C.P.; Bichurin, M.I.; Petrov, V. Magnetoelectric interactions in bilayers of yttrium iron garnet and lead magnesium niobate-lead titanate: Evidence for strong coupling in single crystals and epitaxial films. Appl. Phys. Lett. 2005, 86, 222506. [Google Scholar] [CrossRef]
- Srinivasan, G.; Bichurin, M.I.; Mantese, J.V. Ferromagnetic-ferroelectric layered structures: Magnetoelectric interactions and devices. Integr. Ferroelectr. 2005, 71, 45–57. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharafullin, I.F.; Diep, H.T. Skyrmions and Spin Waves in Magneto–Ferroelectric Superlattices. Entropy 2020, 22, 862. https://doi.org/10.3390/e22080862
Sharafullin IF, Diep HT. Skyrmions and Spin Waves in Magneto–Ferroelectric Superlattices. Entropy. 2020; 22(8):862. https://doi.org/10.3390/e22080862
Chicago/Turabian StyleSharafullin, Ildus F., and Hung T. Diep. 2020. "Skyrmions and Spin Waves in Magneto–Ferroelectric Superlattices" Entropy 22, no. 8: 862. https://doi.org/10.3390/e22080862
APA StyleSharafullin, I. F., & Diep, H. T. (2020). Skyrmions and Spin Waves in Magneto–Ferroelectric Superlattices. Entropy, 22(8), 862. https://doi.org/10.3390/e22080862





