On the Complementarity of the Harmonic Oscillator Model and the Classical Wigner–Kirkwood Corrected Partition Functions of Diatomic Molecules
Abstract
1. Introduction
2. Methods
3. Results
3.1. Vibrational Partition Function of CO
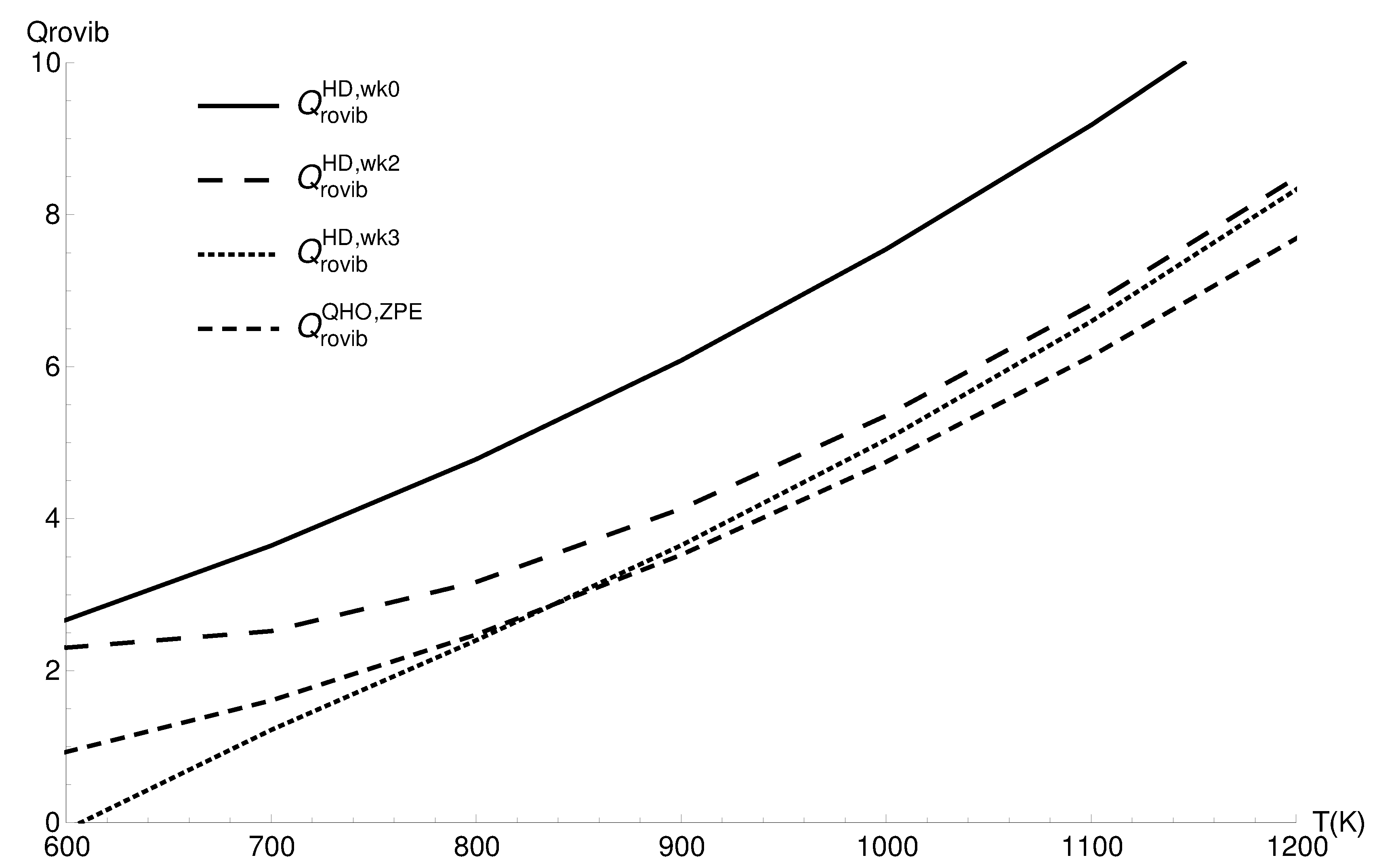
3.2. Rovibrational Partition Function of CO
3.3. Vibrational and Rovibrational Partition Functions of H
4. Conclusions
Funding
Conflicts of Interest
References
- Young, D.A.; Corey, E.M. A new global equation of state model for hot, dense matter. J. Appl. Phys. 1995, 78, 3748–3755. [Google Scholar] [CrossRef]
- Wu, C.J.; Young, D.A.; Sterne, P.A.; Myint, P.C. Equation of state for a chemically dissociative, polyatomic system: Carbon dioxide. J. Chem. Phys. 2019, 151, 224505. [Google Scholar] [CrossRef] [PubMed]
- Buchowiecki, M. Ro-vibrational coupling in high temperature thermochemistry of the BBr molecule. Chem. Phys. Lett. 2018, 692, 236–241. [Google Scholar] [CrossRef]
- Valentini, P.; Norman, P.; Zhang, C.; Schwartzentruber, T.E. Rovibrational coupling in molecular nitrogen at high temperature: An atomic-level study. Phys. Fluids 2014, 26, 056103. [Google Scholar] [CrossRef]
- Zaghloul, M.R. Dissociation and ionization equilibria of deuterium fluid over a wide range of temperatures and densities. Phys. Plasmas 2015, 22, 062701. [Google Scholar] [CrossRef]
- Zaghloul, M.R.; Hassanein, A. Equation-of-state, critical constants, and thermodynamic properties of lithium at high energy density. Phys. Plasmas 2019, 26, 122702. [Google Scholar] [CrossRef]
- Mies, F.H.; Julienne, P.S. The thermodynamic properties of diatomic molecules at elevated temperatures: Role of continuum and metastable states. J. Chem. Phys. 1982, 77, 6162–6176. [Google Scholar] [CrossRef]
- Hill, T.L. Statistical Mechanics; Dover: New York, NY, USA, 1987. [Google Scholar]
- Hill, T.L. Molecular Clusters in Imperfect Gases. J. Chem. Phys. 1955, 23, 617–622. [Google Scholar] [CrossRef]
- Buchowiecki, M. On the exclusion of the negative contribution to the molecular partition function. Mol. Phys. 2019, 117, 1640–1644. [Google Scholar] [CrossRef]
- Buchowiecki, M. High-temperature ideal-gas partition function of the H2+ molecule. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 155101. [Google Scholar] [CrossRef]
- Buchowiecki, M. Partition functions of thermally dissociating diatomic molecules and related momentum problem. Chem. Phys. Lett. 2019, 687, 227–232. [Google Scholar] [CrossRef]
- Buchowiecki, M. Vibrational Partition Function for the Multitemperature Theories of High-Temperature Flows of Gases and Plasmas. J. Phys. Chem. A 2020, 124, 4048–4052. [Google Scholar] [CrossRef] [PubMed]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Quantum Statistics of Almost Classical Assemblies. Phys. Rev. 1933, 44, 31–37. [Google Scholar] [CrossRef]
- Taubmann, G.; Witschel, W.; Schoendorff, L. Calculation of the vibrational partition function of diatomic molecules from a scaled Wigner–Kirkwood expansion. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 2859–2868. [Google Scholar] [CrossRef]
- Liu, Y.F.; Jia, Y.; Shi, D.H.; Sun, J.F. Accurate ab initio potential of CO(X1) at low cost via correlation scaling and extrapolation method. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2296–2302. [Google Scholar] [CrossRef]
- Xie, R.-H.; Gong, J. Simple Three-Parameter Model Potential for Diatomic Systems: From Weakly and Strongly Bound Molecules to Metastable Molecular Ions. Phys. Rev. Lett. 2005, 95, 263202. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.N. Quantum Corrections to the Second Virial Coefficient at High Temperatures. J. Math. Phys. 1968, 9, 1534–1547. [Google Scholar] [CrossRef]
- Kihara, T.; Midzuno, J.; Shizume. T Virial Coefficients and Intermolecular Potential of Helium. J. Phys. Soc. Jpn. 1955, 10, 249–255. [Google Scholar] [CrossRef]
- Qin, Z.; Zhao, J.M.; Liu, L.H. High-temperature partition functions, specific heats and spectral radiative properties of diatomic molecules with an improved calculation of energy levels. J. Quant. Spectrosc. Radiat. Transf. 2018, 210, 1–18. [Google Scholar] [CrossRef]
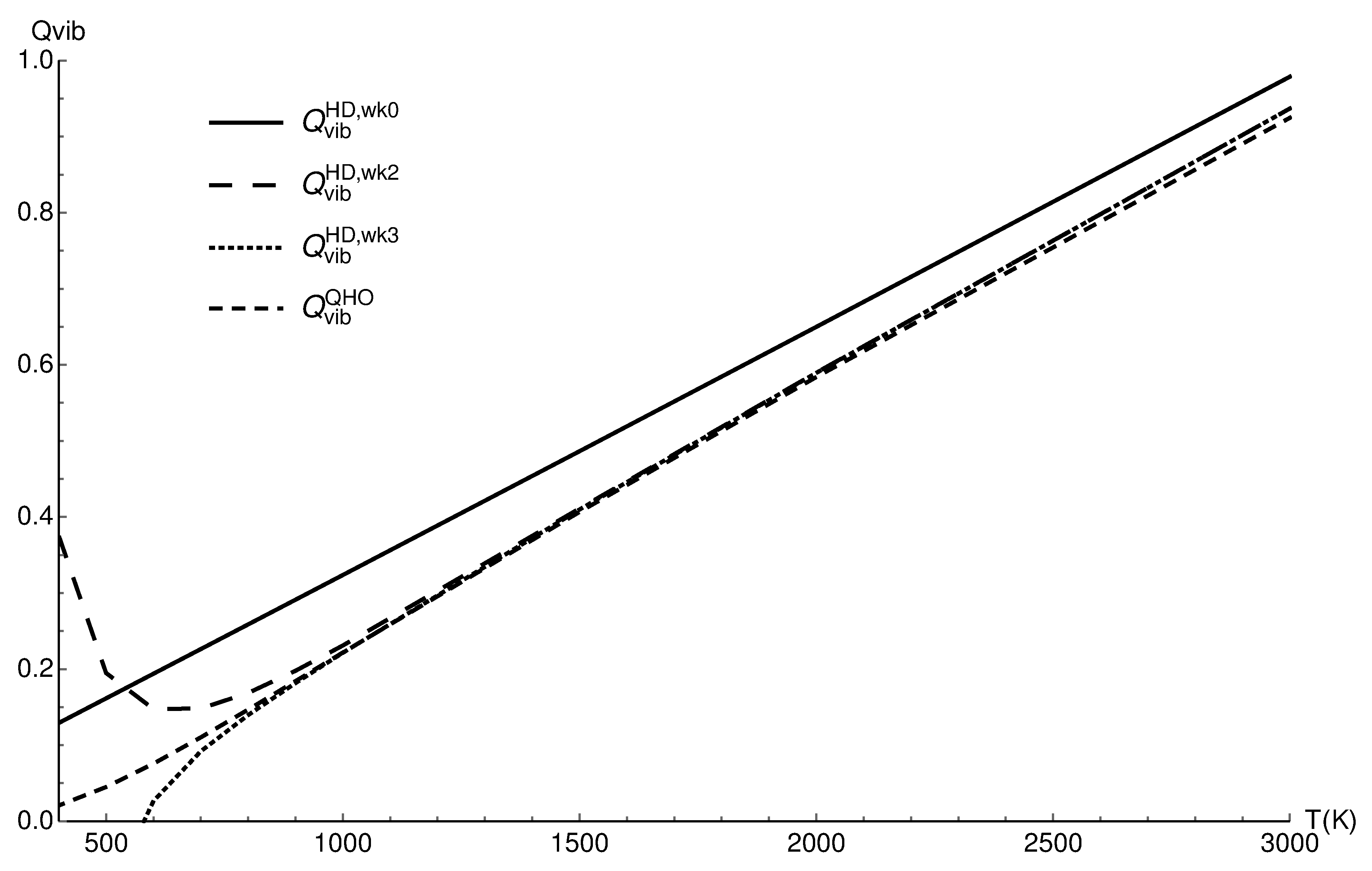
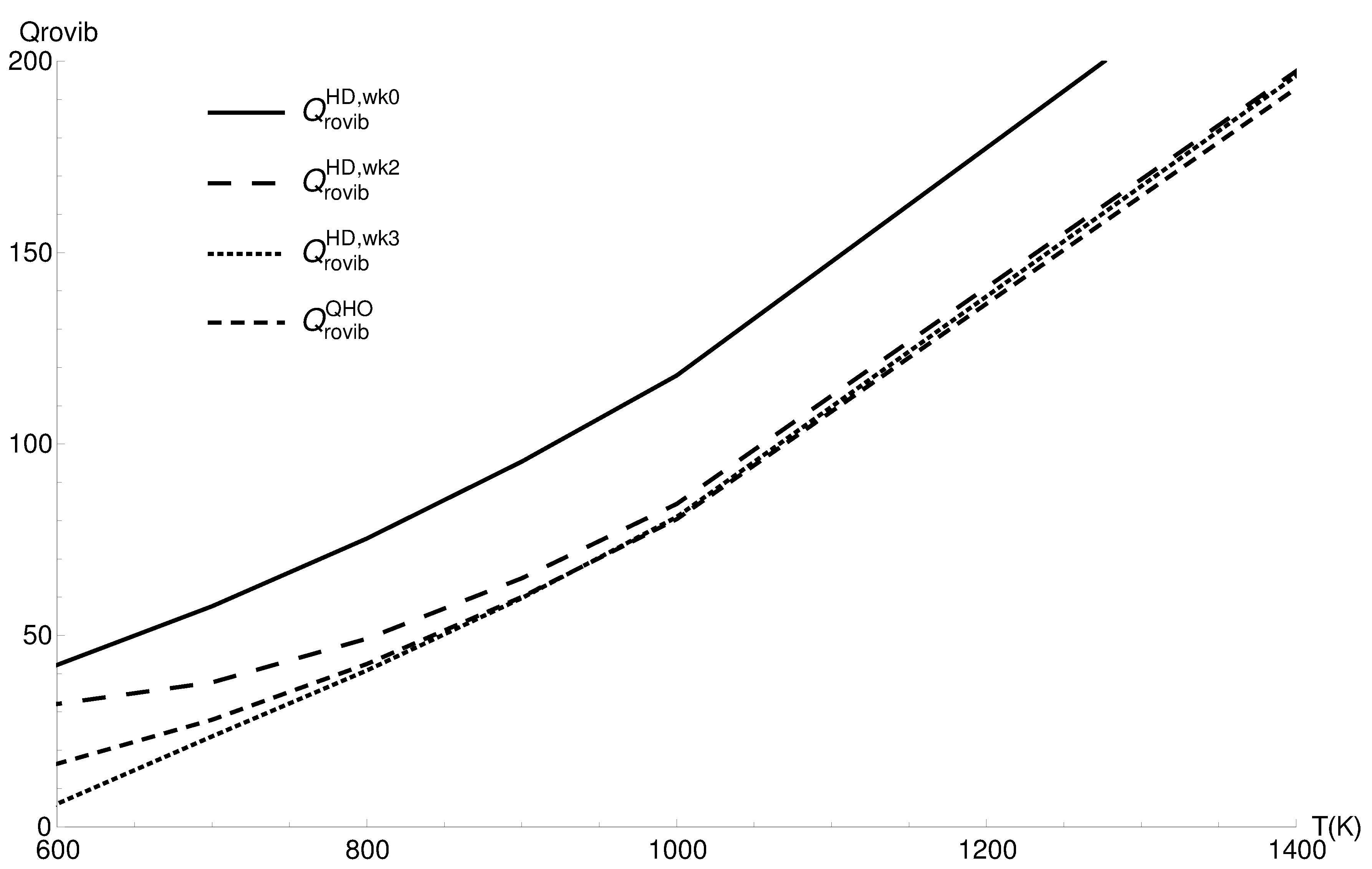
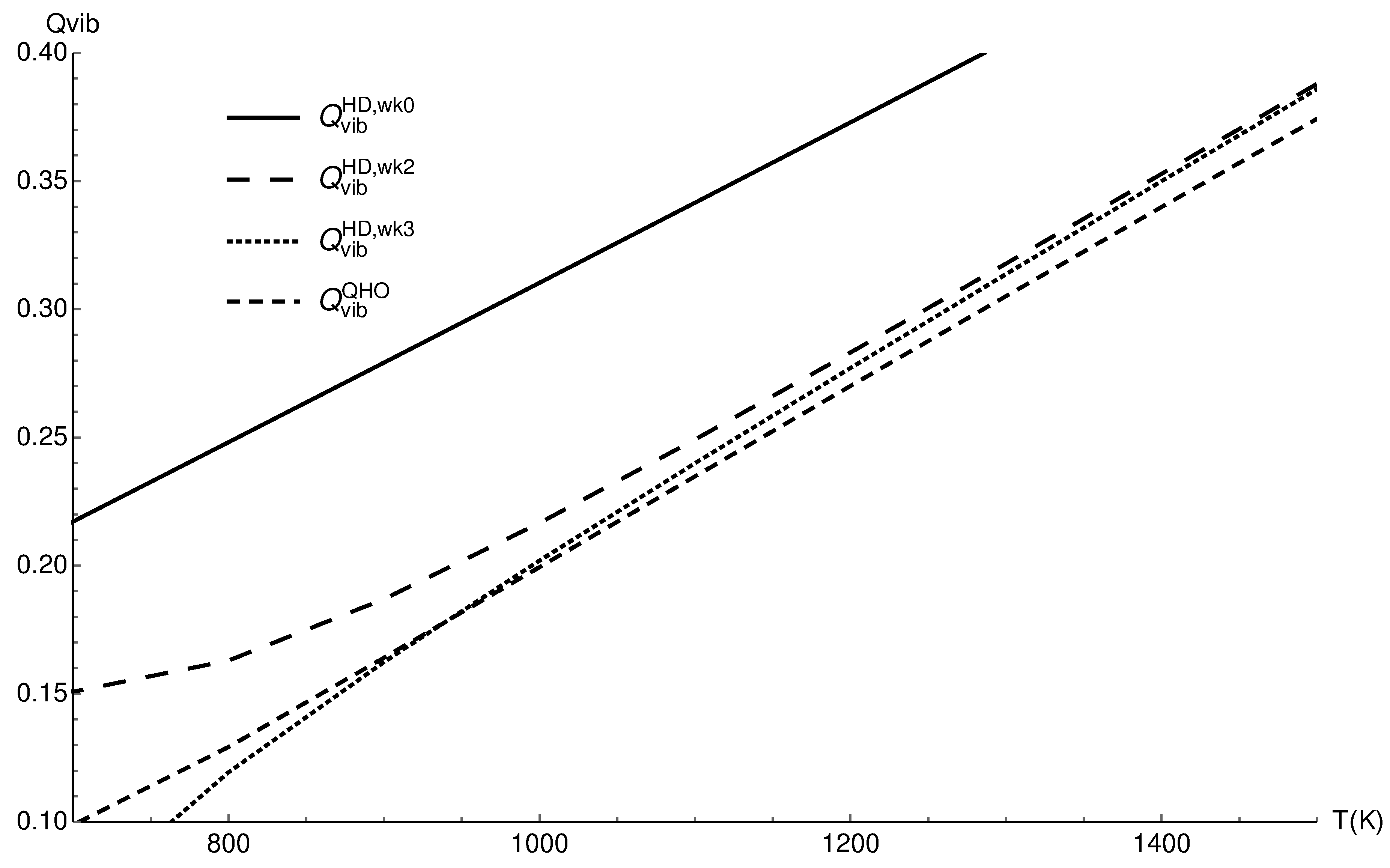
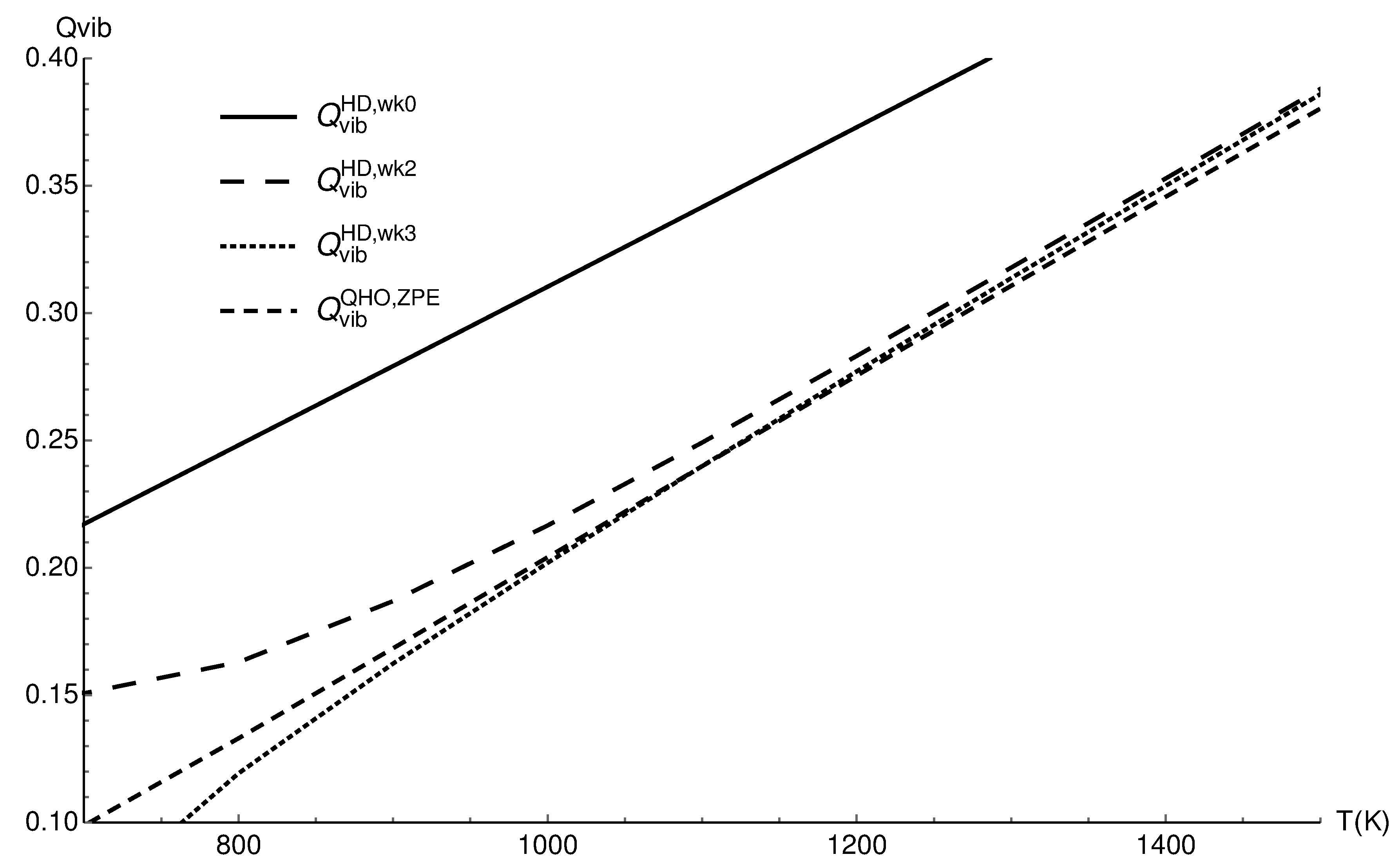
| T (K) | ||
|---|---|---|
| 600 K | ||
| 700 K | ||
| 800 K | ||
| 900 K | ||
| 1000 K | ||
| 1500 K | ||
| 2000 K | ||
| 3000 K |
| T (K) | |||
|---|---|---|---|
| 200 K | |||
| 300 K | |||
| 400 K | |||
| 500 K | |||
| 600 K | |||
| 700 K | |||
| 800 K | |||
| 900 K |
| T (K) | HITRAN | ||
|---|---|---|---|
| 600 K | () | () | |
| 700 K | () | () | |
| 800 K | () | () | |
| 900 K | () | () | |
| 1000 K | () | () | |
| 1500 K | () | () | |
| 2000 K | () | () | |
| 3000 K | () | () |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchowiecki, M. On the Complementarity of the Harmonic Oscillator Model and the Classical Wigner–Kirkwood Corrected Partition Functions of Diatomic Molecules. Entropy 2020, 22, 853. https://doi.org/10.3390/e22080853
Buchowiecki M. On the Complementarity of the Harmonic Oscillator Model and the Classical Wigner–Kirkwood Corrected Partition Functions of Diatomic Molecules. Entropy. 2020; 22(8):853. https://doi.org/10.3390/e22080853
Chicago/Turabian StyleBuchowiecki, Marcin. 2020. "On the Complementarity of the Harmonic Oscillator Model and the Classical Wigner–Kirkwood Corrected Partition Functions of Diatomic Molecules" Entropy 22, no. 8: 853. https://doi.org/10.3390/e22080853
APA StyleBuchowiecki, M. (2020). On the Complementarity of the Harmonic Oscillator Model and the Classical Wigner–Kirkwood Corrected Partition Functions of Diatomic Molecules. Entropy, 22(8), 853. https://doi.org/10.3390/e22080853





