Nonclassical Effects Based on Husimi Distributions in Two Open Cavities Linked by an Optical Waveguide
Abstract
1. Introduction
2. Physical Model
3. Husimi Distribution (HD)
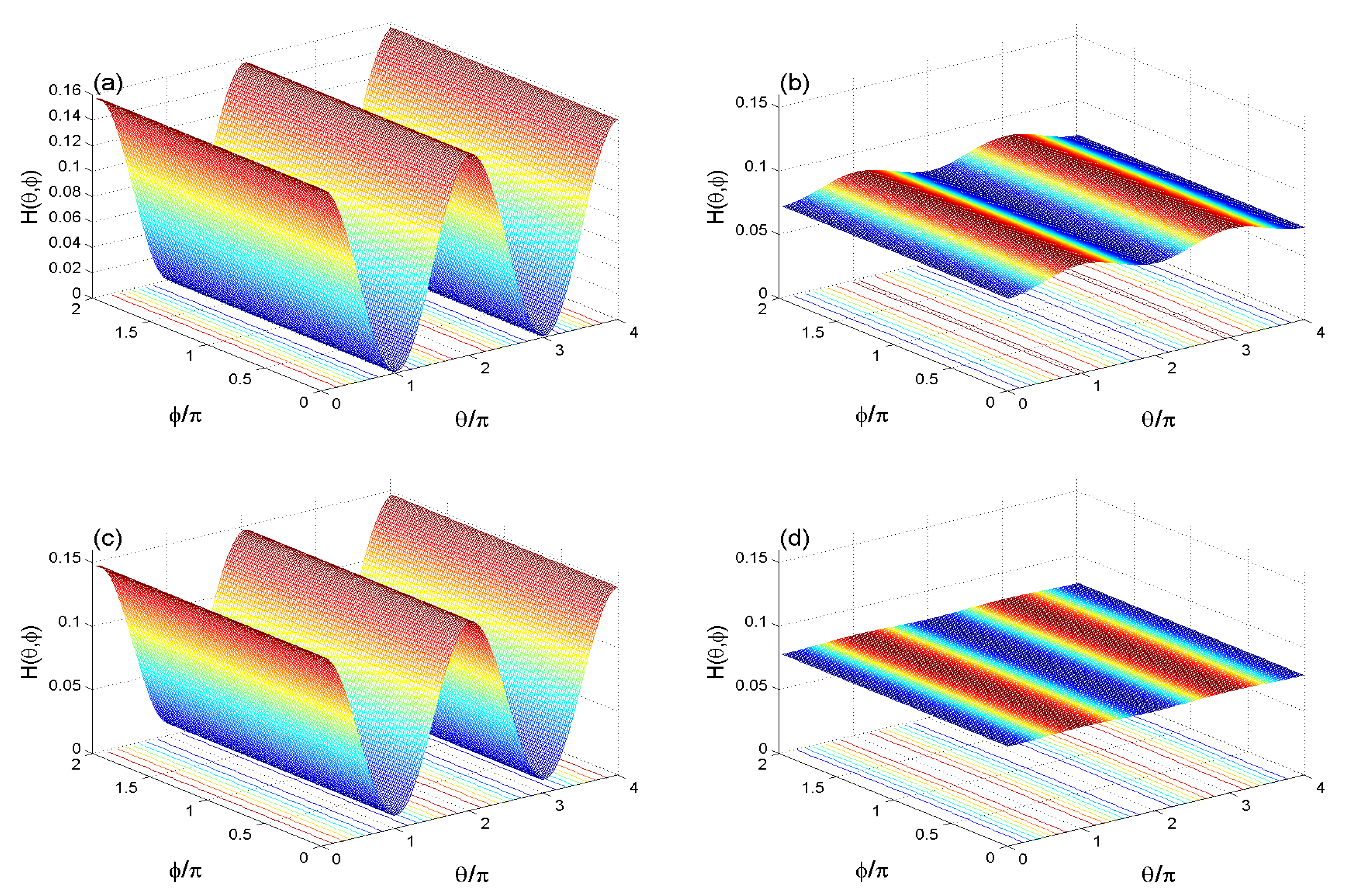
3.1. Phase Space Information of the Husimi Distribution
3.2. Wehrl Entropy
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Walther, H.; Varcoe, B.T.H.; Englert, B.-G.; Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 2006, 69, 1325. [Google Scholar] [CrossRef]
- Miller, R.; Northup, T.E.; Birnbaum, K.M.; Boca, A.; Boozer, A.D.; Kimble, H.J. Trapped atoms in cavity QED: Coupling quantized light and matter. J. Phys. B At. Mol. Opt. Phys. 2005, 38, S551. [Google Scholar] [CrossRef]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565. [Google Scholar] [CrossRef]
- Nogues, G.; Rauschenbeutel, A.; Osnaghi, S.; Brune, M.; Raimond, J.M.; Haroche, S. Seeing a single photon without destroying it. Nature 1999, 400, 239. [Google Scholar] [CrossRef]
- Sayrin, C.; Dotsenko, I.; Zhou, X.; Peaudecerf, P.; Rybarczyk, T.; Gleyzes, S.; Rouchon, P.; Mirrahimi, M.; Amini, H.; Brune, M.; et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 2011, 477, 73. [Google Scholar] [CrossRef] [PubMed]
- Burkard, G.; Gullans, M.J.; Mi, X.; Petta, J.R. Superconductor–semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2020, 2, 129. [Google Scholar] [CrossRef]
- Najer, D.; Söllner, I.; Sekatski, P.; Dolique, V.; Löbl, M.C.; Riedel, D.; Schott, R.; Starosielec, S.; Valentin, S.R.; Wieck, A.D.; et al. A gated quantum dot strongly coupled to an optical microcavity. Nature 2019, 575, 622. [Google Scholar] [CrossRef]
- Kaer, P.; MØrk, J. Decoherence in semiconductor cavity QED systems due to phonon couplings. Phys. Rev. B 2014, 90, 035312. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Quantum correlation control for two semiconductor microcavities connected by an optical fiber. Phys. Scr. 2017, 92, 065101. [Google Scholar] [CrossRef]
- Cirac, J.I.; Ekert, A.K.; Huelga, S.F.; Macchiavello, C. Distributed quantum computation over noisy channels. Phys. Rev. A 1999, 59, 4249. [Google Scholar] [CrossRef]
- Paternostro, M.; Kim, M.S.; Palma, G.M. Non-local quantum gates: A cavity-quantum-electrodynamics implementation. J. Mod. Opt. 2003, 50, 2075. [Google Scholar] [CrossRef]
- Pellizzari, T. Quantum Networking with Optical Fibres. Phys. Rev. Lett. 1997, 79, 5242. [Google Scholar] [CrossRef]
- Mancini, S.; Bose, S. Ponderomotive entangling of atomic motions. Phys. Rev. A 2001, 64, 032308. [Google Scholar] [CrossRef]
- Cho, J.; Lee, H.-W. Generation of Atomic Cluster States through the Cavity Input-Output Process. Phys. Rev. Lett. 2005, 95, 160501. [Google Scholar] [CrossRef] [PubMed]
- Su, S.L.; Shao, X.Q.; Guo, Q.; Cheng, L.Y.; Wang, H.F.; Zhang, S. Preparation of entanglement between atoms in spatially separated cavities via fiber loss. Eur. Phys. J. D 2015, 69, 123. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Masmali, I. Control of the Geometric Phase in Two Open Qubit–Cavity Systems Linked by aWaveguide. Entropy 2020, 22, 85. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Generation and robustness of bipartite non-classical correlations in two nonlinear microcavities coupled by an optical fiber. J. Opt. Soc. Am. B 2018, 35, 47. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Anaya-Contreras, J.A.; Moya-Cessa, H.M.; Zú niga-Segundo, A. The von Neumann Entropy for Mixed States. Entropy 2019, 21, 49. [Google Scholar] [CrossRef]
- Dixit, K.; Naikoo, J.; Banerjee, S.; Alok, A.K. Study of coherence and mixedness in meson and neutrino systems. Eur. Phys. J. C 2019, 79, 96. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A. The effects of thermal photons on entanglement dynamics for a dispersive Jaynes–Cummings model. Phys. Lett. A 2008, 372, 3699. [Google Scholar] [CrossRef]
- Wang, X.; Sanders, B.C.; Pan, S.-H. Entangled coherent states for systems with SU(2) and SU(1,1) symmetries. J. Phys. A Math. Gen. 2000, 33, 7451. [Google Scholar] [CrossRef]
- Sanders, B.C. Review of entangled coherent states. J. Phys. A Math. Theor. 2012, 45, 244002. [Google Scholar] [CrossRef]
- Adesso, G.; Bromley, T.R.; Cianciaruso, M. Measures and applications of quantum correlations. J. Phys. A Math. Theor. 2016, 49, 473001. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Non-local correlations via Wigner Yanase skew information in two SC-qubit having mutual interaction under phase decoherence. Eur. Phys. J. D 2017, 71, 261. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Bipartite non-classical correlations for a lossy two connected qubit–cavity systems: Trace distance discord and Bell’s non-locality. Quantum Inf. Process. 2018, 17, 96. [Google Scholar] [CrossRef]
- Ekert, A.; Richard, J. Quantum computation and Shor’s factoring algorithm. Rev. Mod. Phys. 1996, 68, 733. [Google Scholar] [CrossRef]
- Jennewein, T.; Simon, C.; Weihs, G.; Weinfurter, H.; Zeilinger, A. Quantum Cryptography with Entangled Photons. Phys. Rev. Lett. 2000, 84, 4729. [Google Scholar] [CrossRef]
- Sehati, N.; Tavassoly, M.K. Approximate conditional teleportation of a Λ-type three-level atomic state based on cavity QED method beyond Bell-state measurement. Quantum Inf. Process. 2017, 16, 193. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossin. Theor. Comput. Sci. 2014, 560, 7. [Google Scholar] [CrossRef]
- Puigibert, M.l.G.; Askarani, M.F.; Davidson, J.H.; Verma, V.B.; Shaw, M.D.; Nam, S.W.; Lutz, T.; Amaral, G.C.; Oblak, D.; Tittel, W. Entanglement and nonlocality between disparate solid-state quantum memories mediated by photons. Phys. Rev. Res. A 2020, 2, 013039. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H. High-efficiency quantum state transfer and quantum memory using a mechanical oscillator. Phys. Rev. A 2015, 91, 032309. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264. [Google Scholar]
- Bolda, E.L.; Tan, S.M.; Walls, D. Measuring the quantum state of a Bose-Einstein condensate. Phys. Rev. A 1998, 57, 4686. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221. [Google Scholar] [CrossRef]
- Yazdanpanah, N.; Tavassoly, M.K.; Juárez-Amaro, R.; Moya-Cessa, H.M. Reconstruction of quasiprobability distribution functions of the cavity field considering field and atomic decays. Opt. Commun. 2017, 400, 69. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Coherence and information dynamics of a Λ-type three-level atom interacting with a damped cavity field. Eur. Phys. J. Plus 2017, 132, 75. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023. [Google Scholar] [CrossRef]
- Serafini, A.; Mancini, S.; Bose, S. Distributed Quantum Computation via Optical Fibers. Phys. Rev. Lett. 2006, 96, 010503. [Google Scholar] [CrossRef]
- Liu, T.; Cao, X.-Z.; Su, Q.-P.; Xiong, S.-J.; Yang, C.-P. Multi-target-qubit unconventional geometric phase gate in a multi-cavity system. Sci. Rep. 2016, 6, 21562. [Google Scholar] [CrossRef]
- Didier, N.; Guillaud, J.; Shankar, S.; Mirrahimi, M. Remote entanglement stabilization and concentration by quantum reservoir engineering. Phys. Rev. A 2018, 98, 012329. [Google Scholar] [CrossRef]
- Liu, T.; Su, Q.-P.; Zhang, Y.; Fang, Y.-L.; Yang, C.-P. Generation of quantum entangled states of multiple groups of qubits distributed in multiple cavities. Phys. Rev. A 2020, 101, 012337. [Google Scholar] [CrossRef]
- Santos, J.P.; Céleri, L.C.; Brito, F.; Landi, G.T.; Paternostro, M. Spin-phase-space-entropy production. Phys. Rev. A 2018, 97, 052123. [Google Scholar] [CrossRef]
- Yang, L.-P.; Jacob, Z. Engineering first-order quantum phase transitions for weak signal detection. J. Appl. Phys. 2019, 126, 174502. [Google Scholar] [CrossRef]
- Romera, E.; del Real, R.; Calixto, M. Husimi distribution and phase-space analysis of a Dicke-model quantum phase transition. Phys. Rev. A 2012, 85, 053831. [Google Scholar] [CrossRef]
- Mintert, F.; Życzkowski, K. Wehrl entropy, Lieb conjecture, and entanglement monotones. Phys. Rev. A 2004, 69, 022317. [Google Scholar] [CrossRef]
- Houdre, R.; Weisbuch, C.; Stanley, R.P.; Oesterle, U.; Ilegems, M. Nonlinear Emission of Semiconductor Microcavities in the Strong Coupling Regime. Phys. Rev. Lett. 2000, 85, 2793. [Google Scholar] [CrossRef] [PubMed]
- Giacobino, E.; Karr, J.-P.; Messin, G.; Eleuch, H.; Baas, A. Quantum optical effects in semiconductor microcavities Optique quantique dans les microcavites semi-conductrices. C. R. Phys. 2002, 3, 41. [Google Scholar] [CrossRef]
- Eleuch, H.; Courty, J.M.; Messin, G.; Fabre, C.; Giacobino, E. Cavity QED effects in semiconductor microcavities. J. Opt. B 1999, 1, 1. [Google Scholar] [CrossRef]
- van Enk, S.J.; Kimble, H.J.; Cirac, J.I.; Zoller, P. Quantum communication with dark photons. Phys. Rev. A 1999, 59, 2659. [Google Scholar] [CrossRef]
- Louisell, W.H. Quantum Statistical Properties of Radiation; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Eleuch, H. Photon statistics of light in semiconductor microcavities. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 055502. [Google Scholar] [CrossRef]
- Mohamed, A.-B.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Baas, A.; Karr, J.P.; Eleuch, H.; Giacobino, E. Optical bistability in semiconductor microcavities. Phys. Rev. A 2004, 69, 023809. [Google Scholar] [CrossRef]
- Messin, G.; Karr, J.P.; Baas, A.; Khitrova, G.; Houdré, R.; Stanley, R.P.; Oesterle, U.; Giacobino, E. Parametric Polariton Amplification in Semiconductor Microcavities. Phys. Rev. Lett. 2001, 87, 127403. [Google Scholar] [CrossRef] [PubMed]
- Jabri, H.; Eleuch, H. Interaction of a dipolariton system with squeezed light from a parametric down-conversion process. Phys. Rev. A 2020, 101, 053819. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H.; Obada, A.-S.F. Influence of the Coupling between Two Qubits in an Open Coherent Cavity: Nonclassical Information via Quasi-Probability Distributions. Entropy 2019, 21, 1137. [Google Scholar] [CrossRef]
- van Enk, S.J.; Kimble, H.J. On the classical character of control fields in quantum information processing. Quant. Inform. Comput. 2002, 2, 1. [Google Scholar]
- El-Orany, F.A.A. Atomic Wehrl entropy for the Jaynes–Cummings model: Explicit form and Bloch sphere radius. J. Mod. Opt. 2009, 56, 99. [Google Scholar] [CrossRef]
- Siomau, M.; Fritzsche, S. Quantum computing with mixed states. Eur. Phys. J. D 2011, 62, 449. [Google Scholar] [CrossRef]
- Hou, S.-Y.; Sheng, Y.-B.; Feng, G.-R.; Long, G.-L. Experimental Optimal Single Qubit Purification in an NMR Quantum Information Processor. Sci. Rep. 2015, 4, 6857. [Google Scholar] [CrossRef]
- Collins, D. Qubit-channel metrology with very noisy initial states. Phys. Rev. A 2019, 99, 012123. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-B.A.; Eleuch, H. Nonclassical Effects Based on Husimi Distributions in Two Open Cavities Linked by an Optical Waveguide. Entropy 2020, 22, 767. https://doi.org/10.3390/e22070767
Mohamed A-BA, Eleuch H. Nonclassical Effects Based on Husimi Distributions in Two Open Cavities Linked by an Optical Waveguide. Entropy. 2020; 22(7):767. https://doi.org/10.3390/e22070767
Chicago/Turabian StyleMohamed, Abdel-Baset A., and Hichem Eleuch. 2020. "Nonclassical Effects Based on Husimi Distributions in Two Open Cavities Linked by an Optical Waveguide" Entropy 22, no. 7: 767. https://doi.org/10.3390/e22070767
APA StyleMohamed, A.-B. A., & Eleuch, H. (2020). Nonclassical Effects Based on Husimi Distributions in Two Open Cavities Linked by an Optical Waveguide. Entropy, 22(7), 767. https://doi.org/10.3390/e22070767




