Portfolio Optimization for Binary Options Based on Relative Entropy
Abstract
1. Introduction
Literature Review
2. Maximum Exponential Growth Rate
2.1. The Kelly Criterion
2.2. Extension of the Kelly Criterion to Multiple Wagers
3. Shannon Entropy of Discrete Returns
3.1. Investments Versus Wagers
3.2. Joint Entropy of a Portfolio of Discrete Return Assets
4. Minimum Relative Entropy
4.1. Kullback–Leibler Divergence
4.2. Relative Entropy as a Convex Risk Measure
- (i)
- Monotonicity. If , then ,
- (ii)
- Translation invariance. If , then , and
- (iii)
- Convexity. , for .
- (i)
- Monotonicity. For a risk measure to be monotonic it must satisfy: If and almost surely then almost surely. Using as stated, we have and for discrete distributions P and Q. Because implies as a consequence of the data processing inequality (Cover, 1991) [30], it follows thatalmost surely. Therefore, (16) shows is monotonic.
- (ii)
- Translation invariance. For a risk measure to exhibit translation invariance it must satisfy: If then . Recall the risk measure based on the relative entropy principle is of the form . Since , for all c, it follows that and, thus, we have (17),Therefore exhibits translation invariance.
- (iii)
- Convexity. A risk measure is convex if: For and it follows that: . It is known that is convex in the pair of probability mass functions . If and are two pairs of probability mass functions, then (18) follows,
4.3. Minimum Risk Option Portfolios with Relative Entropy
4.4. Discrete Entropic Portfolio Optimization (DEPO)
4.5. Risk-Adjusted Performance
5. Portfolio Selection Examples with DEPO
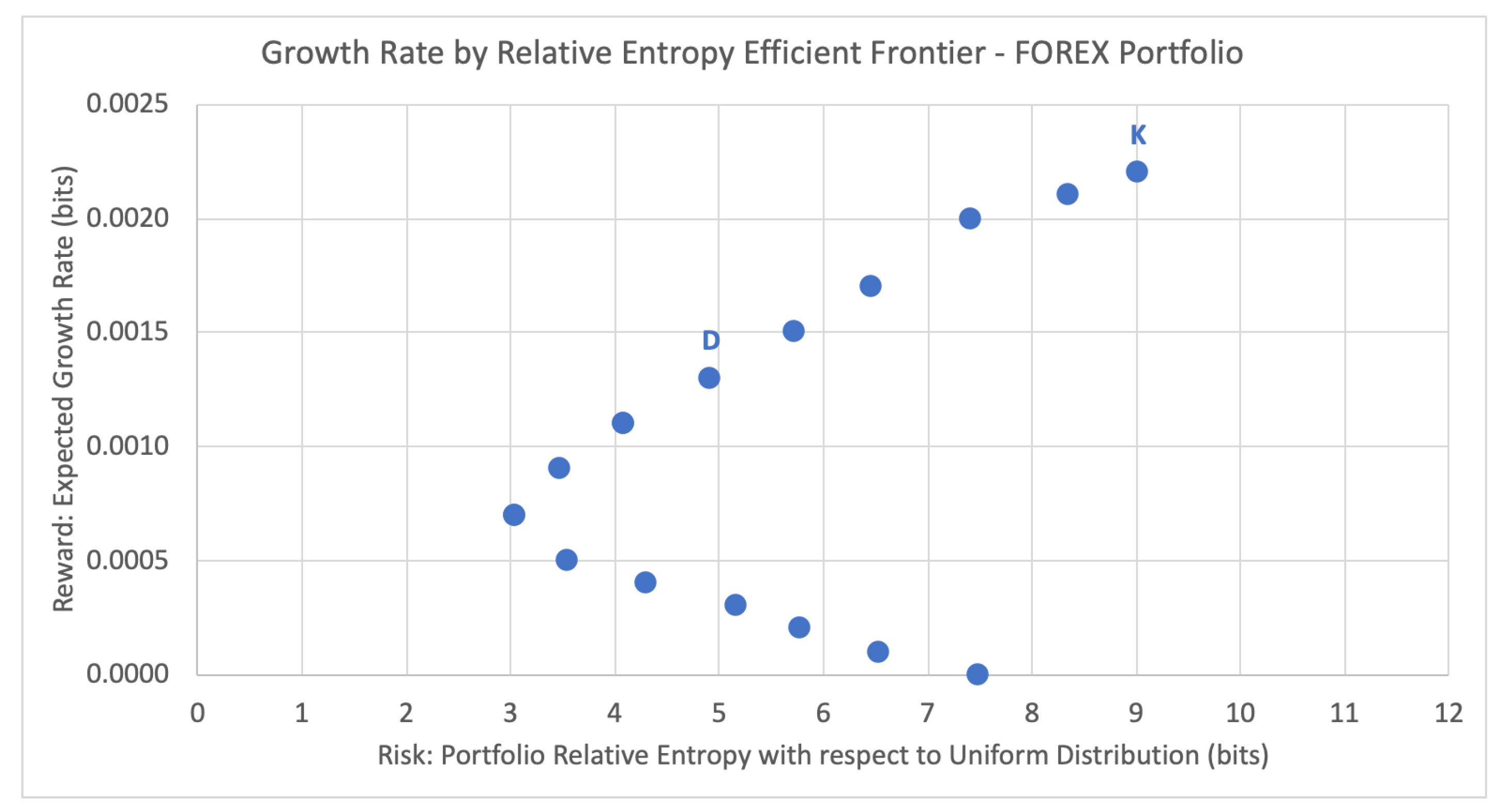
5.1. FOREX Binary Option Portfolio Example
5.1.1. Data
5.1.2. Efficient Frontier and Portfolio Selection
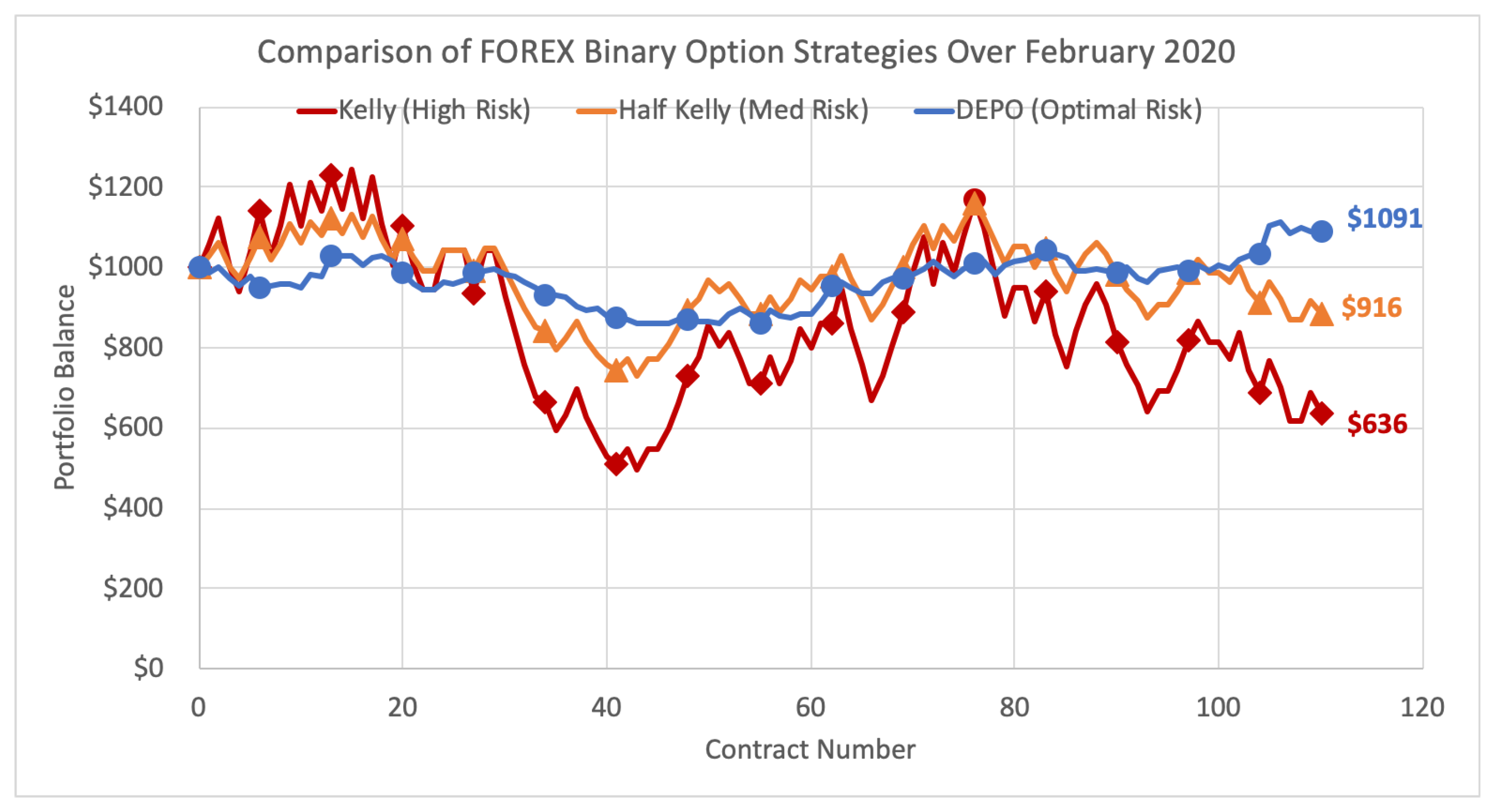
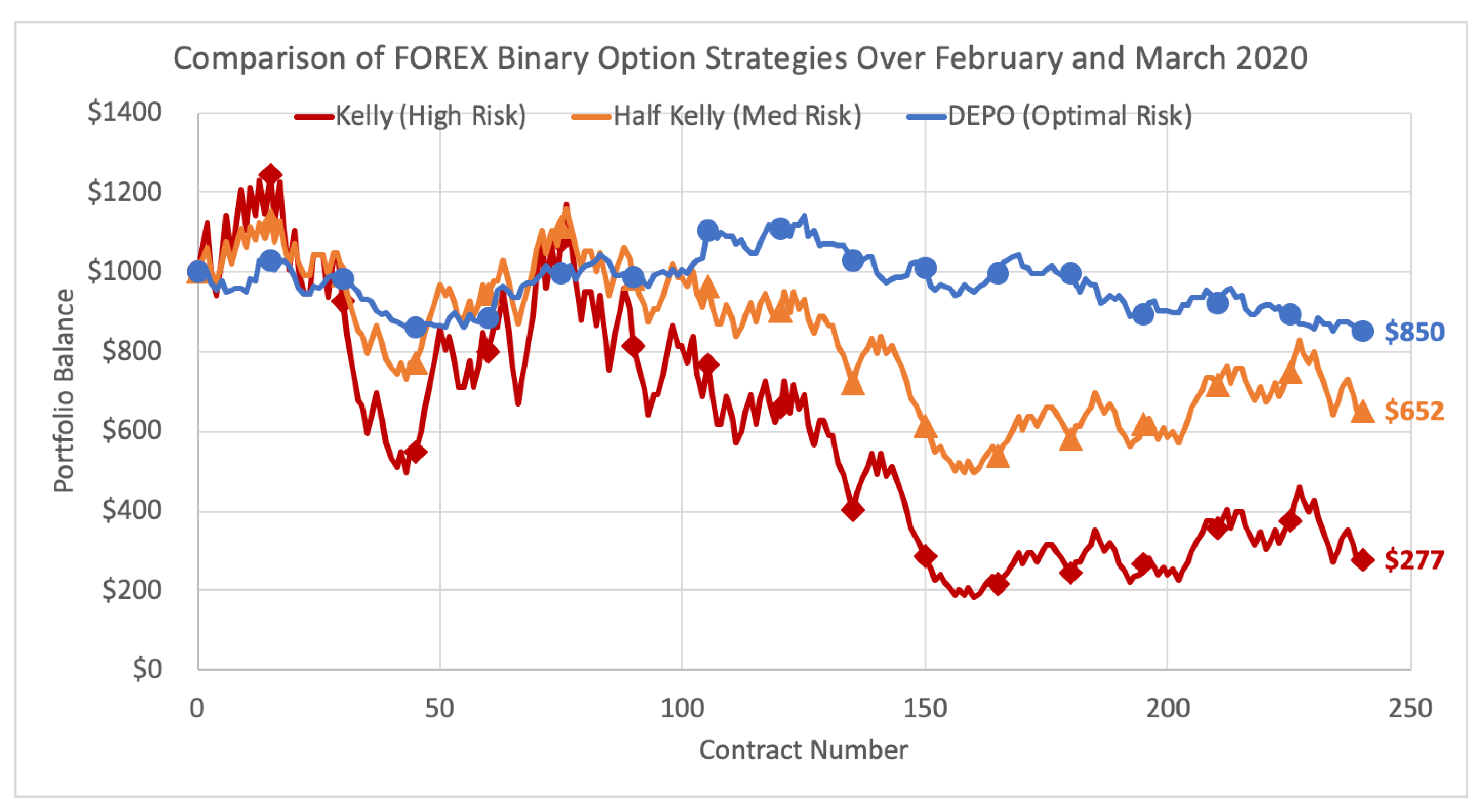
5.1.3. Comparison to the Kelly Criterion over Time
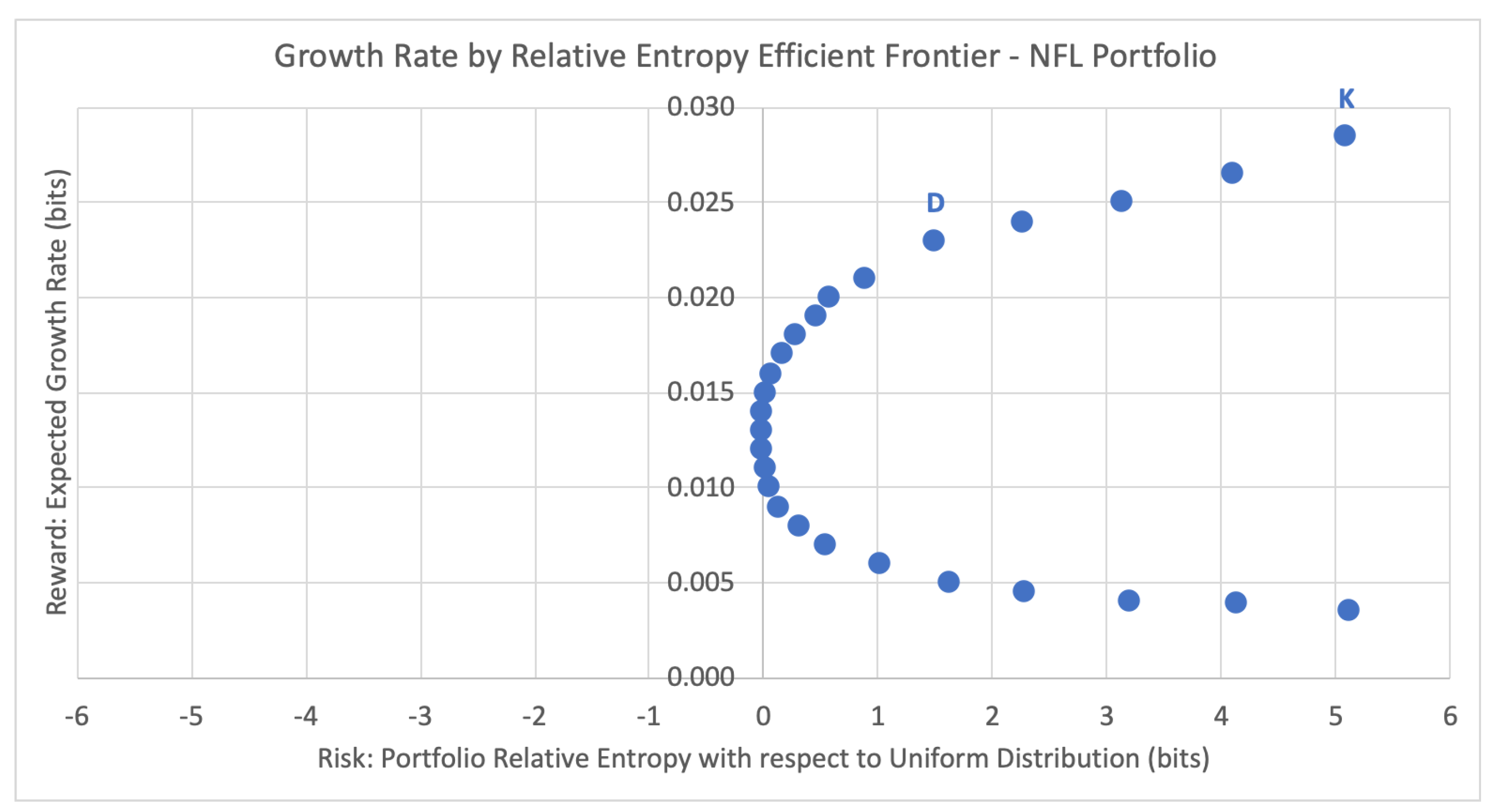
5.2. NFL Sportsbook Example
5.2.1. Data
5.2.2. Efficient Frontier and Portfolio Selection
5.2.3. Comparison to the Kelly Criterion over Time
6. Conclusions
7. Materials and Methods
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AUD | Australian dollar |
| BAL | Baltimore Ravens |
| CAD | Canadian dollar |
| CHF | Confoederatio Helvetica (Swiss) franc |
| DEPO | Discrete entropic portfolio optimization |
| EUR | Euro |
| FOREX | Foreign Exchange |
| FRO | Fixed-return option |
| GBP | Great British pound (sterling) |
| GROUND | Growth rate over uniform divergence |
| IND | Indianapolis Colts |
| JAC | Jacksonville Jaguars |
| JPY | Japanese yen |
| KC | Kansas City Chiefs |
| KL | Kullback-Leibler |
| LAC | Los Angeles Chargers |
| LV | Las Vegas |
| MIA | Miami Dolphins |
| NADEX | North American Derivative Exchange |
| NFL | National Football League |
| REPO | Return-entropy portfolio optimization |
| USD | US dollar |
References
- Mercurio, P.; Wu, Y.; Xie, H. An Entropy-Based Approach to Portfolio Optimization. Entropy 2020, 22, 332. [Google Scholar] [CrossRef]
- Shannon, C. A Mathematical Theory of Communication: Part 1. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C. A Mathematical Theory of Communication: Part 2. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Kelly, J. A New Interpretation of Information Rate. Bell Syst. Tech. J. 1956, 35, 917–926. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; John Wiley and Sons: New York, NY, USA, 1959. [Google Scholar]
- Benello, A.; van Biema, M.; Carlisle, T. Concentrated Investing: Strategies of the World’s Greatest Concentrated Value Investors; John Wiley and Sons: New York, NY, USA, 2016. [Google Scholar]
- Rotundo, L.; Thorp, E. The Kelly Criterion and the Stock Market. Am. Math. Mon. 1992, 99, 922–931. [Google Scholar] [CrossRef]
- Browne, S.; Whitt, W. Portfolio Choice and the Bayesian Kelly Criterion. Adv. Appl. Probab. 1996, 28, 1145–1176. [Google Scholar] [CrossRef]
- MacLean, L. The Kelly Capital Growth Investment Criterion: Theory and Practice; World Scientific: Singapore, 2010. [Google Scholar]
- Das, S. Data Science: Theories, Models, Algorithms, and Analytics. 2016. Available online: https://srdas.github.io/Papers/DSA_Book.pdf (accessed on 1 January 2020).
- Lavinio, S. The Hedge Fund Handbook; McGraw-Hill, Irwin Library of Investment & Finance: New York, NY, USA, 2000. [Google Scholar]
- O’Shaughnessy, D. Optimal Exchange Betting Strategy for Win-Draw-Loss Markets. In Proceedings of the MATHSPORT 2012 11th Australasian Conference on Mathematics and Computers in Sport, Melbourne, Australia, 11–13 July 2012; Volume 1, p. 1. [Google Scholar]
- Baker, R.; McHale, I. Optimal Betting Under Parameter Uncertainty: Improving the Kelly Criterion. Decis. Anal. 2013, 10, 189–199. [Google Scholar] [CrossRef]
- Maclean, L.; Ziemba, W. The Handbook of the Fundamentals of Financial Decision Making; World Scientific: Singapore, 2013. [Google Scholar]
- Sinclair, E. Confidence Intervals for the Kelly Criterion. J. Invest. Strateg. 2014, 3, 65–74. [Google Scholar] [CrossRef]
- Davari-Ardakani, H.; Aminnayeri, M.; Seifi, A. Multistage Portfolio Optimization with Stocks and Options. Int. Trans. Oper. Res. 2016, 23, 593–622. [Google Scholar] [CrossRef]
- Faias, J.; Santa-Clara, P. Optimal Option Portfolio Strategies: Deepening the Puzzle of Index Option Mispricing. J. Financ. Quant. Anal. 2017, 52, 277–303. [Google Scholar] [CrossRef]
- Chu, D.; Wu, Y.; Swartz, T. Modified Kelly Criterion. J. Quant. Anal. Sport. 2018, 14, 22. [Google Scholar]
- Hubacek, O.; Sourek, G.; Zelezny, F. Exploiting Sports-Betting Market Using Machine Learning. Int. J. Forecast. 2019, 35, 783–796. [Google Scholar] [CrossRef]
- Vecer, J. Optimal Distributional Trading Gain: State Price Density Equilibrium and Bayesian Statistics. Working Paper. 2020. Available online: https://ssrn.com/abstract=3616661 (accessed on 3 July 2020).
- Khanna, N. The Kelly Criterion and the Stock Market. 2016. Available online: https://sites.math.washington.edu/~morrow/336_16/2016papers/nikhil.pdf (accessed on 1 March 2020).
- MacKay, D. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Hardy, M. An Introduction to Risk Measures for Actuarial Applications. 2006. Available online: https://www.researchgate.net/profile/Mary_Hardy2/publication/242469445_An_Introduction_to_Risk_Measures_for_Actuarial_Applications/links/0a85e5342bd491d188000000/An-Introduction-to-Risk-Measures-for-Actuarial-Applications.pdf (accessed on 1 March 2020).
- Follmer, H.; Schied, A. Stochastic Finance: An Introduction in Discrete Time; De Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Ahmadi-Javid, A. Entropic Value-at-Risk: A New Coherent Risk Measure. J. Optim. Theory Appl. 2012, 155, 1105–1123. [Google Scholar] [CrossRef]
- Artzner, P.; Delbaen, F.; Eber, J.; Heath, D. Coherent Measures of Risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover Publications: New York, NY, USA, 1996. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; John Wiley and Sons: New York, NY, USA, 1991. [Google Scholar]
- Keren, G.; Charles, L. The Two Fallacies of Gamblers: Type I and Type II. Organ. Behav. Hum. Decis. Process. 1994, 60, 75–89. [Google Scholar] [CrossRef]
- Low, R.; Faff, R.; Kjersti, A. Enhancing Mean–Variance Portfolio Selection by Modeling Distributional Asymmetries. J. Econ. Bus. 2016, 85, 49–72. [Google Scholar] [CrossRef]
- Sharpe, W. Mutual Fund Performance. J. Bus. 1966, 39, 119–138. [Google Scholar] [CrossRef]
- Eling, M. Does the Measure Matter in the Mutual Fund Industry? Financ. Anal. J. 2008, 64, 54–66. [Google Scholar] [CrossRef]
- Rad, H.; Low, R.; Faff, R. The Profitability of Pairs Trading Strategies: Distance, Cointegration and Copula Methods. Quant. Financ. 2016, 16, 1541–1558. [Google Scholar] [CrossRef]
- NADEX. The Components of Binary Option Pricing. 2020. Available online: https://www.nadex.com/learning-center/courses/binary-options/components-binary-option-pricing (accessed on 1 March 2020).

| Currency Pair | Short Name | Mean Outcome | % In-the-Money | Relative Entropy |
|---|---|---|---|---|
| Australian Dollar/Japanese Yen | AUD/JPY | −0.42591 | 0.287045 | 0.135127 |
| Australian Dollar/US Dollar | AUD/USD | −0.868988 | 0.065506 | 0.651076 |
| Euro/Pound Sterling | EUR/GBP | 0.0174 | 0.5087 | 0.000218 |
| Euro/Japanese Yen | EUR/JPY | −0.243882 | 0.378059 | 0.04334 |
| Euro/US Dollar | EUR/USD | −0.109232 | 0.445384 | 0.008624 |
| Pound Sterling/Japanese Yen | GBP/JPY | −0.069511 | 0.465244 | 0.003488 |
| Pound Sterling/US Dollar | GBP/USD | −0.500692 | 0.249654 | 0.18927 |
| US Dollar/Canadian Dollar | USD/CAD | 0.468873 | 0.734437 | 0.164974 |
| US Dollar/Swiss Franc | USD/CHF | −0.889943 | 0.055028 | 0.692615 |
| US Dollar/Japanese Yen | USD/JPY | −0.370885 | 0.314557 | 0.101636 |
| Currency Pair | Contract Strike Price | Market Consensus Edge | P(In-the-Money) |
|---|---|---|---|
| Australian Dollar/Japanese Yen | AUD/JPY > 72.60 | 1.75% | 48.25% |
| Australian Dollar/US Dollar | AUD/USD > 0.6700 | 2.25% | 52.25% |
| Euro/Pound Sterling | EUR/GBP > 0.8420 | 0% | 50% |
| Euro/Japanese Yen | EUR/JPY > 120.20 | 0% | 50% |
| Euro/US Dollar | EUR/USD > 1.1080 | 1.5% | 51.5% |
| Pound Sterling/Japanese Yen | GBP/JPY > 142.80 | 1% | 49% |
| Pound Sterling/US Dollar | GBP/USD > 1.3180 | 1.5% | 51.5% |
| US Dollar/Canadian Dollar | USD/CAD > 1.3240 | 2.625% | 47.375% |
| US Dollar/Swiss Franc | USD/CHF > 0.9640 | 2.5% | 47.5% |
| US Dollar/Japanese Yen | USD/JPY > 108.40 | 2.75% | 47.25% |
| Option Contract | Buy or Sell | Probability of Success | Kelly Wager % |
|---|---|---|---|
| USD/JPY > 108.40 | Sell | 52.75% | 5.5% |
| Option Contract | Buy or Sell | Probability of Success | DEPO Wager % |
|---|---|---|---|
| USD/JPY > 108.40 | Sell | 52.75% | 0.7% |
| USD/CAD > 1.3240 | Sell | 52.625% | 0.7% |
| USD/CHF > 0.9640 | Sell | 52.5% | 0.7% |
| AUD/JPY > 72.60 | Sell | 51.75% | 0.7% |
| EUR/USD > 1.1080 | Buy | 51.5% | 0.7% |
| GBP/USD > 1.3180 | Buy | 51.5% | 0.7% |
| Team Name | Short Name | Mean Outcome | Cover Rate | Relative Entropy (bits) |
|---|---|---|---|---|
| Arizona Cardinals | ARI | 0.056 | 0.528 | 0.002263 |
| Atlanta Falcons | ATL | −0.079365 | 0.460317 | 0.004548 |
| Baltimore Ravens | BAL | −0.081967 | 0.459016 | 0.004852 |
| Buffalo Bills | BUF | −0.04 | 0.48 | 0.001154 |
| Carolina Panthers | CAR | 0.080645 | 0.540323 | 0.004697 |
| Chicago Bears | CHI | −0.031746 | 0.484127 | 0.000727 |
| Cincinnati Bengals | CIN | 0.173554 | 0.586777 | 0.021838 |
| Cleveland Browns | CLE | −0.121951 | 0.439024 | 0.010755 |
| Dallas Cowboys | DAL | −0.02439 | 0.487805 | 0.00043 |
| Denver Broncos | DEN | 0 | 0.5 | 0 |
| Detroit Lions | DET | −0.064516 | 0.467742 | 0.003004 |
| Green Bay Packers | GB | 0.072 | 0.536 | 0.003742 |
| Houston Texans | HOU | −0.02439 | 0.487805 | 0.00043 |
| Indianapolis Colts | IND | 0.088 | 0.544 | 0.005593 |
| Jacksonville Jaguars | JAC | −0.114754 | 0.442623 | 0.00952 |
| Kansas City Chiefs | KC | 0.095238 | 0.547619 | 0.006553 |
| Los Angeles Chargers | LAC | −0.031746 | 0.484127 | 0.000727 |
| Los Angeles Rams | LAR | −0.112903 | 0.443548 | 0.009215 |
| Miami Dolphins | MIA | −0.04065 | 0.479675 | 0.001192 |
| Minnesota Vikings | MIN | 0.193548 | 0.596774 | 0.027194 |
| New England Patriots | NE | 0.2 | 0.6 | 0.02905 |
| New Orleans Saints | NO | 0.129032 | 0.572581 | 0.015254 |
| New York Giants | NYG | −0.00813 | 0.495935 | 0.000047 |
| New York Jets | NYJ | −0.081967 | 0.459016 | 0.004852 |
| Oakland Raiders | OAK | −0.064516 | 0.467742 | 0.003004 |
| Philadelphia Eagles | PHI | −0.055118 | 0.472441 | 0.002192 |
| Pittsburgh Steelers | PIT | 0.024 | 0.512 | 0.000415 |
| Seattle Seahawks | SEA | 0.163934 | 0.581967 | 0.019473 |
| San Francisco 49ers | SF | 0.008 | 0.504 | 0.000046 |
| Tampa Bay Buccaneers | TB | −0.096774 | 0.451613 | 0.006767 |
| Tennessee Titans | TEN | −0.196721 | 0.401639 | 0.028099 |
| Washington Redskins | WAS | −0.015625 | 0.492188 | 0.000176 |
| Away Consensus | Away Team | Home Team | Home Consensus | |
|---|---|---|---|---|
| 70% | Kansas City Chiefs −3.5 | @ | Jacksonville Jaguars | 30% |
| 44% | Tennessee Titans | @ | Cleveland Browns −5.5 | 56% |
| 53% | Atlanta Falcons | @ | Minnesota Vikings −3.5 | 47% |
| 43% | Washington Redskins | @ | Philadelphia Eagles −10.5 | 57% |
| 67% | Baltimore Ravens −7.0 | @ | Miami Dolphins | 33% |
| 63% | Los Angeles Rams −1.5 | @ | Carolina Panthers | 37% |
| 46% | Buffalo Bills | @ | New York Jets −2.5 | 54% |
| 44% | Cincinnati Bengals | @ | Seattle Seahawks −9.5 | 56% |
| 34% | Indianapolis Colts | @ | Los Angeles Chargers −6.0 | 66% |
| 43% | San Francisco 49ers | @ | Tampa Bay Buccaneers −1.0 | 57% |
| 61% | Detroit Lions −2.5 | @ | Arizona Cardinals | 39% |
| 58% | New York Giants | @ | Dallas Cowboys −7.0 | 42% |
| 51% | Pittsburgh Steelers | @ | New England Patriots −5.5 | 49% |
| Bet to Cover | Bet to Not Cover | Probability of Success | Kelly Wager % |
|---|---|---|---|
| Kansas City Chiefs −3.5 | Jacksonville Jaguars | 60% | 20% |
| Bet to Cover | Bet to Not Cover | Probability of Success | DEPO Wager % |
|---|---|---|---|
| Kansas City Chiefs −3.5 | Jacksonville Jaguars | 60% | 5.89% |
| Baltimore Ravens −7.0 | Miami Dolphins | 58.5% | 5.89% |
| Los Angeles Chargers −6.0 | Indianapolis Colts | 58% | 5.89% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercurio, P.J.; Wu, Y.; Xie, H. Portfolio Optimization for Binary Options Based on Relative Entropy. Entropy 2020, 22, 752. https://doi.org/10.3390/e22070752
Mercurio PJ, Wu Y, Xie H. Portfolio Optimization for Binary Options Based on Relative Entropy. Entropy. 2020; 22(7):752. https://doi.org/10.3390/e22070752
Chicago/Turabian StyleMercurio, Peter Joseph, Yuehua Wu, and Hong Xie. 2020. "Portfolio Optimization for Binary Options Based on Relative Entropy" Entropy 22, no. 7: 752. https://doi.org/10.3390/e22070752
APA StyleMercurio, P. J., Wu, Y., & Xie, H. (2020). Portfolio Optimization for Binary Options Based on Relative Entropy. Entropy, 22(7), 752. https://doi.org/10.3390/e22070752






