Measuring Independence between Statistical Randomness Tests by Mutual Information
Abstract
1. Introduction
2. Preliminaries
2.1. Randomness Assessment
NIST Randomness Tests
2.2. Mutual Information
2.3. Problems Associated with Applying too Many Tests
Multiple Problem Tests and Independence between Statistical Randomness Tests
3. Some Previous Results
4. The Proposed Method to Detect the Correlation between Statistical Randomness Tests
- Step 1.
- Select the random number generators.
- -
- The generators used must generate outputs that satisfy the random conditions.
- Step 2.
- Build the data samples using the selected generators.
- -
- Generate n sequences of random numbers of length L to evaluate them using the selected statistical tests.
- Step 3.
- Evaluate each of the n sequences by the k statistical tests and obtain their corresponding n p-values, or test statistics, for each test (with and ).
- Step 4.
- Calculate the mutual information between the sequences of p-values, or test statistics, to detect the presence of correlations.
- -
- Estimate the MI between all the pairs of sequences of p-values or test statistics, to detect the presence of correlation, using the MI expression based on entropy H and some estimator of H with low mean squared error (MSE), over the number n of sequences generated in step 2.
- Step 5.
- Determine the significant correlations to conclude the correlation between the tests. The MI values were grouped by property 1 of the MI in the triangular matrix M:where represents the MI between the i and j. Taking into account property 2 we havewhere represents the entropy of the variable . The resulting matrix is a triangular matrix where the diagonal contains .
| Algorithm 1: Normalized mutual information matrix. |
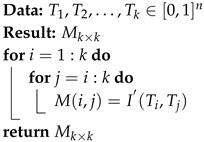 |
- Construct the permuted samples with q the number of permutations used, in such a way that the possible association between and disappears, with being the permutation u of the elements of , that is to say,
- .
- , for .
- is the identity of .
- Estimate the MI of the permuted samples, to obtain , where .
- The p-value associated with the test of the form is calculatedwhere is the defined indicator function of the form
- If , then the null hypothesis is accepted. If , then the null hypothesis is rejected.
5. Correlation Assessment of NIST Tests
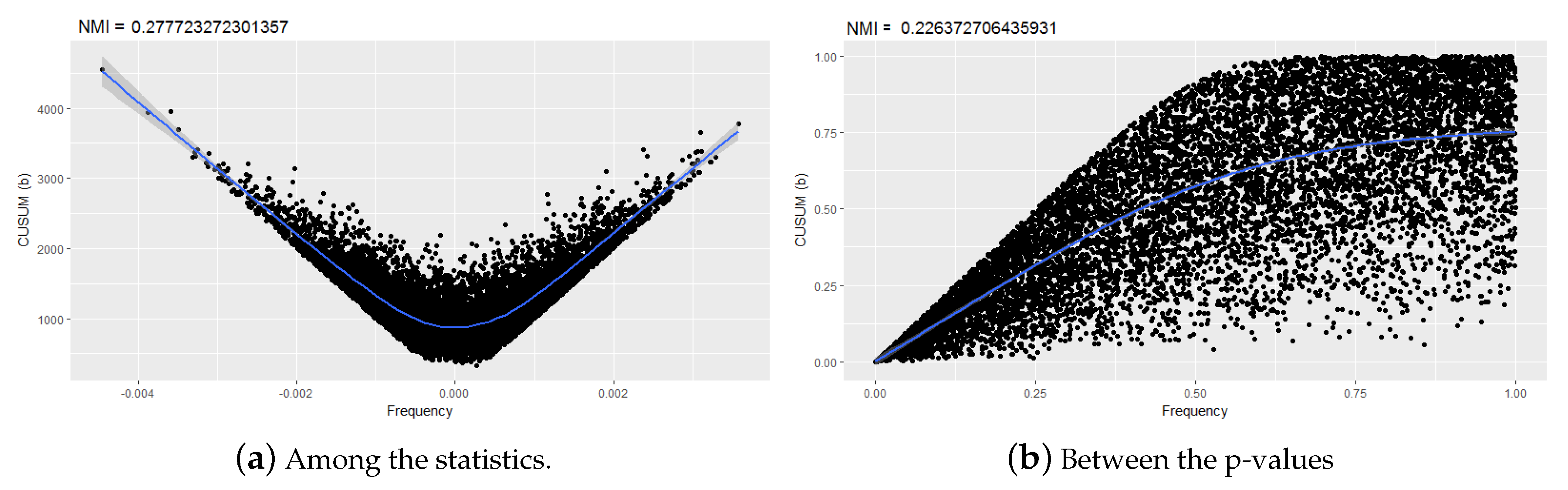
5.1. Selection of the Number of Sequences and MI Estimator
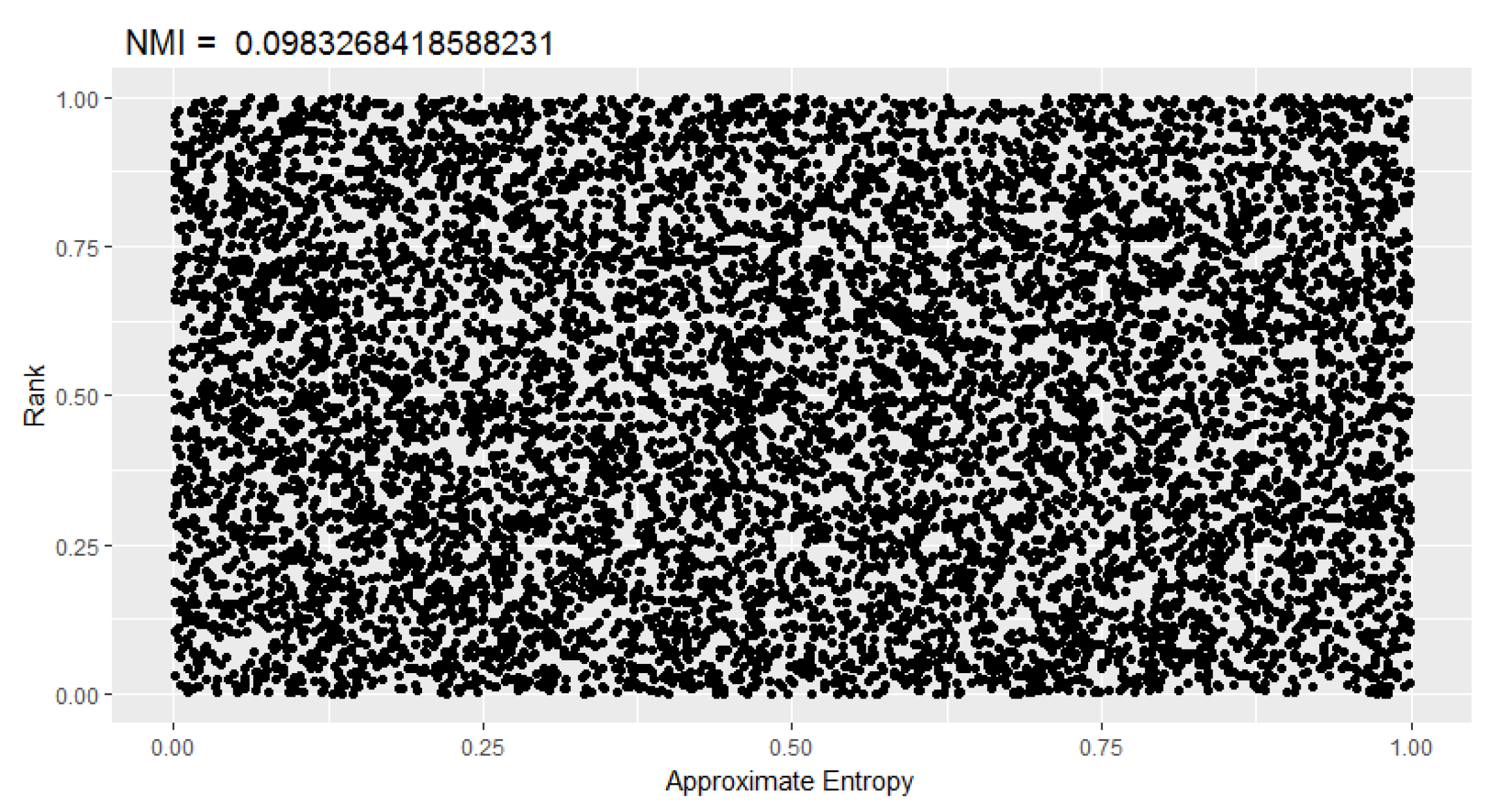
5.2. Sample Discretization
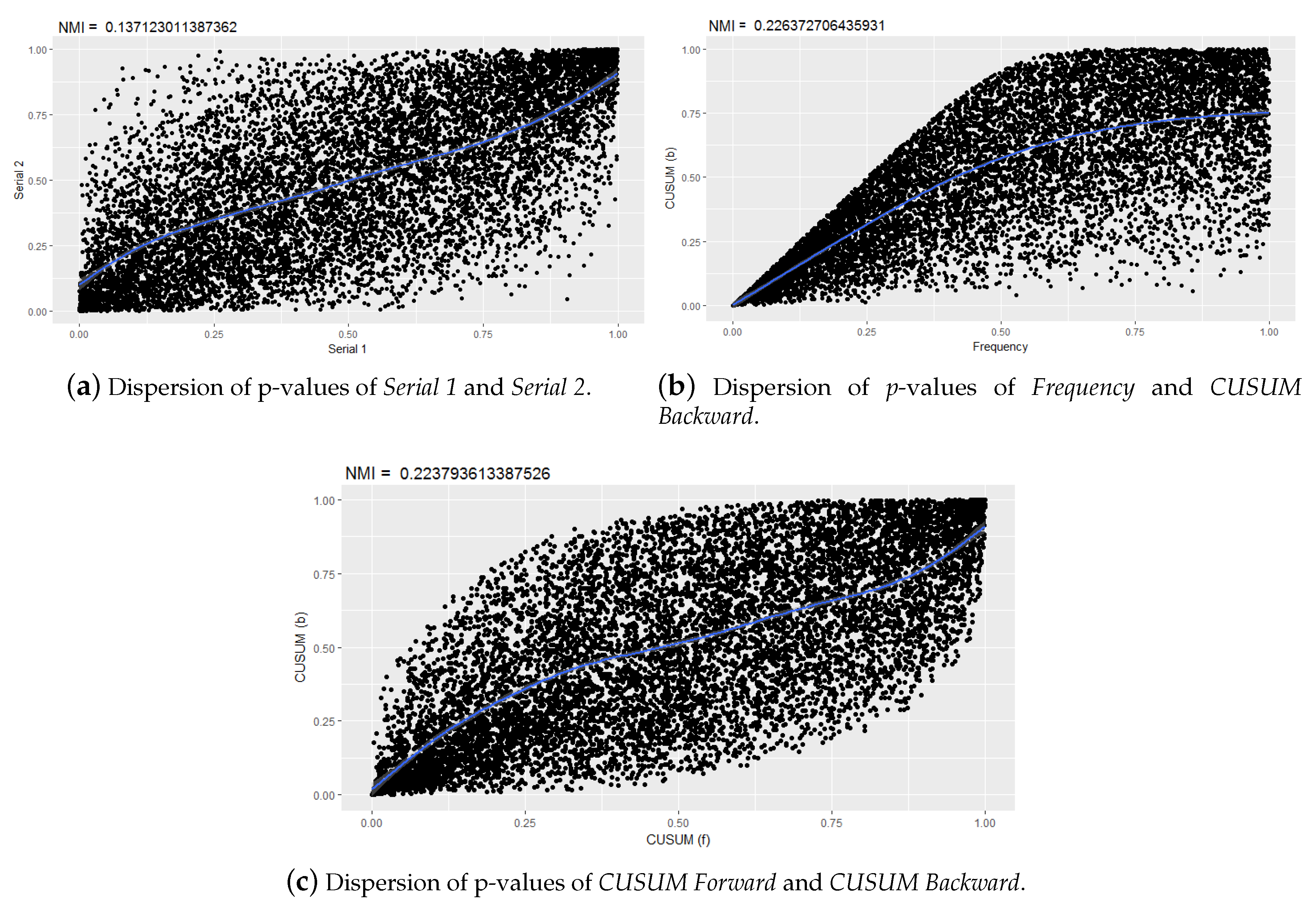
5.3. Correlation between p-Values
Discussion of Correlations between p-Values
5.4. Correlation between Statistics
Discussion of the Correlations between the Statistics
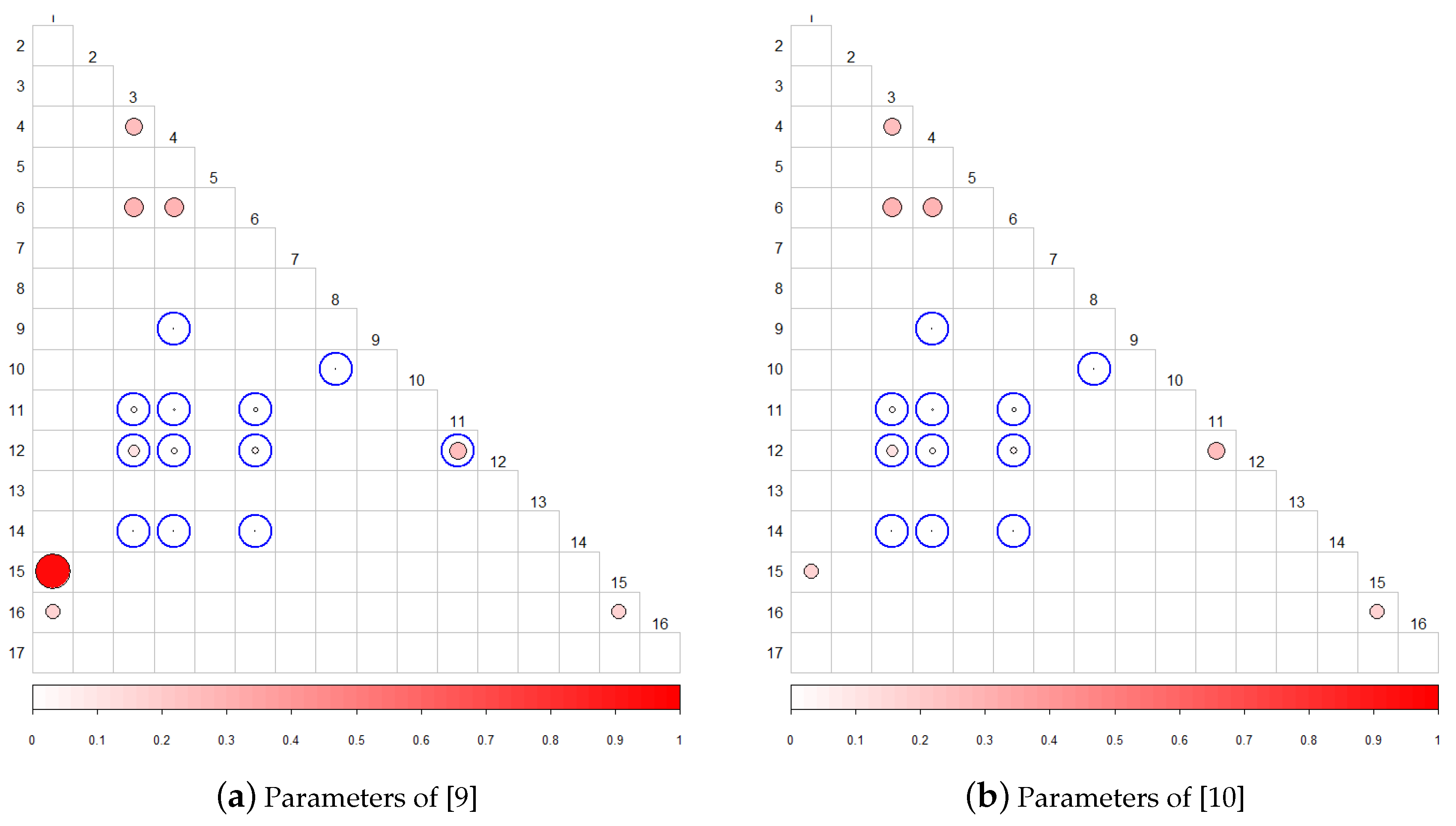
5.5. Comparison of Results with Previous Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sulak, F. Statistical analysis of block ciphers and hash functions. In Publication of the Middle East Technical University Ph.D. Examinations; Supervisor Assoc. Prof. Dr. Ali Doganaksoy; METU: Ankara, Turkey, 2011. [Google Scholar]
- Demirhan, H.; Bitirim, N. Statistical testing of cryptographic randomness. J. Stat. Stat. Actuar. Sci. 2016, 9, 1–11. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, 1st ed.; Addison-Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Koçak, O. A Unified Evaluation of Statistical Randomness Tests and Experimental Analysis of their Relations. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2016. [Google Scholar]
- Bassham, L.E., III; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L. A Statistical Test Suite for Random And Pseudorandom Number Generators for Cryptographic Applications; BoozAllen and Hamilton: McLean, VA, USA, 2001. [Google Scholar]
- Ryabko, B.Y.; Monarev, V. Using information theory approach to randomness testing. J. Stat. Plan. Inference 2005, 133, 95–110. [Google Scholar] [CrossRef]
- Ryabko, B. Time-Adaptive Statistical Test for Random Number Generators. Entropy 2020, 22, 630. [Google Scholar] [CrossRef]
- Demirhan, H.; Bitirim, N. A simulation study on the accuracy of cryptographic randomness tests. Simulation 2017, 93, 1113–1122. [Google Scholar] [CrossRef]
- Doğnaksoy, A.; Ege, B.; Muş, K. Extended results for independence and sensitivity of NIST randomness tests. In Proceedings of the Information Security and Cryptography Conference, Istanbul, Turkey, 25–27 December 2008. [Google Scholar]
- Doǧanaksoy, A.; Sulak, F.; Uǧuz, M.; Şeker, O.; Akcengiz, Z. Mutual correlation of NIST statistical randomness tests and comparison of their sensitivities on transformed sequences. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 655–665. [Google Scholar] [CrossRef]
- Marsaglia, G. The Marsaglia Random Number CDROM, with the DIEHARD Battery of Tests of Randomness. 2008. Available online: http://www.cs.hku.hk/diehard (accessed on 3 April 2020).
- Knuth, D.E. The Art of Computer Programming, 3rd ed.; Addison-Wesley: Reading, MA, USA, 1998. [Google Scholar]
- Caelli, W.; Dawson, E.; Nielsen, L.; Gustafson, H. CRYPT-X Stastical Package Manual, Measuring the Strength of Stream and Block Ciphers; Information Security Research Centre, Queensland University of Technology: Brisbane, Queensland, Australia, 1992. [Google Scholar]
- L’Ecuyer, P.; Simard, R. TESTU01: A Software Library in ANSI C for Empirical Testing of Random Number Generators. TOMS 2007. [Google Scholar] [CrossRef]
- Fan, L.; Chen, H.; Gao, S. A general method to evaluate the correlation of randomness tests. In International Workshop on Information Security Applications; Springer: Berlin/Heidelberg, Germany, 2013; pp. 52–62. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Verdú, S. Empirical Estimation of Information Measures: A Literature Guide. Entropy 2019, 21, 720. [Google Scholar] [CrossRef]
- Hernández, D.G.; Samengo, I. Estimating the Mutual Information between Two Discrete, Asymmetric Variables with Limited Samples. Entropy 2019, 21, 623. [Google Scholar] [CrossRef]
- Carrara, N.; Ernst, J. On the Estimation of Mutual Information. Multidiscip. Digit. Publ. Inst. Proc. 2020, 33, 31. [Google Scholar] [CrossRef]
- Soto, J.; Bassham, L. Randomness Testing of the Advanced Encryption Standard Finalist Candidates; BoozAllen and Hamilton: McLean, VA, USA, 2000. [Google Scholar]
- Turan, M.S.; Doğanaksoy, A.; Boztaş, S. On independence and sensitivity of statistical randomness tests. In International Conference on Sequences and Their Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 18–29. [Google Scholar]
- Georgescu, C.; Simion, E.; Nita, A.P.; Toma, A. A view on NIST randomness tests (in) dependence. In Proceedings of the IEEE 2017 9th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Targoviste, Romania, 29 June–1 July 2017; pp. 1–4. [Google Scholar]
- Burciu, P.; Simion, E. A Systematic Approach of NIST Statistical Tests Dependencies. J. Electr. Eng. Electron. Control Comput. Sci. 2019, 5, 1–6. [Google Scholar]
- Kvålseth, T.O. On normalized mutual information: Measure derivations and properties. Entropy 2017, 19, 631. [Google Scholar] [CrossRef]
- Good, P.I. Permutation, Parametric, and Bootstrap Tests of Hypotheses; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Berry, K.J.; Johnston, J.E.; Mielke Jr, P.W. A Chronicle of Permutation Statistical Methods; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Meyer, P.E.; Meyer, M.P.E. Package ‘infotheo’. In R Package Version; Citeseer: Princeton, NJ, USA, 2009; Volume 1. [Google Scholar]
- Hausser, J.; Strimmer, K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Sechidis, K.; Azzimonti, L.; Pocock, A.; Corani, G.; Weatherall, J.; Brown, G. Efficient feature selection using shrinkage estimators. Mach. Learn. 2019, 108, 1261–1286. [Google Scholar] [CrossRef]
- Boulle, M. Optimal bin number for equal frequency discretizations in supervized learning. Intell. Data Anal. 2005, 9, 175–188. [Google Scholar] [CrossRef]
- Hernandez, J.; Barrero, D.F. Evolutionary generation and degeneration of randomness to assess the indepedence of the Ent test battery. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017. [Google Scholar] [CrossRef]


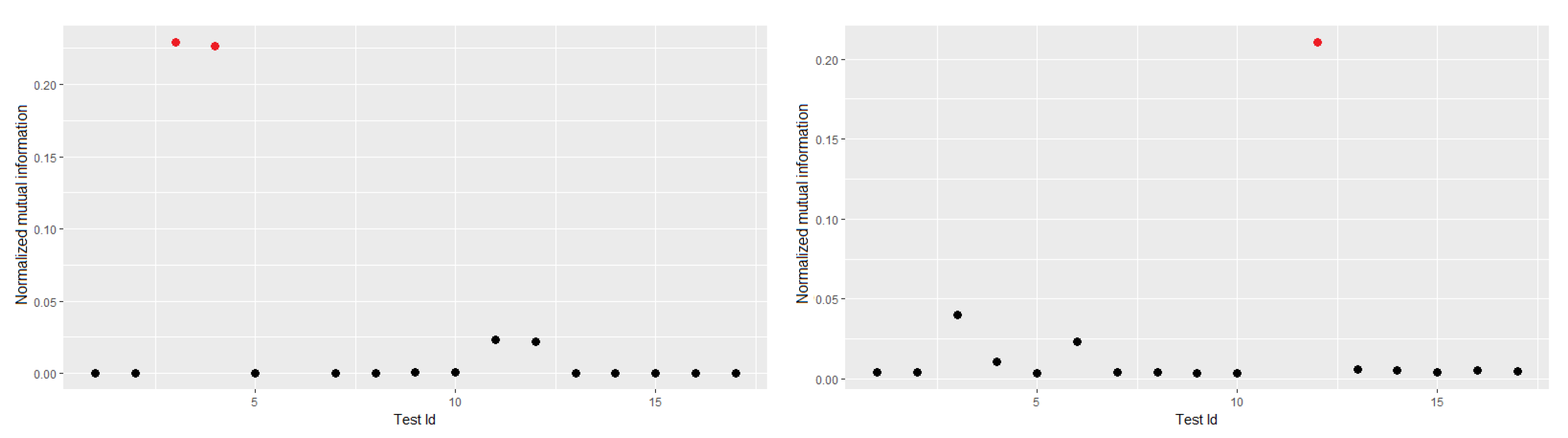
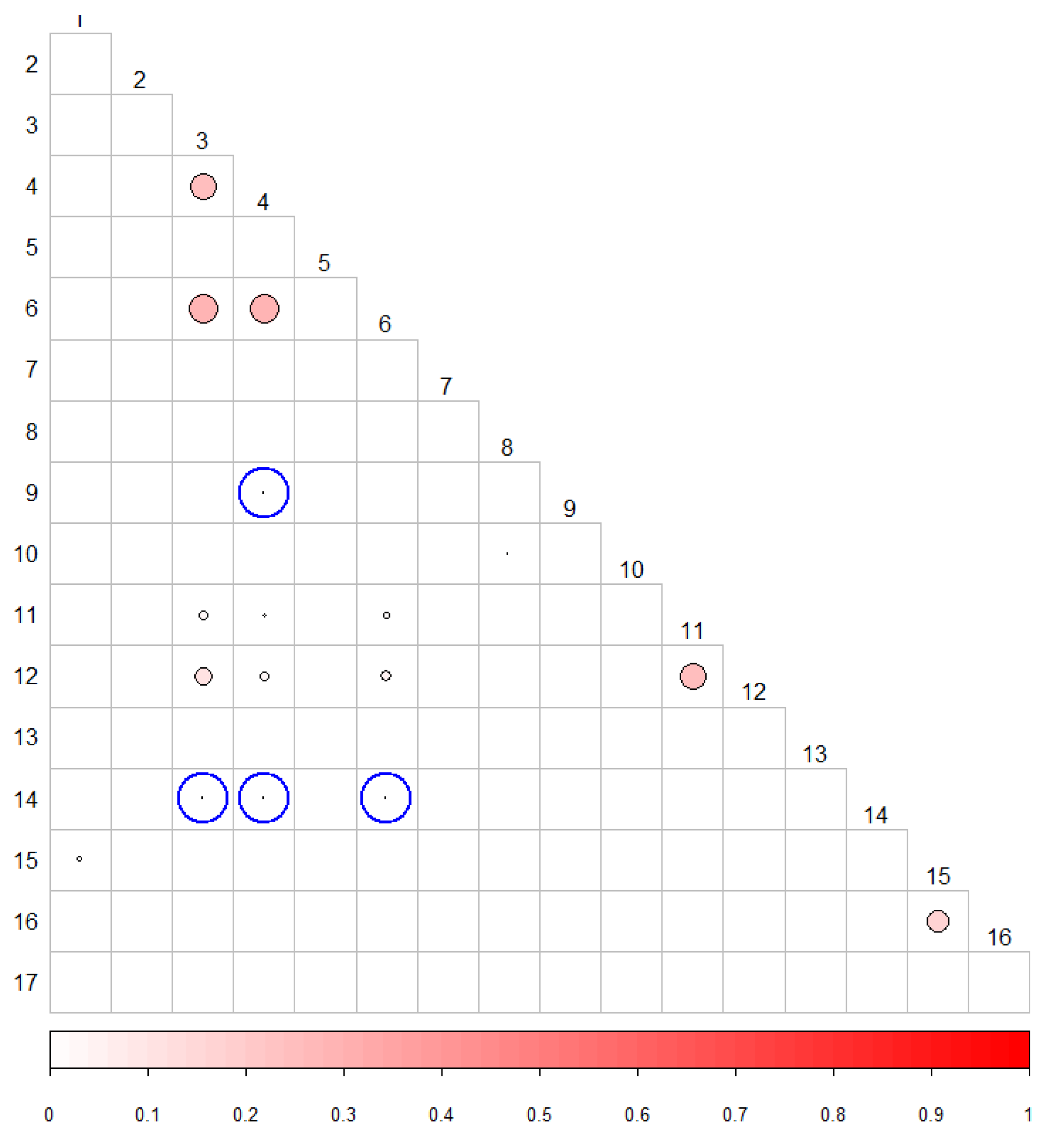

| Randomness Test | Id | Randomness Test | Id |
|---|---|---|---|
| Approximate Entropy | 1 | Overlapping Template | 10 |
| Block Frequency | 2 | Random Excursions | 11 |
| CUSUM (f) | 3 | Random Excursions Variant | 12 |
| CUSUM (b) | 4 | Rank | 13 |
| FFT | 5 | Runs | 14 |
| Frequency | 6 | Serial 1 | 15 |
| Linear Complexity | 7 | Serial 2 | 16 |
| Longest Run | 8 | Universal | 17 |
| Non Overlapping Template | 9 |
| Randomness Tests | Related Tests |
|---|---|
| Frequency | CUSUM(f, b) |
| CUSUM(f) | CUSUM(b) |
| Serial 1 | Serial 2 |
| Approximate Entropy | Serial(1,2) |
| Randomness Tests | Related Tests |
|---|---|
| Frequency | CUSUM, Approximate Entropy |
| Runs | Approximate Entropy, Serial |
| Approximate Entropy | Frequency, CUSUM, Runs, Serial |
| Serial | Runs, Approximate Entropy |
| Randomness Tests | Related Tests |
|---|---|
| Frequency | CUSUM (b, f) |
| CUSUM (b) | CUSUM (f) |
| Serial 1 | Serial 2 |
| Approximate Entropy | Serial(1,2) |
| Random Excursion | Random Excursion Variant |
| est/obs | 1000 | 5000 | 10,000 | 15,000 | 20,000 |
|---|---|---|---|---|---|
| emp | 0.041 | 0.0064 | 0.0034 | 0.0025 | 0.002 |
| mm | 0.0005 | 0 | 0 | 0 | 0 |
| shrink | 0 | 0 | 0 | 0 | 0 |
| sg | 0.0806 | 0.0145 | 0.0074 | 0.0052 | 0.004 |
| max. Dif. | 0.0806 | 0.0145 | 0.0074 | 0.0052 | 0.004 |
| est/obs | 1000 | 5000 | 10,000 | 15,000 | 20,000 |
|---|---|---|---|---|---|
| emp | 0.5761 | 0.5691 | 0.5597 | 0.5592 | 0.5647 |
| mm | 0.5486 | 0.5632 | 0.5567 | 0.5574 | 0.5632 |
| shrink | 0.5585 | 0.5636 | 0.5561 | 0.5565 | 0.5625 |
| sg | 0.6027 | 0.5749 | 0.5626 | 0.5612 | 0.5662 |
| max. Dif. | 0.0541 | 0.0117 | 0.0065 | 0.0047 | 0.0037 |
| Randomness Test | Parameter | Value |
|---|---|---|
| Approximate Entropy | m: first block size | 10 |
| Block Frequency | M: block size | 128 |
| Linear Complexity | M: block size | 500 |
| Longest Run | M: block size | 128 |
| Non Overlapping Template | template | 000000001 |
| Overlapping Template | template | 111111111 |
| Random Excursions | internal state | |
| Random Excursions Variant | internal state | |
| Rank | M: rows of each matrix | 32 |
| Q: columns of each matrix | 32 | |
| Serial | m: block size | 16 |
| Universal | L: block size | 7 |
| Q: initialization blocks | 10 |
| Random Test | Related Test |
|---|---|
| Approximate Entropy | Serial 1 |
| CUSUM (f) | CUSUM (b), Frequency, Random Ex., Random Ex. Variant |
| CUSUM (b) | Frequency, Random Ex., Random Ex. Variant |
| Frequency | Random Ex., Random Ex. Variant |
| Longest Run | Overlapping Template |
| Random Excursions | Random Excursions Variant |
| Serial 1 | Serial 2 |
| Randomness test | Related Test |
|---|---|
| Approximate Entropy | Serial 1 |
| CUSUM (f) | CUSUM (b), Frequency, Random Ex., Random Ex. Variant |
| CUSUM (b) | Frequency, Random Ex., Random Ex. Variant |
| Frequency | Random Ex., Random Ex. Variant |
| Longest Run | Overlapping Template |
| Random Excursions | Random Excursions Variant |
| Serial 1 | Serial 2 |
| Runs | CUSUM (f, b), Frequency |
| Non Overlapping Template | CUSUM (b) |
| Method | Number n of Sequence | Sequence Length L (bits) | Metric Used |
|---|---|---|---|
| [9] | 100,000 | 5000 | Pearson |
| [15] | 300 | 1,000,000 | Setting to distance of Fan [15] |
| [10] | 200,000 | 1024 | Pearson |
| 200 | 1,048,576 | Pearson | |
| Proposed method | 10,000 | 1,000,000 | MI |
| Method | Approximate Entropy | Serial |
|---|---|---|
| [9] | 8 | 9 |
| [10] | 14 | 16 |
| predefined by NIST | 10 | 16 |
| Randomness Tests | Correlated Tests | ||
|---|---|---|---|
| [9] | [10] | Proposed Method | |
| Frecuency | CUSUM(f, b) | CUSUM(f, b) | CUSUM(f, b) Random Ex. Random Ex. Variant Runs |
| App. Entropy | Serial(1,2) | Serial(1,2) | Serial 1 |
| CUSUM(f) | CUSUM(b) | CUSUM(b) | CUSUM(b) Random Ex. Random Ex. Variant Runs |
| CUSUM(b) | CUSUM(f) | CUSUM(f) | CUSUM(f) Non Overlapp. Random Ex. Random Ex. Variant Runs |
| Serial 1 | Serial 2 | Serial 2 | Serial 2 |
| Random Ex. | Random Ex. Variant | Random Ex. Variant | |
| Longest | Overlapp. | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karell-Albo, J.A.; Legón-Pérez , C.M.; Madarro-Capó , E.J.; Rojas, O.; Sosa-Gómez, G. Measuring Independence between Statistical Randomness Tests by Mutual Information. Entropy 2020, 22, 741. https://doi.org/10.3390/e22070741
Karell-Albo JA, Legón-Pérez CM, Madarro-Capó EJ, Rojas O, Sosa-Gómez G. Measuring Independence between Statistical Randomness Tests by Mutual Information. Entropy. 2020; 22(7):741. https://doi.org/10.3390/e22070741
Chicago/Turabian StyleKarell-Albo, Jorge Augusto, Carlos Miguel Legón-Pérez , Evaristo José Madarro-Capó , Omar Rojas, and Guillermo Sosa-Gómez. 2020. "Measuring Independence between Statistical Randomness Tests by Mutual Information" Entropy 22, no. 7: 741. https://doi.org/10.3390/e22070741
APA StyleKarell-Albo, J. A., Legón-Pérez , C. M., Madarro-Capó , E. J., Rojas, O., & Sosa-Gómez, G. (2020). Measuring Independence between Statistical Randomness Tests by Mutual Information. Entropy, 22(7), 741. https://doi.org/10.3390/e22070741







