Re-Optimization of Expansion Work of a Heated Working Fluid with Generalized Radiative Heat Transfer Law
Abstract
1. Introduction
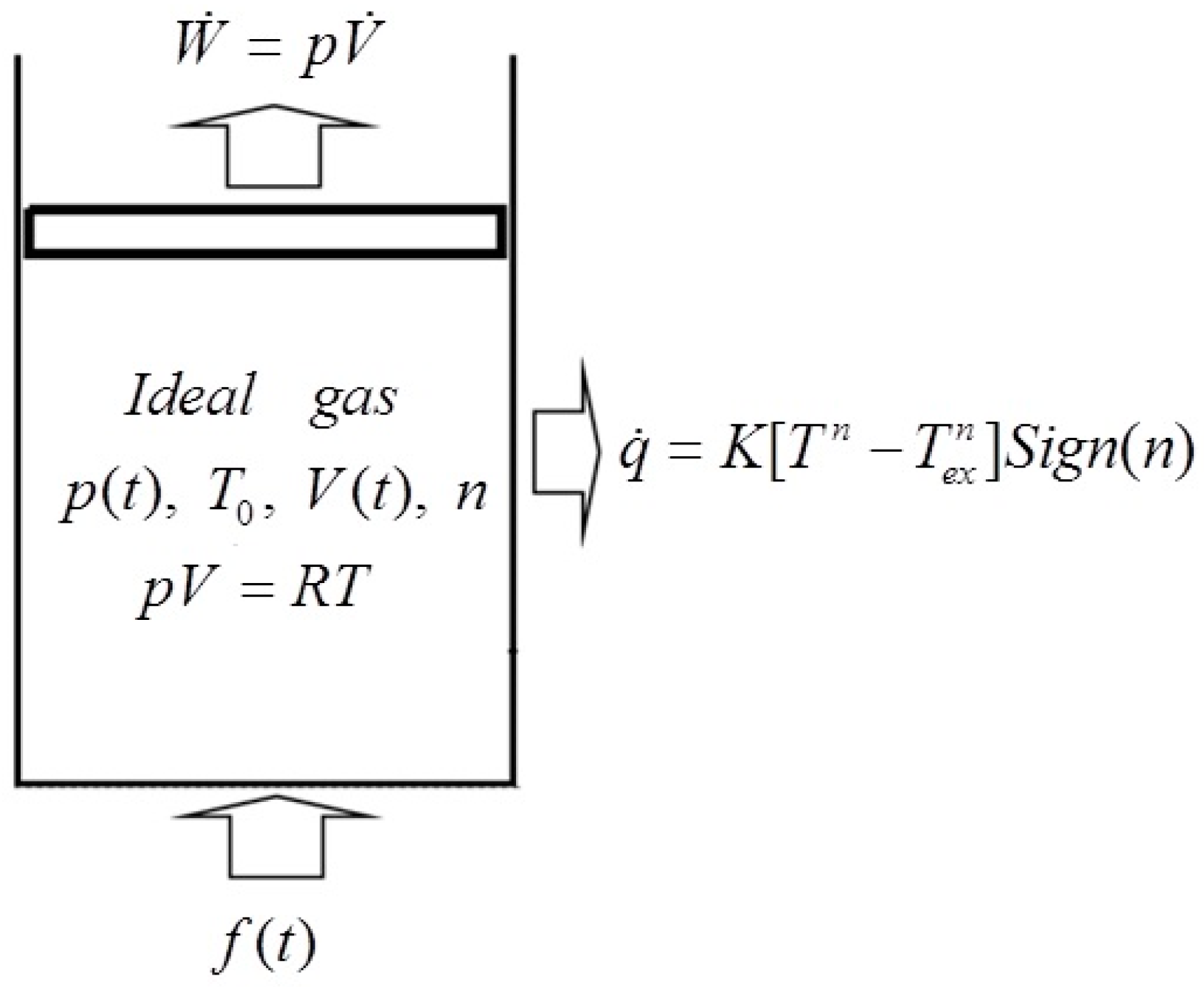
2. Modeling
3. Optimal Solutions
3.1. General Solution
3.2. Case of
3.3. Case of
3.4. Case of
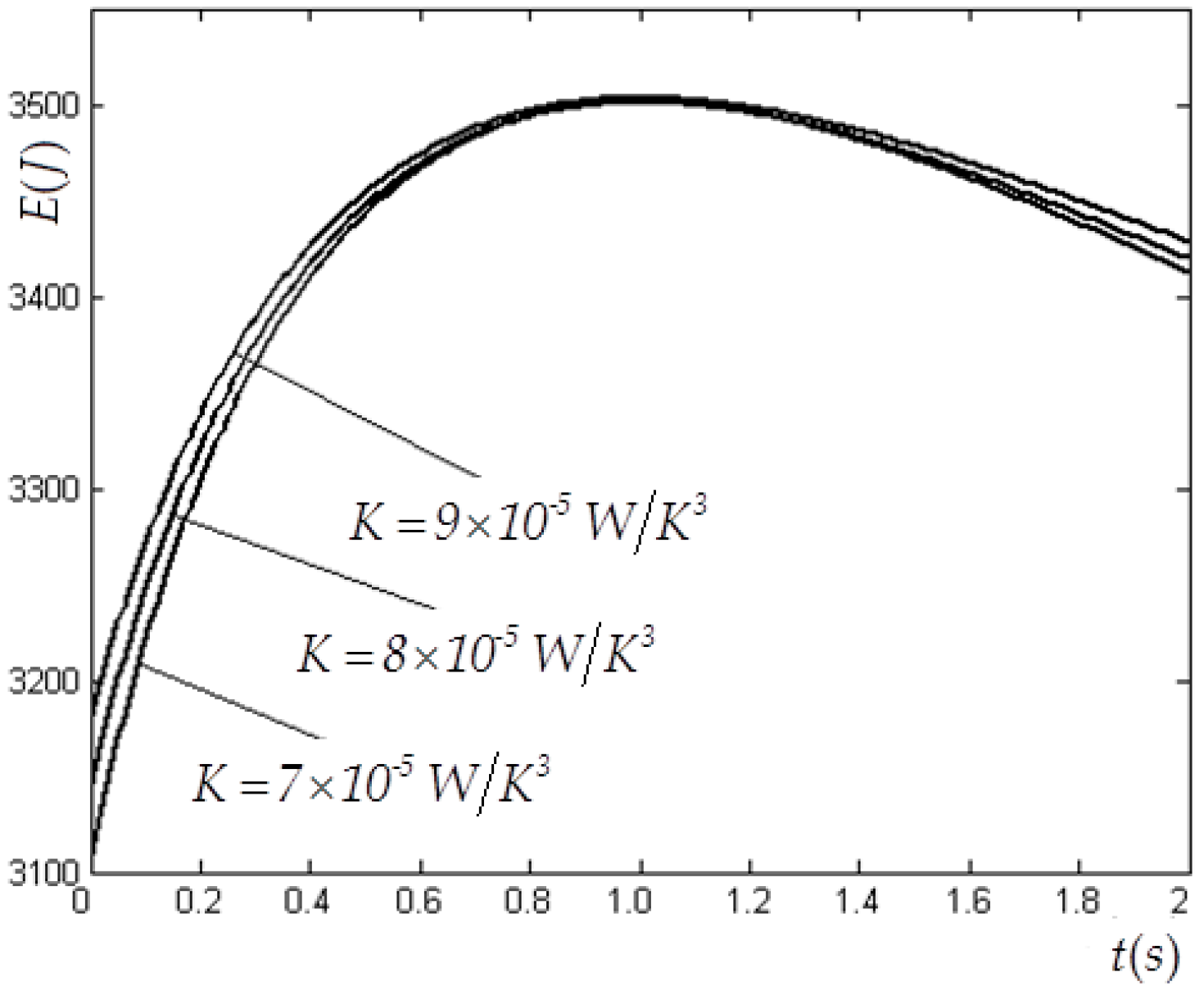
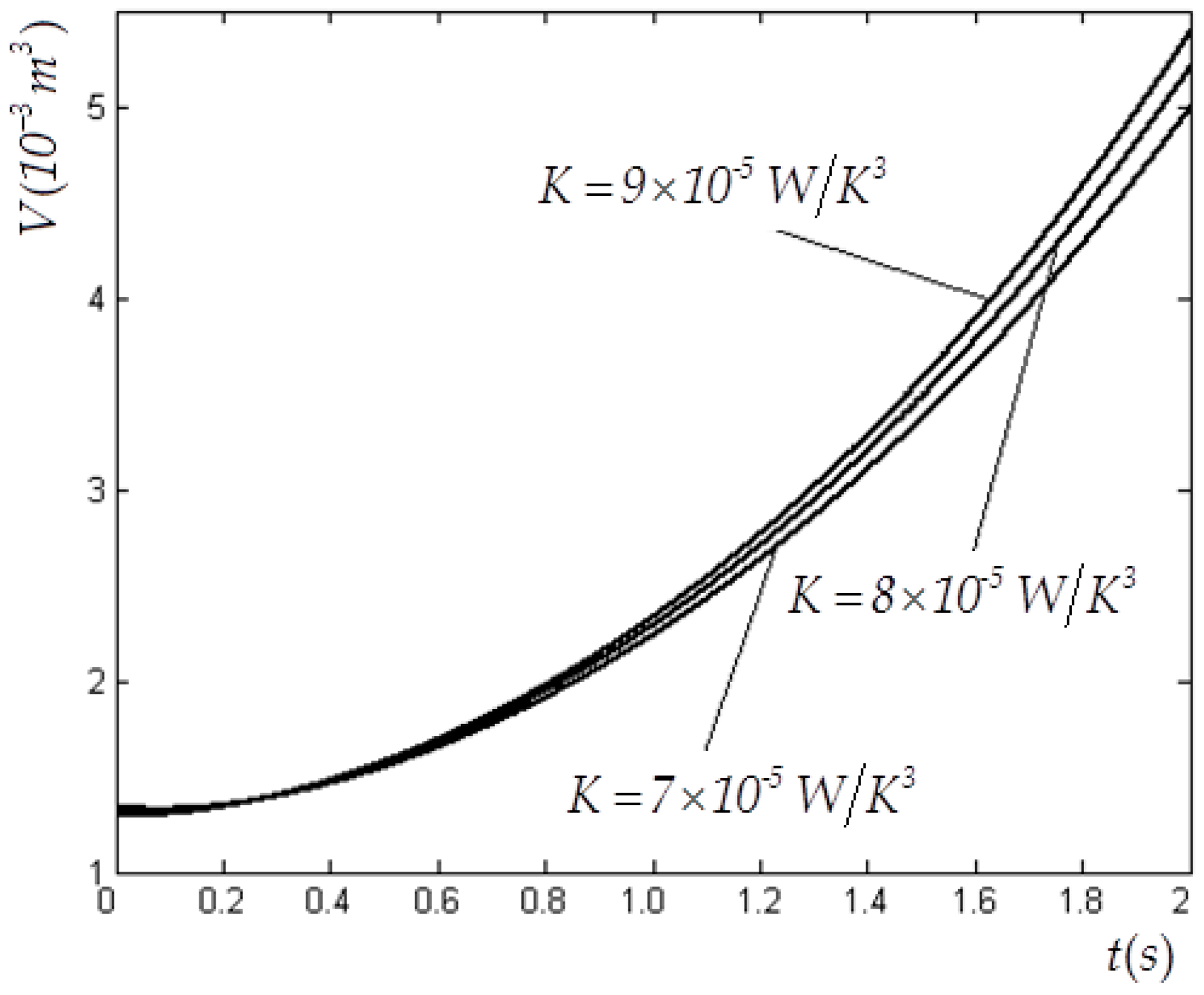
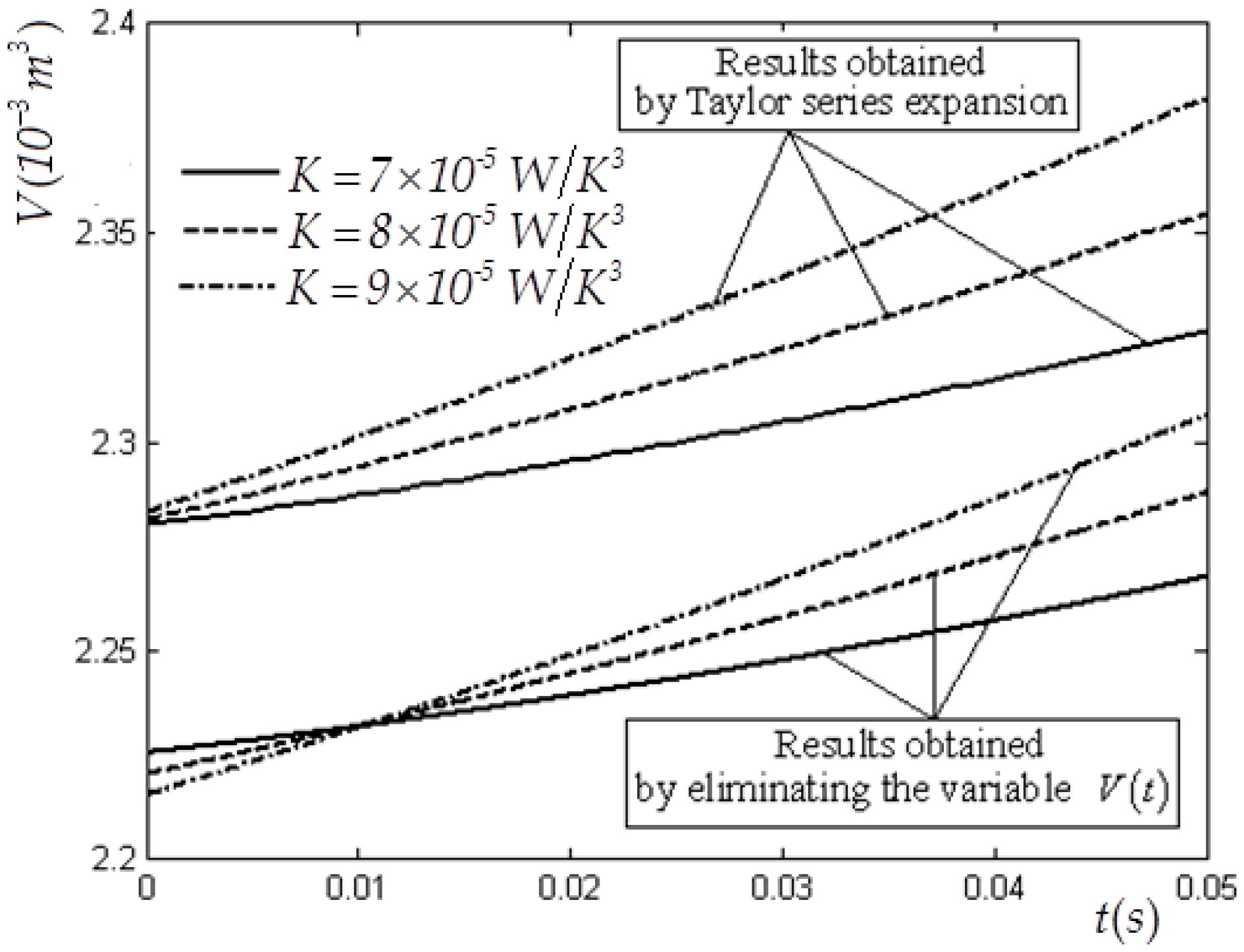
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Molar heat capacity, J/(mol∙K) | |
| Internal energy, J | |
| Rate of heated, W | |
| Heat conductance, W/K | |
| Modified Lagrangian, W | |
| Heat transfer power exponent | |
| Pressure, Pa | |
| Heat flow rate through the cylinder wall, W | |
| Gas constant, J/(mol∙K) | |
| Sign function | |
| Temperature, K | |
| Time, s | |
| Volume, | |
| Work output, J | |
| Greek symbols | |
| Efficiency | |
| Lagrange multiplier | |
| Subscripts | |
| External heat bath | |
| Final state of expansion process | |
| 0 | Ambient or reference |
References
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, 37, 62–70. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. 2011, 50, 2690–2704. [Google Scholar] [CrossRef]
- Chen, L.G.; Meng, F.K.; Sun, F.R. Thermodynamic analyses and optimizations for thermoelectric devices: The state of the arts. Sci. China Technol. Sci. 2016, 59, 442–455. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Progress in finite time thermodynamic studies for internal combustion engine cycles. Entropy 2016, 18, 139. [Google Scholar] [CrossRef]
- Feidt, M. The history and perspectives of efficiency at maximum power of the Carnot engine. Entropy 2017, 19, 369. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J. Progresses in generalized thermodynamic dynamic-optimization of irreversible processes. Sci. Sin. Technol. 2019, 49, 981–1022. [Google Scholar] [CrossRef][Green Version]
- Chen, L.G.; Xia, S.J.; Feng, H.J. Progress in generalized thermodynamic dynamic-optimization of irreversible cycles. Sci. Sin. Technol. 2019, 49, 1223–1267. [Google Scholar] [CrossRef][Green Version]
- Badescu, V. Optimal Control in Thermal Engineering; Springer: New York, NY, USA, 2017. [Google Scholar]
- Band, Y.B.; Kafri, O.; Salamon, P. Maximum work production from a heated gas in a cylinder with piston. Chem. Phys. Lett. 1980, 72, 127–130. [Google Scholar] [CrossRef]
- Band, Y.B.; Kafri, O.; Salamon, P. Finite time thermodynamics: Optimal expansion of a heated working fluid. J. Appl. Phys. 1982, 53, 8–28. [Google Scholar] [CrossRef]
- Salamon, P.; Band, Y.B.; Kafri, O. Maximum power from a cycling working fluid. J. Appl. Phys. 1982, 53, 197–202. [Google Scholar] [CrossRef]
- Aizenbud, B.M.; Band, Y.B. Power considerations in the operation of a piston fitted inside a cylinder containing a dynamically heated working fluid. J. Appl. Phys. 1981, 52, 3742–3744. [Google Scholar] [CrossRef]
- Aizenbud, B.M.; Band, Y.B.; Kafri, O. Optimization of a model internal combustion engine. J. Appl. Phys. 1982, 53, 1277–1282. [Google Scholar] [CrossRef]
- Band, Y.B.; Kafri, O.; Salamon, P. Optimization of a model external combustion engine. J. Appl. Phys. 1982, 53, 29–33. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Wu, C. Optimal expansion of a heated working fluid with phenomenological heat transfer. Energy Convers. Manage. 1998, 39, 149–156. [Google Scholar] [CrossRef]
- Song, H.J.; Chen, L.G.; Sun, F.R. Optimization of a model external combustion engine with linear phenomenological heat transfer law. J. Energy Inst. 2009, 82, 180–183. [Google Scholar] [CrossRef]
- Chen, L.G.; Song, H.J.; Sun, F.R. Optimization of a model internal combustion engine with linear phenomenological heat transfer law. Int. J. Ambient Energy 2010, 31, 13–22. [Google Scholar] [CrossRef]
- Song, H.J.; Chen, L.G.; Sun, F.R. Optimal expansion of a heated working fluid for maximum work output with generalized radiative heat transfer law. J. Appl. Phys. 2007, 102, 094901. [Google Scholar] [CrossRef]
- Ma, K.; Chen, L.G.; Sun, F.R. Optimum expansion of a heated under Dulong-Petit heat transfer law. J. Eng. Therm. Energy Power 2009, 24, 447–451. (in Chinese). [Google Scholar]
- Chen, L.G.; Song, H.J.; Sun, F.R. Optimal expansion of a heated working fluid with convective-radiative heat transfer law. Int. J. Ambient Energy 2010, 31, 81–90. [Google Scholar] [CrossRef]
- Chen, L.G.; Ma, K.; Sun, F.R. Optimal expansion of a heated ideal gas with time-dependent heat conductance. Int. J. Low-Carbon Technol. 2013, 8, 230–237. [Google Scholar] [CrossRef][Green Version]
- Chen, L.G.; Ma, K.; Sun, F.R. Optimal expansion of a heated working fluid for maximum work output with time-dependent heat conductance and generalized radiative heat transfer law. J. Non-Equilib. Thermodyn. 2011, 36, 99–122. [Google Scholar] [CrossRef]
- Chen, L.G.; Ma, K.; Feng, H.J.; Ge, Y.L. Optimal configuration of a gas expansion process in a piston-type cylinder with generalized convective heat transfer law. Energies 2020, 13, 3229. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.; Fischer, A.; Schaller, M.; Schubert, S. Optimal process paths for endoreversible systems. J. Non-Equilib. Thermodyn. 2003, 28, 233–268. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Novikov engine with fluctuating heat bath temperature. J. Non-Equilib. Thermodyn. 2018, 43, 141–150. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Stochastic Novikov engine with Fourier heat transport. J. Non-Equilib. Thermodyn. 2019, 44, 417–424. [Google Scholar] [CrossRef]
- Paéz-Hernández, R.T.; Chimal-Eguía, J.C.; Sánchez-Salas, N.; Ladino-Luna, D. General properties for an Agrawal thermal engine. J. Non-Equilib. Thermodyn. 2018, 43, 131–140. [Google Scholar] [CrossRef]
- Feidt, M.; Costea, M. From finite time to finite physical dimensions thermodynamics: The Carnot engine and Onsager’s relations revisited. J. Non-Equilib. Thermodyn. 2018, 43, 151–162. [Google Scholar] [CrossRef]
- Zaeva, M.A.; Tsirlin, A.M.; Didina, O.V. Finite time thermodynamics: Realizability domain of heat to work converters. J. Non-Equilib. Thermodyn. 2019, 44, 181–191. [Google Scholar] [CrossRef]
- Schwalbe, K.; Hoffmann, K.H. Optimal control of an endoreversible solar power plant. J. Non-Equilib. Thermodyn. 2018, 43, 255–272. [Google Scholar] [CrossRef]
- Wu, Z.X.; Chen, L.G.; Feng, H.J. Thermodynamic optimization for an endoreversible Dual-Miller cycle (DMC) with finite speed of piston. Entropy 2018, 20, 165. [Google Scholar] [CrossRef]
- Dumitrascu, G.; Feidt, M.; Popescu, A.; Grigorean, S. Endoreversible trigeneration cycle design based on finite physical dimensions thermodynamics. Energies 2019, 12, 3165. [Google Scholar]
- Meng, Z.W.; Chen, L.G.; Wu, F. Optimal power and efficiency of multi-stage endoreversible quantum Carnot heat engine with harmonic oscillators at the classical limit. Entropy 2020, 22, 457. [Google Scholar] [CrossRef]
- de Vos, A. Endoreversible models for the thermodynamics of computing. Entropy 2020, 22, 660. [Google Scholar] [CrossRef]
- Masser, R.; Khodja, A.; Scheunert, M.; Schwalbe, K.; Fischer, A.; Paul, R.; Hoffmann, K.H. Optimized piston motion for an alpha-type Stirling engine. Entropy 2020, 22, 700. [Google Scholar] [CrossRef]
- Mozurkewich, M.; Berry, R.S. Finite-time thermodynamics: Engine performance improved by optimized piston motion. Proc. Natl. Acad. Sci. USA 1981, 78, 1986–1988. [Google Scholar] [CrossRef]
- Mozurkewich, M.; Berry, R.S. Optimal paths for thermodynamic systems. The ideal Otto cycle. J. Appl. Phys. 1982, 53, 34–42. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Watowich, S.J.; Berry, R.S. Optimal paths for thermodynamic systems. The ideal Diesel cycle. J. Appl. Phys. 1985, 58, 2125–2134. [Google Scholar] [CrossRef]

| (W/K) | |||
| 1.341 | 1.316 | 1.295 | |
| 3108.480 | 3147.350 | 3181.910 | |
| 4.9940 | 5.205 | 5.388 | |
| 3412.680 | 3419.810 | 3428.710 | |
| 2492.780 | 2567.670 | 2634.600 | |
| 4630.820 | 4661.790 | 4690.000 | |
| 0.603 | 0.607 | 0.611 |
| (W/K) | |||
| 2.226 | 2.221 | 2.216 | |
| 2217.500 | 2220.850 | 2224.2000 | |
| 2.2677 | 2.288 | 2.306 | |
| 2268.590 | 2265.820 | 2264.350 | |
| 978.929 | 983.553 | 988.173 | |
| 2880.230 | 2886.190 | 2892.120 | |
| 0.555 | 0.556 | 0.557 |
| (W/K) | |||
| 2.280 | 2.282 | 2.284 | |
| 2181.93 | 2181.100 | 2179.820 | |
| 2.326 | 2.355 | 2.382 | |
| 2237.070 | 2229.330 | 2222.680 | |
| 981.919 | 986.471 | 991.195 | |
| 2896.100 | 2904.8000 | 2913.4000 | |
| 0.558 | 0.560 | 0.561 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Ma, K.; Ge, Y.; Feng, H. Re-Optimization of Expansion Work of a Heated Working Fluid with Generalized Radiative Heat Transfer Law. Entropy 2020, 22, 720. https://doi.org/10.3390/e22070720
Chen L, Ma K, Ge Y, Feng H. Re-Optimization of Expansion Work of a Heated Working Fluid with Generalized Radiative Heat Transfer Law. Entropy. 2020; 22(7):720. https://doi.org/10.3390/e22070720
Chicago/Turabian StyleChen, Lingen, Kang Ma, Yanlin Ge, and Huijun Feng. 2020. "Re-Optimization of Expansion Work of a Heated Working Fluid with Generalized Radiative Heat Transfer Law" Entropy 22, no. 7: 720. https://doi.org/10.3390/e22070720
APA StyleChen, L., Ma, K., Ge, Y., & Feng, H. (2020). Re-Optimization of Expansion Work of a Heated Working Fluid with Generalized Radiative Heat Transfer Law. Entropy, 22(7), 720. https://doi.org/10.3390/e22070720






